Computational model of cellular metabolic dynamics: effect of insulin on glucose disposal in human skeletal muscle

Abstract

Identifying the mechanisms by which insulin regulates glucose metabolism in skeletal muscle is critical to understanding the etiology of insulin resistance and type 2 diabetes. Our knowledge of these mechanisms is limited by the difficulty of obtaining in vivo intracellular data. To quantitatively distinguish significant transport and metabolic mechanisms from limited experimental data, we developed a physiologically based, multiscale mathematical model of cellular metabolic dynamics in skeletal muscle. The model describes mass transport and metabolic processes including distinctive processes of the cytosol and mitochondria. The model simulated skeletal muscle metabolic responses to insulin corresponding to human hyperinsulinemic-euglycemic clamp studies. Insulin-mediated rate of glucose disposal was the primary model input. For model validation, simulations were compared with experimental data: intracellular metabolite concentrations and patterns of glucose disposal. Model variations were simulated to investigate three alternative mechanisms to explain insulin enhancements: Model 1 (M.1), simple mass action; M.2, insulin-mediated activation of key metabolic enzymes (i.e., hexokinase, glycogen synthase, pyruvate dehydrogenase); or M.3, parallel activation by a phenomenological insulin-mediated intracellular signal that modifies reaction rate coefficients. These simulations indicated that models M.1 and M.2 were not sufficient to explain the experimentally measured metabolic responses. However, by application of mechanism M.3, the model predicts metabolite concentration changes and glucose partitioning patterns consistent with experimental data. The reaction rate fluxes quantified by this detailed model of insulin/glucose metabolism provide information that can be used to evaluate the development of type 2 diabetes.

skeletal muscle accounts for ∼80% of all insulin-mediated glucose uptake (35, 39, 42, 46). A reduction in skeletal muscle insulin sensitivity is therefore a major cause of hyperglycemia (20). Uncontrolled hyperglycemia is the hallmark characteristic of type 2 diabetes mellitus, a state that, if untreated, leads to systemic oxidative stress and inflammation and subsequent microvascular dysfunction (34). Thus, quantitative understanding of the regulatory mechanisms that control insulin-mediated glucose disposal in skeletal muscle, and indeed knowledge of the partitioning of glucose toward oxidative or nonoxidative metabolism, is essential to develop treatments for diabetes (37).

The hyperinsulinemic euglycemic clamp has been widely used to quantify insulin sensitivity (9). Under such controlled conditions, the insulin-stimulated glucose disposal rate (GDR) can be considered an effective and physiological input signal in a mathematical model to analyze the responses (outputs) of skeletal muscle metabolism. Skeletal muscle biopsies obtained during clamp experiments indicate that metabolic species in the cytosol or mitochondria show only modest increases (1, 13, 31); in fact, intracellular glucose has been shown to decrease slightly (11). Nevertheless, noticeable increases in reaction fluxes, such as that of glucose phosphorylation (4), carbohydrate oxidation (16, 23), and energy expenditure (15, 22), occur during hyperinsulinemic conditions. Such information indicates that skeletal muscle becomes more active when stimulated by insulin. To match the substantially increased glucose uptake rate, most reaction fluxes need to be elevated in a coordinated manner because glucose disposal involves a series of pathways and reactions in skeletal muscle. To date, however, clamp experiments have shown elevated enzyme activity or protein content in only a few key enzymes: hexokinase (HK), glycogen synthase (GS), and pyruvate dehydrogenase (PDH) (22–24, 45). Whether these increases are sufficient to stimulate the entire metabolic system of skeletal muscle requires examination.

Due to a shortage of dynamic in vivo human data, the regulatory mechanisms of insulin action on skeletal muscle metabolism are poorly understood. To quantitatively interpret the limited data, a physiologically based mathematical model can be applied. Models related only to the intracellular effects of insulin provide limited mechanistic understanding of the in vivo metabolic effects of insulin on skeletal muscle because they do not include some key elements (8, 29) or are focused only on insulin signaling (36). Instead, a multiscale mathematical model of cellular metabolic dynamics is needed to quantify mechanisms by which insulin regulates skeletal muscle metabolism (21). Furthermore, it is essential to examine the fate of intracellular glucose by investigating oxidative vs. nonoxidative glucose disposal. The model presented in this study incorporates most key metabolites and enzymatic reactions in skeletal muscle to simulate dynamic responses of in vivo metabolism during hyperinsulinemic euglycemic clamp experiments in healthy subjects. Model variations were simulated to investigate three alternative mechanisms (Models M.1, M.2, and M.3) to explain insulin enhancements.

METHODS

Overview

Insulin facilitates glucose uptake and glucose disposal in skeletal muscle through multiple intracellular reactions, including phosphorylation of glucose by HK, glycogen synthesis via GS, glycolysis via PDH, and the TCA cycle (16, 17). We developed a mathematical model for these processes in a skeletal muscle model based on previous work that describes transport and metabolic processes in capillary blood, cytosol, and mitochondria (21). For this study, the model needed the addition of a malonyl-CoA pathway with four reaction fluxes in the cytosol (ATP-citrate lyase, acetyl-CoA carboxylase, malate dehydrogenase, and malonyl-CoA utilization) as well as citrate and malate transport fluxes between the cytosol and mitochondria. The detailed metabolic pathways of the model are shown in Fig. 1.

Fig. 1.

Schematic diagram of biochemical pathways depicting various chemical reactions and species involved in the cellular metabolism of skeletal muscle. Reactions and species are further compartmentalized into cytosolic and mitochondrial reactions and species. Glu, glucose; Gly, glycogen; G6P, glucose 6-phosphate; F6P, fructose 6-phosphate; F16BP, fructose 1,6-biphosphate; GA3P, glyceraldehyde-3-phosphate; 13BPG, 1,3-biphosphate glycerate; PEP, phosphoenolpyruvate; Pyr, pyruvate; Lac, lactate; Ala, alanine; Gr3P, glycerol 3-phosphate; Tgl, triglycerides; Glr, glycerol; FFA, free fatty acid; FAC, fatty acyl-CoA; ACoA, acetyl-CoA; Cit, citrate; AKG, α-ketogluterate; SCoA, succinyl-CoA; Suc, succinate; Mal, malate; Oxa, oxaloacetate; CoA, coenzyme-A (free); PCr, phosphocreatine; Cr, creatine; Pi, inorganic phosphate; NADH, reduced nicotinamide adenine dinucleotide; NAD⁺, oxidized nicotinamide adenine dinucleotide; FADH₂, reduced flavin adenine dinucleotide; FAD, oxidized flavin adenine dinucleotide; MalCoA, Malonyl-CoA; IMS, intermembrane space of mitochondria. Red line, tissue including mitochondrial and cytosolic domains; Blue line, capillary blood domain. Detailed descriptions of reactions are listed in the online supplement (appendix C).

The primary model input is insulin-mediated glucose disposal. To quantitatively analyze the regulatory mechanisms of insulin on skeletal muscle metabolism, three different forms of the model were simulated: M.1, simple mass action; M.2, insulin-mediated activation of key metabolic enzymes (i.e., HK, GS, PDH) M.3, parallel activation by a phenomenological insulin-mediated intracellular signal that modifies the coefficients of specific reaction and transport rates. To validate the model and evaluate many of its parameters, we compared simulated outputs to intramyocellular human data collected during hyperinsulinemic euglycemic clamp experiments.

Experimental Methods

Subjects.

Fifteen lean, healthy human subjects (n = 15; age 24 ± 1 yr, BMI 22.2 ± 0.7 kg/m²) with normal glucose tolerance (NGT) volunteered to undergo a hyperinsulinemic euglycemic clamp. Medical screening excluded individuals with heart, kidney, liver, intestinal, and pulmonary diseases or those taking medications for hypertension, diabetes, or other obesity-related conditions. All volunteers had been sedentary and weight stable for 6 mo prior to the study. The study was approved by the Case Western Reserve University Institutional Review Board, and written informed consent was provided by our subjects in accordance with the guidelines for the protection of human subjects.

Hyperinsulinemic euglycemic clamp experiment.

Clamps were performed as previously described (9, 38). In the morning following an overnight fast, subjects voided urine and were weighed. Intravenous lines were inserted into an antecubital vein (for the infusion of glucose and insulin), and into a heated dorsal vein in retrograde fashion (for arterialized blood sampling). A 2-h primed 40 mU·m⁻²·min⁻¹ insulin infusion proceeded, while a variable-rate 20% dextrose infusion was used to maintain plasma glucose concentrations at 90 mg/dl. Arterialized blood samples were collected every 5 min to measure plasma glucose (Beckman Instruments, Fullerton, CA) to adjust the glucose infusion rate. Space-corrected steady-state GDR was calculated during the last 30 min of the procedure, according to DeFonzo et al. (9). Plasma insulin was assayed via commercial radioimmunoassay (Linco, St. Charles, MO). Free fatty acid concentrations in arterialized blood were determined by colorimetric assay (Wako Chemicals, Dallas, TX). Indirect calorimetry was performed during resting and insulin-stimulated conditions, as previously described (38). Additional experimental data for the concentrations of intracellular species, under the same experimental conditions, were taken from literature reports: glucose [Glu], pyruvate [Pyr], and lactate [Lac] (12); glucose 6-phosphate [G6P] (31); citrate [Cit], malate [Mal], and malonyl-coenzyme A [MalCoA] (2); and glycogen [Gly] (10).

Model Development

Dynamic mass balances.

This model structure is composed of three domains: blood, cytosol, and mitochondria, following a previous model (21) (online supplement, appendix A; supplemental materials are found linked to the online version of this article at the Journal's web site). In the capillary domain, the dynamic mass balance equation of a chemical species j can be expressed as:

$$V_{\mathrm{b}\mathrm{l}}\frac{\mathrm{d}{\mathrm{c}}_{\mathrm{b}\mathrm{l},\mathrm{j}}}{\mathrm{d}t}=Q({\mathrm{C}}_{\mathrm{a}\mathrm{r}\mathrm{t},\mathrm{j}}-{\mathrm{C}}_{\mathrm{b}\mathrm{l},\mathrm{j}})-{\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{c}\mathrm{y}\mathrm{t},\mathrm{j}}^{\mathrm{k}}$$ (1)

where C_art,j is the arterial concentration; C_bl,j is the capillary blood concentration, which approximates the venous concentration C_ven,j; V_bl is the total effective volume of the blood (and interstitial fluid); Q is the tissue blood flow; J_bl↔cyt,j^k is the net mass flux between blood and cytosol that is associated with passive (k = p) or facilitated (k = f) transport. The dynamic mass balance equations for species j in the cytosol and mitochondria have the general forms:

$$V_{\mathrm{cyt}}\frac{\mathrm{d}{\mathrm{C}}_{\mathrm{cyt},\mathrm{j}}}{\mathrm{d}t}=R_{\mathrm{c}\mathrm{y}\mathrm{t},\mathrm{j}}+{\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{cyt},\mathrm{j}}^{\mathrm{k}}-{\mathrm{J}}_{\mathrm{cyt}\leftrightarrow \mathrm{mit},\mathrm{j}}^{\mathrm{k}}$$ (2)

$$V_{\mathrm{mit}}\frac{\mathrm{d}{\mathrm{C}}_{\mathrm{mit},\mathrm{j}}}{\mathrm{d}t}=R_{\mathrm{mit},\mathrm{j}}+{\mathrm{J}}_{\mathrm{cyt}\leftrightarrow \mathrm{mit},\mathrm{j}}^{\mathrm{k}}$$ (3)

where C_x,j is the concentration of species (j) in cytosol (x = cyt) or mitochondria (x = mit); V_x is the effective volume occupied by the cytosol or mitochondria; J_cyt↔mit,j^k is the net mass transport flux of j by mechanism k between the cytosol and mitochondria; and R_x,j is the net rate of the metabolic reaction producing and utilizing substrate j in domain x:

$$R_{\mathrm{x},\mathrm{j}}={\displaystyle \sum _{\mathrm{j}}{\beta }_{\mathrm{j},\mathrm{S}\leftrightarrow \mathrm{P}}{\phi }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P}}}$$ (4)

where φ_x,S↔P is the reaction flux rate that the species j is involved in as substrate (S) or product (P), and β_j,S↔P is the corresponding stoichiometric coefficient. The detailed mass balance equations of each species in each domain are listed in the online supplement (appendix B).

Metabolic fluxes.

The reaction fluxes in cytosol or mitochondria can be expressed as reversible enzyme kinetics (21):

$${\phi }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P}}=\gamma (\mathrm{A},\mathrm{I})\frac{\left[\frac{V_{\mathrm{m}\mathrm{a}\mathrm{x},\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{f}}}{K_{\mathrm{m},\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{f}}}\underset{\mathrm{q}}{\Pi }{\left[{\mathrm{S}}_{\mathrm{q}}\right]}^{{\mathrm{m}}_{\mathrm{q}}}-\frac{V_{\max ,\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{b}}}{K_{\mathrm{m}.\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{b}}}\underset{\mathrm{l}}{\Pi }{\left[{\mathrm{P}}_{\mathrm{l}}\right]}^{{\mathrm{n}}_{\mathrm{l}}}\right]}{\left[1+\frac{1}{K_{\mathrm{m},\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{f}}}\underset{\mathrm{q}}{\Pi }{\left[{\mathrm{S}}_{\mathrm{q}}\right]}^{{\mathrm{m}}_{\mathrm{q}}}+\frac{1}{K_{\mathrm{m},\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{b}}}\underset{\mathrm{l}}{\Pi }{\left[{\mathrm{P}}_{\mathrm{l}}\right]}^{{\mathrm{n}}_{\mathrm{l}}}\right]}$$ (5)

where γ(A, I) represents a controller function that accounts for activation (A) or inhibition (I) (21); [S_q] and [P_l] denote concentrations of substrates and products, and m_q and n_l are stoichiometric coefficients; K_m,S↔P^f and K_m,S↔P^b are Michaelis-Menten constants of forward and backward reactions. The two maximal reaction rate coefficients are not independent, but satisfy μ_x,s↔p = V_max,x,s↔p^b/V_max,x,s↔p^f where μ_x,s↔p is a thermodynamic equilibrium coefficient (21).

Because citrate can activate the reaction of acetyl-CoA carboxylase (ACC), which catalyzes the conversion of acetyl-CoA (ACoA) to malonyl-CoA (MalCoA) (33), the model includes an additional activation modulator:

$${\mathrm{\gamma }}_{\mathrm{A}\mathrm{C}\mathrm{o}\mathrm{A}\leftrightarrow \mathrm{M}\mathrm{al}\mathrm{C}\mathrm{o}\mathrm{A}}(\mathrm{A})=\frac{{\mathrm{C}}_{\mathrm{cyt},\mathrm{Cit}}}{K_{\mathrm{cyt},\mathrm{A}\mathrm{C}\mathrm{o}\mathrm{A}\leftrightarrow \mathrm{M}\mathrm{a}\mathrm{l}\mathrm{C}\mathrm{o}\mathrm{A}}^{\mathrm{Ctrl}}+{\mathrm{C}}_{\mathrm{cyt},\mathrm{Cit}}}$$ (6)

The detailed reaction fluxes of the model are listed in the online supplement (appendix C).

Transport fluxes.

The transport fluxes may be passive (p) or carrier mediated, i.e., facilitated (f). The net transport flux of species between domains and for passive diffusion is

$${\mathrm{J}}_{\mathrm{x}\leftrightarrow \mathrm{y},\mathrm{j}}^{\mathrm{p}}={\lambda }_{\mathrm{x}\leftrightarrow \mathrm{y},\mathrm{j}}({\mathrm{C}}_{\mathrm{x},\mathrm{j}}-{\mathrm{C}}_{\mathrm{y},\mathrm{j}})$$ (7)

and for facilitated transport is

$${\mathrm{J}}_{\mathrm{x}\leftrightarrow \mathrm{y},\mathrm{j}}^{\mathrm{f}}={\mathrm{T}}_{\mathrm{x}\leftrightarrow \mathrm{y},\mathrm{j}}\left(\frac{{\mathrm{C}}_{\mathrm{x},\mathrm{j}}}{{\mathrm{M}}_{\mathrm{x}\leftrightarrow \mathrm{y},\mathrm{j}}+{\mathrm{C}}_{\mathrm{x},\mathrm{j}}}-\frac{{\mathrm{C}}_{\mathrm{y},\mathrm{j}}}{{\mathrm{M}}_{\mathrm{x}\leftrightarrow \mathrm{y},\mathrm{j}}+{\mathrm{C}}_{\mathrm{y},\mathrm{j}}}\right)$$ (8)

where λ_x↔y,j is the effective permeability-surface area product for passive diffusion; T_x↔y,j is the maximal transport rate for facilitated transport and M_x↔y,j is the corresponding Michaelis-Menten (MM) constant. In this model, malonyl-CoA can inhibit the transport of fatty acyl-CoA (FAC) from the cytosol to mitochondria (33). Therefore, in the FAC transport flux:

$${\mathrm{J}}_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{F}\mathrm{A}\mathrm{C}}^{\mathrm{f}}={\gamma }_{\mathrm{FAC}}{\mathrm{T}}_{\mathrm{cyt}\leftrightarrow \mathrm{mit},\mathrm{FAC}}\left(\frac{{\mathrm{C}}_{\mathrm{cyt},\mathrm{FAC}}}{{\mathrm{M}}_{\mathrm{cyt}\leftrightarrow \mathrm{mit},\mathrm{FAC}}+{\mathrm{C}}_{\mathrm{cyt},\mathrm{FAC}}}-\frac{{\mathrm{C}}_{\mathrm{m}\mathrm{i}\mathrm{t},\mathrm{F}\mathrm{A}\mathrm{C}}}{{\mathrm{M}}_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{F}\mathrm{A}\mathrm{C}}+{\mathrm{C}}_{\mathrm{m}\mathrm{i}\mathrm{t},\mathrm{F}\mathrm{A}\mathrm{C}}}\right)$$ (9)

an inhibition modulator is incorporated:

$${\gamma }_{\mathrm{F}\mathrm{A}\mathrm{C}}(\mathrm{I})=\frac{K_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{F}\mathrm{A}\mathrm{C}}^{\mathrm{C}\mathrm{t}\mathrm{r}\mathrm{l}}}{K_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{F}\mathrm{A}\mathrm{C}}^{\mathrm{C}\mathrm{t}\mathrm{r}\mathrm{l}}+{\mathrm{C}}_{\mathrm{c}\mathrm{y}\mathrm{t},\mathrm{M}\mathrm{a}\mathrm{l}\mathrm{C}\mathrm{o}\mathrm{A}}}$$ (10)

Model inputs.

The primary model input is the experimentally measured insulin-mediated GDR, which enters as

$${\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{c}\mathrm{y}\mathrm{t},\mathrm{G}\mathrm{l}\mathrm{u}}^{\mathrm{f}}={\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{c}\mathrm{y}\mathrm{t},\mathrm{G}\mathrm{l}\mathrm{u},0}^{\mathrm{f}}+({\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{c}\mathrm{y}\mathrm{t},\mathrm{G}\mathrm{l}\mathrm{u},\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{p}}^{\mathrm{f}}-{\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{c}\mathrm{y}\mathrm{t},\mathrm{G}\mathrm{l}\mathrm{u},0}^{\mathrm{f}})\left(1-\exp \left(-\frac{t-t_0}{{\tau }_{\mathrm{Glu}}}\right)\right)$$ (11)

where J_{bl↔cyt,Glu,0}^f and J_{bl↔cyt,Glu,clamp}^f are the measured GDRs at rest and during the insulin-stimulated clamp; τ_Glu is the time constant; t₀ is start of the clamp from a resting, steady state. Due to the inhibition of lipolysis in adipose tissue by insulin (35), the concentration of arterial free fatty acids (FFA) decreases substantially under insulin-stimulated conditions:

$${\mathrm{C}}_{\mathrm{a}\mathrm{r}\mathrm{t},\mathrm{F}\mathrm{F}\mathrm{A}}={\mathrm{C}}_{\mathrm{a}\mathrm{r}\mathrm{t},\mathrm{F}\mathrm{F}\mathrm{A},0}+\left({\mathrm{C}}_{\mathrm{a}\mathrm{r}\mathrm{t},\mathrm{F}\mathrm{F}\mathrm{A},\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{p}}-{\mathrm{C}}_{\mathrm{a}\mathrm{r}\mathrm{t},\mathrm{F}\mathrm{F}\mathrm{A},0}\right)\left(1-\exp \left(-\frac{t-t_0}{{\tau }_{\mathrm{F}\mathrm{F}\mathrm{A}}}\right)\right)$$ (12)

where C_a,FFA,0 and C_a,FFA,clamp are the experimentally measured arterial FFA concentrations at rest and during the insulin-stimulated stage of the clamp experiment; τ_FFA is the time constant. Furthermore, insulin can increase substrate availability to skeletal muscle due to increased capillary dilation and net blood flow (7, 15, 26), which changes as

$$Q=Q_0+(Q_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{p}}-Q_0)\left(1-\exp \left(-\frac{t-t_0}{{\tau }_{\mathrm{Q}}}\right)\right)$$ (13)

where Q₀ and Q_clamp are the measured blood flow rates at rest and during insulin stimulation (15); the time constant τ_Q is assumed equal to τ_Glu.

Model Simulation Strategy

Model implementation.

This insulin/glucose metabolism model was used to simulate a hyperinsulinemic-euglycemic clamp experiment in healthy human subjects with NGT. To investigate three alternative mechanisms to explain insulin enhancements, three model variations (M.1, M.2, M.3) were tested. In the basic model (M.1), parameter values are not affected by insulin stimulation, so that responses reflect only the effect of mass action. According to available measurements, model M.2 assumes that insulin stimulates enzyme activity associated only with HK (24, 28, 45), GS (3, 24, 45), and PDH (6, 22, 23); consequently, activity coefficients are incorporated in the corresponding enzymatic reactions. Model M.3 assumes that maximum-rate coefficients of reaction and transport (V_max,S↔P or T_cyt↔mit,j) associated with glucose disposal reactions in tissue will increase during the clamp experiment.

M.2 simulations were based on measured insulin-stimulated changes in enzyme activity of HK (24, 28, 45), GS (3, 24, 45), and PDH (6, 22, 23). The effect of these activated enzymes was simulated by modifying reaction fluxes in Eq. 5:

$${\Phi }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P},\mathrm{i}}^{\mathrm{B}}={\omega }_{\mathrm{E}\mathrm{n}\mathrm{z},\mathrm{i}}(t){\varphi }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P},\mathrm{i}}$$ (14a)

where ω_x,S↔P,i(t)i ∈ (HK, GS, PDH) is the activity coefficient defined as

$${\omega }_{\mathrm{E}\mathrm{n}\mathrm{z},\mathrm{i}}(t)=1+\left({\omega }_{\mathrm{Enz},\mathrm{i}}^0-1\right)\left\{1-\exp \left[-\left(\frac{t-t_0}{{\tau }_{\mathrm{G}\mathrm{l}\mathrm{u}}}\right)\right]\right\}$$ (14b)

where ω_Enz,i⁰ represents the measured enzyme activity at the end of the clamp experiment.

In the simulations of M.3, the reaction fluxes were modified by an enhancement coefficient associated with an apparent stimulation effect of insulin:

$${\Phi }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{p}}^{\mathrm{C}}={\eta }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P}}\left(t\right){\varphi }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{p}}$$ (15a)

The reaction rate coefficient changes according to

$${\eta }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P}}\left(t\right)=1+\left({\eta }_{\mathrm{x},\mathrm{S}\leftrightarrow \mathrm{P}}^0-1\right)\left\{1-\exp \left[-\left(\frac{t-t_0}{{\tau }_{\mathrm{G}\mathrm{l}\mathrm{u}}}\right)\right]\right\}$$ (15b)

where η_x,S↔P⁰ is the maximal value of the enhancement coefficient. Reactions and processes that are not considered to be activated in response to insulin include glycogen phosphorylation, lactate dehydrogenase, lipase, acyl-CoA synthetase, adenylate kinase, creatine kinase, and β-oxidation. Furthermore, values of η_x,S↔P⁰ are assumed identical for reactions in the same pathway, e.g., glycolysis, triglyceride synthesis, TCA cycle, oxidative phosphorylation, and malonyl-CoA branch.

Transport fluxes between cytosol and mitochondria that are closely associated with reaction fluxes can be stimulated indirectly by insulin. To reflect this, we incorporate an enhancement coefficient in the transport flux of the involved chemical species between cytosol and mitochondria except O₂ and CO₂:

$${\mathrm{J}}_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}^{\mathrm{C}}={\eta }_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}\left(t\right){\mathrm{J}}_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}$$ (16a)

where the enhancement coefficient varies with time according to

$${\eta }_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}\left(t\right)=1+\left({\eta }_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}^0-1\right)\left\{1-\exp \left[-\left(\frac{t-t_0}{{\tau }_{\mathrm{G}\mathrm{l}\mathrm{u}}}\right)\right]\right\}$$ (16b)

and η_cyt↔mit,j⁰ is the maximal value of the enhancement coefficient.

Evaluation of steady-state concentrations and fluxes.

The values of resting steady-state concentrations of most species in cytosol and mitochondria were found previously (21). The exceptions were concentration values of malonyl-CoA (2, 27, 32) and of citrate (Cit), malate (Mal), oxaloacetate (OAA), and acetyl-CoA (ACoA), which were based on an assumed distribution between the cytosol and mitochondria (Table 1). Also, the resting steady-state values of the transport fluxes were previously reported (21) and are listed in Table 2.

Table 1.

Species concentrations in muscle tissue cells from literature reports and their compartmentalization (distribution) into cytosol and mitochondria under resting steady-state conditions (mmol/kg tissue wet wt or mM)

	Tissue Cells (100%)	Cytosol (90%)		Mitochondria (10%)
Species	Concentration, mmol/kg wet wt	Mass, %	Concentration, mmol/kg wet wt	Mass, %	Concentration, mmol/kg wet wt
Glu	0.5	100	0.5556	0	0
Pyr	0.05	95	0.0528	5	0.025
Lac	0.78	100	0.8667	0	0
Ala	1.3	100	1.4444	0	0
Glr	0.065	100	0.0722	0	0
FFA	0.45	100	0.50	0	0
CO2 (F)	N/A	N/A	1.403 (46 mmHg)	N/A	1.525 (50 mmHg)
O2 (F)	N/A	N/A	0.0338 (25 mmHg)	N/A	0.027 (20 mmHg)
H+	N/A	N/A	10−7.1 + 3 (pHcyt = 7.1)	N/A	10−7.6 + 3 (pHcyt = 7.6)
Gly	95.0	100	105.56	0	0
G6P	0.25	100	0.2778	0	0
F6P	0.044	100	0.0488	0	0
F16BP	0.06	100	0.0667	0	0
GA3P	0.08	100	0.0889	0	0
13BPG	0.08	100	0.0889	0	0
PEP	0.0049	100	0.00539	0	0
Tgl	15.0	100	16.667	0	0
Gr3P	0.15	100	0.167	0	0
FAC	0.0035	95	0.00369	5	0.00175
PCr	21.0	100	23.333	0	0
Cr	10.5	100	11.667	0	0
ATP (T)	6.2	86	5.924	14	8.68
ADP (T)	0.8	2	0.0178	98	7.84
AMP (T)	0.04	100	0.0444	0	0
Pi	2.75	95	2.903	5	1.375
CoA	0.02	80	0.0178	20	0.04
NADH	0.05	0.5	0.2778E-3	99.5	0.4975
NAD+	0.45	30	0.15	70	3.15
ACoA	0.002	40	8.89E-4	60	0.012
Cit	0.095	50	0.0528	50	0.475
AKG	0.0125	0	0	100	0.125
SCoA	0.125	0	0	100	1.25
Suc	0.095	0	0	100	0.95
Mal	0.095	95	0.10	5	0.0475
Oxa	0.0024	40	0.00107	60	0.0144
FADH2	0.024	0	0	100	0.24
FAD	0.212	0	0	100	2.12
MalCoA	0.000475	100	0.000528	0	0

Cytosolic and mitochondrial species concentrations are calculated from the tissue cells species concentrations according to their approximate volumes of distribution and mass fractions. Most of the species concentrations are the same as those previously reported (21). Definitions are as in Fig. 1.

Table 2.

Transport fluxes and parameters at resting steady state

	Transport Fluxes and Parameters at Resting Steady State
Species	Jbl↔cyt(0), mmol/min	Tbl↔cyt, mmol/min	Mbl↔cyt, mmol/l	λbl↔cyt, l/min	ηbl↔cyt,j0
Blood-cytosol passive or carrier-mediated (facilitated) transport fluxes and parameters
Glu	0.195	0.411	2.5
Pyr	0.012	1.513	1.0
Lac	−0.09	2.217	5.0
Ala	−0.065			0.0579
Glr	−0.008			0.343
FFA	0.073	1.491	1.0
CO2	−2.01			30.597
O2	2.606			193.71
H+	−7.25E-6	5.84E-5	4.78E-5

Species	Jcyt↔mit(0), mmol/min	Tcyt↔mit, mmol/min	Mcyt↔mit, mmol/l	λcyt↔mit, l/min	ηcyt↔mit,j0‡
Cytosol-mitochondria passive or carrier-mediated (facilitated) transport fluxes and parameters
O2	2.606			386.13
CO2	−2.010			16.477
Pyr	0.239	1.3377	0.0528		8
FAC‡	0.082	0.9179	0.00175		1.2
Pi	12.458	69.765	1.375		2
CoA	−0.082	0.4267	0.04		1.3
ATP/ADP†	−12.458	37.374	666.367		2
			0.554
NADH/NAD+†	0.275	0.3716	0.00062		3.2
			15.794
H+	2.9E-05	1.113E-4	2.51E-05		1.3
Cit	−8.95E-3	0.0224	0.475		1.5
Mal	8.95E-3	0.05	0.048		1.5

Resting blood-cytosol species transport fluxes satisfy J_bl↔cyt = UR = Q(C_art–C_ven) at resting steady-state conditions. Resting cytosol-mitochondria species transport fluxes J_cyt↔mit are based on a flux balance analysis at resting steady-state conditions. Transport parameters (λ, T_max) for a species are evaluated from the governing equation of transport flux associated with the specific species at resting steady state. Activation coefficients are optimized to fit the experimental data during the clamp experiment on the basis of the model variation M.3.

^†Transport of ATP-ADP and NADH-NAD⁺ between cytosol and mitochondria follow special carrier-mediated transport mechanisms (21).

^‡Transport of FAC from cytosol to mitochondria is assumed to be inhibited by malonyl-CoA. The corresponding modulation coefficient K_{cyt↔mit,FAC}^Ctrl is estimated by the initial concentration of MalCoA as 5.277E-4.

Simulations for all models start with the same resting steady-state flux balance. From the mass balance equations (Eqs. 1, 2, and 3) at steady state, the reaction and transport fluxes satisfy

$${\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{cyt},\mathrm{j}}^{\mathrm{k}}=Q\left({\mathrm{C}}_{\mathrm{art},\mathrm{j}}-{\mathrm{C}}_{\mathrm{b}\mathrm{l},\mathrm{j}}\right)=Q\left({\mathrm{C}}_{\mathrm{a}\mathrm{r}\mathrm{t},\mathrm{j}}-{\mathrm{C}}_{\mathrm{v}\mathrm{e}\mathrm{n},\mathrm{j}}\right)=\mathrm{U}{\mathrm{R}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{cyt},\mathrm{j}}$$ (17)

$$0=R_{\mathrm{c}\mathrm{y}\mathrm{t},\mathrm{j}}+{\mathrm{J}}_{\mathrm{b}\mathrm{l}\leftrightarrow \mathrm{c}\mathrm{y}\mathrm{t},\mathrm{j}}^{\mathrm{k}}-{\mathrm{J}}_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}^{\mathrm{k}}$$ (18a)

$$0=R_{\mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}+{\mathrm{J}}_{\mathrm{c}\mathrm{y}\mathrm{t}\leftrightarrow \mathrm{m}\mathrm{i}\mathrm{t},\mathrm{j}}^{\mathrm{k}}$$ (18b)

The sequence of evaluation has been described previously (21). Using Eq. 17, the transport fluxes J_bl↔cyt,j^k were determined from the measured uptake rates UR_bl↔cyt,j. Then, by a flux-balance analysis with the other Eqs. 18a and 18b, the reaction rate and the transport fluxes J_cyt↔mit,j^k were evaluated except for citrate, which was assumed to be 1% of the reaction flux of CS because no experimental data were available. Values of the resting steady-state transport and reaction fluxes are listed in Tables 2 and 3, respectively.

Table 3.

Reaction flux and related parameter values at resting steady state, in mmol/min

	ϕ0	Vmax,x,S↔Pf	Vmax,x,S↔Pb	Km,S↔Pf	Km,S↔Pb	Kγ	ηx,S↔P0
Hexokinase	0.195	0.59	4.34E-12	3.29	3.93E-07	27.8	21
Glycogen synthase	0.250	27.777	9.45E-07	17400	158	0	1.8
Glycogen phosphorylase	0.250	0.254	3.50E+6	0.00306	293000	1.87e-5	1
Phosphoglucose isomerase	0.195	1.126	5.37E-01	0.278	0.0486	0	4.12
Phosphofructokinase	0.195	7.852	2.49E-10	0.288	9.42E-08	0.841	4.12
Aldolase +TPI	0.195	2.670	3.30E-01	0.667	0.079	0	4.12
GA3P dehydrogenase	0.382	1.146	7.37E-08	0.0387	1.96E-09	0	4.12
Phosphoglycerate kinase	0.382	1.192	4.09E-02	0.00158	0.0319	0	4.12
Pyruvate kinase	0.382	1.171	3.21E-02	7.61E-09	0.313	0.00267	4.12
Lactate dehydrogenase	0.090	9.76E +44	7.20E-03	1.17E +23	1.3E-15	0	1
Lipases	0.008	0.024	7.43E-19	16.7	4.52E-15	0	1
Gr3P dehydrogenase	0.008	0.025	9.35E-04	1.96E-09	0.0251	0	1.2
Acyltransferase	0.008	0.024	2.34E-06	8.42E-09	0.000273	0	1.2
Acyl-CoA synthetase	0.106	0.318	1.69E-19	0.312	6.21E-14	0	1
ATPase	12.352	29.562	3.52E-11	5.92	1.04E-5	0	1.3
Adenylate kinase	0	200	4.01E-02	132	3.18E-5	0	1
Creatine kinase	0	200	6.65E +0	2.97E-4	20.7	0	1
Alanine aminotransferase	0.065	0.197	1.83E-03	0.0528	1.44	0	1.25
PDH	0.239	0.870	8.21E-12	0.00315	3.81e-7	0.361	32
β-Oxidation	0.0819	0.164	8.8E-189	4.67E-4	6E-6	0	1
Citrate synthase	0.8946	6.454	2.20E-09	0.00048	9.55E-7	0.361	2.25
Isocitrate dehydrogenase	0.886	6.433	1.19E-01	2.99	0.0948	0.361	2.25
AKG dehydrogenase	0.8856	2.663	2.28E-05	0.0158	0.948	0	2.25
SCoA synthetase	0.8856	2.687	2.69E-02	13.5	0.33	0	2.25
Succinate dehydrogenase	0.8856	1.814	0.0127	2.01	0.228	0	2.25
Malate dehydrogenase	0.8946	29.524	2.285E-5	2.99	3.00E-07	0	2.25
Complex I +III+IV	3.753	1.126E +32	1.75E-0	2.05E-6	3.15	0	1.1
Complex II+III+IV	1.459	1.74E +19	9.23E-07	0.0394	2.12	0	1.1
ATP synthase	11.573	1.92E-08	3.76E +0	0.000271	8.68	0	1.2
Citrate lyase	0.00894	0.0268	2.35E-07	0.00557	4.89E-08	0	1.2
ACC	0.00894	0.0537	5.96E-13	0.00739	2.72E-05	5.278E-2	1.2
Malate dehydrogenase	0.00894	0.0286	1.8E-03	2.35E-11	0.015	0	1.2
Malonyl-CoA utilization	0.00894	0.0439	1.71E-02	5.27E-48	0.0125	0	1.2

Value of reaction fluxes is based on flux balance analysis. Michaelis-Menten parameters (K_mγ^f, K_m^bK_γ) are the same as in our previous model (21). Maximal reaction rate coefficients, V_max are evaluated from the governing equation of reaction flux. Activation coefficients η are optimized to fit the experimental data based on model variation M.3.

The model equations were solved numerically using MATLAB (“ode15s”; MathWorks, Natick, MA) to simulate the hyperinsulinemic metabolic responses in blood and skeletal muscle.

Estimation of Model Parameters

Values of the input parameters (τ_Glu, τ_FFA) estimated from least-squares fitting of the model input equations to experimental data (Fig. 2) are listed in Table 4. The transport parameters (λ_x↔y,j, T_x↔y,j) were evaluated from transport fluxes of the specific species at resting steady state. Most Michaelis-Menten parameters K_m,S↔P^f and K_m,S↔P^b, were found previously (21), but those associated with the reaction fluxes for ATP-citrate lyase, ACC, malate dehydrogenase, and malonyl-CoA utilization were estimated from the equilibrium values of the species concentrations (S_q,0, P_k,0):

$$K_{\mathrm{m},\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{f}}=\underset{\mathrm{q}}{\Pi }{\left[{\mathrm{S}}_{\mathrm{q},0}\right]}^{{\mathrm{m}}_{\mathrm{q}}},K_{\mathrm{m},\mathrm{S}\leftrightarrow \mathrm{P}}^{\mathrm{b}}=\underset{\mathrm{l}}{\Pi }{\left[{\mathrm{P}}_{\mathrm{l},0}\right]}^{{\mathrm{n}}_{\mathrm{l}}}$$ (19)

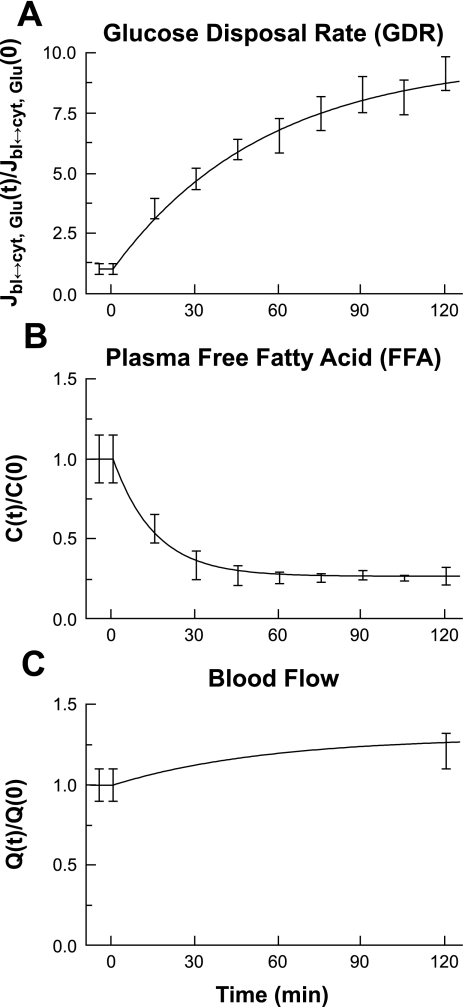
Fig. 2.

Model inputs for intramyocellular metabolic simulations. Each panel represents dynamic changes of model inputs across the time period of the clamp experiment. A 2-h 40 mU·m⁻²·min⁻¹ hyperinsulinemic-euglycemic (90 mg/dl) clamp was performed in 15 healthy human volunteers. A: glucose disposal rate (GDR). B: plasma free fatty acid (FFA). C: blood flow. Experimental data for GDR and FFA were measured in vivo during the clamp. Variables were normalized by dividing the value at each time point by the value measured under resting steady-state conditions (t = 0 min).

Table 4.

Physiological input parameters

Parameter	Description	Value	Reference
tGlu	Time constant of glucose uptake during the clamp	55 min	Estimated
τFFA	Time constant of plasma FFA changes during the clamp	15 min	Estimated
τQ	Time constant of blood flow changes during the clamp	55 min	Estimated
Q	Blood flow at resting, steady state	0.9 l/min	(21)
Qclamp	Blood flow at end of the clamp, 20% increase	1.08 l/min	(15)

For the modulation factors associated with the reaction of ACC (γ_{ACoA↔MalCoA}(A)) and FAC transport (γ_FAC(I)), we assumed that the parameter values corresponded to the resting, steady-state values of the species concentrations K_{cyt,ACoA↔MalCoA}^Ctrl = C_cyt,Cit(t₀), K_{cyt↔mit,FAC}^Ctrl = C_cyt,MalCoA(t₀). From the reaction flux values at resting steady state, maximal reaction rate coefficients (V_max,S↔P^f) were calculated. Also, transport rate coefficients (T_max,j) were calculated from the transport fluxes. These parameter values in transport and reaction fluxes are summarized in Tables 2 and 3, respectively. The values of the activity coefficients ω_Enz,i⁰ of enzymes were based on the relative change of enzyme activities during the clamp experiment, where we set ω_Enz,HK⁰ = 3 (24, 28, 45), ω_Enz,GS⁰ = 2 (3, 24, 45) and ω_Enz,PDH⁰ = 2 (6, 22, 23).

The values η_x,S↔P⁰ and η_cyt↔mit,j⁰ in M.3 were determined by least-squares fitting model simulations to available experimental data of intracellular species concentrations: [Glu], [Pyr], and [Lac] (12); [G6P] (31); [Gly] (10); [Mal], [Cit], and [MalCoA] (2) during clamp experiments (Tables 2 and 3). In the constrained optimization process most η_x,S↔P⁰ and η_cyt↔mit,j⁰, we set the inequality constraints with the lower bound as 1 and upper bounds as 10, except for the reaction of HK and PDH, whose upper bounds are set as 30 and 40, respectively. The nonlinear constrained optimization was achieved using a robust generalized reduced gradient algorithm GRG2, (http://www.maxthis.com/Grg2ug.htm) (21).

RESULTS

Model simulations were compared with experimental data from insulin stimulation of skeletal muscle to provide validation of the mathematical model and to investigate possible mechanisms that are consistent with the data. The data were obtained from human hyperinsulinemic-euglycemic clamp experiments of healthy subjects and from the literature. Possible mechanisms were simulated with three model variations (M.1, M.2, and M.3).

Dynamics of Model Inputs

The simulated model input functions were fitted to glucose disposal and plasma FFA data obtained from clamp experiments (Fig. 2). The change in blood flow during hyperinsulinemia was based on literature data (15). Insulin-stimulated GDRs increased approximately ninefold (Fig. 2A), arterial FFA concentration decreased substantially (∼80%; Fig. 2B), and blood flow increased by ∼20% under these experimental conditions (Fig. 2C).

Species concentration responses.

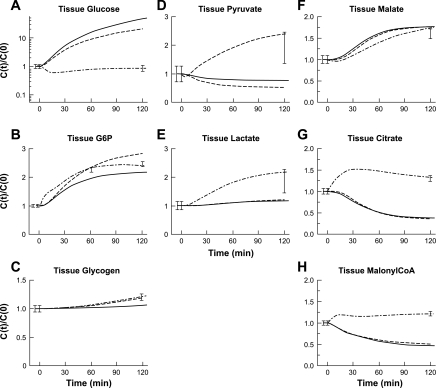
Model simulations of the dynamic responses of intracellular species concentrations for each model variation (Fig. 3) were compared with insulin-response data. Only M.3 fits all of the experimental data. Whereas M.1 and M.2 simulations predicted large increases in [Glu] (Fig. 3A), M.3 predicted a moderate decrease in intracellular [Glu]. Simulations of [G6P] with M.1 and M.2 predicted increases of ∼110 and ∼170%, respectively (Fig. 3B) that deviate from the experimental data, but the M.3 predicted ∼130% increase corresponds more closely to the data. The simulated [Gly] from M.1 showed little change, whereas M.2 and M.3 both predicted a ∼20% increase (Fig. 3C).

Fig. 3.

Model simulation dynamics of intramyocellular concentrations of Glu, G6P, and Gly, Pyr, Lac, Mal, Cit, and MalCoA during a 40 mU·m⁻²·min⁻¹ hyperinsulinemic-euglycemic clamp. Each panel represents dynamic changes of cellular Glu (A), G6P (B), Gly (C), Pyr (D), Lac (E), Mal (F), Cit (G), and MalCoA (H) in response to hyperinsulinemia. Intracellular species concentrations (mmol/kg wet wt or mM) were calculated based on volume-average formula: C_tis = (V_cytC_cyt + V_mitC_mit)/V_tis and were normalized with respect to the value measured under resting steady-state conditions (t = 0 min). Error bars represent measured experimental data (means ± SE). Lines represent M.1 (–), M.2 (- - -), and M.3 (-·-) model simulations. The dynamics of [Glu] were plotted using a semilog (y-axis) transformation.

M.1 and M.2 predict ∼20 and ∼50% decreases in [Pyr] (Fig. 3D) and a minor increase for [Lac] (Fig. 3E), respectively. Compared with the experimental data, M.1 and M.2 simulations were 60 and 70% lower for [Pyr] and ∼50% lower for [Lac]. M.3 simulations of [Pyr] (Fig. 3D) and [Lac] (Fig. 3E) matched the increase of ∼100% during the clamp experiment.

[Mal] increased 70–75% in accord with experimental data (Fig. 3F) in simulations of models M.1, M.2, and M.3. Whereas M.1 and M.2 predicted an ∼35% decrease in [Cit], M.3 simulated a 50% increase at ∼30 min with a good fit to the experimental data (Fig. 3G). Simulations of [MalCoA] with M.1 and M.2 predicted a ∼35% decrease, which was ∼50% lower than the experimental data. M.3 predicted a ∼25% increase of [MalCoA] that fit the experimental data well (Fig. 3H).

Responses of Reaction Fluxes

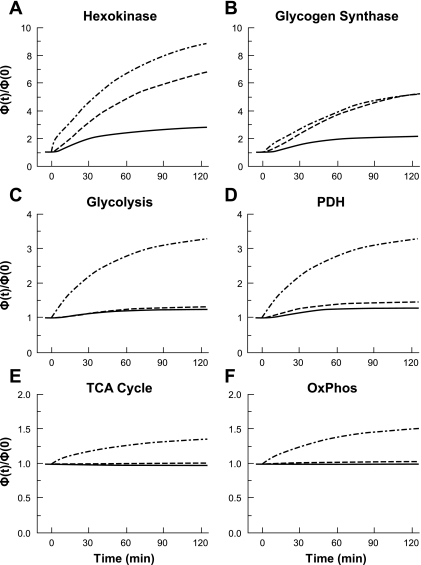
Glucose disposal in tissue is associated with the key reaction fluxes of HK, GS, glycolysis, PDH, the TCA cycle, and oxidative phosphorylation. Simulations with M.3 produced reaction fluxes that were greater than those with M.1 and M.2 (Fig. 4). Simulated responses of the HK reaction flux with M.1, M.2, and M.3 showed increases of ∼150, ∼600, and ∼900%, respectively. The reaction fluxes of GS increased by ∼100% for M.1, and by ∼500% for both M.2 and M.3. The glycolysis reaction flux with M.1 and M.2 showed little change, whereas with M.3 this flux increased ∼250%. Simulated dynamic responses of PDH by M.1 and M.2 showed a 20–40% increase in reaction flux, whereas M.3 predicted a ∼250% increase. M.1 and M.2 simulated responses of the reaction fluxes of the TCA cycle and oxidative phosphorylation showed small changes, whereas the M.3 simulated flux rates increased by ∼35% and ∼50%, respectively.

Fig. 4.

Model simulation dynamics of the reaction fluxes for hexokinase (HK), glycogen synthase (GS), glycolysis, pyruvate dehydrogenase (PDH), TCA cycle, and oxidative phosphorylation (OxPhos), during a 40 mU·m⁻²·min⁻¹ hyperinsulinemic-euglycemic clamp. Each panel represents dynamic changes of cellular reaction fluxes for HK (A), GS (B), glycolysis (C), PDH (D), TCA (E), and OxPhos (F) in response to hyperinsulinemia. Glycolytic reaction flux was represented by GAPDH; TCA cycle flux was represented by citrate synthase; flux in oxidative phosphorylation was represented by the lumped reaction associated with NADH. Flux rates (mmol/min) were normalized with respect to the corresponding flux at resting steady state (t = 0 min). Lines represent M.1 (–), M.2 (- - -), and M.3 (-·-) model simulations.

Contributions to Glucose Disposal Flux

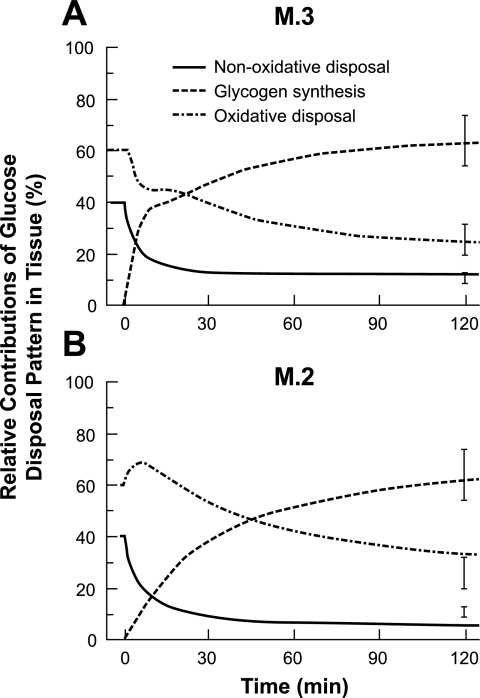
The three components of glucose disposal in tissue are 1) nonoxidative disposal indicated by lactate and alanine transport from tissue to blood, 2) net glycogen synthesis in the cytosol, and 3) oxidative disposal in mitochondria. The relative rates of these glucose disposal mechanisms predicted by M.2 and M.3 were compared with experimental data (23) in Fig. 5. At rest, net glycogen synthesis was zero, whereas nonoxidative and oxidative mechanisms accounted for ∼40 and 60% of GDRs, respectively. Under hyperinsulinemic conditions, the net glycogen synthesis rate increased rapidly in both M.2 and M.3 models and eventually accounted for ∼60% of the glucose disposal. The initial response of M.3 response was faster than the M.2 response. The nonoxidative disposal rates of both M.2 and M.3 decreased rapidly, but the M.3 simulation was closer to the experimental data at the end of the clamp experiment that shows a relative contribution of 15%. With respect to oxidative glucose disposal, the initial rate decreases quickly according to the M.3 model but increases according to the M.2 model. After this initial phase, oxidative disposal rates of both models decrease. At the end of the clamp experiment at which the relative oxidative GDR is ∼25%, the M.3 simulation is closer to the experimental value than the M.2 simulation.

Fig. 5.

Relative contributions of 3 glucose disposal routes predicted by M.2 and M.3 and comparison with experimental data. The dynamics of the relative distribution of the 3 glucose disposal patterns in skeletal muscle during a 40 mU·m⁻²·min⁻¹ hyperinsulinemic-euglycemic clamp are compared with experimental data. Lines represent nonoxidative glucose disposal (–), net glycogen synthesis (- - -), and oxidative glucose disposal (-·-). Nonoxidative disposal is estimated by the release rate of lactate and alanine. Rate of net glycogen synthesis is calculated by the difference between reaction rates of GS and glycogen phosphorylation.

DISCUSSION

Overview

A physiological, cell-based mathematical model of skeletal muscle metabolism was developed to investigate intracellular responses to insulin stimulation with a clamp experiment. This model includes the most important metabolic species with transport and reaction fluxes necessary to describe skeletal muscle metabolism in response to insulin stimulation. Making use of information from previous investigations (8, 29, 30, 36), three alternative mechanisms (M.1–3) were simulated for comparison with the experimental data.

Role of Mass Action and Activated Key Enzymes

The effect of mass action alone (M.1 simulation) or with increased key enzyme activity (M.2 simulation) of HK, GS and PDH cannot account for the experimental responses of the GDR produced by the insulin clamp (Fig. 3). Theoretically, according to the glucose mass balance equation, the rate of glucose utilization (catalyzed by HK) must increase to match the increase in GDR; otherwise, glucose uptake would inevitably cause the accumulation of tissue glucose. Additionally, the increase of other species concentrations during the clamp (Fig. 3) indicates that the rates of all downstream reactions must also increase. However, M.1 simulation produced only minor changes in intracellular species (Fig. 3). Even with increased enzyme activity, the M.2 simulation did not sufficiently increase glycolysis, PDH, TCA cycle, and oxidative phosphorylation (Fig. 4). Therefore, a more complex activation mechanism is needed to stimulate skeletal muscle metabolism in response to insulin.

Effect of Dynamic Reaction and Transport Flux Rates

The large increase in GDR during hyperinsulinemia must be balanced by greater glucose utilization in skeletal muscle to avoid accumulation of metabolic intermediates. This balance can be achieved by allowing the maximal-rate coefficients for reaction or transport, V_max,S↔P or T_cyt↔mit,j, or maximal enhancement coefficients η_x,S↔P⁰ or η_cyt↔mit,j⁰, to increase with the same time constant as GDR, τ_Glu. These factors reflect the phenomenological stimulation effect of insulin on specific reaction and transport processes. This concept was implemented in the M.3 model to achieve a good fit of the simulated output to all experimental data (Fig. 3) and to predict necessary increases in reaction fluxes (Fig. 4).

Reaction flux rates directly reflect the metabolic status of a tissue. Up to now, only sparse in vivo experimental reaction flux data have been available. In young, healthy individuals, ATP synthesis rate increased by ∼40% during a hyperinsulinemic-euglycemic clamp experiment (5, 40, 41). In similar subjects under hyperinsulinemic conditions, the carbohydrate oxidation rate increased about two- to threefold (15, 23). Although skeletal muscle is not contracting during the clamp experiment, the 26% increase in energy expenditure is significant (15). Because carbohydrate oxidation involves a series of reaction pathways (glycolysis, PDH, TCA cycle, oxidative phosphorylation), all the reaction fluxes in response to insulin should increase in a coordinated manner. This is achieved in the M.3 simulation by increasing reaction flux rate coefficients associated with glucose disposal. Consequently, the predicted reaction fluxes (Fig. 4) show remarkable increases in which the HK flux rate is almost the same as the GDR.

These predicted flux rates enable the contributions to the GDR in skeletal muscle to be quantitatively evaluated. After glucose enters skeletal muscle, it can be converted via three possible pathways: 1) glycogen synthesis, 2) conversion to alanine and lactate, or 3) oxidative phosphorylation. After phosphorylation to G6P by HK, glucose can be used to synthesize glycogen, or it can be catalyzed further along the glycolytic pathway to produce pyruvate. Pyruvate is either converted to lactate and alanine, which is then released into the blood (nonoxidative disposal), or it can enter the mitochondria and be oxidized completely via the TCA cycle and oxidative phosphorylation (oxidative disposal). The partitioning of glucose uptake predicted by M.3 simulation was consistent with experimental data obtained during clamp experiments (Fig. 5). In lean, healthy individuals, glycogen synthesis is the primary route for insulin-mediated glucose disposal in skeletal muscle. This provides further evidence that the reaction fluxes predicted by model M.3 are physiologically sound. The activity coefficient (ω_Enz,i⁰) for GS in M.2 almost equals to the enhancement coefficient η_x,S↔P of GS in M.3 (Table 3). Also, the simulated glycogen synthesis flux from M.2 and M.3 are close (Fig. 4B). Correspondingly, the relative fraction of glycogen synthesis in total glucose disposal from M.2 and M.3 are similar (Fig. 5). However, the dynamic simulations of nonoxidative and oxidative glucose disposal of M.2 and M.3 are significantly different.

Stimulatory Mechanisms of Insulin

Skeletal muscle is the most important insulin-sensitive peripheral tissue for glucose disposal (39). Impaired insulin sensitivity of skeletal muscle reduces whole body glucose disposal. Therefore, clarifying the mechanisms of insulin-dependent skeletal muscle metabolism is essential for understanding the etiology of insulin resistance and type 2 diabetes mellitus. Some insulin-dependent processes, the upregulation of GLUT4 translocation, and the activation of key enzymes such as GS, have been well studied (18, 19, 24, 35). However, due to a lack of in vivo experimental data, the mechanisms of insulin-stimulated skeletal muscle metabolism, particularly with regard to reaction flux rates, are still undetermined.

Of the models considered, simulations with the M.3 model incorporating dynamic reaction and transport rate coefficients were most consistent with the experimental data of the skeletal muscle metabolism response to insulin. However, the equations representing the dynamic reaction rate coefficients are phenomenological and not based on experimental measurements of enzyme activity. There is no direct experimental evidence that insulin can increase the activity of the enzymes involved. Data from skeletal muscle biopsies have verified only the increased activities of three enzymes (HK, GS, and PDH) following insulin stimulation (22, 24, 28). In fact, the activity of the key glycolytic enzyme, phosphofructokinase (PFK), does not change during a clamp experiment (14, 25, 43, 44). Although the reaction flux of PFK must increase substantially according to the M.3 simulation, further validation of this effect is required. However, from the M.2 simulation, it is clear that insulin stimulation of just three enzymes, HK, GS and PDH, cannot stimulate skeletal muscle metabolism enough to match the increase in GDR or changes of other intracellular metabolite concentrations. Also, the dynamics of the components of glucose disposal are significantly different between models M.2 and M.3 (Fig. 5). Indeed, more frequent measurements of the three components of glucose disposal during a clamp would be a critical experiment to determine whether the M.3 model reflects the underlying mechanisms. This would mean that a far more complex coordination of intracellular metabolism exists during insulin stimulation.

It is difficult, however, to examine enzyme activities and corresponding reaction fluxes in vivo. If the measured insulin-stimulated changes in enzyme activities reflect their real physiological status, then changes in activity of HK, GS, and PDH could be attributed to a direct effect of insulin via insulin signaling. However, the lack of change in PFK activity during clamp experiments indicates that not all enzymes are under the direct control of insulin. Clearly, the measured enzyme activity change in PFK is inconsistent with the predicted reaction flux response of glycolysis. The discrepancy between the M.2 and M.3 simulations suggest that additional stimulatory factors exist in vivo that increase the reaction rate coefficients as represented phenomenologically. This could be associated with enzyme interactions induced by increased reaction flux rates (40). Therefore, the current in vitro measurements based on biopsy samples are insufficient, and noninvasive in vivo techniques are needed to trace the enzyme activities and corresponding reaction flux changes.

Model Limitations and Future Development

The model developed for this study does not include the regulatory mechanisms of insulin signaling on skeletal muscle metabolism at the molecular level. The current model incorporates a phenomenological stimulatory effect of insulin on muscle metabolism. To improve our understanding of the regulatory mechanism of insulin on skeletal muscle, a quantitative relationship between plasma insulin concentrations and specific reactions in tissue should be established. Some mathematical models of the detailed insulin signaling pathways have been published (36), which could be incorporated into this insulin/glucose metabolic model. Such a mechanistic model could provide investigators with an in silico tool to pursue a systems biology approach to evaluate regulatory mechanisms of insulin on skeletal muscle metabolism in response to potential treatment modalities targeted against insulin resistance.

Conclusion

The model mechanism that produced the best fit of simulated outputs to experimental data assumed that metabolic reaction fluxes associated with glucose disposal increased in parallel coordination with nonconstant reaction rate coefficients. This represents the first in silico study to demonstrate that simple mass action or upregulation of key rate-limiting enzymes (HK, GS, PDH) is insufficient to accurately explain insulin-stimulated changes in the concentration of intracellular species and partitioning of glucose disposal in skeletal muscle. We have demonstrated for the first time that insulin propagates a rather complex coordination of enzymatic reaction fluxes and thus highlights a relatively unexplored research direction. By yielding important predictions about changes of intracellular species concentrations, reaction fluxes, and the partitioning of glucose within skeletal muscle, we have developed a tool that could be used to further explore and ultimately understand the processes of insulin-stimulated metabolism and the mechanism by which they may become impaired.

GRANTS

This work was supported in part by grants (P50 GM-66309, 1F31 GM-084682) from the National Institute of General Medical Sciences (NIH) and by a grant from the National Aeronautics and Space Administration (NNJ06HD81G). Support for the experimental studies was provided in part by NIH grants RO1 AG-12834, T32 HL-007887, and CTSA UL1 RR-024989.

DISCLOSURES

No conflicts of interest are reported by the authors.