Abstract
Electrophysiological alternans is a beat-to-beat alternation of the action potential duration and/or Ca2+ transient amplitude and is linked to ventricular arrhythmias. We investigated the significance of various rate parameters under different experimental conditions with respect to alternans incidence and the propensity for spiral wave formation. Voltage and Ca2+ were optically mapped in monolayers of neonatal rat ventricular myocytes. Alternans did not occur at physiological temperature, but its incidence increased significantly at lowered temperatures. Pacing cycle length for spatially concordant alternans onset (PCLC), PCL for spatially discordant alternans onset (PCLD), and minimum cycle length for loss of 1:1 or 2:2 capture (MCL) also significantly increased with lower temperature but in a way such that the differences between PCLC and MCL and between PCLD and MCL widened. These results provided the rationale to identify the former difference as the alternans vulnerable window (AVW; in ms) and the latter difference as the discordant alternans vulnerable window (AVWD; in ms). Computational simulations showed that interventions that widen AVW, including altered Ca2+ cycling and enhanced K+ currents, also promote alternans, regardless of whether PCLC or MCL increased or decreased. The simulation results were confirmed experimentally by addition of the ATP-sensitive K+ channel agonist pinacidil. Mathematical analysis provided a theoretical basis linking the size of AVW to the incidence of alternans. Finally, experiments showed that the size of AVWD is related to the incidence of spatially discordant alternans and, additionally, to the incidence of spiral wave formation. In conclusion, vulnerable windows can be defined that are strongly correlated with alternans incidence, spatial discordance, and spiral wave formation.
Keywords: electrophysiology, arrhythmia, optical mapping, computational model
electrophysiological alternans in the heart is the beat-to-beat alternation of the action potential duration (APD; in ms) and/or intracellular Ca2+ (Cai2+) transient amplitude, a period-2 rhythm or 2:2 response. This phenomenon results in a highly arrhythmogenic substrate and is linked to ventricular fibrillation and sudden cardiac death (13, 26). Prominent hypotheses for the cause of alternans include intrinsic tissue heterogeneities, a steep relationship between APD and pacing rate (APD restitution), and a steep relationship between Ca2+ release from the sarcoplasmic reticulum (SR) and SR Ca2+ load (12, 17, 25, 26). Alternans can be spatially concordant, alternating in phase at different spatial locations, or spatially discordant, in which regions of myocytes alternate with opposite phase separated by a nodal line at which no alternans is present. Previous studies (25) have demonstrated that the presence of spatially discordant alternans produces a much greater dispersion in refractoriness and greater risk for wavebreaks and arrhythmogenesis. Furthermore, spatially discordant alternans results in a substrate in which a premature ectopic beat or tissue heterogeneities can initiate reentry (11, 17).
The mechanisms that promote or suppress alternans, and their relationship to reentry formation, are not fully understood. We used a well-established condition for alternans induction, lowered temperature (1, 11, 22), to characterize alternans incidence and spiral wave formation in experiments on monolayers of neonatal rat ventricular myocytes (NRVMs). In addition to promoting alternans, lowered temperature slows Ca2+ cycling (15), prolongs APD (19, 21), and increases the minimum cycle length (MCL; in ms) that maintains capture (i.e., decreases the maximum capture rate) (19).
In our study, we investigated how the incidence of alternans and spatially discordant alternans are related to the onset pacing rates of concordant and discordant alternans and to MCL. In the past, alternans has been characterized in terms of the pacing cycle length (PCL; in ms) for alternans onset (PLCC) (3, 11, 14). However, in this study, we propose two new parameters, which we term the alternans vulnerable window (AVW) and spatially discordant vulnerable window (AVWD), and experimentally demonstrate the relationship between these windows to alternans incidence, spatially discordant alternans incidence, and the propensity for spiral wave formation.
Additionally, computational models are a powerful approach to gain insight into mechanisms for alternans generation (9, 18, 27, 28). However, for a given simulation with fixed parameters, the incidence of alternans is deterministic. We used a model of the canine ventricular myocyte with physiological random variation to simulate a cell population to determine how AVW depends on Ca2+ cycling and repolarizing currents and its relationship with the incidence of alternans. Based on the modeling results, we conducted additional experiments using an ATP-sensitive K+ channel agonist to test for increased alternans, spatial discordance, and spiral wave incidence. Finally, we present a theoretical model that relates the incidence of alternans to the vulnerable window we have defined.
METHODS
The use of animals in these studies conformed with the American Physiological Society's “Guiding Principles in the Care and Use of Animals” and with the National Institutes of Health's Guide for the Care and Use of Laboratory Animals (1996). The animal protocol used was approved by the Johns Hopkins Animal Care and Use Committee.
An expanded methods section is available in the Supplemental Material.1 In brief, freshly isolated NRVMs were plated onto coverslips and cultured to form confluent monolayers. Optical mapping of voltage or Ca2+ was performed as previously described (24). For increased spatial resolution, Ca2+ mapping was also performed using an electron multiplying charged-coupled device camera (iXon+ 860, Andor Technology, Belfast, Ireland). Monolayers were mapped at three experimental conditions: physiological temperature (35–37°C), room temperature (24–26°C), or cold temperature (18–20°C). For voltage (or Ca2+) mapping, cell monolayers were stained during (or before) the experiment with 10 μM di-4-ANEPPS (or 5 μM Rhod-2 AM), a fluorescent voltage (or Ca2+)-sensitive dye, and then continually superfused with dye-free Tyrode solution. The ATP-sensitive K+ channel agonist pinacidil (50 μM) was added to a subset of monolayers at room and physiological temperatures.
Point stimulation was applied near the edge of the monolayer using either single-step or decremental pacing. For single-step pacing, 1.5× threshold pulses were applied at a constant PCL starting from rest. For decremental pacing, PCL was shorted by a step size of 20 ms for 10 beats/step starting from a PCL baseline of 340 ms (for physiological and room temperatures) or 600 ms (for cold temperature). PCL was shortened until MCL was reached, which was determined either by the loss of 1:1 or 2:2 capture or by the appearance of wavebreaks or spiral waves. PCL for the onset of concordant alternans and 2:2 response (PCLC) was defined when the average alternans across the entire monolayer became >10% amplitude for Cai2+ alternans or 5-ms duration for APD alternans. PCL for the onset of discordant alternans (PCLD) was determined by the appearance of two distinct out-of-phase regions, each having alternans exceeding the Ca2+ or voltage thresholds just described. Monolayers were categorized as either A when alternans (defined as the occurrence of a 2:2 response) was induced or NA monolayers when alternans was not induced. A monolayers were further categorized as either AC or AD if spatially concordant (but not discordant) or spatially discordant alternans was elicited, respectively. We defined AVW as the range of PCLs between PCLC and MCL. Similarly, AVWD was defined as the range of PCLs between PCLD and MCL.
The temperature sensitivity of electrical parameters was determined by the calculation of Q10 (unitless), which conveys temperature dependence by the following formula:
| (1) |
where PT is the value of the parameter at temperature T and Pref is the value of the parameter at a reference temperature of 20°C (293 K). Q10 values were determined from a linear regression of the following logarithm-transformed relation (19):
| (2) |
The computation of APD, Ca2+ transient duration (CTD; in ms), conduction velocity, electrical and Ca2+ wavelength, and alternans maps for Cai2+, APD, conduction velocity, and cycle length are described in the Supplemental Material. Average data values are given as means ± SE. Two-sample Student's t-tests were performed to determine statistically significant differences. P values of <0.05 were considered significant.
Computational modeling simulations of a single cell were performed using the Shiferaw-Fox canine model (20). For a given simulation with fixed parameters, the incidence of alternans (as well as PCLC and MCL) is deterministic. To simulate the probabilistic nature of alternans (akin to the experiments), the Ca2+-dependent inactivation parameter (γ) of the L-type Ca2+ channel, which, when varied, alters voltage-Ca2+ coupling, was randomly chosen from a Gaussian distribution, with a mean of 1 and a SD of 0.2. A value of 0.7 (or 1.5) for γ results in positive (or negative) coupling (20). Over the range of subspace Ca2+ concentration values in our simulations, the chosen distribution for γ resulted in Ca2+-dependent inactivation levels varying by 5–15%, consistent with previously published variations in the levels for L-type Ca2+ channels (4).
Alternans incidence and AVW were altered by varying the sensitivity of SR Ca2+ release to SR load (i.e., the gain; u) and the relative weight of K+ ionic current (wK). For a given set of parameters (u, wK), 50 simulations were run, with each simulation having a different value of randomly chosen γ. Cells were categorized as either NA or A when no alternans or alternans was induced, respectively. MCL was measured for both groups, and PCLC was determined for A cells. Cai2+ (and APD) alternans thresholds were increased to 16% amplitude (and 7-ms duration) for the determination of PCLC in the simulations to reduce the overall alternans incidence and widen the range of variables that resulted in a fractional incidence.
RESULTS
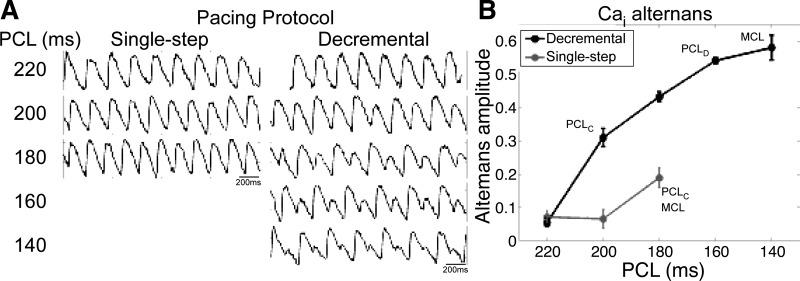
The first step in this study was to establish the baseline incidence of alternans in our NRVM monolayers. At physiological temperature, neither single-step nor decremental pacing induced APD or Cai2+ alternans (n = 23 for APD and n = 15 for Cai2+). However, when the temperature was lowered to room temperature, small-amplitude alternans was induced by single-step pacing (Fig. 1). Decremental pacing induced even larger and more robust Cai2+ and APD alternans and reduced MCL to shorter PCLs. Out of a subset of monolayers mapped using both pacing conditions, decremental pacing significantly shortened MCL by an average of 44 ± 5 ms (n = 18). Furthermore, decremental pacing, but not single-step pacing, induced alternans in 7 of 18 monolayers. In the remaining 11 of 18 monolayers, alternans was induced by both pacing protocols, although decremental pacing induced a significantly wider AVW (average widening of 31 ± 6 ms) and a greater incidence of spatially discordant alternans (6 of 11 vs. 1 of 11 monolayers). Because decremental pacing induced alternans more frequently, this pacing condition was used for the remainder of the experiments in this study.
Fig. 1.
Alternans after single-step or decremental pacing. A: Ca2+ transient signals were recorded at a site ∼2 mm from the pacing site at different pacing cycle lengths (PCLs) after either single-step or decremental pacing. B: intracellular Ca2+ [Cai2+ (Cai)] alternans amplitude as a function of PCL. Cai2+ alternans amplitude at the recording site was averaged over six beats at each PCL. PCLC and PCLD, spatially concordant and spatially discordant alternans onset PCL, respectively; MCL, minimum cycle length for loss of 1:1 or 2:2 capture.
Cai2+ and APD alternans at lowered temperature.
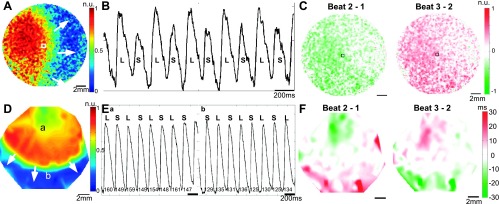
At lowered temperature and after decremental pacing, Cai2+ alternans was observed frequently and with an easily measurable amplitude. A representative Cai2+ mapping experiment is shown in Fig. 2, A–C. The monolayer was cooled to room temperature and paced near the left edge at a PCL of 180 ms (Fig. 2A). A representative trace from near the center of the monolayer showing the typical large-small alternation in the Ca2+ transient amplitude is shown in Fig. 2B. In this example, alternans is spatially concordant, and the alternans amplitude is largest near the pacing site (Fig. 2C).
Fig. 2.
Cai2+ and action potential duration (APD) alternans. A: Ca2+ map of paced propagation. Scale is in normalized fluorescence units (n.u.). B: representative Ca2+ transient signal at the site denoted by the square in A. Large (L) and small (S) transient amplitudes are labeled on the trace. C: Cai2+ alternans map showing spatially concordant alternans. Scale is in fraction of normalized fluorescence (0–1). D: voltage map of paced propagation in a different monolayer. E: representative voltage traces from sites a and b in D. APDs are labeled on the traces, showing out-of-phase long-short alternations. F: APD alternans map showing spatially discordant alternans.
Lowered temperature also facilitated the occurrence of APD alternans. A representative voltage experiment is shown in Fig. 2, D–F. The monolayer was cooled to room temperature and paced near the top edge at a PCL of 220 ms (Fig. 2D). In this example, APD alternans is spatially discordant. A representative trace proximal (or distal) to the pacing site showing the typical long-short (or short-long) alternation in APD is shown in Fig. 2E. The nodal line region in the center of the monolayer showing no alternation in APD is shown in Fig. 2F. A representative example of alternans in both conduction velocity and cycle length is shown in the Supplemental Material (Supplemental Fig. S1).
AVW.
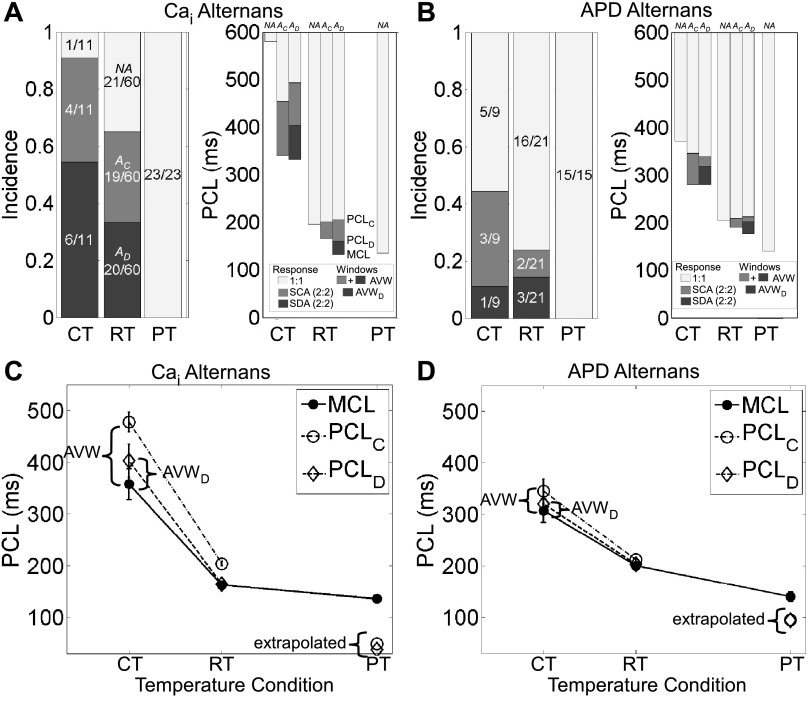
Given that alternans appears at lowered temperature, how do key parameters such as MCL, PCLC, and PCLD change with temperature and relate to the incidence of alternans? Decreasing temperature increased the incidence of Cai2+ and APD alternans (i.e., a larger proportion of A monolayers) and the incidence of spatially discordant Cai2+ alternans (i.e., a larger proportion of AD monolayers; Fig. 3, A, left, and B, left). Lowered temperature also increased PCLC, PCLD, and MCL significantly but in a way such that the differences between PCLC and MCL and between PCLD and MCL widened for both Cai2+ and APD alternans (Fig. 3, C and D, and Supplemental Tables S2 and S3). These results provided the rationale to identify the former difference as AVW and the latter difference as AVWD.
Fig. 3.
Summary of Cai2+ and APD alternans at different temperature conditions. A and B: Cai2+ alternans (A) and APD alternans (B) at physiological temperature (PT), room temperature (RT), and cold temperature (CT). Left: light shaded regions show the incidence of monolayers with no alternans (NA monolayers), medium shaded regions show the incidence of monolayers with spatially concordant alternans (AC monolayers), and dark shaded regions show the incidence of monolayers with spatially discordant alternans (AD monolayers). Values in bars are numbers of monolayers. Right: plot of PCL showing the transitions from the window of 1:1 response (light shaded regions) to the windows of 2:2 response, consisting of regions of spatially concordant alternans (SCA; medium shaded regions) and spatially discordant alternans (SDA; dark shaded regions). These regions, in turn, define the alternans vulnerable window (AVW; medium and dark shaded regions together) and spatially discordant alternans vulnerable window (AVWD; dark shaded region). Error bars are not shown but are given in Supplemental Tables S1–S3. C and D: plots of mean PCLC, PCLD, and MCL for Cai2+ (C) and APD (D) alternans. Solid lines connect measured values of MCL, and dashed lines connect measured values of PCLC and PCLD. Extrapolated values for PCLC and PCLD, determined from Q10 values and Eq. 1, are plotted for PT. Error bars show SEs.
To quantify the temperature sensitivity of the alternans parameters, Q10 values for APD, CTD, and MCL were computed using average values from all monolayers at the three temperature conditions, and Q10 values for PCLC and PCLD were computed using their average values at cold and room temperature (Table 1). For both APD and Cai2+ alternans, PCLC and PCLD had larger Q10 values and increased with greater temperature sensitivity than MCL as temperature was lowered. Because alternans was not observed at physiological temperature, PCLC and PCLD are not measurable for this temperature condition. However, from the Q10 values, it was possible to use Eq. 1 to extrapolate their expected values, and at physiological temperature, both values were less than MCL (Fig. 3, C and D, and Supplemental Table S1), consistent with the finding of no alternans (Fig. 3, A and B, left).
Table 1.
Temperature sensitivity of alternans and functional parameters
| Intracellular Ca2+ Alternans |
APD Alternans |
|||
|---|---|---|---|---|
| Q10 | R2 | Q10 | R2 | |
| PCLC, ms | 4.13 | 1.00* | 2.25 | 1.00* |
| PCLD, ms | 4.49 | 1.00* | 2.14 | 1.00* |
| MCL, ms | 1.75 | 0.78 | 1.61 | 0.96 |
| APD/CTD, ms | 1.40 | 0.94 | 1.41 | 0.70 |
Q10 values were determined from a linear regression of Eq. 2.
Only two temperature conditions [room temperature (RT) and cold temperature (CT)] were used for this calculation, so the linear regression, by definition, will be a “perfect fit.” APD, action potential duration; PCLC and PCLD, spatially concordant and spatially discordant alternans onset pacing cycle length, respectively; MCL, minimum cycle length for loss of 1:1 or 2:2 capture.
Focusing now on when temperature was held constant, AVW was wider and PCLC was longer in AD monolayers compared with AC monolayers; however, these changes were significant only for Cai2+ experiments at room and cold temperatures (Supplemental Tables S2 and S3). MCL of AD monolayers was the shortest, followed by that for AC monolayers and then for NA monolayers, for both Cai2+ and APD experiments (Fig. 3, A, right, and B, right, and Supplemental Tables S2 and S3). The differences in MCL paralleled similar differences in APD or CTD observed for the three groups, although the differences were often small. We also measured the conduction velocity and electrical and Ca2+ wavelengths in NA, AC, and AD monolayers and did not find significant differences between the groups (data not shown). In summary, at a given temperature, alternans was associated with monolayers having wider AVW, higher PCLC, and lower MCL.
As expected, MCL was not significantly different between the Ca2+ and voltage mapping experiments at each temperature condition. However, Cai2+ alternans occurred more frequently than APD alternans, and AVW and AVWD were significantly wider for Cai2+ than for APD at both lowered temperatures.
Altering the vulnerable windows.
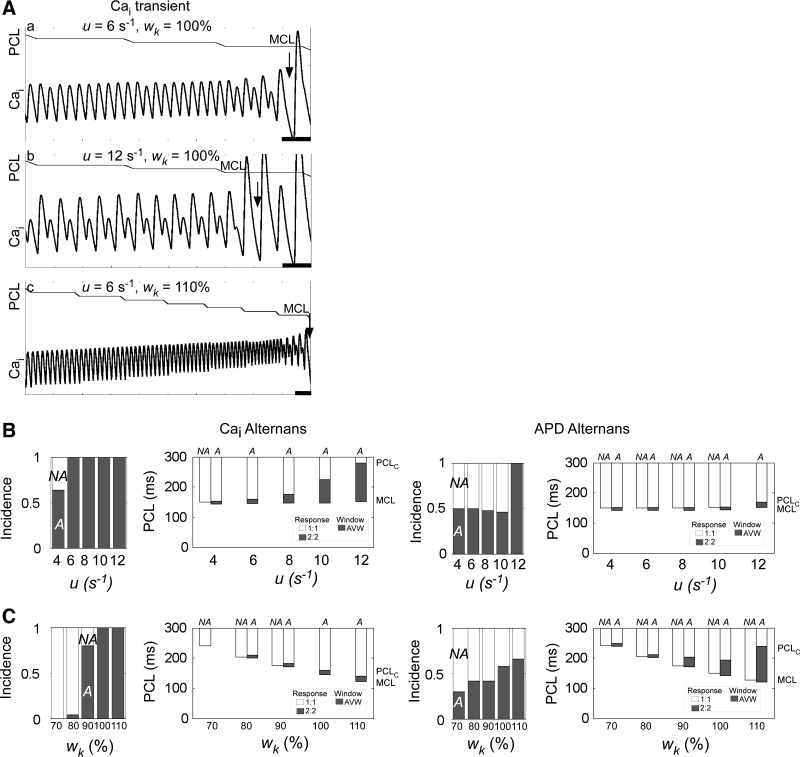
Using the Shiferaw-Fox computational model (20), we found that steepening the SR release dependence of SR load (by increasing u) led to longer PCLC, larger AVW, and larger amplitude alternans for a given PCL (Fig. 4, A,a and b), consistent with previous studies (5, 20) using this model. We also found that increasing the relative weight of the K+ current (by increasing wK) led to alternans onset at a shorter PCL, but at the same time, APD shortened, allowing pacing at shorter cycle lengths and reducing MCL. The net effect was a wider AVW despite the shorter PCLC, which enabled the induction of alternans in the range of short PCLs now made available by the reduction in MCL (Fig. 4A,c).
Fig. 4.
Alternans incidence and vulnerable window in a computational model. A: Ca2+ transients during decremental pacing to MCL for three combinations of the sensitivity of sarcoplasmic reticulum (SR) Ca2+ release to SR load (i.e., the gain; u) and the relative weight of K+ ionic current (wK). The traces at the top of a–c show PCL as a function of time. Loss of 1:1 or 2:2 capture (MCL) is shown in each trace (arrow). a–c start at the same instant of time, but c is shown for 5 s longer. Ca2+-dependent inactivation parameter of the L-type Ca2+ channel (γ) = 1.0. Scale bars = 500 ms. Transmembrane voltages were also computed and had similar results (not shown). B: effects of varying u on the incidence and onset of Cai2+ and APD alternans. Increasing u increased the incidence of Cai2+ and APD alternans (left) and also increased PCLC and, to a lesser extent, MCL, with a net effect of an overall increase in AVW (right). γ = 1.0 and wK = 100%. C: effects of varying wK on the alternans incidence and onset. Increasing wK increased the incidence of Cai2+ and APD alternans (left) and decreased MCL and, to a lesser extent, PCLC, with a net effect of an overall increase in AVW (right). u = 6 s−1. In B, right, and C, right, the left (or right) column of a given pair is average for NA [or alternans (A)] cells. In cases of 0% (or 100%) incidence of alternans, only the NA (or A) columns are shown. Error bars are not shown, but in all cases, SEs were <2 ms.
Simulations were run for a population of cells with γ chosen randomly from a Gaussian distribution, for increasing u and fixed wK or fixed u and increasing wK (see methods). Increasing u increased the incidence of Cai2+ and APD alternans (Fig. 4B, left) and increased both PCLC and MCL while widening AVW (Fig. 4B, right). Increasing wK also increased the incidence of Cai2+ and APD alternans (Fig. 4C, left) but decreased both MCL and PCLC while widening AVW (Fig. 4C, right). In both sets of simulations, for a given value of u or wK value, A cells had a shorter MCL compared with that for NA cells, consistent with our experimental findings. In summary, the computer simulations show that varying Ca2+ cycling or K+ currents can promote alternans and widen the vulnerable window whether PCLC and MCL increase or decrease.
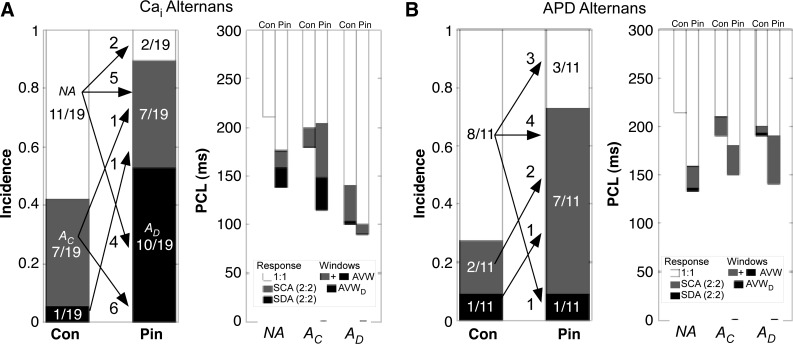
Motivated by the simulation results for increasing K+ current, we next added the ATP-sensitive K+ channel agonist pinacidil, which shortens APD and decreases MCL (2), to a subset of monolayers while keeping temperature constant. At room temperature, pinacidil significantly decreased MCL for all monolayers in Cai2+ and APD experiments by 65 ± 6 ms (n = 19) and 71 ± 10 ms (n = 11), respectively. PCLC also decreased, but by only 29 ± 9 ms (n = 8) and 23 ± 19 ms (n = 3), respectively, leading to widening of AVW. Overall, the incidence of both Cai2+ and APD alternans increased. The majority of NA monolayers became A monolayers after pinacidil treatment (Fig. 5, A, left, and B, left, and Table 2 and Supplemental Table S4). A monolayers remained as A monolayers with pinacidil, and in these monolayers, AVW widened in six of eight Cai2+ experiments (by 28 ± 14 ms overall, n = 5) and in two of three APD experiments (by 20 ± 12 ms overall, n = 3; Fig. 5, A, right, and B, right). The addition of pinacidil also increased the overall incidence of spatially discordant alternans in Cai2+ experiments (Fig. 5A, left) and widened the overall average AVWD (Fig. 5A, right).
Fig. 5.
Incidence of Cai2+ and APD alternans with pinacidil (Pin) treatment of monolayers at room temperature. A: incidence of Cai2+ alternans in control (Con) and after 15-min washin of 50 μM Pin. B: incidence of APD alternans for similar Pin treatment. Left, arrows and numbers show the fate of NA, AC, and AD monolayers with Pin exposure. Right, windows of 1:1 capture, AVW, and AVWD for NA, AC, and AD monolayers before (Con) and after the addition of Pin. In the Con columns, PCLC, PCLD, and MCL and windows of 1:1 capture, AVW, and AVWD are defined as in Fig. 3. In the Pin columns, MCL is averaged from all monolayers in the group, AVW from all A monolayers in the group, and AVWD from all AD monolayers in the group. See the Supplemental Material for further explanation. Error bars are not shown but are given in Supplemental Table S4.
Table 2.
Spiral wave incidence
| Intracellular Ca2+ Alternans |
APD Alternans |
|||||
|---|---|---|---|---|---|---|
| NA Monolayers | AC Monolayers | AD Monolayers | NA Monolayers | AC Monolayers | AD Monolayers | |
| PT | 0/23 (0%) | 0/0 | 0/0 | 0/16 (0%) | 0/0 | 0/0 |
| RT | 2/21 (10%) | 5/19 (26%) | 7/20 (35%) | 1/16 (6%) | 0/2 (0%) | 0/3 (0%) |
| CT | 0/1 (0%) | 1/4 (25%) | 4/6 (66%) | 0/5 (0%) | 1/3 (33%) | 1/1 (100%) |
| Pinacidil subset at RT | ||||||
| Control | 1/11 (9%) | 2/7 (29%) | 1/1 (100%) | 0/8 (0%) | 0/2 (0%) | 0/1 (0%) |
| Pinacidil | 0/2 (0%) | 4/7 (57%) | 8/10 (80%) | 0/3 (0%) | 1/7 (14%) | 1/1 (100%) |
Shown is the incidence of spiral wave formation at physiological temperature (PT), RT, and CT temperature, including the subset of monolayers mapped at RT before and after pinacidil treatment, for monolayers in which alternans was not induced (NA monolayers), spatially concordant alternans was induced (AC monolayers), and spatially discordant alternans was induced (AD monolayers).
At physiological temperature, pinacidil decreased MCL for all monolayers in Cai2+ and APD experiments by 28 ± 14 ms (n = 4) and 23 ± 10 ms (n = 4), respectively. However, MCL remained higher than PCLC extrapolated from our data at lower temperatures for control conditions (Fig. 3, C and D, and Supplemental Table S1), and, consistent with this finding, pinacidil did not elicit pacing-induced Cai2+ or APD alternans.
Spiral wave formation.
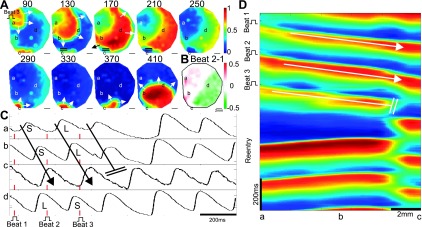
Next, we investigated the relation of spatially concordant and discordant alternans, and of AVW and AVWD, to reentrant spiral wave formation. An example of spiral wave formation is shown in Fig. 6. During Ca2+ mapping at room temperature, the monolayer was paced at 180 ms at the end of a decremental pacing sequence. Spatially discordant alternans was induced (Fig. 6B). After the last stimulus, the propagating wave failed between sites b and c, near the nodal line, seen in the Cai2+ traces from sites spanning the nodal line (Fig. 6C) and in the Cai2+ space-time plot (Fig. 6D). A spiral wave initiated when the wave propagated counterclockwise around the blocked region near site c (Fig. 6A, 170-ms image, black arrow), out of the optical mapping area (at 210–250 ms), and then reentered near site c (at 290 ms).
Fig. 6.
Spiral wave formation after spatially discordant Cai2+ alternans. A: Ca2+ map of propagation after the last beat (beat 3) before spiral wave formation. The Ca2+ wave was blocked near site c (double solid lines), propagated around the block (arrow, 170 ms) and reentered the mapping field near site c (290 ms), initiating a spiral wave. Time is in milliseconds after the beat 3 stimulus. B: Cai2+ alternans for the preceding two beats showing spatially discordant alternans. The site of propagation block falls on the nodal line. C: Cai2+ transients near the site of block and across the nodal line. Sites a–c show the direction of propagation (arrow), the site of block (double solid lines), and spiral wave formation. Site d is out of phase with sites a and b, showing spatial discordance. Large- and small-amplitude Cai2+ transients are shown. D: space-time plot, along the axis joining sites a–c, showing conduction block between sites b and c. The pulse symbol shows the stimulus site in A and the time of stimulation in C and D (along with the red lines in C).
Overall, spiral waves were generally induced by more frequently in A monolayers compared with NA monolayers at room and cold temperatures, whereas no spiral waves were induced at physiological temperature, at which no alternans was induced (Table 2). We also found that the incidence of spiral wave formation increased after the addition of pinacidil. In conclusion, for both cold and room temperature conditions, including the subset of monolayers mapped after the addition of pinacidil, spiral waves occurred more frequently in AD monolayers compared with AC monolayers.
Since spatially discordant alternans has been suggested to be a causative factor for reentry (3), we investigated the dependence of spiral wave incidence on PCLD and AVWD as well as on PCLC, MCL, and AVW (Fig. 7) in Cai2+ mapping experiments. For NA monolayers, AVW and AVWD were assigned values of 0 (and PCLC and PCLD were assigned values equal to MCL), and for AC monolayers, AVWD was set to 0 (and PCLD was set to MCL).
Fig. 7.
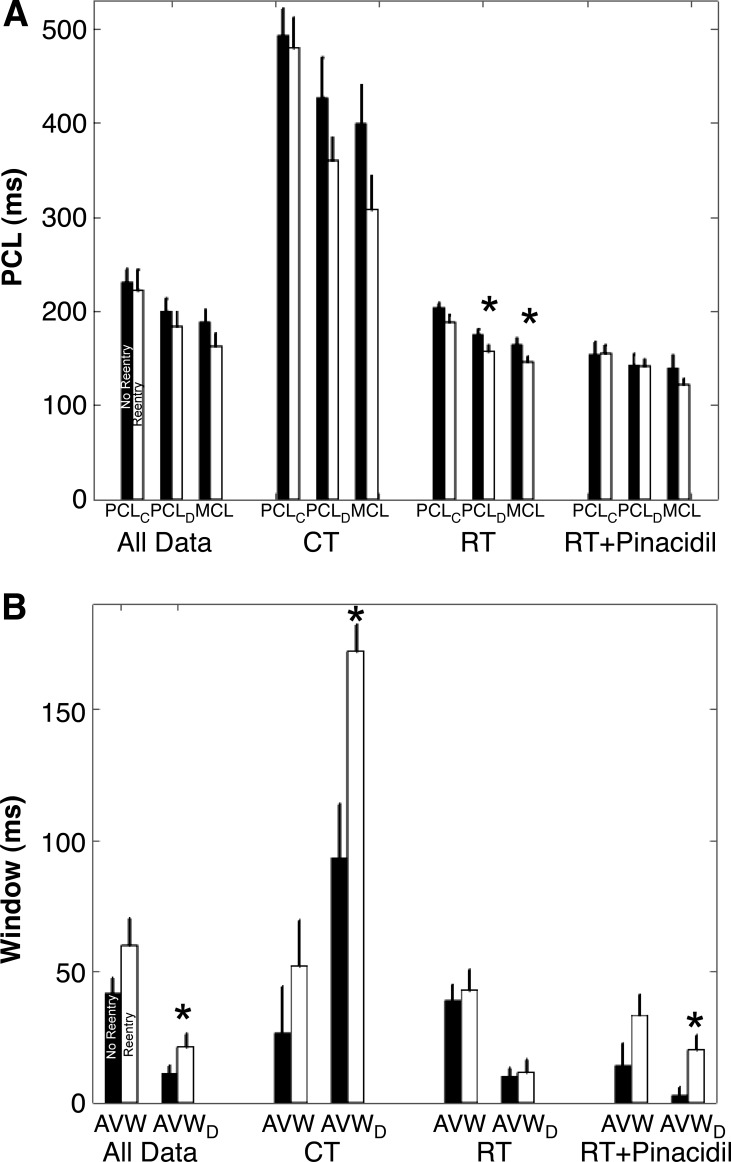
Cai2+ alternans parameters for monolayers in which spiral wave reentry did and did not occur. A: average values for PCLC, PCLD, and MCL. B: average values for AVW and AVWD. The four groups were averaged over all temperature conditions, CT, RT, and the subset of RT monolayers after the addition of Pin. Monolayers mapped at PT were not included because no alternans was induced. For each group, the average values are plotted for monolayers in which no reentry (solid bars) or reentry (open bars) occurred. Error bars show SEs. *Statistically significant difference (P < 0.05) of no reentry compared with the corresponding reentry group.
For all temperature conditions, together as well as individually, PCLC, PCLD, and MCL were shorter (Fig. 7A) and AVW and AVWD were larger (Fig. 7B) in monolayers in which spiral wave reentry occurred (reentry, open bars) compared with monolayers in which it did not (no reentry, solid bars), although in most of the conditions, these differences did not reach statistical significance. AVWD provided the best measure of reentry susceptibility, as it was the only measure to show a statistically significant difference between the two groups for multiple conditions and when all data were combined (Fig. 7B). PCLD and MCL showed a statistical difference only in the subset of monolayers at room temperature (Fig. 7A).
DISCUSSION
We have shown that the occurrence of alternans enables the measurement of a vulnerable window (AVW), which is determined as the difference between PCLC and MCL. Interventions, including lowered temperature and pinacidil treatment, alter PCLC and MCL and, subsequently, the size of the vulnerable window. Regardless of whether PCLC and MCL increased or decreased, a widened AVW accompanied an overall increase in alternans incidence. Computer simulations showed that changes in Ca2+ cycling or ionic currents can promote alternans and, at the same time, widen AVW by altering PCLC and MCL. Additionally, the difference between PCLD and MCL (AVWD) is a measurable parameter for the vulnerable window for spatially discordant alternans, which is associated with the incidence of spatially discordant alternans. Lowered temperature and the addition of pinacidil widened AVWD, which accompanied an overall increase in spiral wave formation.
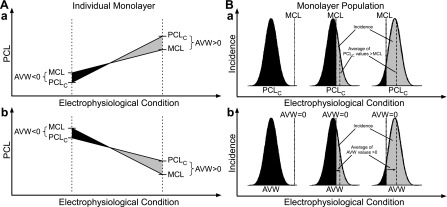
Although alternans has been characterized in the past in terms of PCLC (3, 11, 14), we found the difference between PCLC and MCL to be a more meaningful measurement. Our results are summarized by the generalized concept of the AVW in an individual monolayer (Fig. 8A). A change in a given electrophysiological condition in the system (e.g., temperature, drug concentration, ionic current amplitude, or Ca2+ cycling property) may increase or decrease both PCLC and MCL, but the sign of their relative difference, AVW, determines the occurrence of alternans. Positive AVW (Fig. 8, shaded areas) is associated with alternans, whereas negative AVW (Fig. 8, solid areas) is not. Furthermore, differences in the sensitivities of PCLC and MCL to the condition can limit the range over which AVW can occur. Our experiments and computational simulations demonstrated that the electrophysiological condition on the abscissa can be lowered temperature (Fig. 3) or increased gain of SR Ca2+ release (u; Fig. 4) when PCLC and MCL increase (Fig. 8A,a). When PCLC and MCL decrease (Fig. 8A,b), the variable can be decremental pacing (Fig. 1), increased K+ current (wK; Fig. 4), or the addition of pinacidil (Fig. 5). Furthermore, our study shows that the concept of the vulnerable window is applicable to both the neonatal rat and dog ventricle and to single cells and two-dimensional monolayers, supporting the notion that it is a general relationship.
Fig. 8.
General concept of AVW. A: AVW for an individual monolayer. If AVW, defined as PCLC − MCL, is >0 (shaded region), alternans occurs. If AVW is <0 (solid region), there is no alternans. Differential sensitivities of PCLC and MCL to an electrophysiological condition give different alternans responses at different PCLs. A, a: Case where both PCLC and MCL are increasing and where PCLC increases with greater sensitivity (slope). A, b: Case where both PCLC and MCL are decreasing, and where MCL decreases with greater sensitivity. Both cases result in AVW going from negative to positive. B: AVW for a monolayer population. B, a: For a Gaussian distribution of PCLC values, alternans will be induced in all monolayers that fall to the right of the MCL line (shaded region). The sensitivity of the PCLC distribution or MCL line to an electrophysiological condition can shift the proportion of monolayers in which alternans is induced. B, b: the same concept applies for the more general case where AVW has a Gaussian distribution, as a result of the difference between a Gaussian distribution for both PCLC and MCL, and where the AVW = 0 line separates regions of alternans (shaded region) and no alternans (solid region). A similar concept holds for PCLD, MCL, AVWD, and the incidence of spatially discordant alternans.
Relating the size of AVW to the incidence of alternans requires a consideration of the population of monolayers. For a given monolayer (or myocyte) and a specific set of conditions, a positive AVW is the only requirement for the incidence of alternans (Fig. 8A, shaded area). However, for a population of monolayers and a specific set of conditions, there will be a fractional incidence of alternans. The relationship between the alternans incidence and size of AVW is explained by the generalized concept of the AVW for a population (Fig. 8B, a). We assume that PCLC for the monolayer population has some Gaussian distribution, due to the variability of ionic currents, Ca2+ cycling, and tissue properties. We also assume that MCL is constant for the entire population, although we will loosen this requirement later. The fraction of the total area under the Gaussian curve that lies to the right of the MCL line (shaded area where PCLC > MCL and AVW > 0) represents the fractional incidence of alternans. The difference between the mean value of PCLC in this region (shaded area) and MCL is the average value of AVW. A change in a given electrophysiological condition can potentially shift the PCLC distribution to the left or the right and/or shift MCL to the left or right, thereby affecting the fractional incidence of alternans (shaded area). Any change that increases (or decreases) the fractional incidence of alternans will also increase (or decrease) the mean value of AVW. We can also consider the more general case in which MCL follows a Gaussian distribution rather than a single value (see the appendix for the mathematical proof). In this case, the difference of PCLC and MCL (AVW) also has a Gaussian distribution, and the line AVW = 0 will separate the regions of alternans (Fig. 8B, b, shaded area) and no alternans (Fig. 8B, b, solid area). A condition change that results in an increase (or decrease) in the mean value of AVW will similarly increase (or decrease) the area having positive AVW and, hence, the fractional incidence of alternans.
For the case of a single monolayer or myocyte with all electrophysiological conditions held fixed except for PCL, the discussion of a negative vulnerable window is relevant in the sense that it means that alternans is not induced under these conditions. In this case, the size of the negative window is relevant in that it serves as an index of how “far” the condition is from the bifurcation to alternans. In the context of a population of monolayers or myocytes, only positive AVW values (measured in monolayers in which alternans was induced) are used to compute the average AVW. However, by including negative AVW values as part of the population distribution, we can then define the alternans incidence (measured across all monolayers) as the fraction of positive AVWs, as described earlier. The mathematical formulation that relates average AVW and alternans incidence (presented in the appendix) depends only on the proportion of negative AWV values, and not the AVW size, and is therefore independent of the extrapolation method.
A previous study (8) has demonstrated that ischemia induces alternans through altered Ca2+ handling. During ischemia, ATP-sensitive K+ channels are open due to low levels of ATP, similar to that after the addition of pinacidil (10). Our study suggests that under these conditions, AVW may widen via changes in ionic currents and Ca2+ cycling that alter PCLC and MCL and facilitate an increased incidence of alternans. These findings are consistent with the vulnerable window concept, where the general electrophysiological condition may be the duration or severity of an ischemic episode.
We defined the vulnerable window as the PCL range between PCLC and MCL, because in the models used in our study, alternans was induced during decremental pacing at all tested PCL values below PCLC until MCL was reached. However, in some experimental and computational models, alternans amplitude first increases and then decreases as PCL decreases, demonstrating both an alternans onset and offset PCL, which occur at PCL values larger than MCL (6, 9). In these models, the concept of the AVW still applies, but with the lower bound of the window defined by the alternans offset PCL, instead of MCL.
In our study, we measured the vulnerable window as a range of PCL values. However, the vulnerable window (the variable on the ordinate axis in Fig. 8A) can be defined more generally in terms of other relevant electrophysiological conditions. Therefore, the vulnerable window can be expressed in terms of temperature, drug concentration, ionic current amplitude, Ca2+ cycling property, or other relevant variable. We also only strictly considered the vulnerable window as a function of a single variable (i.e., temperature, K+ current, or SR Ca2+ release gain). However, more generally, the vulnerable window can be considered as a range in multidimensional parameter space and a function of all electrophysiological conditions or variables.
The general concept of the vulnerable window also extends to AVWD. The interplay between PCLD and MCL governs the size of AVWD and the incidence of spatially discordant alternans in both an individual monolayer (Fig. 8A) and the monolayer population (Fig. 8B). Interventions that widen AVWD, such as lowered temperature and pinacidil, were associated with an increase in the incidence of spatially discordant alternans. Larger AVWD was found for monolayers in which reentry could be induced than in monolayers in which it could not be induced (Fig. 7). However, the mechanisms underlying the relationship between AVWD and spiral wave formation remain to be determined. We speculate that a larger AVWD allows the development of larger-amplitude alternans, steeper APD gradients, and greater chance for conduction block and spiral wave formation, because cycle lengths can become significantly shorter than PCLD.
Pastore et al. (11) previously used optical mapping at lowered temperature to study APD alternans. Our study is a comparison of alternans at physiological temperature with that at two lowered temperature conditions and provides several new insights, specifically that AVW, rather than alternans heart rate threshold (PCLC) alone, as used in the Pastore study, measures alternans susceptibility by considering both PCLC and the loss of 2:2 capture (MCL).
De Diego et al. (3) has previously showed that enhancing L-type Ca2+ channel current by Bay K8644 promotes alternans and increases the incidence of spatially discordant alternans. In their study, Bay K8644 increased the mean value of PCLC, PCLD, and MCL. A careful scrutiny of their data reveals that PCLC and PCLD both increased by a greater amount than MCL, indicating that AVW and AVWD widened in concert with the increase in alternans and incidence of spatially discordant alternans, and is consistent with our generalized concept of the vulnerable window (Fig. 8), with L-type Ca2+ current as the independent variable.
Finally, our results differ from those de Diego et al., which were also obtained from NRVM monolayers, in that we did not observe any instances of APD or Cai2+ alternans at physiological temperature, whereas they showed Cai2+ alternans in all monolayers and APD alternans in a majority of monolayers. Although our methods are similar overall, there are some electrophysiological differences that may account for the conflicting results. At 2-Hz baseline pacing, our mean APD was ∼10% longer and mean CTD was ∼14% longer (Supplemental Table S1) than theirs, consistent with a previous study (14) showing that at near physiological temperature, alternans-resistant myocytes have longer APDs compared with those of alternans-prone myocytes. Furthermore, our restitution slope, which was computed using a dynamic pacing protocol (7), was always <1 for all diastolic intervals (Supplemental Fig. S2), whereas de Diego et al. (3) reported a range of diastolic intervals in which slope was >1, revealing greater dynamic voltage instability of their monolayers. Nevertheless, the de Diego et al. results do not preclude our main findings regarding the identification of vulnerable windows in the context of alternans and spatial discordance.
Limitations.
A limitation of this study is that neonatal rat myocyte electrophysiology and Ca2+ cycling differ from those of the human, although we verified our findings in other ways with the use of a computational model based on canine electrophysiology. However, extrapolation of our results regarding alternans and spiral wave formation to human pathoelectrophysiology must await further confirmatory studies.
Our analysis of the vulnerable window as a function of some electrophysiological variable implicitly assumes that the voltage- and Ca2+-driven properties that induce alternans (i.e., that determine PCLC) and loss of complete capture (i.e., that determine MCL) are continuous functions of a common variable. As the myocyte is a complex nonlinear system, this assumption may not strictly hold for all electrophysiological conditions but does appears valid for PCL, as considered in our experimental and computational experiments, and is consistent with previous studies (16, 23) of action potential stimuli-response dynamics. PCLC and MCL are shown as monotonic functions of some electrophysiological condition (Fig. 8A) for simplicity; however, continuity is the only requirement. If either PCLC or MCL or both are nonmonotonic, AVW may first increase and then decrease (or vice versa) as a function of the electrophysiological condition (see the appendix). Alternatively, AVW may always be negative, resulting in the trivial case where no alternans is induced for any case of the varied electrophysiological condition. Regardless, the relationship between AVW and alternans incidence requires only that PCLC and MCL are continuous functions of the electrophysiological condition.
The vulnerable window strictly defines only regions of alternans with amplitude above some threshold. Therefore, the size of the vulnerable window is not necessarily correlated with the alternans amplitude. However, our study shows an association between the AVWd size and spiral wave incidence, which we suggest is related to alternans amplitude and the severity of APD gradients. Nevertheless, a more general use of both vulnerable windows as a measure of alternans severity remains to be validated. Although spatially discordant alternans appears to be an important factor that contributes to the occurrence of spiral wave reentry, it is not the only factor given that spiral wave reentry also arose in a considerable fraction of monolayers that lacked spatially discordant alternans. Furthermore, because the initiation of the spiral wave was not usually mapped in our experiments, we could not determine how initiation typically occurred.
Finally, in our experiments, Cai2+ alternans occurred more frequently than APD alternans and AVW was significantly wider for Cai2+ than for APD at both lowered temperatures, suggesting perhaps that Cai2+ alternans is driving APD alternans. However, the quantitative incidence of alternans and size of the vulnerable window is influenced by the alternans threshold, which was set near the detection limit. It is possible that undetectable APD alternans could have initiated detectable Cai2+ alternans. Therefore, we cannot draw definitive conclusions regarding whether alternans is driven by Ca2+ or voltage instabilities.
GRANTS
Funding for this work was provided by National Heart, Lung, and Blood Institute Grant R01-HL-066239.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
Supplementary Material
ACKNOWLEDGMENTS
The authors thank Brett Eaton and Susan Thompson for preparing the cell monolayer cultures.
APPENDIX: GENERALIZED CONCEPT OF AVW FOR POPULATIONS
Let us consider the more general case described, in which both PCLC and MCL have a Gaussian distribution, and, therefore, AVW also has a Gaussian distribution. To prove that an increase (or decrease) in the average size of AVW results in an increase (or decrease) in alternans incidence, we first define the probability density function [f(x)] for AVW as a Gaussian distribution with mean μ and standard deviation σ as follows:
| (A1) |
where x = AVW, N is the normal Gaussian distribution function, and μ and σ are functions of some electrophysiological condition or variable z. The proportion of positive AVW values (i.e., the alternans incidence; I) is computed by the following:
| (A2) |
The average size of AVW is equal to the expected value of the positive AVW values (W) and is computed by the following:
| (A3) |
We solve for Eqs. A2 and A3 in terms of the AVW population mean μ and standard deviation σ:
| (A4) |
| (A5) |
where erf is the error function. Both Eqs. A4 and A5 are always positive and increase with respect to an increase in μ (Supplemental Fig. S3, A and B). We then solve for the derivatives with respect to z, treating σ as a constant. By the chain rule,
| (A6) |
| (A7) |
By differentiating Eqs. A4 and A5 and combining with Eqs. A6 and A7,
| (A8) |
| (A9) |
The exponential and error functions in the left terms of the righthand side of both Eqs. A8 and A9 are always positive functions, and, therefore, the changes in alternans incidence (Eq. A8) and average AVW (Eq. A9), with respect to z, will depend on the sign of dμ/dz.
By the linear properties of Gaussian distributions, the AVW population mean μ is the difference of the PCLC population mean μP and the MCL population mean μM, as follows:
| (A10) |
| (A11) |
The existence of the derivatives in Eq. A11 assumes that μP and μM are continuous and differentiable, as functions of z. If both PCLC and MCL are monotonically increasing (with respect to z) and PCLC decreases with greater z dependence (Fig. 8A,a), or if both PCLC and MCL are monotonically decreasing (with respect to z) and MCL increases with greater z dependence (Fig. 8A,b), then dμ/dz is positive and both the alternans incidence and average AVW increase with respect to an increase in z. If dμ/dz is negative, then both the alternans incidence and average AVW decrease with respect to an increase in z. Generally, if either PCLC or MCL or both are nonmonotonic with respect to z, then alternans incidence and average AVW will both increase or decrease as dμ/dz varies as a function of z.
Using the chain rule, Eqs. A8 and A9 can be combined to determine the dependence of I on W, as follows:
| (A12) |
| (A13) |
The dependence of the alternans incidence on AVW is in fact independent of the electrophysiological variable z. Equation A13 is the ratio of two positive functions, and, therefore, I increases (or decreases) monotonically with an increase (or decrease) in W. The alternans incidence increases linearly with AVW for small values of AVW and then asymptotes to 1 for large values of AVW (Supplemental Fig. S3C).
Footnotes
Supplemental Material for this article is available at the American Journal of Physiology-Heart and Circulatory Physiology website.
REFERENCES
- 1. Adam DR, Smith JM, Akselrod S, Nyberg S, Powell AO, Cohen RJ. Fluctuations in T-wave morphology and susceptibility to ventricular fibrillation. J Electrocardiol 17: 209–218, 1984. [DOI] [PubMed] [Google Scholar]
- 2. Bian W, Tung L. Structure-related initiation of reentry by rapid pacing in monolayers of cardiac cells. Circ Res 98: e29–e38, 2006. [DOI] [PubMed] [Google Scholar]
- 3. de Diego C, Pai RK, Dave AS, Lynch A, Thu M, Chen F, Xie LH, Weiss JN, Valderrabano M. Spatially discordant alternans in cardiomyocyte monolayers. Am J Physiol Heart Circ Physiol 294: H1417–H1425, 2008. [DOI] [PubMed] [Google Scholar]
- 4. de Leon M, Wang Y, Jones L, Perez-Reyes E, Wei X, Soong TW, Snutch TP, Yue DT. Essential Ca2+-binding motif for Ca2+-sensitive inactivation of L-type Ca2+ channels. Science 270: 1502–1506, 1995. [DOI] [PubMed] [Google Scholar]
- 5. Hayashi H, Shiferaw Y, Sato D, Nihei M, Lin SF, Chen PS, Garfinkel A, Weiss JN, Qu Z. Dynamic origin of spatially discordant alternans in cardiac tissue. Biophys J 92: 448–460, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Hua F, Gilmour RF., Jr Contribution of IKr to rate-dependent action potential dynamics in canine endocardium. Circ Res 94: 810–819, 2004. [DOI] [PubMed] [Google Scholar]
- 7. Kalb SS, Dobrovolny HM, Tolkacheva EG, Idriss SF, Krassowska W, Gauthier DJ. The restitution portrait: a new method for investigating rate-dependent restitution. J Cardiovasc Electrophysiol 15: 698–709, 2004. [DOI] [PubMed] [Google Scholar]
- 8. Kapur S, Wasserstrom JA, Kelly JE, Kadish AH, Aistrup GL. Acidosis and ischemia increase cellular Ca2+ transient alternans and repolarization alternans susceptibility in the intact rat heart. Am J Physiol Heart Circ Physiol 296: H1491–H1512, 2009. [DOI] [PubMed] [Google Scholar]
- 9. Livshitz LM, Rudy Y. Regulation of Ca2+ and electrical alternans in cardiac myocytes: role of CAMKII and repolarizing currents. Am J Physiol Heart Circ Physiol 292: H2854–H2866, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Noma A. ATP-regulated K+ channels in cardiac muscle. Nature 305: 147–148, 1983. [DOI] [PubMed] [Google Scholar]
- 11. Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation 99: 1385–1394, 1999. [DOI] [PubMed] [Google Scholar]
- 12. Pastore JM, Laurita KR, Rosenbaum DS. Importance of spatiotemporal heterogeneity of cellular restitution in mechanism of arrhythmogenic discordant alternans. Heart Rhythm 3: 711–719, 2006. [DOI] [PubMed] [Google Scholar]
- 13. Pham Q, Quan KJ, Rosenbaum DS. T-wave alternans: marker, mechanism, and methodology for predicting sudden cardiac death. J Electrocardiol 36, Suppl: 75–81, 2003. [DOI] [PubMed] [Google Scholar]
- 14. Pruvot EJ, Katra RP, Rosenbaum DS, Laurita KR. Role of calcium cycling versus restitution in the mechanism of repolarization alternans. Circ Res 94: 1083–1090, 2004. [DOI] [PubMed] [Google Scholar]
- 15. Puglisi JL, Bassani RA, Bassani JW, Amin JN, Bers DM. Temperature and relative contributions of Ca transport systems in cardiac myocyte relaxation. Am J Physiol Heart Circ Physiol 270: H1772–H1778, 1996. [DOI] [PubMed] [Google Scholar]
- 16. Qu Z. Dynamical effects of diffusive cell coupling on cardiac excitation and propagation: a simulation study. Am J Physiol Heart Circ Physiol 287: H2803–H2812, 2004. [DOI] [PubMed] [Google Scholar]
- 17. Qu Z, Garfinkel A, Chen PS, Weiss JN. Mechanisms of discordant alternans and induction of reentry in simulated cardiac tissue. Circulation 102: 1664–1670, 2000. [DOI] [PubMed] [Google Scholar]
- 18. Sato D, Shiferaw Y, Qu Z, Garfinkel A, Weiss JN, Karma A. Inferring the cellular origin of voltage and calcium alternans from the spatial scales of phase reversal during discordant alternans. Biophys J 92: L33–L35, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Shah U, Bien H, Entcheva E. Cardiac arrhythmogenesis and temperature. Conf Proc IEEE Eng Med Biol Soc 1: 841–844, 2006. [DOI] [PubMed] [Google Scholar]
- 20. Shiferaw Y, Sato D, Karma A. Coupled dynamics of voltage and calcium in paced cardiac cells. Phys Rev E Stat Nonlin Soft Matter Phys 71: 021903, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Shutt RH, Howlett SE. Hypothermia increases the gain of excitation-contraction coupling in guinea pig ventricular myocytes. Am J Physiol Cell Physiol 295: C692–C700, 2008. [DOI] [PubMed] [Google Scholar]
- 22. Spear JF, Moore EN. A comparison of alternation in myocardial action potentials and contractility. Am J Physiol 220: 1708–1716, 1971. [DOI] [PubMed] [Google Scholar]
- 23. Vinet A, Chialvo DR, Michaels DC, Jalife J. Nonlinear dynamics of rate-dependent activation in models of single cardiac cells. Circ Res 67: 1510–1524, 1990. [DOI] [PubMed] [Google Scholar]
- 24. Weinberg S, Lipke EA, Tung L. In vitro electrophysiological mapping of stem cells. In: Stem Cells for Myocardial Regeneration: Methods and Protocols. Methods in Molecular Biology, edited by Lee RJ. Clifton, NJ: Humana, 2010. [DOI] [PubMed] [Google Scholar]
- 25. Weiss JN, Karma A, Shiferaw Y, Chen PS, Garfinkel A, Qu Z. From pulsus to pulseless: the saga of cardiac alternans. Circ Res 98: 1244–1253, 2006. [DOI] [PubMed] [Google Scholar]
- 26. Weiss JN, Qu Z, Chen PS, Lin SF, Karagueuzian HS, Hayashi H, Garfinkel A, Karma A. The dynamics of cardiac fibrillation. Circulation 112: 1232–1240, 2005. [DOI] [PubMed] [Google Scholar]
- 27. Xie LH, Sato D, Garfinkel A, Qu Z, Weiss JN. Intracellular Ca alternans: coordinated regulation by sarcoplasmic reticulum release, uptake, and leak. Biophys J 95: 3100–3110, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Xie Y, Garfinkel A, Weiss JN, Qu Z. Cardiac alternans induced by fibroblast-myocyte coupling: mechanistic insights from computational models. Am J Physiol Heart Circ Physiol 297: H775–H784, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.