Effects of region and sex on the mechanical properties of the glenohumeral capsule during uniaxial extension

Abstract

Surgical repair of the glenohumeral capsule after dislocation ignores regional boundaries of the capsule and is not sex specific. However, each region of the capsule functions to stabilize the joint in different positions, and differences in joint laxity between men and women have been found. The objectives of this research were to determine the effects of region (axillary pouch and posterior capsule) and sex on the material properties of the glenohumeral capsule. Boundary conditions derived from experiments were used to create finite-element models that applied tensile deformations to tissue samples from the capsule. The material coefficients of a hyperelastic constitutive model were determined via inverse finite-element optimization, which minimized the difference between the experimental and finite-element model-predicted load-elongation curve. These coefficients were then used to create stress-stretch curves representing the material properties of the capsule regions for each sex in response to uniaxial extension. For the axillary pouch, the C₁ (men: 0.28 ± 0.39 MPa and women: 0.23 ± 0.12 MPa) and C₂ (men: 8.2 ± 4.1 and women: 7.7 ± 3.0) material coefficients differed between men and women by only 0.05 MPa and 0.5, respectively. Similarly, the posterior capsule coefficients differed by 0.15 MPa (male: 0.49 ± 0.26 MPa and female: 0.34 ± 0.20 MPa) and 0.6 (male: 7.8 ± 2.9 and female: 7.2 ± 3.0), respectively. No differences could be detected in the material coefficients between regions or sexes. As a result, surgeons may not need to consider region- and sex-specific surgical repair techniques. Furthermore, finite-element models of the glenohumeral joint may not need region- or sex-specific material coefficients when using this constitutive model.

the glenohumeral joint is the most commonly dislocated major joint in the human body, and ∼80% of these dislocations occur in the anterior direction (10). Dislocations occur across all ages and both sexes; however, treatment options that have been developed in an attempt to restore normal joint function do not account for these variables. After surgical repair, return to normal joint function continues to be a problem (3, 37) with unsatisfactory results in 20–25% of patients. Furthermore, up to 23% of patients may need additional surgical repair (23). These repair techniques, which involve plicating and/or shifting excessively stretched capsular tissue in an attempt to restore normal joint stability, are subjective and ignore commonly defined regional boundaries of the capsule as well as other patient-specific information such as sex.

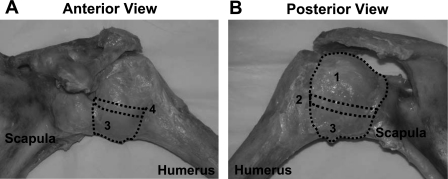
The glenohumeral capsule is a complex sheet of tissue composed of several regions [superior glenohumeral ligament, middle glenohumeral ligament, anterior and posterior bands of the inferior glenohumeral ligament (AB-IGHL and PG-IGHL, respectively), axillary pouch, and posterior capsule] that function collectively to stabilize the joint in extreme ranges of motion (Fig. 1) (15, 41). The thickness of the capsule can vary by 1 mm between regions and over 2 mm between subjects (1, 4, 49). The axillary pouch and posterior capsule are the two largest regions, and both stabilize the joint in different positions. The axillary pouch stabilizes the joint during external rotation and is commonly injured during anterior dislocation (24, 26, 32, 33, 48). The posterior capsule stabilizes the joint during internal rotation (42) and is responsible for the decreased internal rotation in throwing athletes (2, 18, 55). The collagen fibers of both regions do not exhibit a preferred orientation (1, 13).

Fig. 1.

Anterior (A) and posterior (B) view of the glenohumeral capsule. The following structures are shown: the posterior capsule (1), the posterior band of the inferior glenohumeral ligament (2), the axillay pouch (3), and the anterior band of the inferior glenohumeral ligament (4).

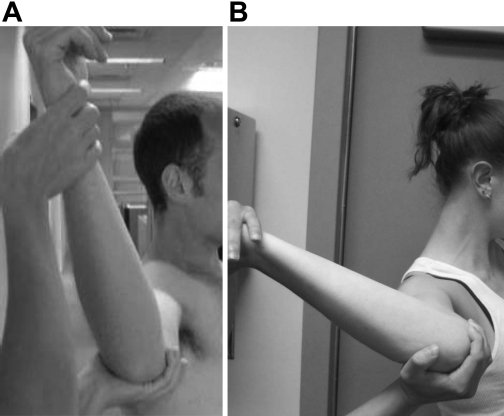
Previous studies (1, 4, 39, 40, 46) have generated conflicting results regarding the relative structural and material properties of these regions. If differences in material properties exist between regions, plicating or shifting across regions may not adequately restore normal joint function, and surgeons may need to consider region-specific repair techniques after dislocation. In addition, the possibility of differences in the material properties of the capsule as a result of sex may also have implications for surgical repair techniques. It has been suggested that increased joint translations, stiffness, and range of motion exist in women compared with men (Fig. 2); however, contradictory data have been reported (5–7, 11, 12, 28, 34, 44). This suggests that the material properties of the glenohumeral capsule between sexes should be examined. Differences in these properties may indicate that different amounts of tissue should be plicated based on patient sex as the overall joint function between sexes has been shown to be different. Therefore, the objectives of this study were to determine the effects of region (axillary pouch and posterior capsule) and sex on the material properties of the glenohumeral capsule.

Fig. 2.

Lateral views of male (A) and female (B) glenohumeral joints demonstrating the possibility of sex differences in the overall range of motion.

METHODS

A combined experimental-computational protocol was used to determine the material coefficients of the axillary pouch and posterior regions of the glenohumeral capsule in response to uniaxial extension (47). A tensile deformation was applied to each tissue sample while the clamp reaction force and clamp displacement were recorded. The tissue was subsequently rotated 90° in the clamps, and the loading protocol was repeated. These experimental data were then used in an inverse finite-element optimization routine to simulate the experimental conditions, optimizing the material coefficients of an isotropic hyperelastic constitutive model until the sum-of-squares difference between the load-elongation curves from experimental measurements and computational predictions was minimized. The optimized coefficients were then used to generate stress-stretch curves representing the response of each region to uniaxial extension for each sex.

Material testing.

Two previous studies performed in our laboratory have quantified the bidirectional material properties of the axillary pouch (40) and posterior capsule (39). Based on the tangent modulus of the axillary pouch and posterior regions, a variation of 40–86% was expected, and an effect size of 1.3 was computed. Assuming equal-sized groups and significance set at α = 0.05, a total of 10 samples/group was required to achieve power of >80%. Fresh-frozen cadaveric shoulders (20 total; 10 from women and 10 from men) were stored at −20°C and thawed for 24 h at room temperature before being tested. The protocol was approved by the University of Pittsburgh Committee for Oversight of Research Involving the Dead (CORID no. 131; the local ethics committee for the use of cadaveric tissue). The average age of the donors was 53 ± 9 yr (women: 51 ± 7 yr and men: 55 ± 10 yr). The shoulders were then dissected free of all skin and musculature. Each joint was examined using radiographs and dissection and determined to be free of pathology, osteoarthritis, and any visible signs of previous injury. The axillary pouch and posterior region of the glenohumeral capsule were identified by determining the margins of the AB-IGHL and PB-IGHL, whose locations were determined by applying distraction and external or internal rotation, respectively, to the joint. These joint positions were chosen as they are the positions in which the bands are most visible (41). Tissue samples from the axillary pouch and posterior region of the glenohumeral capsule were obtained using a cutting guide and scalpel to form square sheets (25 × 25 mm).

Tissue samples were kept hydrated using physiological saline solution throughout the entire testing protocol. The superior margin of the AB-IGHL was used as an anatomic reference for the transverse (perpendicular to the longitudinal axis of the AB-IGHL) and longitudinal (parallel to the longitudinal axis of the AB-IGHL) loading directions during mechanical testing.

Two loading conditions were used in this protocol: 1) tensile deformation applied in the direction parallel to the longitudinal axes of the AB-IGHL (longitudinal) and 2) tensile deformation applied in the direction perpendicular to the longitudinal axes of the AB-IGHL (transverse). The testing order was randomized.

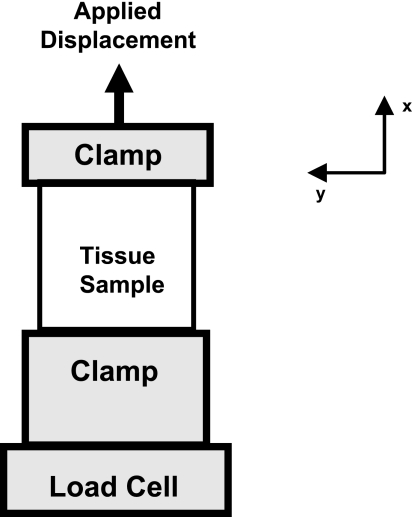
For each tensile deformation (Fig. 3), a preload of 0.5 N was applied to the tissue sample using a materials testing machine (Elf 3200, Enduratec, Eden Prairie, MN). Reaction force was measured with a load cell (Honeywell, Morristown, NJ, accuracy: ±0.1 N and resolution: ±0.05 N). Once the tissue sample was preloaded, the initial width, length, and thickness of the tissue samples were obtained using a ruler (width and length) and digital calipers (thickness). The tissue sample was then preconditioned via 10 cycles of elongation to 1.5 mm (∼10% of width) at a rate of 10 mm/min.

Fig. 3.

Mechanical testing setup for tensile elongations showing the load cell and clamp relationships.

Directly after preconditioning, a displacement of 2.25 mm (∼15% of width) was applied at a rate of 10 mm/min. This elongated the tissue well into the linear region of the stress-strain curve but did not result in tissue damage, as indicated by repeatable curves after the application of this elongation. However, tissue samples from two female specimens failed during the transverse tensile deformation of the posterior capsule. These two tissue samples were not replaced. One of these samples was much smaller compared with the other tissue samples from female specimens: the width of the sample was 55% smaller than the average width of all other female samples. Therefore, the tissue sample could not support the applied loads after being trimmed for rotation in the clamps. The thickness of the second tissue sample that failed was more than twice the average thickness of all other female samples. Even though there were no signs of previous injury based on gross appearance, the increased thickness could be indicative of a previous injury. Therefore, only 18 specimens (8 from women and 10 from men) were included in the analysis of the posterior capsule. Extensive preliminary testing was preformed to establish this testing protocol, which has been successfully used in the past (47). Tissue samples were elongated multiple times after a 30-min recovery period, which resulted in repeatable load-elongation curves. Therefore, the protocol does not result in damage of normal tissue samples.

Tissue samples were allowed to recover for 30 min, at the initial clamp-to-clamp distance, between the two loading conditions. After the recovery period, the tissue sample was removed from both clamps, and the tissue that was previously held within the clamps was carefully dissected away via scalpel transection. The opposite edges of the tissue sample were wrapped in gauze, soaked in saline, and placed in the custom clamps. The tensile deformation protocol was then repeated. The clamp reaction force, tissue sample elongation, and tissue sample geometry were recorded from each tensile deformation.

Parameter optimization.

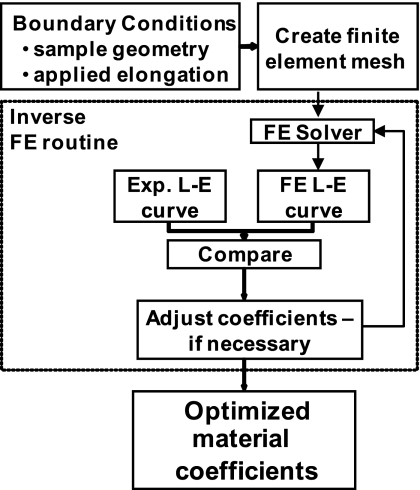
The reaction forces, elongations, and tissue sample geometry (width, thickness, and length) from both experimental loading conditions were used as boundary conditions to determine the material coefficients for an isotropic hyperelastic strain energy function via an inverse finite-element optimization technique (Fig. 4) (53). The strain energy (W) was based on the form originally used by Veronda and Westmann (52) but with an uncoupled dilatational and deviatoric response (54), as follows:

$$W=C_1[e^{C_2({\tilde{I}}_1-3)}-1]-\frac{C_1{C}_2}{2}({\tilde{I}}_2-3)+\frac{1}{2}K{[\ln (\text{J})]}^2$$ (1)

where Ĩ₁ and Ĩ₂ are the deviatoric invariants of the right Cauchy-Green deformation tensor C, 1/2K[ln(J)]² governs the dilatational response of the tissue (where J is the volume ratio), and C₁ and C₂ are the material coefficients that were determined using the inverse finite-element optimization routine, where C₁ scales the magnitude of the stress-stretch curve and C₂ governs the magnitude and nonlinearity of the stress-stretch curve. This strain energy is convex and exhibits physically reasonable behavior under tension, compression, and shear (53, 54).

Fig. 4.

Flowchart of the inverse finite-element (FE) methodology used to determine the material coefficients for the isotropic hyperelastic constitutive model. L-E curve, length-elongation curve; Exp, exponential.

An image obtained using a high-speed video camera (model 1000m, Adimec, Stoneham, MA, resolution: 1,000 × 1,000 pixels) from each loading condition with the tissue sample in the reference strain configuration, or preloaded state, was used to create a finite-element mesh by adjusting nodal points of the mesh until they were aligned with the edges of the tissue samples. Initial estimates for the material coefficients of C₁ = 0.1 MPa and C₂ = 10 were used consistently for the parameter optimization. All finite-element calculations were performed using the nonlinear, implicitly integrated code NIKE3D (30).

The inverse finite-element optimization routine used a sequential quadratic programming method (E04UNF, Numerical Algorithms Group, Oxford, UK). The NAG routine minimized a smooth objective function subject to a set of constraints on the following variables:

$$F(C_1,C_2)=\frac{1}{2}{\displaystyle \sum _{i=1}^m{\left\{y_i-f_i(C_1,C_2)\right\}}^2}$$ (2)

where F(C₁,C₂) is the objective function, y is the experimental clamp reaction force, f(C₁,C₂) is the clamp reaction force from the finite-element simulation, i represents a particular clamp displacement level, and m is the number of discrete clamp displacement levels. Eleven points were used in the present study, based on previous work performed on the medial collateral ligament (19). Both material coefficients were constrained to be >0 to ensure physically reasonable behavior and strong ellipticity but <5 MPa (C₁) or <50 (C₂) (31).

Our research group has shown that the material coefficients of the constitutive model from one tensile deformation are capable of predicting the response of the tissue to a tensile deformation in the perpendicular direction (46, 47). No differences could be detected in the material coefficients between the transverse and longitudinal tensile deformations for tissue samples from the axillary pouch and posterior capsule. Therefore, the material symmetry of both capsule regions was then represented as isotropic. Furthermore, the material coefficients of this constitutive model have been used to represent the capsule properties in three-dimensional finite-element models of the glenohumeral joint successfully (16, 38). Experimentally obtained capsule strains were compared with those predicted by the finite-element models for validation.

The material coefficients from both tensile deformations (longitudinal and transverse) for the present study were averaged to give one set of material coefficients that best described the overall response of each region. The average coefficients were then used to generate stress-stretch curves for uniaxial extension based on region and sex (male and female stress-stretch curves for uniaxial extension for each tissue sample). The stress-stretch relationship was derived from the appropriate deformation gradient tensor. For uniaxial extension and assuming incompressibility, the deformation gradient (F) and Cauchy stress (T) were as follows:

$$F=\left[\begin{array}{ccc}{\lambda }_1& 0& 0\\ 0& \frac{1}{\sqrt{{\lambda }_1}}& 0\\ 0& 0& \frac{1}{\sqrt{{\lambda }_1}}\end{array}\right]$$ (3)

$$T_{11}=\frac{C_1{C}_2({\lambda }_1-1)({\lambda }_1^2+{\lambda }_1+1)\left[2{\lambda }_1{e}^{\frac{C_2({\lambda }_1+2){({\lambda }_1-1)}^2}{{\lambda }_1}}-1\right]}{{\lambda }_1^2}$$ (4)

where λ is stretch. The stress-stretch curves were discretized into 11 points and averaged across all tissue samples. Stress-stretch curves were created for each region (axillary pouch and posterior capsule) and then further subdivided into two additional curves based on sex. Thus, a total of six average stress-stretch curves were generated.

Both statistical differences and clinically significant differences were examined in this study. Statistical differences compared the material coefficients and stress values of the stress-stretch curves using specific statistical tests with significance set at α = 0.05. A sensitivity analysis was performed to provide a measure for clinically significant differences in the material coefficients of the average stress-stretch curves. Based on the analysis, clinically significant differences were 0.3 MPa for C₁ and 3.0 for C₂. These differences resulted in a change in the material properties of the tissue, as indicated by a squared correlation coefficient of <0.9 when two stress-stretch curves were compared (46, 47).

The tissue sample geometry and material coefficients of the constitutive model for each tissue sample were not normally distributed; therefore, nonparametric statistics were performed. The tissue sample geometry of each region was compared using a Wilcoxon signed-rank test. To determine the effect of region on the material properties of the glenohumeral capsule, three comparisons were made. A single statistical comparison of the material coefficients may not be enough to reveal differences in the material properties as the constitutive model is nonlinear and the material coefficients are not linearly independent. Therefore, averaging the individual material coefficients does not yield the same stress-stretch response as averaging the individual stress-stretch curves and determining a set of average material coefficients. To thoroughly address our objective, differences in the material properties were examined in three distinct ways. The first two comparisons were statistical. The third test was for clinical significance and was based on the sensitivity analysis. First, the optimized material coefficients were compared using a Wilcoxon signed-rank test. Next, the stress values of the stress-stretch curves at each of the 11 discretized points were compared using a Freidman test with individual Wilcoxon post hoc tests. Finally, the average stress-stretch curves were fit to the stress-stretch relationship for uniaxial extension (Eq. 4) using the nonlinear Levenberg-Marquardt algorithm to obtain a set of material coefficients representing the average stress-stretch curves for each region. These material coefficients representing the average stress-stretch curves were then compared for clinical significance based on the results of the sensitivity analysis.

The tissue sample geometry was compared between sexes using a Mann-Whitney test. To determine the effect of sex on the material properties of the axillary pouch and posterior capsule, three comparisons were made within each region. First, a Mann-Whitney test was used to compare the individual material coefficients; then, a Kruskal-Wallis test was used to compare the stress values at each of the 11 discretized points representing the average stress-stretch curves. Finally, the material coefficients of the average stress-stretch curves were compared using the results of the sensitivity analysis (0.30 MPa for C₁ and 3.0 for C₂) for clinical significance.

RESULTS

Tissue sample geometry.

Statistically significant differences were found in the tissue sample geometry between capsular regions but not between sexes (Table 1). The thickness and cross-sectional area of the posterior capsule were significantly less than the axillary pouch (P < 0.001). No differences were found in the tissue sample geometry (width, thickness, and cross-sectional area) between sexes within each region. The specimen-to-specimen variation was always greater for the male tissue samples compared with the female tissue samples except for the width in the posterior capsule. In the axillary pouch, the variability in thickness and cross-sectional area were 74% and 44% greater in men compared with women, respectively. Similarly, for the posterior capsule, men exhibited 26% and 5% greater variability in thickness and cross-sectional area, respectively.

Table 1.

Tissue sample geometry for each region of the capsule under tensile elongation

	Width, mm	Thickness, mm	Cross-Sectional Area, mm2
Axillary pouch
Women	17.3 ± 1.8	1.95 ± 0.28	34.1 ± 7.7
Men	18.3 ± 2.1	2.08 ± 0.49	38.3 ± 11.1
Posterior region
Women	17.9 ± 2.1	1.29 ± 0.30	22.9 ± 5.7
Men	17.4 ± 1.3	1.10 ± 0.38	18.9 ± 5.9

Values are means ± SD.

Effects of region on material properties.

The majority of the three comparisons (material coefficients, stress-stretch curves, and material coefficients representing the average stress-stretch curves) could not find differences in the material properties of the axillary pouch and posterior capsule; however, statistically significant differences were found between the 11 discretized points of the stress-stretch curves between regions. There were no significant differences between the material properties of the axillary pouch and posterior capsule based on the optimized material coefficients of the isotropic constitutive model (Table 2). No statistically significant differences were found between regions (p = 0.07 for C₁ and 0.42 for C₂) of the capsule, and the average coefficients differed by 0.17 MPa and 0.47, respectively, between regions. In the axillary pouch, the range of both coefficients (C₁: 0.08–1.35 MPa and C₂: 2.67–13.4) was greater than in the posterior region (C₁: 0.15–0.87 MPa and C₂: 4.25–13.6) of the capsule, indicating greater specimen-to-specimen variation.

Table 2.

Material coefficients for the axillary pouch and posterior region

	C1, MPa			C2
	Women	Men	Combined	Women	Men	Combined
Axillary pouch
Average	0.23 ± 0.12	0.28 ± 0.39	0.25 ± 0.28	7.7 ± 3.0	8.2 ± 4.1	7.97 ± 3.5
Range	0.09–0.48	0.08–1.35	0.08–1.35	4.1–11.8	2.7–13.4	2.67–13.4
Posterior region
Average	0.34 ± 0.20	0.49 ± 0.26	0.42 ± 0.24	7.2 ± 3.0	7.8 ± 2.9	7.50 ± 2.9
Range	0.15–0.64	0.17–0.87	0.15–0.87	4.3–13.6	4.3–13.0	4.25–13.6

Values for averages are means ± SD. C₁ and C₂ are material coefficients.

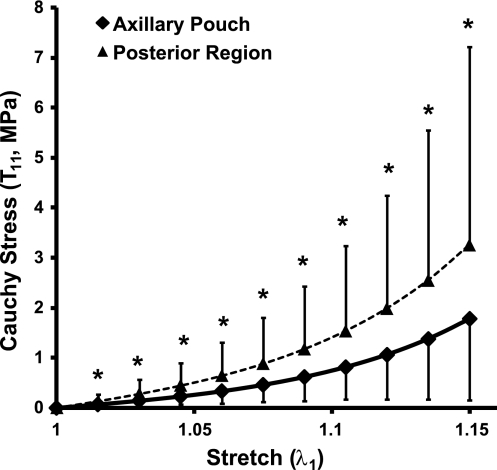
Only one comparison yielded statistically significant differences: the comparison between the 11 discretized points of the stress-stretch curves between regions (Fig. 5). The stress in the posterior capsule was 84% greater than that in the axillary pouch at a maximum stretch of λ = 1.15. However, despite these statistical differences, no clinically significant differences were found between the material coefficients representing the average stress-stretch curves for each region (Table 3). The value of the C₁ coefficient was 0.18 MPa greater in the posterior capsule than in the axillary pouch. However, the value of the C₂ coefficient was greater in the axillary pouch than in the posterior capsule by 0.8. Again, based on the criteria from our sensitivity analysis, differences of >0.3 MPa for C₁ and >3.0 for C₂ were considered significant (46, 47). Therefore, no differences in the material coefficients representing the average stress-stretch curves of each region were found.

Fig. 5.

Stress-stretch curves for the axillary pouch and posterior region under uniaxial extension. Values are means ± SD. *Statistical significance between regions.

Table 3.

Material coefficients representing the average stress-stretch curves for uniaxial extension

	Axillary Pouch			Posterior Region
	Women	Men	Combined	Women	Men	Combined
C1, MPa	0.17	0.14	0.16	0.29	0.37	0.34
C2	9.4	9.3	9.3	8.0	8.9	8.5

Effects of sex on material properties.

All three comparisons of the material properties of each capsule region between sexes yielded no significant differences. Within each region, no statistically significant differences in the optimized material coefficients were found between sexes (axillary pouch: P = 0.24 for C₁ and 0.94 for C₂ and posterior capsule: P = 0.18 for C₁ and 0.66 for C₂; Table 2). In the axillary pouch, the C₁ coefficients differed by 0.05 MPa; however, the variability was 212% greater in the tissue samples from men (range: 0.08–1.35 MPa) compared with those from women (range: 0.09–0.48 MPa). The C₂ coefficient was 37% greater in men than in women by 0.5. Again, the male tissue samples demonstrated a greater variability (range: 2.7–13.4) than tissue samples from females (range: 4.1–11.8). The posterior capsule exhibited similar results. The C₁ coefficient was 0.15 MPa greater in men than in women, and the variation was 27% greater in men (range: 0.17–0.87 MPa) compared with women (range: 0.15–0.64 MPa). For the C₂ coefficient, a difference of 0.6 existed between sexes, and the variance was almost equal (2% greater in women).

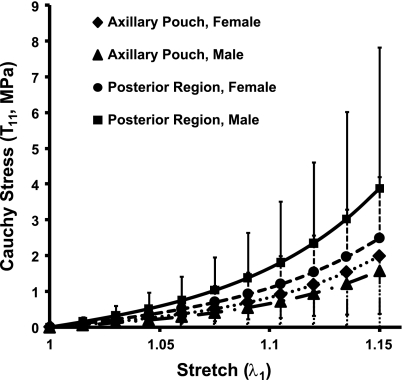
No statistically significant differences were found between sexes for either region when the stress values at each of the 11 discretized points of the stress-stretch curves for uniaxial extension were compared (Fig. 6).

Fig. 6.

Stress-stretch curves for the axillary pouch and posterior region under uniaxial extension for each sex. Values are means ± SD.

Finally, no significant differences were found between the material coefficients representing the average stress-stretch curves for the axillary pouch or posterior capsule between sexes (Table 3). The value of the C₁ material coefficient describing the response of the axillary pouch to uniaxial extension was 0.03 MPa greater in women than in men. Similarly, the C₂ coefficient was only 0.1 higher in women compared with men. For the posterior capsule, differences in both the C₁ and C₂ material coefficients, between sexes, describing the response of the posterior capsule to uniaxial extension were 0.08 MPa and 0.9, respectively. Both capsule regions exhibited differences in the material coefficients between sexes that were <0.3 MPa for C₁ and <3.0 for C₂. Therefore, no significant differences were found in the material coefficients representing the average stress-stretch curves between sexes.

DISCUSSION

In this study, a combined experimental-computational methodology was used to determine the effects of region and sex on the material properties of the axillary pouch and posterior region of the glenohumeral capsule. A hyperelastic isotropic constitutive model was used to describe the material response of each tissue sample to tensile deformations in two perpendicular directions. The effects of region and sex were evaluated by comparing 1) material coefficients for each tissue sample, 2) average stress-stretch curves, and 3) material coefficients representing the average stress-stretch curves.

Studies (9, 21, 22, 27, 35, 50, 51) examining arthroscopic plication procedures have reported anywhere from 2 to 12% recurrence; in addition, 8–9% of patients felt that they had poor outcomes, and 11% of patient have been reported to have poor joint function after surgery. Furthermore, 11–20% of patients did not return to their preoperative activity levels due to complications (21, 51). Therefore, these procedures result in inadequate outcomes, and current repair techniques can be improved. However, the majority of comparisons between the material coefficients from the axillary pouch and posterior capsule performed in this study suggest that these regions do not have different material properties. Significant differences were not found when the material coefficients for the individual tissue samples or the material coefficients representing the average stress-stretch curves were compared. These results support current repair techniques, which ignore regional boundaries of the capsule during plication. As no differences in the material properties of the capsule exist between regions, it is unlikely that plicating along regional boundaries would improve patient outcome. Therefore, other factors potentially leading to the poor patient outcome should be examined. These results further imply that in models of the glenohumeral joint, the axillary pouch and posterior capsule could be represented using the same material coefficients when using this isotropic hyperelastic constitutive model.

The results of this study further suggest that the material properties of the axillary pouch and posterior region of the glenohumeral capsule may not be dependent upon sex when characterized by an isotropic hyperelastic constitutive model. Therefore, when implementing this constitutive model in finite-element models of the glenohumeral joint, sex-specific material coefficients are not necessary. Furthermore, current surgical repair techniques do not need to alter their capsular plication or shift procedures to account for differences in sex.

No statistically significant or clinically relevant differences were found during the sex analyses. Therefore, even though differences in overall joint function (5–7, 11, 12, 28, 34, 44) and tensile properties of other ligaments and tendons (28) have been shown between sexes, sex-specific repair procedures may not improve clinical outcome when only the behavior of the tissue is considered. The tensile properties of the glenohumeral capsule cannot be directly compared with most previous studies (1, 36, 39, 40, 49), since in the present study we did not perform failure tests and used the isotropic hyperelastic constitutive model to describe the behavior of the tissue samples.

The differences in tissue sample thickness and structural properties between sexes have not been reported; however, the differences between regions found here are consistent with other findings reported in the literature. For example, a previous study (25) reported the posterior capsule (1.0 ± 0.4 mm) to be significantly thinner than the anterior (1.8 ± 0.3 mm) and inferior (1.5 ± 0.3 mm) capsule. The same study (25) also reported that the tensile strength and modulus of elasticity were significantly greater in the posterior capsule compared with the anterior and inferior capsule regions. Although the results of this study were not statistically significant, the stress in the posterior capsule was 84% greater than that in the axillary pouch at a maximum stretch of λ = 1.15. Therefore, region- and sex-specific repair techniques may still be needed to restore structural properties based on differences in tissue thickness.

In this study, the variability in the material coefficients of C₁ and C₂ was found to be 112% and 44%, respectively, for the axillary pouch and 57% and 39%, respectively, for the posterior capsule. Similar variability has been reported in material coefficients for other ligaments. For example, the variability of model parameters in the medial collateral ligament, anterior cruciate ligament, posterior cruciate ligament, and patellar tendon has been reported to range from 16% to 102%, 18% to 60%, 28% to 130%, and 19% to 104%, respectively (8, 20, 43, 45, 53).

The cadaveric specimens used in this study were from an older age group, which may not be entirely representative of the younger, athletic population commonly experiencing glenohumeral dislocation. Previous work has shown that the mechanical properties of capsular tissue decrease with age (29). Thus, the combined effect of age and sex on the material properties of the axillary pouch and posterior capsule should also be evaluated to determine if age-specific rehabilitation and repair techniques are necessary. For example, in older patients, surgeons may need to plicate the capsule less to restore structural properties appropriate for that particular age group.

Three comparisons of the material properties of the glenohumeral capsule were made between regions and sex. Post hoc power analyses were then performed on the material coefficients and the 11 stress values on the stress-stretch curves between region and sex due to the loss of 2 tissue samples. The comparisons between each region were found to have sufficient power (>80% for material coefficients and stress-stretch curves). The power of the comparisons between each sex was <80% for the material coefficients and stress-stretch curves of both capsule regions. However, a third comparison was made between the material coefficients representing the average stress-stretch curves based on our sensitivity analysis, and still no differences were detected. Therefore, despite the power of the comparisons between each sex, our results adequately provided insight into the effect of sex on the material properties of the glenohumeral capsule.

Determining the coefficients of a constitutive model is an advantage over only collecting experimental measurements since the response of the tissue sample can then be predicted for loading conditions that were not examined experimentally. Specifically, the coefficients can be input into finite-element models of the glenohumeral joint, as done previously by our research group (14, 16, 17, 38), and the response of the tissue to complex loading conditions can be examined. However, more robust constitutive models may elucidate other findings, for example, structural constitutive models could provide insight into the differences in the contributions of the ground substance and collagen fibers to the stress-strain response of the tissue between regions and/or sexes. Based on our results, region- or sex-specific techniques are unlikely to improve the current methods of plicating and shifting the capsule to restore normal joint stability. Further studies comparing the structural properties of the capsule between sexes as well as contributions from muscles and bony geometry to joint stability will provide additional insight for the improvement of treatment strategies.

GRANTS

This work was funded by National Institute of Arthritis and Musculoskeletal and Skin Diseases Grants R01-AR050218 and R01-AR047369.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).