Familial Resemblance for Loneliness

Abstract

Social isolation and loneliness in humans have been associated with physical and psychological morbidity, as well as mortality. This study aimed to assess the etiology of individual differences in feelings of loneliness. The genetic architecture of loneliness was explored in an extended twin-family design including 8,683 twins, siblings and parents from 3,911 families. In addition, 917 spouses of twins participated. The presence of assortative mating, genetic non-additivity, vertical cultural transmission, genotype–environment (GE) correlation and interaction was modeled. GE interaction was considered for several demographic characteristics. Results showed non-random mating for loneliness. We confirmed that loneliness is moderately heritable, with a significant contribution of non-additive genetic variation. There were no effects of vertical cultural transmission. With respect to demographic characteristics, results indicated that marriage, having offspring, more years of education, and a higher number of siblings are associated with lower levels of loneliness. Interestingly, these effects tended to be stronger for men than women. There was little evidence of changes in genetic architecture as a function of these characteristics. We conclude that the genetic architecture of loneliness points to non-additive genetic influences, suggesting it may be a trait that was not neutral to selection in our evolutionary past. Sociodemographic factors that influence the prevalence of loneliness do not affect its genetic architecture.

Introduction

Humans are obligatorily gregarious. The average person spends nearly 80% of waking hours in the company of others, most of which is spent in small talk (Emler 1994). Kahneman et al. (2004) used the day reconstruction method (DRM) to determine how 1,018 employed women spent their time. These workers reported spending 3.4 of their waking hours alone. Time with co-workers (5.7 h), clients (4.5 h), spouses/significant others (2.7 h), friends (2.6 h), bosses (2.4 h), and relatives (1 h) constituted the approximately 80% of the waking hours spent in the company of others. The time spent with friends, relatives, spouse, children, clients, and coworkers (but not bosses) was rated as more enjoyable than the time spent alone. Respondents indicated that their most enjoyable activities were intimate relations and socializing—activities that promote bonding and high quality relationships. Their least enjoyable activities were commuting and working. These results are consistent with survey data. When asked “what is necessary for happiness?” the majority of respondents rate “relationships with family and friends” as most important (Berscheid 1985). In a large study conducted by the National Opinion Research Center, individuals who reported having contact with five or more intimate friends in the prior 6 months were 60% more likely to report that their lives were “very happy” (Burt 1986; Myers and Diener 1995).

Social isolation is associated with broad-based morbidity and mortality (House et al. 1988). Importantly, when individuals have control over the amount of time spent alone, perceived social isolation (i.e., loneliness) is a more important predictor of adverse health outcomes than objective social isolation (i.e., time spent alone; e.g., Cole et al. 2007; Hawkley et al. 2006; Penninx et al. 1997; Seeman 2000; Sugisawa et al. 1994). In a developmental study, Caspi et al. (2006) found that loneliness in adolescence and young adulthood predicted how many cardiovascular risk factors (e.g., body mass index, waist circumference, blood pressure, cholesterol) were elevated in young adulthood.

The first scientific treatments of loneliness depicted loneliness as “a chronic distress without redeeming features” (Weiss 1973, p. 15), perhaps resulting from poor social skills (Marangoni and Ickes 1989) or a discrepancy between actual and desired social relationships (e.g., Peplau and Perlman 1982). Cacioppo and Patrick (2008) have suggested that humans are not only obligatorily gregarious, but that their survival depends on their collective abilities rather than on their individual might. Given survival depends on the inclusion and participation in a social group, there is an adaptive benefit to having a strong response (i.e., loneliness) when a member’s inclusion might be in jeopardy, just as there is a benefit to having aversive signals for other conditions critical for their survival (e.g., hunger, pain). Such an evolutionary perspective implies that individuals might inherit differing tendencies to experience loneliness. Longitudinal studies have confirmed that loneliness is stable (1 year test–retest = .75, 3 years test–retest = .70, Cacioppo et al. 2006), and adoption and twin studies have suggest that loneliness has a heritable component in children (Bartels et al. 2008; McGuire and Clifford 2000) and in adults (Boomsma et al. 2005, 2006a, 2007). The measures of loneliness in these studies have been somewhat idiosyncratic, so our first aim is to determine the heritability of loneliness using a measure developed and validated for use in large surveys and proven to be predictive of mental health outcomes in population-based studies (Hughes et al. 2004).

Secondly, we want to explore the genetic architecture of loneliness by using an extended twin-family design. Twin studies are powerful to establish whether or not genetic variation contributes to variation in complex traits, such as loneliness. The extended twin study, which includes siblings, spouses, and parents of twins (e.g., Eaves 1972; Martin et al. 1997; Boomsma et al. 2002; Maes et al. 2009) offers the possibility to test for several refinements in genetic architecture that go beyond the quantification of heritability, such as the presence of vertical cultural transmission and genotype–environment correlation. Data from additional siblings increase the statistical power to analyze genetic non-additivity and shared environment (Boomsma and Molenaar 1987; Heath et al. 1985; Posthuma and Boomsma 2000).

According to the similarity-attraction hypothesis, people are more likely to form long-term relationships with those who are similar to themselves in terms of attitudes and personality (Byrne et al. 1970). The characteristics on which similarity operates, move from obvious characteristics (e.g., physical traits, attitudes) to less obvious ones (personality, cognitive-structural similarity) as relationships develop and deepen (Neimeyer and Mitchell 1988). Loneliness reflects a reaction to the absence of intimate and social needs and influences social cognition (see Ernst and Cacioppo 1998), reactions to others (Hawkley et al. 2006), depressive symptomatology (Cacioppo et al. 2006, in press), and overall subjective well being (Cacioppo et al. 2008). Although feelings of loneliness can be transient, stable individual differences in loneliness are hypothesized to have sufficiently broad effects on social cognition, emotion, and behavior to produce similarity-based matching. i.e., positive “phenotypic” assortative mating. Another mechanism that can lead to assortment is the larger probability to meet for those individuals who share a social background and cultural environment i.e., social homogamy. These two mechanisms of mate selection have different implications for genetic analyses. An extended twin design that includes data on spouses of twins allows the possibility to test whether phenotypic assortment or social homogamy is most likely (Eaves et al. 1989; Heath and Eaves 1985; van Grootheest et al. 2008).

The influence of genetic factors does not need to be constant across age, sex, or different environments. Earlier we established that for loneliness there is little evidence for age-by-genotype or sex-by-genotype interaction. In this paper, we investigate the effects of environmental exposures, such as sociodemographic factors, on the heritability and environmental contributions to the variance of loneliness. The inclusion of these factors as moderators of heritability amounts to the study of gene–environment interaction (e.g., Boomsma and Martin 2002; Eaves 1984). Also, we explore if these environmental exposures influence the prevalence of loneliness. Prior research in population-based samples in the United States has shown that loneliness is lower the greater the education level and lower in married than in unmarried individuals (Hawkley et al. 2008; Hughes et al. 2008). We sought to replicate these findings in Dutch and Belgian twin families, and to explore other demographic predictors of loneliness. Loneliness was defined as a sum score (the sum of 3 items) and the extent to which these scores differed the modification of genetic influences as a function of sex, age and other demographic characteristics was investigated. In order to address these research questions, the loneliness items must measure the same underlying trait across groups so that group differences in the sum scores only reflect group differences with respect to loneliness. A necessary condition for this is that the questionnaire displays measurement invariance with respect to the groups under consideration (Mellenbergh 1989; Meredith 1993). We apply multiform confirmatory factor analysis to establish whether the loneliness scale is measurement invariant with respect to sex, age, marital status, twin zygosity status, parental status, twin status and country of living.

Method

Participants and procedure

Participants were registered with the Netherlands Twin Register (NTR, Boomsma et al. 2002; 2006b) or with the East Flanders Prospective Twin Survey (EFPTS, Derom et al. 2006). In 2004, twins and their parents, siblings and spouses were invited by mail to complete a survey concerning health, lifestyle, personality, and psychopathology (Distel et al. 2007). The total sample for genetic analyses comprised 8,683 twins, siblings and parents from 3,911 families. Among those, 4,818 were members of a twin pair, 817 were siblings of a twin pair, 1,350 were fathers and 1,698 were mothers of a twin pair. There were 308 brothers and 509 sisters. There were 479 families with monozygotic male twins (MZM), 278 with dizygotic males (DZM), 1,145 with monozygotic females (MZF), 617 with dizygotic females (DZF), and 728 with opposite sex twin pairs (DOS). The mean age was 34.25 for the twins (18–86, SD = 11.24), 36.90 for the siblings (16–90, SD = 11.53), and 58.01 for the parents (34–87, SD = 6.53). In addition, for the study of the mechanisms of assortment we used data from the spouses of the twins (580 male and 337 female spouses). Zygosity of same-sex Dutch twins was determined either from DNA polymorphisms or answers to validated survey questions. For Belgian twins zygosity was assessed at birth through sequential analysis based on sex, fetal membranes, umbilical cord blood groups and placental alkaline phosphatase until 1985. After that time, DNA fingerprinting was used. In case of missing or insufficient DNA information, the zygosity of the same-sex twins was based on survey items on physical twin resemblance and confusion of the twins (see Derom and Derom 2005). The Dutch and the Belgian sample are highly similar regarding loneliness scores and demographic characteristics.

Measures

Loneliness was assessed with the short scale for measuring loneliness in large surveys, developed by Hughes et al. (2004). The three items that compose this scale were selected from the R-UCLA Loneliness Scale (Russell et al. 1980): “How often do you feel left out”, “How often do you feel isolated from others”, and “How often do you feel that you lack companionship”. Response categories were: “Hardly ever” (1), “Some of the time” (2), and “Often” (3). Responses were summed, with higher scores indicating greater loneliness. Hughes et al. (2004) obtained a reliability of .72 for the Three-Item Loneliness Scale (TILS) and a correlation of .82 between the TILS and the R-UCLA scale. The scale was translated into Dutch by a professional translator and back to English by a native English speaker. The back translation was approved by one of the developers of the TILS. We collected re-test data 6 months after the original data collection from 200 unrelated individuals. The test–retest reliability for the TILS was .63.

The selection of relevant sociodemographic characteristics variables was based on previous studies on the predictors of loneliness (Hawkley et al. 2008; Hughes et al. 2008). Marital status was measured with the question “Are you currently married or do you have a durable relationship?” (“no”, “yes, living together”, and “yes, but not living together”).

The participants reported the highest educational level achieved, choosing between 4 categories, from primary education to university degree. Work status was assessed with the question: “What kind of work do you currently do?” with 8 answer categories: 1-paid work > 32 h per week, 2-paid work, 12–32 h, 3-paid work < 12 h, 4-student, 5-unemployed, 6-pension, 7-housewife/man, and 8-retired. As we were interested in the amount of time spent working, we coded category 4-student as missing; we merged categories 5–8 as unoccupied, and categories 2–3 as part-time workers. The three resulting categories were recoded so that a higher value reflected more hours of work. Finally, participants reported how many children and siblings they have.

Measurement invariance analysis

To study loneliness in different groups (e.g., twins and parents, or men and women) it must first be established that the TILS is measurement invariant (MI), meaning that given a certain level of loneliness (the factor score), individuals from different groups have the same probability of a particular response on one of the 3 items of the TILS. MI was examined in a multi-group confirmatory factor (MGCF) analysis that specified one latent factor on which the 3 items loaded. For the 3 ordinal items a threshold model was assumed with a liability distribution that separated participants into 3 categories by specifying 2 thresholds. MI was tested for sex (men–women), marital status (durable relationship—durable relationship but not living together—no durable relationship), zygosity (monozygotic–dizygotic twins), parental status (parent–non-parent), twin status (twin–non-twin), age (younger individuals (<43 years old)—older individuals (>43 years old)) and country of living (The Netherlands–Belgium).

Three types of MI were tested that form a nested hierarchy and are represented by increasing levels of cross-group equality constraints. The first level of MI is metric invariance. Metric invariance holds if the latent factor scores predict the item responses equally across groups. Metric invariance is tested by constraining the factor loadings of the 3 items to be equal across the groups under consideration (e.g., across men and women). If metric invariance holds, the next level of MI is strong factorial invariance which can be tested by imposing constraints on the thresholds. If thresholds and factor loadings are the same across groups, this means that any difference in loneliness among groups is the result of differences in the latent factor mean. The final step is to test whether differences in variances of the liability distributions of the items are only caused by differences in variances of the latent factor between the groups (strict invariance). If strict MI holds, differences in means and variances in loneliness among groups are due to a true difference on the latent factor, and not due to differences in measurement of this construct. It is then allowed to interpret differences in both means and (co)variances of the latent factor scores across groups as true differences in the latent construct (Gregorich 2006).

MI was tested in Mplus Version 5.0 using the DELTA parameterization (Muthén and Muthén 2005). The Weighted Least Squares Mean Variance adjusted (WLSMV) estimator in combination with the ‘complex’ option was used to correct for dependency among observations, which has shown to be effective in the context of family data (Rebollo et al. 2006). Since chi-squared difference tests are strongly affected by sample size and model complexity (Herzog et al. 2007; Schermelleh-Engel et al. 2003; Yu 2002), alternative goodness-of-fit indices were employed. The Root Mean Error of Approximation (RMSEA), the Tucker–Lewis Index (TLI) and the Comparative Fit Index (CFI) were shown to be adequate fit statistics for confirmatory factor analysis with ordinal data (Yu 2002). RMSEA value smaller than .05 indicate good fit, values between .05 and .08 indicate adequate fit, values between .08 and .10 mediocre fit whereas values larger than .10 are not acceptable. CFI and TLI values larger than .95 are considered as good fit (Yu 2002). More technical details about the MCGF model for ordinal data can be found in Flora and Curran (2004) or Millsap and Yun-Tein (2004).

Genetic analyses

Descriptive statistics were obtained from SPSS 14.0 (Norusis 2005). In the genetic analyses, data from monozygotic (MZ) and dizygotic (DZ) twin pairs were analyzed simultaneously with data from their parents and siblings. In the classic twin design (CTD), the difference in genetic relatedness between MZ and DZ twins, who share respectively, 100 and 50% (on average) of their segregating genes, forms the basis to estimate the amount of variance that can be ascribed to genetic and environmental factors. Genetic variance can be decomposed into additive genetic variance (A) and non-additive, or dominance, genetic variance (D). Environmental variance is decomposed as variance due to environmental factors common to family members (C), and due to environmental factors unique to the individual (E). The components C and D can not be simultaneously estimated under the CTD. Adding data from parents of the twins has been shown to reduce parameter bias and aid in distinguishing between additive and non-additive genetic effects (Heath et al. 1985; Keller and Coventry 2005; Rebollo et al. 2007). Adding data from siblings of twins increases the statistical power to detect variance due to A, C and/or D (Posthuma and Boomsma 2000). Also, the extended twin family design (ETFD) allows the consideration of assortative mating, vertical cultural transmission and the gene-environment correlation induced by simultaneous genetic and cultural transmission.

To distinguish between mechanism of assortment, i.e., phenotypic assortment or social homogamy, data from spouses of MZ and DZ twins were analyzed. According to Heath and Eaves (1985), social homogamy leads to (1) a correlation between spouses of MZ twins identical to the one between spouses of DZ twins; (2) a correlation between a twin and his cotwin’s spouse which does not differ between MZ and DZ twins; and (3) a correlation between husband and wife equal to that between a twin and his cotwin’s spouse. The presence of phenotypic assortment would be indicated by a larger correlation between husband and wife than between a twin and his cotwin’s spouse.

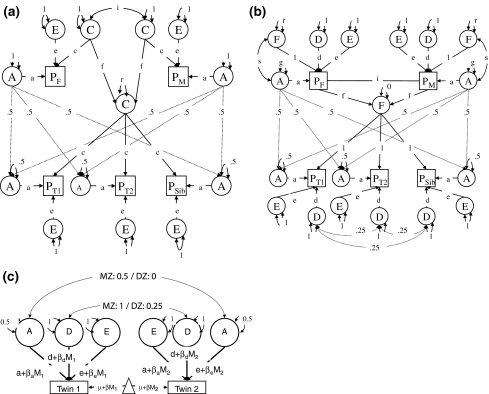
The contribution of genetic and environmental factors to the variation of loneliness was estimated, both in a model that assumed social homogamy, and in a model that assumed phenotypic assortment. For social homogamy, the model as described by Eaves et al. (1989) and depicted in Fig. 1a was fitted to the data. Here, the strength of the assortment, entirely due to cultural environment, is represented by the correlation between the C factors of the parents of the twins. The environment of the parents contributes directly (f) to the environment shared by offspring. The parameter r represents the variance of the shared environment, which does not come from the parental environment.

Fig. 1.

a Path diagram of social homogamy model. Squares represent the phenotypes of a DZ twin pair (P_T1 and P_T2) with one sibling (P_Sib), and both parents (P_F and P_M). Latent factors represent A-additive genetics, C-common environment, E-non-shared environment. Path coefficients represent r-variance due to non parental shared environment, f-cultural transmission, i-assortment. b Path diagram of phenotypic assortment model. Squares represent the phenotypes of a DZ twin pair (P_T1 and P_T2) with one sibling (P_Sib), and both parents (P_F and P_M). Latent factors represent A-additive genetic variance, D-dominance genetic variance, E-non-shared environment, and F-Vertical cultural transmission. Path coefficients represent s-gene–environment covariance, r-variance due to vertical cultural transmission, g-variance of additive genetic factors, i-assortment. c Path diagram of moderator model. β_a, β_d and β_e represent the moderating effects of the moderator (covariate) on the variance components A, D, and E, respectively. M₁ to M₂ represent the observed value on the moderator for twin 1 and twin 2. β represents the main effect of the moderator, with is included in the model for the means. μ is the intercept of the model for the means (Figure does not include the parents and sibling for simplicity)

To model phenotypic assortment, the approach described by Fulker (1982), and Neale et al. (1994) was applied which assumes spouse correlations arise through positive phenotypic assortative mating (Fig. 1b). The spouse correlation is represented in Fig. 1b by a copath (i), which represents an extrinsic correlation that influences the covariance structure of both antecedent and subsequent factors, but does not contribute to their variance (Cloninger 1980). In the CTD, cultural transmission is accounted for as C. In an ETFD cultural transmission can be distinguished from other forms of shared environment, assuming that vertical cultural transmission (VCT) from parents to offspring is based on the measured phenotype of the parents rather than on a latent variable. Non-transmissible shared environment comprises environmental conditions shared by relatives reared together within a generation (Cloninger et al. 1979). With univariate data, a model that includes both VTC and C is not identified; thus based on the pattern of correlations, we decided to assume that non-transmissible shared environment (C) was zero for loneliness. When parents transmit both genes and environment to their offspring, a passive genotype–environment correlation (s) occurs. We assume that the population is at equilibrium, and thus genetic and cultural transmission, assortative matting and gene–environment covariance are constant from generation to generation. Therefore, the parameters that represent those components in the parental generation are constrained in the model fitting as a function of the parameters of the offspring generation.

Summing up, the phenotypic variance is modeled as a function of additive (A) and dominance genetic variation (D), vertical cultural transmission (f), non-shared environment (E), and gene–environment correlation (s). The estimates incorporate the effects of assortative mating. Variance due to D is not expected to change as a product of assortative mating, under the assumption that loneliness is affected by a large number of genes (Crow and Kimura 1970, p. 156). Finally, it should be noted that under the current design D and VCT can not be estimated simultaneously, because their effects on twin and intergenerational correlations are opposite (Heath et al. 1985).

Gene–environment interaction

The second goal of this study is to explore the effects of sociodemographic factors on the prevalence and heritability of loneliness. The moderator model (see Fig. 1c) described by Purcell (2002) was applied in which the effect of a moderator is introduced on the prevalence (i.e., the main effect of the moderator), and the variance components (i.e., GE interaction effect of the moderator). Inclusion of moderator effects on the prevalence implies partialling out the effect of the moderator, after which the remaining variance is decomposed into genetic and environmental components. These variance components are allowed to vary depending on the level of the moderator. i.e., each variance components is partitioned into a part that is independent of the moderator, and a part that is a linear function of the moderator. The model thus allows for a different variance decomposition for different levels of the moderator.

General model fitting procedure

Structural equation modeling with maximum likelihood estimation of parameters was conducted. To analyze an ordinal dependent variable a threshold model was specified, in which it is assumed that the ordered categories reflect an imperfect measurement of an underlying liability distribution (Neale and Cardon 1992). From the prevalence for each category c-1 (c = number of categories) thresholds are estimated, which represent the values in the liability distribution that discriminate between categories. The scale of the latent distribution is constrained to have a mean of zero and a variance of 1. Nested models were evaluated to arrive at the best model, starting with a saturated model in which all parameter estimates (means, variances, and covariances between relatives) were allowed to vary freely. More constrained models were compared by subtracting differences in the log-likelihood (−2LL), obtaining a chi-square statistic. A non-significant p value indicates that the restricted model can be retained without a significant loss of fit. Because of the large sample size, a p value of .01 was chosen. We also used the RMSEA (Steiger 1990), the Bayesian Information Criterion (BIC, Schwarz 1978) and the Akaike Information Criterion (AIC; Akaike 1987) in selecting the best model. RMSEA is more robust to sample size and model complexity than the chi-square test (Schermelleh-Engel et al. 2003). Good models have an RMSEA of .05 or less. Models whose RMSEA is .10 or more have poor fit. BIC and AIC are information theoretic criteria designed to minimize the amount of information required to express the data and the model. Thus, those models that are the most parsimonious and efficient representations of the data are selected. Models producing smaller values of BIC and AIC can be thought of as more efficiently approximating the true model (Markon and Krueger 2004). All models included a main effect of age on the thresholds, and all genetic models also included the main effect of marital status (the moderator with the strongest main effect). All model fitting utilized the software package Mx (Neale et al. 2006).

Results

Measurement invariance

Table 1 gives prevalences of the three loneliness items in different groups of individuals. To test whether the differences in prevalence between the groups represent true differences, multiform confirmatory factor analysis was applied. Table 2 shows the results of the MI analyses. Based on the CFI and TLI, all three levels of MI hold for all groups. The RMSEA values also indicate adequate to good fit except for strict factorial invariance for the three marital status groups (.124 and .095, respectively).

Table 1.

Prevalences of the three loneliness items

	Item 1			Item 2			Item 3
	Almost never	Sometimes	Often	Almost never	Sometimes	Often	Almost never	Sometimes	Often
Men	.60	.37	.03	.71	.26	.02	.80	.18	.02
Women	.50	.44	.05	.62	.34	.04	.75	.22	.03
Not married/no durable relationship	.31	.56	.13	.56	.38	.06	.68	.27	.06
Married/durable relationship	.60	.37	.02	.68	.29	.03	.80	.18	.02
Durable relationship but not living together	.48	.47	.05	.64	.32	.04	.75	.21	.04
MZ twins	.50	.43	.07	.64	.31	.05	.77	.20	.03
DZ twins	.51	.44	.06	.66	.31	.04	.78	.18	.03
Parents	.56	.41	.03	.66	.31	.03	.75	.23	.03
Non-parents	.53	.42	.05	.65	.31	.04	.78	.19	.03
Twin	.50	.44	.06	.65	.31	.04	.77	.19	.03
Non-twin	.57	.40	.03	.66	.31	.03	.77	.21	.02
Young	.51	.44	.06	.65	.31	.04	.78	.19	.03
Old	.58	.39	.03	.66	.31	.03	.76	.22	.02
Dutch	.56	.41	.04	.66	.31	.03	.79	.19	.02
Belgian	.45	.47	.08	.62	.33	.05	.69	.27	.05

Table 2.

Model fitting results for three levels of measurement invariance

		N	χ2	df	#par	CFI	TLI	RMSEA
Men vs. women	Metric invariance	10,218	1.794	2	15	1.000	1.000	.000
	Strong factorial invariance	10,218	18.644	3	14	.999	.999	.032
	Strict factorial invariance	10,218	22.397	5	11	.999	.999	.026
Not married/no durable relationship vs. married/durable relationship vs. durable relationship but not living together	Metric invariance	9,922	9.862	5	21	1.000	1.000	.017
	Strong factorial invariance	9,922	364.624	7	19	.981	.981	.124
	Strict factorial invariance	9,922	341.988	11	13	.982	.989	.095
MZ twins vs. DZ twins	Metric invariance	4,862	1.211	2	15	1.000	1.000	.000
	Strong factorial invariance	4,862	1.630	3	14	1.000	1.000	.000
	Strict factorial invariance	4,862	5.231	5	11	1.000	1.000	.004
Parents vs. non-parents	Metric invariance	10,230	7.374	2	15	1.000	.999	.023
	Strong factorial invariance	10,230	54.931	3	14	.998	.996	.058
	Strict factorial invariance	10,230	69.745	6	11	.997	.998	.046
Twin vs. non-twin	Metric invariance	10,230	8.175	2	15	1.000	.999	.025
	Strong factorial invariance	10,230	69.304	3	14	.997	.995	.066
	Strict factorial invariance	10,230	91.457	6	11	.996	.997	.053
Young vs. old	Metric invariance	10,230	13.172	2	15	.999	.999	.033
	Strong factorial invariance	10,230	97.861	3	14	.996	.993	.079
	Strict factorial invariance	10,230	107.763	6	11	.995	.996	.058
Dutch vs. Belgian	Metric invariance	10,230	2.986	2	15	1.000	1.000	.010
	Strong factorial invariance	10,230	35.414	3	14	.998	.997	.046
	Strict factorial invariance	10,230	38.992	6	11	.998	.999	.033

N number of individuals, χ ² adjusted chi-square difference test statistic, df adjusted difference in degrees of freedom between fitted and comparison models (note that this is not simply the difference in number of free parameters), #par number of free parameters in the model, CFI comparative fit index, TLI Tucker–Lewis index, RMSEA root mean square error of approximation

Descriptive statistics

Table 3 shows the distribution for the loneliness scores and for each of the measured moderators, separately for the parent and offspring generation. The means and standard deviations for the three-item loneliness scale were very similar to those obtained by Hughes et al. (Mean = 3.89, SD = 1.34, 2004, p. 663). The fact that most people report low levels of loneliness produces a fairly skewed distribution. Analyzing this score as a continuous variable is problematic, and therefore we treated it as ordinal with 4 categories, with the first one representing low levels of loneliness.

Table 3.

Description of the sample for loneliness and demographic variables

	Offspring generation	Parental generation
Loneliness
Mean score; SD	4.18; 1.36	4.12; 1.29
Sum score of 3	40.9%	43.0%
Sum score of 4	26.5%	26.5%
Sum score of 5	13.6%	12.8%
Sum score of 6	11.8%	13.1%
Sum score of 7	3.4%	2.7%
Sum score of 8	1.5%	1.3%
Sum score of 9	1.3%	.6%
Marital status
1 Not married/no durable relationship	26.8%	6.7%
2 Married/durable relationship	62.8%	83.9%
3 Durable relationship but not living together	8.5%	3.5%
Having children
1 No	54.3%	0%
2 Yes	44.7%	100%
Educational level
1 Primary education	1.4%	7.7%
2 Low secondary	16.2%	32.4%
3 High secondary	26.7%	23.2%
4 University	51.1%	28.4%
Work status
1 Full time	46.1%	25.5%
2 Part time 12–32 h	23.0%	15.6%
3 Part time <12 h	2.6%	3.0%
4 Student	7.3%	1.3%
5 Unemployed	2.1%	16.5%
6 Pension	1.7%	15.2%
7 Housewife/man	4.7%	3.9%
8 Retired	1.2%	25.5%
Number of siblings
Mean; SD; range	2.84; 1.89; 0–15	3.64; 2.84; 0–17
1	16.1%	15.1%
2	39.8%	16.6%
3	20.7%	16.1%
4	8.6%	11.8%
5	5.7%	9.4%
6+	8.2%	21.6%

The distribution of marital status varied considerably between generations. The third category of stable relationship without cohabitance showed low endorsement. Given that the main interest is in the impact of having a stable relationship on loneliness, we merged categories 2 and 3. The variable having children showed variability only in the offspring generation, as obviously 100% of parents have children. With respect to educational level, there is a shift of the offspring generation towards a higher educational level.

Mechanism of assortment

Table 4 shows the model fitting results from testing different predictions for spouse correlations regarding the possible mechanism of assortment. At the bottom of the table, estimates of twin–spouse correlations are summarized. The estimates suggest a zygosity difference in the correlation between the twin and his co-twin’s spouse, which would suggest the presence of phenotypic assortment. However, this difference was not significant. Models 3–5 in Table 4 tested the conditions described by Heath and Eaves (1985) for the presence of social homogamy. None of the models showed a significant deterioration of the fit, implying that social homogamy is a likely mechanism of spouse resemblance for loneliness. In model 6 the overall presence of assortment was tested, and found to be significant. It should be noted that the number of spouses available by zygosity, once the data are structured in pairs was rather small (see Table 4), and the results of the model fitting procedure may be an artifact of the lack of power. Thus, we proceeded to test both models specifying phenotypic assortment and social homogamy with genetic modeling.

Table 4.

Model fitting results for the study of the mechanisms of mate selection and estimates of twin-spouse, cotwin–spouse and spouse–spouse correlations

Model	−2LL	df	Versus	χ2	Δdf	p
1 Full unconstrained	13914.247	5,722
2 Spouse–Spouse equal for MZ & DZ	13916.039	5,723	1	1.791	1	.181
3 Spouse–Spouse = 0	13916.468	5,724	2	.429	1	.512
4 Twin–cotwin’s spouse equal for MZ & DZ	13917.633	5,725	3	1.165	1	.280
5 Twin–cotwin’s spouse = husband–wife	13919.276	5,726	4	1.643	1	.199
6 Twin–cotwin’s spouse = husband–wife = 0	13930.556	5,727	5	11.274	1	<.001

	Full Model		Model 5
	MZ	DZ	MZ	DZ
Twin-own spouse	.17 (N = 476)	.17 (N = 381)	.13	.13
Twin-cotwin spouse	.12 (N = 390)	.02 (N = 260)	.13	.13
Twin spouse-cotwin spouse	−.05 (N = 79)	.24 (N = 55)	.00	.00

−2LL = −2 log-likelihood of the model, df degrees of freedom, vs versus, χ ² difference in −2 LL between nested models, Δdf difference in degrees of freedom between nested models, p p value associated with χ², MZ monozygotic, DZ dizygotic

Best fitting model indicated in bold

Saturated model

Table 5 shows the model fitting results for the saturated model. Models 2 and 3 show that thresholds for loneliness do not differ between zygosity groups or between generations. Models 4–4.2 show no sex differences in the thresholds or in the effects of age. The effect of marital status on loneliness differed significantly between men and women. Models 5.1 and 5.2, show that age and marital status affect levels of loneliness. Model 6 confirmed that assortative mating is significant for loneliness. Models 7.1–7.3 showed no sex differences in parent–offspring correlations, and models 8.1–8.3 showed no sex differences either in twin correlations. Thus, in subsequent genetic analyses parameters representing the influence of A, D and E were constrained to be the same for men and women.

Table 5.

Model fitting results from saturated model and maximum likelihood estimates for parameters (familial correlations, thresholds and regression of age and marital status on thresholds) under the best model (indicated in bold)

Model	−2LL	df	Versus	χ2	Δdf	p
1. Fully saturated	20897.068	8,651
Tests on the model for the thresholds (ts)
2. ts MZ = ts DZ	20911.400	8,657	1	14.332	6	.026
3. ts parents = ts offspring	20925.113	8,663	2	13.713	6	.030
4. ts males = ts females	20931.989	8,666	3	6.87	3	.076
4.1 βmarriage males = βmarriage females	20944.534	8,667	4	12.54	1	<.001
4.2 βage males = βage females	20935.866	8,667	4	3.87	1	.049
5.1 βage = 0	20946.444	8,668	4.2	10.57	1	.001
5.2 βmarriage = 0	21123.093	8,669	4.2	187.22	2	<.001
Tests on the correlations
6. Spouse correlation = 0	20955.396	8,668	4.2	19.53	1	<.001
7.1 Father–son = Father–daughter	20935.998	8,668	4.2	.132	1	.716
7.2 Mother–son = Mother–daughter	20936.741	8,669	7.1	.743	1	.388
7.3 Mother–offspring = Father–offspring	20938.134	8,670	7.2	.393	1	.234
8.1 MZM = MZF	20939.978	8,671	7.3	1.844	1	.174
8.2 DZM (SibMM) = DZF(SibFF)	20945.376	8,672	8.1	5.38	1	.020
8.3 DZ = OS	20945.461	8,673	8.2	.085	1	.770

Table 6 presents the estimates of the correlations from the final saturated model. Twin (rMZ = .40, rDZ = .05) and parent–offspring (rPO = .12) correlations suggest a moderate heritability, and non-additive genetic effects. The parent–offspring correlation being slightly higher than the DZ/Sibling correlation might be a result of the combination between non-additive genetic effects and assortative mating. Non-additive genetic effects result in a fast decrease of the DZ correlations (Eaves 1972), and assortative mating inflates the parent–offspring correlation to a larger extent than it does to the sibling correlation (Crow and Kimura 1970). This pattern of correlations could also be a result of vertical cultural transmission, which usually results in a greater intergenerational correlation than it would be expected under additive genetic effects (Heath et al. 1985).

Table 6.

Estimates of the correlations from the final saturated model (8.3)

	r
Monozygotic twin	.397
Dizygotic/sibling	.047
Parent–offspring	.122
Spouse	.163

The thresholds represent the cut point of a normal distribution that an individual has to achieve in order to endorse the next loneliness score, independently of the effects of the covariates. The thresholds did not differ between males and females or between parents and offspring. The β for age was estimated at .155, suggesting that older people show a higher prevalence in the lower categories, i.e., they are less lonely. The β for marital status was estimated at .239 for males and .132 for females indicating that people who are married or engaged in a stable relationship are less likely to feel lonely. This effect was stronger for men than for women.

Genetic modeling

Table 7 shows the results of the genetic model fitting. The first model assumed social homogamy. Models 2 and 3 are complementary, and estimate dominance and cultural transmission respectively, assuming phenotypic assortment. Although the chi-square of these models leads to a significant p value, the RMSEA indicates that all models provide an acceptable fit to the data. The dominance model seems to provide the best fit according to BIC and AIC. In model 4, both cultural transmission and dominance are constrained at zero. The comparison of this model against the prior two models (model 2 and 3) suggests that both dominance and cultural transmission make a significant contribution to the variance of loneliness. Model 5 and 6 indicate that additive genetic effects and assortment are significantly different from zero.

Table 7.

Genetic model fitting results and parameter estimates from social homogamy and phenotypic assortment models

Parameter	Model
	1	2	3	4	5	6
a: Additive genetic path	.545	.423	.629	.513	–	.443
c: Shared environmental patha	.059	–	–	–	–	–
d: Non-additive genetic path	–	.433	–	–	–	.418
e: Unique environmental path	.836	.793	.801	.852	1.000	.793
i: Assortative mating path	47.986	.164	.159	.152	.165	–
g: Variance of A factors	–	1.031	1.058	1.044	1.000	1.000
r: C variance (non transmitted)	.975	–	.018	–	–	–
s: Genotype–environment covariance	–	–	−.062	–	–	–
f: Cultural transmission path	.016	–	−.089	–	–	–
−2 Log likelihood	20965.81	20955.43	20959.40	20970.28	21090.90	20974.98
Degrees of freedom	8,674	8,674	8,674	8,675	8,676	8,675
Number of parameters	12	12	13	11	10	11
Root mean square error of approximation	.048	.034	.040	.041	.118	.047
				.035
Bayesian information criterion	−25,333	−25,339	−25,337	−25,335	−25,279	−25,333
Akaike information criterion	18.35	7.97	11.93	20.82	139.44	25.51
Versus	SAT	SAT	SAT	1	3	1
				2
χ2	20.351	9.978	13.939	14.844	120.618	19.541
				10.883
p value	<.001	.001	<.001	<.001	<.001	<.001
				.001

Model 1: Social homogamy model

Number of constraints included in this model = 3; the total variance in twins, the total variance in parents and the shared environmental variance in twins are constrained to equal 1

Model 2: Phenotypic assortment: Dominance model

Number of constraints included in this model = 2; the total variance is constrained to equal 1 and the parameter g in the parental generation are constrained as a function of the parameters in the offspring generation

Model 3: Phenotypic assortment: Cultural transmission model

Number of constraints included in this model = 4; the total variance is constrained to equal 1 and the parameters g, r and s in the parental generation are constrained as a function of the parameters in the offspring generation

Model 4: As model 2 + no dominance

Model 5: As model 4 + no additive genetic influences

Model 6: As model 2 + no assortative mating

^aShared environment not induced by cultural transmission

Best fitting model indicated in bold

Under social homogamy genetic differences explain 29.7% of the variance, and the remaining 70% is explained by non-shared environment. The non-parental shared environment explained a small percentage of .3%, and the parental 0%. Under phenotypic assortment, additive genetic influences explain 18% of the variance, with .5% due to assortment. Dominance explains 19% of the variance and the remaining 63% is explained by non-shared environment. Under the cultural transmission model (model 3), additive genetics would explain 42% of the variance, with 2% due to assortment. Negative cultural transmission would explain 2% of the variance, and the negative gene–environment correlation would explain 8% of the variance. A negative estimate of cultural transmission implies that parents try to educate their children in an opposite direction to their own phenotypes. Heath et al. (1985) demonstrated that, the effects of dominance tend to mask those of VCT, and thus increase the number of individuals necessary to estimate VCT. However, their simulation study showed that the current sample is sufficient to estimate an effect of cultural transmission of .3 under the presence of genetic dominance with sufficient power. Heath et al. (1985) also demonstrated that, in the absence of VCT, dominance leads to negative estimates of cultural transmission parameters, which is precisely the pattern of results encountered here. We can thus conclude with a certain level of confidence that the dominance model is the most appropriate to explain individual differences in loneliness.

Main and moderating effects of covariates

Based on the dominance model we tested the moderating effects of a series of sociodemographic covariates on the variance components of loneliness, as well as their main effects. Table 8 shows the estimates (first the main effect for men and women and then variance components and their moderation) for each of the covariates. All covariates had significant main effects on loneliness, with a tendency for stronger effects in men. Married people, with children, a higher education and a larger number of siblings are less likely to feel lonely. The work situation affects men and women in opposite directions. Men who work more feel less lonely, whereas for women the pattern is the opposite. It should be noted though that these effects are rather small. For each covariate we tested their moderating effects on the non-shared environmental variance (β_e), the variance due to dominance (β_d), and the additive genetic variance (β_a). Most moderating effects on the variance components were not significant. The moderating effects of marital status and number of siblings on the dominance component were marginally significant (p < .05 but p > .01). According to these results the proportion of variance explained by dominance would be lower for married people with a larger number of siblings.

Table 8.

Parameter estimates from full moderator models (significant estimates in bold)

	Marriage	Children	Education	Work	Siblings
βmain♂	−.181	−.113	−.029	−.013	−.059
βmain♀	−.106	−.034	.008	.019	−.022
Additive genetic	.297	−.305	.266	.348	−.268
βa	.043	−.017	.022	−.007	−.044
Dominance genetic	.367	.356	.370	.321	.331
βd	−.084	−.038	−.023	−.005	−.031
Unique environment	.566	.571	.594	.573	.589
βe	.007	.006	−.005	.003	−.003

Discussion

The present study extends the prior work on the genetics of loneliness. Firstly, we established that the instrument that was used in this study showed measurement invariance (MI) with respect to sex, age, zygosity, parental and twin status. Only for marital status, MI could not be established. Secondly, consistent with prior research, we found that loneliness is moderately heritable. A genetic model that included non-additive genetic variation provided the best fit to the data. It is likely, that loneliness has a stable trait-like component, independent of environmental situations. Individuals may inherit different sensitivities to social pain. Just as some people are sensitive to physical pain and respond more strongly to protect themselves, some people may be more sensitive to the social pain caused by real or perceived rejections. Individuals who are especially sensitive to social painful may tend to engage in self-protective cognition and behavior in interpersonal interactions which, paradoxically, results in their thinking and acting in off-putting ways. Alternatively, individuals may inherit different propensities to feel lonely given a specific social context. That is, people may differ in their propensity to extract and burn social nutrients, much like people differ in the propensity to extract and burn calories from the food they eat. Neither a high or low propensity is best in an absolute sense, each is best in different environmental conditions. Results from a recent fMRI study are consistent with this hypothesis. Participants were exposed to pleasant social pictures (e.g., a smiling couple) and equally pleasant pictures of objects (e.g., a sun setting over the ocean) while in an fMRI scanner. Individuals low in loneliness were more likely to show activation of the ventral striatum, a reward area in the limbic lobule, when viewing the pleasant social pictures than when viewing the pleasant nonsocial pictures, whereas individuals high in loneliness showed the opposite response (Cacioppo et al. 2009). It was as if individuals low in loneliness are affected more positively when exposed to people in pleasant circumstances than are individuals high in loneliness.

The presence of genetic variation due to dominance suggests that a given trait has probably not been neutral to selection (Eaves et al. 1999; Keller et al. 2005). Penke et al. (2007) demonstrate that recurring selection in different directions tends to deplete the additive genetic variance and increase the proportion of non-additive genetic variance. Thus, selection pressures on loneliness and other personality traits must vary across environments and/or across time, so that the net fitness effects are neutral if averaged. This process is known as “balancing selection” by environmental heterogeneity. This would suggest that different extremes of the continuum of loneliness might be adaptable in different kinds of environments. However, based on the present study other explanations for selection pressures cannot be excluded since there may be a survival effect present for loneliness.

Thirdly, the small but significant effect for assortive mating indicated that non-lonely individuals tend to bear children with non-lonely individuals, whereas lonely individuals tend to bear children with lonely individuals. Prior research indicates that lonely individuals are perceived more negatively than non-lonely individuals (e.g., Lau and Gruen 1992), an effect that is greater for lonely than non-lonely perceivers (Rotenberg and Kmill 1992). Lonely individuals also have more difficulty developing strong relationships with classmates than non-lonely individuals (Anderson and Martin 1995; Duck et al. 1994) and they perceive their friends as less similar to themselves than do non-lonely individuals (Bell 1993). Given lonely individuals are perceived to be less interpersonally attractive than non-lonely individuals, positive assortative mating may occur because non-lonely individuals are more likely to achieve the joint consent necessary for marriage with non-lonely individuals, leaving the relatively unpopular lonely individuals with fewer options (Nurmi et al. 1997).

We also examined predictors of loneliness. Marriage, the number of children, years of education, and the number of siblings are associated with lower levels of loneliness. Interestingly, these effects tended to be stronger for men than women. Tornstam (1992) examined the loneliness of 2,795 Swedish residents 15–80 years. As in the current study, married individuals were less lonely than unmarried individuals and this effect was stronger for men than women. Work, on the other hand, appeared to have quite different effects on men and women, with men showing lower levels of loneliness and women higher levels of loneliness when employed. The effect of age on loneliness was equal for males and females. The positive association indicated that younger individuals feel lonelier than older individuals. The literature typically shows that loneliness does not vary with age until late in life (over ages 80 or 85), when disabilities and limitations increase loneliness (Dykstra et al. 2005; Victor et al. 2005; Savikko et al. 2005; Jylhä 2004). This oldest age group is highly underrepresented in our sample in which loneliness is greatest in the young adults.

Finally, Fowler et al. (2009) provided evidence recently for the heritability of the social network attributes of transitivity (the likelihood that two of a person’s contacts are connected), centrality (the fraction of paths in a network that pass through a given individual), and in-degree (the number of times a person is named as a friend). The heritability of these network characteristics suggests the existence of intrinsic node characteristics, that is, heritable attributes and behaviors of the individuals comprising the social network. Given the present results for the heritability of loneliness and prior research showing that loneliness predisposes more negative social perception and behavior (Cacioppo and Patrick 2008), loneliness may serves as an intrinsic node characteristic underlying the heritability of social networks. For instance, Fowler et al. (2009) found the pattern network heritability was explained best by an “Attract and Introduce” model in which: (a) some individuals were inherently more likely to receive friendship nominations, and (b) some individuals are inherently more likely to introduce new friends to existing friends. As noted above, lonely individuals are identifiable by both lonely and nonlonely individuals and are liked less than nonlonely individuals (e.g., Anderson and Martin 1995), as posited in (a). If lonely individuals are also less likely to introduce new friends to existing friends, as would be expected given the effects of loneliness on social cognition (Cacioppo and Patrick 2008), then the trait of loneliness would meet both conditions specified by Fowler et al. (2009) to produce the heritability of the social network attributes they observed.

Several limitations should be kept in mind when interpreting the results of this study. Firstly, spouses may actively influence each others’ loneliness scores through marital interaction. If spouses are more similar in their loneliness scores as a function of the duration of the relationship this is not captured in the present analyses. We therefore calculated the correlation between the differences in the loneliness scores of two spouses with the duration of the relationship. Based on data from 1,091 spouse pairs a correlation of −.056 was estimated which was not significantly different from zero. It is thus unlikely that marital interaction influenced our results. A second more general limitation, related to the first one, concerns social interactions among family members. In the present study we tested for vertical cultural transmission, i.e., a direct influence of the parental phenotype on the phenotype of their offspring. However, the offspring in this study consisted of adults (mean age 35 years, SD = 11.6) so most offspring will not longer live at home with their parents. Thus, it may be that there is a direct influence of parental loneliness on offspring loneliness, but only as long as parents and offspring share the same house. The same concern applies to social interaction among siblings. Sibling interaction effects for threshold variables are indicated if there are prevalence differences between MZ and DZ twins (or siblings). Table 1 shows that there is very little evidence for such differences. Moreover, comparisons of DZ and sibling correlations showed little/no evidence for a special twin environment. Again, when interpreting the results one should keep in mind that siblings in this study do no longer share a house.

In conclusion, a relatively simply model seems to suffice to explain individual differences in loneliness. Several demographic variables including marriage, having siblings and children and educational attainment explain part of the variance in loneliness. Genetic factors, both additive and non-additive, explain about 37% of the variance. The influence of genetic factors is not modified by any these demographic traits.