Novel representation of physiologic states during critical illness and recovery

Abstract

Clinicians depend on recognizing particular critical illnesses (such as sepsis and cardiac failure) from patterns of vital signs. The relationship between a vital sign pattern and a specific condition is explored.

In the previous issue of Critical Care, Cohen and colleagues [1] offer a new approach to identifying and describing states of critical illness. The work follows a path, launched by John Siegel and colleagues [2,3] almost two decades ago, toward letting the data themselves define densely populated regions of physiologic state space that collectively represent a clinical condition. Areas of densely and of sparsely populated regions of the state space arise spontaneously from interconnections among various organ systems and their constituent tissues [4].

What Cohen and colleagues have added to the analysis are bioinformatic tools developed, applied, and validated in the service of genomic analysis. Heat maps representing relative expression and hierarchical clustering give a sense of similarity of states and their adjacencies in physiologic state space, respectively. But the report has a deeper significance that perhaps can be grasped by inspection of Figure 1.

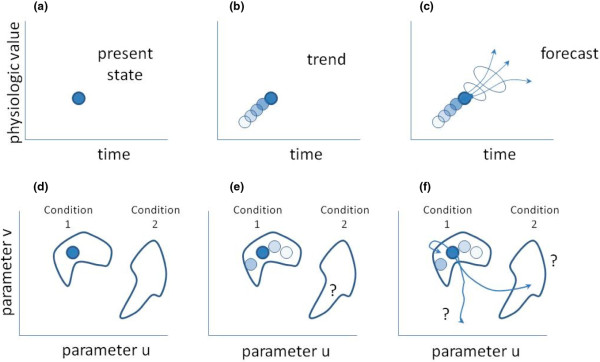
Figure 1.

Temporal evolution of physiologic state. (a-c) Conventional display; (d-f) state space representation. Panels (a-f) are defined in the text of the commentary.

When we clinicians glance up at a bedside physiologic display ('monitor') and look at the heart rate and blood pressure, we obtain the picture seen in Figure 1a. The difficulty is that the present state can be reached from many trajectories, so that the important inverse problem, namely 'what condition led to the particular values of the blood pressure and heart rate', is ill posed in the sense of Hadamard [5,6]. There are essentially an infinite number of trajectories that lead to this point. One approach to clarifying the problem is to generate a mathematical model and then ask what sort of perturbation would offer the most clarification as to the actual condition of the patient [7]. Another approach is to look backwards in time, as in Figure 1b, to see whether there is a clue concerning a trend. Either way, the question/answer that many clinicians think they wish to know is represented in Figure 1c: 'what will the patient's physiology look like at some time in the future, and what is my level of confidence in that forecast?'

What Cohen and colleagues have done is remind us that our real interest lies in Figure 1d-f. At the time of observation (Figure 1d), the patient appears to be in condition 1. Looking backwards in time (Figure 1e), one notes that the patient remains in condition 1. The question that really interests most clinicians is whether the patient will remain in condition 1, transition to condition 2, or head off in some other direction (Figure 1f). Cohen and colleagues have described the shape of the conditions ('clusters') and the distances between them. If the trend information offers a sense of the velocity (magnitude and direction!) through which the patient is moving through the space, and the space has an underlying probability density, then we can make an educated prediction about whether the patient is staying in condition 1, heading toward condition 2, or heading toward some other condition entirely. We neither need nor want to predict the state values specifically. Rather, we want to know in what cluster they will lie. That is a simpler and perhaps more tractable question than predicting precise physiologic values a minute from right now.

It would be very helpful to understand whether the topology of these clusters is general or whether it is specific to certain populations. Using this methodology, additional studies looking at similarly injured populations and also at different but equally ill populations could confirm the value of the approach. It will be interesting and especially informative to eventually tease out whether the transitions toward more favorable states follow from specific interventions or whether they arise simply as a matter of relaxing itinerancy after the underlying problem is fixed. Put differently, do we clinicians actually affect the rate of recovery, or is the best we can do a matter of giving the patient sufficient time to heal?

Competing interests

TB performs research in this field and receives funding from federal and nonfederal not-for-profit agencies to support this research. He is also President of the Society of Complexity in Acute Illness, and one of the authors of the related-research manuscript is a Program Chair for the next annual meeting.

See related research by Cohen et al., http://ccforum.com/content/14/1/R10