Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Jun 17.
Published in final edited form as: Ann Thorac Surg. 2010 May;89(5):1546–1553. doi: 10.1016/j.athoracsur.2010.02.036

The First Finite Element Model of the Left Ventricle with Mitral Valve: Insights into Ischemic Mitral Regurgitation

Jonathan F Wenk 1,2,5, Zhihong Zhang 1,5, Guangming Cheng 1,5, Deepak Malhotra 1,5, Gabriel Acevedo-Bolton 4,5, Mike Burger 6, Takamaro Suzuki 1,5, David A Saloner 4,5, Arthur W Wallace 3,5, Julius M Guccione 1,2,5, Mark B Ratcliffe 1,2,5
PMCID: PMC2887313  NIHMSID: NIHMS207713  PMID: 20417775

Abstract

Background

Left ventricular remodeling after postero-basal myocardial infarction can lead to ischemic mitral regurgitation. This occurs as a consequence of leaflet tethering due to posterior papillary muscle displacement.

Methods

A finite element model of the left ventricle, mitral apparatus, and chordae tendineae was created from magnetic resonance images from a sheep that developed moderate mitral regurgitation after postero-basal myocardial infarction. Each region of the model was characterized by a specific constitutive law that captured the material response when subjected to physiological pressure loading.

Results

The model simulation produced a gap between the posterior and anterior leaflets, just above the infarcted posterior papillary muscle, which is indicative of mitral regurgitation. When the stiffness of the infarct region was reduced, this caused the wall to distend and the gap area between the leaflets to increase by 33%. Additionally, the stress in the leaflets increased around the chordal connection points near the gap.

Conclusions

The methodology outlined in this work will allow a finite element model of both the left ventricle and mitral valve to be generated using non-invasive techniques.

Keywords: Myocardial Infarction, Mitral Regurgitation, Finite Element

Introduction

Ischemic mitral regurgitation (MR) affects 1.2 to 2.1 million patients in the United States, with more than 400,000 patients having moderate-to-severe MR. [1] Chronic ischemic MR of 2+ severity discovered at cardiac catheterization for symptomatic coronary artery disease has a 1-year mortality of approximately 17% [2] and the one-year mortality for 3+ and 4+ ischemic MR is approximately 40%. [2]

Ischemic MR is usually managed with mitral annuloplastyalone. [3,4] However, the need for surgical therapy and the type of surgical therapy remains unclear. For instance, the type of annuloplasty(flexible vs. rigid, complete vs. incomplete) is controversial [3,4] and the role of surgical remodeling with devices including the Acorn CorCap [5] and Coapsys [6] is unclear.

Finite element (FE) modeling of the heart and heart valves is becoming more and more common. For instance, there have been numerous FE modeling studies of the aortic valve, either as a bioprosthesis or as native tissue. In contrast, the mitral valve is structurally more complex and includes the contracting left ventricular (LV) wall as a structural element. As a consequence, most FE models of the mitral valve assume that the papillary muscles are fixed in space. Examples include the work of Kunzelman et al [7,8], who generated the first FE model of an isolated mitral valve. Finite element models of the isolated mitral valve have now been used to determine the effect of artificial chordae on valve deformation [9], the effects of leaflet and annular curvature on leaflet stress [10], and the effects of innovative annuloplasty ring shape. [11,12] More recently, modeling of the mitral leaflets has become more realistic [13] and fluid structure interaction (FSI) has been added. [14]

On the other hand, FE models of the LV that incorporate myocardial contractility have been described and used to determine the effect of myocardial infarction on structure and function. [15–17] Additionally, the efficacy of various surgical procedures has been simulated with the FE method. [18,19] Most recently, a method for determining myocardial material properties non-invasively was developed using FE modeling and optimization [20]. To date, however, FE models of the LV have not included the mitral valve.

In the current study, we expand our previous FE models of the LV [20] to incorporate the leaflets and chordae of the mitral valve. The model is based on MRI data from a sheep that has developed moderate ischemic MR after postero-basal myocardial infarction. [21,22] We demonstrate the utility and power of the method by using the FE model to test the hypothesis that a reduction in infarct stiffness will increase dyskenesis of the posterior LV wall, increase the displacement of the posterior papillary muscle and thereby increase ischemic mitral regurgitation.

Material and Methods

The animal used in this study was treated in compliance with the “Guide for the Care and Use of Laboratory Animals” prepared by the Institute of Laboratory Animal Resources, National Research Council, and published by the National Academy Press, revised 1996.

Myocardial infarction

A single adult sheep underwent posterobasal myocardial infarction as previously described. [21,22] In brief, a castrated male Dorsett sheep was anesthetized (Ketamine, 1 gm, intramuscularly; Isoflurane, 2–4% inspired) and mechanically ventilated (Model 309-0612-800, Ohio Medical Products, Madison, WI).

The exhaled pCO2 was continuously monitored and tidal volume and respiratory rate adjusted to maintain a pCO2 less than 40 mm Hg. During a left thoracotomy, ligatures were placed around the second and third obtuse marginal coronary arteries immediately above the atrioventricular groove. After the thoracotomy was closed, the sheep recovered from anesthesia.

Eight weeks after myocardial infarction, the sheep underwent trans-diaphragmatic echo and magnetic resonance imaging (MRI) as previously described. [23]

Echocardiography

A midline sub-xyphoid incision was made and subdiaphragmatic two-dimensional long axis images were obtained using an Acuson Sequoia C256 with a 3V2c (2–3 MHz) probe. The severity of mitral regurgitation (MR) was assessed quantitatively as the area of the regurgitant jet as a percentage of left atrial area in the apical four-chamber view. The following grading was used: grade 1: <20%; grade 2: 20–40%, grade 3: 40–60% and grade 4: >60% of the left atrial area.

MRI

LV pressure was measured with a non-ferromagnetic transducer-tipped pressure catheter (model SPC-350; Millar Instruments, Houston, TX) as described previously by Guccione et al. [24] A series of orthogonal short- and long-axis magnetic resonance images were acquired (Figure 1) as described previously by Guccione et al. [24]

Figure 1.

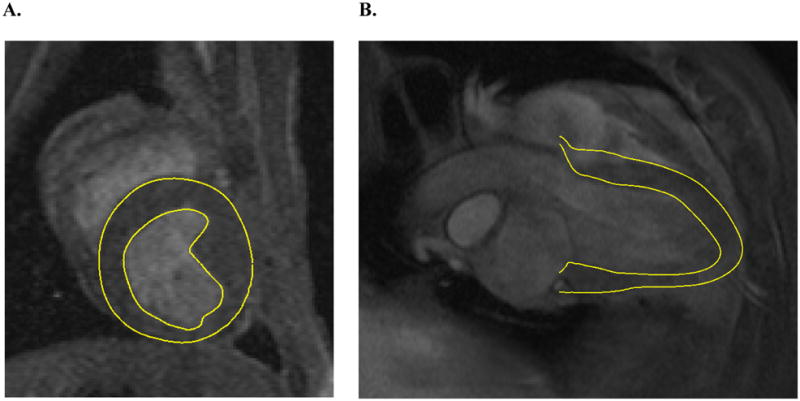
Figure 1

Open in a new tab

A. Short-axis and B. long-axis MRI slices with contour lines.

Image analysis

The images used to build the model were from the last MRI time step before mitral valve opening. The choice of this time point made tracing of the mitral leaflets and reconstruction of chordae easier. Although these images were within the latter part of isovolumic relaxation the model produced was assumed to be in a zero stress state.

A customized version of the MRI post-processing software, FindTags (Laboratory of Cardiac Energetics, National Institutes of Health, Bethesda, MD) was used to contour the endocardial and epicardial LV surfaces (Figure 1), and also to segment the systolic tags for each image slice. [25] The mitral valve annulus and leaflets were identified from the magnetic resonance images using the custom software Find Contours (Cardiac Biomechanics Laboratory, San Francisco VA, San Francisco, CA). Within each long-axis slice, 3 points were selected along the posterior leaflet and 4 points were selected along the anterior leaflet. The annulus was constructed from a total of 12 points around the perimeter of the mitral valve. The chordae tendineae could not be identified on the magnetic resonance images and thus could not be contoured. However, the computational reconstruction of the chordae was approximated from anatomic images of a mitral valve from an excised heart, which included the attached chordae and papillary muscles. [26]

FE model

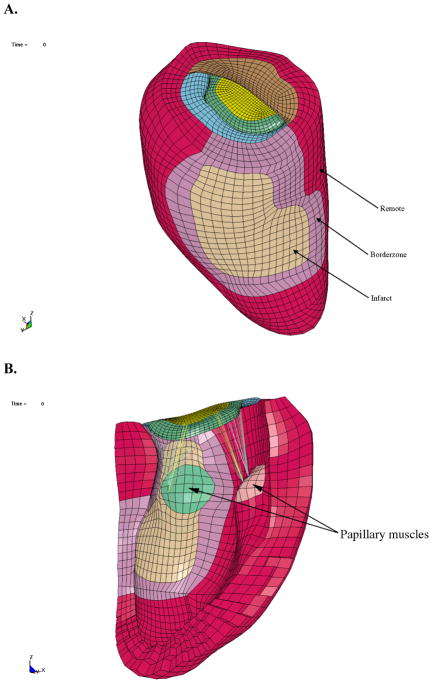
A FE model was created. Infarct, remote, and borderzone regions of the LV were determined based on the LV wall thickness using Find Contours. Specifically, the borderzone region was defined as the steep transition in wall thickness between the remote and infarcted regions. [27] Surface meshes were then created from the LV contours to replicate the in-vivo geometry (Rapidform, INUS Technology, Inc., Sunnyvale, CA), as shown in Figure 2A. The spaces between the endocardial and epicardial surfaces were filled with 8-node trilinear brick elements, with a single integration point for computational efficiency, to generate a volumetric mesh that was 4 elements thick transmurally (Truegrid, XYZ Scientific Applications, Inc., Livermore, CA) (Figures 3A and B). Each region, infarct, remote, and borderzone, was assigned different material properties.

Figure 2.

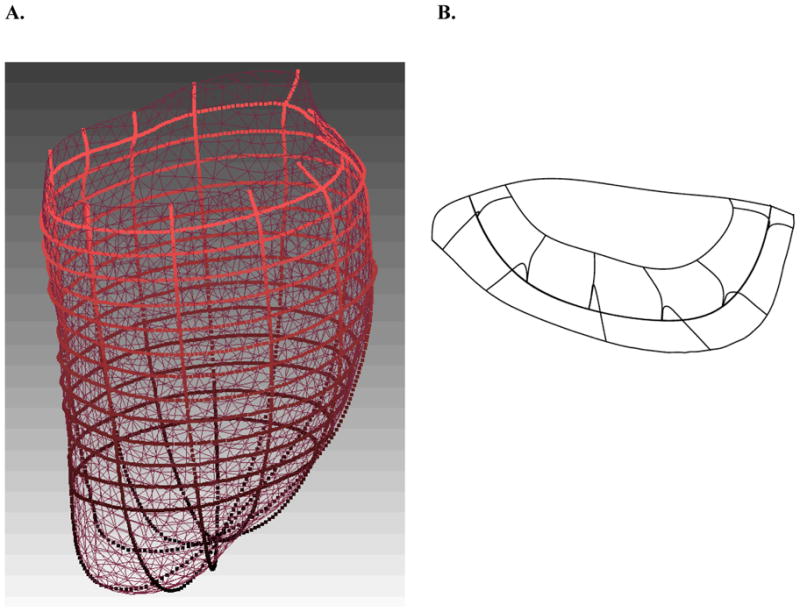
Figure 2

Open in a new tab

Surface geometry developed in Rapidform. A. Epicardial contour lines (imported from FindTags) and surface and B. mitral valve leaflet and annulus contour lines (imported from Find Contours), along with the iges surface.

Figure 3.

Figure 3

Open in a new tab

Finite element model in the undeformed configuration. A. Exterior view of the LV showing postero-basal MI B. Interior view of LV with chordae connected to the papillary muscles

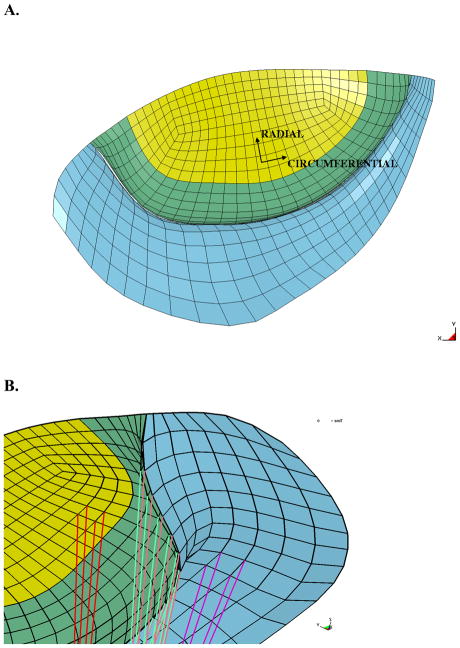
Surface meshes of the mitral valve leaflets were composed of B-spline curves that were fit to the points generated from the magnetic resonance images(Figure 2B). The thickness of the posterior leaflet (blue) was 0.8 mm, while the anterior leaflet was set to 0.8 mm in the edge region (green) and the center region (yellow) was set to 1.0 mm. [28] The posterior and anterior mitral valve leaflets were composed of 4-node bilinear shell elements, and were also assigned different material properties, since the anterior leaflet has a higher relative stiffness. The leaflet response was assumed to act like a flexible membrane, as opposed to a shell that is overly stiff in bending, and was implemented using a single integration point through the thickness of the leaflet.

The chordae tendineae were composed of 2-node beam elements. The strut (basal) and edge (marginal) chordae were assigned different material properties, and were connected directly between the papillary muscles and the mitral leaflets, without branching. More specifically, 24 edge chordae were attached to the nodes on the free-edge of each leaflet to replicate the splay at the connection points seen in-vivo, while 8 strut chordae were distributed over two small regions in the mid-section of each leaflet. The connection points of the chordae on the papillary muscles were chosen to distribute the load, as seen in-vivo, rather than concentrating them at a single point (Figures 3B and 4B).

Figure 4.

Figure 4

Open in a new tab

Mitral valve in the undeformed configuration. A. Atrial view of the mitral valve with coordinate system defined. B. The underside of the mitral valve showing the chordal insertion points. Note the edge chordae attachments along the free-edge and the strut chordae attachments at the mid-section of the leaflets. The anterior leaflet is green and yellow, and the posterior leaflet is blue

Cardiac myofiber angles at the epicardium and endocardium were assigned to be −37° and 83°, respectively, (counterclockwise when viewed from the epicardium) with respect to the circumferential direction, with a linear variation transmurally through the wall. [29] However, the fiber angles in the papillary muscles were assigned to be 90° (in the apex-to-base or longitudinal direction). The fibers in the mitral valve were aligned with the circumferential and radial directions of each leaflet (Figure 4A), where the circumferential direction follows the curvature of the leaflets and the radial direction is normal to it.

Loading conditions

The basal nodes of the LV were extended above the plane of the mitral leaflets and material was added in between, in order to reduce the interaction of the boundary constraints and the leaflets. The extended basal nodes were fully constrained in all directions. The endocardial wall was loaded to the measured in-vivo end-diastolic and end-systolic LV pressures. The leaflets were loaded in order to represent the pressure gradient between the atrium and ventricle, which is given by an inward pressure from the atrium during diastole and an outward pressure from the ventricle during systole.

Constitutive models

Nearly incompressible, transversely isotropic, hyperelastic constitutive laws for passive [30] and active myocardium [31] were modeled in a user-defined material subroutine in the explicit FE solver, LS-DYNA (Livermore Software Technology Corporation, Livermore, CA). The key equations can be found in prior work by Walker et al. [32] The mitral valve leaflets were also modeled with a nearly incompressible, transversely isotropic, hyperelastic material response. The soft tissue material model (*MAT_091), which is built into LS-DYNA [33] and is based on the constitutive law developed by Quapp and Weiss [34], was used to model the leaflet response. An overview of several widely used material models for the mitral valve is given by Weinberg and Mofrad. [35] The chordae tendineae were modeled with a cable element formulation (*MAT_071), which allows a load to be carried only in tension and does not sustain bending. [33] Rather than using a strain energy function, the uniaxial stress-strain curve was used directly in the model as a look-up table.

The material properties of the myocardium were averaged from previous studies [17,36] and are shown Table 1. The infarct was assigned a value roughly 10 times greater than the remote, but with no contractility. The contractility in the borderzone was reduced by 50%, relative to the remote region. [17,36] The material properties for the mitral leaflets were estimated by comparing the stress-strain curves from experimental data [37] and model simulations performed with the soft tissue model using LS-DYNA. The values were determined manually, rather than using a formal optimization, and are shown in Table 2. Unfortunately, it was not possible to exactly reproduce the curves. The stress-strain relation for the chordae tendineae was based on data from Kunzelman and Cochran. [38]

Table 1.

Material properties for the remote, borderzone, and infarct regions of the myocardium. The passive material parameters (C, bf, bt, bfs) are based on the constitutive law from Guccione et al. [30] and the active material parameter (Tmax) is based on the constitutive law from Guccione et al. [31]

Region C (kPa) bf bt bfs Tmax (kPa)
Remote 0.3 49.25 19.25 17.44 180
Borderzone 0.3 49.25 19.25 17.44 90
Infarct 3.6 49.25 19.25 17.44 0
Open in a new tab

Table 2.

Mitral valve leaflet material properties corresponding to the constitutive law from Quapp and Weiss. [34] The subscript ‘cir’ represents the exponential response in the circumferential direction and the subscript ‘rad’ represents the radial direction.

Leaflet C1 (kPa) C2 (kPa) C3,cir (kPa) C3,cir C4,rad (kPa) C4,rad
Anterior 100 0.0 1.5 25 1.0 23
Posterior 40 0.0 3.0 16 1.0 16
Open in a new tab

Results

The pressure in the LV was determined, via catheter, to be 6.09 mmHg and 91.46 mmHg at end-diastole and end-systole, respectively. Atrial pressure was not measured, but the pressure applied to the leaflets during diastole was assumed to be 1.12 mmHg [39], while the pressure applied during systole matched that of the LV.

The severity of MR was quantified from the echocardiograph images (Figure 5). The grade of MR was found to be 2+ in the animal used in this study. It was not possible to ascertain the presence of a gap in the images, due to low resolution. However, the presence of a regurgitant jet is indicative of an open passage between the LV and atrium.

Figure 5.

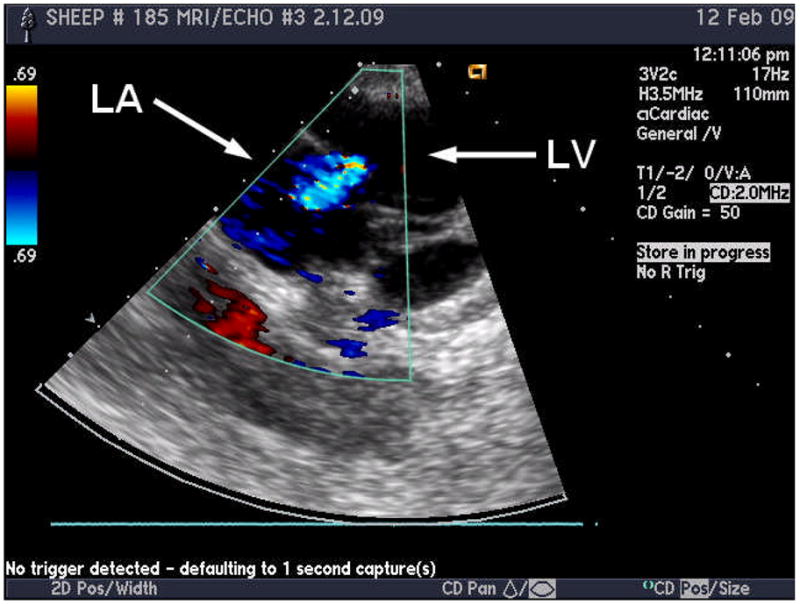
Figure 5

Open in a new tab

Echocardiograph image of a sheep with 2+ MR, where the blue region indicates the regurgitant jet

Mitral valve deformation in the FE model

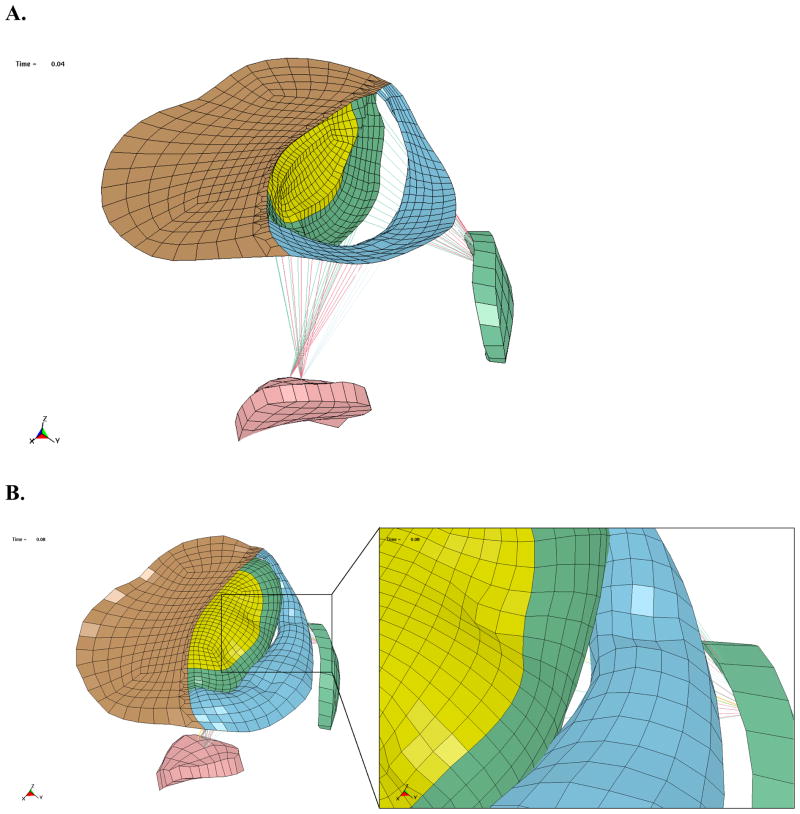
The deformation of the mitral valve is shown in Figure 6, with the chordae and papillary muscles displayed, and the myocardium hidden. The mitral valve is forced open during diastole, due to the pressure gradient from the atrium to the ventricle. In contrast, the pressure in the LV is significantly higher than the atrium during systole, which forces the valve closed. The simulations produced a gap between the posterior and anterior leaflets at the end of the systole, which was located above the infarcted posterior papillary muscle (Figure 6B). The gap was caused by the fact that the papillary muscle was recessed into the wall, due to wall thinning, which tethers the leaflets preventing them from coapting. In addition, the reduced contractility of the infarct and borderzone inhibits the wall from moving inward during systole, which also causes tethering in this region.

Figure 6.

Figure 6

Open in a new tab

A. Oblique view of mitral valve deformation at end-diastole, wall elements have been hidden. B. Oblique view of mitral valve deformation at end-systole, with close up view of the gap.

End-systolic stress computed in FE model

In the baseline case, the effective stress in the center of the anterior leaflet was roughly 119 kPa, while the effective stress in the center of the posterior leaflet was 91 kPa. The average effective stress in the entire leaflet was 85.4 kPa and 72.9 kPa in the anterior and posterior leaflets, respectively. The average end-systolic myofiber stress was 22.1 kPa, 25.6 kPa, and 24.3 kPa in the remote, borderzone, and infarct regions, respectively.

The effect of papillary muscle displacement on simulated results

The infarct material properties were varied to investigate the effects on deformation in the mitral valve leaflets. When the infarct stiffness, C, was reduced from 3.6 kPa to 0.3 kPa, the wall deformation increased significantly (Figure 7). The area of the gap between the leaflets was estimated by placing a cut plane through the gap and measuring the area of the bounded region. The area of the gap was found to increase by roughly 33%, from 3.74 mm2 to 4.96 mm2, when the stiffness of the infarct was reduced, as seen in Figure 8. The stress in the leaflets also increased due to the increased wall deformation. The average effective stresses at several locations in the leaflets are given in Table 3. It is worth noting that the stress in the center of the posterior leaflet did not increase significantly during this simulation.

Figure 7.

Figure 7

Open in a new tab

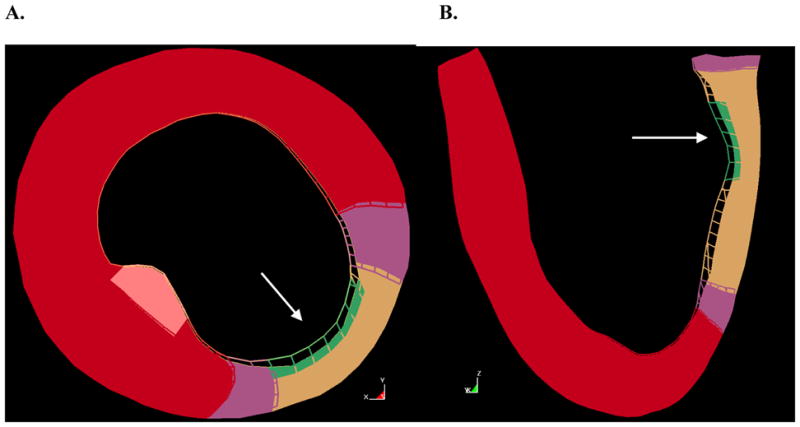
Overlay of stiff infarct model (wire mesh) and soft infarct model (solid) at end-systole. A. Short axis slice, B. long axis slice. The white arrow indicates the location of the posterior papillary muscle.

Figure 8.

Figure 8

Open in a new tab

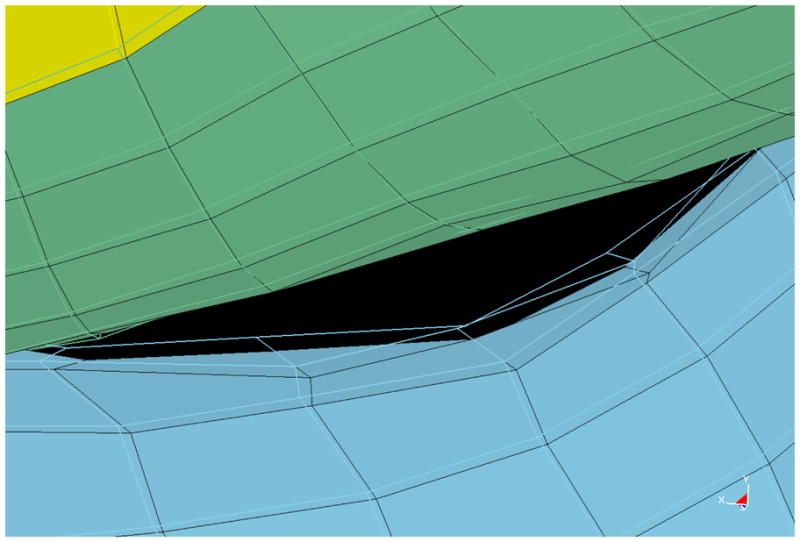
Overlay of stiff infarct model (wire mesh) and soft infarct model (solid) at end-systole, with a close-up view of the gap between the mitral valve leaflets.

Table 3.

Average effective stress values within the posterior and anterior leaflets at several key locations.

Location within leaflets Stress in baseline case, C = 3.6 kPa Stress in case with decreased infarct stiffness C = 0.3 kPa
Center of anterior leaflet 119 kPa 129 kPa
Posterior leaflet near the gap 116 kPa 123 kPa
Anterior leaflet near the gap 58 kPa 62 kPa
Open in a new tab

Comment

In summary, we have described an FE model of the LV that includes myocardial contractility and the mitral valve. To the best our knowledge, this is the first finite element model of LV mechanics that includes the mitral valve. Dayan and colleagues used computer animation software to animate the motion of radiographic markers on the LV and mitral valve. [40] However, that model did not incorporate realistic material laws or material parameters and could not be used to test mechanic hypotheses. Peskin and McQueen [41] used the immersed boundary method to analyze flow dynamics in a whole heart with both the aortic and mitral valves. However, the myocardium in that study was approximated as a fiber-reinforced fluid composite. [41] The fiber-in-fluid model does not allow the myocardium to support a load that is perpendicular to the myofiber direction.

The sheep model of ischemic MR

Ligation of the second and third obtuse marginal coronary arteries in the sheep causes MR to gradually develop over 6 weeks until it reaches a moderate (2–3+) level. [21,22] Ischemic MR in the sheep is the mechanical result of leaflet teathering (Carpentier type 3B mitral leaflet motion [42]) and annular dilation. As a consequence of LV remodeling after the postero-basal myocardial infarction, the posterior papillary muscle moves laterally. [43,44] This causes both anterior and posterior mitral leaflets to be tethered and ischemic MR to occur. The mitral annulus also dilates. For instance, Gorman et al. found that the area of the annulus increased 9.2% at end-systole [45]. While there are differences between human and sheep mitral anatomy [46], the mechanism of ischemic MR in the sheep model is thought to be similar to the mechanism of ischemic MR in humans.

Our model of the LV with mitral valve was able to demonstrate the presence of ischemic MR. For instance, a gap was seen between the anterior and posterior leaflet in the A3P3 region at end-systole. In addition, the model was faithful to the other anatomic characteristics of ischemic MR. Specifically, the shape of the mitral annulus in the model was relatively flat. This has been observed by Ryan et al. [47] in sheep with MR. The deformed shape of the leaflets showed a slight billowing effect in the center of the leaflets, while the strut chordae attachment points on the leaflets were restrained. [44]

The effect of infarct stiffness

We used the finite element model of LV with mitral valve to test the hypothesis that a reduction in infarct stiffness will increase ischemic mitral regurgitation. Specifically, we were able to demonstrate that a reduction in infarct stiffness caused further displacement of the posterior papillary muscle at end-systole. As a consequence, there was an increase in the gap between the anterior and posterior leaflets in the A3P3 region.

The ability of lateral papillary muscle displacement to decrease mitral leaflet coaptation and increase mitral regurgitation has been previously shown using an isolated mitral valve preparation [48] and a finite element model of the mitral valve. [11] In both of those studies, papillary muscle location was manually proscribed whereas in our model, the location of the papillary muscle was solved for by simulating the motion of the myocardial wall.

Leaflet stress

The stress distribution varied significantly over the leaflets in the present study, due to the nonsymmetric geometry and tethering. Leaflet stress in isolated mitral valve models has been reported [28], but most of these studies apply a ventricular pressure of 120 mmHg to models that are symmetric, whereas in the present study we apply a ventricular pressure of 91.46 mmHg. However, it was found that the magnitude of stress in the center of the leaflets was roughly the same order of magnitude as that shown in recent studies. For example, the effective stress in the center of the anterior and posterior leaflets was reported by Prot and colleagues [28] to be roughly 220 kPa and 130 kPa, respectively. In another study, Salgo and colleagues [10] reported much higher stresses in a mitral valve model that were on the order of 4 to 400 MPa. However, it should be noted that the study was conducted with a linear orthotropic material law.

Limitations

The geometry of the mitral valve does not include the clefts in the posterior leaflet. This could affect the deformation of the leaflets near the end points of the free-edges. Second, the leaflets were not modeled to include contact, thus there is some penetration of the anterior leaflet into the posterior. The inclusion of contact would most likely change the shape of the non-coapting region. However, the result of the model simulation would still produce a gap, indicative of MR. Third, the material model for the leaflets does not capture the rapid stiffening effect from the fibers at the critical stretch, but rather has a more gradual stiffening effect. This most likely contributes to the slight billowing in the leaflet deformation. Finally, the material properties used for the myocardium have not been validated, but are based on average values.

Conclusions and future directions

The methodology presented here provides a systematic framework for generating an accurate model of the LV model with mitral valve. The model presented in this study was able to capture the presence of MR, which was seen as a gap between the leaflets and to show the effect of displacement of the papillary muscle on ischemic MR.

We plan to improve the model of the LV with mitral valve in a number of ways. For instance, future models will be made more anatomically correct with the use of co-registered 3 dimensional echocardiography and magnetic resonance images. Second, a contact algorithm to prevent penetration between the leaflets and implementation of a more widely used material model for leaflet stiffness will be integrated into the model. Third, the model will be expanded to incorporate the effect of blood flow and flow structure interaction. This will generate a more accurate profile of the loading applied on the endocardium and mitral valve. Last, we will employ our material optimization techniques to calculate actual myocardial and mitral annular material properties.

The success of this study opens the way for further finite element based studies of therapy for ischemic mitral regurgitation. First and most obvious would be a more detailed study of infarct stiffness which would determine the infarct stiffness that optimally reduces mitral regurgitation and mitral leaflet stress. Models of passive cardiac constraint are being developed in our laboratory and a logical next step would be to simulate the effect of the Acorn CorCap on ischemic MR. Beyond that there are numerous possibilities including the determination of optimal annuloplasty ring material properties and shape and the effect of Coapsys-like intraventricular struts on LV and mitral valve function.

Ultimately, the goal is to use the model to determine the optimal surgical repair of ischemic MR. We believe that as this model improves, it will be a powerful tool for planning future clinical and animal trials, thus reducing the need for expensive and time consuming studies.

Acknowledgments

This study was supported by NIH grants R01-HL-84431 (Dr. Ratcliffe), R01-HL-63348 (Dr. Ratcliffe), R01-HL-77921 (Dr. Guccione), and R01-HL-86400 (Dr. Guccione) This support is gratefully acknowledged.

References

  • 1.Gorman R, Gorman JI, Edmunds LJ. Ischemic mitral regurgitation in cardiac surgery in the adult. In: Cohn L, Edmunds LH Jr, editors. Cardiac Surgery in the adult. New York: McGraw-Hill; 2003. pp. 1751–1770. [Google Scholar]
  • 2.Hickey MS, Smith LR, Muhlbaier LH, et al. Current prognosis of ischemic mitral regurgitation. Implications for future management. Circulation. 1988;78:I51–59. [PubMed] [Google Scholar]
  • 3.Gillinov AM, Wierup PN, Blackstone EH, et al. Is repair preferable to replacement for ischemic mitral regurgitation? J Thorac Cardiovasc Surg. 2001;122:1125–1141. doi: 10.1067/mtc.2001.116557. [DOI] [PubMed] [Google Scholar]
  • 4.Bolling SF, Pagani FD, Deeb GM, Bach DS. Intermediate-term outcome of mitral reconstruction in cardiomyopathy. J Thorac Cardiovasc Surg. 1998;115:381–386. doi: 10.1016/S0022-5223(98)70282-X. discussion 387–388. [DOI] [PubMed] [Google Scholar]
  • 5.Acker M, Bolling S, Mann D, et al. American Association of Thoracic Surgery. San Francisco: 2005. Mitral valve surgery in heart failure: Results of the Acorn CorCap randomized trial. [Google Scholar]
  • 6.Grossi EA, Woo YJ, Schwartz CF, et al. Comparison of Coapsys annuloplasty and internal reduction mitral annuloplasty in the randomized treatment of functional ischemic mitral regurgitation: impact on the left ventricle. J Thorac Cardiovasc Surg. 2006;131:1095–1098. doi: 10.1016/j.jtcvs.2005.11.046. [DOI] [PubMed] [Google Scholar]
  • 7.Kunzelman K. Engineering analysis of mitral valve structure and function. University of Texas Southwestern; 1991. [Google Scholar]
  • 8.Kunzelman KS, Cochran RP, Chuong C, et al. Finite element analysis of the mitral valve. J Heart Valve Dis. 1993;2:326–340. [PubMed] [Google Scholar]
  • 9.Kunzelman K, Reimink MS, Verrier ED, Cochran RP. Replacement of mitral valve posterior chordae tendineae with expanded polytetrafluoroethylene suture: A finite element study. Journal of Cardiac Surgery. 1996;11:136–145. doi: 10.1111/j.1540-8191.1996.tb00028.x. [DOI] [PubMed] [Google Scholar]
  • 10.Salgo IS, Gorman JH, Gorman RC, et al. Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation. 2002;106:711–717. doi: 10.1161/01.cir.0000025426.39426.83. [DOI] [PubMed] [Google Scholar]
  • 11.Maisano F, Redaelli A, Soncini M, et al. An annular prosthesis for the treatment of functional mitral regurgitation: Finite element model analysis of a dog bone-shaped ring prosthesis. Annals of Thoracic Surgery. 2005;79:1268–1275. doi: 10.1016/j.athoracsur.2004.04.014. [DOI] [PubMed] [Google Scholar]
  • 12.Votta E, Maisano F, Bolling SF, et al. The geoform disease-specific annuloplasty system: A finite element study. Annals of Thoracic Surgery. 2007;84:92–102. doi: 10.1016/j.athoracsur.2007.03.040. [DOI] [PubMed] [Google Scholar]
  • 13.Prot V, Haaverstad R, Skallerud B. Finite element analysis of the mitral apparatus: annulus shape effect and chordal force distribution. Biomech Model Mechanobiol. 2009;8:43–55. doi: 10.1007/s10237-007-0116-8. [DOI] [PubMed] [Google Scholar]
  • 14.Kunzelman KS, Einstein DR, Cochran RP. Fluid-structure interaction models of the mitral valve: function in normal and pathological states. Philos Trans R Soc Lond B Biol Sci. 2007;362:1393–1406. doi: 10.1098/rstb.2007.2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Dang AB, Guccione JM, Mishell JM, et al. Akinetic myocardial infarcts must contain contracting myocytes: finite-element model study. Am J Physiol Heart Circ Physiol. 2005;288:H1844–1850. doi: 10.1152/ajpheart.00961.2003. [DOI] [PubMed] [Google Scholar]
  • 16.Guccione JM, Moonly SM, Moustakidis P, et al. Mechanism underlying mechanical dysfunction in the border zone of left ventricular aneurysm: a finite element model study. Ann Thorac Surg. 2001;71:654–662. doi: 10.1016/s0003-4975(00)02338-9. [DOI] [PubMed] [Google Scholar]
  • 17.Walker JC, Ratcliffe MB, Zhang P, et al. MRI-based finite-element analysis of left ventricular aneurysm. Am J Physiol Heart Circ Physiol. 2005;289:H692–700. doi: 10.1152/ajpheart.01226.2004. [DOI] [PubMed] [Google Scholar]
  • 18.Dang AB, Guccione JM, Zhang P, et al. Effect of ventricular size and patch stiffness in surgical anterior ventricular restoration: a finite element model study. Ann Thorac Surg. 2005;79:185–193. doi: 10.1016/j.athoracsur.2004.06.007. [DOI] [PubMed] [Google Scholar]
  • 19.Walker JC, Ratcliffe MB, Zhang P, et al. Wall stress after linear repair of left ventricular aneurysm: A finite element analysis validated with tagged-MRI. Ann Thorac Surg. 2005 Submitted. [Google Scholar]
  • 20.Sun K, Stander N, Jhun C-S, et al. A computationally efficient formal optimization of regional myocardial contractility in a sheep with left ventricular aneurysm. J Biomech Eng. 2009:131. doi: 10.1115/1.3148464. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Llaneras MR, Nance ML, Streicher JT, et al. Large animal model of ischemic mitral regurgitation. Ann Thorac Surg. 1994;57:432–439. doi: 10.1016/0003-4975(94)91012-x. [DOI] [PubMed] [Google Scholar]
  • 22.Llaneras MR, Nance ML, Streicher JT, et al. Pathogenesis of ischemic mitral insufficiency. J Thorac Cardiovasc Surg. 1993;105:439–442. discussion 442–433. [PubMed] [Google Scholar]
  • 23.Ratcliffe MB, Wallace AW, Teerlink JR, et al. Radio frequency heating of chronic ovine infarct leads to sustained infarct area and ventricular volume reduction. J Thorac Cardiovasc Surg. 2000;119:1194–1204. doi: 10.1067/mtc.2000.105826. [DOI] [PubMed] [Google Scholar]
  • 24.Guccione JM, Walker JC, Beitler JR, et al. The effect of anteroapical aneurysm plication on end-systolic three-dimensional strain in the sheep: a magnetic resonance imaging tagging study. J Thorac Cardiovasc Surg. 2006;131:579–586. e573. doi: 10.1016/j.jtcvs.2005.07.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Guttman MA, Zerhouni EA, McVeigh ER. Analysis and visualization of cardiac function from MR images. IEEE Comp Graph Appl. 1997;17:30–38. doi: 10.1109/38.576854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Ritchie J, Warnock JN, Yoganathan AP. Structural characterization of the chordae tendineae in native porcine mitral valves. Annals of Thoracic Surgery. 2005;80:189–197. doi: 10.1016/j.athoracsur.2005.02.011. [DOI] [PubMed] [Google Scholar]
  • 27.Moustakidis P, Maniar HS, Cupps BP, et al. Altered left ventricular geometry changes the border zone temporal distribution of stress in an experimental model of left ventricular aneurysm: a finite element model study. Circulation. 2002;106:I168–175. [PubMed] [Google Scholar]
  • 28.Prot V, Haaverstad R, Skallerud B. Finite element analysis of the mitral apparatus: annulus shape effect and chordal force distribution. Biomechanics and Modeling in Mechanobiology. 2009;8:43–55. doi: 10.1007/s10237-007-0116-8. [DOI] [PubMed] [Google Scholar]
  • 29.Omens JH, May KD, McCulloch AD. Transmural distribution of three-dimensional strain in the isolated arrested canine left ventricle. Am J Physiol. 1991;261:H918–928. doi: 10.1152/ajpheart.1991.261.3.H918. [DOI] [PubMed] [Google Scholar]
  • 30.Guccione JM, McCulloch AD, Waldman LK. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J Biomech Eng. 1991;113:42–55. doi: 10.1115/1.2894084. [DOI] [PubMed] [Google Scholar]
  • 31.Guccione JM, Waldman LK, McCulloch AD. Mechanics of active contraction in cardiac muscle: Part II--Cylindrical models of the systolic left ventricle. J Biomech Eng. 1993;115:82–90. doi: 10.1115/1.2895474. [DOI] [PubMed] [Google Scholar]
  • 32.Walker JC, Ratcliffe MB, Zhang P, et al. Magnetic resonance imaging-based finite element stress analysis after linear repair of left ventricular aneurysm. J Thorac Cardiovasc Surg. 2008;135:1094–1102. 1102, e1091–1092. doi: 10.1016/j.jtcvs.2007.11.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Halquist JO. LS-DYNA Theory Manual. 2006 [Google Scholar]
  • 34.Quapp KM, Weiss JA. Material characterization of human medial collateral ligament. Journal of Biomechanical Engineering-Transactions of the Asme. 1998;120:757–763. doi: 10.1115/1.2834890. [DOI] [PubMed] [Google Scholar]
  • 35.Weinberg EJ, Kaazempur-Mofrad MR. On the Constitutive Models for Heart Valve Leaflet Mechanics. Cardiovascular Engineering. 2005;5:37–43. [Google Scholar]
  • 36.Sun K, Stander N, Jhun C-S, Zhang Z, Suzuki T, Saeed M, Wallace AW, Tseng EE, Baker AJ, Saloner D, Einstein DR, Ratcliffe MB, Guccione JM. A computationally efficient formal optimization of regional myocardial contractility in a sheep with left ventricular aneurysm. J Biomech Eng. 2009;131:111001. doi: 10.1115/1.3148464. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.May-Newman K, Yin FCP. A constitutive law for mitral valve tissue. Journal of Biomechanical Engineering-Transactions of the Asme. 1998;120:38–47. doi: 10.1115/1.2834305. [DOI] [PubMed] [Google Scholar]
  • 38.Kunzelman KS, Cochran RP. Mechanical properties of basal and marginal mitral valve chordae tendineae. ASAIO Trans. 1990;36:M405–408. [PubMed] [Google Scholar]
  • 39.Aubert AE, Ronaszeki A, De Geest H. Relationship between diastolic atrio-ventricular pressure gradient and Doppler determined rapid inflow. Computers in Cardiology. 1994;1994:469–472. [Google Scholar]
  • 40.Dayan JH, Oliker A, Sharony R, et al. Computer-generated three-dimensional animation of the mitral valve. J Thorac Cardiovasc Surg. 2004;127:763–769. doi: 10.1016/s0022-5223(03)00959-0. [DOI] [PubMed] [Google Scholar]
  • 41.Peskin CS, McQueen DM. A three-dimensional computational method for blood flow in the heart: (I) immersed elastic fibers in a viscous incompressible fluid. Journal of Computational Physics. 1989;81:372–405. [Google Scholar]
  • 42.Carpentier A. Cardiac valve surgery--the “French correction”. J Thorac Cardiovasc Surg. 1983;86:323–337. [PubMed] [Google Scholar]
  • 43.Gorman RC, McCaughan JS, Ratcliffe MB, et al. Pathogenesis of acute ischemic mitral regurgitation in three dimensions. J Thorac Cardiovasc Surg. 1995;109:684–693. doi: 10.1016/S0022-5223(95)70349-7. [DOI] [PubMed] [Google Scholar]
  • 44.Liel-Cohen N, Guerrero JL, Otsuji Y, et al. Design of a new surgical approach for ventricular remodeling to relieve ischemic mitral regurgitation: insights from 3-dimensional echocardiography. Circulation. 2000;101:2756–2763. doi: 10.1161/01.cir.101.23.2756. [DOI] [PubMed] [Google Scholar]
  • 45.Gorman JH, 3rd, Jackson BM, Gorman RC, et al. Papillary muscle discoordination rather than increased annular area facilitates mitral regurgitation after acute posterior myocardial infarction. Circulation. 1997;96:II-124–127. [PubMed] [Google Scholar]
  • 46.Degandt AA, Weber PA, Saber HA, Duran CM. Mitral valve basal chordae: comparative anatomy and terminology. Ann Thorac Surg. 2007;84:1250–1255. doi: 10.1016/j.athoracsur.2007.05.008. [DOI] [PubMed] [Google Scholar]
  • 47.Ryan LP, Jackson BM, Parish LM, et al. Regional and global patterns of annular remodeling in ischemic mitral regurgitation. Annals of Thoracic Surgery. 2007;84:553–559. doi: 10.1016/j.athoracsur.2007.04.016. [DOI] [PubMed] [Google Scholar]
  • 48.He S, Jimenez J, He Z, Yoganathan AP. Mitral leaflet geometry perturbations with papillary muscle displacement and annular dilatation: an in-vitro study of ischemic mitral regurgitation. J Heart Valve Dis. 2003;12:300–307. [PubMed] [Google Scholar]

RESOURCES