Mode-Locked Spike Trains in Responses of Ventral Cochlear Nucleus Chopper and Onset Neurons to Periodic Stimuli

Abstract

We report evidence of mode-locking to the envelope of a periodic stimulus in chopper units of the ventral cochlear nucleus (VCN). Mode-locking is a generalized description of how responses in periodically forced nonlinear systems can be closely linked to the input envelope, while showing temporal patterns of higher order than seen during pure phase-locking. Re-analyzing a previously unpublished dataset in response to amplitude modulated tones, we find that of 55% of cells (6/11) demonstrated stochastic mode-locking in response to sinusoidally amplitude modulated (SAM) pure tones at 50% modulation depth. At 100% modulation depth SAM, most units (3/4) showed mode-locking. We use interspike interval (ISI) scattergrams to unravel the temporal structure present in chopper mode-locked responses. These responses compared well to a leaky integrate-and-fire model (LIF) model of chopper units. Thus the timing of spikes in chopper unit responses to periodic stimuli can be understood in terms of the complex dynamics of periodically forced nonlinear systems. A larger set of onset (33) and chopper units (24) of the VCN also shows mode-locked responses to steady-state vowels and cosine-phase harmonic complexes. However, while 80% of chopper responses to complex stimuli meet our criterion for the presence of mode-locking, only 40% of onset cells show similar complex-modes of spike patterns. We found a correlation between a unit's regularity and its tendency to display mode-locked spike trains as well as a correlation in the number of spikes per cycle and the presence of complex-modes of spike patterns. These spiking patterns are sensitive to the envelope as well as the fundamental frequency of complex sounds, suggesting that complex cell dynamics may play a role in encoding periodic stimuli and envelopes in the VCN.

INTRODUCTION

Spike timing is thought to play an important role in the neural representation of sound. It has long been studied in the context of phase-locking, in which a neuron tends to fire at a given phase of a periodic stimulus. This effect is robust in the auditory nerve (AN) and brain stem discharges to low-frequency tones (Rose et al. 1967) and complex harmonic sounds such as vowels (Palmer et al. 1986; Winter and Palmer 1990) and in responses to amplitude-modulated tones (for a review, see Joris et al. 2004). More recently, information theoretic studies have revealed how spike timing can be used to detect (Gai and Carney 2008) or distinguish categories of arbitrary spiking patterns to arbitrary stimuli (Huetz et al. 2006; Schnupp et al. 2006). However, this last approach does not consider the role of the dynamic properties of neurons in the encoding of stimulus information.

Stellate cells in the VCN are well characterized with respect to both their biophysical and coding properties. These cells exhibit highly regular spiking (chopping response) in response to constant stimulation (for both current steps and pure tones) (Manis and Marx 1991; Rhode et al. 1983). They also encode the frequency of AM using the temporal pattern of firing: they display a band-pass vector strength (VS) (Rhode and Greenberg 1994) and their interspike interval (ISI) statistics are related to the temporal periodicity of the stimuli presented (Wiegrebe and Winter 2001). These response properties are thought to result from summation of the inputs from auditory nerve fibers, temporal integration, and a simple spiking mechanism. Simulations of Hodgkin-Huxley (HH) type (Banks and Sachs 1991; Wang and Sachs 1995) or integrate-and-fire models (Hewitt et al. 1992), reproducing the linear subthreshold current-voltage (I-V) curve of stellate cells, have successfully replicated their responses to pure tone at characteristic frequency (CF), the VS in response to AM tones and the responses to other periodic stimuli.

In this article, we complement previous simulation studies using a mathematical theory explaining how nonlinear dynamical systems synchronize to time varying input. We observe higher-order temporal patterns, called “mode-locked” in response to several different classes of periodic stimuli: AM tones, steady-state vowels, and cosine-phase harmonic complexes. Mode-locking, of which phase-locking is a subset, results from the interaction between the dynamics of a nonlinear oscillator and a periodic stimulus. Such spiking patterns have been previously described in generic neuron models similar to models of stellate cells [for instance HH (Aihara et al. 1984; Lee and Kim 2006) or leaky integrate-and-fire (LIF) (Brette 2004; Coombes and Bressloff 1999; Keener et al. 1981)] and have been observed in vitro under DC injection (Aihara et al. 1984; Brumberg and Gutkin 2007; Guttman et al. 1980; Shreiber et al. 2004). Mode-locked responses are often stable across regions of parameter space called Arnold tongues (for a review, see Pikovsky et al. 2001). Our report is the first description of mode-locking in the auditory system and under sensory stimulation in vivo.

METHODS

Experimental data collection

The data were collected from 54 healthy adult pigmented guinea pigs (Cavia porcellus), weighing in the range of 300–400 g, which also provided extensive data for other studies. We analyzed the responses of 11 cells (not previously published) to SAM tones of 3-s duration presented 10 times with a range of modulation frequencies. Seven of these cells were classified as chopper units, two as onset choppers, and two as unusual. We also analyzed the responses of 24 chopper units and 33 onset units in response to vowels and harmonic complexes (previously published in Winter et al. 2003).

The animal preparation has been described in detail previously (Winter and Palmer 1995) and will only be given very briefly. Animals were anesthetized with a single injection (1.3 g/kg ip) of 20% urethan (2 g urethan, Sigma U-2500, in 10 ml distilled water). Atropine sulfate (120 μg sc) was administered to reduce bronchial secretions (atropine sulfate injection BP 600 μg/ml). Depth of anesthesia was indirectly monitored using the pedal withdrawal reflex, and maintenance doses of phenoperidine (1 mg/kg im, intramuscular Operidine 1 mg/ml, Janssen Pharmaceuticals) were applied when required.

All procedures were carried out in a double-walled sound-attenuated chamber and in accordance with UK Home Office regulations. The animal was tracheotomized to allow artificial ventilation when necessary. The animal's core body temperature was monitored rectally and maintained in the range 37–38°C by a heating blanket. The animal was placed in a stereotaxic frame, the left earbar of which had been replaced with a hollow Perspex (Plexiglas) speculum. A silver-wire electrode was placed on the round window of the cochlea via an opening in the bulla to monitor the compound action potential. A polythene tube was inserted into the opening to equalize middle ear pressure, and the hole was resealed with petroleum jelly. A posterior craniotomy exposed the cerebellum. The dura was removed and the exposed cerebellum was covered with 1.5% agar.

Single-unit extracellular recordings were made from the CN of the guinea pig using tungsten-in-glass microelectrodes (Bullock et al. 1988) inserted into the left VCN using stereotaxic co-ordinates. The microelectrode signal was passed via a high-impedance headstage (Axon Instruments HS-2) to an Axoprobe 1A microelectrode amplifier. The signal was filtered (300–2,000 Hz) before being further amplified. A spike discriminator produced an electrical pulse when the spike voltage exceeded a threshold level and a CED1401 laboratory interface time-stamped the electrical pulses with an accuracy of 10 μs.

Pure tone and SAM stimuli were produced by a Hewlett Packard HP3325A synthesizer/function generator. SAM tones were 3 s long with a 6.5-s repetition period and presented at 20 dB above unit threshold. The signals were attenuated before reaching the driver amplifier for a reverse-driven Brüel and Kjær 4134 12.7-mm condenser microphone, coupled to a damped, 4-mm inside-diameter probe tube. This earphone was fitted into the speculum at the left ear. The sound system was calibrated at the start of each experiment. An anti-distortion network and safe driving voltage level were used to ensure that harmonic distortion products from the condenser microphone were negligible.

Steady-state vowels were produced using the Klatt software synthesizer and sampled at 10 kHz. The vowel /a/ had a fundamental of 100 Hz and three formants at 730, 1,090, and 2440 Hz with bandwidths (BW) of 90, 110, and 170 Hz, respectively. The vowel /i/ had a fundamental of 125 Hz and formants at 270 Hz (BW 90 Hz), 2,290 (BW 110 Hz), and 3,010 (BW 170 Hz). Harmonic complexes were cosine-phase and consisted of the first 50 harmonics all at equal levels. Stimuli were presented at ∼80 dB SPL with an interstimulus interval of 240 ms and repeated 100 times.

Data analysis

SYNCHRONIZATION MEASURES: PERIOD-HISTOGRAMS, VECTOR STRENGTH, AND MODE-LOCKING.

Spike times were analyzed for the sustained part of the evoked response to AM tones, from 50 to 3,000 ms. Vowels and harmonic complex stimuli were analyzed within a window from 30 to 120 ms after stimulus onset. Synchronization was initially assessed using the conventional method of constructing period histograms (using 100 bins, independently of the modulation frequency) and calculating the vector strength (VS) (Goldberg and Brown 1969)

$$\text{VS}=\frac{1}{N}\left|{\displaystyle {\sum }_{n=1}^N{e}^{i{\varphi }_n}}\right|$$

where ϕ_n is the phase of the nth spike in the data and N the number of spikes in response to the stimulus. The VS takes a value of 1 if all spikes occur at one precise phase and 0 for a uniform distribution of phases across the modulation cycle. The VS gives a good indication as to whether a phase preference exists in the data.

Mode-locking constitutes a general description of discharge patterns synchronized to periodic stimulation. A neuron with periodic input has a q:p mode-locked responses if it fires periodically p spikes during q cycles of the stimulus (p and q being any arbitrary integers). These synchronized periodic discharges are the result of the interaction between an intrinsic membrane property (e.g., temporal integration) and the periodicity of the input. Mode-locked spike trains can be described through either 1) their spike times sequence: T_n = ([n/p] + ϕ_n)qΔ where T_n denotes the nth spike time, [.] is the integer part of n/p and ϕ_n, one of the p phases defining the spiking pattern, or 2) their sequence of ISI, ISI_n = T_n+1 − T_n. A mode-locked sequence is thus defined by a set of p phases, or p ISIs, which repeats every qΔ (where Δ is the input period). The presence of ISI patterns can be displayed using ISI scattergrams, where each ISI is plotted against its following ISI. Because a periodic sequence of p ISIs is constituted of ordered pairs of ISIs, the sequence appears as a set of p points (see Fig. 1). ISI scattergrams have been used to reveal deterministic dynamic properties of datasets (Kantz and Schreiber 1997; Sauer 1994) and in electrophysiology, to show the presence of bursts in spike trains (Krahe and Gabbiani 2004).

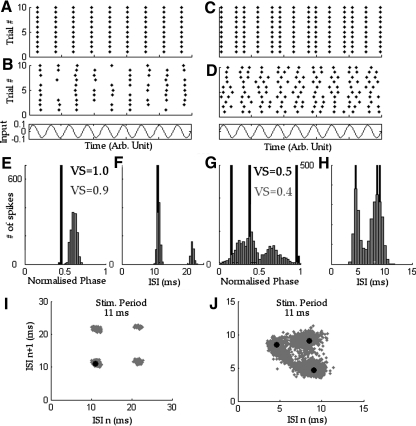
Fig. 1.

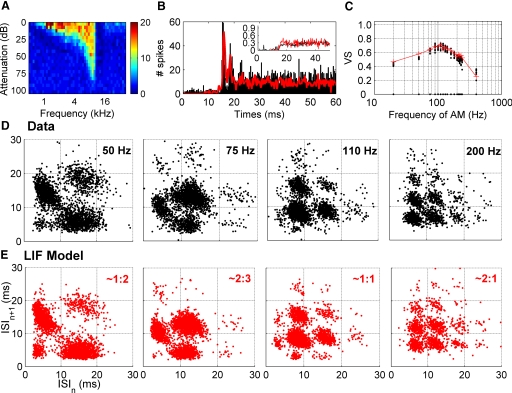
Examples of different patterns of spike timing in response to a periodic signal, demonstrated using a leaky integrate-and-fire (LIF) model with a sinusoidally modulated input. From top to bottom: A, precise phase-locked pattern of discharge [LIF parameters: τ = 7 ms, V_o = −65 mV, V_Thres = −50 mV, V_Reset = −70 mV, I(t) = 11.9*cos(2π*90*Hz*t) mV/ms]. B: the influence of additive Gaussian noise added to the input (D = 0.025 V/√s). The noise creates the random skipping behavior and widens the period histogram. C: an example of a 2:3 mode-locked pattern [LIF parameters: τ = 7 ms, V_o = −65mV, V_Thres = −50 mV, V_Reset = −70 mV, I(t) = 2.1 + 3.9*cos(2π*90*t) mV/ms]. The sequence of discharges is defined by a set of 3 phases and gives a low VS (0.51). D: adding Gaussian noise (D = 0.025 V/√s) to the previous LIF model broadens the distribution of phases decreasing the VS. E and F: period histogram and interspike interval (ISI) distribution of the 1:1 mode (black) and the stochastic 1:1 (gray). G and H: period histogram and ISI distribution of the 2:3 mode (black) and the stochastic 2:3 (gray). I and J: ISI scattergram representation of the modes. Black dots represent the sequence of intervals for the deterministic modes.

SURROGATE SPIKE TRAINS AND MODE-LOCKING CRITERION.

Mode-locked spike trains have by definition both specific ISI sequences and a set of preferred phases of spiking within an AM cycle. Displaying preferred ISI pairs with ISI scattergrams could have nothing to do with mode-locking. This would be the case if a spike train possessed the observed conditional ISI preference but was not locked to the AM cycle. Conversely, the observed conditional ISI structure could simply be inherited from a preference for spiking around certain phases. In this case, the observed ISI sequence would not be much different from phase-locking in the AN where it doesn't matter in which cycle a spike occurs as long as its phase within the cycle follow a given distribution. It is natural to conclude that chopper responses constitute a stochastic mode-locked spike train if the observed ISI dependencies were not sufficient to explain the stimulus locked structure (condition A) and if the stimulus locked structure was not enough to account for the observed ISI structure (condition B). Hence for the spike train to be mode-locked, we specified that the timing of spikes needed to match both the phase and ISI description of mode-locked discharges.

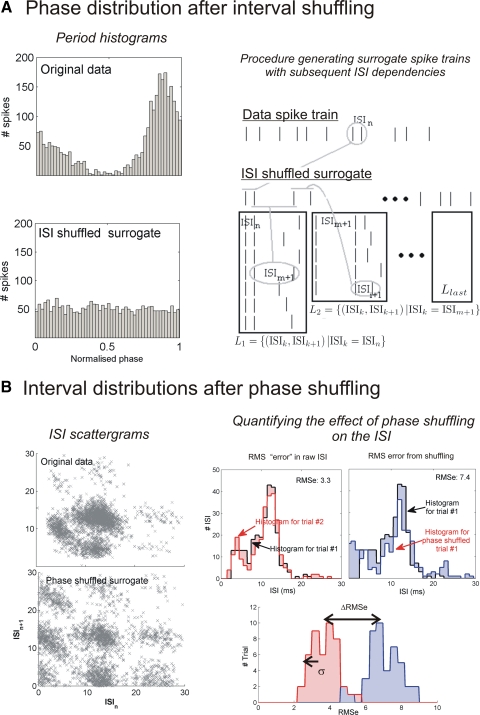
To test condition A, we created surrogate ISI sequences which maintain the subsequent ISI dependencies using the following shuffling procedure (see Fig. 3A): 1) randomly pick from the data one ISI, say ISI_n, and assign ISI_n to the surrogate sequence. 2) Find {k|ISI_k = ISI_n}, i.e., all the ISIs equal to ISI_n, and build the list of ISI pairs: L₁ = {(ISI_k, ISI_{k +1})}. And 3) randomly pick one pair from L₁, say (ISI_m, ISI_{m +1}) and assign ISI_{m +1} to the surrogate sequence. This maintains the ISIs pair dependencies: in the surrogate sequence an ISI of duration ISI_n is followed by one of duration ISI_{m +1} with a similar probability than the original ISI sequence. Then we repeat steps 1–3 until no more pairs remain. So we find in the data all ISIs that are equal to ISI_{m +1} build L₂ = {(ISI_i, ISI_{i +1})}, choose a pair in L₂ and assign ISI_{i +1} to surrogate sequence. To assess whether ISI dependencies are enough to produce phase-locking, we tested the surrogate spike train using a standard Rayleigh test. We denote by R_is the value of this test in the rest of this article.

Fig. 3.

Criteria for mode-locking using surrogate spike trains. A: phase distribution after interval shuffling. Period histogram (top) for spike trains from unit 808009 obtained from 10 repetitions of a 3-s-long AM tone (75 Hz, 20 dB above threshold) and after (bottom) the interval shuffling of a surrogate spike train obtained from a shuffling scheme keeping subsequent ISI dependencies. The phase preference observed in the original period-histogram is destroyed by the procedure. Right: the explanatory schema of the procedure used to maintain subsequent ISI dependencies. The procedure relies on finding pairs of ISI with similar 1st ISI, and re-ordering these pairs (see methods for more details.) B: ISI scattergram of the same unit before (top) and after (bottom) phase shuffling of the spike trains. The original ISI scattergram structure is destroyed. Right-most panel: how a z score is generated that measures how much ISI structure is lost by phase shuffling.

To test condition B, a surrogate spike train is created by randomly shuffling the phases of the genuine spike train (see Fig. 3B). The dissimilarity of ISI sequences for surrogate versus genuine spike trains was assessed by computing the root mean squared error (RMSe) between their ISI distributions. We compared this RMSe from the phase shuffling to the RMSe within data trials. The resulting statistic is expressed in the results as a z score (Z_ps)

$${\text{Z}}_{\text{ps}}=\frac{{\text{RMSe}}_{\text{ps}}-{\text{RMSe}}_{\text{Trials}}}{{\sigma }_{\text{Trials}}}$$

We considered that the phase shuffling had destroyed some of the original ISI structure if the z score was >2 (i.e., the distance between the means was above 2 SD of the intertrial variability—see Fig. 3B). Because the trial length was different between the vowel and harmonic stimuli (120 ms) compared with AM tones (3 s), vowels and harmonic stimuli trials were grouped into sets of 30 randomly chosen trials to obtain a valid estimation of the phase distribution.

A neuron was considered to show stochastic mode-locking if conditions A and B were satisfied. For the AM stimulus, for which a few units were tested with many AM frequencies, we focus in the population statistic on the number of cells showing mode-locking. We consider that a neuron was mode-locking if conditions A and B were satisfied for >50% of modulation frequencies tested. For vowels and harmonic complex stimuli, for which the number of stimuli tested varied from unit to unit, we give the population statistic in terms of numbers of mode-locked responses. Hence we consider the presence of mode-locking for the response of each unit to each stimulus separately.

One possibility that concerned us was that the phase shuffling procedure introduced many very short intervals (<1ms) that could not occur in the data simply due to refractory effects. To check that these short intervals were not affecting the z scores, we devised an alternative procedure to obtain surrogate spike trains with identical phase distributions but no ISIs <1 ms. To do so, we used a nonhomogenous Poisson process with a 1-ms dead time (absolute refractoriness) the intensity of which was obtained from the phase distribution. We computed for all units the z score required to pass condition B using this nonhomogenous Poisson process with dead time. This z score is denoted by Z_Poisson and is also shown in Figs. 4 and 5. The Z_Poisson values are generally lower than the z scores, indicating that some of the measured difference was attributable to this refractory effect. However, these values remain well above two whenever the phase shuffle generated z score is high. Note that this is not quite the same as a Poisson process being driven by the input to the unit.

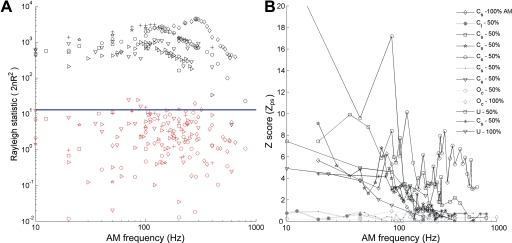
Fig. 4.

A: Rayleigh statistics for all 11 units recorded for AM pure tone stimulation (black symbols) and for their surrogate spike trains (red symbols) obtained from 1st shuffling scheme. For all cells, most surrogate conditions are below the significance level (blue line, R_is = 13.8). Hence, the locked structure is not a result of the ISI dependencies. B: z score index (Z_ps) for the phase shuffled surrogate (scheme 2, see methods). This index shows that the root mean squared error (RMSe) between data and phase-shuffled surrogate is >2 SD of intertrial variability for 5 of 7 choppers. Hence for all but 2 chopper units and 2 onset units, maintaining the phase preference isn't enough to explain the ISI structure. The symbol given for each unit is shown in the legend and is similar in A and B.

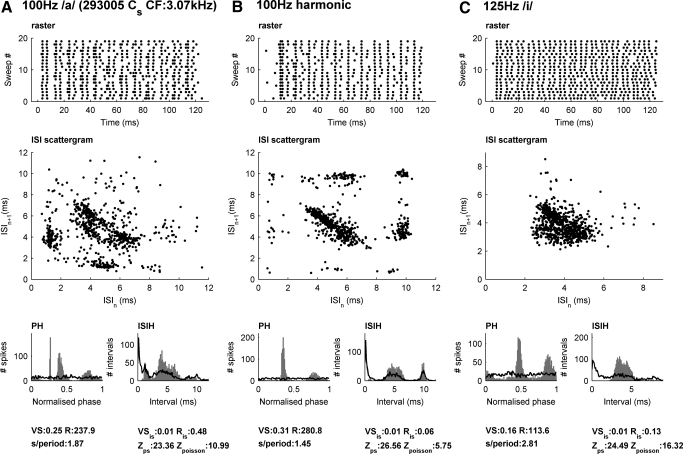
Fig. 5.

An example of a sustained chopper unit [3-kHz characteristic frequency (CF)] that shows complex modes of firing in response to vowels and harmonic complexes. A: the response to a steady-state 100-Hz vowel /a/. B: The response to a 100-Hz cosine-phase harmonic complex. C: the response to a 125-Hz vowel /e/. Top: a raster plot of spike times for 20 different presentations of the stimulus. Second row: ISI scattergrams. Third row: period histograms and 1st-order interval spike histograms for each stimulus. The histograms for the interval-shuffling (on the PH) and the period shuffling (on the ISIH) are superimposed in black. Bottom: measures of the firing behavior for the data and for the shuffled data. An R_is score of <13.8 (Rayleigh criterion) and a z score of ≥2 is required to meet our criterion for “mode-locking.”

BOOTSTRAPPING TEST OF SIGNIFICANCE.

Comparisons of some experimental measures across onset and chopper unit populations were made using bootstrap methods to predict the probability that two populations with the measured difference in means could arise if the two groups belonged to the same underlying population. The samples from both original populations were pooled, and then repeatedly randomly redistributed into two groups (500 times). For each resampling, the mean difference between the two groups was calculated. This generated a distribution of differences for the means, and allowed us to estimate the probability (our P value) that these two groups could have the observed difference in the mean if the samples were drawn from a single population.

Model

PERIODICALLY FORCED LIF MODEL.

We used a LIF model throughout this article to exemplify mode-locked response patterns, to reproduce the mode-locked pattern of discharges of recorded cells, and finally to help understand the organization of the responses to AM tones for a whole range of stimulation parameters (Supplementary Fig. S4).¹ The model has linear subthreshold properties, similar to a stellate cell, and generates action potentials by an ad hoc threshold mechanism. The dynamics of the membrane potential are given by the following equation

$$\frac{\text{d}V}{\text{d}t}=-\frac{\left(V-V_0\right)}{t}+I_{\text{appl}}\left(t\right)$$

where V denotes the membrane potential, V₀ the resting potential, τ the membrane time constant and I_appl (t) the input applied to the model. The input I_appl was either deterministic of the form I_appl(t) = I_o+ ε_ocos(2πft) or stochastic with I_appl(t) = I_o+ ε_ocos(2πft) + √2Dξ(t) where ξ(t) is the additive Gaussian noise and D its intensity (see Fig. 1). When fitting the data, we used shot noise driven by a model of the auditory periphery (see details in next paragraph). Whenever the voltage reaches the value V_Thres, it is reset to V_Reset. This highly nonlinear reset mechanism leads to complex synchronized patterns in response to periodic stimuli.

STOCHASTIC INPUT USED WHEN FITTING THE LIF MODEL TO VCN CHOPPER UNITS.

In our simulations of chopper unit responses to acoustic stimuli, the LIF neuron model received its input from an AN model of the guinea pig cochlea (Sumner et al. 2003b). This first stage employed a dual resonance nonlinear (DRNL) filter-bank simulating the nonlinear mechanical filtering in the ear (Meddis et al. 2001), a neural transduction stage from a model of the inner hair cell (Sumner et al. 2002), and a nonhomogeneous Poisson process with a dead time modeling the AN discharges. These discharges were low-pass filtered (1st-order Butterworth, cut-off: 300 Hz) to simulate the effect of the dendrite on auditory nerve excitatory post synaptic potential (EPSPs) (following Hewitt and Meddis 1993). Parameters are given in Supplementary Table S1.

The LIF neuron model was fitted to the data by varying several model parameters (by hand). Characteristic frequencies of the input AN fibers were always set at the BF of the chopper unit. Bandwidths and gains of the nonlinear part of the DRNL filter were varied to match the frequency response area recorded from the data. For each cell from the data set, only one type of fiber (high medium or low spontaneous rate) was input to the LIF neuron model. The type was selected by varying two calcium parameters of the IHC synaptic release (G_Camax, [Ca_thr]). Four more parameters were varied in the LIF neuron model to replicate the ISI scattergram pattern: the membrane time constant, the threshold voltage, the synaptic strength of the AN inputs, and the numbers of AN fibers.

RESULTS

Spike timing and mode-locking in response to periodic stimulation

Models of neurons often show synchronized spike trains in response to a periodic input (Aihara et al. 1984; Keener et al. 1981). These patterns of synchronization can be described as q:p “mode-locked” spike trains when p spikes occur in an orderly manner during q input periods. Infinitely many periodic spiking patterns of this sort can be defined (2:3, 5:13, q:p, etc.). Figure 1 shows two artificial examples of such firing patterns as well as their stochastic analogue. Figure 1A shows a 1:1 mode-locked spiking pattern in which there is one precisely timed spike on every cycle. The raster below it (Fig. 1B) shows a stochastic version of the 1:1 discharge pattern. Spikes no longer occur on every cycle but are still fairly precisely centered around a given phase. The VS quantifies the jitter around that single phase (Fig. 1E) and decreases when the noise increases. ISIs of the deterministic 1:1 mode are distributed at the period of stimulation (Fig. 1F). For the stochastic input, the ISI distribution has a multi-peaked structure centered at integer multiples of the stimulation period.

Figure 1C presents an example of a more complex spiking pattern: a 2:3 mode. The discharge pattern is defined by three precisely timed spikes distributed over two cycles. The phase distribution is multi-peaked leading to a VS = 0.5 although spikes are perfectly synchronized to the stimulus. A stochastic mode-locked response has even lower vector strength (Fig. 1D). Noise jitters the phases, widening their distribution. The ISI distribution for the deterministic pattern has three distinct intervals, but this structure is blurred for the stochastic 2:3 pattern (Fig. 1H).

To unravel mode-locked responses to a noisy periodic input, we use ISI scattergrams, which plot one interval against the next. Figure 1J shows that the deterministic 2:3 mode consists of three consecutive ISIs (9, 4.5, and 8.5 ms), which yields three points (black points at [9, 4.5], [4.5, 8.5] and [8.5, 9]) in the ISI scattergram. Note that the sum of ISIs adds ≤22 ms, twice the period of the stimulus. One can roughly consider two different actions of a noisy input (e.g., random arrivals of EPSPs from AN fibers) on the periodic response: a spike can be delayed or advanced (spike jitter), blurring the position of the points in the scattergram (Fig. 1, I and J; gray points) and a spike creation or deletion can occur. Examples of spike deletion occur in Fig. 1I for the 1:1 mode. The absence of a spike will create an ISI twice as long as normal that appears on the ISI scattergrams as a regular grid of points.

The responses in Fig. 1 were obtained from a LIF model of neuron driven by a 90-Hz sinusoidal input. The mode-locking is the result of the interaction between the time needed for the LIF neuron model to integrate an input up to threshold and the periodicity of its input. LIF models are a type of nonlinear oscillator that often show mode-locking behavior when stimulated periodically and for which a considerable body of mathematics exists.

Chopper VCN unit responses to AM tones

Because LIF models like the example in Fig. 1 have successfully reproduced many aspects of VCN chopper unit responses, we reasoned that chopper cells should show these complex modes of firing. Examples of ISI scattergram representations are given for a VCN chopper unit (808009) in Fig. 2. This unit shows a regular (CV = 0.3 - Fig. 2B quadrant) “chopping” response in its peristimulus time histogram (PSTH, B) in response to pure tones at CF, which classified it as a sustained chopper (C_s) (Blackburn and Sachs 1989). The unit also shows a band-pass VS (Fig. 2C) in response to AM tones at CF (100% modulation depth) with a best modulation frequency of 90 Hz. However, the modulation transfer function conceals a more complex temporal structure.

Fig. 2.

Example unit 808009. A: frequency response area. B: peristimulus time histograph (PSTH) of the unit (black) in response to a pure tone at CF 50 dB above threshold. The PSTH of the fitted LIF is superimposed in red. Inset: coefficient of variation increases but remains <0.3 (black: data, red: LIF model). C: synchronization index for all the frequencies tested. D: different examples of ISI scattergrams for 4 of 17 modulation frequencies presented. The ISI scattergrams have a structure similar to the one displayed for the fitted LIF model (E). For an AM of 50 Hz, the discharge rate per modulation cycle is 1.74, and the ISI scattergram pattern resembles the theoretical pattern with 2 points at coordinates (15 ms, 5 ms) and (5 ms, 15 ms). The underlying deterministic modes are given for each AM frequency.

Figure 2D shows ISI scattergrams for four different AM frequencies. The clusters in the ISI plane demonstrate ordered timing of spikes over a wide range of modulation frequencies. The discharge rate per cycle drops with increasing frequency of AM. Starting with a pattern of intervals close to a 1:2 mode (rate/cycle = 1.74, close to the theoretical 2 spike/cycle of a 1:2 mode) for a modulation frequency of 50 Hz, then passing through a 2:3 mode around 75 Hz (rate/cycle = 1.17, in theory 1.5 for a 2:3 mode) and a 1:1 around 100 Hz (rate/cycle = 0.94) before heading to a more sparse pattern of the form q:1 with q > 1 (1 spike every q cycle). One can check that the sum of the ISIs constituting one pattern adds up to an integer multiple of the modulation period. For instance, at 50 Hz, the two main clusters have ISI coordinates close to (5, 15) and (15, 5) adding up to the 20-ms period. Similarly, spike pattern clustering methods (Fellous et al. 2004; Schreiber et al. 2004) can be used to demonstrate the existence of different preferred phases. We show in Supplementary Fig. S1 how a 2:3 mode can be sorted in cycles with one spike and cycles with two spikes (see supplementary methods and Fig. 1).

Figure 2E (see also red lines in B and C) shows that a LIF model can match the sequential temporal response of this chopper unit. We used a model of guinea pig auditory nerve fiber activity (Sumner et al. 2002) as input for a LIF model (see methods). The fit of the LIF parameters was realized for two of the frequencies of AM presented (1st and last quadrant of Fig. 2E). The LIF model gives ISI scattergrams very similar to the data at all AM frequencies (see supplementary movies). We interpret this match for all AM frequencies as a demonstration that the chopper unit and LIF model responses are constrained by the same underlying dynamic: their discharges are in both cases reminiscent of mode-locked states.

Mode-locking criteria from surrogate spike trains

The patterns of intervals seen in Fig. 2 were typical of those seen in other cells in our sample, indicating that the stimulus envelope was being encoded by mode-locked patterns rather than just phase-locked (see supplementary movie). To quantify this, we considered that mode-locking arose from an interaction of the time since the last spike and the phase within the AM cycle. Therefore mode-locked spiking patterns are characterized by a dependence on both the spiking phases and ISIs. We used two different shuffling schemes to rule out the possibility that the observed spike train temporal structure could arise solely from either the phase preference or the conditional dependence between successive ISIs (see methods). The first shuffled spike trains aimed at determining whether the ISI clusters observed were only due to a specific pair dependency of ISIs without any link to the periodicity of the stimulus. The second scheme was to clarify the difference between mode-locked discharge patterns and discharges showing solely phase preference, such as those observed at the level of the auditory nerve. Figure 3, A–C, shows the effect of each shuffling scheme on the period histogram and the ISI scattergram.

We applied a statistical criterion to each unit of our data set for both shuffling schemes. Specifically, we tested that after interval shuffling, there was no longer a significant phase preference at the modulation frequency (R_is < 13.8) and that the mean squared error between ISI distributions before and after phase shuffling was at least twice the intertrial variability of the raw ISIs (Z_ps > 2; see methods). Figure 3A shows how interval shuffling is performed. Figure 4A shows the results of ISI shuffling on the AM responses. Maintaining pair statistics is not enough to explain the locking observed. Figure 3B shows scattergrams for the same unit before and after the phase shuffling, and diagrams of the derivation of the z score measure. Essentially this test compares how single trial ISI histograms differ before and after shuffling, relative to the intertrial variability of the unshuffled ISIs (see methods). Figure 4B shows that nearly all chopper units (5/7) of our dataset had very different ISI statistics when only their phase preference was maintained. This in turns means that most units showed significant mode-locking behavior. Modulation depth was important: mode-locking was observed in half of the cells tested with 50% modulation depth (6/11 units including 5/7 choppers, 2/2 unusual, 0/2 onset), while in 75% of the cells tested at 100% modulation depth (3/4 choppers). Each chopper displaying a mode-locking spiking pattern could be fitted with a LIF model (see supplementary table). The root mean squared (RMS) error between the VS of the data and of the LIF model over all seven chopper cells and for all their AM frequencies, was 0.087 (the Fig. 2 fit achieves an RMS error of 0.108).

Mode-locked spike trains in response to complex harmonic stimuli

To further explore the extent to which complex spiking patterns occurred to other periodic stimuli, we then applied similar analyses to the responses of a larger population of chopper and onset units. This previously published dataset (Winter et al. 2003) described the relationship between different measures of temporal coding (ISI histogram peak, auto-correlation, and VS) and the fundamental frequency (F0) of spectrally extended stimuli (vowels and cosine phase harmonic complexes). We reasoned that responses to these stimuli might also show stochastic mode-locked spiking patterns. We considered 24 chopper and 33 onset units, all with CF >1.5 kHz, so as to minimize the role of locking to individual harmonics.

Figure 5 shows the responses of a sustained chopper (C_s unit 293005) with high CF (3 kHz) to three different stimuli. In A and B, we display the responses to two stimuli with similar fundamental frequency of a 100 Hz: a 120-ms steady-state vowel /a/ (A) and a cosine phase harmonic complex (B). Figure 5A shows responses close to a 1:2 mode (rate per cycle = 1.87) with clusters in the ISI scattergram at (4 ms, 6 ms) and (6 ms, 4 ms), but almost no 10-ms intervals. Hence first-order ISIs would not show F₀ encoding in this case. In Fig. 5B, this unit responds to a complex tone with same F₀ but with a different spiking pattern. The ISI scattergram shows in part similar clusters at (4, 6) and (6, 4) but shows also locking to the fundamental period (10-ms intervals), which is clear even in the spike raster (the 1st 20 repetitions of 100 are shown). Therefore periodic stimuli with the same period but different envelopes create patterns of spiking organized around a different structure of intervals. In C, we show the responses of the same chopper unit to the vowel /i/ with a fundamental of 125 Hz. The pattern of spikes is centered more closely around the [2, 6]-ms ISI range but still considerable regularity is clear in the raster. Two clusters are just about visible in the scattergram at (5, 3) ms and (3, 5) ms. A bimodal structure is also clear in the period and interval histograms for these stimuli. Indeed the phase distribution resulted in low VS despite the precision of firing within the phase.

For all three stimuli, the spiking patterns of this unit could not be accounted for by their phase or paired ISI structure. Applying the same phase and interval shuffling tests as for the AM stimuli gave a nonsignificant Rayleigh test (R_is < 13.8, shuffled phase is superimposed in black in Fig. 5) and large Z score (Z_ps, >2, shuffled ISI is shown in black in Fig. 5). The CF of the unit is important here (3 kHz) as it falls above the phase locking limit but is still well driven by the vowel stimuli. This unit is unlikely to be responding to significant energy from the low-numbered harmonics. Instead it is most likely driven by envelope of the harmonics around 3 kHz. From this example, it is clear that broadband harmonic stimuli produce complex yet noisy periodic spiking patterns in chopper units, and that the particular pattern of spiking is sensitive to the stimulus envelope. Two further examples of chopper units are given in the supplementary material.

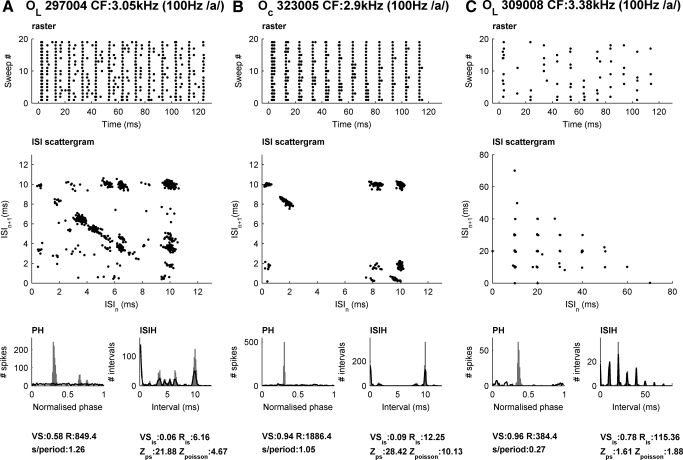
We also observed complex responses in VCN onset units. Figure 6 shows further examples of responses to the vowel /a/ (100-Hz fundamental) from three different onset units. All three units have a high probability of firing at a particular phase, but although all have a similar CF (∼3 kHz), they respond quite differently in other respects. The left-most panel (an O_L unit) is an example of a highly complex pattern of spikes, and our criteria indicates that neither phase nor intervals alone can account for this spiking pattern. In between the spikes at the dominant phase, which form a large number of 10-ms intervals seen as in the scattergram at (10, 10) ms and also in the ISIH, further spikes produce several sets of intervals, forming a diagonal set of interval pairs in the ISI scattergram. These diagonals tend to occur in our data whenever the dominant interval corresponds to the fundamental, and the unit is firing in close to a 1:1 mode. This cell is firing almost once per cycle (1.26 spike/period, this is very clear in the raster) and thus is almost perfectly entrained to the F₀. However, the extra intervals markedly reduce the VS. The O_c unit in the middle panel is even more nearly perfectly entrained to the 100-Hz fundamental (VS 0.94, 1.05 spike/period) with an occasional extra spike occurring precisely 2 ms after the dominant phase. This unit also shows a high z score, but the Rayleigh indicates that the amount of phase structure that can be accounted for by the interval structure alone is significant. In the right-most column of Fig. 6 is an example of an O_L unit that behaves much like a modulated Poisson-process. Both the phase and interval structure are well described by the shuffled versions of each other. The resemblance to a modulated Poisson process is further supported by the fact that we also find a low z score if, instead of using phase shuffled surrogate, we use a surrogate spike train from a nonhomogenous Poisson process with a 1-ms dead time that is modulated by the measured phase distribution. We also thereby verify that short ISIs in the phase shuffled surrogate do not underlie high z scores (see methods). The stochastic but locked nature of the firing is clear in the raster, and also in the ISI scattergram, by the grid-like pattern of intervals, decaying approximately exponentially with increasing intervals. In general, onset units were consistent with previous reports (Godfrey et al. 1975; Rhode and Smith 1986; Winter et al. 2003) in locking excellently to the fundamental, but they differed greatly in the way they did this. Some were almost perfectly entrained, some showed some extra structure, and some fired stochastically while still having a high VS.

Fig. 6.

The responses of 3 different onset units (all with a CF ∼ 3 kHz) to a 100-Hz vowel /a/. The representation is the same as for Fig. 4. A: onset-C unit showing “complex-modes of firing” (i.e., meeting our criteria for mode-locking). B: an onset-C unit that shows almost perfect entrainment (1:1 mode-locking). C: an onset-L unit that behaves like a Poisson process.

Figure 7 shows summary statistics for a population of units (24 chopper units, 33 onset units, all with CF >1.5 kHz) in response to the 100-Hz /a/, the 100-Hz harmonic complex, and the 125-Hz /i/ (thus each unit can be counted more than once if multiple stimuli were presented). These were classified according to the criteria of Blackburn and Sachs (1989) for chopper units, and Winter and Palmer (1995) for onset units. We found that of 55 responses in the chopper units, 44 (80%) met our criteria for displaying spiking patterns reminiscent of mode-locked states, almost irrespective of whether they were classed as transient (79%) or sustained (82%) choppers. In the case of onset cells, 37/90 (41%) responses (39% of O_L responses, 46% of O_c responses, and none of 4 O_I met our criteria.

Fig. 7.

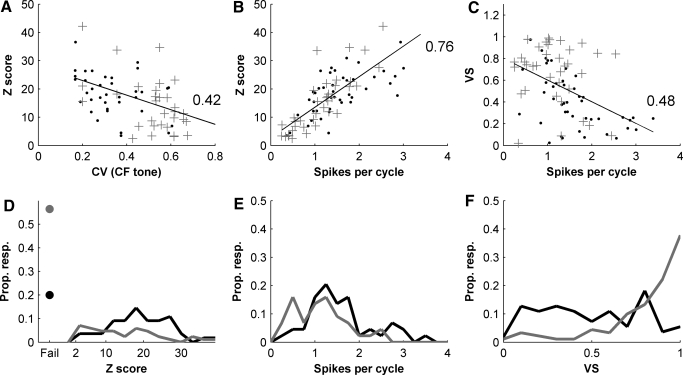
Population measures of the responses to complex periodic stimuli in chopper (blue points) and onset (red crosses) units. Blue lines and points indicate chopper unit responses. Red lines and crosses indicate onset unit response. Numbers within axes give correlation coefficients (see text for statistical significance). A: regularity of a pure tone at CF, 50 dB above unit threshold (calculated from 30 to 50 ms after tone onset) vs. Z score for units passing mode-locking criteria (ML units). B: z score vs. number of spikes per cycle for ML units. C: vector strength (VS) vs. spike per cycle for ML units. D: distribution of z scores across units. Non-ML units are shown as points at “fail.” E: distribution of spikes per cycle across ML units. F: distribution of VS across all units irrespective of ML criteria.

For the units that met the mode-locking criteria, we observed a negative relationship between the CV in response to a pure tone at CF and the z score (Fig. 7A, R = 0.42, P < 0.0001) and between the rate per cycle and the z score (Fig. 7B, R = 0.76, P ≪ 0.0001). The relationship between z score and CV partly reflects differences between choppers and onset units. In our sample of cells that passed both our criteria, we found that onset cells have on average a significantly lower z score than choppers (chopper units: 19.4 ± 9.3; onset units: 15.1 ± 10.6, means ± SD; P < 0.05 nonparametric bootstrap test), and onset cells also tend to have a higher average CV than chopper units (due to the tendency of onset units to show less sustained discharge to a pure tone) (Winter and Palmer 1995). However, this relationship is not simply a difference between different cell types. Noticeably the relationship still holds when considering choppers responses alone (R = 0.5, P < 0.001). This negative relationship between the regularity (CV) of the response and the z score implies that more regular units tend to show more complex ISI structure in response to sounds with envelope modulations.

The second relationship, between z score and spikes per cycle, again partly reflects differences between unit types. In addition to having slightly higher z scores, chopper units have a larger number of spikes per period (1.6 ± 0.7) than the onset population (1.1 ± 0.6, different at P < 0.01 for a bootstrap test). However, this relationship is also strong in the chopper and onset populations considered separately (chopper units: R = 0.62, P ≪ 0.001; onset units: R = 0.72, P ≪ 0.001). This suggests that the more spikes per period, the less of the interval structure could be accounted for by the phase structure. It is important to note that this is not what would be expected of a Poisson process, where spike rate increases without any increase in z score (there was no correlation in a simulation of modulated Poisson processes—not shown). There was also a relationship between the number of spikes per cycle and VS (Fig. 7C, R = 0.48, P ≪ 0.0001). This of course fits with the example models shown in Fig. 1, which makes it clear that VS does not well characterize the precision of periodic coding when there is more than one spike per period. We observed no correlation between VS and z score. All these relationships held if we derived the z score from a modulated Poisson-process with a 1-ms dead time (see methods).

The points on the left of Fig. 7D indicate the proportion of each population that failed the Rayleigh test. In other words, after interval shuffling the phase locking to the fundamental was still significant. Clearly, a much larger proportion of onset responses (56%) failed this first criteria compared with choppers (20%). These proportions correspond almost exactly to the proportions that passed both tests, indicating that almost all failed to make the criteria for mode-locking because they failed the Rayleigh test. We observed that the failure of the Rayleigh test only happens when VS is high. We interpreted this in the following way: very reliably spiking near the same phase was resulting in very small phase jitter buildup during interval shuffling and hence in a significant phase locking after ISI shuffling. This is true for both the chopper (0.81 ± 0.11) and the onset (0.91 ± 0.11, P < 0.01 for a bootstrap test of significance) populations. Thus we see that nearly all cells fail to pass our test for mode-locking because they are phase locking almost perfectly to the fundamental. However, VS and the Rayleigh test do not distinguish between Poisson like stochastic firing at a particular phase in the period, and when a cell is reliably firing on every cycle, as in a 1:1 ratio mode-locked state, or entrainment. The number of spikes per cycle for the chopper units that failed was close to 1 (0.96 ± 0.28), suggesting that these cells were well entrained to the stimulus period. For onset cells the number of spikes per cycle was slightly lower and more variable (0.77 ± 0.46, the difference of means was not significant for a bootstrap test). Our interpretation here is that some cells are behaving in a roughly Poisson like manner, while others are responding in a 1:1 mode.

From these analyses, it is clear that both chopper and onset units show complex spiking patterns in response to periodic stimuli of different types. Consistent with our starting hypothesis these are reminiscent of mode-locking, poorly described by the vector strength and strongest in chopper units. Furthermore, these spiking patterns are sensitive to both the fundamental and the spectrum of the stimulus.

DISCUSSION

We have shown here the existence of mode-locked spiking patterns in VCN chopper units in response to SAM tones, steady-state vowels, and harmonic complexes. Mode-locking behavior is observed in chopper and onset units (all of which are presumed to be multipolar cells) but is strongest in chopper units. Our insights originate from a LIF model that reproduces the sequential pattern of ISIs. The mode-locked behavior in VCN neurons is stochastic, and although clearly not-random, it is difficult to ascribe a particular mode to a particular spike train.

We specifically hypothesized that chopper unit responses should show mode-locked responses because of the previous success of LIF models in modeling them. The model best fits were obtained for few ANF inputs (4–14, see supplementary table), close to estimations obtained in mice VCN slices using minimal ANF electrical stimulation (Ferragamo et al. 1998). Although we did not attempt to fit models to the responses to vowels, the responses seen to these stimuli were nevertheless qualitatively similar to the mode-locking seen in response to AM, and it is likely that a large portion of these responses could be reproduced with fairly simple LIF based models (Hewitt and Meddis 1993).

Two of the 11 units stimulated with AM tones were onset-choppers, and these also showed clustered interspike interval scattergrams, which could be accounted for by the phase distribution alone. This tendency was also evident in the population of onset units stimulated with broad band signals (complex tones and vowel sounds) where around 50% of the spiking patterns observed can be explained by their phase preference. However, the other half of onset units showed more complex spiking patterns. In many instances, onset cells locked almost perfectly to the fundamental. This behavior, often called entrainment, corresponds to a 1:1 mode with a single preferred phase and ISI. Onset-choppers are stellate cells, they show regular spiking in response to injected current (type-I spiking) (Oertel et al. 1990) and considerable temporal integration (Palmer and Winter 1996), but they differ from other stellate cells in their intrinsic currents (Oertel et al. 1990). They also receive convergent inputs from many different ANFs. These factors may conspire to ensure that firing in these cells remains close to the 1:1 mode.

In VCN, the regular spiking of stellate cells contrasts with the phasic spiking of bushy cells and octopus cells (Bal and Oertel 2001), known to come from I_KLT (Rothman and Manis 2003), a low-threshold potassium current, present in bushy and octopus cells. This current limits integration and fosters coincidence detection. For spherical bushy cells responses are similar to those of the auditory nerve because they are connected by only a few large auditory nerve synapses (endbulbs). Thus we can expect both types of bushy cells to show a stochastic type of behavior more similar to the ANFs. We did not have any data from primary-like units with which to test this hypothesis. However, it is possible that some of the onset responders in our sample are octopus cells.

We have undertaken here a description of the observed spiking pattern from the point of view of forced dynamical systems. An alternative approach is to use a purely statistical description of spike times. Johnston and colleagues (1986) modeled chopper responses to pure tones in the lateral superior olive using stochastic point processes. In this case, the point process needs to be more regular than a Poisson process, i.e., the model has a preferred ISI. Rather than obtaining regularity through the hazard function of a renewal process, we set it from biophysical parameters in the LIF model, one advantage being that the description remains valid for time varying stimuli, such as AM tones. It also shows that chopper intrinsic dynamics is a main feature of the response to periodic stimuli. The intrinsic frequency of chopper units was already crucial in some pitch processing models (Wiegrebe and Meddis 2004) and has been reported by Kim et al. (1990) to correlate with the best temporal modulation frequency.

The relation between intrinsic chopping frequency and best temporal modulation frequency is clearly addressed by the theoretical framework of mode-locked synchronization. Indeed there is a clear organization of mode-locked responses in chopper units across frequency of AM as is displayed in Fig. 2 (see also the supplementary movies). For the fitted model, reducing the noise shows how mode-locked discharges are organized in an orderly manner in parameter space (see Supplementary Fig. S4). Progressively increasing stimulation frequency, one goes from p > q modes, through the 1:1 mode and toward q > p modes for higher frequencies. The observation of Kim et al. is thus in accordance with our observation that the 1:1 mode displays the strongest VS and that in models with sufficiently low noise, the 1:1 mode converges to the chopping frequency at 0% modulation depth (Supplementary Fig. S4). Previous studies on spike timing reliability (Hunter et al. 1998; Schreiber et al. 2009) also point at maximum reliability at a modulation frequency equal to the intrinsic frequency.

In conclusion, this study demonstrates mode-locked spiking responses to AM tones, vowels, and harmonic complexes in VCN chopper and onset units. Early work (Knight et al. 1972) on 1:1 locking pointed at the deleterious effect that synchronization represents for stimulus encoding in LIF populations when compared with asynchronous firing. However, recent work has shown how LIFs complex spiking patterns can provide specific coding advantages (e.g., nonuniform sampling stimulus reconstruction) (Lazar 2005). The ISI dependencies displayed by mode-locked spike trains are intriguing as it is known that subsequent ISI dependencies can increase information transfer by spike trains (Chacron et al. 2004). Moreover, knowledge of both the phases and p:q value are important to characterize precisely the stimulus parameters. For example, although a 1:2 mode exists at 44 Hz with 100 to 30% of modulation depth in Supplementary Fig. S4C, the phases at 100 to 30% are different (as seen by the change in VS) and allow disambiguation. Likewise AM depth, frequency, and envelope shape all influence the mode-locked spike train pattern. For example, it is clear in Fig. 5 (and the supplementary figures) that the patterns of spikes are sensitive to whether the stimulus is a vowel or a harmonic complex. Hence the exact sequence of ISIs might carry additional information about the stimulus. For instance, ramped and damped AM tones, which are known to affect neural responses in CN (Pressnitzer et al. 2000) and change roughness perception (Pressnitzer and McAdams 1999), will produce different sets of mode-locked patterns. Mode-locking could thus play a role in encoding multiple features of complex stimuli, possibly more sensitive to stimulus parameters than a pure Poisson based coding. Further work, describing the responses to a larger range of stimuli (such as IRNs or periodic signals in noise) is needed to fully relate mode-locking to auditory temporal processing. A linear analysis of spatiotemporal interactions along the frequency axis has already proven to be advantageous for temporal representation (e.g., Shamma 1985). Thus a full characterization of spatiotemporal mode-locked encoding constitutes an attractive problem from both the experimental and theoretical perspective.

GRANTS

J. Laudanski was supported by a Marie Curie Early Stage Researcher Training Fellowship from the European Commission (EC Contract No: MEST-CT-20050-020723). C. Sumner and A. R. Palmer were supported by the Medical Research Council.