Antisaccade Cost Is Modulated by Contextual Experience of Location Probability

Abstract

It is well known that pro- and antisaccades may deploy different cognitive processes. However, the specific reason why antisaccades have longer latencies than prosaccades is still under debate. In three experiments, we studied the factors contributing to the antisaccade cost by taking attentional orienting and target location probabilities into account. In experiment 1, using a new antisaccade paradigm, we directly tested Olk and Kingstone's hypothesis, which attributes longer antisaccade latency to the time it takes to reorient from the visual target to the opposite saccadic target. By eliminating the reorienting component in our paradigm, we found no significant difference between the latencies of the two saccade types. In experiment 2, we varied the proportion of prosaccades made to certain locations and found that latencies in the high location-probability (75%) condition were faster than those in the low location-probability condition. Moreover, antisaccade latencies were significantly longer when location probability was high. This pattern can be explained by the notion of competing pathways for pro- and antisaccades in findings of others. In experiment 3, we further explored the degrees of modulation of location probability by decreasing the magnitude of high probability from 75 to 65%. We again observed a pattern similar to that seen in experiment 2 but with smaller modulation effects. Together, these experiments indicate that the reorienting process is a critical factor in producing the antisaccade cost. Furthermore, the antisaccade cost can be modulated by probabilistic contextual information such as location probabilities.

INTRODUCTION

The saccadic eye movement system is an excellent model for studying the flexibility of human behaviors because of its extensively investigated neurophysiological basis (Basso and Wurtz 1997; Carpenter 1999; Schall 2004; Schall and Hanes 1993; Schiller and Kendall 2004; for review see Schall 2001, 2009; Schall and Thompson 1999). It is well known that pro- and antisaccades reflect the operation of different cognitive components. Over the last decade, researchers have shown that the saccadic eye movement system can be influenced by a wide range of cognitive factors, including attention (Baldauf and Deubel 2008; Deubel and Schneider 1996; Hoffman and Subramaniam 1995; Kristjansson 2007; Kristjansson et al. 2001, 2004;), learning (Carpenter and Williams 1995), working memory (Geng et al. 2008; Stuyven et al. 2000), and decision-making processes (Ludwig et al. 2005; Milstein and Dorris 2007). Such differences between pro- and antisaccade latencies highlight the flexible control of the oculomotor system. Indeed, patients with prefrontal lobe lesions display difficulties in this control (for review, see Everling and Fischer 1998; Munoz and Everling 2004). These patient studies on cortical lesions are valuable as they provide us with insights into how the brain performs the antisaccade task. Together these clinical studies and analysis of performance among healthy subjects may give clues to advance our understanding of these aspects of saccadic eye movements.

Prosaccade and antisaccade tasks

In the laboratory, different types of saccade tasks have been designed to study the underlying mechanisms of pro- and antisaccades. In a prosaccade task, subjects are instructed to saccade their eyes to a peripheral target. In an antisaccade task, subjects need to suppress the impulse to look automatically toward a singleton, and instead, look away to the target's mirror position. This involves manipulation of stimulus-response compatibility that decouples the stimulus encoding stage and response preparation stage (Juan et al. 2004, 2008; Sato and Schall 2003) and has been widely used in clinical studies (Hutton 2008; Munoz and Everling 2004). Many researchers have reported a qualitative difference between pro- and antisaccades. Specifically, antisaccades are more prone to errors and take longer to initiate. The prolonged latency is often referred to as the antisaccade cost (Hallett 1978). To explain the antisaccade cost, Everling and Fischer (1998) argued for an important role of inhibition and proposed that antisaccades require two subprocesses: suppression of an automatic response and generation of a saccade in the opposite direction. In addition, studies have also indicated that damage to human frontal cortex can increase the number of erroneous prosaccades in an antisaccade paradigm (Munoz and Everling 2004).

Role of attention in saccade generation

Kristjansson et al. (2001) explored the role of attention in antisaccade performance by asking participants to perform them as part of a dual task paradigm. The main task was to make either a prosaccade when the fixation cross suddenly moved away from the center of the display to periphery or an antisaccade to the mirror location of the target. The secondary task was a detection task involving randomly moving dots, which required the deployment of attentional resources. Each participant performed in two conditions. In one condition, participants had to perform the saccade task and ignore the secondary task. In the other condition, they had to perform the secondary task at various time points before target onset. Surprisingly, when the secondary task was introduced, antisaccade latencies became faster than in the saccade-only condition. This increase in efficiency was not observed for prosaccades. Kristjánsson et al. suggested that introducing a secondary task at or before the initiation of saccade interfered with the tendency to make a reflexive prosaccade, thereby generating faster antisaccades. Kristjansson and colleagues (Kristjansson 2007; Kristjansson et al. 2001, 2004) further proposed that these results are consistent with the “competing pathway” concept of pro- and antisaccades, which states that inhibiting one type of saccade improves performance on the opposing one.

Studies have addressed the issue of pro- and antisaccades engaging different oculomotor components (Kristjansson 2007; Munoz and Everling 2004). What is unclear is why antisaccades have longer latencies than prosaccades, even across many different paradigms. Some neurophysiological studies using antisaccades with macaque monkeys have found minimal or no antisaccade cost (Gold and Shadlen 2003; Gottlieb and Goldberg 1999) or even latency benefits for antisaccades (Amador et al. 1998; Gottlieb and Goldberg 1999). Recently, Juan et al. (2008) applied a task composed of pro- and antisaccade trials to study the temporal and functional role of the human frontal eye field (FEF) in covert attention and saccade preparation. In their paradigm, participants were instructed to make an eye movement either toward or away from a colored singleton, depending on its orientation (e.g., vertical: prosaccade; horizontal: antisaccade). They showed that FEF is critically involved in the task in two distinct time windows. The early window was argued to be related to visual processing of the singleton and the latter one for saccade preparation. The pattern of these results was consistent with previous findings in awake-behaving monkeys (Juan et al. 2004). Furthermore, in the behavioral results, it was shown that the antisaccade cost that was present in a blocked design was diminished in an interleaved design. These results could be explained by the different attentional requirements between a blocked and an interleaved design: in an interleaved design, participants do not know which type of saccade to program and execute until a cue is given, thus the programming of a pro- or antisaccade have to be withheld until the cue has been fully analyzed. In addition, Olk and Kingstone (2003) systematically compared performance between pro- and antisaccades with three manipulations (interleaved design, oculomotor inhibition, fixation effect) in various conditions. In their paradigm, participants made a saccade in response to a peripheral arrow. In the blocked design, the direction of the arrowhead was irrelevant, and a significant antisaccade cost was found. In the interleaved design, however, the arrowhead was critical for deciding which type of saccade to make. Therefore in this paradigm, the analysis of the peripheral target always preceded the preparation of a saccade, making the peripheral cue not only critical to selection of target location but also selection of saccadic type. Olk and Kingstone found that antisaccade latencies were always longer than prosaccades in all conditions although the magnitude of the difference varied. Based on this finding, they highlighted two processes that are unique to antisaccades and are possibly the cause of its latency cost: first, the application of inhibitory processes, and second, the process of reallocating attention from the visual target toward the required saccadic location. In experiment 1, we test their second proposal, the reallocating attention hypothesis, by removing attentional reorientation from a version of their saccade task.

Expectancy and saccadic performance

A number of studies have shown that people are sensitive to the degree of expectancy of where a target will be presented, such that targets in likely locations are detected more quickly than targets in less likely locations (Carpenter and Williams 1995; Gmeindl et al. 2005; Milstein and Dorris 2007; for a review see Summerfield and Egner 2009). In animal studies, Basso and Wurtz (1997) first described how the firing rate buildup of neurons in monkey superior colliculus was reduced when previous task experience (probability) increased the certainty of a target location. Dorris and Munoz (1998) also studied how saccadic reaction times and buildup of neuronal activity in monkey superior colliculus were affected by probability. Data showed that, when saccades were directed toward a particular receptive field more frequently than to other locations, the firing rates of the neurons for that particular receptive field would become higher before the initiation of each saccade. These results suggest that the probabilities of saccadic locations can modulate the buildup of neuronal activity, which consequently influences saccade latencies.

Moreover, Miller (1988) studied the effects of absolute and relative target position. A target letter had to be detected in a sequence of four letters in which one location had a higher probability of containing the target. The letter sequence was occasionally offset in horizontal position so it could be determined whether the effects of this higher probability on performance depended on absolute position or the position in the sequence (relative position). It was found that target location probability benefited from both types of spatial relationship. In a related series of studies, Geng and Behrmann (2005) investigated the role of targets' spatial probabilities in a visual conjunction search task. Their experiments addressed how probabilistic regularities of the target can bias visual processing, and how any observed modulatory effect can be related to the concepts of endogenous and exogenous attentional cues. They contrasted the probability cue (random, high, or low) against a standard explicit arrow cue (explicit endogenous cue) and a salient exogenous flash in the periphery (exogenous cue). They found that spatial probability is independent of any benefit afforded by the explicit endogenous cue (the effect was purely additive) but interacted with the salient exogenous cue. These results led them to hypothesize that the probability cue operated through a conjunction of spatial and object information and was processed within a system shared by explicit spatial cues. All in all, these studies showed how motor behaviors can be modulated both physiologically and behaviorally.

In this study, we aimed to investigate whether the probability effects observed in the context of covert visual selection can be extended to the pro- and antisaccade task to elucidate the dynamic mechanisms of cognitive flexibilities in humans.

METHODS

General methods

The three experiments of this study used the same general paradigm. First we describe the general methods which applied to all three.

PROCEDURE AND DESIGN.

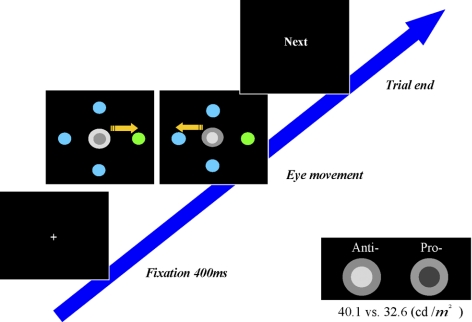
Before the experiment, participants were informed about the nature of the task they were to perform. Participants were seated in a dimly lit room and were asked to place their heads on a chinrest that was 85 cm from the monitor. A calibration procedure was performed at the start of the experiment. Experiments started with 60 practice trials, followed by the formal experimental sessions. Each trial started when participants fixated at the central fixation point (0.5°) for 400 ms. A search display consisted of a saccadic indicator in the center and four stimuli in the periphery was then presented. Participants were required to make a single saccade (Fig. 1) in the direction specified by the saccadic indicator. The saccadic indicator consisted of two concentric circles in the center. If the inner circle was darker than the outer circle, participants were to perform a prosaccade to the colored singleton in the periphery. If the inner circle was brighter than the outer one, an antisaccade away from the colored singleton was required. Participants were instructed to perform the task as quickly and accurately as possible. After the completion of each trial, the computer displayed a “Next” in the center. The participant could either rest or press the space bar to continue onto the next trial at anytime. To perform this task, two cognitive steps should be applied. One is to decide whether a pro- or anti-saccade should be executed and the other is to localize the position of the singleton for the saccadic location. It may be disadvantageous to process the location of the singleton before the discrimination of the central task, because participants may need to refrain from a motor preparation programming from the singleton (if it was an antisaccade task). Therefore the most efficient way to perform the task is to discriminate the contrast in the center at first and then to localize the singleton for saccade position.

Fig. 1.

The fixation cross was presented for 400 ms. After that, the target and the cue was displayed until participants responded or 2.5 s of no response. In this paradigm, participants were instructed to make a prosaccade toward the colored singleton when the inner circle was darker than the outer concentric circle. When the inner circle was brighter than the outer one, participants needed to make an antisaccade away from the colored singleton (the arrows were not presented on the screen during the actual task).

APPARATUS AND STIMULI.

Stimuli were presented on a 19-in color CRT (View Sonic Professional Series P95+) with 1,024 × 768-pixel resolution and 100-Hz refresh rate. Eye movements were recorded by means of an Eyelink II eye-tracker (SR Research, Ontario, Canada) with a 500-Hz sampling rate. An eye movement was considered a saccade when its velocity exceeded 30°/s and its acceleration exceeded 8,000°/s². Only the first saccade made by the participant was collected. In the search display, the saccadic indicator (concentric circles 2°, contrast of brightness 40.1/32.6 cd/m²; Fig. 2) was always in the center, and the four circles were 6.5° from the fixation cross at the left, right, up, and down positions. There were two versions of the singleton that were blue (Commission International de l'Eclairage, x = 0.18, y = 0.19) among green (x = 0.27, y = 0.51) circles and green among blue circles. Colors in the array were approximately isoluminant (blue, 27.7 cd/m²; green, 28.4 cd/m²) presented on a uniform gray background.

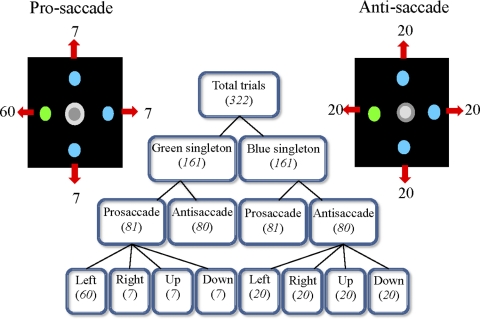
Fig. 2.

Illustration of the design in experiment 2. The number in the figure is the number of trials requiring saccades to the 4 locations. Note that this example is only 1 block that the left position has the higher probability to be the prosaccade target.

Experiment 1

The purpose of experiment 1 was to test the reallocating attention hypothesis. We use a new paradigm that was designed to equate the reorienting process between pro- and antisaccades. Unlike Olk and Kingstone's paradigm (2003), in this paradigm, the saccadic indicator was always in the center of the display, so the participants did not need to move their attention away from the center before initiating a saccade. If antisaccade cost indeed originates from attention reorientation, as argued by the reallocating attention hypothesis, we would expect to observe no significant differences between pro- and antisaccade latencies in this paradigm.

PARTICIPANTS.

Eight students between the age of 18 and 25 yr from the National Central University participated in experiment 1. All of them had normal or correct-to-normal vision. Each participant received monetary reward for their participation on completion of the experiment.

DESIGN.

Participants first performed 60 practice trials and then proceeded to one block of 240 trials. Pro- and antisaccade trials were interleaved (Juan et al. 2008; Olk and Kingstone 2003), which means that the programming of a pro- or antisaccade had to be withheld until participants had finished the analysis of the central saccadic indicator. The order of trial types was randomized and equal in number in the interleaved block.

Experiment 2

To test whether location probability would affect antisaccade cost as predicted by the competing pathway account, we applied one level of location probability (75%) in two blocks (1 with the prosaccade target 75% on the right and 1 with the target 75% on the left). To the best of our knowledge, no one has systematically tested the effect of target location probability on antisaccade cost (cf. Koval et al. 2004). According to the literature on the latencies of prosaccades and antisaccades, it is intuitive to first manipulate location probability on prosaccade trials. The manipulation of probability on the antisaccade trials with this paradigm would provide less clear-cut data because the saccadic location is contingent on the position of the singleton. Therefore the prosaccades will be inevitably sharing the probability benefit that was designed to be beneficial only for the antisaccades. Consequently, we only manipulated the probability of prosaccades in this study. According to the aforementioned ideas relating to spatial probability (Geng and Behrmann 2005) and the competing pathways (Kristjansson 2007; Kristjansson et al. 2001, 2004) between pro- and antisaccade, we formulated three predictions for this experiment. 1) Prosaccades made to locations of higher probability (i.e., 75%) would be faster than those with lower probability because of the effect of probability. 2) Faster prosaccades implies that it is more difficult to suppress the urge to program/perform prosaccades; therefore a slower antisaccade RT will be observed in those trials with the high probability location. Consequently, a significant antisaccade cost would indicate that the underlying competing pathway has been biased by the prosaccade. 3) In experiment 1, we showed that, when location probability was held constant, antisaccade RT did not significantly differ from prosaccades RT. We therefore predict that the antisaccade cost will not be observed in locations with low prosaccade probabilities.

PARTICIPANTS.

Ten students between the age of 18 and 25 yr from NCU participated in experiment 2. All had normal or correct-to-normal vision. Participants received monetary reward on the completion of the experiment. Participants were naïve to the purpose of the study.

DESIGN.

Participants had to perform a total of 644 trials, which included two blocks (75% right and 75% left). Block ordering was counterbalanced across participants and pro- and antisaccade trials within each block were interleaved. Figure 2 shows one example of the blocks with high location probability in the left. The manipulation of probability was applied only to prosaccade trials and not antisaccade trials. In each block, 75% of prosaccade trials were made to the high-probability location and the remaining 25% of trials were evenly distributed to the other three low-probability locations. Therefore each block consisted of an uneven distribution of prosaccade probabilities and an even distribution of antisaccade probabilities. Apart from the high-probability location, saccade directions were randomly assigned regardless of the saccade types. The colored singleton could appear on four locations randomly taking into account the probability manipulation. Participants were not explicitly informed of the change in probability design across blocks, and performed the two blocks successively without any explicit interval for rest between blocks.

Experiment 3

In the previous experiments we observed no significant difference in SRT between the two saccade types when probability was held equal. When we manipulated probability as a variable, we found that prosaccade RT under the high-probability condition was faster than under the low-probability condition (see also Geng and Behrmann 2005). Given this facilitatory effect of probability, one might ask whether such an effect still exists when probability is lowered, but not eliminated. Would the antisaccade cost change in a step-like function according to the change in magnitude in probability? To answer this question, we used the same paradigm as in experiment 2, but with a slightly reduced high probability. The predictions were identical to those from experiment 2, except that a smaller magnitude of both the antisaccade cost and the facilitatory probability effect on prosaccades trials under high probability was expected.

The second purpose of this experiment was to test the modulation of the antisaccade cost. Combining the data here with those from experiments 1 and 2 would introduce different levels of location probability. The rationale here was to see how different levels of probability would interact with difficulty to modulate prosaccades to the high-probability location. If the facilitatory effect of probability manifests itself in a graded and continuous manner on prosaccade RT, the corresponding antisaccade cost should also be continuously correlated. Therefore by combining antisaccade cost and levels of prosaccade probability, this study investigated whether antisaccade cost is systematically modulated by location probability. In particular, according to the logic of the competing pathway hypothesis, antisaccade cost should decrease as probability decreases.

PARTICIPANTS.

Ten students between the age of 18 and 25 yr from NCU participated in experiment 3. None had participated in experiment 2. All had normal or correct-to-normal vision. Participants received monetary reward on completion of the experiment. Participants were naïve to the purpose and design of the study.

DESIGN.

The general design was identical to experiment 2 except for a reduction in the high probability for location (65% instead of 75%). Each participant had to perform a total of 640 trials, which were presented in two blocks (65% right and 65% left). The order of the blocks was counterbalanced. Pro- and antisaccade trials were presented in an interleaved design. Again, we only manipulated location probability in prosaccade trials while keeping antisaccade probability evenly distributed among the four locations. Participants were not explicitly informed of the change in probability design across blocks and performed the two blocks without interruption.

RESULTS

Experiment 1

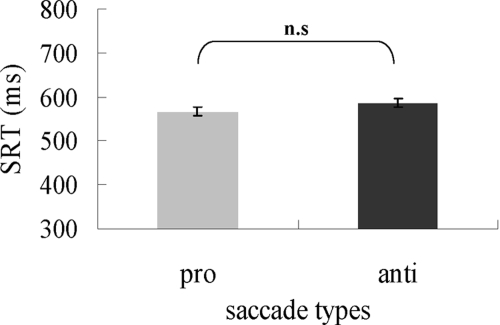
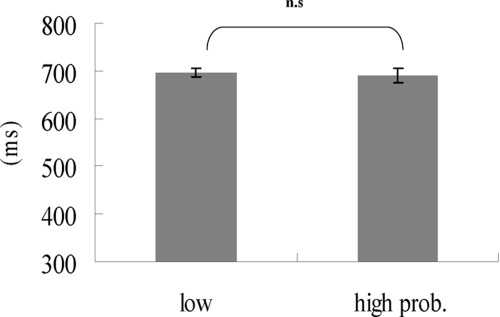
A saccade was identified as correct when it landed within 2° of the correct target. Saccade latency was defined as the time interval between target onset and the initiation of a saccadic eye movement. Mean percent correct of total trials was 88.4% (pro = 88.5%, anti = 88.3%). To exclude outliers, a boxplot was used to identify data that were 1.5× interquartile range (subtracting the first quartile from the third quartile) lower than the first quartile or 1.5× interquartile range higher than the third quartile. The boxplot developed by Tukey concerns the median, the lowest and highest data points to convey the level, spread, and symmetry of a distribution of the data. Before analyzing the data, it is beneficial to look at the pattern of data and, conveniently, it can also be easily used to identify outlier data. Less than 3% of trials were excluded from further analysis. Our main measures were the mean latencies of correct pro- and antisaccades. In particular, the antisaccade cost was examined. Results from the paired t-test (pro- and antisaccade; Fig. 3) showed that the latency of antisaccades did not significantly differ from prosaccades [pro- vs. antisaccades: 571.5 vs. 578.4 ms, t(7) = −0.85, P = 0.42]. Therefore we observed no antisaccade cost in this experiment. In addition, saccade latencies across the vertical and horizontal directions were not significantly different [vertical saccades: t(7) = −0.33, P = 0.75; horizontal saccades: t(7) = −0.74, P = 0.49).

Fig. 3.

Saccade reaction time as a function of the 2 types of saccade. Error bars are SE.

Experiment 2

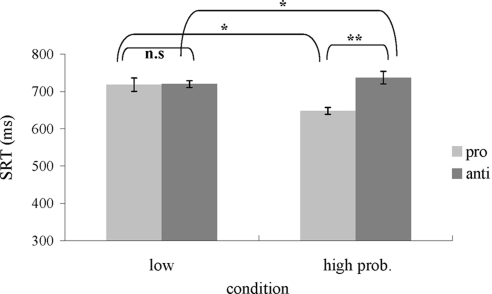
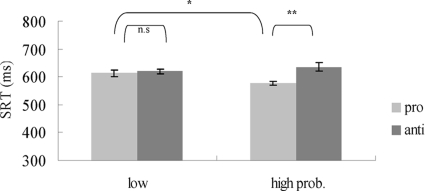
A saccade was identified as correct when it landed within 2° from the correct target. Mean percent correct of total trials was 86% (pro = 89.5%, anti = 83.1%). On average, 2.9% of trials per participant were discarded because of the false execution of a prosaccade when an antisaccade was required. Other trials were excluded because of premature responses (latencies <100 ms), responses with erroneous saccade endpoints, and no-responses (timeout duration: 2.5 s). Using a boxplot, 2.7% of data were identified as outliers (any data lying 1.5× interquartile range lower than the first quartile or higher than the third quartile) and were excluded from further analysis. All trials were categorized under two independent variables: saccade type (pro- and antisaccade) and location probability (high and low). Note that high location probability included prosaccades made to high probability location (75% of all prosaccade trials) and antisaccades made away from the high probability location (25% of all antisaccade trials). The low probability location condition consisted of prosaccades made to the three low-probability locations (totaling 25% of all prosaccade trials) and antisaccades made away from the three low-probability locations (totaling 75% of all antisaccade trials). A repeated-measure two-way (pro-/antisaccade × high/low prob.) ANOVA of saccade RT (Fig. 4) showed no main effect of saccade type [F(1.9) = 4.17, MS error = 4,955.7, P = 0.07], but a significant effect of probability [F(1.9) = 7.43, MS error = 945.2, P < 0.02] and a significant interaction between saccade type and probability [F(1.9) = 32.78, MS error = 586.1, P < 0.01]. Post hoc analysis showed that RT difference between pro- and antisaccades was significant in high probability locations [pro- vs. antisaccade RT: 647.8 vs. 737.1 ms, t(9) = −4.37, P < 0.01] but not in low probability locations [pro- vs. antisaccades RT: 718.1 vs. 720 ms, t(9) = −0.06, P = 0.95]. The effect of probability also reached significance [low vs. high probability location: 718.1 vs. 647.8 ms, t(9) = 4.46, P < 0.01] within prosaccade trials. Latency of antisaccades in the high probability condition were significantly longer than the low probability condition [t(9) = −2.28, P = 0.048]. Thus we observed faster prosaccades and slower antisaccades when the location probability was high. This is consistent with the competing pathway hypothesis.

Fig. 4.

Results of experiment 2. Mean saccade reaction times are plotted as a function of saccade type and the 2 conditions. The right bar in the high probability condition refers to antisaccades away from the color singleton. Error bars represent SE. *Significant post hoc P < 0.05. **Significant P < 0.01.

To examine whether there was any difference between horizontal and vertical saccades, we split the data from the experiment into horizontal and vertical conditions. Because the results of experiment 1 showed that there was no significant difference between vertical and horizontal saccades and in the interests of decreasing the total number of trials, location probability was only manipulated in the the horizontal axis (high prob. Vs. low prob.). Therefore only the low probability condition was presented in the vertical axis. The data showed that the difference between pro-/anti saccade latencies in vertical locations was not significant [paired t-test: t(9) = 1.2, P = 0.25]. In addition, in the low probability condition, the difference between the antisaccade latencies in the vertical and horizontal positions was not significant [paired t-test: t(9) = 0.16, P = 0.88]. However, in the low probability condition, the prosaccade latencies in the horizontal positions were quicker than those in the vertical positions [paired t-test: t(9) = 2.9, P = 0.02]. It is unclear if, as the pattern of latencies suggests, this pattern of results is a consequence of the location probability generalizing to some extent for the horizontal axis as a whole. To clarify the effect, we further compared whether the prosaccade latencies in the high probability location was faster than those in the horizontally opposite position. The results showed that prosaccade latencies in the high probability location were faster than those in the low probability location, a result that approached significance [t(9) = 2.1, P = 0.06]. This pattern of results did not interact with our observation that the significant antisaccade cost only occurred in the high probability location [t(9) = −4.4, P < 0.01] but not in the low probability ones [up: t(9) = −0.84, P = 0.42; right: t(9) = −0.33, P = 0.75; down: t(9) = 1.9, P = 0.09; left: t(9) = −1.2, P = 0.25].

REPETITION PRIMING ANALYSIS.

The probability effect we report here can also be explained by the repetition priming effect. Because there were more trials with a high-probability target location (75%), these identical trials could occur consecutively more often than by chance alone. As a result, faster prosaccades to the high-probability location could simply be caused by repetition priming on a trial-to-trial basis (Geyer et al. 2007; Maljkovic and Nakayama 1996; Walthew and Gilchrist 2006; for a review, see Kristjansson 2008).

To rule out this possibility, we divided prosaccade trials of high location-probability (75%) into two groups based on their previous trials' location. If the previous trial ended with a low-probability target location, there could not have been a repetition priming effect, and the RT of the current trial could be attributed solely to the effect of probability. Alternatively, if the previous trial ended in the same high-probability target location, the RT of the current trial would be a combination of the facilitation from repetition priming and high probability. A significant difference between the two RTs would indicate a strong repetition priming effect that could explain our findings. A paired-sample t-test showed no significant difference between the two groups [repetition vs. nonrepetition: 664.9 vs. 673.5 ms, t(18) = −0.46, P = 0.65]. In general, repetition priming could occur in all locations regardless of the probability manipulation. Our results showed that the priming effects were not larger in the high probability locations than low ones. Therefore the repetition priming effect cannot explain our findings, a pattern of results consistent with the findings of Geng and Behrmann (2005).

PROBABILITY EFFECT TRANSFER TO ANTISACCADE TRIALS.

We also studied whether the effect of probability would transfer to antisaccade trials. If the effect of probability were simply determined by saccadic eye movements irrespective of type, we would expect to observe a benefit whenever a saccade is made to the high-probability location whether or not it was a pro- or antisaccade. Therefore we compared RT from antisaccades made to high-probability location with those made to other locations. The results (Fig. 5) showed that the effect of probability was only present in prosaccade trials not in antisaccade trials [low vs. high probability location: 726.5 vs. 715.5 ms, t(9) = 1.57, P = 0.17].

Fig. 5.

Mean antisaccade reaction time for the 2 conditions. Error bars denote SE. The left bar represents the antisaccades that were made toward the low probability location. The right bar represents the antisaccades that were made toward the high probability location.

Experiment 3

Only correct saccades were included in the analysis (2 visual degrees within the periphery of correct target); 2.3% of data were categorized as inaccurate or erroneous prosaccades and were discarded. We also used boxplot to identify data that were 1.5× interquartile range (subtracting the 1st quartile from the 3rd quartile) lower than the first quartile or 1.5× interquartile range higher than the third quartile. This method excluded 3.1% of data as outliers. Mean percent correct of total trials was 88.1% (pro = 90.7%, anti = 85.5%). Like experiment 2, we divided the data based on their saccade type as well as their associated probability (high or low). Data are provided in Fig. 6. Two-way repeated-measures ANOVA was conducted with factors of saccade type (pro- or antisaccade) and probability (high or low) to evaluate saccade reaction times. Data showed no main effect of blocks [F(1,9) = 1.24, MS error = 701.1, P = 0.29] or saccade type [F(1,9) = 4.75, MS error = 2,509.8, P = 0.07], but a significant interaction between the two was found [F(1,9) = 19.6, MS error = 382.1, P < 0.01]. Post hoc paired t-test showed that prosaccades were significantly faster than antisaccades when presented in high probability location condition (pro- vs. antisaccades RT: 576.2 vs. 635.9 ms, t(9) = −3.9, P < 0.01) but not in low-probability locations [pro- versus antisaccades RT: 613.1 vs. 619.5 ms, t(9) = −0.39, P = 0.7]. Also, prosaccades made to the high-probability location were faster than prosaccades made to the low-probability locations [low vs. high probability location: 613.2 vs. 576.2 ms, t(9) = 2.8, P = 0.02], which indicated a significant probability effect.

Fig. 6.

Result of experiment 3. Mean saccade reaction time as a function of saccade type for the 2 conditions. Error bars denote SE. *Significant post hoc P values (α = 0.05).

However, we did not observe a significantly slower generation of antisaccades in the high-probability condition compared with the low-probability condition [low- vs. high-probability location: 619.5 vs. 635.9 ms, t(9) = −2.1, P = 0.069]. Therefore a significant probability effect was not found among the antisaccade trials.

The latencies of saccades across vertical and horizontal directions were not significantly different. Pro- and antisaccade latencies in vertical locations were not significantly different [paired t-test: t(9) = 1.3, P = 0.9]. Furthermore, in the low-probability condition, the difference between prosaccade latencies in the vertical and horizontal positions was not significant [paired t-test: t(9) = −8.7, P = 0.41]. Similar results were observed in antisaccade trials [paired t-test: t(9) = 0.94, P = 0.37].

Here again we ruled out the possibility of repetition priming [repetition vs. nonrepetition: 563.7 vs. 565.3 ms, t(18) = −0.21, P = 0.83].

MODULATION OF ANTISACCADE COST.

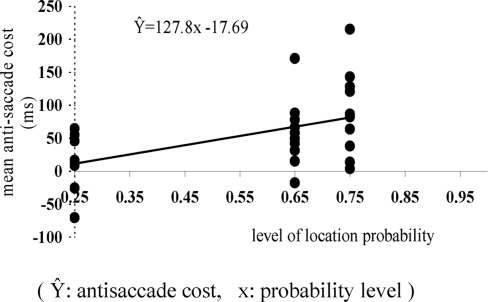
We analyzed the antisaccade cost data from all three experiments, using it as a dependent variable. In experiment 1, we did not manipulate location probability; thus the location probability was 25% (among 4 locations). The antisaccade cost data from experiments 2 (75%) and 3 (65%) formed the high-probability location conditions. One-way ANOVA on probability (25, 65, and 75%) showed a significant effect of probability [F(2,25) = 4.33, MS error = 2,212.4, P = 0.025]. Bonferroni post hoc tests showed that only the antisaccade cost with 25% probability significantly differed from that for 75%. Figure 7 presents the linear regression function plot of mean antisaccade cost across different probability conditions (R² = 0.24, P < 0.01). If we view antisaccade cost as a result of the underlying competition between pro- and antisaccades, this analysis of antisaccade cost does indeed show a positive trend with increasing (prosaccade) location probability.

Fig. 7.

The mean antisaccade cost with 3 levels of location probability. Each data point denotes each participant's mean antisaccade cost. The simple linear regression line is the best fit for these data.

DISCUSSION

Experiment 1

In the experiment 1, we used a modified version of Olk and Kingstone's (2003) paradigm and observed no antisaccade cost in terms of saccade latency. The lack of agreement between these findings and those of Olk and Kingstone can therefore be attributed to the difference between the two paradigms. In their paradigm, before a saccade could be initiated, participants needed to move their attention away from the center cross to a peripheral indicator to determine whether a pro- or antisaccade was appropriate. In our paradigm, participants did not need to orient their attention away from the center to determine which saccade type to make. This difference in saccadic indicator locations between the two paradigms was enough to eliminate the latency difference of pro- and antisaccade. In addition, our interleaved design required participants to analyze the saccadic indicator before deciding on a pro- or antisaccade. Thus we eliminated the reflexive nature of prosaccades and forced it to be programmed on-line. Similar results were also reported in previous research that used an interleaved design (Juan et al. 2008). This inhibitory process may be active in every trial because subjects could not determine the saccade type that was to be made until each visual search array was presented. The saccade task used here was not a reflexive task, the saccadic indicator needs to be processed/analyzed before the direction of saccade can be determined. Moreover, pro- and antisaccade trials were interleaved within blocks. Consequently, saccade latencies were longer than those from other studies using a reflexive saccade task. Several studies that used similar modified antisaccade tasks, such as Olk and Kingstone (2003); Kristjansson et al. (2004) and Juan et al. (2008), all reported relatively longer saccade latency in comparison to those of a reflexive task. In our pilot experiments, we found that saccade latencies were mainly affected by the discrimination task in the center. The longer latencies here are likely to be a consequence of the intensive attentional demand of the discrimination task required to determine saccadic direction, a requirement not typically present in pro/anti-saccade tasks.

As well as studying the effect of probabilities of trial types in the task (Juan et al. 2008), we also wanted to test whether the implicit information relating to target location would also affect the antisaccade cost in humans. In experiment 2, we varied location probability to bias visual attention. The hypothesis was that, if participants from experiment 1 truly did not move their attention away from the center, varying location probabilities should bias attention allocation to locations with higher probabilities. Therefore by biasing spatial attention to respond faster toward highly probable locations, we would expect an antisaccade cost to surface in locations with high prosaccade probabilities.

Experiment 2

These results generally confirm our predictions. Results from the low-probability condition can be seen as a replication of experiment 1 with no significant difference between pro- and antisaccade latencies. Critically, significant antisaccade cost was only observed in the high-probability location rather than the low locations. These results indicate that participants were able to make use of the regularities whenever they were to make a prosaccade. This factor of location probability strengthened the tendency of generating a prosaccade. Consequently, as prosaccade latencies dropped, generation of antisaccades also became slower even though they were not deliberately biased. If we view location probability as having an effect similar to a secondary task, effects of manipulation of location probability is in accordance with the competing pathway account (Kristjansson et al. 2001, 2004; Kristjansson 2007).

Previous studies have also reported a similar magnitude of probability effect (∼60 ms) and showed that probability could influence saccadic eye movements (Geng and Behrmann 2002, 2005). These results suggest that highly predictable location probability could override the salience of a singleton in visual search. Although there are many differences between their paradigm and ours, the similar effect found here may be pointing to the same underlying mechanism. Furthermore, this probability effect cannot be explained by repetition priming (Geng and Behrmann 2005; Geyer et al. 2007; Kristjansson 2008; Maljkovic and Nakayama 1996; Walthew and Gilchrist 2006).

Although the proportions of antisaccade required to each of the four locations were the same, we tested whether antisaccade made to the high-probability location would be faster than other locations. This was based on the rationale that the high-probability location was the most frequent target location of pro- but not antisaccades. Therefore if the effect of probability were simply determined by the location information itself, antisaccades made to the high-probability location would be faster than other locations. This was not the case (Fig. 5). This suggested that probability only had an effect when operating through a combination of location and saccade type. These results are consistent with the probability effect hypothesis (Geng and Behrmann 2005), which proposed that the probability cue operates through a conjunction of spatial and object information. Furthermore, the observation that subjects had no significant decrement or increment on saccade latencies when they antisaccade toward or away from the high probability locations indicate that actual saccade location can be dissociated from the probability effects. This pattern of results suggests an independent relationship between saccadic eye movements and visual selection shown by manipulations on probability. This is consistent with the findings from our previous work (Juan et al. 2004, 2008).

Experiment 3

In this experiment, we decreased the high location probability from 75 to 65%. We found a similar pattern as experiment 2. Moreover, the antisaccade cost was smaller in magnitude when the relative probability of the prosaccade location was lower. Again, these results provide evidence for the competing pathway hypothesis between pro- and antisaccades. Significant antisaccade costs only occurred in high-probability conditions and not in low-probability conditions. Also, the probability effect did not transfer to antisaccade trials [low vs. high probability location: 616.6 vs. 621 ms, t(9) = − 0.36, P = 0.73), suggesting the change in antisaccade cost was primarily a result of changes in prosaccade latency. The second aim of this experiment was to see whether the magnitude of the antisaccade cost would be affected by different levels of probability. Results from one-way ANOVA and regression analysis seem to support this view. This suggests that antisaccade cost is indirectly sensitive to spatial probability. Higher location probability demands more attention to likely locations, thereby creating higher difficulty in inhibiting the automatic prosaccades. Our analyses here quantified this process and support the prediction of the competing pathway hypothesis. The critical new result here is that the magnitude of the antisaccade cost could be determined by the probability that a location would be the target of a prosaccade.

General conclusion

In this study, we conducted three experiments to explore how location probability may play a role in antisaccade performance. In experiment 1, we successfully reduced the antisaccade cost by removing the attentional reorientation processes. These results could be argued to be consistent with the reallocating attention hypothesis that was put forth by Olk and Kingstone (2003). The absence of difference between pro- and antisaccade latencies is also consistent with Juan et al. 2008. In experiment 2, we manipulated location probability in prosaccade trials (75%). Significant antisaccade costs were only found in this high-probability condition and not in the low-probability condition. As previously discussed, if we view location probability as a form of a secondary task, our results from experiment 2 are consistent with the idea of competing pathways as proposed by Kristjansson (2007). In experiment 3, similar results to those from experiment 2 were found except for a reduced magnitude for the antisaccade cost as a consequence of the lowered probability manipulation (65%). We showed that differing levels of probability can result in different antisaccade costs. Together, these results suggest that the antisaccade cost can be systematically changed with the different levels of location probability.

As previous studies have suggested (Geng and Behrmann 2002, 2005), the underlying mechanism for the acquisition of location probabilities may be related to those that support repetition priming. Because the effect of probability has to be learned over time, such cumulative frequency is likely to be temporarily stored in one's short-term memory. Studies have shown such statistical learning is often learned implicitly (Fiser and Aslin 2001), leaving no trace of awareness (Chun and Jiang 1998; Geng and Behrman 2005). In our study, only some participants noticed the manipulation of location probability (experiment 2, 3; experiment 3, 4). Our manipulation therefore is consistent with the aforementioned studies on implicit learning. Fiser and Aslin (2001) suggested that the mechanism that mediates statistical -learning may apply to other modalities and species. We found this statistical- earning of probability could also exist in the antisaccade paradigm and for the visual domain. The main advantage of this implicit modulation is that it may lessen one's cognitive load, leaving resources for other information to be processed consciously.

The paradigm used here is not identical to the conventional antisaccade task (for a review, see Munoz and Everling 2004). It is more like the modified task reported in Olk and Kingstone (2003) and Kristjansson et al. (2003). The conventional antisaccade task is usually carried out in a blocked design. Therefore the inhibitory processes are less involved in the prosaccade trials and result in a significant antisaccade cost. This task is a revised version of Juan et al. (2004, 2008); which intermixes pro- and antisaccade trials and requires active attentional control and visual selective processes before a saccadic direction is determined. The pattern of our results suggests that, once attentional control is more demanded by the task, the antisaccade cost is less apparent (see also Kristjansson et al. 2003, 2004).

In this study, we showed that antisaccade cost can be modulated by location probability. This effect can be categorized as a top-down cognitive factor, along with other knowledge-based factors such as focus of attention toward items that share the same features with the target (Folk et al. 1992), familiarity effects (Wang et al. 1994), and expectancy effects for locations that have a high likelihood of containing the target (Dorris and Munoz 1998; Geng and Behrmann 2005). These results highlight the importance of spatial regularity in visual search task and the flexibility of inhibition in the oculomotor system. It seems that probability is a key determinant for motor preparation despite its form, such as location (Dorris and Munoz 1998; Geng and Behrmann 2005), task type (Juan et al. 2008; Chiau et al. 2009) or context (Tseng et al. 2009, for a review, see Summerfield and Egner 2009). Given the implicit nature of the task and its brief duration, the oculomotor system is still sensitive enough to adapt to available probabilistic information. This situational-based learning biases motor preparation toward the highly probable location at the onset of every trial, thus modulating the upcoming saccade latency.

It is noteworthy that the location probability effects only occurred with the prosaccades, but not antisaccades, toward the location. This specific pattern of results indicates that the probability effects observed in this study do not take place at a general spatial representation level. Many studies have suggested that the competition between prosaccades and antisaccades could be modulated within/between several neural substrates, such as frontal eye fields (FEF) (Everling and Munoz 2000; Sato and Schall 2003; Schall and Thompson 1999), supplementary eye fields (SEF) (Schlag-Rey et al. 1997), and the superior colliculus (SC) (Dorris and Munoz 1998;) (for reviews see: Kristjansson 2007; Munoz and Everling 2004). The location probability effects observed in this study are contingent on the match of both location and saccadic type. Therefore the effects could have originated from high cognitive control areas such as SEF and dorsolateral prefrontal cortex (Desouza et al. 2003) and propagate to, and take effect in, the eye movement control areas like FEF and SC. The location probability effects are likely to take place in the FEF and the SC by increasing the motor preparation level and consequently decreasing the saccade latencies (Connolly et al. 2002, 2005; Koval et al. 2004; Manoach et al. 2007).

In summary, we showed that antisaccade cost is not only affected by bottom-up processes, but also top-down factors such as implicit probability, a context-based knowledge. By elucidating how the visual system can perform efficient search, one can gain much insight into the issue of how we internalize meaningful regularities between objects and events in the external world. Further research is needed to differentiate the effect of probability from motor preparation and attentional bias (Geng and Behrmann 2002) and shed light on the possible functional role of neural substrates underlying these phenomena.

GRANTS

This work was sponsored by the National Science Council, Taiwan (96-2413-H-008-001-MY3, 97-2511-S-008-005-MY3, 98-2410-H-008-010-MY3, 98-2517-S-004-001-MY3, 97-2511-S-008-008-MY5). N. G. Muggleton was supported by the UK Medical Research Council. C.-H. Juan was supported by the National Science Council, Taiwan (98-2918-I-008-011) and the Fulbright Scholarship.