Mechanisms and Distribution of Ion Channels in Retinal Ganglion Cells: Using Temperature as an Independent Variable

Abstract

Trains of action potentials of rat and cat retinal ganglion cells (RGCs) were recorded intracellularly across a temperature range of 7–37°C. Phase plots of the experimental impulse trains were precision fit using multicompartment simulations of anatomically reconstructed rat and cat RGCs. Action potential excitation was simulated with a “Five-channel model” [Na, K(delayed rectifier), Ca, K(A), and K(Ca-activated) channels] and the nonspace-clamped condition of the whole cell recording was exploited to determine the channels' distribution on the dendrites, soma, and proximal axon. At each temperature, optimal phase-plot fits for RGCs occurred with the same unique channel distribution. The “waveform” of the electrotonic current was found to be temperature dependent, which reflected the shape changes in the experimental action potentials and confirmed the channel distributions. The distributions are cell-type specific and adequate for soma and dendritic excitation with a safety margin. The highest Na-channel density was found on an axonal segment some 50–130 μm distal to the soma, as determined from the temperature-dependent “initial segment–somadendritic (IS-SD) break.” The voltage dependence of the gating rate constants remains invariant between 7 and 23°C and between 30 and 37°C, but undergoes a transition between 23 and 30°C. Both gating-kinetic and ion-permeability Q10s remain virtually constant between 23 and 37°C (kinetic Q10s = 1.9–1.95; permeability Q10s = 1.49–1.64). The Q10s systematically increase for T <23°C (kinetic Q10 = 8 at T = 8°C). The Na channels were consistently “sleepy” (non-Arrhenius) for T <8°C, with a loss of spiking for T <7°C.

INTRODUCTION

Whole cell recording of neurons faces a vexing technical contradiction: on the one hand, the complexity of the neural geometry makes it difficult to achieve the space-clamped condition necessary for unequivocal data interpretation. Nonspace-clamped experimental records, on the other hand, implicitly harbor full information that cannot be unequivocally extracted. Here we add temperature, as an independent, easily manipulated variable, to eliminate some of the ambiguity in that information extraction.

The modeling of the nonspace-clamped recordings is done in multicompartment analyses of morphologically reconstructed neurons, whose dendritic processes and axon are divided into short segments (compartments). The added feature of nonspace clamping is the electrotonic current, which is the current that flows across the boundary between neighboring compartments (i.e., from one compartment directly into its neighbor). The electrotonic current carries information of the changing electrical status in the dendrites and axon to the recording site of the soma and is subject to change with temperature.

In the retina, previous studies have examined the relationship between temperature and the kinetics of retinal function, such as photoreception (Baylor et al. 1983; Donner et al. 1988), amacrine cell synaptic release (Veruki et al. 2003), the electroretinogram (Schellart et al. 1974), and the ganglion cell's ability to respond to light or contrast (e.g., Aho et al. 1993; Dhingra et al. 2003). Our study evaluates action potentials across a large temperature range, to estimate the spatial distribution of ion channels in the retinal ganglion cell, from the kinetic changes that occur. In the process, we evaluate elements of channel gating that continue to function in concert and coherence to generate the action potentials across that large temperature range.

Almost all retinal ganglion cells, including “phasic off-center cells” (e.g., Lankheet et al. 1989), respond with at least a short period of tonic repetitive firing to constant depolarizing current injected into the soma. Our method of analysis (“phase plots”) is highly discriminating of the precise waveform of action potentials and exploits the impulse repetition to enhance the signal-to-noise ratio. The shape of the action potential changes with temperature and it does so in conjunction with temperature-dependent changes in the “waveform” of the electrotonic current at the soma. It is these changes in the waveform that allow us to exploit the nonspace-clamped recording condition to determine the necessary spatial parameterization and to estimate the distribution of ion channels throughout the encoder region of the neural morphology.

METHODS

Experiments were performed on acutely isolated retinas of male Long–Evans rats (175–300 g) and cats (Felis domesticus). Animals were killed and retinas were prepared as described previously (Cohen 1998; Newman 2003). Animals were treated in accordance with the guidelines of the Institutional Animal Care and Use Committees of the University of Minnesota, Yale University, or the Department of Health and Human Services.

Rat retina

Rat retinas were held in place in a superfusion chamber with nylon threads attached to a Pt ring and superfused at 2 to 3 ml/min with bicarbonate-buffered Ringer solution containing (in mM): NaCl, 111.0; KCl, 3.0; CaCl₂, 2.0; MgSO₄, 1.0; NaH₂PO₄, 0.5; dextrose, 15.0; and NaHCO₃, 32; pH 7.44, equilibrated with 5% CO₂-95% O₂. Before reaching the chamber, the superfusate was heated or cooled with a Peltier thermoelectric module. A microthermistor within the recording chamber monitored the temperature of the retinal preparation.

Current-clamp records were obtained from the rat ganglion cell somata near the vitreal surface of isolated retinas using whole cell patch-clamp recording. Nerve impulse trains were obtained at closely spaced temperatures throughout the range of 7.2 through 37.1°C, each in response to the minimum multiple of 20 pA that yielded maintained (tonic) repetitive firing (Fig. 1). The standard protocol began near room temperature (∼23°C), which was then stepwise lowered until spiking ceased, subsequently stepwise increased to mammalian temperatures, then lowered to yield room-temperature controls at the beginning, middle, and end of the experiment. Cell membrane potential was recorded with an Axon Instruments MultiClamp 700A amplifier (Molecular Devices, Union City, CA) and was digitized at 10, 20, or 40 kHz. Cells were stimulated with depolarizing current pulses passed through the recording pipette. The patch pipette/intracellular solution contained (in mM), Na-methanesulfonate, 5.0; K-methanesulfonate, 128.0; MgCl₂, 2.0; K-EGTA, 5.0; glutathione, 1.0; MgATP, 2.0; NaGTP, 0.2; Fluo-4 pentapotassium salt, 0.1; and HEPES, 5.0 (pH 7.4).

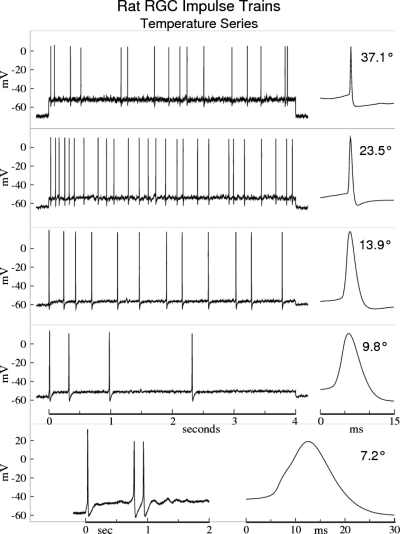
Fig. 1.

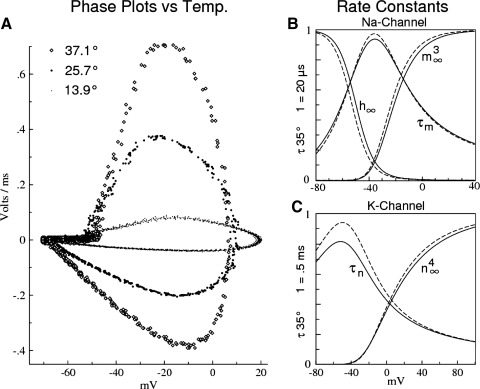
Impulse trains from a rat retinal ganglion cell (RGC) taken at 5 different temperatures show distinct differences in their action potential (AP) kinetics. Insets at right show the durations and waveforms of a single AP from each impulse train. The highest amplitude impulses and lowest threshold currents occur in the temperature range 13–16°C. Spiking is somewhat noisy at mammalian temperatures (37.1°C), with somewhat lower impulse amplitudes. The most regular spiking, with systematic adaptation, occurs for T <13°C (except for T <8°C, where the Na channels become “sleepy”; see the following text and Fohlmeister 2009). Step stimulus currents were the minimum multiples of 20 pA to yield repetitive firing at each temperature (320, 120, 40, 40, and 20 pA, at 37.1, 23.5, 13.9, 9.8, and 7.2°C, respectively).

Cat retina

Cat retinal tissue was held in a microscopic chamber and superfused with a gravity-fed Ringer solution (5 ml/min) that was warmed by an in-line heater just before entering the retinal chamber. The temperature was monitored by a thermocouple at the entrance to the chamber. Physiological temperature recordings from the isolated retina used a bicarbonate-buffered Ringer solution containing the following salts (in mM): NaCl, 120; KCl, 3.1; KH₂PO₄, 0.5; NaHCO₃, 23.0; Mg₂SO₄, 1.2; CaCl₂, 1.15; 0.5% equine serum; 26 vitamins and amino acids, equilibrated with 5% CO₂-95% O₂ (Ames and Nesbett 1981).

The action potentials of X (Beta) and Y (Alpha) cat ganglion cells were recorded from the soma in current clamp using the whole cell recording technique. Membrane potential was recorded with a DAGAN 3900A patch-clamp amplifier (Dagan, Minneapolis, MN) and digitized at 18.5 kHz using a VR10B data recorder (Instrutech, Mineola, NY); the data were corrected for series resistance and junction potentials. Cells were stimulated with depolarizing current pulses in 50- or 100-pA steps passed through the recording pipette. The patch-pipette intracellular solution contained (in mM) K-methanesulfonate, 120; KCl, 4; MgCl₂, 2; HEPES, 5; CaCl₂, 0.5, EGTA, 5; glutathione, 1.0, NaATP, 1.0, NaGTP, 0.5, and lucifer yellow 0.05% methoxycarbonyl salt (pH 7.2), and neurobiotin/biocytin (0.5%; Molecular Probes, Eugene, OR) for cell identification (for details, see Cohen 1998, 2000).

Morphological reconstruction of RGCs

Retinal ganglion cells (RGCs) were labeled in isolated retinas with either neurobiotin or DiIC18(3) (for details, see Cohen 1998; Mangrum et al. 2002). The retinas were fixed in 4% paraformaldehyde and embedded in either PBS-glycol 1:1 or aqueous phosphate-buffered polyalcohols. Stained ganglion cells were manually digitized using a Neurolucida morphological reconstruction system (Microbrightfield, Williston, VT). A total of 12 RGCs were reconstructed: rat (n = 4), cat Alpha (n = 4), and cat Beta (n = 4). The membrane surface areas of these 12 RGCs had a bimodal distribution; small-area cells (Rat Type I and Cat Beta/“X” RGCs) had somal surface areas ranging from 1,105 to 1,573 μm² and dendritic areas from 3,332 to 6,147 μm², whereas large-area cells (Rat Type II and Cat Alpha/“Y” RGCs) had somal areas of 1,653–4,047 μm² and dendritic areas of 14,934–28,247 μm². Dendritic diameters for Alpha/Type II RGCs range from 0.19 to 5.38 μm, with 95% broadly distributed between 0.39 and 1.79 μm; for Beta/Type I RGCs these ranges are somewhat narrower, with the extreme range 0.16–2.49 μm, 95% of compartments between 0.31 and 1.24 μm, and 50% between 0.47 and 0.68 μm. Typical examples of each morphological type are shown in Fig. 2.

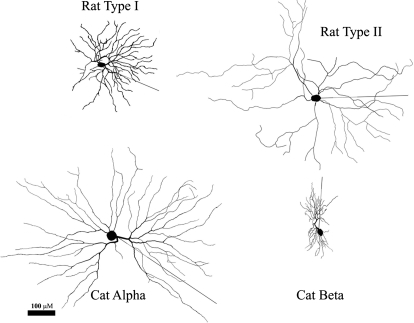
Fig. 2.

Examples of traced RGCs from the rat (top) and cat (bottom) used for model generation. Top left: “Type I” RGC, which corresponds to the Alpha or RG_A2 type (Peichl 1989; Sun et al. 2002). Top right: “Type II” RGC, may correspond to the RG_C3 type. Bottom left: cat Off-α ganglion cell (Peichl and Wässle 1983). Bottom right: cat Off-β ganglion cell. See methods for reconstruction details.

The axon was divided into three segments: the axon hillock or initial segment (IS; length = 45 μm), a thinner segment immediately adjacent (also called trigger segment [TS]; l = 90 μm; Fohlmeister and Miller 1997b; cf. also Van Wart et al. 2007), and the axon proper (AX; l = 2 mm). Typical diameters of IS, TS, and AX are, respectively, 1, 0.6, and 1 μm (Rat Type I and Cat Beta), and 2, 1.2, and 1.6 μm (Rat Type II and Cat Alpha).

Model simulations

The morphological data were converted into “.hoc” model file format using cvapp (http://neuron.duke.edu/cells/download.html) and compartmentalized for computer simulations with the program NEURON (Carnevale and Hines 2006). The (maximum) compartment length was 15 μm. The compartments were supplemented with the model gating kinetics and gating rate constants to simulate membrane ion currents. The channel densities of the individual ion currents (i.e., the open channel [G-bar] conductances) were distributed uniformly within each of the following neural regions: dendrites, soma, axon hillock, trigger segment, and axon. The specific values of these regional G-bars were determined in analysis and form a part of the results (Table 1).

Table 1.

G-bar conductances at 35°C (mS/cm²)

Channel	Dendrites	Soma	IS	TS	Axon
Rat RGC Type I (1,661 dendritic compartments)
Na	79.50	72.00	141.10	231.1	124
K	23.40	50.40	67.80	74.6	50
Ca	1.20	1.20	0.753	0.0	0
Rat RGC Type II (2,379 dendritic compartments)
Na	56.70	88.40	176.60	378.6	124
K	43.10	94.80	134.60	134.6	50
Ca	0.765	0.765	0.510	0.0	0
Cat Beta RGC (“X”) (1,175 dendritic compartments)
Na	63.90	69.40	100.00	244.5	124
K	13.40	32.00	50.10	50.1	50
Ca	1.39	1.39	0.836	0.0	04
Cat Alpha RGC (“Y”) (3,298 dendritic compartments)
Na	60.80	158.00	277.00	448.5	124
K	41.20	36.10	50.10	46.7	50
Ca	2.23	2.23	1.39	0.0	0

Multiplicative factors for modified “Cat Alpha RGC” (Fig. 9)
	Surface Area		Na Conductance
	Soma	Dendrites	Soma	Dendrites	Impulse Frequency
A (Control)	1.00	1.00	1.00	1.00	1.00
B	1.00	0.54	0.75	1.00	2.16
C	1.00	0.95	0.75	1.30	1.17
D	2.80	1.00	0.75	0.80	0.59
[1]	2.80	0.95	0.67	0.90	0.79
[2]	0.41	1.00	1.40	1.18	1.16
(*) Beta RGC	0.27	0.16	0.44	1.05	6.40

Top section: Distributions of ion channels (G-bar conductances at 35°C) throughout the processes of the traced RGCs of Fig. 2. The diameters of IS (Initial Segment), TS (Trigger Segment), and Axon used in simulation were, respectively, 1, 0.6, and 1 μm (Rat “Type I” and Cat Beta) and 2, 1.2, and 1.6 μm (Rat “Type II” and Cat Alpha). Phase-plot homology is maintained when the Na-channel density of each of these axonal segments is inversely varied with its diameter. Bottom section: Multiplicative factors applied to the Cat Alpha RGC (Fig. 2) to modify the normal morphology and ion channel densities (G-bar conductances) for the phase plots and spike trains shown in Fig. 9. Each modification maintained phase-plot homology with original Cat Alpha RGC. Two further phase-plot homologous modifications (not plotted in Fig. 9) are: [1] The combination of C and D (thinned dendritic trunks plus enlarged soma) and [2] the converse of D (reduced soma; unaltered dendrites).

(*) “Cat Alpha RGC” modified to match membrane areas, channel densities, and phase-plot homology with “Cat Beta RGC” (see text).

The integration step used with NEURON was 0.0001 ms. A typical run duration took 21 min to generate a 400-ms record of a Type I/Beta RGC; the durations were about threefold longer for Type II/Alpha RGCs. Reducing the integration step to 0.00001 ms (factor of 10) resulted in a maximum difference in all state variables of 0.009% (m, h, n, c, V, dV/dt; at 37.1°C). Increasing the integration step to 0.001 ms resulted in a maximum error of 0.73% (at 37.1°C). These percentage differences were smaller for lower temperatures (reduced dV/dt).

Electrotonic current

The instantaneous membrane potential varies from compartment to compartment and it does so in conjunction with “electrotonic current,” which is the current that flows across the boundaries between the neighboring compartments. Because there are no current sources or sinks within the compartments (except injected stimulus current into the soma compartment), conservation of current requires that the sum of all currents flowing across the entire boundary of any individual compartment must always be zero (or I_STIM). Each compartment's boundary consists of its plasma membrane (considered a surface), plus its intercompartmental interfaces (cytoplasmic cross sections across which all current is electrotonic). We therefore computed the net electrotonic current to be the residual current that equals—in magnitude—the sum of all instantaneous membrane currents, including ion channel, capacitive, and leak (minus I_STIM). With regard to the algebraic sign, we define positive electrotonic current as the net positive charge flowing into the compartment (from its neighboring compartments). Note that this is counter to the convention for membrane currents (e.g., positive Na⁺ ions flowing into the compartment = negative Na current). The algebraic sign reversal is a visual aid in associating specific features of the net electrotonic current with peaks of the membrane currents in the figures [it also corresponds with the normal usage of stimulus current, for which depolarizing (i.e., “positive”) stimulus = net positive charges injected into the cell]. All figure plots showing electrotonic current are of the soma compartment, which is both the stimulating and recording site. The net electrotonic current of the soma compartment is a measure of both the instantaneous dendritic load and of impulses initiated elsewhere than the soma (most prominently the initial segment–somadendritic [IS-SD] break).

Complement of channels and gating kinetics

The underlying currents for the simulated impulse trains were generated by a five-channel model (Fohlmeister et al.1990) based on voltage-clamp data from retinal ganglion cells of both rat (Lipton and Tauck 1987) and tiger salamander (Lukasiewicz and Werblin 1988), which appear to share the major channel types; the gated currents of the model are I_Na, I_K, I_Ca, I_K,A, and I_K,Ca.

All model fits were obtained with I_K,A = 0 because the experimental data did not exhibit a decisive phase-plot signature for that inactivating potassium current—i.e., a decreased postspike undershoot with wider impulses (Fohlmeister and Miller 1997a). This does not imply the absence of I_K,A across RGC membranes. In agreement with earlier reports (Lankheet et al. 1989), it does, however, confirm that I_K,A is small relative to the delayed rectifier I_K in retinal ganglion cells. Modeling showed that the absence of a decisive signature places an upper limit for I_K,A of about 15% of the total I_K + I_K,A.

The following rate constants for the gating kinetics are modified from Fohlmeister and Miller (1997a) and give the best fits to the present data (see results and discussion regarding the Alternate rate constants for T ≤23°C and also for rate constants in the transition region of 23–30°C). The underlined coefficient on the right side of each equation is temperature dependent and is given for 35°C. For temperatures other than 35°C, multiply these coefficients by the “Kinetic Q10 Factors” listed in Table 2.

Table 2.

Q10s and neural parameters as functions of temperature

	Q10
	Gating Kinetic		Conductance		Action Potential*
Temperature, °C	Na	K	Na	K	Amplitude, mV	Width, ms	Stimulus, pAmp
37.1	1.95	1.9	1.64	1.61	49.8	0.30	440
34.9	1.95	1.9	1.64	1.61	53.1	0.34	320
29.9	1.95	1.9	1.59	1.52	63.5	0.50	120
23.5	1.95	1.9	1.64	1.49	71.1	0.71	120
16.7	3.00	3.0	2.97	3.10	72.5	1.60	80
14.1	3.70	3.7	3.08	3.60	79.4	2.16	40
13.9	3.70	3.7	2.85	3.60	81.6	2.10	40
13.0	4.30	4.3	2.95	3.30	82.5	2.09	40
9.8	8.00	8.0	11.70	4.60	72.6	4.35	40
7.7**	520,000†	9.0	3,300	270	62.0	10.44	160

	Q10 Factors
	Gating Kinetic		Conductance		Equilibrium Potentials, mV
Temperature, °C	Na, Ca	K	Na, Ca	K	Na	K	Leak	Ri, Ω·cm
37.1	1.151	1.144	1.109	1.105	61.02	−102.03	−65.02	136.6
35.0	1.000	1.000	1.000	1.000	60.60	−101.34	−64.58	143.2
34.9	0.993	0.994	0.995	0.995	60.58	−101.31	−64.56	143.5
29.9	0.711	0.720	0.777	0.791	59.60	−99.67	−63.51	160.4
23.5	0.463	0.478	0.566	0.610	58.34	−97.56	−62.17	185.0
13.9	0.132	0.136	0.219	0.165	56.45	−94.40	−60.16	234.9
9.8	0.0563	0.0580	0.0845	0.0988	55.65	−93.05	−59.30	251.2
7.7	0.00347†	0.0358	0.00670	0.0441	55.23	−92.36	−58.86	263.3

Top section: Gating Kinetic and Conductance Q10s for a series of closely spaced temperatures as determined by model fits to experimental phase plots from Rat RGCs. “Stimulus” was the minimum multiple of 20 picoamperes (injected into the soma) to yield sustained repetitive firing.

(*) Amplitude, the impulse peak through afterhyperpolarization; Width, measured at the midpoint of the voltage extremes.

(**) Q10 (7.7°C) computed as: exp{[ln x(7.7°C) ln x(9.8°C)]/[7.7 − 9.8)/10]}; x = coefficient of rate constant (voltage-independent) and/or G-bar conductance, except (†).

(†) This “Q10” is equivalent to applying Q10 = 9 to the rate constants for 9.8°C, followed by an additional reduction of a factor of 10, resulting in “sleepy” Na channels at 7.7°C. Bottom section: Multiplicative “Q10 Factors” to be applied to the gating kinetic Rate Constants and G-bar Conductances, for other than 35°C (these correspond to the temperatures of Q10s in the top section). Equilibrium Potentials (mV) were computed by applying the factor (T + 273°)/(37° + 273°) to 37°C values (Woodbury 1965). See methods for computation of Ri (cytoplasmic resistivity). (†) “Sleepy” Na channels at 7.7°C (“Q10 Factor” for Ca = 0.0347).

1) Standard gating rate constants for T >30°C

Na activation

$$\begin{array}{l}{\alpha }_{\mathrm{m}}\left(\mathrm{V}\right)=-\underline{2.725}\left(\mathrm{V}+35\right)/\left\{\exp \left[-0.1\left(\mathrm{V}+35\right)\right]-1\right\}\hfill \\ {\beta }_{\mathrm{m}}\left(\mathrm{V}\right)=\underline{90.83}\exp \left[-\left(\mathrm{V}+60\right)/20\right]\hfill \end{array}$$

Na inactivation

$$\begin{array}{l}{\alpha }_{\mathrm{h}}\left(\mathrm{V}\right)=\underline{1.817}\exp \left[-\left(\mathrm{V}+52\right)/20\right]\hfill \\ {\beta }_{\mathrm{h}}\left(\mathrm{V}\right)=\underline{27.25}/\left\{1+\exp \left[-0.1\left(\mathrm{V}+22\right)\right]\right\}\hfill \end{array}$$

K activation (delayed rectifier)

$$\begin{array}{l}{\alpha }_{\mathrm{n}}\left(\mathrm{V}\right)=\underline{-0.09575}\left(\mathrm{V}+37\right)/\left\{\exp \left[-0.1\left(\mathrm{V}+37\right)\right]-1\right\}\hfill \\ {\beta }_{\mathrm{n}}\left(\mathrm{V}\right)=\underline{1.915}\exp \left[-\left(\mathrm{V}+47\right)/80\right]\hfill \end{array}$$

Ca activation

$$\begin{array}{l}{\alpha }_{\mathrm{c}}\left(\mathrm{V}\right)=-\underline{1.362}\left(\mathrm{V}+13\right)/\left\{\exp \left[-0.1\left(\mathrm{V}+13\right)\right]-1\right\}\hfill \\ {\beta }_{\mathrm{c}}\left(\mathrm{V}\right)=\underline{45.41}\exp \left[-\left(\mathrm{V}+38\right)/18\right]\hfill \end{array}$$

2) Alternate rate constants for T ≤23°C

Na activation

$$\begin{array}{l}{\alpha }_{\mathrm{m}}\left(\mathrm{V}\right)=-\underline{2.804}\left(\mathrm{V}+35\right)/\left\{\exp \left[-0.1\left(\mathrm{V}+35\right)\right]-1\right\}\hfill \\ {\beta }_{\mathrm{m}}\left(\mathrm{V}\right)=\underline{93.46}\exp \left[-\left(\mathrm{V}+60\right)/18\right]\hfill \end{array}$$

Na inactivation

$$\begin{array}{l}{\alpha }_{\mathrm{h}}\left(\mathrm{V}\right)=\underline{1.869}\exp \left[-\left(\mathrm{V}+55\right)/20\right]\hfill \\ {\beta }_{\mathrm{h}}\left(\mathrm{V}\right)=\underline{28.04}/\left\{1+\exp \left[-0.1\left(\mathrm{V}+25\right)\right]\right\}\hfill \end{array}$$

K activation

$$\begin{array}{l}{\alpha }_{\mathrm{n}}\left(\mathrm{V}\right)=-\underline{0.0984}\left(\mathrm{V}+32.5\right)/\left\{\exp \left[-0.1\left(\mathrm{V}+32.5\right)\right]-1\right\}\hfill \\ {\beta }_{\mathrm{n}}\left(\mathrm{V}\right)=\underline{1.969}/\exp \left[-\left(\mathrm{V}+58.5\right)/76\right]\hfill \end{array}$$

Ca activation

$$\begin{array}{l}{\alpha }_{\mathrm{c}}\left(\mathrm{V}\right)=-\underline{1.4}\left(\mathrm{V}+15\right)/\left\{\exp \left[-0.1\left(\mathrm{V}+15\right)\right]-1\right\}\hfill \\ {\beta }_{\mathrm{c}}\left(\mathrm{V}\right)=\underline{46.68}\exp \left[-\left(\mathrm{V}+40\right)/18\right]\hfill \end{array}$$

The kinetic structure is that of Hodgkin and Huxley (1952). A noninactivating (H-type) Ca current is added with parameterization similar to that of Na activation and with variable equilibrium (Nernst) potential dependent on intracellular calcium ion concentration ([Ca²⁺]_i). The Ca-activated K current I_K,Ca is gated as follows

$$g\left(\mathrm{K},\text{CA}\right)=G\text{-}\text{bar}\left(\mathrm{K},\text{CA}\right)\frac{{\left({\left[{\mathrm{Ca}}^{2+}\right]}_{\mathrm{i}}/{\mathrm{Ca}}_{\text{diss}}\right)}^2}{\text{1+}{\left({\left[{\mathrm{Ca}}^{2+}\right]}_{\mathrm{i}}/{\mathrm{Ca}}_{\text{diss}}\right)}^2}$$

where Ca_diss = 10⁻⁶ molar (dissociation constant) and, in the absence of Ca influx, [Ca²⁺]_i = 10⁻⁷ molar (residual internal Ca concentration).

A leakage current (I_Leak) was adjusted to match the input resistance and time constant of RGCs. The five-channel model was originally constructed to yield the measured input resistance of about 1 GΩ (tiger salamander RGCs; cf. Fohlmeister and Miller 1997a,b). Mammalian RGCs, in contrast, commonly show lower input resistance (35–150 MΩ for cat Alpha and Beta RGCs, respectively; Cohen 2001; O'Brien et al. 2002); the low value for Alpha RGCs is possibly due to dendritic gap junctions (cf. Cook and Becker 1995; Hu and Bloomfield 2003; Xin and Bloomfield 1997; cf. also Ceelen et al. 2001). A membrane conductance (leak) value of 10,000 Ω/cm² was found to fit most cells, and had a Q10 factor of 1.85. However, as with the Ca-activated K current, the effect of leakage on the impulse waveform is negligible, even with the lowest input resistance (35 MΩ).

Cytoplasmic resistivity

The temperature dependence of cytoplasmic resistivity (Ri) was based on the analysis of Robinson and Stokes (1954) and the results of Trevelyan and Jack (2002). Specific intermediate values of Ri (listed in Table 2) were determined by logarithmic interpolation with Q10 = 0.8 applied to Ri = 140 Ω·cm at 36°C.

Temperature control in modeling

The following four elements were subjected to temperature control and analysis:

• 1) Gating-kinetic rate constants

• 2) G-bar (open channel) conductance, magnitudes, and distribution

• 3) Ion equilibrium (Nernst) potentials (given in Table 2)

• 4) Cytoplasmic resistivity (given in Table 2).

Data analysis

Phase plots from digitized data.

A phase plot of a tonic nerve impulse train is the closed (cyclical) curve generated by plotting the temporally advancing time rate of change, dV/dt, against the simultaneously advancing membrane potential V as shown in Fig. 3B (the dV/dt variable is replaced by capacitive and ionic currents in this plot and some other plots). Only the shape of the phase plot is of significance; the variable of time is typically not marked along the curve. The curve, for most of its length, expresses features of the action potential; the remaining short curve segment represents the interspike interval (ISI) (see Figs. 3B and 4A for more details). Phase plots of the experimental action potential data were used as templates to be fit by phase plots of model-simulated impulse trains.

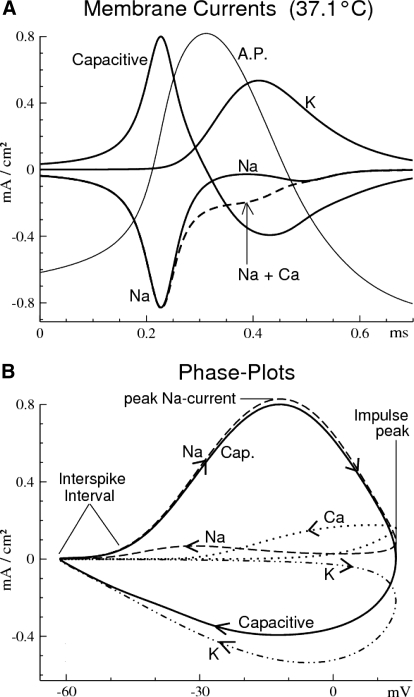
Fig. 3.

Demonstration of the method of analyzing the AP waveform using phase-plot analysis, which allows estimation of the membrane currents underlying the AP. A: model membrane currents associated with an AP at 37.1°C. B: phase plots of the ionic and capacitive currents [ordinate], plotted as functions of the membrane potential V [abscissa] throughout one impulse cycle. The ionic currents are +/− inverted (mirror-symmetrically flipped about the abscissa) to facilitate comparison with the capacitive current, which is conventional. Arrows = direction of time; curve segments with right (left) pointing arrow-components occur during the rising (falling) phase of the AP. Vertical slices (constant V) across rising- or falling-phase segments occur at the same time. Phase plots of the ionic currents do not cross the abscissa (i.e., each ionic current flow remains in the same direction across the membrane throughout the AP).

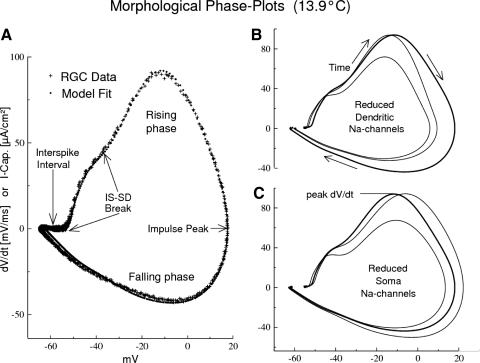
Fig. 4.

Demonstration of the sensitivity to channel distribution of the model fit to experimental phase plots (of the AP waveform) at a single temperature. A: model phase plot fit to rat RGC data at 13.9°C. B and C: sensitivity of the phase plot to modifications of the channel distribution. Channel distributions are modified on the dendrites and soma relative to the model fit from A to the real data (heavy curve). Thin curves: reduced peak dV/dt [ordinate] = dendritic or soma Na channels reduced by 50%; the original peak dV/dt is restored by increasing Na channels on the complementary membrane (G-bars are multiplied by factors of 1.29 on the soma or 1.44 on the dendrites; see text for interpretation). The percentage errors (see text) are the average deviation from the control curve, taken from 16 radial line samples crossing the curves from the center axis of the control curve (centroid). The line samples were spaced by equal time intervals (average angular spacing = 22.5°).

Digitized impulse train data provide sample points at equal time increments. Because dV/dt varies, these points are unequally spaced along the phase-plot curve. However, cycling over multiple action potentials fills in the gaps between the plotted points (it also provided signal averaging). This occurs because the digitization rate and impulse frequency are not synchronized.

It is critical that the two components (V, dV/dt) of the plotted points be isochronic everywhere along the curve of the phase plot. However, because the computation of dV/dt involves (at least) two sampling times, time is ill-defined for dV/dt. This makes digitized results highly prone to systematic phase-plot distortions, which increase with increasing sampling interval. This problem is largely eliminated by applying a first-order “correction” to the raw data. The correction assumes that the time of dV/dt is midway between the two consecutive sample times (used in its calculation) and shifts the plotted value of V to that temporal midpoint by linear interpolation, thus

$$\begin{array}{cc}Abscissa& \\ & V\left[i\right]=\left(f\left[i\right]+f\left[i+1\right]\right)/2\end{array}$$

$$\begin{array}{cc}Ordinate& \\ & \text{d}V/\text{d}t\left[i\right]=\left(f\left[i+1\right]-f\left[i\right]\right)/\Delta \tau \end{array}$$

where f[i] is the ith sample of membrane potential (raw data corrected for junction potential) and Δτ is the sampling interval. The phase plot consists of the i sequence of (V[i], dV/dt [i]).

Removing the systematic time discrepancy of Δτ/2 associated with direct use of V[i] = f[i] eliminates a gross distortion in the phase plot during the rising phase of the action potential (i.e., when dV/dt is large) and increases the acceptable maximum sampling interval by a factor of about 10. Both experimental and model impulse train data were digitized with the same Δτ = 0.1 ms (for T <25°C) and Δτ = 25 μs (T >25°C). Although this procedure yields accurate channel-density distributions, these noninfinitesimal digitization intervals Δτ continue to somewhat underestimate the peak excursions of dV/dt in phase plots.

Membrane currents and their phase plots.

In contrast to the experimental data, which consist exclusively of membrane potential V as a function of time, the model data add the underlying membrane currents. Relationships of these currents (I_Na, I_K, I_Ca, I_Capacitive) to the voltage during one action potential are shown in Fig. 3 for a space-clamped spherical soma (single-compartment model). Figure 3A shows the currents plotted linearly against time at 37.1°C. Note that, in contrast to the Hodgkin–Huxley model of the squid giant axon, the optimal Na and K currents are sequentially active— i.e., nonoverlapping in time (Fohlmeister 2009).

Figure 3B shows the same membrane currents plotted cyclically in the form of phase plots. Here, dV/dt is replaced by each of the ionic membrane currents, so that these phase plots consist of instantaneous pairs [V(t) (abscissa), I(t) (ordinate)]. The arrows indicate the direction of advancing time through the action potential waveform(s). Because the model is a single compartment, the absence of electrotonic current renders Kirchoff's law a zero-sum statement of the membrane currents: I_Cap + ∑_i I_i = I_STIM. Thus the instantaneous sum of the three major ionic currents (I_Na, I_K, I_Ca), plus capacitive current [I_C = C_m(dV/dt)], nearly equals zero throughout the action potential (contributions from I_K(Ca) and stimulus currents are negligible). More specifically, the Na and capacitive currents are nearly identical throughout the rising phase of the impulse because the K and Ca currents are near zero during that phase (Fig. 3B). Near the peak and during the falling phase of the action potential (negative capacitive current), the difference between K and capacitive currents is balanced by Ca current, the Na channel being inactivated.

Equivalence of dV/dt and capacitive current.

Phase plots of [V, I_C (capacitive current)] and of [V, dV/dt] are, point for point (i.e., in principle), numerically identical in both the space-clamped (Fig. 3B) and nonspace-clamped cases (Fig. 5, C and D). This is true because all membrane currents (capacitive and ionic) are local at the soma, which is also the recording site of the membrane potential V and therefore of dV/dt. This equivalence allows one to detect and quantify the effects of the nonspace-clamping (“electrotonic effects”) by comparing the recorded voltage waveform of the action potential with the underlying local ionic currents, as determined in model fitting. To convert capacitive current I_C to dV/dt, simply replace the ordinate units [μAmp/cm²] with [mV/ms], the proportionality factor being C_M = 1 [μFarad/cm²] (i.e., unity).

Fig. 5.

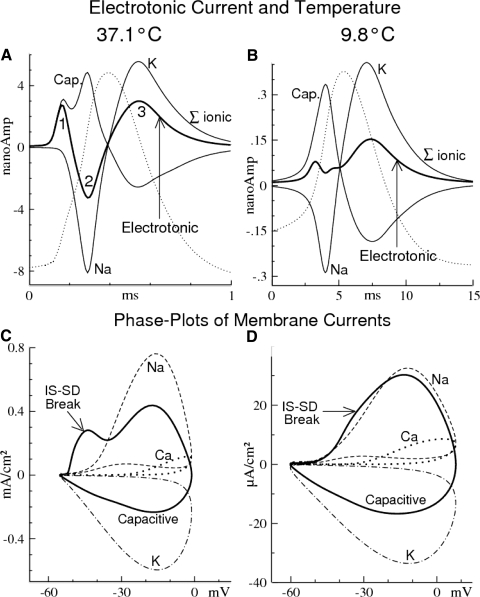
Comparison of the effect of high and low temperatures on the electrotonic current during an AP. A and B: electrotonic current (heavy curves), capacitive (“Cap.”), and summed ionic membrane currents (“Σ ionic”) at the soma during APs (thin dotted curves) at 37.1 and 9.8°C. The current peaks of “Σ ionic” are almost purely sodium (“Na”) and potassium currents (“K”). The plotted capacitive (and ionic) currents are only those from the recorded compartment (soma); membrane currents (including capacitive) of all other compartments contribute to, and are contained in, the electrotonic current. For ease in associating the electrotonic current peaks, the convention used here is negative electrotonic current = positive charge flowing out of the soma (thus negative trough 2 is positive electrotonic charge flowing away from the soma). The numbered peaks (and trough) of the electrotonic current are associated with: 1, almost pure capacitive membrane current (initial segment–somadendritic [IS-SD] break); 2, Na current of the regenerative phase of the AP; 3, K current during the recovery phase of the AP. Note the changes with temperature of both scales (abscissa and ordinate). C and D: phase plots corresponding to A and B, respectively. Capacitive (currents) = fits to one rat Type II RGC (see Equivalence of dV/dt and capacitive current in methods). Note that the large inequality of Na and capacitive currents in C (37.1°C) is small in D (9.8°C). The difference (inequality) is the subtraction of electrotonic current, which is absent for the space-clamped soma given in Fig. 3B.

Minimizing the residual error: uniqueness of the solutions.

A “solution” is defined to be a set of regional G_Na, G_K, and G_Ca that yields a model phase-plot congruency with the phase plot of experimental data at a given temperature; the ability to achieve congruency proves the existence of a solution. The model fitting of phase plots was done by hand, using the eye for signal averaging (e.g., Fig. 4A). The resulting solution was confirmed by computer minimization, in a process that also confirmed the uniqueness of the solution (see following text). Minimized was the global deviation (i.e., equal weight at all points) of the model-generated phase plots along the corresponding curves of experimental records. Varied were the regional G_Na, G_K, and G_Ca on the dendrites and soma (cf. Fig. 4, B and C) and on the initial segment (IS) and trigger segment (TS). At each step of the process the ion conductances were moved either singly, or in combinations, as required and suggested by the convergence properties observed in the earlier steps; the process was therefore one of interpolation among the earlier approximate fits. Each cell was fit separately at every temperature. Examples of phase-plot fits are given in Figs. 4 (13.9°), 7 (33.5°, 36.1°), 8 (35°), and 10 (7.2°C).

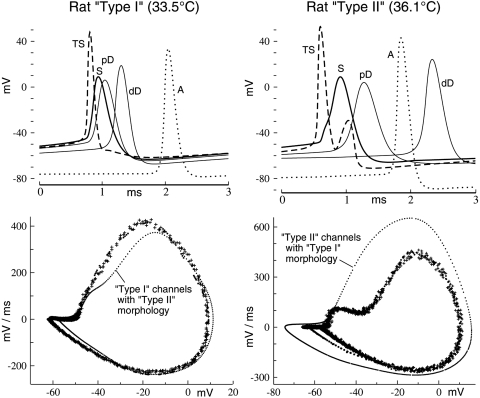
Fig. 7.

Comparison of AP initiation and propagation throughout 2 rat ganglion cell morphological models. Top panels: plots of AP initiation, shape, and time of occurrence at different RGC locations. Each set of records are of a 3-ms segment taken from the steady-state phase of model impulse trains. TS, trigger segment (site of impulse initiation); S, soma; pD, proximal dendrite (∼25% into the dendritic tree); dD, distal dendrite (near the dendritic tips); A, axon (900 μm distal to TS). Note the 2 depolarizations in the record for TS of RGC Type II (see text for interpretation). Bottom panels: phase plots of experimental impulse trains (+) of the 2 RGCs are independently fit by the model (heavier dots). The strong sensitivities to cell geometry become apparent when the distributed ion channels (model fits) are applied to the complementary RGC morphologies (small dots).

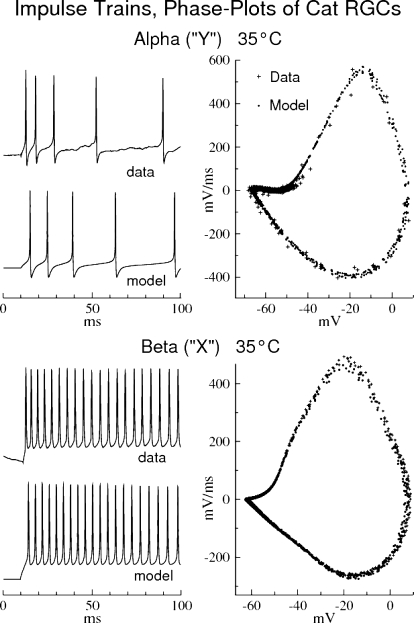
Fig. 8.

Comparison of impulse trains of recorded and model cat ganglion cells with their corresponding phase plots. Left panels: impulse trains of Alpha (“Y”) and Beta (“X”) RGCs of the Cat, at 35°C (top record of each pair, experimental data; bottom record, model simulation with the Cat RGCs shown in Fig. 2 with the channel densities listed in Table 1). Right panels: phase plots of the impulse train records at their left; experimental (+), model (dots).

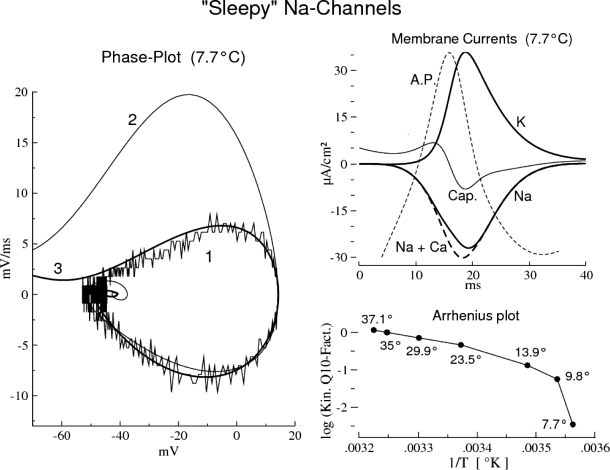
Fig. 10.

“Sleepy” Na channels. Phase plot 1 computed from a single impulse (rat RGC Type I) at 7.7°C. Thin curve 2 is the attempted model “fit” with standard (“nonsleepy”) gating kinetics. The model fit (heavy curve, 3) was obtained by applying an additional Na-channel–specific factor of 0.1 to the rate constants α_m (V), β_m (V), α_h (V), and β_h (V), which renders that channel “sleepy.” Membrane currents: ionic and capacitive currents and action potential (“A.P.”) of the model fit in A (compare Fig. 3A). Arrhenius plot: the logarithm (base 10) of the Na-channel gating rates, normalized to unity at 35°C (“Gating Kinetic Q10 Factors” in Table 2), plotted against inverse absolute temperature, 1/T (°Kelvin). The significant deviation from linear for 7.7°C indicates the non-Arrhenius behavior of “sleepiness” in the Na-channel gating (plotted points are specified in °C).

Uniqueness of the hand-fitted results was confirmed by computer with the minimization package SUBPLX—this package “uses the subplex method [a generalization of the Nelder–Mead simplex method which requires no derivative approximations] to solve unconstrained optimization problems. The method is well suited for optimizing objective functions that are noisy or discontinuous at the solution” (computer code and quote by T. Rowan, Department of Computer Sciences, Univ. of Texas, Austin). The minimization run for each phase plot was repeated 2,500 times from different random initial conditions (regional G_Na, G_K, and G_Ca). The initial conditions were generated from the 30,000 pseudorandom numbers [uniformly distributed on the interval (0, 1)], which are returned by the program RANDOM (Wichmann and Hill 1982). The 2,500 minimization runs for each “solution” were submitted as one “batch job,” which typically required 10 days to complete.

The “curve” to be fitted was defined by the sequential points of the phase plot determined from the (digitized) data points of a single experimental action potential and this was repeated for several action potentials. The test phase plots were generated from model data with the same digitization interval. The results were screened by increasingly limiting the acceptable residual norm, a process that strongly converged onto a unique solution for each cell. Specifically, the computer runs led to numerous local minima with large residual norms and incongruent phase plots. All runs that terminated with a small residual norm (and congruent phase plots; ∼2 to 4% of each “batch job”) also yielded channel densities near those listed in Table 1. The gating-kinetic Q10s (Table 2) were also confirmed by adjusting the underlined coefficients of the gating rate constants to minimize those residual norms. The values listed in Tables 1 and 2, however, were determined from precision fits done by hand.

RESULTS

General analytical considerations

Phase-plot sensitivity to alterations in somadendritic channel distribution.

Figure 4A gives an example of the quality of the model fits to the experimental phase plots of the action potential waveforms. The model fits occur with a unique morphological distribution of the primary ionic currents (see immediately above), whose conductance G-bars are listed in Table 1. Deviations from the listed values lead to the following distortions, which provide another form of evidence for the uniqueness of the solutions.

The sensitivity of the phase plots to shifting channel populations among the morphological regions is seen in Fig. 4B, which gives the example of reducing the dendritic Na-channel density by 50%. This results in the curve of reduced peak dV/dt (ordinate). The curve deviates from control (heavy curve), with an average error of −29.6% (see Fig. 4 caption for “centroid” error). The attempt to reestablish peak dV/dt with a compensating increase in somal Na channels (second thin curve) results in a −19.8% error.

Conversely, reducing the somal Na-channel density by 50% (Fig. 4C) causes a similar reduction in peak dV/dt (−23.8% error) and another form of failed correction by adding Na channels to the dendrites (+12.1% error). Note that the IS-SD break (an axonal phenomenon) is also affected by the relative channel distribution in the somadendritic region.

Increasing I_Na and/or I_K (maintaining their morphological proportions) “squares” the shape of the phase plot (i.e., flattens and slightly increases the peak and/or minimum ordinate excursions). The phase-plot distortions attributed to the transferring of channels between morphological regions or to proportionately increasing channel densities are sufficiently large to allow the Na- and K-channel distribution of the G-bars to be determined with <5% uncertainty for a single temperature.

The 50% regional channel reductions applied in Fig. 4, B and C resulted in excitation failure (loss of spiking) for some of the RGC morphologies of the same cell type. Spiking failure and irregularities increase with increasing temperature and can occur with as little as 20% reduced Na channels on the dendrites at 37°C. Since all real RGCs were excitable, this suggests that the channel densities are distributed in a relatively “sparing” and efficient manner, specifically to ensure action potential excitation for each RGC, particularly at mammalian temperatures. The distributed G-bars listed in Table 1 are for typical cells and are near the mean values found for each cell type.

Temperature's effects on the electrotonic current during the action potential.

Electrotonic current flows longitudinally inside the relatively slender neural processes of the dendrites and axon in response to nonzero spatial gradients of the membrane potential. This is the current that flows across the boundaries between neighboring compartments. The electrotonic current (at a given location) was calculated as the negative sum of all instantaneous membrane currents of the local compartment (including capacitive, ion channel, leak, and any injected stimulus). This sum is balanced by the electrotonic current from the requirement of current conservation (see methods).

The experimentally recorded membrane potential at the soma is therefore the result of weighted contributions from the local membrane currents, stimulus current plus electrotonic current due to regional membrane currents from the dendrites, and the impulse initiation site of the axon. Using a fixed distribution of ion channels, Fig. 5 shows significant differences in the contribution of the electrotonic current in shaping the model action potentials at high and low temperatures (Fig. 5, A and B, respectively). At 37.1°C there is a large negative electrotonic current (trough 2 in Fig. 5A) in response to the local (somatic) Na current associated with the regenerative phase of the somatic action potential. This negative electrotonic current became smaller at 23.5°C, remained detectable at 13.9°C (neither is shown), but is entirely absent at 9.8°C (Fig. 5B).

These changes in trough 2 reflect shifting weights in the contributions of the regional membrane currents to the somatic action potential. The temperature-related changes are caused by differences in the temperature dependence among the contributing factors. The rates of channel gating are the most strongly affected, whereas electrotonic effects (i.e., the spatial spreading of local changes in membrane potential) are determined by the relatively weaker temperature-dependent Ri and Rm and the temperature-independent morphological diameters. At high temperatures (Fig. 5A), the fast de- and repolarization rates allow little time for spatial spreading during the short duration of the action potentials, which can lead to steep spatial gradients in membrane potential.

Thus the fast gating kinetics at high temperatures cause the action potential on the trigger segment (TS) to be near its peak by the time it begins to rise regeneratively at the soma (cf. Fig. 7 in the following text). This implies a steep (descending) gradient between TS and the soma. The positive charge flowing into the soma by the resulting electrotonic current (“peak 1”) causes the initial, smaller peak in the capacitive current (Fig. 5A), which is associated with the IS-SD break (cf. Fig. 5C).

Trough 2 of the electrotonic current occurs at the subsequent time of maximum rate of depolarization at the soma. It occurs, in part, in response to the large spatial gradient (descending) from the depolarizing soma into the dendrites (which are still subthreshold) and, in part, to the similar gradient in the axonal direction, where the fast gating kinetics have (nearly) repolarized TS. The peak rate of depolarization at the soma (peak capacitive current) is associated with maximum regenerative Na influx (Fig. 5A). Note that the electrotonic current at trough 2 draws off about half of the positive charge introduced into the soma by the regenerative Na current (Fig. 5C).

At lower temperatures, the relatively slower depolarization rate allows more time for spatial equilibration. This expands the spatial reach (extent) of concurrent regenerative activity (Na current) that, at 9.8°C, comes to encompass TS, the soma, and well into the dendritic tree. Further, the various phases of the action potentials are instantaneously more nearly the same across these three regions (i.e., the action potentials overlap), which reduces the spatial gradients. Thus at 9.8°C, peak 1 of the electrotonic current is substantially reduced relative to the membrane currents and trough 2 is entirely eliminated (Fig. 5B), even though at the time there is significant regenerative Na influx.

Figure 5, C and D shows the corresponding changes in the phase plot between the two temperatures (37.1 and 9.8°C). The phase plots are of the type [V, I_x], as in Fig. 3B, except nonspace-clamped. In Fig. 5C (37.1°C), there are two peaks of capacitive current during the rising phase of the action potential, due to the IS-SD break and the regenerative somatic action potential. Note that the phase plot for the Na current does not show a corresponding peak associated with the IS-SD break in the phase plot for capacitive current. Thus the IS-SD break (the initial abrupt rate of rise in membrane potential that triggers the local soma action potential) is not associated with a local Na current. Because only the sodium and electrotonic currents are potentially capable of generating a rapid membrane depolarization, this absence of a corresponding Na-current peak in the phase plot confirms that the IS-SD break is a purely electrotonic effect at the soma, due to a Na-current–induced depolarization elsewhere (i.e., on the axonal impulse trigger zone). In Fig. 5A, the IS-SD break is the leftmost of the pair of peaks in capacitive current (associated with peak 1 of the electrotonic current).

Except for the IS-SD break (absent in the single-compartment simulation of Fig. 3), the capacitive current in multicompartment simulation is significantly reduced relative to that of the single compartment (about halved at 37.1°C, both ± ordinate excursions relative to zero; compare Figs. 5C and 3B), and this is due to the electrotonic load (trough 2 in Fig. 5A). The peak Na current is also somewhat lower than that in single-compartment simulations (related to the same cause); the peak K currents, however, are nearly the same.

In contrast to 37.1°C, the membrane currents I_Na, I_K, and I_C are significantly smaller at 9.8°C and I_Na matches I_C more closely during the rising phase of the action potential (compare Fig. 5, C and D). Note also that I_Ca is larger relative to I_Na and I_K, which is due to the greater impulse amplitude at 9.8°C. Further, I_C is much greater at 37.1°C because of the much faster kinetics, the much shorter action potential width, and thus much higher dV/dt (see van Rossum et al. 2003). Nevertheless, despite these large electrotonic and temperature differences, the optimally fitted Na-, K-, and Ca-channel distributions (G-bars) are nearly identical for 9.8 and 37.1°C. This confirms the uniqueness of the model-determined channel distribution for a given RGC and these are the G-bar conductances listed in Table 1.

Morphological distribution of membrane currents by RGC type

Table 1 lists the distributions of open channel conductances, G-bar (mS/cm²) at 35°C, for I_Na, I_K, and I_Ca throughout the neural processes, as determined for the four ganglion cells (RGCs) shown in Fig. 2. The median deviations from the listed G-bar values among members of the same cell-type were about ±6%; the maximum observed deviation was 14% (cf. Relation of channel distribution to cell morphology in the following text). For temperatures other than 35°C, apply the “Conductance Q10-Factors” (Table 2, bottom panel).

Temperature Q10s

The temperature Q10s of the sodium and potassium channel gating-kinetic rates and of G-bar conductances are listed in Table 2. The four Q10s were derived from phase-plot fits (rat RGC data) for a series of closely spaced temperatures, which allowed each Q10(T) to be recognized as a continuous, monotonic function of temperature. Each of the four Q10s remains constant (and relatively small) in the range 23 to 37°C. The Q10s systematically increase as the temperature is reduced from 23 to about 7°C. Spiking terminates for RGCs at 7°C (see “Sleepy” sodium channels in the following text and discussion).

Voltage and temperature dependence of the gating rate constants

The voltage dependence of the gating-kinetic rate constants yielding the best phase-plot fits remains unchanged across two temperature spans: T >30°C (Standard gating rate constants) and T <23°C (Alternate rate constants in methods). There is, however, a noticeable steepening in the steady-state fractions of open gates, m_∞³ and n_∞⁴ (as functions of V), when temperature is reduced from 30 to 23°C. The steady-state fractions and the gating time constants are shown in Fig. 6B (Na channels) and Fig. 6C (K channels). The steeper voltage dependence was observed in control impulses at T <23°C, taken both before and after the higher temperatures, indicating that the effect is reversible. Possible causes are given in the discussion. Phase plots are superposed in Fig. 6A at three widely spaced temperatures.

Fig. 6.

Temperature's effects on rate constants. A: phase plots as a function of temperature (rat Type I RGC). B and C: steady states of gating and time constants of the “Standard” rate constants for T >30°C (continuous curves) and “Alternate” rate constants for T <23°C (dashed curves) for Na- and K-channel gating, respectively. The steady-state fractions of open gates, m_∞³(V), h_∞(V), n_∞⁴(V), are computed as: x_∞(V) = α_x(V)/[α_x(V) + β_x(V)], (x = m, h, n), and vary on the ordinate interval (0, 1). The dashed and solid curves of m_∞³ and of n_∞⁴ intersect at −61.09 and at −19.24 mV, respectively (see text for interpretation). Time constants are computed as: τ_x(V) = 1/[α_x(V) + β_x(V)], with ordinate scales specified for T = 35°C.

Both sets of the rate constants (Standard and Alternate) are nominally listed for T = 35°C—this allows a direct comparison of the gating time constants, τ_m and τ_n, in Fig. 6, B and C. To obtain rate constants for other temperatures T <23°C or T >30°C, apply the multiplicative “Kinetic Q10 Factors” (Table 2) to the underlined coefficients of the set of rate constants that applies to that temperature. The same “Kinetic Q10 Factors” apply to both sets; they scale the overall rates of channel gating (i.e., τ_m,h,n), but do not affect the voltage sensing [i.e., m_∞³ (V), h_∞ (V), n_∞⁴ (V)].

The transition from “Standard” to “Alternate” rate constants appears to be smooth. Thus for rate constants in the range of 23°C < T < 30°C, apply linear interpolation between all corresponding numerical values of the two sets of rate constants and the “Kinetic Q10 Factors” to the result.

Impulse initiation and propagation (rat cell type, IS-SD break)

The bimodal distribution of total membrane area of RGCs suggests two broad morphological cell types (see methods, Reconstruction of RGCs for model simulation). These appear to be distinguished by the relative prominence of the IS-SD break and the simulation results confirm that cell “type” correlates with overall cell size. The top panels of Fig. 7 show examples of the temporal development of excitation throughout the two morphological types from rats (Fig. 2). Following activation at the thin segment (or trigger segment [TS]), the nascent impulses propagate into the somadendritic tree (S, pD, dD) and down the axon (A). The channel-density distributions used are listed under “Rat RGC Type I” and “Rat RGC Type II” in Table 1.

For the type I cell, action potential initiation occurs as a single impulse at TS (near its junction with the initial segment [IS]) and diverges as a pair of impulses in two directions. The temporal sequence for the Type II cell, on the other hand, involves a substantial nonregenerative (passive) initial depolarization of the soma (the IS-SD break; cf. Fig. 5C), which is electrotonically associated with the newly triggered impulse on TS. Simulations show that the greater electrotonic load of the larger cells can delay the regenerative excitation onset at the soma (see Fig. 9F in the following text). The delayed somal action potential can cause a second depolarization of TS, as seen in Fig. 7 (a combination of electrotonic and locally active currents). This second depolarization of TS could therefore again become suprathreshold, which is a potential mechanism for propagating spike doublets on the axon.

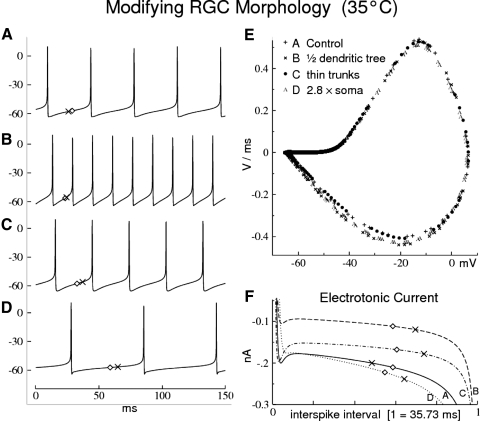
Fig. 9.

Repetitive firing effects of modifying an Alpha ganglion cell's somadendritic morphology while retaining its impulse waveform. The somatic G_Na-bar is reduced, specifically to maintain the optimal match with the control impulse phase plot. A (Control): “Cat Alpha RGC” of Fig. 2 (soma = 4,047 μm²; dendrites = 28,247 μm²; surface ratio = 0.143), with G-bars of Table 1. B: the rightmost dendritic tree, including its trunk, is removed at the soma. C: the thick, right-side dendritic branch and trunk diameters are halved. D: the soma is enlarged. Quantitative changes are listed in Table 1 as multiplicative factors relative to A; among membrane conductances, only the G_Na-bar was adjusted. E: phase-plot homology is maintained throughout, for which the somatic G_Na-bar was reduced to 75% in B, C, and D (relative to A). Left panel: impulse trains in steady-state repetitive firing (stimulus = 0.2 nA injected into the soma); note the changes in impulse frequency. F: electrotonic currents at the soma during the interspike interval (ISI) associated with the conditions of A–D: the ISI durations were normalized to A (=35.73 ms) by adjusting the injected stimulus current, thus A (control; stim = 0.2 nA; continuous curve), B (stim = 0.1195 nA; dashed), C (stim = 0.178 nA; dash-dot), D (stim = 0.2384 nA; dots). () = the point at which the electrotonic current becomes larger (in magnitude) than the injected stimulus current (the effective stimulus to the soma becomes negative); (◊) = the point of minimum dV/dt during the ISI (the depolarization rate changes from the initial deceleration, to subsequent acceleration; see text).

Exchanging the ion channel distributions between the two morphological types again produced poor phase-plot correlation with the observed data (small dots in the bottom panels of Fig. 7). Nevertheless, the highest Na-channel density was found on the membrane of “TS” in every tested RGC (Van Wart et al. 2007). Despite this, and although the impulses in Fig. 7 are initiated on TS, the initiation point can vary from the soma to the proximal axon to a distance of about 200 μm, depending on the magnitude of stimulus and on spiking history (cf. Fohlmeister and Miller 1997b; Sheasby and Fohlmeister 1999).

Phase plots of cat RGCs

Impulse train records and phase plots from cat Alpha (“Y”) and Beta (“X”) RGCs at 35°C were fitted to the RGC model, as shown in Fig. 8. The best cat RGC model fits occurred with the same rate constants used for the rat RGC simulations. The two species thus appear to share similar gating kinetics. Differences in the phase plots (action potentials) are due to morphological effects (see following text and Fig. 7). Although both X and Y cells show high Na-channel densities on their trigger segments TS, similar to those of rat “Type I” and “Type II” cells (Table 1), the cat RGCs show little IS-SD break in their phase plots.

Relation of channel distribution to cell morphology

Despite the geometric complexity of individual RGCs, general rules exist for maintaining phase-plot homology with cell-type–specific channel distributions. To generate these rules, two initial observations are helpful. 1) As shown in Table 1, the somadendritic distribution of Na channels is relatively uniform across most RGCs (70 ± 10 mS/cm²), except that the larger cells show a higher G_Na bar on the soma (particularly the 158 mS/cm² of the large cat Alpha RGC), and 2) the soma-to-dendritic ratios of membrane area are significantly higher for the small-area Type I cells (mean ratio = 0.289 among our traced RGCs) than they are for the large-area Type II cells (mean ratio = 0.125; see methods, Reconstruction of RGCs for model simulation).

The relationship between Na-channel distribution and area parameters was explored by systematically modifying the somadendritic morphology of the most exceptional cell in Table 1, i.e., “Cat Alpha RGC” of Fig. 2. Figure 9 shows the control (A) and the results of modifications that include removing a large dendritic tree (B), thinning dendrites (C), and enlarging the soma (D). These modifications all loosely retain the original action potential waveform (i.e., a similarly shaped phase plot; Fig. 9E), while reducing the somatic G_Na-bar to 75% of the original Cat Alpha RGC value given in Table 1. Each modification also increases the cell's soma-to-dendritic area ratio (the control area ratio = 0.143). All changes in membrane parameters are listed in the bottom panel of Table 1, in the form of fractions relative to control.

The effects of these modifications on impulse frequency (constant stimulus current) are seen in the model spike train records in the left panel of Fig. 9. The frequency changes significantly (Fig. 9, B–D), whereas the action potentials remain of similar shape (Fig. 9E). Furthermore, these results exemplify the following generally observed rules. Rules 1 and 2 apply to RGCs in general, with rule 2 establishing the overall soma-to-dendritic Na-channel density ratio based on membrane area. Additional rules 3 and 4 serve to modulate regional Na-channel densities based on the diameters of the soma and dendritic processes.

1. The impulse frequency (for given stimulus current) is inversely related to the total somadendritic surface area and is directly (but weakly) related to the distal extent of the dendritic arbor (see following text).

2. The ratio of soma-to-dendritic Na-channel densities (G_Na bar) is inversely related to the ratio of soma-to-dendritic surface areas. Further, the relative proportions of the Na-channel densities on the initial segment (IS), the trigger segment (TS), and on the soma remain nearly constant.

3. The Na-channel density of a given neural process (soma, dendrites) is inversely related to the diameter of that process (this also applies to the axon; cf. caption of Table 1).

4. Overall the Na-channel densities (soma and dendrites) are inversely related to the size of the soma.

Because the soma-to-dendritic area ratio is roughly cell type specific, rules 3 and 4 apply primarily within a given cell type. Substantial deviations from rules 2, 3, and 4, particularly as they apply to the higher channel densities required for thinner processes, can result in excitation failure.

The effect on the impulse waveform when the control Na-channel densities are retained with the modified (mod.) morphologies can be inferred from the phase-plot changes in Fig. 4. Dendrites may be partially severed in the “slice preparation,” for example (corresponding to mod. B). This will lead to an increased impulse amplitude with increased peak dV/dt and a somewhat reduced IS-SD break (i.e., invert the effect demonstrated in Fig. 4C). The impulse frequency generated by mod. B (with control Na channels) will lie between those of Fig. 9, A and B. This is because the reduced membrane area of mod. B increases the frequency relative to that in Fig. 9A (rule 1, listed earlier), but the deeper afterhyperpolarization associated with the greater impulse amplitude lengthens the ISI of Fig. 9B. Thus the rules implicitly explain the exceptionally high G_Na bar found on the soma membrane of the unmodified “Cat Alpha RGC” in Fig. 2 and further suggest that, for all RGCs, the observed channel densities are determined by the criterion of the minimally necessary ionic currents for excitation, with a “safety margin” in the range of 15 to 35%.

Repetitive firing, dendritic load, and impulse frequency

Previous studies of RGCs found that electrotonic load on the encoder is a primary factor in reducing the impulse frequency in low-frequency repetitive firing (Fohlmeister and Miller 1997b). This load is reflected in the large dendritic areas of cat Alpha RGCs, which have a significantly lower total membrane resistance than that of their smaller-area Beta RGC counterparts (Cohen 2001; O'Brien et al. 2002). For reduction of impulse frequency, the salient electrotonic current occurs during the ISI (Fig. 9F), which is one to three orders of magnitude smaller than its maxima during an action potential. Figure 9F shows that the electrotonic current is negative (hyperpolarizing) throughout the ISI for all modifications of the Alpha RGC. The curves go off-scale near their ends, as a result of the active membrane currents associated with action potentials.

As shown in Fig. 9F, the magnitude of the electrotonic current in the ISI is strongly dependent on morphology. The algebraic sum of injected stimulus current plus electrotonic current is initially depolarizing (injected current dominates) and later hyperpolarizing (electrotonic current dominates). This algebraic sum is the effective stimulus (of the soma), which equals the sum of all external currents, either injected or electrotonic, i.e., originating in other compartments. The (×) marks the point in the ISI at which the injected current balances the electrotonic current—i.e., the point of zero net stimulus, beyond which the effective stimulus is hyperpolarizing. For the control curve (A, solid in Fig. 9F), the injected current (0.2 nA) is balanced at −0.2 nA of electrotonic current (negative electrotonic current = net positive charge flowing out of the compartment into its neighboring compartments; see methods). The durations of the ISIs for the modified Alpha cells (modifications B–D) were normalized to that of control (35.73 ms) by adjusting the injected stimulus current. Modifications B and C required <0.2 nA of injected stimulus; D required >0.2 nA (see Fig. 9 caption). Note that the balancing electrotonic current is the negative of the stimulus current in all cases and that the changeover point (×) from depolarizing to hyperpolarizing effective stimulus occurs significantly later in the ISI for all three modifications (B, C, D), relative to control (A).

The membrane potential, however, continues to depolarize monotonically throughout the interval, despite the changeover to a hyperpolarizing effective stimulus at the soma. Indeed, the initially slowing rate of depolarization subsequently increases. This is due to Na-activation gating, which continues in the soma. The increasing Na current is the cause of the increasing magnitude of the (negative) electrotonic current. The electrotonic current, in turn, reduces the rate of depolarization and therewith the rate of Na-activation gating, which lengthens the ISI (reduces impulse frequency). Because it is a response to (i.e., instantaneously induced by) the increasing depolarization, the electrotonic current acts like a “dashpot” (a form of negative feedback, or drag) that can slow, but cannot reverse, the continuing depolarization. A similar phenomenon occurs in the action potential, where the descent into “trough 2” of electrotonic current in Fig. 5A slows the rate of regenerative Na-activation gating (widens the impulse).

The changeover point in depolarization rate (minimum dV/dt), which is marked (♢) in Fig. 9F, occurs at a more uniform location within the ISI. (This inflection point on the voltage wave shape is also marked by the diamond (♢) in the first ISI of Fig. 9, A–D.) Thus the morphological modifications do not significantly affect the interspike trajectory of the membrane potential. Note, however, that the onset of hyperpolarizing effective stimulus (×) occurs after minimum dV/dt (♢) for all three modifications (B–D), whereas it occurs prior to minimum dV/dt in the control record (A). This reflects the 25% reduced somal Na channels associated with the modifications and shows the insignificance of Na-channel gating in the control of the ISI trajectory (see Fohlmeister 2009).

“Sleepy” sodium channels

Although rat RGCs generate large-amplitude impulses at the lower temperatures (Fig. 1, bottom panels), the Na channels become “sleepy” for T <8°C and spiking abruptly ceases for T <7°C. The non-Arrhenius kinetic behavior of “sleepiness” manifests itself in an abrupt slowing of the Na-channel gating kinetics (cf. Matteson and Armstrong 1982). Action potentials generated in the range of 7–8 °C with “sleepy” Na channels are of abnormally long duration (12 to 15 ms; bottom right of Fig. 1 and thin dashed curve in the top right of Fig. 10; see also Table 2).

Figure 10 (left panel) shows phase plots of experimental impulse data at 7.7°C (noisy curve 1) and of model impulses generated with “nonsleepy” (curve 2) and “sleepy” Na-channel kinetics (curve 3). The “sleepy” model responses were generated by a 16.22-fold reduction of the Na-channel rate constants in going from 9.8 to 7.7°C (corresponding to “Q10” = 520,000; Table 2); Na-activation and Na-inactivation gating, α (m, h) and β (m, h), are equally affected. This large Q10 is reflected in the Arrhenius plot (Fig. 10, bottom right), which shows an abrupt deviation from the linear for T <9.8°C. The 16.22-fold reduction is equivalent to first applying the nonsleepy gating kinetic Q10 = 9 to all Na-channel rate constants for 9.8°C, followed by an additional multiplicative factor of 0.1 (Q10 = 9 was determined for K-channel gating, which remains nonsleepy at 7°C).

The top right panel of Fig. 10 shows the ionic and capacitive membrane currents and the action potential of the “sleepy” model as it was fit in the phase plot. Note the simultaneous flow (temporal overlapping) of the “opposing” Na and K currents, which is a characteristic of the Hodgkin–Huxley model for the squid giant axon, and is absent in the nonsleepy five-channel model (cf. Fig. 3). The subthreshold oscillations and repetitive firing responses of “sleepy” RGCs (Fig. 1, bottom) are also characteristic of the Hodgkin–Huxley model (see Fohlmeister 2009).

DISCUSSION

Temperature has proven to be a strong independent variable in the analysis of action potentials in retinal ganglion cells in situ. It offered a previously underused “dimension,” along which to exploit the inherent nonspace-clamped condition to determine and constrain nonuniformly distributed membrane features. The range of 7 to 37°C is sufficiently large for the gating rates of ion channels to change by more than one order of magnitude. Given that degree of change, it was not known a priori that the best model fits to experimental phase plots would emerge with the uniquely same result at all temperatures. The fact that this occurred has yielded the nonuniform distribution of membrane currents throughout a substantial portion of the morphology of RGCs, to a high degree of certainty and accuracy.

Building on the channel mechanisms of the Hodgkin–Huxley model (1952), we were able to obtain good fits to mammalian RGC action potentials by simple modifications to the channel-gating kinetic rate constants. The ease with which experimental phase plots were fit implies a reasonably accurate description of the membrane currents during action potentials, despite the fact that the mammalian impulse waveform differs significantly from that of the squid giant axon. The waveform of the squid axon is associated with considerable K current during the regenerative phase of the action potential (including at impulse threshold) and, further, a large majority of the Na current (85% at 6.3°C) occurs during the falling phase of the action potential. With the rate constants of mammalian RGCs, in contrast, there is almost no temporal overlap of these currents throughout the action potential (see Fig. 3A). This absence of competition between the major ionic currents represents a metabolic optimization of the Hodgkin–Huxley kinetic framework (Fohlmeister 2009).

Model simulations show optimally concerted ionic currents during action potentials at all temperatures. Thus the curves of the membrane currents shown in Fig. 3A retain their character, with only the scales of current magnitude (ordinate) and time (abscissa) changing with temperature. These results reflect the finding that, first, the voltage dependence of the channel gating (rate constants) remains unchanged throughout a large temperature range (7 to ∼23°C). The voltage dependence changes somewhat in the mammalian temperature range, particularly for T >30°C, but remains functionally the same, in that the ionic currents remain optimally concerted throughout the action potentials. Second, at each temperature the Q10s are nearly the same across the gating processes (Table 2). The readily detected exception is the abrupt change in the Q10 of Na-channel gating (“sleepy channels”) at low temperatures (7–8°C). The slowing of Na-channel gating associated with “sleepiness” causes the Na and K currents to overlap competitively during the action potential at these low temperatures, thus making the “sleepy” RGCs somewhat similar to the original Hodgkin–Huxley model (Fohlmeister 2009).

Complement of ion channels: voltage-gated ion channel subtypes found in RGCs

To form a perhaps more definitive model, one would ideally prefer to use the specific isotypes of sodium and potassium channel reported in retinal ganglion cells. However, considerable controversy exists over which ion channel types are present in mammalian retinal ganglion cells and in what location and proportions. At present there are between 13 and 17 ganglion cell types found in most vertebrate retinas.

Kaneda and Kaneko (1991) found that sluggish or W-cells in the cat had sodium currents with slower rates of recovery than those of brisk X-type ganglion cells. Studies using antibodies or in situ hybridization of sodium channels have reported the existence of sodium channel types Na_V1.1, 1.2, 1.3, and 1.6 in the retinal ganglion cell layer (Boiko et al. 2001; Caldwell et al. 2000; Craner et al. 2003; Khaliq et al. 2003). However, studies disagree on the RGC locations of these ion channel subtypes and whether they are expressed in all ganglion cell types. For example, Na_V1.6 was reported by Caldwell et al. (2000) and Boiko et al. (2001) to be located exclusively in the inner segment of the axon, whereas Craner et al. (2003) and Kaneko et al. (2007) reported hybridization in the ganglion cell body and axon as well. Finally, virtually nothing is known about the phosphorylation state of the sodium channels in RGCs (Hidaka and Ishida 1998).

The distribution of voltage-gated potassium channels in RGCs is also poorly understood. The potassium channel subunits Kv1.1–1.6 have been reported to hybridize to ganglion cells (Henne et al. 2000; Höltje et al. 2007; Pollock et al. 2002). Lasater and Witkovsky (1990) found differences in ganglion cell spiking properties reflected in the kinetics of inactivation of outward currents (presumably due to potassium channels; cf. also Lukasciewicz and Weblin 1988).

The ability of the five-channel model to accurately simulate action potentials does not exclude other ion channels. Small currents (including Ca-activated K currents, low-threshold T-type Ca currents: Henderson and Miller 2003; Lee et al. 2003; I_h currents: Pape 1996; Tabata and Ishida 1996; etc.), some of which may be involved in the precise timing of the occurrence of impulses, remain undetected (effectively masked) in phase plots by the dominance of the large currents of the action potential. The A current appeared small in our model because the experimental data did not exhibit a decisive “phase-plot signature” for the inactivating I_K(A) in the action potential. Although other models of cat RGC spiking have used estimated channel kinetics (e.g., van Rossum et al. 2003) and have examined the ISI, our study has focused principally on the mechanism of the nerve impulse.

Temperature Q10s

Previously reported Q10s of gating kinetics vary by channel type, among the gates of a given channel, the direction of the gating-kinetic step (i.e., opening or closing the channel), the temperature range under consideration, and also with the experimental method. Thus Q10s for K-channel gating range from Q10 = 1.5 (Tiwari and Sidkar 1999) to 3.63 (Clay and Shrier 2002). Frankenhaeuser and Moore (1963) found in the frog node of Ranvier (5–20°C): Q10 = 3.2 for α_n, 2.8 for β_n, and differential Q10s = 1.76 and 2.87 for Na-channel activation (m) and inactivation (h) gating, whereas Collins and Rojas (1982) found Q10s = 2.34 and 2.9, respectively, for the latter.

Larger Q10s have also been determined, particularly in mammalian preparations at lower temperatures. Thus Q10s >4 are reported for both ionic and gating (asymmetric displacement) currents of Shaker K⁺ channels in the range 2–22°C (Rodriguez et al. 1998). A Q10 as high as 7.31 is reported for a slow, external K⁺-activated K current [“I(deltaK)”] in cortical and hippocampal neurons (Filippov and Krishtal 1999). Beam and Donaldson (1983) reported Q10 = 6 for K-channel activation in rat skeletal muscle in the range 1–10°C; this reduced to Q10 = 2 for the range 30–38°C. Our Q10s fall into the general pattern of these reports, but are more highly constrained because of the sensitivity of phase-plot analysis.

In mammalian RGCs, we find that nearly the same gating-kinetic Q10 applies to all rate constants of the spiking Na and K currents. Different Q10s among the channel types, or among the rate constants of a given channel, result in phase-plot distortions or spiking failure (cf. Klockner et al. 1990). This finding is one of the major conclusions that follows from the RGCs' ability to generate action potentials throughout a temperature range that is sufficiently large to change the kinetic rates by more than one order of magnitude. A small difference of Q10 = 1.95 and 1.9 between Na- and K-channel gating, respectively, is seen throughout the range of 23–37°C. As is commonly observed in mammalian preparations, the gating-kinetic Q10s increase as temperature is lowered below T <23°C (Table 2) and our values are remarkably consistent with those of Beam and Donaldson (1983). The large Q10s at low temperature may indicate a departure from the enzyme kinetics of conformational changes in a single protein molecule and may suggest a more complex gating mechanism involving channel subunits (Catterall 1995; Hanlon and Wallace 2002).

Effect of temperature on channel gating

One of the aims of the present study was to extend rate constants obtained for tiger salamander RGCs at 22°C (Fohlmeister and Miller 1997a,b) to mammalian preparations and temperatures. It was found that the rate constants of the mammalian preparations undergo a noticeable change in range of 23–30°C (dashed to solid curves in Fig. 6, B and C). The effect is benign to the normal signaling function of the neuron (i.e., its encoding flexibility; cf. Fohlmeister 2009). It does have a potential metabolic advantage (Na-K-ATPase pumping) in that, at the highest temperatures (T >35°C), the “standard” rate constants are capable of maintaining spiking with about 10% lower channel densities. This capability, however, appears to be in the nature of an additional “safety factor” because the fitting of phase-plot data (i.e., phase-plot congruency) occurs with the same (i.e., unchanged) morphological distribution of ion channel densities at all temperatures.

Among the temperature-dependent differences in the rate constants is a reduced steepness in the voltage dependence of m_∞³ (V) and n_∞⁴ (V) for T >30°C relative to that for T <23°C (see Fig. 6, B and C) and this may be a capacitive effect. Earlier work has shown that membrane capacitance decreases with increasing temperature (e.g., Robinson and Stokes 1954; White 1975) and this may indicate an increased thickness in the hydrophobic portion of the bilayer membrane, possibly associated with thermodynamic phase transitions (e.g., Boheim et al. 1980). An increased thickness implies a lower transmembrane electric field, dV/dx, for a given membrane potential (x = transmembrane direction). Because the “voltage sensor” of channel gating responds directly to the electric field (not to the membrane potential), a thicker membrane will reduce the steepness in voltage dependence of channel gating.

The dashed and solid curves of m_∞³ (V) and n_∞⁴ (V) in Fig. 6, B and C intersect at different membrane potentials (equal m_∞³ occurs at −61.09 mV; equal n_∞⁴ at −19.24 mV). The offsets from zero may partially be explained by differential surface charges (e.g., Gilbert and Ehrenstein 1969; McLaughlin and Harary 1974). Note also that the h_∞ curve simply shifts on the voltage axis and does not intersect. This may be an indication that Na-inactivation gating is linked to Na-activation gating without an independent voltage sensitivity. There are, however, differences in the voltage dependence between the “standard” and “alternate” rate constants that cannot be attributed to these biophysical effects alone, such as differential gating effects between a given transition and its inverse (e.g., α_n and β_n).

These gating effects may be associated with the same cause as is the Q10s' behavior change as a function of temperature. Note that the changes from “alternate” to “standard” rate constants begin to arise at about the same temperature as does the onset of constant and low gating-kinetic Q10s (=1.9, 1.95), i.e., about T >23.5°C—thus consider that mammalian channel gating may involve two simultaneous processes of widely different temperature Q10s and with distinct voltage dependencies. The overall voltage response of gating may combine the two voltage dependencies in such a way that the voltage dependence of the rate-limiting process is dominantly expressed and “masks” that of the other (faster) process. Thus the high-Q10 process (Q10 ≃ 8) will be considerably slower and therefore rate limiting at sufficiently low temperatures (expressing “alternate” rate constants), but will speed up rapidly at high temperatures where the low-Q10 process (Q10 ≃ 2) then becomes rate-limiting (and “standard” rate constants are expressed).

The concept of two simultaneous and complementary active processes in mammalian channel gating is supported by a comparative analysis with the squid giant axon (Fohlmeister 2009). The high-Q10 component of channel gating appears to be missing in the squid axon. The action potential of the squid axon has a duration of only 2.5 ms at 6.3°C (the primary temperature of the Hodgkin–Huxley model) and a comparison with the mammalian RGC action potentials shows that the gating-kinetic Q10 of the squid axon remains constant (Q10 = 2) down to 6.3°C. This Q10 = 2 is very near to the Q10s = 1.9 to 1.95, which remain constant in RGCs in the partial temperature range of T >23.5°C. It is possible that these relatively low Q10s (=1.9 to 2) are associated with the irreducible minimum mechanism necessary for channel function and are therefore conserved across species (possibly related to the α-subunit of the channel) and that the mammalian channel gating is more complex and involves secondary processes of high Q10 that do not occur in the squid axon (possibly associated with the channel β-subunits). These secondary processes may also possibly be associated with the functional differences of the various mammalian channel subtypes Na_V1.1–1.6 and Kv1.1–1.6.

Summary.

Varying the temperature of the action potential kinetics has allowed us to estimate the regional distributions of ion channels on the dendrites, soma, and proximal axon of retinal ganglion cells. We were able to use relationships of these channels with temperature to detect and to quantify details of their gating kinetics and their Q10s. The same (five-channel) model could be applied to anatomically reconstructed RGCs in two species. The voltage dependence of channel-gating changes between 23 and 30°C, but remains invariant outside this transition range. The gating-kinetic Q10s and ion-permeability Q10s remain constant for all T >23°C and both systematically (but independently) increase for T <23°C. These features maintain an “optimum” relationship between the Na and K currents, which is broken only by “sleepy” Na channels for T <8°C. The high degree of coherence in these results may be applicable to impulse-encoding mechanisms in other mammalian neurons.

GRANTS

This research was supported in part by National Eye Institute Grant R01EY-012833 to R. F. Miller.