A Robust Approach towards Recognizing Valid Arterial Blood Pressure Pulses

Abstract

We propose a projection method based on Singular Value Decomposition (SVD) to validate Arterial Blood Pressure (ABP) signal in order to avoid artifacts and noise in subsequent processing. The projection has been done on 567 validated ABP beats collected from 51 patients hospitalized in UCLA medical center. Then we compare the performance of the proposed projection method with that of a previously developed algorithm; Signal Abnormality Index (SAI); which is a value and trend based approach and has shown to be effective in cleaning the ABP waveforms. The testing dataset consists of 1336 ten-second ABP segments (18472 ABP beats) of both valid and invalid pulses selected randomly from Multi-Parameter Intelligent Monitoring for Intensive Care (MIMIC II) database. The proposed projection approach which validates the signal based on the shape of the waveform achieves a True Positive Rate (TPR) of 99.06%; 5.43% higher than that of the SAI; and a False Positive Rate (FPR) of 7.69%; 17.38% lower than that of SAI. Integration of some of the SAI value based abnormality conditions to the validation process of SVD based method can further improve the performance by reducing the FPR to 3.92% while keeping the TPR at the high rate of 99.05%.

I. Introduction

In any application which involves information extraction from clinical recordings of physiological signals, noise and artifacts are a constantly existing problem that can not be neglected. In the Intensive Care Unit (ICU), different events can cause noise and artifacts in the monitoring signals, e.g., catheter flush, patient movement, pressure transducer blockage, power-line interference, signal amplification, quantization and device saturation which results in clipping the signal. As a result, inadequate addressing of noise and artifacts creates an overwhelmingly large number of false alarms in the ICU [1],[2] which can lead to the disruption and decreased quality of care [3],[4], desensitization of clinical staff to warnings and slowing of response times [5]. The presence of noise and artifacts can also challenge the performance of different algorithms designed for the detailed analysis of morphology of pulsatile physiological signals [6],[7]. As a result, the noise handling has to be an intrinsic component of such algorithms to ensure their high performance.

Various strategies have been employed to improve estimates of noisy physiological parameters, such as filtering [8],[9], averaging [10] and machine learning [11]. Averaging and machine learning methods can reduce the effect of transient artifacts, but at the cost of smoothing true physiological changes or causing a high complexity due to the large amount of data needed for model training [12]. On the other hand, Kalman filtering methods have shown to be able to reliably identify artifacts from physiological signals [13],[14].

Sun et al. in [15] have defined a parameter named Signal Abnormality Index (SAI) to distinguish valid Arterial Blood Pressure (ABP) pulses from the noisy ones. The algorithm flags ABP beats by intelligently setting some constraints on physiological, noise/artifact and beat to beat variation values and has shown to achieve a reasonable level of performance for validating ABP signal. More recently, this ABP SAI algorithm has been utilized to provide better heart rate extraction [12] and to reduce false alarms for critical arrhythmias [16],[17].

In our previous work [18], we proposed a projection method using the Singular Value Decomposition (SVD) to validate Intracranial Pressure (ICP) pulse signal. The algorithm decomposes the pulses in a validated reference pulse library to a signal and a noise subspace. Then it applies a validity criterion based on the ratio of the energy of the projected signal over that of the projected noise, to evaluate any new ICP pulse. It was shown that the proposed projection method has a high level of performance with reasonably low computational complexity comparing to other correlation based methods [6].

Since no proprietary ICP features were incorporated in the proposed algorithm, it can be potentially applied to process any pulsatile signals usually seen in clinical environment including Pulse Oximetry (SpO2) and ABP. To investigate this idea further, in this work we implement the same projection method on an expert-validated reference library of 567 ABP pulses collected from 51 patients hospitalized at UCLA Ronald Reagan medical center. Then the resultant signal and noise subspaces have been used to validate 1336 ten-second ABP segments (18472 ABP beats) which were randomly selected from 120 patient records in PhysioNet's Multi-Parameter Intelligent Monitoring for Intensive Care (MIMIC) II database [19],[20] whose waveforms include simultaneous ECG and ABP signals. Comparison of the performance of the proposed projection method with that of the SAI algorithm concludes that the SVD based projection method performs better in validating both ABP segments and individual ABP beats, because of introducing a higher True Positive Rate (TPR) and a much lower False Positive Rate (FPR). Then we demonstrate that the integration of the proposed SVD based method with some abnormality conditions adopted in the SAI method can reduce the FPR to as low as 3.92% while keeping the TPR at a high rate of 99.05%.

In this paper, we first review the basics of both the SVD based projection and signal abnormality index methods. Then the results of applying the described methods to the testing dataset collected from MIMIC II database are presented. A detailed discussion on the accountability of each of the SAI abnormality conditions and the possibility of integrating them to the SVD based method has been delivered. At the end, weaknesses and possible improvements to the proposed integrated method have been discussed.

II. METHODS AND MATERIALS

A. Using Singular Value Decomposition to Validate an ABP Pulse

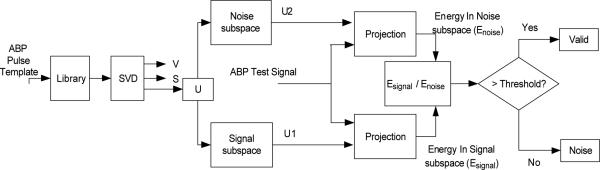
Suppose that the ABP reference library consists of N valid ABP pulses in the time domain. The goal is to decompose the pulses in the library to a signal and a noise subspace and then establishing a validity criterion based on the ratio of the energy of the projected signal over that of the projected noise. We adopt the singular value decomposition (SVD) as a subspace decomposition technique. The flowchart of this algorithm has been shown in Fig. 1.

Fig. 1.

Flowchart of recognizing valid ABP pulses using singular value decomposition.

The algorithm starts by normalizing each pulse in a reference library in both time and amplitude scale so that all pulses have the same length in time, are zero-mean, and have unit standard deviations. Then the library can be represented by a matrix A_M×N as [P₁,...,P_n,...,P_N] where P_n is n^th normalized pulse in the library. A is decomposed by SVD to A = UΣV^T where we assume the same convention that columns of U and V are arranged in a descending order of their corresponding singular values [21], [22]. Based on a chosen signal space dimension I, orthonormal matrix U can be further separated into a signal part and a noise part where the former contains the first I columns of U.

In practice, choosing the optimum value of I is dependent on the nature of data. As it is shown in [18], for the pulsatile signals, the knee point of the curve E_K; the percentages of the total energy existing in the space whose bases are the singular vectors corresponding to the K largest singular values of the matrix A; can be a good candidate for the value of parameter I. (A knee point is defined as the point with the maximum perpendicular distance from the straight-line which connects the beginning and end point of the concave region of the curve [6].)

Now let us use b to represent a test ABP pulse that goes through the same normalization process. To determine whether b is a valid pulse, we first project b onto the signal subspace as $b_p=U_1.U_1^T.b$, where U₁ = [u₁ u₂ ... u_I]. Then a ratio measure can be calculated as the following,

$$Rati{o}_{Energy}=\frac{E_{signal}}{E_{noise}}=\frac{{\Vert b_p\Vert }^2}{{\Vert b-b_p\Vert }^2}.$$ (1)

This ratio will be compared with a threshold (ϖ) to determine the validity of b. For more details on using SVD method to validate a pulsatile pulse, the readers are referred to [18].

B. A Review on ABP Signal Abnormality Index

Sun et al. in [15] have suggested an algorithm named Signal Abnormality Index (SAI) to detect abnormal beats in the ABP waveforms. Since this approach has shown to be effective to select clean ABP waveforms with an acceptable level of performance, it would be interesting to compare the performance of our proposed projection method with that of the SAI method. As a result, in this subsection, we will review the basics of the SAI algorithm.

SAI flags an ABP beat as an invalid beat by intelligently setting constraints on the physiologic, noise/artifact and beat to beat variation values. In other word, a beat is flagged if either of the following abnormality conditions is satisfied,

$$\begin{array}{cc}\hfill & C1:\{\begin{array}{cc}\hfill P_s>300mmHg\hfill & \hfill \left(a\right)\hfill \\ \hfill P_d<20mmHg\hfill & \hfill \left(b\right)\hfill \\ \hfill P_m<30or{P}_m>200mmHg\hfill & \hfill \left(c\right)\hfill \\ \hfill f<20orf>200bpm\hfill & \hfill \left(d\right)\hfill \\ \hfill P_s-P_d<20mmHg\hfill & \hfill \left(e\right)\hfill \\ \hfill w<-40mmHg∕100ms\hfill & \hfill \left(f\right)\hfill \end{array}\phantom{\}}\hfill \\ \hfill & C2:\{\begin{array}{cc}\hfill \mid P_s\left[k\right]-P_s[k-1]\mid >20mmHg\hfill & \hfill \left(g\right)\hfill \\ \hfill \mid P_d\left[k\right]-P_d[k-1]\mid >20mmHg\hfill & \hfill \left(h\right)\hfill \\ \hfill \mid T\left[k\right]-T[k-1]\mid >2∕3\text{sec}\hfill & \hfill \left(i\right)\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (2)

Where P_s, P_d and P_m are systolic, diastolic and mean arterial blood pressures, respectively. T is the duration of each beat and $f=\frac{60}{T}$ beats per minute. w is a measure of the noise and is defined as the mean of all the negative slopes.

As (2) shows, the first 6 conditions (a) to (f) are absolute value based abnormality conditions (C1) whereas the last three (g) to (i) are trend based abnormality conditions (C2). The decision rule used in the SAI algorithm to validate the segments of ABP signal is as the following; an ABP segment is declared as an invalid segment if any of its beats is flagged. (if any of the above 9 abnormality conditions is satisfied for any of the beats.)

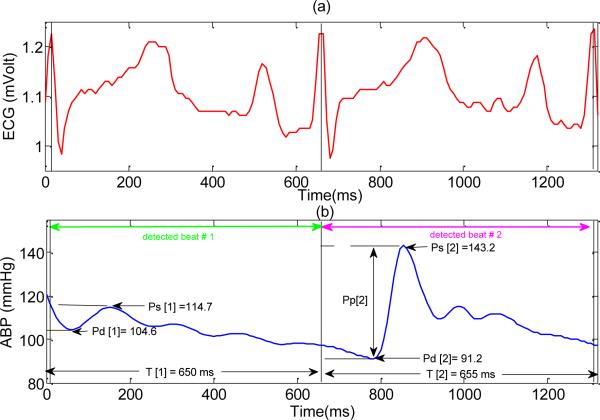
Although the SAI algorithm has proven its effectiveness in its ability to select the clean ABP segments, there exist some concerns regarding the proposed signal validation method. For example, based on the condition (f) which is the noise detector criterion, SAI method would be exclusively sensitive to the high frequency noise which causes a large negative slope. As a result, the existing method would not be able to correctly evaluate an ABP beat distorted by a low frequency noise such as baseline wanders or thermal fluctuation. The other concern regarding the proposed method is that its performance has not been optimized for the individual recognition of valid ABP beats (contrasting to recognition of valid ABP segments). This is partially due to the fact that the SAI algorithm applies the trending based abnormality conditions (C2) to all the detected beats regardless of being preceded by a noisy beat or not. Consequently, if a beat is invalid due to satisfying any of the conditions (a), (b) or (c), then the next beat would also be flagged as an invalid beat if it is truly a valid one. Fig. 2 shows an example of this case. Please note that in this example, the second beat would be wrongly evaluated as invalid beat because of satisfying abnormality condition (g).

$$\begin{array}{cc}\hfill & \mid P_s\left[2\right]-P_s\left[1\right]\mid =\mid 143.2\text{-}114.7\mid =28.5>20mmHg\hfill \\ \hfill & \Rightarrow \text{Beat}\#2\text{is declared as invalid}.\hfill \end{array}$$ (3)

Fig. 2.

An example of a valid ABP beat (preceded by a noisy beat) which would be wrongly evaluated as noise by SAI algorithm due to applying trend based abnormality conditions. (a) ECG signal (b) ABP signal. For the first detected ABP beat P_m [1] = 105.16 mmHg, w[1] = –5.26 mmHg / 100 ms and for the second detected beat P_m[2] = 107.37 mmHg, and w[2] = –10.16 mmHg / 100ms.

As this example shows, applying C2 to all the beats (regardless of the validity of the preceding beats) would definitely decrease TPR. To avoid such a problem, we can apply the C2 abnormality conditions only to the beats preceded by a valid beat. This new approach; let us name it the modified SAI; guarantees a higher TPR. The effect of this modification on the FPR would be later investigated in this paper.

C. Combining SVD Based Projection Method and SAI Algorithm

Since the proposed SVD projection method starts by normalizing each pulse in the reference library both in time and amplitude scale so that all pulses are equal-length in time, zero-mean and unit-variance, it validates each beat based on the shape of the pulse rather than the absolute values of its features. As a result, this approach is different from the one proposed in SAI algorithm; a value and trend based approach. So it would be interesting to investigate whether combining the two methods would improve the performance of the ABP beat validation. We use the SVD based projection method with each of the nine SAI abnormality conditions to compute the performance of the ABP beat recognition on a testing dataset which will be described in the next section.

D. Patient Data

To define the noise and signal subspace, we perform the SVD on a library of validated ABP pulses which has been constructed as the following. Signal segments were selected from the archived ABP and ECG signals of 51 patients, including 16 females and 35 males, who were seen as inpatients at the UCLA Ronald Reagan medical center, neurosurgery unit for different related conditions, e.g. Subarachnoid Hemorrhage (20 cases), Traumatic brain injury (15 cases), Hydrocephalus (8 cases), Intracranial hypertension (3 cases), Slit ventricle syndrome (1 case), brain tumor (1 case), cervical cord injury (1 case), Arterio-Venous Malformation (1 case) and shunt failure (1 case). The average age of these patients was 50 (ranging from 14 to 81 years old). During their hospitalization, these patients received continuous cardiovascular monitoring using the bedside GE monitors. ABP and lead II of ECG signals were archived using either a mobile cart at the bedside that was equipped with the PowerLab TM SP-16 data acquisition system (ADInstruments, Colorado Springs, CO) or the BedMasterTM system that collects data from the GE Unity network which the bedside monitors were connected to. Majority of signals were recorded using the PowerLab system, which sampled ECG and ABP signals at 400 Hz. Sampling rate used in the Bedmaster system was 240 Hz. Signal files in this archive were transformed into the Chart™ Binary file format for further processing.

A 3 to 5 minutes segment of data was randomly selected, in an interval of 12 Hours for each patient, without avoiding noisy regions. These signal segments were subsequently processed by the MOCAIP algorithm [6] and a dominant ABP pulse was generated for every 30 seconds recording. The generated dominant pulses were assessed by an expert and annotated as valid or invalid pulses (The invalid dominant pulses were caused majorly by noise in the data and/or by the wrong QRS detections). A total of 567 dominant pulses (from the assessed valid pulses) were randomly selected to form a library of ABP pulses. The mean ABP of these pulses was 77.61±41.76 mmHg. The use of these archived waveform data in an anonymous fashion has been granted a wavier of consent by the UCLA IRB.

For the testing data set, we used the Multi-Parameter Intelligent Monitoring for Intensive Care II (MIMIC II) database accessed via Physionet [19]. We randomly selected 120 patients whose waveforms included simultaneous ABP and ECG signals. A total of 222 hours of data were generated by randomly choosing a record with time duration of less than 24 hours. Then a 10 second segment of simultaneous ABP and ECG signals was randomly selected, in an interval of 10 minutes; resulting in 1336 ABP and ECG segments. Between different available beat detection algorithms [23],[24], we chose the one proposed in [25] to mark the onset of each ABP beat and consequently, a total of 18472 ABP pulses were detected. The number of valid ABP beats, as assessed by an experienced researcher, was 15469 accounting for 83.74% of all the detected beats. Using the ABP segment validation criterion of SAI algorithm results in identifying 978 valid ABP segments accounting for 73.20 % of all the selected ABP segments.

E. Data analysis and Validation Protocol

We chose the 90^th percentile of the lengths of all the pulses in the library to resize them. Then the singular value decomposition was performed on the matrix A whose columns are the normalized (zero-mean and unit-variance) ABP pulses in the library. For the energy ratio comparison, the threshold ϖ was set as the minimum of the computed Ratio_Energy among all the 567 pulses of the ABP library. This threshold setting guarantees the correct assessment of any ABP pulse similar to any of the pulses in the validated library.

The projection method described in the previous section was used to find the validity of all the 18472 detected beats generated from the MIMIC II database and the following parameters were calculated; TPR, FPR, Accuracy (Ac), positive predictive value (PPV) and negative predictive value (NPV). Then the SAI segment validation criteria were used to evaluate each of the 1336 ABP segments and the same performance parameters were calculated. The performance of the proposed projection method was compared to that of the SAI and the modified SAI methods. As a final step, comparing the performance of validating ABP beats using the combination of SVD projection method and the SAI algorithm was conducted.

III. RESULTS

The number of valid ABP beats in the testing dataset, as assessed visually by the experiences researcher, was 15469 for 83.74% of all the 18472 detected beats. Applying the ABP segment validation criterion of SAI algorithm results in identifying 978 valid ABP segments accounting for 73.20% of all the 1336 selected ABP segments.

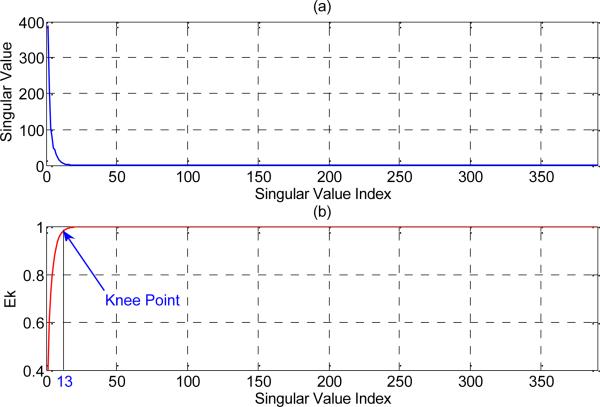
Fig. 3-(a) shows the singular spectrum of the matrix A constructed from the library of 567 validated ABP pulses (The plot of singular values versus their index number). We observe that matrix A has only a limited number of significant singular values. Fig. 3-(b) is the plot of the previously defined E_K. The knee point of this curve (I = 13) is selected as the number of basis vectors to construct the signal subspace.

Fig. 3.

(a) Singular value spectrum of the matrix A constructed from the library of 567 validated ABP pulses. (b) Plot of E_K (percentage of the total energy which exists in the space define by the first K singular vector of matrix A) and the corresponding knee point for the ABP library.

Table I presents the results of valid ABP beat recognition on the testing data set using the proposed projection method, SAI method, and modified SAI method. We observe that not only TPR of the proposed projection method (0.990) is higher than that of the SAI method (0.936), but also its FPR (0.076) is also significantly lower than the FPR of the SAI (0.250). Therefore, the SVD based projection method has better performance than that of the SAI algorithm.

TABLE I.

THE RESULTS OF VALID ABP BEAT RECOGMITION ON THE TESTING DATASET USING DIFFERENT METHODS

	SVD based projection	SAI method	Modified SAI method
(TP)	15323	14483	14784
(FP)	231	753	963
(FN)	146	986	685
(TN)	2772	2250	2040
(FPR)	0.0769	0.2507	0.3207
(TPR)	0.9906	0.9363	0.9557
(Ac)	0.9796	0.9059	0.9108
(PPV)	0.9851	0.9506	0.9388
(NPV)	0.9500	0.6953	0.7486

TP= number of True Positive cases, FP=number of False Positive cases, FN=number of False Negative cases, TN=number of True Negative cases, Ac=Accuracy, PPV=Positive Predictive Value, NPV= Negative Predictive Value.

We also observe that applying the trend based abnormality conditions exclusively to the beats preceded by a valid ABP beat (modified SAI method) increases both the number of true positive cases (TP) and the number of false positive (FP) cases. Please note that although the amount of the increase in TP (301) is slightly more than that of FP (210), since the total number of valid ABP beats is 5.1 times of the invalid ones, the effect of ignoring trend based abnormality conditions (C2) will be dominated by a much higher increase in FPR relative to its TPR counterpart.

Table II summarizes the validation results of the ABP segments. We need to note that the definition of a TP case in this paper (a valid beat) is different than that of [15]. Taking into account this difference, we observe that our segment validation results for the SAI algorithm are consistent with those reported in [15] and the proposed SVD based projection method has better performance than that of the SAI method; especially the FPR of the projection method (0.02) is much lower than FPR of the SAI (0.12). We also note that the results of ABP segment validations for SAI method and modified SAI method are exactly the same.

TABLE II.

THE RESULTS OF RECOGNIZING VALID 10-SECOND ABP SEGMENTS ON THE TESTING DATASET USING DIFFERENT METHODS

	SVD based projection	SAI method	Modified SAI method
(TP)	917	872	872
(FP)	10	45	45
(FN)	61	106	106
(TN)	348	313	313
(FPR)	0.0279	0.1257	0.1257
(TPR)	0.9376	0.8916	0.8916
(Ac)	0.9469	0.8869	0.8869
(PPV)	0.9892	0.9509	0.9509
(NPV)	0.8509	0.7476	0.7476

TP= number of True Positive cases, FP=number of False Positive cases, FN=number of False Negative cases, TN=number of True Negative cases, Ac=Accuracy, PPV=Positive Predictive Value, NPV= Negative Predictive Value.

The results of applying any of the SAI abnormality conditions to the SVD based projection method are summarized in Table III. We observe that integrating different SAI abnormality conditions to SVD projection method can have different effects on the performance of the ABP beat validation. For example, applying abnormality conditions (b) or (c) has an improving effect whereas applying conditions (e), (f), (g) or (h) degrades the performance and conditions (a), (d) or (i) does not change the performance significantly. As the last row of table III shows, the combination of SVD projection method and the first four SAI abnormality conditions decreases the FPR of ABP beat validation to 3.92% while keeping its TPR as high as 99.05%.

TABLE III.

THE RESULTS OF COMBINING SAI ABNORMALITY CONDITIONS AND PROPSOED SVD PROJECTION METHOD FOR VALID ABP BEAT DETECTION

Method	FPR	TPR	PPV	NPV
SVD projection	0.0769	0.9906	0.9851	0.9500
SVD projection +SAI condition (a)	0.0769	0.9905	0.9851	0.9499
SVD projection +SAI condition (b)	0.0449	0.9905	0.9912	0.9515
SVD projection +SAI condition (c)	0.0402	0.9905	0.9921	0.9514
SVD projection +SAI condition (d)	0.0759	0.9905	0.9853	0.9500
SVD projection +SAI condition (e)	0.0589	0.9669	0.9883	0.8466
SVD projection +SAI condition (f)	0.0765	0.9847	0.9851	0.9215
SVD projection +SAI condition (g)	0.0722	0.9654	0.9856	0.8389
SVD projection +SAI condition (h)	0.0722	0.9795	0.9858	0.8978
SVD projection +SAI condition (i)	0.0769	0.9901	0.9851	0.9480
SVD projection +SAI conditions (a) to (d)	0.0392	0.9905	0.9923	0.9515

IV. Discussion

The lower TPR of the SAI method, comparing to that of its modified version as proposed in the present work, can be partially blamed on applying trend based abnormality conditions (C2) to all candidate beats regardless of the validity of the preceding beats (please note that the number of true positive cases increases from 14483 to 14784 when we replace the SAI method with its modified version). The amount of increase in the number of FP cases, resulting from replacing SAI method with its modified version, shows that there exist considerable numbers of invalid ABP beats preceded by another invalid beat which does not satisfy any of the value based abnormality conditions (C1) and as a result, the only way for their correct recognition is applying trend based abnormality conditions of (C2).

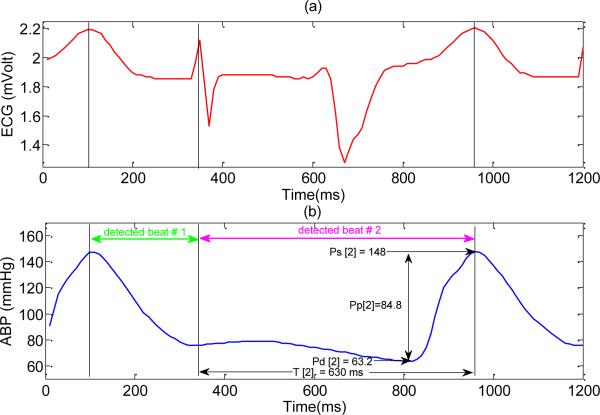
The careful assessment of these 210 beats shows that a majority of them resulted from the wrong QRS detections and consequently they are chopped or shifted version of some valid ABP beats. So they cannot be correctly evaluated just by applying the value based abnormality conditions. Fig. 4 shows an example where the second invalid beat will be wrongly evaluated as a valid one by the modified SAI.

Fig. 4.

An example of invalid ABP beats resulted from spurious beat detection where a spiky T wave is falsely detected as a QRS complex. As a result, each true beat has split into multiple ones. (a) ECG signal (b) ABP signal. Note that for the second ABP beat P_m[2] = 83.13 mmHg, w[2] = –5.84 mmHg / 100ms. Since this beat does not satisfy any of the value-based abnormality conditions, the modified SAI algorithm will wrongly evaluate it as a valid one (due to ignoring trend based abnormality conditions).

The similarity of the ABP segment validations results of SAI method and modified SAI method can be explained as the following. According to the SAI segment validation criterion, a segment is declared invalid if at least one of its beats is flagged. Therefore, applying trend based abnormality conditions to the beats preceded by a noisy beat does not increase the number of FP cases, because that segment is already labeled as an invalid one due to invalidity of the preceding beat.

Applying conditions (g) and (h) to the SVD projection method degrades the performance because these conditions reject some of the valid ABP beats, which are preceded by a noisy beat. This is the same problem with SAI abnormality conditions as discussed before. The value based conditions (e) and (f) also degraded the performance due to producing a low TPR. The careful assessment of the valid beats rejected by these conditions concludes that the defined threshold value for the pulse pressure (20 mmHg) and mean negative slope as a measure of noise (−400 mmHg/s) seem to be stringent.

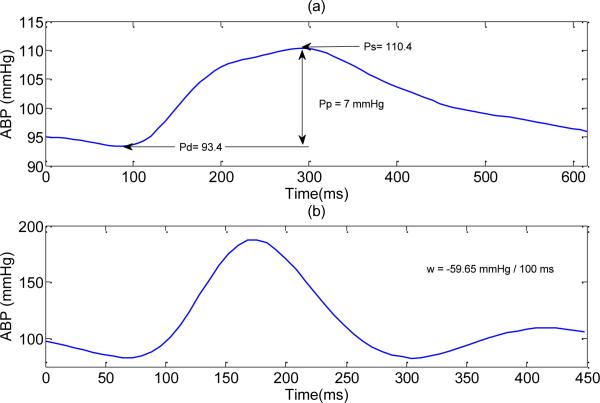
As a result, some of the valid ABP beats in the testing dataset with pulse pressure below than 20 mmHg or with mean negative slope of less than the defined threshold have been wrongly rejected by these two conditions. Fig. 5 shows two examples of valid ABP beats, which were rejected by the stringent conditions of (e) and (f).

Fig. 5.

An example of two valid ABP beats, which would be wrongly evaluated as noise by applying SAI value based abnormality conditions. (a) affected by condition (e): P_p = 7 < 20 mmHg, (b) affected by the condition (f) : w = –59.65 < –40 mmHg / 100ms.

While it seems that applying conditions (a), (d) and (i) does not change the performance of ABP beat validation in this specific testing dataset, we believe that including physiological value based conditions (a) and (d) will have an improving effect in general on the performance of the proposed SVD based projection method whereas the trend based condition (i) will degrade it by rejecting the valid beats preceded by the noisy beats.

Note that the goal of this study was solely the recognition of the valid beats versus the invalid ones from the beats which are already detected (using any method of beat detection). As a result, the invalid beats in this study have to be either caused by the noise/artifacts or by the wrong beat detection. In other words, we aimed to show that the proposed SVD based method is capable of this recognition regardless of the original source of invalidity of the beats (noise/artifacts or wrong beat detection). Therefore, using another method of beat detection, even a method with higher rate of correct beat detection, would not make difference in fulfilling our goal of assessing the proposed method for the valid beat recognition.

V. Conclusion

We proposed an SVD based projection method to validate the ABP signals. The algorithm development and evaluation were conducted using two completely different sets of data. The results on validating the 1336 ten-second-long ABP segments indicate that the proposed SVD method has 4.6% higher TPR and 9.78% lower FPR comparing to SAI. Our algorithm compares favorably again with the SAI method when it comes to validating the individual ABP beats by achieving a 5.43% higher TPR and 17.38% lower FPR. We showed that the SAI algorithm performance is not optimized for the individual assessment of ABP beats because applying the SAI trend based conditions to every beat in general is questionable and also some of the SAI value based threshold has been set too stringent to take into account abnormalities arising from the physiological disturbances like arrhythmia and hypotension. Finally, we demonstrated that the careful integration of the proposed SVD based method with some of the value-based abnormality conditions of the SAI method can reduce the FPR to as low as 3.92% while keeping the TPR at high rate of 99.05%.

Biographies

Shadnaz Asgari received her M.Sc. and Ph.D. in Electrical Engineering from University of California, Los Angeles i n 2005 and 2008, respectively. Since May 2008, she has been a post-doctoral scholar in Neural Systems and Dynamics Lab (NSDL) of UCLA neurosurgery department where she is doing statistical signal processing, detection and estimation towards effective clinical decision making.

Marvin Bergsneider received a B.S. in Electrical Engineering in 1983 from the University of Arizona, followed by a M.D. degree in 1987 from the University of Arizona College of Medicine. He obtained his neurosurgical residency training at UCLA, where he joined the faculty in 1994. He is a Professor of Neurosurgery and a faculty member of the UCLA Biomedical Engineering Interdepartmental Program. His research interests include modeling of intracranial fluid biomechanics and hydrocephalus, plus bioMEMS development.

Xiao Hu received the B.S. and M.S. from the University of Electronic Science and Technology of China in 1996 and 1999, respectively. He received a Ph.D. degree in Biomedical Engineering from the University of California, Los Angeles in 2004. He joined the division of neurosurgery at the UCLA Medical Center as an assistant researcher in 2004 and then as an assistant professor in December 2006. He has a broad research interest in biomedical modeling, signal processing, and biomedical informatics. He currently directs the Neural Systems and Dynamics Laboratory (NSDL) at UCLA.