Correction of motion artifacts in cone-beam CT using a patient-specific respiratory motion model

Abstract

Purpose: Respiratory motion adversely affects CBCT image quality and limits its localization accuracy for image-guided radiation treatment. Motion correction methods in CBCT have focused on the thorax because of its higher soft tissue contrast, whereas low-contrast tissue in abdomen remains a challenge. The authors report on a method to correct respiration-induced motion artifacts in 1 min CBCT scans that is applicable in both thorax and abdomen, using a motion model adapted to the patient from a respiration-correlated image set.

Methods: Model adaptation consists of nonrigid image registration that maps each image to a reference image in the respiration-correlated set, followed by a principal component analysis to reduce errors in the nonrigid registration. The model parametrizes the deformation field in terms of observed surrogate (diaphragm or implanted marker) position and motion (inhalation or exhalation) between the images. In the thorax, the model is obtained from the same CBCT images that are to be motion-corrected, whereas in the abdomen, the model uses respiration-correlated CT (RCCT) images acquired prior to the treatment session. The CBCT acquisition is a single 360° rotation lasting 1 min, while simultaneously recording patient breathing. The approximately 600 projection images are sorted into six (in thorax) or ten (in abdomen) subsets and reconstructed to obtain a set of low-quality respiration-correlated RC-CBCT images. Application of the motion model deforms each of the RC-CBCT images to a chosen reference image in the set; combining all images yields a single high-quality CBCT image with reduced blurring and motion artifacts. Repeated application of the model with different reference images produces a series of motion-corrected CBCT images over the respiration cycle, for determining the motion extent of the tumor and nearby organs at risk. The authors also investigate a simpler correction method, which does not use PCA and correlates motion state with respiration phase, thus assuming repeatable breathing patterns. Comparison of contrast-to-noise ratios of pixel intensities within anatomical structures relative to surrounding background tissue provides a quantitative assessment of relative organ visibility.

Results: Evaluation in lung phantom, two patient cases in thorax and two in upper abdomen, shows that blurring and streaking artifacts are visibly reduced with motion correction. The boundaries of tumors in the thorax, liver, and kidneys are sharper and more discernible. Repeat application of the method in one thorax case, with reference images chosen at end expiration and end inspiration, indicates its feasibility for observing tumor motion extent. Phase-based motion correction without PCA reduces blurring less effectively; in addition, implanted markers appear broken up, indicating inconsistencies in the phase-based correction. In structures showing 1 cm or more motion excursion, PCA-based motion correction shows the highest contrast-to-noise ratios in the cases examined.

Conclusions: Motion correction of CBCT is feasible and yields observable improvement in the thorax and abdomen. The PCA-based model is an important component: First, by reducing deformation errors caused by the nonrigid registration and second, by relating deformation to surrogate position rather than phase, thus accommodating breathing pattern changes between imaging sessions. The accuracy of the method requires confirmation in further patient studies.

INTRODUCTION

There is increasingly widespread use of cone-beam CT for guiding radiation treatment of cancer with C-arm accelerators.¹ In thoracic and abdominal disease sites that are subject to respiratory motion, however, CBCT image quality is adversely affected. The resultant poorer image quality reduces the ability to discern soft tissue boundaries, compromising target and organ at risk (OAR) localization.

Different methods have been investigated to reduce motion in CBCT. Respiration-correlated CBCT (RC-CBCT) produces images at different motion states using retrospective sorting of projection images into different breathing phase bins.^{2, 3, 4} The limited number of projections per phase bin reduces the contrast resolution and introduces streak artifacts caused by sparse projections; thus, the method is more suited to detecting high-contrast objects such as tumor in parenchymal lung. Moseley et al.⁵ have used a multiple breath-hold technique to reduce motion artifacts in CBCT images of liver. A limitation is that not all patients can perform repeated and reproducible breath holds. In addition, breath-hold anatomical positions may not be representative of free breathing or gated treatment, as the contraction of respiratory muscles is different. We have investigated gated CBCT to reduce motion artifacts.⁶ A limitation is the low duty cycle for imaging (20%–30%), resulting in correspondingly longer (4–5 min) acquisition times.

A more desirable approach is to combine high CBCT scan efficiency (100% duty cycle) with motion correction of the images. Li et al.⁷ have investigated CBCT motion compensation with different approaches for deriving the phase-based motion model. Clinical evaluation was limited to one CBCT acquisition done with four gantry rotations, thus considerably lengthening the acquisition time. Rit et al.⁸ compensate for respiratory motion during reconstruction of the projection images from a 1 min 200 ° CBCT scan, using a prior motion model estimated from a respiration-correlated planning CT (RCCT). Their method assumes that the phase-based respiratory motion during the CBCT acquisition is identical to that of the RCCT. The above investigations have focused mostly on the thorax because of its higher soft tissue contrast, whereas low-contrast tissue in abdomen remains a challenge.

We report here on a method to correct motion artifacts in 1 min RC-CBCT scans using a patient-specific motion model, and investigate its effectiveness in the thorax and abdomen. The model provides a means to deform the RC-CBCT images to a common point in the respiratory cycle. The deformed images are combined into a single CBCT image set, thus improving the detectability of tumor and OAR, and hence localization accuracy. Our preliminary results in the thorax suggest it is feasible to derive the model directly from the RC-CBCT scan, whereas in the abdomen, the model is derived from a RCCT scan acquired prior to treatment. An important component of the method is a principal component analysis (PCA) to reduce artifacts and noise in the data. Because the motion model is parametrized by the temporal variation in surrogate position such as the diaphragm, it can accommodate changes in breathing pattern between imaging sessions. In addition, the method can generate CBCT image sets over the respiratory cycle, thus providing a means of evaluating target and OAR motion information at treatment, which may differ from the respiratory motion observed at simulation.^{9, 10}

METHODS

We briefly outline the overall approach, followed by a more detailed description of each step. The basic concept of the motion model can be separated into two parts: First, adaptation of the model to a particular patient using a calibration respiration-correlated image set; and second, application of the model to correct motion artifacts in CBCT.

Motion model calibration

Calibration of the motion model requires a respiration-correlated image set. In the thorax, the calibration uses the same RC-CBCT images that are to be subsequently motion-corrected. CBCT projection images and respiration signals are passively recorded during CBCT-guided hypofractionated treatments. The data were analyzed retrospectively for this study with IRB approval. A gantry-mounted kilovoltage imaging system (Varian Medical Systems, Palo Alto, CA) provides CBCT capabilities. The CBCT scan consists of a 1 min gantry rotation while recording patient respiration with an external monitor [Varian real-time position management (RPM) system]. The projection images are sorted into bins of approximately equal numbers of projections, according to the RPM-determined phase of the respiratory signal. The choice of number of bins (six in thorax, ten in abdomen) is described below. Each bin is reconstructed using software based on the Feldkamp algorithm¹¹ to produce a series of RC-CBCT images $I\left(\vec{x},t\right)$, where $I\left(\vec{x},t\right)$ denotes the intensity of voxel at position $\vec{x}$ and at phase bin t. We use a research version of the Varian reconstruction software, with no correction for cupping or ring artifacts, the latter caused by noisy detector elements. In the thorax, the choice of six RC-CBCT subsets (six phase bins) is a compromise between residual motion within each bin and sufficient image quality to guide the nonrigid image registration for model calibration and subsequent motion correction.

In abdomen, the low soft tissue contrast precludes model calibration from RC-CBCT subsets. Instead, we calibrate the motion model from an RCCT of the patient at simulation about 1 week prior and apply the model to correct the RC-CBCT subsets. An eight-slice scanner (LightSpeed, GE HealthCare, Waukesha, WI) acquires repeat CT images for a complete respiratory cycle at each couch position while recording patient respiration (Varian RPM). The CT images are retrospectively sorted (GE Advantage 4D) to produce a series of RCCT images at ten respiratory phase points. The time resolution of each CT slice (i.e., gantry rotation period) is 0.5 s; CT slice thickness is 2.5 mm. Since the RC-CBCT subsets are not used for model calibration in abdomen, we sort the CBCT projections into ten bins to yield comparable residual motion within each bin to that in the RCCT image set.

The patient-specific motion model¹² uses nonrigid image registration to calculate a set of deformation fields that deforms each image in the respiration-correlated image set to a reference image at the desired motion state, denoted by $I\left(\vec{x},t_{\text{ref}}\right)$. Each nonrigid registration defines a voxel-dependent displacement field $\vec{u}\left(\vec{x},t\right)$, such that a point$\vec{x}+\vec{u}\left(\vec{x},t\right)$ in the deformed (study) image corresponds to point $\vec{x}$ in the reference image. Note that in the application of the model to motion-corrected CBCT in this study, the nonrigid registration is performed in the opposite direction to that in Ref. 12. The nonrigid registration uses a fast free-form algorithm,¹³ which minimizes a cost function consisting of two terms: A sum of squared intensity differences between corresponding voxels in the reference and study images, and a smoothing term that limits sharp gradients in the vector displacement field $\vec{u}$.

Each image in the respiration-correlated set is tagged by two surrogate signals that are visible in the 3D images. In three of the clinical examples, we determine the displacement of the apex of the diaphragm along the superior-inferior relative to its position in the reference image (i.e., at the reference motion state). The two surrogate signals for an image thus consist of the diaphragm displacement in the image and its displacement in the image approximately one third of a respiratory cycle prior, to distinguish between the inspiration and expiration portions of the respiratory cycle. In one of the clinical examples in abdomen where the diaphragm is not within the field-of-view, we instead use a fiducial marker implanted in the liver as surrogate.

Next, a PCA is performed to reduce errors in the nonrigid registration and to relate the surrogate signals to the model parameters given by the time-varying displacement fields. We first construct a set of vectors with discrete indices, given by p_j=[u_1,1,j,u_1,2,j,u_1,3,j,…,u_M,3,j]^T, where u_m,i,j is the ith component (i=1–3) of displacement for voxel m (m=1,M) at phase index j (j=1,J). We want to connect p_j with s_j=[s_1j,…,s_nj]^T, where s_n,j is the displacement of the nth surrogate (n=2 in this study) at phase index j. Next we construct a matrix $P=\left[{\tilde{p}}_{1,}{\tilde{p}}_{2,}\dots ,{\tilde{p}}_j,\dots ,{\tilde{p}}_J\right]$, composed of centered vectors ${\tilde{p}}_j=p_j-\overline{p}$, where the mean vector$\overline{p}=1∕J{\sum }_{j=1}^J{p}_j$ represents the respiration-averaged motion state. The size of matrix P is (3M×J). The covariance matrix PP^T (size 3M×3M) is positive semidefinite, meaning its eigenvalues are non-negative. We can calculate its nonzero eigenvectors e_i(i=1,…,J−1) according to the procedure described previously.¹² The result is that each motion state ${\tilde{p}}_j$ is approximated as a weighted sum of K eigenvectors e_k with the largest eigenvalues

$${\tilde{p}}_j\approx \sum _{k=1}^K{w}_{kj}{e}_k$$ (1)

or in matrix notation

$$P\approx EW,$$ (2)

where matrix E=[e_1,…,e_K] consists of the first K eigenvectors to approximate the motion states and W=[w_kj] with size K×J. Note that for known ${\tilde{p}}_j$ and e_k, one can calculate the weighting factors $w_{kj}=e_k^T{\tilde{p}}_j∕e_k^T{e}_k$. Our previous study indicated that K=2 is sufficient to describe motion states in the thorax.¹²

Instead of expressing the motion states in terms of phase-index-dependent weighting factors, we wish to express them in terms of the surrogate signals. We rewrite Eq. 1 as

$${\tilde{p}}_j\approx \sum _{k=1}^K{w}_{kj}{e}_k=E{w}_j=EV{s}_j,$$ (3)

with

$$w_j=\left[\begin{array}{l}{w}_{1j}\hfill \\ \cdot \hfill \\ \cdot \hfill \\ w_{Kj}\hfill \end{array}\right]=V{s}_j.$$ (4)

V is a matrix to be determined with size K×n. Equations 3, 4 are valid for the above J distinct phases; thus we rewrite Eq. 4, in matrix notation as

$$W=VS,$$ (5)

where the observed S=[s₁,…,s_J]=[s_nj] and calculatedW=[w₁,…,w_J]=[w_kj] are obtained from the model calibration and calibration image set. One can prove that the best solution to Eq. 5 is

$$V=W{S}^T{\left(S{S}^T\right)}^{-1},$$ (6)

such that ${\sum }_{j=1}^J{\parallel w_j-V{s}_j\parallel }^2$ is minimized. Substituting Eq. 6 into Eq. 3, we have

$$\tilde{p}=E\left(W{S}^T{\left(S{S}^T\right)}^{-1}\right)s.$$ (7)

Therefore, given surrogate signals s=[s₁s₂]^T in the image set to be corrected, we can calculate the corresponding displacement field $\tilde{p}$. Note that there is no dependence on phase bin in Eq. 7: The model-predicted displacement field depends only on the surrogate signals of the image.

Model application and evaluation

Basic steps in motion correction are, first, to correct each RC-CBCT image by applying the motion model, so as to deform the image to the same reference motion state in the breathing cycle; second, to combine the corrected RC-CBCT images to obtain a high-quality CBCT at the reference motion state.

To correct each RC-CBCT image, one image is chosen as reference, and the position of surrogates observed in the images are calculated as displacements relative to their position in the reference image, as described above. The surrogate signals are substituted into Eq. 7 to obtain the centered vectors $\tilde{p}\left(t\right)$. Adding to this the mean vector $\overline{p}$ yields the displacement field p, which is applied to deform each RC-CBCT image into the reference RC-CBCT motion state. Since the model is calibrated with the RC-CBCT image set to be motion-corrected, the displacement fields are already registered to the images. In abdomen, skeletal registration of RCCT to CBCT defines the location of the deformation fields in the CBCT coordinate system.

A difficulty of using the RC-CBCT data to calibrate the model is the effect of strong streaking artifacts caused by the sparse projections in the filtered back-projection reconstruction of each of the RC-CBCT subsets. The artifacts are oriented differently in each RC-CBCT subset and thus influence the nonrigid registration, such that the artifacts align with those in the reference RC-CBCT. To counteract this tendency, we define a volume of interest (VOI), whose boundary is ∼2 mm outside the patient surface and include only voxels inside the VOI in the nonrigid registration cost function. In addition, to avoid deformation of the vertebral column, the VOI excludes the delineated vertebrae. The VOI is delineated on a CBCT reconstructed from all projections and transferred to the reference RC-CBCT. The deformation field is zero outside the VOI except near the VOI boundary, subject to the smoothing term in the cost function. The choice of VOI allows for some expansion and contraction at the patient’s anterior surface in the nonrigid registration. The resultant deformation fields are used to calibrate the model via PCA as before, followed by model application for motion correction.

We evaluate the geometric accuracy of the method in a software phantom that simulates respiration. The 4D NURBS-based cardiac torso (NCAT) phantom provides a model of the human torso, in which organ shapes are constructed from nonuniform B-splines (NURBS), based on the 3D visible human CT data set.¹⁴ For this study, the phantom includes a spherical lesion of 2 cm diameter in the right lung, 5 cm superior of the diaphragm at end expiration. The NCAT phantom models respiratory motion and generates CT image sets at different motion states; we generate ten motion states over a breathing cycle, using 2 cm for diaphragmatic contraction and 0.5 cm for chest wall expansion with tidal breathing, which represents the upper range of excursion observed in patients with RCCT at our institution. Next, we simulate the effect of respiration during a CBCT scan by generating a complete set of projections, i.e., digitally reconstructed radiograph, from the NCAT CT image sets at each motion state, then select a temporal sequence of projections corresponding to a breathing period of 4 s and a 360 ° CBCT acquisition over 1 min at ten projections∕s. The projections are generated to simulate half-fan CBCT acquisition with laterally offset image detector. The projections are respiration-sorted into six bins, reconstructed and processed in the same way as described above. Because the lateral extent of the NCAT phantom outside the rib cage is considerably larger relative to the patients considered in this study, we define the lateral extent of the VOI to be approximately 3 cm outside the rib cage, consistent with the patient data.

For comparison with the PCA-model-based motion correction, we also investigate a simpler method, which does not use PCA and correlates motion state with respiration phase, referred to here as phase-based correction. For each RC-CBCT subset at a given phase bin, the phase-based correction applies the deformation field from the nonrigid registration of the calibration image (i.e., RC-CBCT in thorax, RCCT in abdomen) at the same phase, and the deformed RC-CBCT subsets are added together. In the application to abdomen, the phase-based method thereby assumes that the breathing pattern in the RCCT (e.g., motion amplitude and correlation of internal anatomy to external RPM signal) is the same as in the RC-CBCT. In the remainder of the paper, “phase-based correction” refers to correction by deformation fields directly from the nonrigid registration and selected according to the phase bin of the image [Eq. 1 withK=J−1], whereas “PCA-model-based correction” refers to correction using the two principal components of the deformation fields and selected according to the surrogate signals [Eq. 7].

Visual evaluation compares CBCT images before motion correction, phase-based motion correction to the end expiration state, and PCA-model-based correction to end expiration. In order to quantitatively evaluate CBCT quality and organ visibility, we define a contrast-to-noise ratio as CNR=(S₁−S₂)∕σ₁, where S₁ and S₂ are the average voxel intensities in an annular volume inside the organ boundary and a background region outside the boundary, respectively. σ₁ is the rms variation in voxel intensity inside S₁. The organ to be evaluated is delineated on the RCCT image at end expiration, and the S₁ and S₂ regions are generated as a 5 mm thick volume contraction and expansion, respectively, from the organ boundary. In liver, S₂ excludes the ribs, which are brighter than the liver and the surrounding background tissue. The organ contours are transferred to the CBCT and manually aligned in 3D on the axial, sagittal, and coronal view images, using the end expiration RCCT as a visual guide. The manual alignment is performed three times by the same observer to assess reproducibility of the CNR calculation. The following structures evaluated in this way: Tumor in lung, main-stem bronchus, distal bronchus, and diaphragm in the thoracic CBCT; liver and kidneys in the abdominal CBCT.

RESULTS

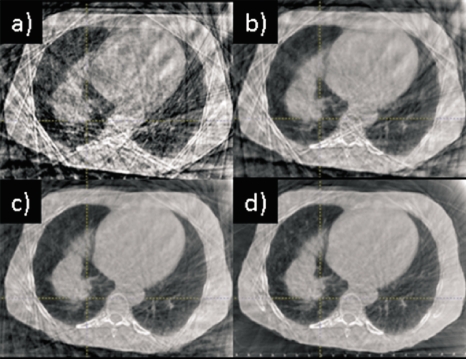
Figure 1 illustrates the influence of the different motion correction methods on a thoracic CBCT (Patient 1). Figure 1a shows an axial cut through the RC-CBCT subset at end expiration. Strong streaking artifacts are visible, caused by the sparse and nonuniformly spaced projections. When one combines the RC-CBCT images after nonrigid registration alone (phase-based correction), strong streaking artifacts are still present, as in Fig. 1b. PCA-model-based motion correction eliminates much of the noise in the nonrigid registration associated with the artifacts, clearly reducing the artifacts in the motion-corrected image shown in Fig. 1c, although not entirely eliminating them. Confining the nonrigid registration within the VOI almost completely eliminates the artifacts [Fig. 1d]. The subsequent examples of phase-based and PCA-model-based correction in thorax use nonrigid registration within the VOI.

Figure 1.

Influence of different motion correction methods on a thoracic CBCT reconstruction: (a) RC-CBCT subset at end expiration with no correction; (b) phase-based correction without VOI limitation in the nonrigid registration; (c) PCA-model-based correction without VOI limitation in the nonrigid registration; and (d) PCA-model-based correction with VOI limitation in the nonrigid registration. Display window settings are the same for all images.

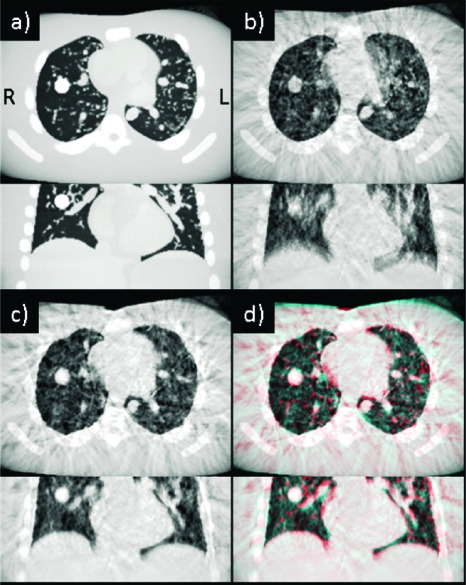
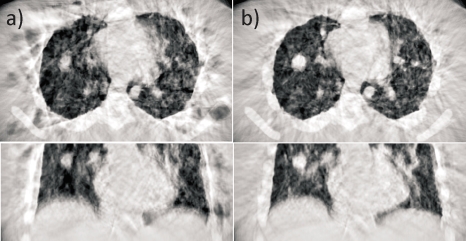
We examine the behavior of the method with the NCAT phantom. Figure 2a is a simulated CBCT reconstruction of the static phantom at end expiration; with axial and coronal sections chosen through the spherical lesion in lung. Figure 2b is the reconstruction with simulated respiration during the CBCT scan, but with no motion correction. Considerable blurring of the diaphragm, heart, lung airways, and lesion is evident (cardiac motion was not simulated). Figure 2c shows the result after PCA-model-based correction at the end expiration motion state. The blurring is considerably reduced, except for that caused by residual motion within each phase bin. Figure 2d is a red-blue overlay of the static phantom [Fig. 2a] and motion-corrected images [Fig. 2c], showing that the motion-corrected lesion position and shape are consistent with those of the static lesion (ground truth). Difference in the motion-corrected and ground truth lesion centroid positions (3D vector magnitude) is 2.0 mm, comparable to the voxel size of 1.5 mm.

Figure 2.

(a) Axial and coronal CBCT sections of the static NCAT phantom at end expiration. Spherical lesion is visible in the right lung. (b) CBCT of phantom with simulated respiratory motion with no correction. (c) CBCT with PCA-model-based correction at end expiration. (d) Red-blue overlay of static and motion-corrected images. Display window settings are the same for all images.

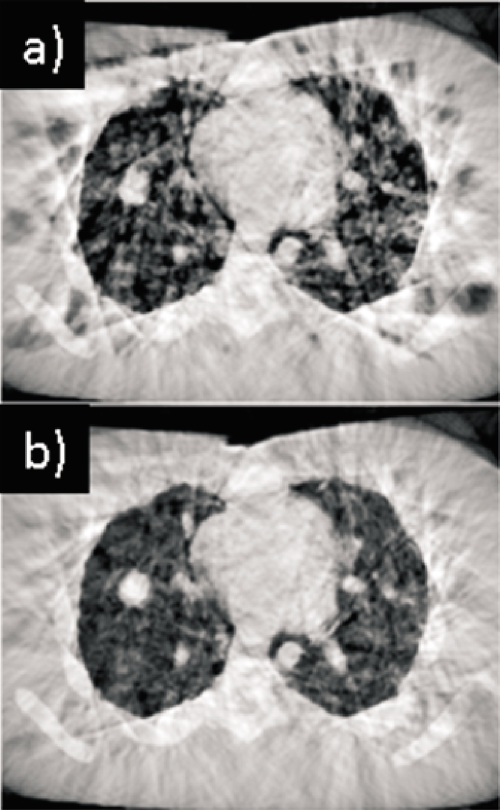
Figure 3 illustrates the effect that discarding smaller principal components has on reducing errors in the motion-corrected images caused by the influence of streaking artifacts on the deformable registration. Figure 3a shows the phase-based corrected image, in which the effects of streaking are clearly evident and result in distortions throughout the image. Note that the influence of streaking is considerably more pronounced than in the patient case [Fig. 1b]; thus the phantom study is a more challenging test of the motion correction method. The PCA-model-based correction [Fig. 3b] considerably reduces the streaking artifacts and distortions, although it does not completely eliminate them in this case. We explain this in more detail in Sec. 4.

Figure 3.

Axial CBCT section of phantom with simulated respiratory motion (a) with phase-based motion correction and (b) with PCA-model-based correction. Display window settings are the same for all images.

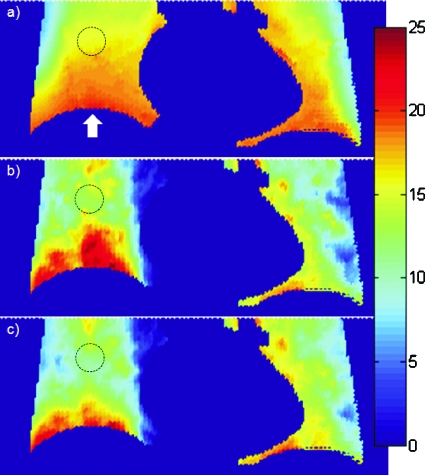
We quantify the accuracy of the method by examining displacement fields in the phantom study. We use as ground truth the displacement field resulting from nonrigid registration between the end expiration and end inspiration (EE-to-EI) CT images of the phantom. Figure 4a shows the magnitude (3D vector) of the resultant displacement field in the lungs and along a coronal cut through the center of the spherical lesion (dashed black circle). Figure 4b shows the corresponding EE-to-EI displacement field from nonrigid registration of the CBCT images, and Fig. 4c shows the EE-to-EI prediction from the PCA model. We note that displacement within the lesion is 15–16, 13–15, and 12–14 mm in Figs. 4a, 4b, 4c, respectively. Near the diaphragm apex (arrow), displacement is 20, 15–23, and 16–21 mm, respectively. The larger fluctuations in Fig. 4b relative to ground truth are caused by noise and streak artifacts in the phase-binned CBCT images. The PCA model [Fig. 4c] reduces the fluctuations but slightly underestimates (by 2–3 mm) the lesion displacement. We note that the discrepancy is largest in the EE-to-EI case, but is correspondingly less between other motion states. Since the motion-corrected image is an average of images deformed between different motion states, the resultant error in the image is less, as observed in Fig. 2.

Figure 4.

Coronal section of displacement field in NCAT phantom lungs (a) from deformable registration between end expiration and end inspiration CT images (ground truth); (b) from deformable registration between EE and EI cone-beam CT images; and (c) from PCA model prediction of cone-beam CT between EE and EI. Color denotes magnitude (3D vector) of displacement in mm. The dashed black circle indicates location of spherical lesion; the arrow indicates location of diaphragm apex.

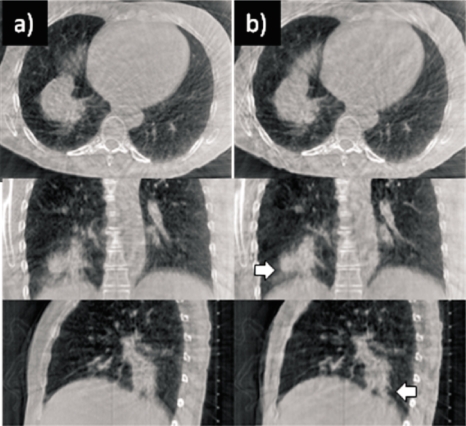
Figure 5 shows CBCT images of the same patient as in Fig. 1, with no correction (left panel) and with PCA-model-based correction (right). Note that the blurring is visibly reduced with motion correction, revealing structure of tumor in lung (arrows) not visible in the uncorrected image.

Figure 5.

Axial, coronal, and sagittal views of an example thoracic CBCT (Patient 1) (a) with no correction and (b) with PCA-model-based motion correction at end expiration. Arrows indicate tumor. Display window settings are the same for all images.

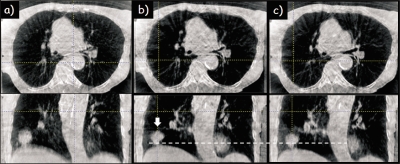
Figure 6 illustrates the ability to reconstruct different motion states from the same CBCT of a second thoracic patient (Patient 2). Left images are with no correction, middle images are PCA-model-based corrected at the end expiration motion state, and right images are corrected at the end inspiration motion state. Reduced blurring with motion correction and displacement of the diaphragm and tumor (arrow) between motion states is clearly evident.

Figure 6.

Thoracic CBCT of Patient 2 (a) no correction, (b) PCA-model-based motion correction at end expiration, and (c) PCA-model-based at end inspiration. Arrow indicates tumor. The dotted horizontal line serves as an aid to visualize motion extent. Display window settings the same for all images.

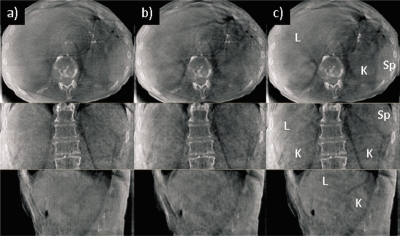
Figure 7 shows an abdominal CBCT (Patient 3) with no correction (left), phase-based correction (middle), and PCA-model-based correction (right). The liver, kidneys, and spleen are difficult to discern with no correction, and phase-based correction yields little apparent improvement. With PCA-based correction, the organ boundaries are sharper and more distinct, illustrating the feasibility of the approach even in the more challenging abdominal sites.

Figure 7.

Axial, coronal, and sagittal views of an abdominal CBCT example (Patient 3) (a) no correction, (b) phase-based correction at end expiration, and (c) PCA-model-based correction at end expiration. L denotes liver,K=kidney, and Sp=spleen. Display window settings are the same for all images. No correction is made for cupping artifacts (bright area at edge of images) or ring artifacts (visible on the axial view images) caused by noisy detector elements in the Feldkamp reconstruction.

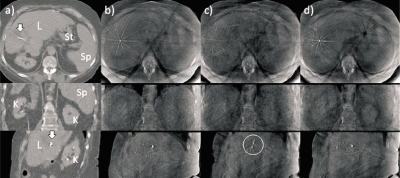
Figure 8 shows a second abdominal case (Patient 4): Respiration-correlated CT at end expiration (left), CBCT with no correction (second column), phase-based correction (third column), and PCA-model-based correction (right). Since the diaphragm is not within the reconstructed field-of-view in all phase bins, an implanted fiducial marker (arrows) serves instead as the surrogate signal. In the uncorrected CBCT [Fig. 8b], organs are difficult to discern, and motion-induced streaking is evident in the axial image. The implanted marker in the sagittal view shows motion-induced blurring and streaking. Phase-based correction reduces blurring only slightly relative to no correction [Fig. 8c]; in addition, the implanted marker appears broken up (circle), indicating inconsistencies in the nonrigid registration. This is at least partly a result of a phase lag in the internal motion observed in the CBCT relative to the prior RCCT (Fig. 9); thus, the assumption of same breathing pattern results in errors in the phase-based motion correction. With PCA-model-based correction [Fig. 8d], boundaries of liver, kidneys, spleen, stomach, and implanted marker are sharper and more discernible.

Figure 8.

Axial, coronal, and sagittal views of a second abdominal example (Patient 4). (a) Respiration-correlated CT at end expiration. L denotes liver, K=kidney, St=stomach, and Sp=spleen. The arrow indicates implanted fiducial marker. (b) CBCT with no correction. (c) CBCT after phase-based motion correction at end expiration. Implanted marker appears broken up (circle) owing to errors in the phase-based motion correction. (d) CBCT after PCA-model-based motion correction. Display window settings the same for all CBCT images. No correction is made for cupping artifacts (bright area at edge of images) or ring artifacts (visible on the axial view images).

Figure 9.

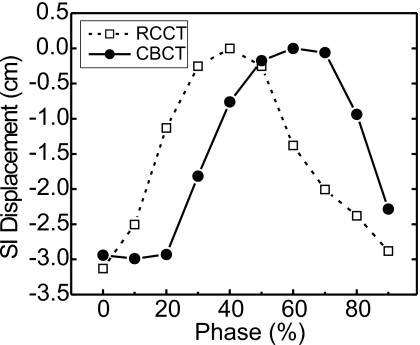
Comparison of the superior-inferior displacement of a liver-implanted fiducial marker from its end expiration (superiormost) position vs RPM phase, as observed in the RCCT and RC-CBCT images from Patient 4. The example illustrates the interfraction changes in internal respiratory motion pattern that can affect phase-based motion correction of CBCT based on a prior RCCT.

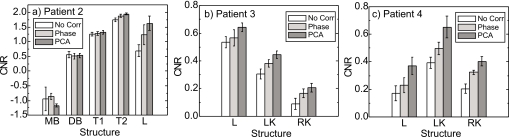
Figure 10 compares CNR values in Patients 2–4 (an RCCT scan for delineating structures of Patient 1 was not available). In the thoracic CBCT scan [Fig. 10a], there is little or no improvement in CNR with phase-based or PCA-based motion correction in the main-stem bronchus, distal bronchus, or tumor T1 (midway between apex and diaphragm of the right lung). Inspection of the RCCT shows little respiratory motion for these structures: The motion excursion (3D vector displacement of centroid) between end inspiration and end expiration is 4, 1, and 1 mm, respectively. In contrast, tumor T2 (attached to the diaphragm and shown in Fig. 3) and liver have larger motion excursions of 16 and 11 mm, respectively. Consequently, CNR improves with motion correction, with PCA-model-based correction showing more improvement than phase-based correction. In the two abdominal CBCT scans [Figs. 10b, 10c], CNR of the liver and kidneys improves with motion correction, with PCA-model-based correction showing more improvement than phase-based in all cases. Further, the difference between PCA-model-based CNR and phase-based CNR is larger than the intraobserver variability in registration (error bars).

Figure 10.

Comparison of contrast-to-noise ratios of anatomical structures in CBCT images with no correction, phase-based correction, and PCA-model-based correction. Wide vertical bars indicate the mean CNR for three repeat measurements and error bars indicate standard deviation. (a) Patient 2 thoracic CBCT. MB denotes main-stem bronchus, DB=distal bronchus, T1=tumor 1 (midway between lung apex and diaphragm), T2=tumor 2 (near diaphragm), and L=liver. (b) Patient 3 abdominal CBCT. L denotes liver, LK=left kidney, and RK=right kidney. (c) Patient 4 abdominal CBCT.

DISCUSSION AND CONCLUSIONS

Initial results indicate that motion correction of 1 min CBCT scans is feasible and yields clearly observable improvement in image quality in both thorax and abdomen. The PCA-based model is an important component in the motion correction method. Our previous study of RCCT in the thorax indicated several characteristics of the model relevant to motion correction.¹² First, two principal components appear sufficient to accurately model 3D respiration-induced motion while suppressing errors in the nonrigid registration caused by image artifacts. Second, the model does not assume repeatable breath cycles, but is parametrized by the temporal variation in surrogate position, thus accommodating interfraction changes in breathing pattern. The model is thus applicable to modeling interfraction organ variations, which is relevant for model calibration with a prior image set. The assumption that two principal components are sufficient is based on a limited number of patient thoracic studies and may not be applicable in all cases. Söhn et al.¹⁵ have reported using four principal components to model deformation of male pelvic organs. We note that the model can be expanded to a larger number of principal components if necessary. This can be determined using a patient’s RCCT image set, for example, by comparing the actual image and model-generated image at end inspiration (assuming the reference image is at end expiration).¹² One can increase the number of principal components as needed until good agreement is achieved.

To provide an intuitive sense of PCA, we summarize several properties of the covariance matrix PP^T.¹⁶ The diagonal terms are the variance of the individual voxel displacements comprising ${\tilde{p}}_j$, while the off-diagonal elements are the covariances in displacement between different voxel pairs. Large variances correspond to large motion or “signal” in the data, while small values represent no motion or noise introduced by the nonrigid registration. Large covariances correspond to highly correlated motion between voxel pairs and indicate redundancy in the data, since the motion of neighboring voxels will be highly correlated, while small covariances correspond to low redundancy. PCA seeks to minimize redundancy as measured by covariance and maximize the signal in the data as measured by variance. It does so by determining eigenvectors that are linear combinations of the ${\tilde{p}}_j$, such that the covariance matrix corresponding to the eigenvectors is diagonal; hence, redundancies are minimized. Second, PCA selects directions in the high-dimensional space along which the variances in ${\tilde{p}}_j$ are largest and presumed most important. This is done by selecting the eigenvectors with the largest eigenvalues. Eigenvectors with small or zero eigenvalues constitute noise in the data and are neglected.

The results in thorax indicates that it is feasible to calibrate the model with the same CBCT scan to be motion-corrected, thus requiring no assumptions of sameness of anatomical deformations between calibration and motion-corrected imaging sessions. Such changes may be caused by tumor growth or shrinkage, changes in atelectasis, or fluid in the lungs. In their previous study, Li et al.⁷ have found that a motion model derived from nonrigid registration of RC-CBCT subsets limited the performance of their motion correction method. Leng et al.¹⁷ have proposed a motion correction technique in which they estimate and remove sparse projection streaking artifacts in the RC-CBCT by means of a CBCT image constructed from all available projections. In an evaluation of one clinical thoracic CBCT example, they found that their method reduced streaking artifacts but did not eliminate them.

Our results indicate that three factors contribute to reducing errors caused by streaking artifacts: (1) Confining the nonrigid registration to a VOI defined at the patient surface limits the magnitude of streaking-induced deformation to be less than or comparable to respiration-induced deformation; (2) the dependence of streaking-induced deformations with time bin is different than that for respiration-induced deformations; and (3) the PCA-based model favors larger deformation which correlates with surrogate motion. This can be understood as follows. The first contributing factor prevents streaking-induced deformation from becoming the dominant principal component. The second contributing factor means that the linear combination of the ${\tilde{p}}_j$ corresponding to maximal respiration-induced variance is different from that for maximal streaking-induced variance; thus respiration-induced and streaking-induced motions are partially separated into different principal components. Figure 11 shows the phantom CBCT images corrected using each of the first two principal components separately. We observe that streaking-induced deformation is more pronounced in the first principal component, while respiration-induced deformation is more pronounced in the second (i.e., less blurring). It is interesting to note that the phantom has a large volume outside the lungs that is affected by streaking, thus resulting in a larger variance in the PCA than does respiration. Streaking is evident in different amounts in all the principal components, including the smallest three (data not shown). The third contributing factor reduces streaking partly by discarding the smallest principal components, and partly by replacing the phase-index-dependent weighting factors [w_kj n Eq. 1] with ones expressed in terms of the surrogate signals [Eqs. 5, 6]. The matrix V in Eq. 6 minimizes ${\sum }_{j=1}^J{\parallel w_j-V{s}_j\parallel }^2$, thus the weights w_j that correlate with the surrogate signals s_j are favored relative to those which correlate less. This has the effect of enhancing the contribution of the principal component with more pronounced respiration-induced deformation.

Figure 11.

Axial and coronal CBCT section of phantom with PCA-model-based motion correction (a) using first principal component only and (b) using second principal component only. Display window settings are the same for all images.

Application of the method in thorax relies partly on confining the nonrigid registration to a VOI defined at the patient surface. The VOI allows some chest and abdominal expansion, subject to the smoothing term that limits sharp gradients in the vector displacement field. Nevertheless, a potential limitation is the underestimation of respiration-induced motion in the transaxial direction. The results demonstrate the feasibility of the approach but indicate the need for further studies to investigate more sophisticated constraints in the nonrigid registration.

Motion correction in abdomen precludes model calibration with the same CBCT because of the inherently low soft tissue contrast and strong sparse projection artifacts in the RC-CBCT subsets. Instead, the model is calibrated with a prior RCCT, thus assuming that deformation fields do not change between RCCT and CBCT sessions. In this study, the RCCT was acquired at simulation 2 weeks prior to treatment. In order to investigate whether tissue deformation changes between simulation and treatment, further patient studies will acquire another RCCT on the same day as treatment. A comparison of the two RCCT data sets will test the model reproducibility.

Further studies are planned to investigate the geometric accuracy of motion-corrected CBCT. Studies with deformable analytical¹⁴ and physical¹⁸ phantom provide a known ground truth for comparison. The second means of validation is a patient imaging study, in which patients will receive an additional CBCT gated at end expiration⁶ that acts as a bronze standard for comparison to the motion-corrected CBCT.