Arrangement of 3D structural motifs in ribosomal RNA

Abstract

Structural 3D motifs in RNA play an important role in the RNA stability and function. Previous studies have focused on the characterization and discovery of 3D motifs in RNA secondary and tertiary structures. However, statistical analyses of the distribution of 3D motifs along the RNA appear to be lacking. Herein, we present a novel strategy for evaluating the distribution of 3D motifs along the RNA chain and those motifs whose distributions are significantly non-random are identified. By applying it to the X-ray structure of the large ribosomal subunit from Haloarcula marismortui, helical motifs were found to cluster together along the chain and in the 3D structure, whereas the known tetraloops tend to be sequentially and spatially dispersed. That the distribution of key structural motifs such as tetraloops differ significantly from a random one suggests that our method could also be used to detect novel 3D motifs of any size in sufficiently long/large RNA structures. The motif distribution type can help in the prediction and design of 3D structures of large RNA molecules.

INTRODUCTION

RNA is a remarkably versatile molecule participating in enzymatic reactions (1), gene transcriptional regulation (2) and biological information transfer. According to the RNA world hypothesis (3), which is not entirely settled, RNA preceded DNA and protein in the first stage of life development. Thus, a detailed understanding of RNA folding and structure would serve to elucidate how RNA can carry out so many different functions in the cell. RNA is a modular biomolecule, composed primarily of conserved structural motifs comprising the RNA secondary structures. Progress in X-ray crystallography has enabled the structure determination of large RNA molecules; e.g. the 2.4-Å crystal structure of the Haloarcula marismortui large ribosomal subunit (HM LSU 23 S rRNA) (4,5). With current crystallographic data on transfer RNA, ribozymes and large ribosomal RNAs (rRNA) along with anticipated new structures, it is important to develop tools for annotating RNA structures and finding structural or 3D motifs.

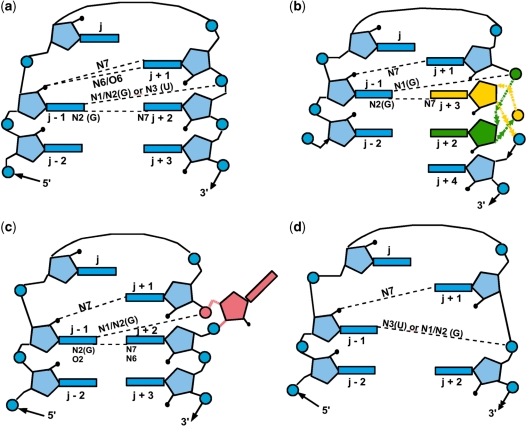
RNA 3D motifs can be defined generally as ‘recurrent structural elements containing multiple intramolecular RNA–RNA interactions’ (6). They are frequently observed among known RNA structures and serve architectural roles in RNA folding and tertiary-structure stabilization. They typically comprise hairpin 1-loop, which links the 3′- and 5′-ends of a double helix, or internal 2-loops, which separates the RNA double helix into two segments by the insertion of residues that are not Watson–Crick paired in one/both strands (7). The most common and well-studied hairpin 1-loop motifs are the tetraloops with characteristic four-residue sequences, connecting two anti-parallel chains of a double-helical RNA. They are biologically important as they are implicated in (i) initiating RNA folding, (ii) stabilizing helical stems and (iii) binding proteins and long-range tertiary interactions (8–11). Isolated tetraloops exhibit well-defined structure and are thermodynamically stable. Tetraloops have been classified according to their sequence and conserved structures into five types: (i) GNRA (12,13), (ii) UNCG (14–16), (iii) ANYA (17–19), (iv) (U/A)GNN (20) and (v) CUYG (21–23), where N is any nucleotide, R is a purine (G or A) and Y is a pyrimidine (C or U). Recently, they have been classified according to their deviations from the standard tetraloop motif (11), as illustrated in Figure 1. An example of internal 2-loop motifs is the kink-turn, which is formed by two strands in a helix–internal loop–helix arrangement (5,24,25), and is important for tertiary interaction with proteins (5). As the name implies, a sharp bend or kink is formed in the phosphodiester backbone of the strand, bringing the minor side of the two nearby helices together. The local 3D motifs that appear in 3D structures have been classified in the SCOR database (26).

Figure 1.

Schematic diagrams showing the various tetraloop motifs and their hydrogen-bonding interactions, adapted from Hsiao et al. (11), Figure 3. (a) The standard tetraloop. (b) A tetraloop with a 3–2 switch where the bases of the j+2 and the j+3 residues are switched. (c) A tetraloop with insertion where a residue (in pink) is inserted between the j+1 and the j+2 residues. However, >1 residue can be inserted and if extensive enough, would produce a strand clip. (d) A tetraloop with deletion where the j+2 residue in the standard tetraloop is absent so the j+3 residue becomes the j+2 residue. Rectangles, pentagons and circles denote base, sugar and phosphate groups, respectively, while dashed lines denote characteristic hydrogen bonds.

Automated tools for 3D motif recognition require, as input, a query structure representing a known 3D motif and some measure of structural similarity, which is mainly based on different shape and pattern recognition methods such as geometric hashing (27), spherical harmonics (28), shape distributions (29,30) and moment invariants (31). Since 3D motifs involving hairpin and internal loops possess distinct backbone conformations (32), new methods based on analyzing and classifying RNA backbone conformations have been developed to search for recurrent motifs in 3D RNA structures. Methods such as PRIMOS (33) and COMPADRES (34) employ a reduced representation of the RNA backbone (using two pseudotorsion angles) to analyze the RNA backbone conformation and identify recurrent RNA backbone conformations. In particular, COMPADRES has been used to identify novel RNA 3D motifs comprising ≥5-nt such as π-, Ω-turn and α-loop (34). All the backbone torsion angles have also been used to identify RNA conformational motifs in the HM LSU 23 S rRNA (32,35). Instead of using torsion angles, NASSAM (36) employs a reduced vectorial representation of the RNA structure to convert the problem of searching for recurrent 3D motifs to the subgraph isomorphism problem. FR3D (37) uses a combination of geometric, symbolic and sequence information to search a query motif in the RNA structure for local and composite recurrent 3D motifs. The 3D structure of short RNA sequences have been represented as shape histograms and used to find 3D motifs in the HM LSU 23 S rRNA structure (30). Furthermore, the distribution of RNA motifs along the sequence has been used to align rRNAs (38).

The aforementioned approaches for RNA motif classification, however, do not recognize all 3D motifs in a given RNA molecule and may yield false positives. Notably, none of these methods (to the best of our knowledge) provide statistical information on the distribution of a given 3D motif along the RNA chain, although the locations of various motifs such as kink-turns in 23 S rRNA and A-minor motifs in 16 S rRNA have been determined (5,39,40). This may be due partly to the low occurrence frequency of a given 3D motif in the RNA chain for most of the known motifs and the lack of highly reliable motif recognition methods. This raises the following intriguing questions: (i) Do the recurrent 3D motifs distribute randomly or do they cluster together or disperse along the RNA chain? (ii) Is it possible to identify known stable and important 3D motifs such as tetraloops by their statistically significant non-random distribution? Information on 3D RNA motif distributions might aid conformational sampling, which usually neglects long-range correlations, and thus energy-based prediction of RNA tertiary structure (41,42). This information could also help to verify and improve theoretical descriptions of RNA folding, and provide additional evidence for the biological significance of the motifs.

The key objectives of this work are to develop a novel strategy to characterize the distributions of 3D motifs along a RNA chain and identify those motifs that have a truly non-random distribution. The distributions of 3D motifs along a RNA chain were determined using a recently developed algorithm designed for finding keywords in a single text without using a corpus of documents taken as a reference (43,44). The algorithm takes into account the frequencies of the words in the text and their spatial distribution along the text. Keyword detection is based on the premise that relevant words are significantly clustered, whereas irrelevant words are distributed randomly in the text. In our case, RNA 3D motifs such as tetraloops represent ‘words’, while the entire RNA molecule is considered as ‘text’. The structural similarity of the 3D motifs (‘words’) was estimated using the shape histogram approach in combination with the root-mean-square deviation (RMSD) of their backbone atoms (30). The distribution of a given 3D motif along the chain relative to a random one was estimated by a scoring function based on statistical methods. Key 3D motifs (representing keywords) were identified as those that not only attract, but also repel one another along the RNA chain in a statistically significant manner. The HM LSU 23 S rRNA (1jj2.pdb, chain 0) was employed as a test system because it is known from previous work (11) to contain 21 standard tetraloops (Figure 1a) and 10 tetraloops with deletions at position 2 (Figure 1d), and the crystal structure contains 2754 bases, which suffice for statistical analyses. Hence, our novel strategy was used to determine the distribution of all 3-, 4- and 5-mer motifs in HM LSU 23 S rRNA.

METHODS

Representing RNA fragment structure using shape histogram

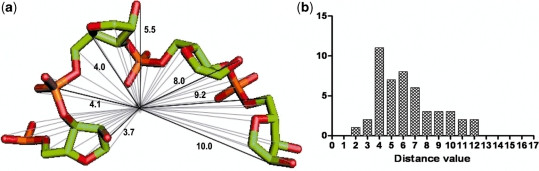
The structure of a short RNA sequence or fragment was described using the shape histogram approach (30), which has been successful in finding 3D motifs given a query pattern. Only backbone atoms (P, O5′, C5′, C4′, O4′, C3′, O3′, C2′, O2′, C1′, OP1, OP2) of the RNA fragment were considered because flexibility of the bases may lead to possible false results in structural similarity comparisons. For a given RNA fragment, the centroid with respect to the phosphorus atoms of the fragment and its distance to each backbone atom were computed, as illustrated in Figure 2a. Next, the distances are rounded to the nearest integer (e.g. a distance of 3.65 Å is rounded to 4 Å). The frequency of each integer distance value is plotted as a 2D histogram and represented by a histogram vector h = (h₁,…,h_n), where h_i is the frequency of the integer distance d_i (Figure 2b). The shape histogram of a RNA fragment, which is a distribution of Euclidean distances of the RNA backbone atoms from the centroid, can be considered as a signature of the fragment structure.

Figure 2.

The shape histogram of a given RNA fragment. (a) The backbone atoms of a RNA fragment 1794–1797 and some of their distances to a centroid. (b) The shape histogram of a given RNA fragment represented by the frequency of an integer distance in Angstrom.

Measuring structural similarity by comparing shape histograms

Following previous work (30), the difference between 2 RNA fragments, characterized by histogram vectors h and g, was estimated by the cosine of the angle formed by h and g:

(1)

A Cos of 1 means perfect overlap between the shape histograms of the two RNA fragments. Since using only Cos as a measure of similarity has been shown to be less effective than its combination with the backbone RMSD (30), the latter was also computed using the SVDSuperimposer package of BioPython (http://www.biopython.org). Given a threshold of x for Cos and y for RMSD, two RNA fragments were deemed to be similar if their Cos is ≥x and their RMSD is ≤y.

Determining the different 3D motifs along a RNA chain

A RNA fragment can be considered as a ‘word’ containing structural information described by a shape histogram. However, a word has fixed spelling and discrete letters, so two words are either equal or not equal, whereas the Cos and RMSD, describing the difference between two RNA fragments, are continuous variables. Therefore, a combination of Cos and RMSD thresholds was used to assign the structural similarity of two RNA fragments (equivalence of two words). In this way, motifs are treated as discrete objects like words. For a RNA consisting of N nucleotides, there will be N − l + 1 RNA fragments composed of l-nucleotides (l-mer or ‘l-letter word’) starting from each nucleotide. The l-mer fragment starting at position i was compared with all the other N − l l-mer fragments starting at position i + 1, i+2, … , N − l + 1, 1, 2, 3, … , i−1; a match was recorded by the position of the matching fragment, denoted by the position of its first nucleotide, a_i. If there are >10 matches, then the l-mer fragment starting at position i is a potential motif, whose distribution along the RNA chain is described by the positions of the ‘word’ along the text, S_i = (a₁, a₂, a₃…). Note that an l-mer RNA fragment that repeats ≤10 along the chain was not considered as a motif for distribution analyses due to the lack of statistics.

Representative motifs obeying the transitivity of ‘words’

In literal text, if word X is equal to word Y, and word Z is equal to word Y, then X and Z represent the same word (transitive relation). In a RNA molecule, the equivalence of ‘words’, determined according to the Cos and RMSD thresholds, contains some fuzziness. According to given RMSD and Cos threshold values, ‘word’ X is similar to ‘word’ Y, and ‘word’ Z is similar to ‘word’ Y, but ‘words’ X and Z are different if the corresponding RMSD or Cos exceeds the threshold. To adopt the statistics applied in finding keywords in literal texts to finding ‘key’ motifs along the RNA (see below), the following procedure was employed to ensure the transitive relation of l-mer RNA fragments (‘words’): for two sets, S_i and S_j, if one of these two sets possess >70% l-mer RNA fragments in common, and if set S_i contains more ‘words’ than set S_j, then set S_i was used to represent the distribution of a motif whose representative l-mer is at position i. However, if S_i and S_j have the same number of words, then set S_i was compared with another set S_k. With this protocol, the problem of choosing between two sets with the same number of ‘words’, but with partially different content of ‘words’, did not arise. All representative l-mers are considered to be different ‘words’. l-mers that are similar to the representative l-mer at position i according to the Cos and RMSD thresholds are treated as ‘equal to’ the representative l-mer, thus satisfying the transitive relation. Since the number of ‘words’ common to two different motifs is small and depends on the Cos and RMSD thresholds, only those representative l-mers that are conserved upon successive changes of the Cos or RMSD similarity threshold were considered. This protocol gives all possible representative motifs, each containing a set of similar ‘words’ and their positions, with no or only a few ‘words’ in common with a set of ‘words’ comprising another motif.

Random distribution of a 3D motif

Words of importance such as keywords do not randomly occur throughout the text, but rather appear in a specific context. Likewise, key motifs may not be randomly distributed along the RNA chain, but might self-attract or self-repel one another. From extensive simulation of random texts (generated as random binary sequences where ‘1’ models a word in a text with probability p and ‘0’ accounts for the rest of the words with probability 1−p), the geometric distribution was found to be a very good model in describing the distribution of random words in a text (43); it becomes the exact distribution if the desired word has a fixed probability of occurrence in infinitely long text (45). Since ‘motifs in the RNA’ correspond to ‘words in the text’, the geometric distribution was used to describe the distribution of the motifs occurring randomly along the RNA chain. Let d_i = a_i – a_i−1 denote the separation of the same consecutive motifs (‘words’) along the RNA chain (‘text’), and D = (d₁, d₂, …., d_N) denote the set of integer distances. The probability of distance d, P(d), in set D in the case of random placement of the motif along the RNA chain (or a word along the text) is described by the geometric distribution:

(2)

In Equation (2), p, the probability of the motif occurring randomly in the RNA chain, is given by the occurrence frequency of the l-mer motif divided by the number of all l-mer fragments. Other distributions have not been shown to describe the distribution of random words, and hence have not been employed as a null hypothesis. Notably, Poisson distribution was not used as it describes the random distribution of continuous distances, and hence is not valid for ‘words’ with integer separations. Using another distribution type for the null hypothesis would not be expected to change the conclusions obtained herein, if it is close to the geometric distribution.

Evaluating if a 3D motif distribution is random or not

Requirements for local/global folding, long-range interactions and evolutionary history may all affect the distribution of RNA motifs along the 1D sequence and in the 3D structure, resulting in non-random distribution of the motifs. Notably, a highly non-random motif distribution may reflect the importance of that motif. To determine if a given motif has a non-random distribution, a fully random distribution, which was not obtained from the RNA sample space, was employed as a reference. The set of D-values that differs from those described by the geometric distribution in Equation (2) was estimated by σ, the ratio of the normalized mean square deviations for elements of set D to those in the geometric distribution:

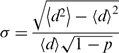(3)

Since σ and thus P(σ) depends on the occurrence frequency of the motif, n, artificial clustering caused by fluctuations is possible for motifs that occur infrequently along the RNA chain. This is because for rare motifs (small n), the distribution P(σ) is broad, so the probability of large σ by chance is non-negligible; i.e. a rare random l-mer fragment would be misidentified as a key motif. Thus, the deviation of the distribution of D-values from a geometric distribution was also evaluated using a Z-score measure, which depends on the self-attraction/repulsion of a l-mer motif and its frequency:

(4)

In Equation (4), 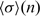is the mean value of σ for the case of randomly placed motifs with small n number of counts and 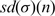is the corresponding standard deviation. From the extensive simulation of random texts using random binary sequences (43), the n dependence of the mean <σ> and the standard deviation sd(σ) of the distribution P(σ) can be approximated as:

(5)

Since the C score accounts for finite size corrections, but σ does not, it is more reliable and may not correlate with σ if finite size corrections are important. Nevertheless, both types of scores should indicate the same type of motif distribution; i.e. the l-mers of a given 3D motif are either clustered or dispersed along the RNA chain. The l-mers of a given 3D motif are clustered along the RNA chain if σ > 1 or C > 0, but are dispersed if σ < 1 or C < 0; they are randomly distributed if σ = 1 or C = 0.

Determining motifs of interest

A 3D motif was identified to be of interest if (i) its distribution is significantly non-random, (ii) its distribution type (clustered/dispersed along the RNA) is conserved when the similarity measure (Cos or RMSD) was altered and (iii) it is conserved with small changes in its length. First, all l-mer motifs were derived using a RMSD threshold, y = 1.5 Å, and a Cos threshold, x = 0.93, 0.94, 0.95 or 0.96, as well as x = 0.95 and y = 2.0 Å. Next, statistical scores (σ and C) describing their distribution type were computed according to Equations (3−5). All motifs with significantly non-random distributions that conserve their distribution type (same C score sign) under changes of the Cos or RMSD similarity threshold and persist with increasing motif length were considered to be of potential interest.

Relating the distribution of RNA motifs in 1D to that in 3D

The distributions of motifs found along the 1D sequence may not correlate with those in the 3D structure. To relate an l-mer distribution along the RNA sequence to that in the 3D structure, the distance between any two l-mers was computed as the distance between the centroids of the two l-mers. Hence, the distances between any two centroids of all l-mer motifs in the 1jj2 structure were computed and averaged to yield 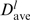. The D_ave distances between any two centroids of all 3-, 4- and 5-mer motifs are 12.54, 12.56 and 12.57 Å, respectively. For a given l-mer motif, the distances between the centroid of each l-mer and the centroid of its nearest neighbor were computed and averaged to yield d_ave. Since d_ave reflects the mean distance between an l-mer and its nearest neighbor pertaining to the same motif, whereas D_ave(l) reflects the mean distance between any two l-mers belonging to any motif, a d_ave >> D_ave(l) would imply that the motif is dispersed in the 3D structure.

RESULTS

Length distribution of RNA helices and non-helical regions

To evaluate the optimal length of the RNA fragments to represent the key motifs in rRNA, the number of nucleotides in RNA helices and between RNA helices were evaluated. RNA helices were defined as ≥2 contiguous Watson–Crick base pairs, using the base-pairing data from the NDB database (http://ndbserver.rutgers.edu/). According to this definition, there are 178 helices in the 1jj2 structure containing ≥2 contiguous Watson–Crick base pairs. The distributions of the number of nucleotides in RNA helices and between RNA helices (Supplementary Figure S1) show a mean of 4 ± 2 bp with a maximum of 10 in helices and a mean of 4 ± 3 bases between the helices. This indicates that motifs in the 1jj2 structure RNA likely contain 4 nt in both helical and non-helical regions. Since motifs of interest should be conserved upon small changes in length (see above), 3-, 4- and 5-mer motifs that deviate significantly from a random distribution and persist under changes of the similarity measure were identified. As tetraloops have been well characterized in the HM LSU 23 S rRNA structure and can be compared with the 4-mer motifs, the latter are first presented followed by 3- and 5-mer motifs.

4-mer motif distributions

4-mer motifs whose distributions are significantly non-random (i.e. C scores < −1.5 or > 5) and whose distribution type remains the same (i.e. same C score sign) when the Cos/RMSD threshold was changed were identified as 4-mer RNA motifs of interest (‘Methods’ section). Those derived using Cos = 0.95 and RMSD = 1.5 Å are listed in Table 1 according to decreasing occurrence frequency along the RNA chain. The results in Table 1 show that the most common key motif, whose representative 4-mer is at position 178 (‘Methods’ section), is clustered along the RNA chain (C > 5 and σ > 1) with most successive motifs separated by 1-nt (Supplementary Figure S2). The 178–181 4-mer matched the first 4-nt of both strands of all 84 helices in the 1jj2 structure containing ≥4 contiguous Watson–Crick base pairs with a mean RMSD = 0.83 ± 0.45 Å and a mean Cos = 0.96 ± 0.03. This indicates that the most common 4-mer motif corresponds to a helical motif (Figure 3a). The mean distance between the centroid of a 4-mer helical motif and the centroid of its nearest neighbor (d_ave ∼ 5.2 Å) is significantly shorter than that between the centroids of all 4-mer motif pairs in the 1jj2 structure (D_ave⁴ = 12.54 Å), indicating clustering of the helical regions in the 3D structure as well.

Table 1.

4-mer motifs derived using Cos = 0.95 and RMSD = 1.5 Å

Motifa	Frequencyb	Cc	σd	dave/Davee	Consensus sequencef
178	1029	8.55	1.26	0.41	C (30%) G (32%) G (36%) G (36%)
1052	117	−1.75	0.83	1.26	G (38%) C (33%) G (32%) G (47%)
1794	34	−1.90	0.66	2.16	G (65%) A (50%) A (65%) G (35%)
209	23	−1.84	0.61	2.22	C (35%) G/C (30%) C (48%) A (56%)
2689	16	−1.93	0.53	2.98	C (37%) C (62%) A (56%) G (50%)

^aPosition of the representative l-mer of the motif along the RNA chain (‘Methods’ section); number in bold corresponds to the representative of the tetraloop motif.

^bThe number of times the l-mer motif is found along the RNA chain.

^cC score calculated according to Equations (4 and 5).

^dσ score calculated according to Equation (3).

^eThe average of the distances between the centroid of each l-mer and the centroid of its nearest neighbor divided by the average of the distances between any two centroids of all l-mer motifs in the 1jj2 structure.

^fThe consensus sequence with percentage frequency of each base in parentheses.

Figure 3.

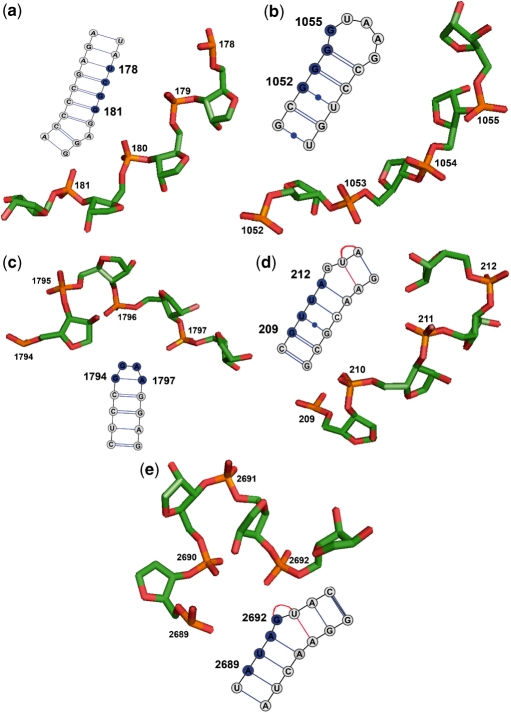
Three-dimensional backbone and secondary-structures corresponding to the representative 4-mer motifs in Table 1: (a) helical motif, 178−181, (b) part of an internal loop, 1052−1055, (c) tetraloop motif, 1794−1797, (d) part of an internal loop, 209−212 and (e) part of an internal loop, 2689−2692. In the secondary structures, circles denote the residues, while filled ones denote residues comprising the 4-mer motif. Single and double lines denote one and two hydrogen bonds, respectively, dot on the line singles out non-Watson–Crick base pairs, while red lines represent base triples. Secondary structures were prepared by the program, VARNA (47).

In contrast to the helical motif, the other four key 4-mer motifs exhibit C scores <−1.5, σ < 1 and 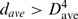, indicating that these four motifs are both sequentially and spatially dispersed. Without the need to input a query structure, our new strategy could yield known motifs in the SCOR database (26). The motif whose representative 4-mer is at position 1052 is the most common motif that is both sequentially and spatially dispersed along the RNA chain (Table 1, frequency = 117). According to the SCOR database, the 1052–1055 4-mer connects with the 1055–1059 hairpin loop and is part of the 1052, 1065 internal loop (the comma separates residues belonging to different strands), which belongs to the class of stacked duplexes with one non-Watson–Crick pair (Figure 3b). The motif whose representative 4-mer is at position 1794 is found 34 times along the RNA chain and encompass many of the known tetraloops (see below and Figure 3c). The motif, represented by the 209−212 4-mer, overlaps with the 210−215, 225−229 internal loop in the SCOR database where the bulged base forms a dinucleotide platform (sequential bases that are side-by-side, coplanar and non-Watson–Crick base-paired), which in turn is part of a base triple (Figure 3d). The least common motif that is both sequentially and spatially dispersed is represented by the 2689−2692 4-mer, which overlaps with the 2690−2694, 2701−2704 internal loop with a dinucleotide platform and a base triple that is annotated in the SCOR database (Figure 3e).

Comparison with known tetraloops

Our new strategy could predict most of the known tetraloops without using a known tetraloop as a query structure, even though it was aimed at identifying 3D motifs with significantly non-random distributions rather than detecting all tetraloops without false positives. Comparison of the set of 4-mers encompassing tetraloops with the 43 tetraloops reported by Hsiao et al. (11) in Table 2 shows that our method predicted 19 of the 21 standard tetraloops (Figure 1a), 8 of the 10 tetraloops with deletion of the j+2 residue in the standard tetraloop (Figure 1d), one of the three tetraloops with insertion of a residue between residues j+1 and j+2 in the standard tetraloop (Figure 1c), and all tetraloops with a 3−2 switch where the bases of residues j+2 and j+3 are exchanged (Figure 1b). The two missing standard tetraloops at position 734 and 1238 as well as the two missing tetraloops with deletion at position 625 and 1992 superposed with the known tetraloop at position 1794 with a backbone RMSD of 1.43 Å (Cos = 0.94), 1.54 Å (Cos = 0.97), 1.58 Å (Cos = 0.94) and 1.65 Å (Cos = 0.95), respectively. Thus, they were missed using a RMSD threshold ≤1.5 Å and Cos threshold ≥0.95.

Table 2.

All 4-mers encompassing tetraloop motifs derived using Cos = 0.95 and RMSD = 1.5 Å

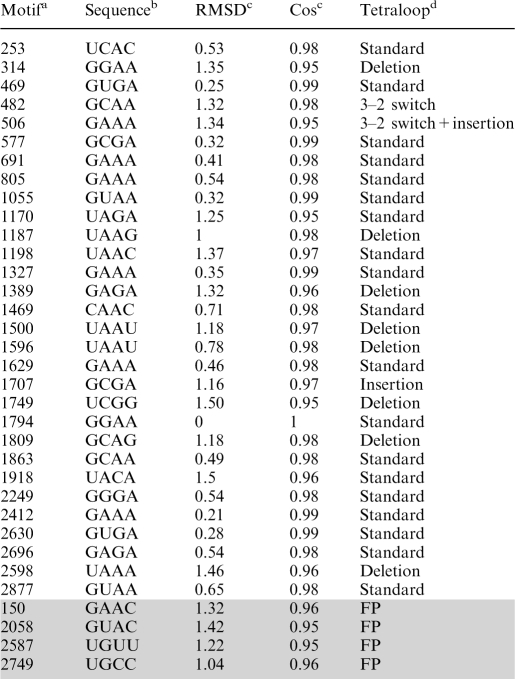^aPosition of the first residue of the 4-mer along the RNA chain.

^bSequence of 4-mer.

^cComputed relative to the backbone atoms of the 1794−1797 fragment.

^dTetraloop type, according to the annotation by Hsiao et al. (11), Figure 4 (see also Figure 1); FP means false positive; i.e. the 4-mer is not one of the 43 tetraloops annotated by Hsiao et al., and is shaded grey.

The 4-mers at position 150, 2058, 2587 and 2749 along the RNA chain do not belong to any of the annotated tetraloops in the 1jj2 structure (11), even though they superposed with the known tetraloop at position 1794 with backbone RMSDs < 1.5 Å and Cos ≥ 0.95 (Table 2). This is because they do not exhibit hydrogen-bonding interactions between the j−1 and j+2 bases, characteristic of tetraloops (Figure 1), but instead form hydrogen-bonding interactions with other non-tetraloop bases. The 150−153 4-mer has two base-pair interactions (152:A–G: 185, 153:C–G:184), the 2058–2061 4-mer has also two base-pair interactions (2060: A–U:2076, 2061: C–G:2075), the 2587–2590 4-mer has one base-pair interaction (2588: G–G:2617), while the 2749–2752 4-mer has three base-pair interactions (2732:U–G: 2750, 2731: G–C:2751, 2730:G–C: 2752).

Notably, the 21 known standard tetraloops are characterized by C = −2.27, σ = 0.52, verifying that tetraloops tend to be dispersed along the RNA chain. To verify that they are also dispersed in the 3D structure, the distances between each of the 21 standard tetraloops and the nearest standard tetraloop in the structure, d_tt, were computed. The d_tt distances are all ≥14.1 Å (Supplementary Table S1). As the d_tt distances reflect the proximity of two nearest standard tetraloops, the distances between any two standard tetraloops would be much greater than 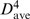, indicating that the standard tetraloops are indeed dispersed in the 3D structure. All the standard tetraloops cap left and/or right-stranded helices whose backbone conformations correspond to the helical motif, represented by the 178–181 4-mer, except for tetraloops at position 2696 and 2877. The distances between each standard tetraloop and the helical motif that it caps, d_th, are <11 Å with a mean distance of 7.60 ± 1.53 Å.

3-mer motif distributions

As for the 4-mer motifs in Table 1, 3-mer motifs whose distributions are significantly non-random (C < −1.5 or >5) and whose distribution type remains the same when the Cos/RMSD threshold was changed were deemed to be of interest. Those motifs derived using Cos = 0.95 and RMSD = 1.5 Å are listed in Table 3 according to decreasing occurrence frequency along the RNA chain. These were matched against the first or last three residues of each of the 4-mer motifs in Table 1 using shape histograms (Cos) and RMSD values. Four of the 3-mer motifs were found in the respective 4-mer motifs. The most common 3-mer motif, whose representative is at position 304, is part of the helical 4-mer motif: comparison of its representative 3-mer at position 304 with the first and last three residues of the helical 4-mer at 178 gives Cos = 0.97, RMSD = 1.08 Å and Cos = 0.97, RMSD = 1.12 Å, respectively. Like the 4-mer helical motif, the 3-mer helical motif is clustered along the RNA (C > 5, σ > 1) and in the 3D structure (d_ave is half of 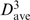). The 3-mer at 232 is similar to the first three residues of the 4-mer at 1052 (Cos = 0.95 and RMSD = 0.90 Å), while the 3-mers at 2588 and 356 are similar to the last three residues of the 4-mer at 1052 (Cos = 0.96, RMSD = 0.35 Å) and at 2689 (Cos = 0.96, RMSD = 0.36 Å), respectively. Like their 4-mer motifs, these 3-mer motifs are also dispersed along the chain (C < −1.9 and σ < 1) and in the 3D structure (d_ave > 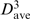), except the 3-mer at 2588. The 3-mers that are part of tetraloops also exhibit dispersed distributions along the RNA but they are not listed in Table 3, as their C scores are >−1.5.

Table 3.

3-mer motifs derived using Cos = 0.95 and RMSD = 1.5 Å^a

^aSee footnotes to Table 1.

^bShaded motifs are found as part of 4-mer motifs in Table 1; the motifs in italics do not overlap with known motifs in the SCOR database.

In addition to the 3-mer motifs that are part of 4-mer motifs, three other motifs in Table 3 overlap with known motifs in the SCOR database. The 521–523 3-mer overlaps with the 517–522 internal loop. For the 3-mer motif whose representative is at 2098, its constituent 312–314 3-mer overlaps with the known 313–318 hairpin loop in the SCOR database. The 264–266 3-mer overlaps with the second strand of the 246–248, 261–265 kink turn. The remaining 3-mer motifs in Table 3 (in italics) do not match any motifs in the SCOR database or the triloop motif (46). Although the backbone conformations of these two 3-mer motifs are conserved, their base interactions vary widely. For the 3-mer motif whose representative is at position 1942, 27% exhibit antiparallel Watson–Crick base pairing and 7% show no base pairing, whereas for the 3-mer motif whose representative is at position 2278, 31% exhibit antiparallel Watson–Crick base pairing and 12.5% show no base pairing. Thus, these two motifs do not exhibit any consensus secondary structures or specific sequences.

5-mer motif distribution

The same protocol used to identify the 4- and 3-mer motifs was applied to 5-mer RNA motifs occurring >10 times along the RNA chain. The motifs derived using Cos = 0.95 and RMSD = 1.5 Å are listed in Table 4. They were compared with the 4-mer motifs in Table 1 by matching the latter against the first or last four residues of each 5-mer motif. They were also compared with the 3-mer motifs in Table 3 by matching the latter against the consecutive triplets comprising each 5-mer motif. Kink-turns were not among the motifs in Table 4 as only eight (local and composite) are found in the 1jj2 structure and are thus not amenable to statistical analyses on their distribution (‘Methods’ section).

Table 4.

5-mer motifs derived using Cos = 0.95 and RMSD = 1.5 Å^a

^aSee footnotes to Table 1.

^bShaded motifs are found as part of 4-mer motifs in Table 1.

The 5-mer motifs in Table 4 match the 4-mer motifs in Table 1 with Cos ≥ 0.96 and RMSD ≤ 1.10 Å and/or the 3-mer motifs in Table 3 with Cos ≥ 0.95 and RMSD ≤ 1.25 Å. The first three and four residues of the most common 5-mer motif, whose representative is at position 1547, match the 3- and 4-mer helical motifs. This 5-mer motif also exhibit clustering of helical regions along the RNA chain (C > 10, σ > 1) and in the 3D structure (d_ave/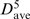 = 0.41 Å). In contrast to the 5-mer helical motif, the other three key 5-mer motifs exhibit negative C scores, σ < 1, and d_ave/ 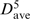> 2.3, indicating that these 5-mer motifs are both sequentially and spatially dispersed. The first three and last four residues of the representative 5-mer at 312 match the 2098−2100 3-mer and the known 313−318 hairpin loop in the SCOR database, respectively. The last four residues of the representative 5-mer at 2411 match the 2412−2415 tetraloop (Table 2). The first three and last four residues of the representative 5-mer at 1530 match the 521−523 3-mer and the 2689−2692 4-mer.

Distribution of binding residues in the l-mer motifs

To reveal whether the 3-, 4- and 5-mer motifs in Tables 1, 3 and 4, which deviate significantly from a random distribution and persist under changes of the similarity measure, play a role in binding, the fraction of ‘binding’ residues in these motifs was compared to that in all l-mers. A ‘binding’ residue was defined as one with non-hydrogen atoms within vdW contact (≤4.0 Å) of a non-hydrogen atom of a protein or another RNA chain. This yielded 1238 binding residues. Compared to the fraction of binding residues in all l-mers, which is equal to 1238/(2755−l), the fraction of binding residues in the 4 or 5-mer motifs with a dispersed distribution in Table 1 or 4 is significantly higher: the fraction of binding residues in the 4 or 5-mer dispersed motifs (1.10 or 0.98) is 2.4 or 2.2 times greater than that in all 4- or 5-mers (∼0.45). In contrast, the fraction of binding residues in the 3-mer dispersed motifs in Table 3 (0.48) is similar to the fraction of binding residues in all 3-mers (0.45). The fraction of binding residues in the ubiquitous 3-, 4- or 5-mer helical motif (0.66, 0.58 or 0.61) is not significantly greater than that in all 3-, 4- or 5-mers.

Sequence signatures of the recurrent motifs

To find out if the recurrent motifs identified by our new method have specific or non-specific sequences, the sequences for all 3-, 4- and 5-mer motifs derived using Cos = 0.95 and RMSD = 1.5 Å were analyzed. For a given l-mer motif, the frequency of each base type is computed for each position and the most common base at each position is found. Those motifs with base occurrence probabilities ≥0.60, ≥0.55 and ≥0.50 for the 3-, 4- and 5-mers, respectively, are listed in Table 5. Notably, the first and last four residues of the 5-mer motifs whose representatives are at 469 and 690, respectively, correspond to the known tetraloops. Interestingly, the fraction of binding residues in the 3-, 4- or 5-mer motifs in Table 5 (1.56, 1.05 or 1.22) is significantly greater than that in all 3-, 4- or 5-mers (0.45), indicating that these motifs with specific sequences may be part of binding sites for proteins and other molecules. In contrast, commonly occurring structural motifs such as the helical motif do not exhibit a clear sequence–structure relationship; e.g. the most common base at each position of the 3-, 4- or 5-mer helical motif occurs with a probability of ∼0.30−0.38, indicating that this motif does not have a strong sequence preference.

Table 5.

Sequence signatures of the recurrent motifs derived using Cos = 0.95 and RMSD = 1.5 Å^a

Motif	Frequency	C	σ	dave/Dave	Consensus sequence
3-mer
212	11	−0.12	0.84	3.62	A (81%) G (81%) U (72%)
534	11	0.54	0.99	3.23	G (63%) A (63%) A (90%)
552	14	−0.63	0.77	3.16	A (71%) C (85%) C (64%)
4-mer
567	16	−0.34	0.84	2.79	C (56%) G (81%) A (81%) A (75%)
1389	28	−1.65	0.67	2.45	G (64%) A (57%) A (71%) A (75%)
1862	14	−1.33	0.62	3.32	C (57%) G (71%) A (57%) A (64)
5-mer
469	16	−1.12	0.69	3.12	G (75%) A (50%) A (68%) A (81%) G (62%)
690	16	−2.61	0.39	3.34	C (50%) G (81%) A (50%) A (68%) A (81%)

^aSee footnotes to Table 1.

DISCUSSION

The successful prediction and design of 3D structures of large RNA molecules requires knowledge of not only the modular and hierarchical characteristics of structural motifs, but also their distribution type. Furthermore, some structural motifs that are not deemed to be important could be distributed in a very specific manner and their distributions in predicted structures might serve as a test of the reliability of a theoretical model or reveal the importance of the motif. Thus, we have developed a novel strategy for characterizing the distribution of motifs along the RNA chain. The clustering or dispersion of the same 3D motif along the RNA chain was evaluated by its deviation from a random distribution using statistical scores that account for finite size effects. Herein, the following three features were used to identify 3D motifs of interest: (i) the l-mer motif occurs >10 times along the RNA chain to allow for a statistical description of its distribution, (ii) its distribution along the RNA is significantly non-random (C < −1.5 or >5), and its distribution type (clustering or dispersion of a given motif along the RNA chain) is conserved despite changes in the similarity measures (RMSD and Cos threshold values) and (iii) the l-mer motif is conserved with increasing length of the motif. For example, the tetraloop motif, whose representative 4-mer is at position 1794, occurs 34 times along the RNA chain (Table 1). It has a significantly non-random distribution (C < −1.5), and the motifs remain dispersed along the RNA chain (C remains <−1.5) even when the Cos/RMSD threshold was changed. The tetraloop motif persists as part of the 5-mer motif whose representative is located at 2411. Although RMSD and Cos values were used in this work, other similarity measures incorporating B-factors, sequence and base pairing information could also be used to identify 3D motifs of interest satisfying the criteria defined above.

Statistical analysis of the distribution of structural motifs in the HM LSU 23 S rRNA structure shows that different motifs exhibit different sequential and spatial distributions as well as functional roles. The most common l-mer motifs (l = 3, 4 and 5) correspond to helical regions, which tend to cluster together both along the RNA chain and in the 3D structure. They display non-specific sequences and comprise a similar number of binding residues as all l-mers. In contrast, motifs such as tetraloops and the 5-mer motifs in Table 4 tend to be dispersed along the RNA chain and in the 3D structure. They as well as recurrent motifs associated with specific sequences in Table 5 contain more binding residues than all 4- or 5-mers. Thus for these motifs, their specific backbone conformations appear to be correlated with a role in binding.

Our novel strategy for characterizing the sequential and spatial distributions of motifs could detect well-known important motifs annotated in the SCOR database, validating our hypothesis that the arrangement of these motifs along the RNA chain is truly non-random. Notably, it can automatically discover key 3D motifs without prior experimental knowledge; e.g. a known tetraloop as a query structure. Hence, it can potentially discover novel 3D motifs that could be of biological interest. The sequential and spatial distributions of a motif could help to (i) verify a new example of that motif in rRNA and (ii) validate tertiary-structure predictions; e.g. if a new tetraloop were found in rRNA or if a predicted rRNA structure contains tetraloops, then the tetraloops should be dispersed sequentially (negative C-values) and spatially (d_ave > D_ave) with d_tt distances >14 Å.

One of the limitations of the present motif distribution analyses is that a relatively rare l-mer RNA fragment occurring ≤10 times along the chain was not considered for distribution analyses due to insufficient statistics for determining the motif distribution. However, some biologically important motifs that are binding sites for another RNA/proteins occur <10 times, and hence do not allow for a statistical description of their distributions. Furthermore, motifs such as kink-turns (5) occur <10 times but may play important roles in RNA structures. Hence the present approach would not work well in small RNAs such as small nuclear RNAs or group I and II introns containing relatively rare but important motifs. Another limitation of the present method is that it cannot automatically discover motifs involving two RNA strands simultaneously (two-strand motifs) such as composite kink-turns and tetraloop receptors, as the analogy between two-strand motifs and words in text is not straightforward. Furthermore, it is not clear if the geometric distribution can still be used to describe the distribution of two-strand motifs occurring randomly along the RNA chain, as in the case of one-strand motifs. These issues and improved similarity measures are subjects for further research.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Council, Taiwan (NSC 95−2113−M−001−038−MY5). Funding for open access charge: National Science Council Taiwan.

Conflict of interest statement. None declared.