Abstract
Context: Quantitative estimates of the magnitude, direction, and rate of change of health inequalities play a crucial role in creating and assessing policies aimed at eliminating the disproportionate burden of disease in disadvantaged populations. It is generally assumed that the measurement of health inequalities is a value-neutral process, providing objective data that are then interpreted using normative judgments about whether a particular distribution of health is just, fair, or socially acceptable.
Methods: We discuss five examples in which normative judgments play a role in the measurement process itself, through either the selection of one measurement strategy to the exclusion of others or the selection of the type, significance, or weight assigned to the variables being measured.
Findings: Overall, we find that many commonly used measures of inequality are value laden and that the normative judgments implicit in these measures have important consequences for interpreting and responding to health inequalities.
Conclusions: Because values implicit in the generation of health inequality measures may lead to radically different interpretations of the same underlying data, we urge researchers to explicitly consider and transparently discuss the normative judgments underlying their measures. We also urge policymakers and other consumers of health inequalities data to pay close attention to the measures on which they base their assessments of current and future health policies.
Keywords: Health inequalities, measurement, ethics, health policy
Measuring and evaluating health inequalities are often considered to be separate tasks. Broad policy frameworks, such as the U.S. Department of Health and Human Services’ Healthy People 2010 and the World Health Organization's Commission on the Social Determinants of Health's recent report, present powerful moral arguments for reducing health inequalities (U.S. Department of Health and Human Services 2000; WHO Commission on Social Determinants of Health 2008). However, they seldom specify precise numerical targets, and even when they do, they rarely identify a specific measurement strategy to determine whether progress is being made toward these goals or discuss the rationale for selecting specific measures and strategies. Conversely, scientific literature on measuring health inequalities often presents data without fully discussing the moral considerations relevant to the measurement process. It is generally assumed that the measurement of health inequalities is a value-neutral process and that the resulting data provide an objective basis for creating and assessing value-driven policies.
This assumption is flawed. Normative judgments—statements about whether inequality is right or wrong or whether one situation is better or worse than another—underlie many descriptive efforts to measure the magnitude of, and trends in, health inequalities. These judgments provide implicit justifications for choosing one measurement strategy to the exclusion of others and for selecting the type, significance, and weight assigned to the variables being measured. As a result, descriptive measures of the magnitude of health inequalities often contain implicit judgments about the moral value of those inequalities, and in some cases, these judgments may determine the presence, absence, or direction of an inequality (Harper and Lynch 2005, 2007).
In this article, we present five case studies in which normative judgment is integral to some of the most basic decisions underlying the measurement of health inequalities. We conclude with a call for greater transparency and more widespread acknowledgment of the normative justifications underlying measurement decisions.
Inequality and Normative Judgments
Inequality is conventionally thought to be a relatively straightforward concept. Many discussions of health inequalities define inequality as a simple descriptive numerical comparison, in contrast to the more complex inequity, which involves normative judgments regarding justice and fairness.1 For example, Kawachi and Kennedy begin their glossary of health inequalities by stating that “inequality and equality are dimensional concepts, simply referring to measurable quantities. Inequity and equity, on the other hand, are political concepts, expressing a moral commitment to social justice” (Kawachi and Kennedy 2002, p. 647). More generally, philosopher Iris Marion Young observes that “judgments of equality or inequality in themselves … are simply factual comparisons of amounts or degrees of some variables between or among entities. Such comparisons by themselves do not yield judgments with the moral force that claims about social, economic, or political equality usually carry” (Young 2001, p. 6).
In this conventional view, measurement—that is, determining the magnitude, direction, and rate of change of health inequalities—is a value-neutral process. Choosing the appropriate variables, metrics, and measurement strategy is a technical matter whose goal is producing accurate and unbiased data. Judgments about whether a particular distribution of health is just, fair, or socially acceptable may guide the interpretation of the data, but it is conventionally assumed that measures of inequality are essentially value free.
In contrast to this conventional account, we contend that judgments about inequity are often embedded in measures of inequality. Measurement is an inherently value-laden enterprise, and judgments about justness, fairness, and social acceptability are inextricably bound to the selection of measures and statistical strategies, and thus frequently precede determinations of the magnitude, direction, and rate of change in inequality. As Norman Daniels observed about equality of access to health care,
To arrive at a notion of equal access, we must already have made various decisions about what kinds of considerations ought to count in judging when access is equal. These decisions reflect our purpose or interest in making the judgment about equality, and some of these discriminations are themselves of a moral nature. Moral considerations … are already included in the specification of equality and are not held at bay until we get to decisions about equity. (Daniels 1982, p. 53)
The same can be said of measuring inequalities in health more generally: to arrive at a notion of health (in)equality, we must already have made normative decisions about what kinds of considerations ought to count in judging when health is (un)equal. This point is exemplified by the recent debate over whether the World Health Organization should measure health inequalities across all individuals in a population (e.g., Le Grand 1987) or between social groups. Those arguing for measuring across all individuals emphasized the value of maximizing comparability across countries (Murray, Gakidou, and Frenk 1999), whereas others argued that moral concern for social group differences in health has traditionally been the foundation of health inequalities research (Braveman, Krieger, and Lynch 2000).
Normative judgments often underlie choices about whether to use one measurement strategy rather than another, which variables to include or exclude in measurement, and how these variables should be compared and weighted. In rare cases, measures require us to explicitly state these judgments in order to assess the magnitude of inequality. More commonly, judgments about what is just, fair, or acceptable are implicitly embedded in the measures themselves.
Case Study 1: Relative and Absolute Inequality
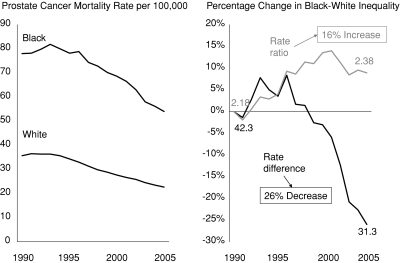
The left panel of figure 1 shows trends in age-adjusted prostate cancer mortality from 1990 to 2005 for black and white men in the United States (National Cancer Institute Surveillance Research Program 2009). This figure clearly indicates that mortality rates for both groups decreased during this period, albeit at different rates. There is also a clear and persistent racial inequality in mortality rates across the entire period. How do we determine whether the situation is better or worse in 2005 than in 1990?
Figure 1.
Trends in Prostate Cancer among Black and White Males, and Percentage Change in the Black-White Rate Ratio and Rate Difference, 1990–2005.
Note: The rate ratio is calculated as the black mortality rate divided by the white mortality rate. The rate difference is calculated as the black mortality rate minus the white mortality rate.
Source: Authors’ calculations using SEER*Stat Software (National Cancer Institute Surveillance Research Program 2009), with underlying data provided by the National Center for Health Statistics 2009a, 2009b.
The right panel plots the percentage change over time for two simple and widely used measures of inequality, the rate ratio (Rblack÷ Rwhite) and the rate difference (Rblack− Rwhite). The rate ratio indicates that black-white inequality increased by roughly 16 percent during this period (measured as the excess rate ratio [rate ratio2005− rate ratio1990]/[rate ratio1990− 1]), while the rate difference indicates that inequality decreased by 26 percent. Both measures are technically correct, but when considered in isolation, they support opposing answers to the question of whether or not black-white inequality in prostate cancer mortality is decreasing. Despite this ambiguity, studies often use only the rate ratio and conclude that inequalities in prostate cancer mortality between black and white men increased during the 1990s (Chu, Miller, and Springfield 2007; DeLancey et al. 2008).
As a number of authors have pointed out (Mechanic 2007; Scanlan 2006), in the context of improving health for two groups, the situation demonstrated in figure 1—increasing relative but decreasing absolute inequality—occurs when the rate of improvement is smaller for the group with the worst initial health. In this case, prostate cancer mortality declined by 36.4 percent for whites and 30.8 percent for blacks, which is why relative inequality increased. This has led some to argue that relative measures of inequality are more useful for tracking progress (Levine et al. 2001; Low and Low 2006; Victora et al. 2000), since in the context of improving health for all groups, reductions in relative inequality imply a faster relative rate of health improvement among disadvantaged groups (which, by definition, necessarily leads to decreases in absolute inequality as well).
While this is technically correct, is the relative rate of reduction necessarily the best metric for assessing trends in inequality? One could just as easily measure trends in prostate cancer mortality on an absolute scale, in which case blacks made more progress than whites between 1990 and 2005. The rate for blacks declined by 24 deaths/100,000 population, while the white rate declined by 13 deaths/100,000, leading to a drop in absolute inequality. In a situation like this, a constant or increasing rate ratio accompanied by a declining rate difference could be considered evidence of progress (though perhaps not ideal progress). To take an extreme example, suppose that through some intervention, the white rate fell from its 2005 value of 22.7/100,000 to 1.0, and the black rate fell from 54/100,000 to 2.2. If we looked only at ratio measures, we would likely conclude that no progress had been made toward reducing black-white inequalities, since the rate ratio increased slightly after the intervention. Yet the rate difference fell by nearly 100 percent, and the rates for both blacks and whites dropped almost to zero. It is difficult to imagine that most observers would assess this prostate cancer scenario as being worse than the situation in 1990, yet that is precisely what exclusive reliance on the ratio measure suggests.
Deciding whether to use absolute or relative measures requires us to consider whether health equality has “independent normative significance” (Temkin 2003, p. 63)—that is, whether it is a valuable goal in itself, independent of other considerations. In this example, we must consider whether a reduction in relative inequality per se is a moral good, independent of other considerations, such as overall population health and the absolute rates of disease for each group. The rate ratio measures relative inequality alone and does not contain any information about changes in overall population health or the absolute rates of disease for each group. Using the rate ratio alone thus implicitly endorses the very strict egalitarian position that what matters is equality in itself, independent of other considerations. Looking at the rate difference as well allows us to take other considerations into account; for example, the fact that whatever led to the decline in prostate cancer mortality appears to have done so in a Pareto improving fashion, benefiting both groups and harming neither (Deaton 2002).2
Now consider a situation in which overall health is not improving but worsening. The rapid increase in U.S. obesity rates in recent decades has affected virtually all demographic groups but has done so in an unequal fashion (Wang and Beydoun 2007). Zhang and Wang (2004) reported the respective prevalence of obesity among adult males with low versus high education as 13.8 percent and 8.6 percent between 1976 and 1980, and 24.1 percent and 17.1 percent between 1988 and 1994. In this case the rate difference between education groups increased from 5.2 percent to 7 percent, but the rate ratio declined from 1.60 to 1.41. If one considers the rate of change exclusively, the less educated did better, since their relative increase in obesity was 75 percent, compared with 99 percent for the more educated. Yet if one considers the absolute level of obesity, the less educated rose by 10.3 percentage points, compared with 8.5 points for the more educated. If we consider only the rate ratio—again implicitly endorsing the position that equality matters most—then we must conclude that educational inequalities in obesity are decreasing and that we are making progress toward health equality. However, if we consider the rate difference—implicitly endorsing the position that inequality matters but it is not all that matters—we would conclude that inequality is worsening in this case because the absolute increase in the rate of obesity has been greater for the disadvantaged.
The distinction between relative and absolute inequality has been frequently discussed (Mechanic 2002, 2007; Oliver, Healey, and Grand 2002), and both measures are reported more often now than in the past (e.g., Houweling et al. 2007; Mackenbach et al. 2008). Nevertheless, explicit discussions of why one measure is chosen to the exclusion of another remain rare, especially when they conflict. For example, recent reports on long-term trends in socioeconomic inequalities in mortality in the United Kingdom (Gregory 2009) and the United States (Warren and Hernandez 2007) conclude that little or no progress was made during the entire twentieth century in reducing inequalities, but neither considers absolute inequality or makes a case for why relative inequality should be of primary concern.
These examples illustrate the fact that determining whether an inequality is increasing or declining is a normative as well as a mathematical exercise. In particular, reporting only a measure of relative inequality provides an accurate but only partial assessment of the situation and implicitly endorses the egalitarian position that equality alone takes precedence over other considerations. Our point here is not that the rate ratio (or any summary measure of relative health inequality) is an inaccurate or biased measure but that using it to the exclusion of other measures may embed normative judgments in apparently objective descriptions of health trends.
Case Study 2: Who Counts?
Table 1 shows the results of measuring geographic inequalities in life expectancy across U.S. Census regions, divisions, states, and counties for two periods, 1969–1973 and 1999–2003. It uses two measures of health inequality: one (the Mean Log Deviation) that weights the contribution of each area to inequality by its population size, and one (the Index of Disparity) that does not (Keppel and Pearcy 2009; Pearcy and Keppel 2002; see the appendix for the formula). Table 1 also shows the percentage change over time in inequality for both measures. What can we conclude about geographic inequalities in mortality in the United States from this table?
TABLE 1.
Comparison of Population-Weighted and -Unweighted Measures of Geographic Inequality in Life Expectancy at Birth in the United States, 1969–1973 and 1999–2003
| Life Expectancy at Birth |
Measure of Health Inequality |
||||
|---|---|---|---|---|---|
| Geographic Unit | Units | Min. | Max. | Unweighted Index of Disparity | Weighted Mean Log Deviation |
| 1969–1973 | |||||
| Census region | 4 | 70.2 | 72.2 | 1.67 | 0.050 |
| Census division | 9 | 69.7 | 72.4 | 1.80 | 0.072 |
| State | 51 | 65.9 | 74.3 | 4.36 | 0.137 |
| Countya | 3,087 | 56.2 | 85.0 | 16.77 | 0.423 |
| 1999–2003 | |||||
| Census region | 4 | 76.2 | 78.5 | 1.61 | 0.074 |
| Census division | 9 | 74.7 | 78.7 | 2.02 | 0.097 |
| State | 51 | 73.0 | 80.7 | 4.43 | 0.150 |
| Countyb | 3,140 | 62.0 | 96.1 | 20.35 | 0.379 |
| % Change, 1969–73 to 1993–2003 | |||||
| Census region | −3.6% | +48.0% | |||
| Census division | +12.2% | +34.7% | |||
| State | +1.6% | +9.5% | |||
| County | +21.2% | −10.4% | |||
Notes: The Index of Disparity is calculated as the average deviation of each area's life expectancy from the area with the highest life expectancy, giving each area equal weight and expressed as a proportion of the life expectancy of the area with the highest life expectancy and multiplied by 100. The Mean Log Deviation weights each area by its population size and is calculated as the average difference between the logarithm of each area's life expectancy and the logarithm of the population average life expectancy (see the appendix for formulas).
One county with a life expectancy at birth of 19.8 was excluded.
Two counties with life expectancies at birth estimated as 4.0 and 102.0 were excluded.
Source: Authors’ calculations using SEER*Stat Software (National Cancer Institute Surveillance Research Program 2009), with underlying data provided by the National Center for Health Statistics 2009a, 2009b.
First, it is clear that the choice of geographic unit has a discernible impact on the magnitude and direction of changes in health inequalities. For example, the Mean Log Deviation indicates that state-level inequalities increased by 9.5 percent during this time period but that county-level inequalities decreased by 10.4 percent. Each measure accurately reflects trends in inequality, so it would be correct to conclude either that geographic inequalities in life expectancy increased or decreased during this time period. However, there is no a priori statistical reason to prefer one geographic unit over the other. We must rely on some normative criterion to determine the most appropriate geographic unit. For example, we might prefer to compare states, because many federal public health resources are distributed on a per-state basis in the United States. Alternatively, we might prefer to compare counties because they better reflect underlying racial or socioeconomic inequalities, and looking only at states may ignore disadvantaged populations within relatively “healthy” states.
Second, using weighted or unweighted measures has a significant impact on the magnitude and direction of changes in inequality. Among counties, unweighted inequality increased by 21.2 percent between 1969–1973 and 1999–2003, but weighted inequality decreased by 10.4 percent. Again, each measure accurately reflects trends in inequality, so it would be correct to conclude that geographic inequalities either increased or decreased during this time period. While both measures are accurate, choosing between them requires normative judgment.
The question of whether or not to weight by population size is complicated and politically significant, as reflected in the bicameral legislature of the U.S. Congress, which contains a Senate that weights states equally and a House of Representatives that weights individuals equally. A number of arguments can be used to justify one or another measure. For example, one might argue that geographic units such as countries, states, or counties have normative importance regardless of their size and should thus be treated with equal respect. If we have already determined that a geographic unit such as a state has moral or political significance, why should we consider a health inequality that disadvantages a relatively small state any less significant than one that disadvantages a larger one? The same logic holds for inequalities across social group categories: if we have already determined that equality between different racial groups is a priority, why should the relative size of each racial group matter? In this view, using weighted measures is counterproductive because it implicitly endorses the judgment that health inequalities are more significant when they affect a larger proportion of the population.
By contrast, one might argue that it is the health of the individuals within those geographic units that is morally significant and that it makes little sense to talk about the health of geographic units in the abstract. County-level health inequalities are unjust not because counties themselves are morally significant but because the individuals who reside in those counties are. Indeed, we weight individuals equally to calculate measures of average health, like average prevalence and mortality, so why should we weight them unequally to calculate measures of health inequality (Ravallion 2004)? Put another way, why should the roughly 20,000 individuals from Lamoille County, Vermont, each count 500 times more than each of the 10 million individuals living in Los Angeles County when measuring health inequality?
Weighted measures also account for the fact that the distribution of individuals across social or geographic groups often changes over time owing to migration or changes in social policies (Heller, McElduff, and Edwards 2002; Illsley 1999). If the relative size of a minority group triples, doesn't it make sense that their significance also should triple? If a state's population falls from 25 percent to 0.25 percent of the national population, can it still lay claim to the same relative share of health resources? By contrast, unweighted measures implicitly assume that the relative importance of a social group or geographic unit is essentially static, remaining unaffected by changes in size or composition.
Case Study 3: Weighing Lives
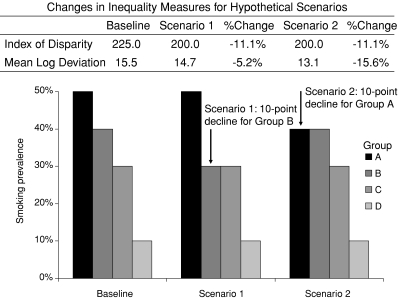
Figure 2 shows a hypothetical distribution of a health outcome (smoking prevalence) for four unordered social groups (e.g., race/ethnicity or geographic areas). To simplify this example we have fixed the population size of each group to be exactly the same, so that the problem of population weighting discussed in the previous section is irrelevant. At baseline, the respective smoking rates in groups A, B, C, and D are 50, 40, 30, and 10 percent. In scenario 1, the smoking rate in the group with the second highest baseline smoking rate (group B) declines from 40 to 30 percent, with no changes in any other group. In scenario 2, the smoking rate in the group with the highest baseline smoking rate (group A) declines from 50 to 40 percent, with no changes in any other group. It should be clear that in both cases overall inequality has declined, but by how much? Should the fact that the smoking rate has declined in group A or B have any bearing on the magnitude of the change in overall smoking inequality among these four groups?
Figure 2.
Changes in Inequality in Smoking Prevalence according to the Index of Disparity and Mean Log Deviation for Two Hypothetical Changes in the Distribution of Smoking across Social Groups.
Note: The Index of Disparity is calculated as the average deviation of each group's smoking rate from the group with the lowest rate, giving each group equal weight and expressed as a percentage of the rate in the group with the lowest rate. The Mean Log Deviation weights each group by its population size and is calculated as the average difference between the logarithm of each group's smoking rate and the logarithm of the population average rate of smoking (see the appendix for formulas).
As readers may have guessed, it depends on the measure used. Suppose we are interested in measuring only changes in relative inequality in smoking. One measure for unordered groups is the average percentage difference between each group's rate and the smoking rate in the best group (Keppel and Pearcy 2009), elsewhere called the Index of Disparity (Pearcy and Keppel 2002; see the appendix for the formula). This measure is equally sensitive to a change in smoking rates, regardless of which group improves. Figure 2 shows that when using the Index of Disparity to measure inequalities, scenarios 1 and 2 generate exactly the same change in health inequality (an 11 percent decline).
Now consider another measure of health inequality, the Mean Log Deviation. Whereas the Index of Disparity takes the absolute difference between rates, the Mean Log Deviation takes the difference between the logarithm of rates. The use of the logarithm guarantees that the contribution to the change in overall inequality of a change in health of x units will vary depending on where in the health distribution that change occurs. Figure 2 shows that when using the Mean Log Deviation to measure inequalities, the magnitude of the change in inequality is three times larger (16 percent versus 5 percent) when the group with the highest prevalence shows improvement (scenario 2) than when the group with the next-to-highest prevalence shows improvement (scenario 1).
Both the Index of Disparity and the Mean Log Deviation provide mathematically accurate measures of the change in overall inequality among these populations, but they reflect different normative judgments about what should be taken into consideration when measuring equality. The Index of Disparity is “utilitarian” in the sense that its measure of total inequality is insensitive to which part of the health distribution benefits most from changes in health inequality. Other things being equal, a five-unit change in health decreases inequality by exactly the same amount, regardless of whether that change comes from the least healthy group or another group. The Mean Log Deviation is “prioritarian” in the sense that it attaches greater value to reductions in inequality among less healthy groups. Other things being equal, a five-unit change in health affects overall inequality more if it occurs in a less healthy group.
The distinction between these two measures is important in two respects. First, care must be taken in selecting a measure that will accurately reflect one's normative judgments. If one believes that reducing overall inequality is a valuable social goal in itself and is indifferent to exactly how that reduction is achieved, then the Index of Disparity is an appropriate measure. But if one believes that, other things being equal, it is better to reduce inequality by first improving the health of the least healthy, the Index of Disparity is a poor choice of inequality measure because it is insensitive to which group's health improves.
Care must also be taken in using these measures as a basis for making policy decisions. Suppose that the two scenarios reflect the impact of different interventions. If he were unaware that this measure assigns equal priority to all groups, a prioritarian who reviews only the Index of Disparity might erroneously conclude that neither intervention is preferable, despite the fact that he would likely prefer scenario 2, since he assigns priority to a reduction in the worst-off group. Similarly, if she were unaware that this measure prioritizes reductions in groups with higher baseline smoking rates, a utilitarian who reviews only the Mean Log Deviation might erroneously conclude that the intervention in scenario 2 is “better” (i.e., reduces inequality more).
Case Study 4: Quantifying Aversion to Inequality
While the Mean Log Deviation provides a means for weighing different groups because it uses differences in the logarithm of rates, it assigns those weights in an arbitrary fashion (Cowell 2000). Other measures allow one to determine more explicitly how these weights are assigned.
One common measure of socioeconomic inequality in health is the Concentration Index (CI) (Kakwani, Wagstaff, and van Doorslaer 1997, see the appendix for the formula), which may be measured on the relative or absolute scale (the relative CI is mathematically equivalent to the more commonly used Relative Index of Inequality) (Wagstaff, Paci, and van Doorslaer 1991). The CI uses information on all socioeconomic groups; it weights by population size; and, most important, it reflects the direction of the socioeconomic gradient in health—that is, when illness increases with increasing socioeconomic disadvantage, the index is negative, and when illness decreases with increasing disadvantage, the index is positive (Wagstaff, Paci, and van Doorslaer 1991). The CI thus reflects the normative judgment that it is important to distinguish between health inequalities that systematically disadvantage already disadvantaged groups (i.e., CI is negative) and health inequalities that systematically disadvantage already advantaged groups (i.e., CI is positive).
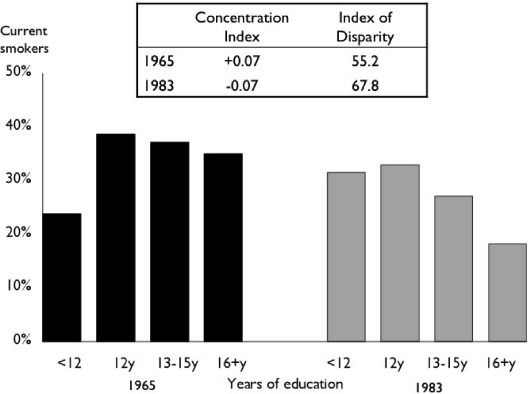
Figure 3 shows U.S. women's rates of smoking by years of completed education in 1965 and in 1983, using two measures of relative inequality. The Index of Disparity, which ignores the ranking of the social groups, registers a roughly 20 percent increase in education-related smoking inequality. The CI registers similar relative magnitudes of the gradient in both periods. But whereas in 1965 smoking was more concentrated among higher-educated women (a positive CI of 0.07), by 1983 smoking was more concentrated among lower-educated women (a negative CI of 0.07). If one is primarily concerned about the health of disadvantaged populations, the change in sign suggests that the situation in 1983 is considerably worse than in 1965, even though the magnitude of relative inequality is unchanged. One could argue, however, that systematic health inequalities that disproportionately affect any social group, regardless of whether or not they are socioeconomically advantaged, should be minimized, in which case the CI might be a less appealing measure, since it is relatively insensitive to inequalities that disproportionately affect groups in the middle of the socioeconomic distribution.
Figure 3.
Concentration Index and Index of Disparity for Education-Related Inequality in Current Smoking among U.S. Women in 1965 and 1983.
Note: The Concentration Index is calculated as two times the covariance between the smoking rate of each group and its relative rank in the cumulative distribution of the population, ranked by education, divided by the population average smoking rate. The Index of Disparity is calculated as the average deviation of each group's smoking rate from the group with the lowest rate, giving each group equal weight and expressed as a percentage of the rate in the group with the lowest rate (see the appendix for formulas).
Source: Authors’ calculations of National Health Interview Survey data (National Center for Health Statistics 2009b).
The CI places additional weight on the health of disadvantaged groups relative to advantaged groups by including an “inequality aversion” parameter that differentially weights health as a function of socioeconomic position (see the appendix for the formula). The concept of inequality aversion in the measurement of inequality has a long history in economics (Atkinson 1970; Cowell 2000; Sen and Foster 1997) but has thus far received less attention in the measurement of health inequality. For the “standard” CI, the value of the parameter (ν) is 2, which leads to respective weights of 2, 1.5, 1, 0.5, and 0 for the health of individuals at the 0th, 25th, 50th, 75th, and 100th percentile of the cumulative distribution according to socioeconomic position (Wagstaff 2002). Thus the health of the poorest person in the population is weighted by 2, and thereafter the weights decline with increasing socioeconomic rank. Since this inequality aversion parameter may be adjusted, one can specify exactly how much weight to give to each social group.
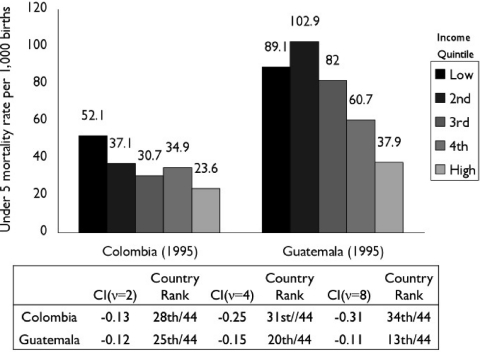
Figure 4 shows the distribution of childhood (under five) mortality in Colombia and Guatemala in 1995, as measured by the World Bank's Demographic and Health surveys (Gwatkin et al. 2007). In both countries, mortality generally declines as income increases, leading to a negative value for socioeconomic mortality inequality as measured by the CI. However, the ranking of the two countries among the forty-four participating countries differs substantially depending on how much weight is given to mortality among the poorest group. For the standard CI (ν= 2), Colombia ranks 28th and Guatemala ranks 25th; but as the weight placed on the health of the poorest group increases by increasing ν to 4 and then 8, Colombia's CI continues to increase, whereas Guatemala's remains nearly constant. The reason is that in Colombia, the lowest income quintile has a mortality rate considerably higher than the rest of the quintiles, whereas in Guatemala, the poorest group has a rate closer to the population average rate.
Figure 4.
Concentration Index with Varying Inequality Aversion Parameters (ν) for Relative Socioeconomic Inequality in Childhood (under Five) Mortality according to Household Income Quintile, Colombia and Guatemala, 1995.
Note: Country rank refers to the ranking of countries with respect to the CI, with the least negative value ranked highest. The Relative Concentration Index is calculated as two times the covariance between the mortality rate of each group and its relative rank in the cumulative distribution of the population, ranked by education and divided by the population average mortality rate (see the appendix for the formula). The parameter ν represents the weight attached to the health of the poorest group, which decreases as socioeconomic rank increases.
Source: Data from Gwatkin et al. 2007, with calculations by the authors.
Since the inequality aversion parameter can be set to different values, the CI can reflect a range of judgments about the relative value of the health of different segments of the population. However, while many studies use the CI to measure health inequalities (Harper et al. 2008, 2009; Hosseinpoor et al. 2005; Smith, Frank, and Mustard 2009; Zhang and Wang 2007), in most cases the standard CI is used without explicit discussion of how much to weigh the health of the poor. This is unfortunate because the “standard” value of ν= 2 is no less a normative judgment of the relative value of the health of the poor than any other value one might choose. Also, as in the previous case study, care must be taken when using these measures as a basis for policy decisions. A policymaker reviewing a ranking of countries’ progress toward achieving health equality may be unaware that small adjustments to the CI can have a large impact on their relative rank.
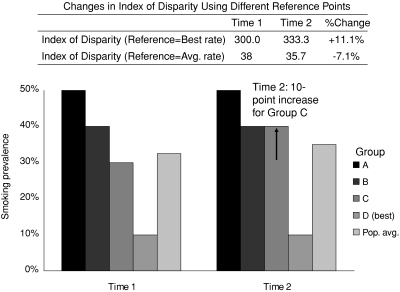
Case Study 5: Reference Points
Measuring health inequality means measuring differences in health, regardless of whether they are between individuals or between social groups. But differences from what standard? Figure 5 demonstrates how the choice of the reference point affects conclusions about changes in health inequality. Again we consider smoking prevalence among four hypothetical groups; in this case, we measure relative inequality using the Index of Disparity and two different reference points: the population average rate and the best observed rate. At time 1, the prevalences are 50, 40, 30, and 10 percent; while at time 2, group C's smoking rate has increased from 30 to 40 percent. If we use the best observed rate (group D) as the reference group, then we would conclude that inequality has increased by 11.1 percent. But if we use the population average rate as the reference, we would conclude that inequality has decreased by 7.1 percent, since groups A and B are now closer to the population average rate.
Figure 5.
Effect of Changing the Reference Point for the Index of Disparity When Calculating Relative Inequality in Smoking across Four Hypothetical Groups.
Note: The Index of Disparity is calculated as the average deviation of each group's smoking rate from the rate in the reference group, giving each group equal weight and expressed as a percentage of the rate in the reference group. In the first case the reference group is the group with the lowest rate of smoking, and in the second case it is the population average smoking rate.
As in the other case studies, both reference groups produce a mathematically correct result, but they imply different normative positions (Ruger 2006). Choosing to measure inequality as the difference from the best observed rate implies that we care about health inequality, but inequality is not all that matters. More specifically, it implies an unwillingness to tolerate reductions in inequality that may come from worsening health among those who are healthier to begin with. It also implies a preference for reducing inequality by raising the level of health among less healthy groups. Except in the case when the rate in the healthiest group worsens, the only way for inequality to decrease using the best group rate as the reference point is if the other groups’ health improves.
By contrast, measuring inequality as the difference from the population average implicitly values equality most highly and indicates a willingness to accept reductions of inequality achieved by worsening health for some groups. Ironically, this normative criterion may simply be a by-product of the fact that many standard statistical measures of inequality are derived from economics, which generally use the population average income as the reference point. Since income is a transferable good, it is plausible that policies for reducing inequality might consider redistributing wealth from rich to poor. Yet health status is a nontransferable good, so the same redistributive logic cannot apply. Moreover, even if it were transferable, it is unlikely that anyone but the strictest egalitarian would be willing to accept worsening health among the healthy in order to reduce health inequality.
One might also consider other reference points. For example, when measuring health across a social group category, one might choose to use the health of the most socially advantaged group (e.g., highest socioeconomic position) rather than best health as the reference point, which would imply a greater sensitivity to social group equality than to health outcomes per se. Or one might measure inequality as differences between each group and a fixed, desirable level (e.g., maximum health). This idea has much in common with the concept of “shortfall” equality in welfare economics (Sen 1981, 1992), although only a few measures of shortfall inequality currently exist (Erreygers 2009). Regardless, as with previous examples, producers and consumers of health inequality data should be cognizant of the normative judgments implicit in the choice of reference points.
Conclusion
The challenges outlined here are by no means an exhaustive list of the value judgments implicit in measuring health inequalities. Normative considerations also arise when determining the causes of health inequalities and when deciding among possible intervention strategies to reduce inequalities. Moreover, many of the challenges outlined here are not confined to the study of health inequality but apply to the study of inequality more generally. The same normative issues that shape judgments about levels and trends in health inequality apply to inequality in the distribution of other factors, such as income or residential location. For example, assessing the levels and trends in global economic inequality depends on whether or not countries are weighted by population size, by whether one considers inequality on an absolute or relative scale, and by the amount of weight placed on different parts of the income distribution (Firebaugh 2003; Milanovic 2005; Ravallion 2004).
Because inequality is a complex, multidimensional concept (Sen and Foster 1997; Temkin 1993), we do not believe that there is a single, one-size-fits-all strategy for determining how best to measure and interpret health inequalities. Nor do we have a strong preference for any particular measure or suite of measures. We do believe that the producers and consumers of health inequality data must pay more attention to the normative choices inherent in measurement, and we make the following three recommendations for future work.
First, researchers should recognize that relying exclusively on a single measure of health inequality may implicitly endorse normative judgments and that this endorsement is an unavoidable by-product of the structure of those measures. As our case studies demonstrate, choosing one or another statistical measure does not necessarily reflect bias or sloppy analysis because any of the measures can be adequately defended on technical grounds. Nevertheless, choosing one or another measure to the exclusion of others may introduce normative criteria regarding the relative importance of inequality per se, whether individuals or groups count more, which groups (if any) should be prioritized and by how much, and what the appropriate target of inequality reduction should be. We thus urge researchers to avoid uncritically using a single measure (such as a rate ratio) simply because it is widely accepted practice to do so, and to consider the implicit normative judgments embedded in many measures of inequality.
Second, we urge researchers to strive for transparency in identifying the moral significance of the measures that they use. Whenever possible, researchers should clearly describe the normative judgments underlying seemingly straightforward measurement decisions, including the selection of one measurement strategy to the exclusion of others, or the selection of the type, significance, and weight assigned to the variables being measured. We believe that doing so will have several positive effects: it will improve the quality and consistency of reporting on health inequalities; it will make analyses of health inequalities more useful for guiding future health interventions and policy changes; and it will forestall criticisms of the selective reporting of statistics on health inequalities.
Finally, we urge policymakers and other consumers of health inequalities data to pay close attention to the measures on which they base their evaluations of current and future health policies for remedying health inequalities. Wherever possible, these evaluations should be based on a full consideration of the broadest range of measures possible. Although the measures may not be “biased” in the conventional sense of the term, using one exclusively or uncritically may bias a decision because of the implicit normative judgments contained in the measure itself.
Acknowledgments
S. Harper and N. King are the primary authors, contributed equally to this work, and drafted and revised the manuscript. S. Harper, N. King, and J. Lynch conceptualized and designed the study and interpreted the data. S. Harper analyzed the data. S.C. Meersman, M.E. Reichman, N. Breen, and J. Lynch assisted in revising the manuscript. All authors approved the final version.
The authors thank the editor, three anonymous reviewers, Barry Miller, and Sue Krebs-Smith for providing valuable feedback on a draft of the manuscript. This project was carried out under contract with the National Cancer Institute (contract 263-MQ-611198). N. King received funding from the Robert Wood Johnson Health and Society Scholars program. The content of this publication does not necessarily reflect the views or policies of the National Cancer Institute.
Appendix
Formulas for Selected Measures of Health Inequality
Index of Disparity
The formula for the Index of Disparity is (Pearcy and Keppel 2002)
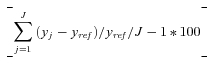 |
where y is health, j indexes each of the J social groups, and yref is the group with the best rate of health (i.e., the lowest smoking rate). If the population average rate is used as the reference group, then one takes the absolute value of the difference between each group's rate and the reference population and divides by J instead of J– 1 groups.
Mean Log Deviation
The Mean Log Deviation may be written as (Firebaugh 1999)
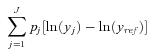 |
where pj is the population share in group j, y is health, and yref is average rate of health in the population.
Concentration Index (CI)
The general formula for the relative CI for grouped data is given by Kakwani and colleagues (Kakwani, Wagstaff, and van Doorslaer 1997) as
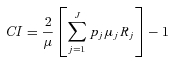 |
where pj is the group's population share, μj is the group's mean health, and Rj is the relative rank of the jth socioeconomic group, which is defined as
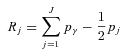 |
where pγ is the cumulative share of the population up to and including group j, and pj is the share of the population in group j. Rj essentially indicates the cumulative share of the population up to the midpoint of each group interval.
Extended Concentration Index (CI)
Wagstaff (2002) shows that the extended CI (with the inequality aversion parameter) for individuals may be written as
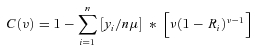 |
where yi represents the health of individual i, μ is mean health, Ri represents an individual's fractional rank in the cumulative socioeconomic distribution of the population (defined earlier), and ν is the aversion parameter. The CI can therefore be thought of as a weighted average of each individual's health share (yi/nμ), with the weights equal to ν(1 –Ri)ν−1 (see Wagstaff 2002 for derivation for grouped data).
Endnotes
In this article, we limit ourselves to the terms inequality and inequity and do not use the term disparity except when discussing the Index of Disparity. There is some disagreement over whether “disparity” is synonymous with inequality or with inequity, although in the United States it is commonly understood to refer to the latter (Thomson et al. 2006, pp. 24–25).
Similar concerns with relying solely on measures of relative effect have recently led to a greater emphasis on measures of absolute risk in the context of observational epidemiology (Lynch et al. 2006; Poole 2007) and clinical trials (Cook and Sackett 1995; Schwartz et al. 2006).
References
- Atkinson AB. On the Measurement of Inequality. Journal of Economic Theory. 1970;2:244–63. [Google Scholar]
- Braveman P, Krieger N, Lynch J. Health Inequalities and Social Inequalities in Health. Bulletin of the World Health Organization. 2000;78:232–34. [PMC free article] [PubMed] [Google Scholar]
- Chu KC, Miller BA, Springfield SA. Measures of Racial/Ethnic Health Disparities in Cancer Mortality Rates and the Influence of Socioeconomic Status. Journal of the National Medical Institute. 2007;99:1092–104. [PMC free article] [PubMed] [Google Scholar]
- Cook RJ, Sackett DL. The Number Needed to Treat: A Clinically Useful Measure of Treatment Effect. British Medical Journal. 1995;310:452–54. doi: 10.1136/bmj.310.6977.452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowell FA. Measurement of Inequality. In: Atkinson AB, Bourguignon F, editors. Handbook of Income Distribution. Amsterdam: Elsevier; 2000. pp. 87–166. [Google Scholar]
- Daniels N. Equity of Access to Health Care: Some Conceptual and Ethical Issues. The Milbank Quarterly. 1982;60:51–81. [PubMed] [Google Scholar]
- Deaton A. Policy Implications of the Gradient of Health and Wealth. Health Affairs. 2002;21:13–30. doi: 10.1377/hlthaff.21.2.13. [DOI] [PubMed] [Google Scholar]
- DeLancey JO, Thun MJ, Jemal A, Ward EM. Recent Trends in Black-White Disparities in Cancer Mortality. Cancer Epidemiology Biomarkers Prevention. 2008;17:2908–12. doi: 10.1158/1055-9965.EPI-08-0131. [DOI] [PubMed] [Google Scholar]
- Erreygers G. Can a Single Indicator Measure Both Attainment and Shortfall Inequality? Journal of Health Economics. 2009;28:885–93. doi: 10.1016/j.jhealeco.2009.03.005. [DOI] [PubMed] [Google Scholar]
- Firebaugh G. Empirics of World Income Inequality. American Journal of Sociology. 1999;104:1597–630. [Google Scholar]
- Firebaugh G. The New Geography of Global Income Inequality. Cambridge, MA: Harvard University Press; 2003. [Google Scholar]
- Gregory IN. Comparisons between Geographies of Mortality and Deprivation from the 1900s and 2001: Spatial Analysis of Census and Mortality Statistics. British Medical Journal. 2009;339:b3454. doi: 10.1136/bmj.b3454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gwatkin DR, Rutstein S, Johnson K, Suliman E, Wagstaff A, Amouzou A. Socio-economic Differences in Health, Nutrition, and Population within Developing Countries: An Overview. Washington, DC: World Bank, Health, Nutrition, and Population and Human Development Network; 2007. [PubMed] [Google Scholar]
- Harper S, Lynch J. Methods for Measuring Cancer Disparities: A Review Using Data Relevant to Healthy People 2010 Cancer-Related Objectives. Washington, DC: National Cancer Institute; 2005. [Google Scholar]
- Harper S, Lynch J. Selected Comparisons of Measures of Health Disparities Using Databases Containing Data Relevant to Healthy People 2010 Cancer-Related Objectives. Washington, DC: National Cancer Institute; 2007. [Google Scholar]
- Harper S, Lynch J, Meersman SC, Breen N, Davis WW, Reichman ME. An Overview of Methods for Monitoring Social Disparities in Cancer with an Example Using Trends in Lung Cancer Incidence by Area-Socioeconomic Position and Race-Ethnicity, 1992–2004. American Journal of Epidemiology. 2008;167:889–99. doi: 10.1093/aje/kwn016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper S, Lynch J, Meersman SC, Breen N, Davis WW, Reichman ME. Trends in Area-Socioeconomic and Race-Ethnic Disparities in Breast Cancer Incidence, Stage at Diagnosis, Screening, Mortality, and Survival among Women Ages 50 Years and Over (1987–2005) Cancer Epidemiology Biomarkers Prevention. 2009;18:121–31. doi: 10.1158/1055-9965.EPI-08-0679. [DOI] [PubMed] [Google Scholar]
- Heller RF, McElduff P, Edwards R. Impact of Upward Social Mobility on Population Mortality: Analysis with Routine Data. British Medical Journal. 2002;325:134–36. doi: 10.1136/bmj.325.7356.134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosseinpoor AR, Mohammad K, Majdzadeh R, Naghavi M, Abolhassani F, Sousa A, Speybroeck N, Jamshidi HR, Vega J. Socioeconomic Inequality in Infant Mortality in Iran and across Its Provinces. Bulletin of the World Health Organization. 2005;83:837–44. [PMC free article] [PubMed] [Google Scholar]
- Houweling TA, Kunst AE, Huisman M, Mackenbach JP. Using Relative and Absolute Measures for Monitoring Health Inequalities: Experiences from Cross-National Analyses on Maternal and Child Health. International Journal for Equity in Health. 2007;6:15. doi: 10.1186/1475-9276-6-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Illsley R. Reducing Health Inequalities: Britain's Latest Attempt. Health Affairs. 1999;18:45–46. doi: 10.1377/hlthaff.18.3.45. [DOI] [PubMed] [Google Scholar]
- Kakwani N, Wagstaff A, van Doorslaer E. Socioeconomic Inequalities in Health: Measurement, Computation, and Statistical Inference. Journal of Econometrics. 1997;77:87–103. [Google Scholar]
- Kawachi I, Kennedy BP. Health of Nations. Why Inequality Is Harmful to Your Health. New York: New Press; 2002. [Google Scholar]
- Keppel KG, Pearcy JN. Healthy People 2010: Measuring Disparities in Health. Chance. 2009;22:6–9. [Google Scholar]
- Le Grand J. Inequalities in Health: Some International Comparisons. European Economic Review. 1987;31:182–91. [Google Scholar]
- Levine RS, Foster JE, Fullilove RE, Fullilove MT, Briggs NC, Hull PC, Husaini BA, Hennekens CH. Black-White Inequalities in Mortality and Life Expectancy, 1933–1999: Implications for Healthy People 2010. Public Health Reports. 2001;116:474–83. doi: 10.1093/phr/116.5.474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Low A, A Low. Importance of Relative Measures in Policy on Health Inequalities. British Medical Journal. 2006;332:967–69. doi: 10.1136/bmj.332.7547.967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch J, Smith G Davey, Harper S, Bainbridge K. Explaining the Social Gradient in Coronary Heart Disease: Comparing Relative and Absolute Risk Approaches. Journal of Epidemiology and Community Health. 2006;60:436–41. doi: 10.1136/jech.2005.041350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackenbach JP, Stirbu I, Roskam AJ, Schaap MM, Menvielle G, Leinsalu M, Kunst AE, the European Union Working Group on Socioeconomic Inequalities Socioeconomic Inequalities in Health in 22 European Countries. New England Journal of Medicine. 2008;358:2468–81. doi: 10.1056/NEJMsa0707519. [DOI] [PubMed] [Google Scholar]
- Mechanic D. Disadvantage, Inequality, and Social Policy. Health Affairs. 2002;21:48–59. doi: 10.1377/hlthaff.21.2.48. [DOI] [PubMed] [Google Scholar]
- Mechanic D. Population Health: Challenges for Science and Society. The Milbank Quarterly. 2007;85:533–59. doi: 10.1111/j.1468-0009.2007.00498.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milanovic B. Worlds Apart: Measuring International and Global Inequality. Princeton, NJ: Princeton University Press; 2005. [Google Scholar]
- Murray CJL, Gakidou EE, Frenk J. Health Inequalities and Social Group Differences: What Should We Measure? Bulletin of the World Health Organization. 1999;77:537–43. [PMC free article] [PubMed] [Google Scholar]
- National Cancer Institute Surveillance Research Program. SEER*Stat Software. 6.5.2 ed. Bethesda, MD: National Cancer Institute. 2009. Available at http://www.seer.cancer.gov/seerstat accessed December 17, 2009.
- National Center for Health Statistics. Mortality Data. 2009a. Available at http://www.cdc.gov/nchs/deaths.htm accessed January 5, 2010.
- National Center for Health Statistics. National Health Interview Survey. 2009b. Available at http://www.cdc.gov/nchs/nhis.htm accessed January 5, 2010. [Google Scholar]
- Oliver A, Healey A, Grand JL. Addressing Health Inequalities. The Lancet. 2002;360:565–67. doi: 10.1016/s0140-6736(02)09713-1. [DOI] [PubMed] [Google Scholar]
- Pearcy JN, Keppel KG. A Summary Measure of Health Disparity. Public Health Reports. 2002;117:273–80. doi: 10.1016/S0033-3549(04)50161-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poole C. Coffee and Myocardial Infarction. Epidemiology. 2007;18:518–19. doi: 10.1097/EDE.0b013e31806466e5. [DOI] [PubMed] [Google Scholar]
- Ravallion M. Competing Concepts of Inequality in the Globalization Debate. Brookings Trade Forum. 2004:1–38.. [Google Scholar]
- Ruger JP. Measuring Disparities in Health Care. British Medical Journal. 2006;333:274. doi: 10.1136/bmj.333.7562.274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scanlan JP. Can We Actually Measure Health Disparities? Chance. 2006;19:47–51. [Google Scholar]
- Schwartz LM, Woloshin S, Dvorin EL, Welch HG. Ratio Measures in Leading Medical Journals: Structured Review of Accessibility of Underlying Absolute Risks. BMJ. 2006;333:1248–50. doi: 10.1136/bmj.38985.564317.7C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen A. Public Action and the Quality of Life in Developing Countries. Oxford Bulletin of Economics and Statistics. 1981;43:287–319. doi: 10.1111/j.1468-0084.1981.mp43004001.x. [DOI] [PubMed] [Google Scholar]
- Sen AK. Inequality Reexamined. Cambridge, MA: Harvard University Press; 1992. [Google Scholar]
- Sen AK, Foster JE. On Economic Inequality. Oxford: Clarendon Press; 1997. [Google Scholar]
- Smith P, Frank J, Mustard C. Trends in Educational Inequalities in Smoking and Physical Activity in Canada: 1974–2005. Journal of Epidemiology and Community Health. 2009;63:317–23. doi: 10.1136/jech.2008.078204. [DOI] [PubMed] [Google Scholar]
- Temkin LS. Inequality. New York: Oxford University Press; 1993. [Google Scholar]
- Temkin LS. Equality, Priority or What? Economics and Philosophy. 2003;19:61–87. [Google Scholar]
- Thomson GE, Mitchell F, Williams M, National Research Council . Examining the Health Disparities Research Plan of the National Institutes of Health: Unfinished Business. Washington, DC: National Academy Press; 2006. [PubMed] [Google Scholar]
- U.S. Department of Health and Human Services. Healthy People 2010: Understanding and Improving Health. Washington, DC: 2000. [Google Scholar]
- Victora CG, Vaughan JP, Barros FC, Silva AC, Tomasi E. Explaining Trends in Inequities: Evidence from Brazilian Child Health Studies. The Lancet. 2000;356:1093–98. doi: 10.1016/S0140-6736(00)02741-0. [DOI] [PubMed] [Google Scholar]
- Wagstaff A. Inequality Aversion, Health Inequalities and Health Achievement. Journal of Health Economics. 2002;21:627–41. doi: 10.1016/s0167-6296(02)00006-1. [DOI] [PubMed] [Google Scholar]
- Wagstaff A, Paci P, van Doorslaer E. On the Measurement of Inequalities in Health. Social Science and Medicine. 1991;33:545–57. doi: 10.1016/0277-9536(91)90212-u. [DOI] [PubMed] [Google Scholar]
- Wang Y, Beydoun MA. The Obesity Epidemic in the United States—Gender, Age, Socioeconomic, Racial/Ethnic, and Geographic Characteristics: A Systematic Review and Meta-Regression Analysis. Epidemiologic Reviews. 2007;29:6–28. doi: 10.1093/epirev/mxm007. [DOI] [PubMed] [Google Scholar]
- Warren JR, Hernandez EM. Did Socioeconomic Inequalities in Morbidity and Mortality Change in the United States over the Course of the Twentieth Century? Journal of Health and Social Behavior. 2007;48:335–51. doi: 10.1177/002214650704800401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO Commission on Social Determinants of Health. Closing the Gap in a Generation: Health Equity through Action on the Social Determinants of Health. Final Report of the Commission on the Social Determinants of Health. Geneva: World Health Organization, Commission on Social Determinants of Health; 2008. [Google Scholar]
- Young IM. Equality of Whom? Social Groups and Judgments of Injustice. Journal of Political Philosophy. 2001;9:1–18. [Google Scholar]
- Zhang Q, Wang YF. Trends in the Association between Obesity and Socioeconomic Status in U.S. Adults: 1971 to 2000. Obesity Research. 2004;12:1622–32. doi: 10.1038/oby.2004.202. [DOI] [PubMed] [Google Scholar]
- Zhang Q, Wang YF. Using Concentration Index to Study Changes in Socio-economic Inequality of Overweight among US Adolescents between 1971 and 2002. International Journal of Epidemiology. 2007;36:916–25. doi: 10.1093/ije/dym064. [DOI] [PubMed] [Google Scholar]