Reconciling Coherent Oscillation with Modulationof Irregular Spiking Activity in Selective Attention:Gamma-Range Synchronization between Sensoryand Executive Cortical Areas

Abstract

In this computational work, we investigated gamma-band synchronization across cortical circuits associated with selective attention. The model explicitly instantiates a reciprocally connected loop of spiking neurons between a sensory-type (area MT) and an executive-type (prefrontal/parietal) cortical circuit (the source area for top-down attentional signaling). Moreover, unlike models in which neurons behave as clock-like oscillators, in our model single-cell firing is highly irregular (close to Poisson), while local field potential exhibits a population rhythm. In this “sparsely synchronized oscillation” regime, the model reproduces and clarifies multiple observations from behaving animals. Top-down attentional inputs have a profound effect on network oscillatory dynamics while only modestly affecting single-neuron spiking statistics. In addition, attentional synchrony modulations are highly selective: interareal neuronal coherence occurs only when there is a close match between the preferred feature of neurons, the attended feature, and the presented stimulus, a prediction that is experimentally testable. When interareal coherence was abolished, attention-induced gain modulations of sensory neurons were slightly reduced. Therefore, our model reconciles the rate and synchronization effects, and suggests that interareal coherence contributes to large-scale neuronal computation in the brain through modest enhancement of rate modulations as well as a pronounced attention-specific enhancement of neural synchrony.

Introduction

During covert selective attention to locations or features of the visual scene, visual cortical neurons are modulated selectively in both their firing rate (Desimone and Duncan, 1995; Reynolds and Chelazzi, 2004) and their gamma-range synchronization (Fries et al., 2001, 2008b; Womelsdorf et al., 2006; Gregoriou et al., 2009). Several studies suggest that gamma-range synchronization facilitates attentional processing (Salinas and Sejnowski, 2001; Womelsdorf and Fries, 2007; Tiesinga et al., 2008). However, single-neuron studies indicate that spatial attention only reduces modestly the high irregularity of neuronal spiking (McAdams and Maunsell, 1999a; Mitchell et al., 2007), contrary to what would be expected from a robust enhancement of oscillatory firing. These contrasting temporal aspects of attentional modulation must be reconciled to specify the dynamics of cortical network activity, and its sensitivity to synchronization for attentional processing.

The fact that attentional enhancement of network oscillations does not impact greatly on single-neuron irregularity may constrain models that evaluate the functional role of neural synchronization in selective attention. Typically, strong synchrony-based attentional effects require that neurons enter an oscillator regime during behaviorally relevant contexts (Börgers et al., 2005, 2008; Tiesinga, 2005; Mishra et al., 2006; Buehlmann and Deco, 2008; Buia and Tiesinga, 2008; Zeitler et al., 2008; Masuda, 2009). It remains to be analyzed how attentional synchronization affects information processing in networks that consistently reside in oscillatory regimes with highly irregular neural spiking (Brunel and Hakim, 1999; Brunel and Wang, 2003; Geisler et al., 2005; Brunel and Hansel, 2006).

Attention modulates associative visual cortex responses presumably through top-down inputs from the frontoparietal network (Colby and Goldberg, 1999; Corbetta and Shulman, 2002; Bressler et al., 2008). Indeed, attention enhances coherence between signals recorded simultaneously from visual and frontoparietal areas (Saalmann et al., 2007; Gregoriou et al., 2009). It has been hypothesized that the source area of the top-down attentional signal is a working memory circuit of the parietal or prefrontal cortex (Desimone and Duncan, 1995; Corbetta and Shulman, 2002). Neurons in such circuits present sustained selective firing (Gnadt and Andersen, 1988; Quintana et al., 1988; Funahashi et al., 1989), possibly oscillatory (Pesaran et al., 2002; Compte et al., 2003; Joelving et al., 2007), during the delay period between sensory cue extinction and motor response, and provide input to neurons in associative sensory circuits (Moore and Armstrong, 2003). Thus, working memory circuits can maintain an internal copy of the attentional set, and modulate both firing rates and oscillations in upstream visual areas, as suggested experimentally (Gregoriou et al., 2009).

Here, we reconcile the dichotomy between modulations of local field potential synchrony and Poisson-like firing in attention using a network of two interacting cortical microcircuits in visual and working memory areas (Ardid et al., 2007). Using a manipulation that specifically abolishes interareal coherence, we assess the impact of synchronized sensory and executive circuits on the attentional modulations of sensory firing rates (McAdams and Maunsell, 1999b; Reynolds et al., 1999; Treue and Martínez Trujillo, 1999; Martinez-Trujillo and Treue, 2004). We find that, in a regime of irregular single-neuron spiking, interareal synchrony has a profound impact in gamma-range coherence across circuits, but only a limited effect on the firing rate of neurons in the sensory circuit.

Materials and Methods

The model network.

Each of the two network modules represents a local circuit of the cortex. The sensory network represents a local circuit of the visual middle-temporal area (MT). We refer to the working memory module as a local circuit of the prefrontal cortex (PFC) for the sake of simplicity, although working memory and selective attention are likely to be subserved by both prefrontal and parietal cortices (Colby and Goldberg, 1999; Corbetta and Shulman, 2002; Corbetta et al., 2008). The MT and PFC circuits had exactly the same wiring structure; they only differed in the strength of the synaptic connectivity within each module. A detailed account of the local circuit model can also be found in (Compte et al., 2000). For each circuit, pyramidal cells (N_E = 1024) and interneurons (N_I = 256) were spatially distributed on a ring simulating the cortical columnar organization, labeled by their preferred direction of motion (θ_N, from 0 to 360°). Their axonal collaterals differentially targeted neighboring (isodirectional) and distant (cross-directional) neurons. This was implemented by taking the synaptic conductance between neuron i and neuron j to be g_syn,ij = W(θ_i − θ_j)G_syn, where W(θ_i − θ_j) was either a constant for unstructured connections [W(θ_i − θ_j) = 1] or the sum of a constant term plus a Gaussian: W(θ_i − θ_j) = J⁻ + (J⁺ − J⁻)exp(−(θ_i − θ_j)²/2σ²). This last expression depends on two parameters, J⁺ and σ, while J⁻ is determined from a normalization condition (Compte et al., 2000). In both networks, only the excitatory-to-excitatory connectivity was structured with σ_EE = 14.4° and J_EE⁺ = 1.62 (Compte et al., 2000). The excitatory-to-inhibitory, inhibitory-to-excitatory, and inhibitory-to-inhibitory connections were unstructured, i.e., the cross-directional and isodirectional components of feedback inhibitory connections were equally strong. This simplification was introduced to constrain the number of free parameters and because inhibitory tuning can easily be obtained by additionally tuning excitatory-to-inhibitory connections without affecting much the rest of network operation (Compte et al., 2000). Following the notations by Compte et al. (2000), the parameters defining the strengths of local connections in the two networks were as follows: in PFC: G_EE,AMPA = 0.459 nS, G_EE,NMDA = 0.557 nS (pyramid to pyramid); G_EI,AMPA = 0.352 nS, G_EI,NMDA = 0.430 nS (pyramid to interneuron); G_IE = 3.20 nS (interneuron to pyramid); G_II = 2.50 nS (interneuron to interneuron); in MT: G_EE,AMPA = 0.801 nS, G_EE,NMDA = 1.10 nS (pyramid to pyramid); G_EI,AMPA = 0.684 nS, G_EI,NMDA = 2.00 nS (pyramid to interneuron); G_IE = 7.34 nS (interneuron to pyramid); G_II = 7.34 nS (interneuron to interneuron). Thus, although recurrent synaptic conductances were very strong in both modules, recurrent inputs in MT were at least three times stronger than in PFC. On the other hand, both networks operated in an inhibition-dominated regime (Compte et al., 2000): recurrent excitatory and inhibitory inputs into excitatory neurons during stimulus response averaged 4.8467 nA and 9.4006 nA in area MT, respectively, and 1.4094 nA and 1.5515 nA in area PFC, respectively. This corresponds to an inhibition-to-excitation ratio of 1.94 in MT and 1.10 in PFC.

Both pyramidal cells and interneurons were modeled as leaky integrate-and-fire neurons, with the same parameters as for neurons in the network model of Compte et al. (2000). Specifically, each type of cell was characterized by six intrinsic parameters: the total capacitance C_m, the total leak conductance g_L, the leak reversal potential E_L, the threshold potential V_th, the reset potential V_res, and the refractory time τ_ref. The values used were C_m = 0.5 nF, g_L = 25 nS, E_L = −70 mV, V_th = −50 mV, V_res = −60 mV, and τ_ref = 2 ms for pyramidal cells; and C_m = 0.2 nF, g_L = 20 nS, E_L = −70 mV, V_th = −50 mV, V_res = −60 mV, and τ_ref = 1 ms for interneurons. All cells received random background excitatory inputs. This unspecific external input was modeled as uncorrelated Poisson spike trains to each neuron at a rate of v_ext = 1800 Hz per cell (or equivalently, 1000 presynaptic Poisson spike trains at 1.8 Hz), except for excitatory cells in PFC where v_ext = 2010 Hz. This input was exclusively mediated by AMPARs, with the maximum conductances g_ext,E = 2.8 nS on pyramidal cells and g_ext,I = 2.38 nS on interneurons, in PFC; and g_ext,E = 17 nS and g_ext,I = 9.2 nS in MT. High external conductances in MT produced the high-variance strong external input that allowed high firing rates (>60 Hz) with irregular spiking statistics (CV ≈ 1) in our integrate-and-fire neurons.

Neurons received their recurrent excitatory inputs through AMPAR- and NMDAR-mediated transmission and their inhibitory inputs through GABA_ARs. These conductance-based synaptic responses were calibrated by the experimentally measured dynamics of synaptic currents. Thus, postsynaptic currents were modeled according to I_syn = g_syns(V − V_syn), where g_syn is a synaptic conductance, s a synaptic gating variable, and V_syn the synaptic reversal potential (V_syn = 0 for excitatory synapses, V_syn = −70 mV for inhibitory synapses). AMPAR and GABA_AR synaptic gating variables were modeled as an instantaneous jump of magnitude 1 when a spike occurred in the presynaptic neuron followed by an exponential decay with time constant 2 ms for AMPA and 10 ms for GABA_A. The NMDA conductance was voltage dependent, with g_syn multiplied by 1/(1 + [Mg²⁺]exp(−0.062V_m)/3.57), [Mg²⁺] = 1.0 mm. The channel kinetics was modeled by the following equations:

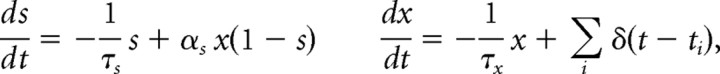where s is the gating variable, x is a synaptic variable proportional to the neurotransmitter concentration in the synapse, t_i are the presynaptic spike times, τ_s = 100 ms is the decay time of NMDA currents, τ_x = 2 ms controls the rise time of NMDAR channels, and α_s = 0.5 kHz controls the saturation properties of NMDAR channels at high presynaptic firing frequencies. Parameters for synaptic transmission were taken from Compte et al. (2000).

The MT and PFC network modules were interconnected through bottom-up and top-down AMPAR-mediated connections (see scheme in Fig. 1B). Both bottom-up and top-down connectivities were topographic, so that for both the bottom-up and top-down pathways, neurons sharing the same preference were more strongly coupled than neurons with disparate preferences. This connectivity was described by a Gaussian function: g_syn = G_synexp(−(θ_i − θ_j)²/2σ²)/σ$\sqrt{2\pi }$. We used for the bottom-up connection onto PFC pyramids G_EE^MT→PFC = 0.005 nS and σ = 36°, for the bottom-up connection onto PFC interneurons G_EI^MT→PFC = 0, for the top-down connection onto MT pyramids G_EE^PFC→MT = 0.146 nS and σ = 72°, and for the top-down connection onto MT interneurons G_EI^PFC→MT = 0.098 nS and σ = 72°. The less specific connectivity in the top-down direction is supported by recent evidence in area MT, showing that the directionality index for responses to behaviorally relevant stimuli located far from the receptive field, and presumably reflecting top-down input, was approximately half that of responses to stimuli in the receptive field (Zaksas and Pasternak, 2005). The divergence of bottom-up projections to PFC was chosen equal to bottom-up inputs from V1, which were in turn determined by fitting typical tuning curve widths for motion direction in area MT (see below).

Figure 1.

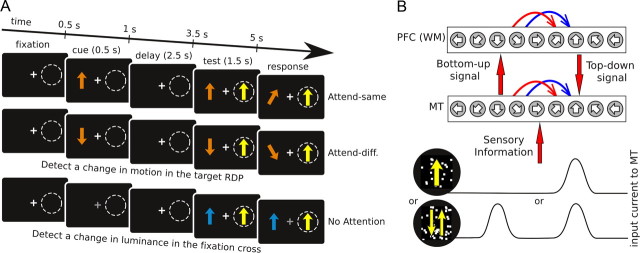
Schematic description of simulated task and model architecture. A, The simulated task consisted of various task epochs (columns) and trial types (rows). In attention trials (top two rows) a cue stimulus is presented, indicating the motion direction of the stimulus to be attended. After a delay period without any motion stimulation, the target and test stimuli appear on the screen outside and inside the receptive field, respectively. The direction of motion of the test stimulus can match the attended target direction (top row) or not (middle row). B, Scheme of the model architecture (red is excitation, blue is inhibition). Each of the two circuits includes excitatory pyramidal cells and inhibitory interneurons (not shown in scheme). The MT circuit contains neurons selective for the same receptive field and are differentially selective to motion direction. Neurons in the PFC circuit are also selective to motion direction but not to spatial location. Local connections within each circuit and cross-areal connections between excitatory cells depend on their respective preferred stimulus features (motion stimulus direction). Top-down projection from the working memory (WM) circuit targets both excitatory and inhibitory cells in the sensory circuit. Two kinds of random-dot motion stimuli are considered (yellow arrows signal motion directions): single (top input current) and transparent (bottom input current) motion.

The integration method used was a second-order Runge–Kutta algorithm with a time step of Δt = 0.02 ms. We confirmed that using Δt = 0.002 ms did not alter the dynamics of our control network. The custom code for the simulations was written in C++.

Monosynaptic latencies.

Our code implementation considers the possibility of introducing independent latencies for each synapse in recurrent connections and also between the two networks. The values for these latencies come from two terms, an identical constant term for all the connections from a specific neuron of the same kind (recurrent vs loop connection) plus a variable term, selected at random from an exponential distribution given its SD. We have tried other types of random distributions (Gaussian truncated by discarding negative latencies; gamma; and uniform distributions) without showing significant quantitative differences in the results. We used this technique because it allowed us to study two different issues using monosynaptic latencies. On the one hand, we could increase drastically the monosynaptic latency variability (SD 100 ms) so as to break completely the synchrony between the two networks (see Fig. 6). By doing that, we do not pretend to consider a plausible physiological scenario, but to quantitatively analyze the role of oscillations and synchrony per se on sensory encoding in the MT network (see Figs. 7–10). On the other hand, from a plausible biophysical point of view using reasonable variances [1–2 ms (Ghosh and Porter, 1988; Fanardjian and Papoyan, 1997; Sirota et al., 2005; Le Bé et al., 2007)], the technique allowed us to see to which degree the effects of synchronization persist in more realistic conditions (supplemental Fig. 6, available at www.jneurosci.org as supplemental material). In some recurrent connections, fixed synaptic delays were used (<1 ms), but these did not have a significant impact in network synchronization.

Figure 6.

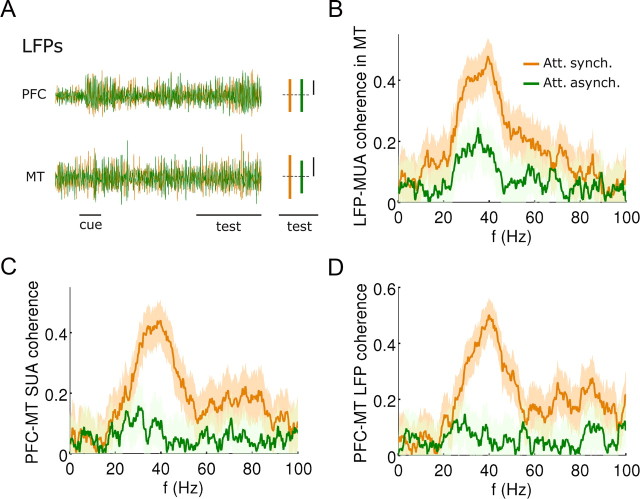
Random conduction latencies in the top-down signal disrupt selectively gamma band synchronization between the two networks. A, Sample gamma-band filtered LFP signals (20–70 Hz) from the PFC and MT networks in the control attention case (orange) and in the case with randomly dispersed top-down synaptic latencies of SD 100 ms (green). Bar plots to the right of LFP traces represent the SD of LFP signals during the test period in each condition, and show that top-down latencies affect LFP fluctuations in MT but not in PFC. B, Gamma coherence between MUA and LFP signals from the MT network drops after introduction of random synaptic latencies of SD 100 ms in the top-down connection (before = orange, after = green) (computed as in Fig. 4A). C, Same for the SUA–SUA coherence between MT and PFC (computed as in Fig. 5A). D, Same for LFP-LFP coherence between networks (computed as in Fig. 5D).

Figure 7.

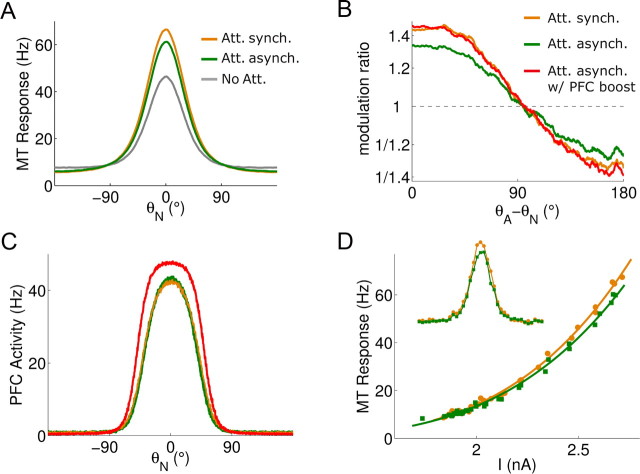
Gamma band synchronization between PFC and MT specifically enhances the firing rate effects attributed to selective visual attention, in a similar way as PFC rate increases. A, Trial-averaged (N_t = 20) population activity during the test period in attention (orange), nonattention (gray), and random top-down latencies (green) cases. Attention enhances selectivity, and interareal gamma band synchronization contributes. B, Modulation ratios [i.e., point-by-point division of attentional rates by nonattentional rates (Martinez-Trujillo and Treue, 2004) in A] are accentuated in the control case (orange) relative to the case with asynchronous top-down input (green). Attentional modulation is recovered when, in addition, PFC neurons receive external injected current (red). C, PFC activity for the cases depicted in B. Activity is boosted by external current injection (red), and this results in a recovered modulation ratio through asynchronous top-down signal in B. D, Interareal synchronization increases the exponent of the power-law relationship between MT neuron activity and input (I = I_S + I_A). The exponent increases from 3.79 to 3.92. Inset, Tuning curves with interareal synchrony (orange) and without (green).

Figure 8.

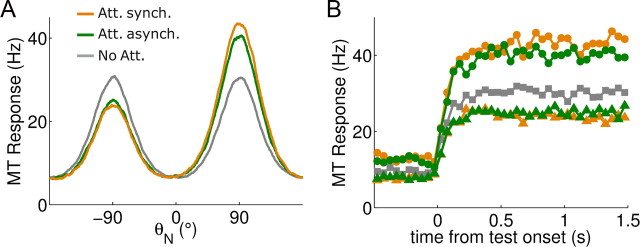
Gamma-range synchronization strengthens the attentional bias of network responses to multiple stimuli (transparent motion). A, Trial-averaged population activity in MT when two transparent motion components were simultaneously presented in the receptive field (N_t = 20), in the nonattended (gray), and attended with (green) and without (orange) random top-down latencies. Synchronized top-down inputs enhance attentional effects. Neurons are labeled on the x-axis according to their preferred direction (θ_N). B, The attentional bias is enhanced by interareal synchrony when attention is directed to the neuron's preferred direction of motion (circles, stimuli at 90° and −90°, neuron θ_N = 90°, attention at 90°; see A), and reduced when attention is focused to the neuron's null direction of motion (triangles, stimuli at 90° and −90°, neuron θ_N = −90°, attention at 90°; see A). The nonattention condition is plotted to observe the attentional bias magnitude (squares, stimuli at 90° and −90°, neuron θ_N = 90°; see A).

Figure 9.

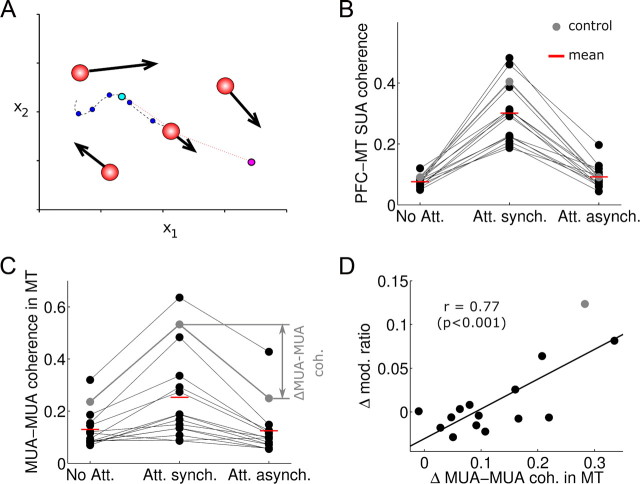
An automated optimization procedure found 14 additional MT networks, all of which showed little dependence of firing rate modulations on interareal synchronization. A, Simplified schematic representation of the optimization algorithm (particle swarm optimization). Each network configuration is determined by fixing 13 free parameters of the simulation, i.e., each network is represented by one “particle” in a 13-dimensional space. We represent here graphically an analogous bidimensional situation (parameters x₁, x₂). Several networks (typically 50, a “swarm”) are simulated in parallel (here 4 red particles). For one of the particles (center), a path with previously visited locations (dark blue dots) is drawn. The particle updates its velocity stochastically toward the location with best fitness value visited previously by this particle (cyan dot) and toward the best location found by the whole swarm (magenta dot). The fitness of a given location is determined by running 7 network simulations with the corresponding parameters for various stimuli conditions, and checking how well neural responses approach quantitatively experimental values for MT neurons in the literature (supplemental Methods, available at www.jneurosci.org as supplemental material). An optimization run finishes when the swarm converges to a global optimum. If the global optimum is not reached within 50 algorithm iterations, the optimization run is stopped and all particles are discarded. B, Interareal coherence is enhanced in attention trials, and abolished by top-down random latencies. Average maximal PFC–MT SUA coherence (mean in ±10 Hz from coherence peak) for each of 15 networks in three different conditions: nonattention trials (No Att.), attention trials (Att. synch.), and attention trials with random top-down conduction latencies (Att. Asynch.). The control network shown in previous figures is indicated in gray. C, Effects of attention in MT MUA–MUA coherence are abolished when introducing top-down random latencies. Average maximal MT–MT coherence (mean in ±10 Hz from coherence peak) for each of 15 networks in the three different conditions of B. The control network shown in previous figures is indicated in gray. D, The effects of top-down random latencies on MT–MT coherence (ΔMUA–MUA coh., indicated on C) and on changes in rate modulations of maximally activated neurons (modulation ratio averaged across neurons where θ_A − θ_N ∈ [0°, 45°]) correlate strongly across the population of 15 networks. Despite large changes in coherence (x-axis), firing rate modulations of coding populations are affected very modestly by interareal synchronization (y-axis).

Figure 10.

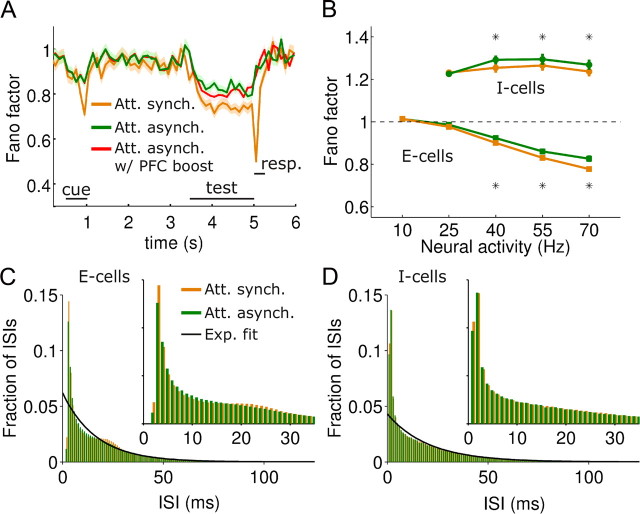
Interareal synchronization reduces neuronal firing variability but Fano factors remain high, due to burstiness. A, Fano factor of high-rate MT neurons (averaged over 101 neurons around θ_N = 0°, see Materials and Methods) through the periods of the task for attention (orange), attention trials with top-down asynchronous input (green) and attention trials with top-down asynchronous input and PFC boost (red) (Fig. 7). The overlap of the red and green curves, for which test-period firing rates are identical (Fig. 7), demonstrates that interareal synchronization, not rate, was responsible for the attentional Fano factor modulation in the test period shown in A. Shaded regions indicate SEM over the 101 neurons considered. B, Fano factor versus binned firing rate for model neurons. At high rates, interareal synchronization had the effect of reducing the Fano factor (compare case with interareal synchrony, in orange, and case without, in green; stars indicate t test significance at p < 0.05). The Fano factor was calculated individually for each neuron, following the approach that is used experimentally (Mitchell et al., 2007) (see Materials and Methods). C, ISIHs (N_t = 128) for excitatory neurons of intermediate rates (neurons firing in the range 47–62 Hz) in attention trials (orange) and attention trials with top-down asynchronous input (green) (Fig. 6). Burstiness is reflected in the high first bins of the histogram (compare with expected Poisson histogram fit delineated in black). Oscillations appear as a small secondary peak at ∼23 ms for the attention trials. D, Same for inhibitory neurons. Oscillations are not observed.

Simulated feature-based attentional tasks.

The chosen simulation protocol resembled other behavioral protocols used in monkey attention experiments (Martinez-Trujillo and Treue, 2004) (Fig. 1A). In attention trials, attention is focused on the direction of motion of a peripheral stimulus, whereas in nonattention trials, attention is directed elsewhere (for instance to the fixation cross luminance). Furthermore, we included a delay period, between the presentation of the stimulus to pay attention to (cue stimulus), and the presentation of the stimulus to respond to (target stimulus). Specifically, all trials consist of four periods: cue (0.5 s), delay (2.5 s), test (1.5 s), and response. In the cue period, a cue stimulus appears indicating the type of trial: a random dot pattern (RDP) stimulus in coherent motion indicates attention trial and the attended feature (direction of motion), whereas a change in fixation cross luminance (not specifically modeled) indicates nonattention trial. In the delay, no visual stimulus is presented so that all task instructions have to be maintained mnemonically. During the test period, one or two transparently moving RDPs (test stimuli) are presented in the neuron's receptive field (RF). These stimuli are behaviorally irrelevant, but in attentional trials they may be similar or dissimilar to the direction of motion of the behaviorally relevant attended stimulus (target stimulus), which is away from the neuron's RF. Using this protocol, one can gradually separate the test and the target features in attention trials. To model consistently the neural mechanism for this behavioral task and the flow of sensory information through MT to PFC, one would require the simulation of two different motion-selective MT circuits feeding into a motion-selective PFC circuit; one MT network would be selective to the RF where the cue appears, and the other one would be selective to the RF where the test is presented. We noted, however, that the temporal separation of the cue and test period makes activity in these two periods independent for both MT circuits. This justifies reducing the model to a single MT circuit, which is responsive to motion stimuli presented in either RF. This is, however, a simplifying abstraction, and interpretation of cue activations in MT should be regarded as occurring in neurons selective for the corresponding stimulus location. In the response period, a brief and transient change in the target RDP direction of motion or in the luminance of the fixation cross occurs, and the subject has to detect it and respond in a prescribed time window. Our model does not include these aspects of the task.

Task-related extrinsic inputs.

Cells in area MT received external inputs from primary visual area V1 that were selective to the direction of motion of the visually presented stimulus (Born and Bradley, 2005) (Fig. 1B). We thus modeled motion stimuli presentation by injecting external currents to MT neurons that mimicked outputs from V1 to MT. We tried with Poisson-triggered synaptic inputs, and our conclusions remained unaffected. When there was a single motion direction (θ_S), the current injected to a neuron labeled by θ_i was I(θ_i) = I₀ + I₁exp(μ(cos(θ_i − θ_S) − 1)), for MT pyramidal cells we used I₀^E = 1.65 nA and I₁^E = 0.74 nA, for MT interneurons we used I₀^I = 1.4 nA and I₁^I = 1.39 nA, and for both cell types μ = 2.63 [this choice of μ gives a connectivity profile very close to a Gaussian with a constant baseline, with the same width as MT-to-PFC connections, which gives tuning widths in MT compatible with physiological data (Snowden et al., 1992; Treue and Martínez Trujillo, 1999)]. When two overlapping directions of motion were visually presented, the current impinging on MT neurons was the sum of the currents corresponding to the two single stimuli, normalized so that the maximal current was still I₀ + I₁ (supplemental Methods and supplemental Fig. 1B, available at www.jneurosci.org as supplemental material). This normalization was derived from the observation that the maximal response of a direction-selective V1 neuron remains the same for either single-motion or transparent-motion stimuli (Snowden et al., 1991). When a stimulus suddenly appears or disappears from the visual scene, we simulate smooth current transitions where injected current from V1 to MT changes exponentially with a time constant of 50 ms.

Moreover, since here we want to analyze dynamical aspects of neural activity and how this dynamics is modified when feature-based attention is involved, we incorporate the experimental fact that stimulus-specific oscillations occur at gamma-range frequencies in V1 neural activity (Friedman-Hill et al., 2000). Specifically, we introduce a new oscillatory component added to the constant bottom-up input from V1, I(θ_i) (see above). This oscillatory component is constructed as the sum of sinusoidal terms with frequencies f_i = 15, 16, … 55 Hz, random phases in the range [0, 2π], and amplitudes pondered by a factor coming from a Gaussian function, Aexp(−(f_i − f_c)²/2σ²), with f_c = 35 Hz, σ = 10 Hz, and A = I(θ_i)/16. Such oscillatory input adds to the oscillations that are generated internally in MT through the recurrent excitation–inhibition loop. Oscillations in the input from V1 affect the overall oscillatory character of MT neural activity in passive conditions (see Fig. 4, blue lines), but not its modulations by attention or the effect of top-down conduction latencies.

Figure 4.

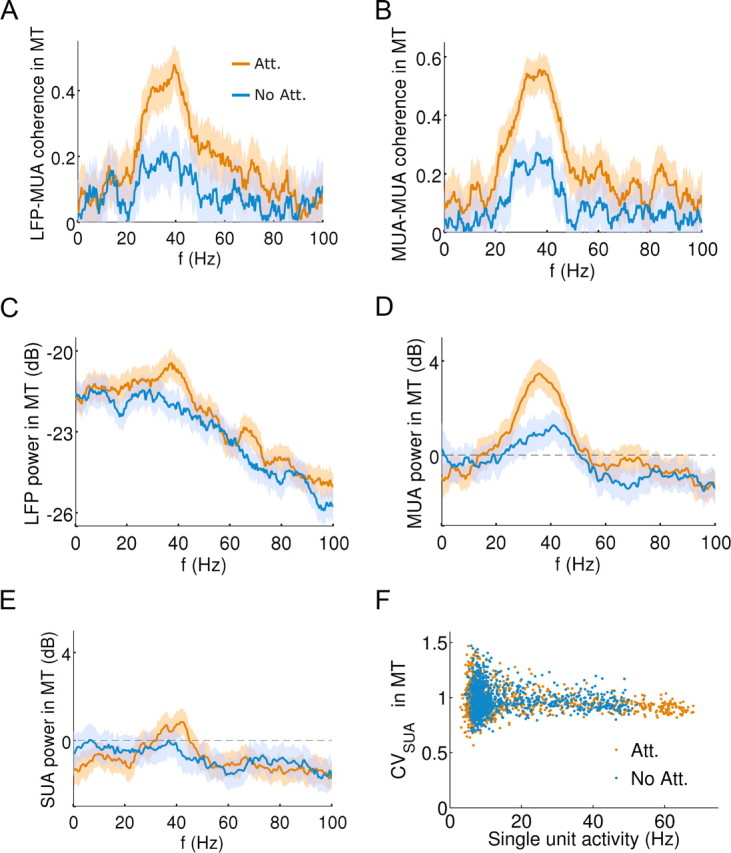
Gamma band oscillations are detected locally in both networks. A, Average coherence between the LFP and MUA in MT increases in the gamma-range for attention (orange) relative to nonattention (blue) trials during test stimulus presentation (N_t = 20). B, Same between neighboring MUAs in MT. C, The power spectrum of the LFP reveals a gamma peak enhancement in attended trials (orange) relative to nonattended trials (blue). D, Synchrony enhancement in spike train power spectra remains by constructing a MUA with 3 neighboring SUA (N_t = 20). E, Averaged power spectrum of MT test-period SUA does not show significant synchrony enhancement (N_t = 20). F, Coefficients of variation (CVs) for the excitatory MT neuron population remain very high (≈1) both in attention (orange) and nonattention (blue) trials. CV data for the 1024 neurons comes from the 1.5 s test period in a single simulation.

PFC model neurons received motion-specific sensory inputs only through the MT-to-PFC pathway. These inputs were weak enough so they would not drive the PFC network into a bump attractor state by themselves (see Fig. 2E). In all our simulation trials and during the attentional cue period, all PFC neurons also received a constant current injection of 0.025 nA. This current was not selective, and thus it did not carry any direction of motion information. It was too weak to trigger by itself a persistent activity pattern in the PFC network (see Fig. 2A, No Att.), but strong enough so that, when presented coincidentally with a visual stimulus, the PFC stored the directional information from MT (see Fig. 2A, Att.). Such a “gating input” (Ardid et al., 2007) allows our model to differentiate the attentional cue from an identical visual stimulus presented during the test period (see Fig. 1A). This gating input could emanate from phasic alertness circuits in the superior temporal gyrus or in the thalamus (Sturm and Willmes, 2001; Fan et al., 2005; Thiel and Fink, 2007), or phasic neuromodulation from the locus coeruleus (Aston-Jones and Cohen, 2005).

Figure 2.

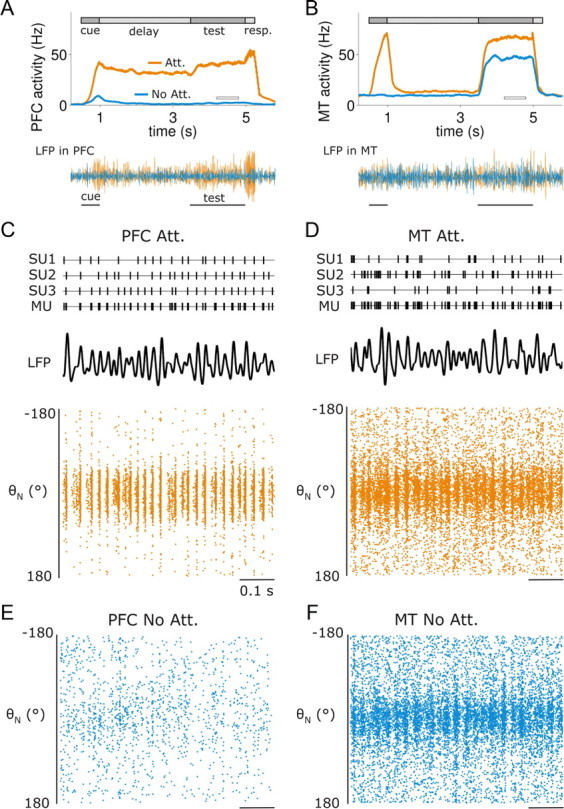
Network oscillations emerge in two-area loop model. A, Top, Average firing rate of a PFC neuron selective to the test stimulus. The PFC neuron activated only in attention trials, from cue onset, through delay until the response period. Bottom traces, Bandpass filtered LFPs (20–70 Hz) for the two attentional conditions. Attentional LFP amplitude increase reveals local synchrony enhancement at gamma frequencies. B, Same for a neuron from the MT network, also selective to the test stimulus. The MT neuron activated during cue and test in attention trials and only during the test in nonattention trials, when no cue was presented. C, Dynamics of 3 single units (SU), multiunit (MU, pooled spikes from top SUs), LFP (bandpass filtered 20–70 Hz), and spatiotemporal graph of spiking activity (bottom) in the PFC area network in a fragment of the test period (white horizontal bar in A) and in the attended condition. D, Same for MT network. E, Spatiotemporal graph of network spiking activity in the nonattention condition and in the test period for the PFC network. F, Same for MT network.

LFP signal from simulation data.

LFP signals reflect a summation of synaptic potentials, subthreshold membrane oscillations, and spike afterpotentials rather than spiking activity (Logothetis and Wandell, 2004; Rauch et al., 2008). In area MT, LFPs also show selectivity to direction of motion (Liu and Newsome, 2006), although the tuning properties for LFPs are usually poorer than for spiking activity (Liu and Newsome, 2006). We built the LFP signal as the sum of EPSCs from 129 neurons selected uniformly among those with selectivity θ_i within 90° of a given central location (typically 0°). In our loop model, there are three contributions to the LFP signal related to the recurrent excitatory input (we only consider the AMPAR contribution), the loop excitatory input (from the other network), and the external Poisson excitatory input. No significant differences appeared when we also considered recurrent NMDAR-mediated and GABA_AR-mediated synaptic inputs in the LFP. The sampling frequency used for the LFP was 1 kHz.

SUA/MUA signal from simulation data.

Our SUA (MUA) signal comes from the spike train of one (three) randomly selected neuron(s) for each trial simulation, where the specific selection is done using a uniform probability distribution within the interval: center ± 30°, and center represents the relevant direction of motion and is typically 0° or 180°. This reflects the fact that in experimental studies, different SUA/MUA recordings are averaged together, based on an approximately similar (but not exactly equal) selectivity.

Measures of variability.

To characterize the irregularity of neural spiking, we measured coefficients of variation (CVs) and Fano factors. To evaluate the CV, we computed interspike intervals (ISIs) of spike trains during the test period for each neuron, lumping together ISIs from each of 20 model simulations. For each neuron, we thus obtained its CV as the ratio of SD to mean of its ISIs. The population average CV was then obtained as the mean of each neuron's CV. The Fano factor was calculated also individually for each neuron, following the approach that is used experimentally (Mitchell et al., 2007). For Figure 10A, we took spike trains corresponding to 101 neurons around θ_N = 0° in 20 simulations, each of which included cue (θ_A = 0°), delay, test (θ_S = 0°), and response periods and lasted 6 s. These spike trains were fragmented in non-overlapping pieces of duration 100 ms. For each neuron and time window, we thus had 20 spike train fragments, from which we obtained 20 spike counts. The Fano factor for each cell was computed as the variance over the mean of these spike counts. The population Fano factor for each time window was then computed as the average over the neurons' Fano factors in that time window. For Figure 10B, we took spike trains corresponding to a given neuron in 128 simulations, in each of which the test period lasted 5 s. These spike trains were fragmented in non-overlapping pieces of duration 500 ms. For each neuron, we thus had 1280 spike train fragments, from which we obtained 1280 spike counts. The Fano factor for each cell was computed as the variance over the mean of these spike counts. The population Fano factor was then computed as the average over the neurons' Fano factors.

Frequency domain analysis.

We used the Chronux data analysis toolbox (http://chronux.org) for the spectral analysis of model data. We estimated quantitatively the amount of oscillations in our model computing the power-spectra of time-series (LFP) and/or point-process (SUA/MUA) signals. To study synchrony between two signals, we used the coherence measure C(f) = S₁₂(f)/$\sqrt{S_1\left(f\right)S_2\left(f\right)}$, where S_i(f) represents the spectrum estimation for each signal, and S₁₂(f) the cross-spectrum estimation between both of them. All spectral quantities (power spectra and coherences) were computed by using 9 orthogonal Slepian tapers and a bandwidth of 10 Hz. In Figures 3C–F and 5C and supplemental Figure 4, A and B (available at www.jneurosci.org as supplemental material), we performed time-resolved sliding window spectral analyses. These analyses consisted in the spectral evaluation of spectra/coherence in time windows of length 500 ms, which were moved along the signals in steps of 25 ms. In Figure 3C–F and supplemental Figure 4, A and B (available at www.jneurosci.org as supplemental material), we plotted the average power in the range 30–50 Hz (normalized to firing rate for the case of MUA spectra) over 20 trial simulations.

Figure 3.

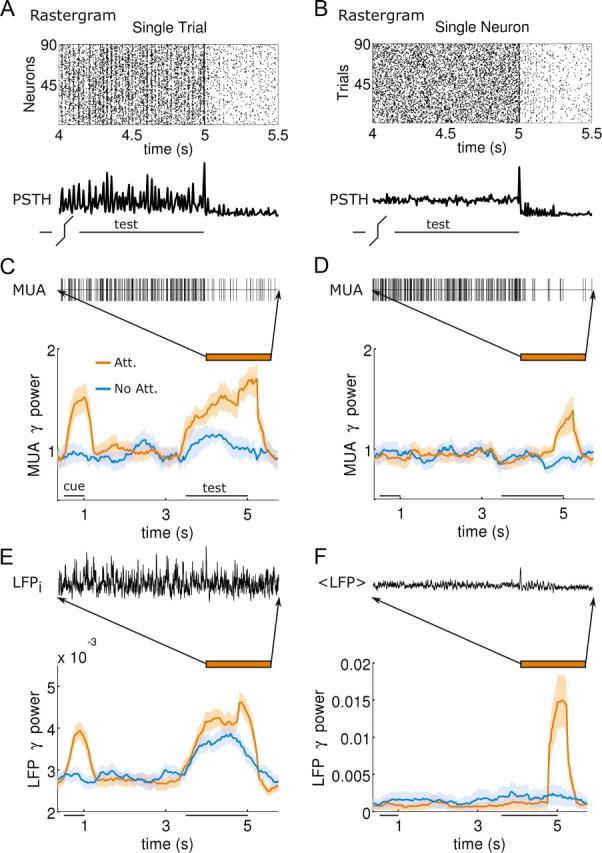
Attentional synchrony enhancement in MT is not phase locked to stimulus, but to response. A, Spike-time rasters of 90 neurons (y-axis) in time (x-axis) in a single trial, and their PSTH (below) show clear gamma oscillations. B, This oscillatory regime is not revealed in the spike-time rasters or PSTH of a single neuron in 90 different stimulus-aligned trial simulations (y-axis). C, MUA formed by collapsing spikes from 3 adjoint neurons in A shows different gamma-range spectral power (average power in 30–50 Hz normalized to MUA firing rate) during stimulus presentation for attention (orange) and nonattention (blue) trials (N_t = 20). D, Same analysis for MUA formed from the spiking activity of a neuron in 3 consecutive trials fails to show attentional gamma enhancement during test stimulus, but it emerges during response. E, Gamma power spectrum (see C) of LFP (sample LFP above) averaged over 70 simulations shows gamma enhancement during stimulus and response. F, Gamma power spectrum of average LFP (LFP averaged over 70 trials, above) does not show attentional enhancement during stimulus, as oscillations are not phase locked to stimulus, but shows it during response, indicating phase locking of gamma to response onset.

Figure 5.

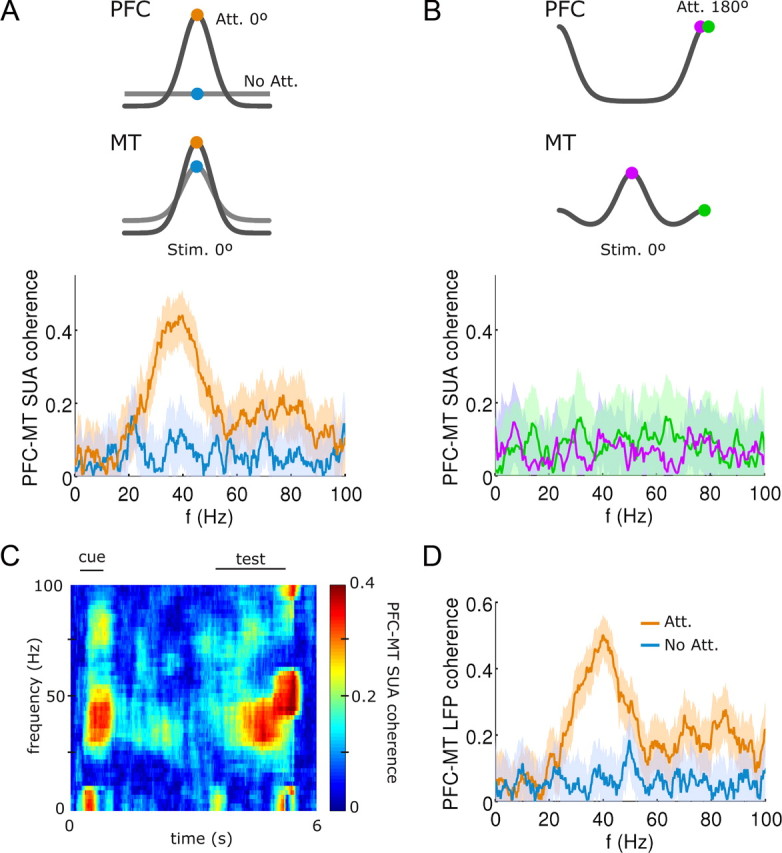
Coherent neuronal activity between PFC and MT in the gamma band occurs selectively and only in attention trials. A, Trial-averaged (N_t = 20) coherence between spikes from one PFC neuron and one MT neuron [selected at θ_center ≈ 0° (see Materials and Methods), circles in the top scheme] shows gamma-range enhancement during attention-to-test (orange) relative to nonattention (blue) trials. B, In contrast to A, no gamma-range effect is observed when the test stimulus was orthogonal to the attended stimulus, both when taking neurons with similar selectivity (green, see top scheme) or with distant selectivity and maximal response (violet, see top scheme) in either network. C, Temporally resolved PFC–MT SUA coherence analysis through an attention trial shows strong gamma coherence during cue, test, and response periods. D, Averaged coherence between local field potentials at θ_center ≈ 0° (see Materials and Methods) in the two networks mimics results in A.

Statistical analysis.

Ninety-five percent confidence intervals in power spectra and coherence measures in Figures 3–6 and supplemental Figures 4 and 5 (available at www.jneurosci.org as supplemental material) were computed following a jackknife approach over simulation trials (identical simulation parameters but each one with different random number generation; typically N_t = 20, except in Fig. 3C–F, where N_t = 70). The extent of these confidence intervals is shown as shadowed areas around the mean curves. We performed unpaired t tests (unless indicated otherwise) to establish significant differences between the means of two distributions. As the t test relies on the assumption of normally distributed errors, we tested our data with the Kolmogorov–Smirnov normality test to establish that the data did not violate the normality assumption (p > 0.05). For the cases where the assumption was violated, we applied instead the nonparametric unpaired Mann–Whitney test. All analyses were performed using the Matlab package (The MathWorks).

Parameter optimization to find a diversity of MT models.

We designed an unbiased, automated optimization procedure to find the parameters of suitable MT networks. This procedure consisted in randomly initializing 13 free parameters (I₀^E; I₁^E; I₀^I; I₁^I; μ; G_EE,AMPA; G_EE,NMDA; G_EI,AMPA; G_EI,NMDA; G_IE; G_II; g_ext,E; g_ext,I; each within a prespecified range of values) for each of 50 networks, henceforth called particles (see Fig. 9A). Such networks were simulated to evaluate their responses to background activity, to single presented stimuli, and to two stimuli presented with varying separation (30°, 60°, 90°, 120°, and 180°). Evaluation was performed with predefined functions that rated the degree of accomplishment of specified target behaviors (maximal and minimal firing rates, response to two stimuli compared to single stimulus, etc., supplemental Methods, available at www.jneurosci.org as supplemental material) for each particle. Based on the overall rating of each particle, and the history of best rating for each particle and for the collection of particles (swarm), a particle swarm optimization algorithm (Kennedy and Eberhart, 1995) updated the parameters of each particle in the swarm. This procedure was repeated iteratively until the swarm converged to a network that accomplished the required functional output (typically within 50 iterations). Such swarm simulations were computationally intensive (10,000 CPU hours each) and required specialized grid computing management software [Grid SuperScalar (Sirvent et al., 2006)]. For more details, see supplemental Methods (available at www.jneurosci.org as supplemental material). We ran several swarm simulations and identified 15 different MT networks with similar functional output (supplemental Fig. 1, available at www.jneurosci.org as supplemental material) but largely divergent parameters (supplemental Fig. 2 and supplemental Table 1, available at www.jneurosci.org as supplemental material). We used this set of models to test the generality of our results (see Fig. 9; supplemental Fig. 9, available at www.jneurosci.org as supplemental material), and show that they are unlikely to emerge from a specific, singular combination of parameter values.

Results

The model architecture is described in a previous paper (Ardid et al., 2007). The model includes two interacting cortical networks at different stages in the processing hierarchy, one of them is a sensory area and the other one a working memory (WM) area. To be able to evaluate the spiking statistics of neurons in each area, single cells are described by a spiking (integrate-and-fire) neuron model. Excitatory and inhibitory neurons are interconnected through AMPA receptor and NMDA receptor-mediated excitatory synapses and GABA_A receptor-mediated inhibitory synapses, so that biologically realistic oscillations can be generated through synaptic interactions in the model networks (Fig. 1B and see Materials and Methods). To simulate the neural encoding of an analog quantity (such as direction of motion), these synaptic connections are topographically organized, so that the strength of neuronal connectivity depends parametrically on the similarity of presynaptic and postsynaptic neuron selectivities. Then, the two networks are interconnected through weaker, topographically organized excitatory AMPA receptor-mediated synapses that provide selective bottom-up inputs to the WM area and selective top-down inputs to the sensory area. Parameter values were calibrated based on available physiological and anatomical evidence. Some parameter values (typically synaptic strengths) were relatively unconstrained by existing data and were manipulated to find operating regimes that reproduced the neuronal responses recorded experimentally in areas MT and PFC of behaving monkeys (for details, see Ardid et al., 2007). We focus on these two areas to specify our hypotheses and extract specific data from the literature. These areas have been shown to be anatomically connected (Barbas, 1988; Schall et al., 1995; Burman et al., 2006; Roberts et al., 2007), but our model might equally apply to other combination of sensory and WM-supporting associative areas, such as V4-PFC or MT-LIP. In fact, we apply a generalization principle so that in those aspects where no data are available from area MT, we extrapolate from results in area V4.

This model has been shown to integrate most attentional modulations of the firing rate in visual extrastriate neurons (Ardid et al., 2007): biased competition (Desimone and Duncan, 1995; Reynolds et al., 1999), multiplicative scaling of tuning curves (McAdams and Maunsell, 1999b; Treue and Martínez Trujillo, 1999), and selective enhancement with inhibitory surround of population activity profiles (Martinez-Trujillo and Treue, 2004; Chen et al., 2008). In addition, this biophysical computational model provides a plausible mechanistic basis for the feature-similarity gain principle proposed by Treue and Martínez-Trujillo (Treue and Martínez Trujillo, 1999; Martinez-Trujillo and Treue, 2004). According to this principle, the attentional modulation of the firing rate response of a given extrastriate neuron to arbitrary visual stimuli is given by a multiplicative factor (“modulation ratio”) that only depends on how similar the attended feature is to the neuronal preferred feature (Martinez-Trujillo and Treue, 2004). Our model network is architecturally identical to this earlier model (Ardid et al., 2007), but we operated some parameter value modifications to reproduce all the firing rate effects accounted for in (Ardid et al., 2007) plus the statistics of single neuron firing in these areas (McAdams and Maunsell, 1999a; Mitchell et al., 2007), and attentional local and long-range synchronization effects (Fries et al., 2001, 2008b; Womelsdorf et al., 2006; Saalmann et al., 2007). Using a computationally intensive search algorithm in parameter space (see Fig. 9A and Materials and Methods), we found 15 network realizations that reproduced satisfactorily the required phenomenology (supplemental Figs. 1, 2, available at www.jneurosci.org as supplemental material). We report here detailed data about one of these networks and test some of our conclusions in the rest of network models to evaluate the generality of our results.

A model simulation followed a typical protocol of selective visual attention tasks: A first cue stimulus indicates what needs to be attended, a random-duration delay forces the subject to maintain actively such attentional set in memory, and during the test period a sensory stimulus appears that is to be processed under the specific attentional condition established by the first cue (Fig. 1A and see Materials and Methods). We specify this general visual attention task by assuming that stimuli are moving random dot patterns and the relevant stimulus feature is direction of motion. This type of stimulus is effective in eliciting responses in area MT (Born and Bradley, 2005) and also in PFC (Zaksas and Pasternak, 2006). Persistent working memory activity in single neurons has not yet been located in the primate brain for this type of stimulus (Zaksas and Pasternak, 2006), but there is evidence of category-based delay activity for motion stimuli in area LIP (Freedman and Assad, 2006).

Gamma oscillations in network dynamics

Figure 2, A and B, shows sample firing rate activity from two neurons, one in each network, which were selective to the direction of motion of the test and attended stimulus. Both neurons interacted synaptically, as they were mutually coupled because of their similar selectivity. Enhanced synchronization in the test period of attention trials relative to nonattention trials is reflected by the larger fluctuation amplitudes in the local field potential (LFP) signals of either network (Fig. 2A,B). Spatiotemporal patterns of network activity in attention (Fig. 2C,D) and nonattention (Fig. 2E,F) trials revealed network oscillatory activity in all high-activity states in both networks (Fig. 2C,D,F). Interneurons showed similar patterns of activity (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). Despite these marked population oscillations, spike trains of MT neurons were highly variable (Fig. 2D). Coefficients of variation (CVs) of interspike intervals of MT excitatory and inhibitory neurons, combining data from 20 test-period simulations, were 0.98 ± 0.06 and 1.11 ± 0.04, respectively (mean ± SD, N_E = 1024 and N_I = 256, respectively). These high values of variability (Poisson spike trains have a CV of 1) are in qualitative agreement with experimental data (see Figs. 4F, 10A,B) (Softky and Koch, 1993; McAdams and Maunsell, 1999a; Mitchell et al., 2007), and they reflect in part the fact that spike trains had a bursty character (see Fig. 10C,D) (Bair et al., 1994; Constantinidis and Goldman-Rakic, 2002). Oscillatory firing was difficult to identify both in individual MT neuron spike trains (single unit activity, SUA) and event trains formed by collapsing spikes from several neighboring neurons (multiple unit activity, MUA) (Fig. 2D), and only became clear in the collective network activity and filtered local field potential (LFP) (Fig. 2D). The LFP was obtained from the model as the summated synaptic currents produced by a large number of neurons (see Materials and Methods). This sparse participation of neurons in the population rhythm, where oscillations are revealed in the LFP and not in the SUA, is characteristic of cortical activity during cognitive tasks (Fries et al., 2001; Pesaran et al., 2002). Theoretical work has shown that such a regime can be obtained with strong inhibitory feedback within the network (Brunel and Wang, 2003; Geisler et al., 2005), as it indeed happened in our MT network (recurrent inhibitory currents exceeded recurrent excitatory currents by a factor close to 2). However, no previous study has addressed how these regimes are modulated by oscillating top-down inputs.

Gamma-range rhythms are not phase locked to stimulus but to response

We then investigated what specific analyses of experimentally accessible signals could reveal such weak population rhythms. It is instructive to compare SUA, MUA, and/or LFP recordings from several trials (similar to typical experimental data) (Fig. 3B) with simultaneous activity of a population of neurons in a single trial (Figs. 2, 3A). We found that raster plots and peristimulus time-histograms (PSTHs) of SUA spike trains over several trials (Fig. 3B) failed to reflect the oscillatory dynamics that were readily observed for simultaneously recorded spike trains in a single trial (Fig. 3A). This can be further demonstrated by pooling together spikes from 3 different SUAs to generate a MUA spike train, and computing its average power content around the peak of the gamma oscillation (30–50 Hz) in the course of the trial (Fig. 3C,D). When the SUAs came from 3 simultaneously recorded neurons, attentional gamma-band power enhancement was observed during stimulus presentation (Fig. 3C), whereas it was absent when the MUA was formed by spike trains from a given neuron in 3 different trials (Fig. 3D). This reveals that the stimulus-triggered population rhythm was not phase locked to the stimulus onset time on different trials. This also underlies the lack of oscillatory marks in the power spectrum of event-related potential (average LFP over trials) during stimulus presentation (Fig. 3F), which were instead present when power spectra of each individual LFP were first computed and only then averaged over trials (Fries et al., 2008a) (Fig. 3E).

Only one synchronization effect remains in the multiple-trial analyses of Figure 3, D and F: a gamma-band oscillation locked to the response onset time. This effect is dependent on how the response period is simulated. Network response here consisted in the erasure of PFC persistent activity by means of general excitation of the PFC pyramidal population (Compte et al., 2000). Such sudden activity surge in PFC generated a synchronization enhancement in MT that was phase locked to response time, and was thus detectable from both trial-averaged spectral measures and event-related potential measures (Fig. 3E,F). Such synchronization did not emerge if we reset PFC persistent activity through excitation of the PFC interneuron population. In a recent experiment, marked additional increases in gamma-band oscillations were found in area V4 right at the time of change detection in an attention task (Fries et al., 2008b). Our model would thus suggest that erasure of the maintained attentional set at the end of behavioral trials occurs through synchronizing excitation (Gutkin et al., 2001), rather than inhibition. This also shows how the degree of oscillatory synchrony in PFC can change qualitatively the temporal properties of MT responses: sudden strong oscillations in PFC reset the phase of gamma-range activity in MT, whereas this does not happen for weaker PFC oscillations as during the delay and test periods.

Local-circuit synchronization without neural oscillators

At the local circuit level, attention modulated the microcircuit oscillations. Similar to experiments in area V4 (Womelsdorf et al., 2006; Fries et al., 2008b), greater coherence was observed between MT MUA and LFP signals when the PFC maintained oscillating persistent activity in attention trials than when it did not in nonattention trials (Fig. 4A,B). Such strong attentional enhancement of gamma-range oscillations was also clearly reflected in the LFP power spectrum (Fig. 4C) and in the MUA power spectrum, obtained by pooling several simultaneously recorded SUAs (Fig. 4D). The time course of LFP spectral enhancement in the gamma range paralleled firing-rate changes in MT through the task (supplemental Fig. 4, available at www.jneurosci.org as supplemental material), as it has also been observed experimentally (Fries et al., 2008b). However, at the level of single neuron firing, the attentional enhancement of oscillatory activity was barely reflected in either the power spectrum (Fig. 4E) or the coefficient of variation (Fig. 4F). These two calculations approached the expected features of highly irregular Poisson spike trains. Therefore, strong coherence effects in the population are not a signature of neurons switching to the regime of a neural oscillator.

Selective long-range synchronization

We quantified how attention modulated the synchrony between the two areas by computing the coherence between SUAs extracted from the two networks. Gamma-range synchronization was observed between equal-selectivity neurons in the two networks, but only when they fired in response to an attended stimulus (Fig. 5A), and mostly during the cue, test, and response periods (Fig. 5C). Notably, coherence between neurons in the two networks was absent if the presented stimulus was dissimilar to the stimulus being attended (Fig. 5B). This occurred because the oscillating top-down input had a limited connectivity footprint, and could only synchronize the firing of those MT neurons being targeted by the activated PFC neurons. In addition, such synchronization was only effective if these MT neurons were firing coherently in response to a preferred stimulus. Thus, neurons of distant selectivity in the two networks did not synchronize even though they were both firing at high rates (Fig. 5B, violet), and neurons of equal selectivity in the two networks did not synchronize either, if the attended feature differed from the feature being presented (Fig. 5B, green). Analogous results were obtained for the coherence between LFPs extracted from either network (Fig. 5D). Enhanced interareal synchronization during attention has been reported experimentally (Saalmann et al., 2007; Gregoriou et al., 2009), showing in addition that synchronization occurs only between neurons with overlapping receptive fields (Gregoriou et al., 2009). Our results predict that this selectivity projects to feature space: synchronization affects only those neurons in the two networks that are firing above baseline and only if the attended feature and the test feature coincide.

We tested the role of local-circuit AMPA receptors in generating the attentional enhancement of synchronization (supplemental Fig. 5, available at www.jneurosci.org as supplemental material). We found that when AMPA receptors were replaced by NMDA receptors in MT recurrent connections, both oscillations in MT and synchronization across MT and PFC were reduced significantly. Removing AMPA receptors from PFC totally abolished interareal synchronization and reduced the attentional effects on local-circuit oscillations in MT. Therefore, fast recurrent dynamics in both networks were necessary to implement synchronization enhancement by attention but had little effect on the irregular firing statistics of MT neurons.

Random top-down latencies disrupt interareal synchronization

What are the functional consequences of this temporal coordination of spiking activity in the two network areas? One way to address this question is to selectively abolish interareal coherence in the network and assess the computational consequences. To this end, we introduced long (nonphysiological) random conduction latencies in the top-down signal from PFC excitatory neurons to MT neurons. These latencies were taken randomly from an exponential distribution of SD 100 ms, and chosen independently for each pair of presynaptic and postsynaptic neurons (see Materials and Methods). This nonphysiological manipulation [the SD in conduction latencies between cortical areas is typically <2 ms (Ghosh and Porter, 1988; Fanardjian and Papoyan, 1997; Sirota et al., 2005; Le Bé et al., 2007)] produced the temporal shuffling of all top-down synaptic events onto MT, but no significant change in the total number of top-down events received (see Fig. 7C, orange and green lines). Thus, we expected rate effects due to the top-down signal to remain, while specific effects of the temporal organization of top-down spikes should be removed. Indeed, the temporal fluctuations of the LFP signals extracted from the MT network were significantly diminished by this manipulation (SD of MT LFP 0.74 ± 0.04 nA before and 0.70 ± 0.05 nA after introducing random latencies; mean ± SD, N_t = 20 trials, t test p < 0.001) (a single trial is illustrated in Fig. 6A), while there was no such effect in PFC (SD of PFC LFP was 0.23 ± 0.01 nA before, and 0.22 ± 0.01 nA after introducing random latencies; mean ± SD, N_t = 20 trials, t test p > 0.05) (Fig. 6A). When we repeated the coherence analyses of Figures 4 and 5 on the data from the long-latency top-down input, we confirmed that the attentional synchronization enhancement was significantly reduced at the local level (Fig. 6B) and practically vanished at the interareal level (Fig. 6C,D).

Interareal synchronization affects attentional rate modulations weakly

The firing-rate effects of feature-based attention (Martinez-Trujillo and Treue, 2004; Ardid et al., 2007) were diminished by the introduction of random top-down latencies, albeit by a small amount (Fig. 7). In particular, the selectivity enhancement of population activity induced by attention was reduced (Fig. 7A,B). Thus, attentional modulation of MT activity can be considered as composed of two different contributions: a main term, proportional to the mean PFC input, and another weaker contribution, that depends on the interareal synchronization.

We confirmed that a physiologically realistic dispersion of synaptic latencies in long-range connections [∼1.2 ms (Ghosh and Porter, 1988)] was insufficient to eliminate the effect of interareal synchronization in the attentional modulations of firing rate responses in area MT (supplemental Fig. 6, available at www.jneurosci.org as supplemental material). Because attentional selectivity enhancement is thought to underlie the behavioral advantage of selective attention (Lee et al., 1999), our finding identifies a specific way through which interareal synchronization may contribute to distributed cortical network processing.

We wondered whether it would be possible to dissociate these two effects of the attentional signal. We ran simulations in the attended condition with random top-down latencies, now with the addition of an oscillating (at 35 Hz) external input (with zero mean) to MT that restored the intra-MT coherence to the control values of Figure 4. Because top-down input from PFC retained long, random top-down latencies, there was no coherence between MT and PFC in these simulations, and we could specifically test how the sole change in intra-MT coherence during attention trials with an asynchronous top-down input from PFC affected rate modulations in area MT. Our simulations revealed that the same rate effect was achieved whether MT synchrony was enhanced by virtue of a synchronizing top-down input from our PFC network, or via synchronization by a separate input pathway (supplemental Fig. 7, available at www.jneurosci.org as supplemental material). It is important to note that, in these simulations, the additional oscillatory input was attention specific, and spatially tuned the same way as the top-down asynchronous input. The result shows that the overall attentional effect observed in the control condition can be decomposed into two additive components.

On the other hand, interareal synchronization during attention acts similarly as modest rate increases in the area from which the attentional signal originates. We demonstrated this by injecting additional current into active neurons (∼0.04 nA) of the PFC network, when random top-down latencies disrupted interareal synchronization. We calibrated this injected current so that the modulation ratio in MT recovered the modulation ratio of the original network with intact interareal synchrony (Fig. 7B, red and orange curves). The average firing rate in the PFC population increased by 25% (from 10.6 Hz to 13.3 Hz), while peak rates increased by 12% (from 42.2 Hz to 47.5 Hz) (Fig. 7C). Thus, synchrony between the sensory and WM network achieved a given attentional effect on MT population rate coding with lower PFC firing. This metabolic efficiency represents an advantage of interareal synchronization. In addition, the same correspondence between interareal synchronization and rate increases suggests that MT populations with enhanced oscillations (Fig. 7B, orange) will have greater impact on their downstream targets by virtue of their enhanced synchronization (Salinas and Sejnowski, 2001), much as if they were firing at a higher rate.

We also tested the multiplicative scaling of tuning curves in our network by running simulations with the test stimulus at different directions of motion θ_S (n = 36) while attention was maintained at a fixed direction θ_A = 0° (Martinez-Trujillo and Treue, 2004; Ardid et al., 2007). Firing rates and input currents were recorded for an MT neuron located within the focus of attention, both in simulations with and without top-down random latencies. Interareal synchronization steepened the power law relating current input and firing rate in MT neurons (Fig. 7D). Earlier studies have shown that input fluctuations underlie the power-law relationship between firing rate and input currents in neurons, and that the higher the exponent in this power law, the more multiplicative the responses to additive currents are (Murphy and Miller, 2003). Consistent with this, input current fluctuations in our network were reduced by 10% when the desynchronizing top-down latencies were introduced (SD of total ± current in an active MT neuron went from 2.67 0.05 nA to 2.39 ± 0.03 nA; mean ± SD, N_t = 20 trials, t test, p < 0.001), and this manipulation also compromised slightly the multiplicative character of neural response modulations to additive top-down biases (supplemental Fig. 8, available at www.jneurosci.org as supplemental material).

We then studied how interareal synchronization affected the attentional processing of competing stimuli in area MT. The modulation of competitive interactions between simultaneously presented stimulus representations is a fundamental component of attentional processing (Desimone and Duncan, 1995; Reynolds et al., 1999). Similar biased competition effects as those observed in V4 (Reynolds et al., 1999) have been found in MT neural activity driven by transparent motion stimuli (Wannig et al., 2007; Patzwahl and Treue, 2009), as our model predicted [Fig. 8 and Ardid et al. (2007)]. In our model, desynchronizing random top-down synaptic latencies reduced slightly the attentional bias of responses to either competing stimulus (Fig. 8A,B). Therefore, interareal synchronization might constitute an incremental mechanism behind biased competition in the cortex.

Testing generality in a population of network models

Our analysis showed that interareal synchronization had effects on all major attentional rate modulations in area MT. However, these effects were small and did not attribute a major computational role to synchronization-based rate enhancements in selective attention. We were concerned about the generality of our results: was the weak role of synchronization in our network a particular result of our specific parameter selection? To address this in our simulations, we designed an unbiased optimization procedure on 13 of our network parameters (Materials and Methods, and supplemental Methods, available at www.jneurosci.org as supplemental material). In brief, we let these parameters take values within a prespecified region of a 13-dimensional hyperspace (Fig. 9A), and we evaluated the neural responses of the corresponding MT network models upon the presentation of one and two motion stimuli. An optimization procedure based on the particle swarm optimization algorithm (Kennedy and Eberhart, 1995) was guided by the known properties of passive responses to random dot patterns in area MT (Maunsell and Van Essen, 1983; Albright, 1984; Mikami et al., 1986; Snowden et al., 1991, 1992; Britten et al., 1992) (supplemental Methods and supplemental Fig. 1, available at www.jneurosci.org as supplemental material). Repeated optimization runs starting from different random initial conditions allowed us to obtain 14 additional MT networks consistent with these data. These networks were highly diverse in terms of the varied parameters (coefficients of variation of the various parameters were in the range 0.26–0.93, with a mean at 0.47 and SD 0.19) (see supplemental Fig. 2 and supplemental Table 1, available at www.jneurosci.org as supplemental material). By construction, these different MT networks had similar activity upon stimulus presentation (supplemental Fig. 1, available at www.jneurosci.org as supplemental material), and for each of them, we manually tuned top-down connections from our PFC network to generate also similar attentional firing rate enhancements (supplemental Fig. 9, orange traces, available at www.jneurosci.org as supplemental material), compatible with experiments (Treue and Maunsell, 1996; Treue and Martínez Trujillo, 1999; Martinez-Trujillo and Treue, 2004; Zaksas and Pasternak, 2005). We studied the synchronization properties of the resulting MT–PFC networks and found the following in all the available 15 networks: (1) the PFC and MT circuits synchronized at gamma frequencies in attention trials (Fig. 9B) (mean peak PFC–MT SUA coherence in the attended condition was 0.30 ± 0.10 at a frequency of 40 ± 2 Hz, and in the nonattended condition 0.08 ± 0.02 at 41 ± 16 Hz; n = 15, mean ± SD; coherence values were different, paired t test, p < 0.001); and (2) randomization of top-down latencies disrupted this interareal synchronization (Fig. 9B) (mean peak PFC–MT SUA coherence in attention was reduced by random latencies to 0.09 ± 0.04; mean ± SD; n = 15, p < 0.001; not significantly different from nonattention coherence, p > 0.1). For most of the 15 networks, the attentional top-down input from PFC enhanced existing gamma-range oscillatory dynamics in area MT (Fig. 9C) (mean peak MUA–MUA coherence in MT was 0.25 ± 0.17 at 40 ± 8 Hz for attended, and 0.13 ± 0.07 at 39 ± 14 Hz for nonattended trials; n = 15, mean ± SD; coherence values were different, paired t test, p < 0.001); and random top-down latencies abolished attentional synchrony effects in MT (Fig. 9C) (random latencies brought mean peak MT MUA–MUA coherence down to 0.12 ± 0.09; mean ± SD; n = 15, p < 0.001; not significantly different from nonattention levels, p > 0.1). This confirms that our results of Figures 4–6 are generally valid for many MT networks that are functionally constrained by the experimental data detailed above. We then tested what impact interareal synchronization had on MT firing rate enhancements by attention in the population of 15 models. Despite the large variance in parameter values, all the networks responded similarly at the level of the peak firing rate to the abolishment of interareal synchronization through the introduction of random top-down synaptic latencies: The attentional enhancement at the peak of population rate responses was unaffected or only slightly modified by interareal synchronization removal (Fig. 9D; supplemental Fig. 9, available at www.jneurosci.org as supplemental material). From all the tested networks, the control network that we illustrate in Figures 2–8 and 10 is the one that showed the most pronounced effects on MT firing rates by interareal synchronization (Fig. 9D, gray dot).

Interareal synchronization reduces slightly the high variability of neuronal firing

Neural spiking was highly irregular in our MT network, with CVs and Fano factors (FFs) close to unity, the expected value for Poisson spike trains (Figs. 4F, 10A,B). Fano factors were higher for interneurons than for pyramidal neurons (1.24 ± 0.05 and 0.97 ± 0.10, respectively; mean ± SD, n = 256, 1024 neurons, Mann–Whitney test, p < 0.001) (Fig. 10B). Despite the pronounced effect of attentional modulatory inputs on the coherence of neuronal firing (Fig. 5), the attentional effects on irregularity were much less pronounced (Fig. 10A,B) and were only sizable if PFC presented very strong oscillations (response period in Fig. 10A). We designed a test to show how much of this modest attentional modulation was specifically due to interareal synchronization and not to changes in the firing rate of MT neurons. We computed the Fano factor of stimulus-activated pyramidal neuron spike trains in the attentional condition in the three different cases shown in Figure 7, B and C: control case with intact interareal synchronization, case with largely dispersed top-down random latencies, and case with top-down random latencies and PFC boost to recover the firing rate modulations of the intact case. Fano factors increased significantly by a small amount when random synaptic latencies were included in top-down connections, regardless of whether MT neurons responded with a higher or lower firing rate to the presented test stimulus (Fig. 10A). This proves that the attentional modulation of Fano factor was primarily due to interareal synchronization, and not to changes in the firing rate of MT neurons (Mitchell et al., 2007). Together, our results are consistent with available data on spike count variability in neurons of area V4 (McAdams and Maunsell, 1999a; Mitchell et al., 2007), and suggest that a portion of the reduction in Fano factor during attention observed experimentally (Mitchell et al., 2007) might be due to an oscillating top-down signal, which regularizes V4 neuronal firing slightly. Importantly, the Fano factor of MT neurons remains generally very high in our model, even in the coherent oscillating dynamics regime that characterizes the attentional state in our network (FF ≈ 0.8). We found that this fact was explained by the bursty character of MT neurons spike trains, also detected experimentally (Bair et al., 1994). Indeed, the distribution of interspike intervals (ISI) presented an overrepresentation of short ISIs (Fig. 10C,D) and interareal synchrony enhanced only slightly ISI probability in E-cells within the 20–30 ms range, corresponding to gamma-range synchronization (Fig. 10C).

Discussion

In this study, we investigated network synchronization induced by attention in a computational model of two interacting, sensory and executive, cortical areas. Apart from attentional rate effects (Ardid et al., 2007), the model matched both the synchronization and the irregular statistics of neuronal firing in these areas (McAdams and Maunsell, 1999a; Fries et al., 2001; Womelsdorf et al., 2006; Mitchell et al., 2007; Gregoriou et al., 2009). These measures offer conflicting views on the impact of temporal dynamics modulations in attentional processing, and our model integrates these results in a single coherent framework. We show that significant attentional modulation of local and long-range coherence is compatible with little attentional modulation of highly irregular statistics in single-neuron firing. We then evaluated the impact that such weak interareal synchronization had on attentional processing in our network. The impact of synchrony was assessed by comparing rate-based attentional modulations in MT with or without coherence with PFC. Random latencies in PFC-to-MT connections removed totally the attentional MT synchrony enhancement, taking it to nonattention levels, while only marginally affecting MT neuron Fano factors. Furthermore, we show that the temporal organization of top-down incoming spikes into MT is responsible for not more than 10–15% of the various attentional modulations of firing rate identified experimentally. The modest effects of synchronization on MT firing rates are in contrast with the marked and highly selective effects of interareal synchronization on the coherence of neural activity across areas. This suggests that selective attention might encode in activity coherence across areas the results of selection and detection, adding this information to the rate code of sensory areas.

This model integrates and helps to clarify multiple, hitherto disconnected, experimental results on attentional modulations of neural dynamics. Oscillations in the local cortical circuit in extrastriate cortex are enhanced by a synchronizing top-down input (Fries et al., 2001, 2008b; Womelsdorf et al., 2006; Gregoriou et al., 2009), with a time course that parallels that of rate modulations (Fries et al., 2008b). This local network synchrony is concomitant with enhanced synchronization between neurons in the sensory and associative networks (Saalmann et al., 2007; Gregoriou et al., 2009). However, such increase in oscillatory dynamics does not affect greatly the high variability of extrastriate neuron firing (McAdams and Maunsell, 1999a; Mitchell et al., 2007). An element that contributes to firing variability is the incidence of bursty firing in a significant proportion of neurons (Bair et al., 1994; Constantinidis and Goldman-Rakic, 2002). All these results are integrated in our network model, where population oscillations and synchrony are compatible with neuronal irregular firing: rhythmic activity emerges as a population phenomenon, without entraining individual neurons into a clock-like oscillatory regime (Brunel and Wang, 2003; Geisler et al., 2005). Then, top-down inputs modulate local and long-range synchronization significantly, without affecting much single neuron firing statistics. However, we found that interareal synchronization induces a small but significant decrease in Fano factor at high rates (Fig. 10A,B). This suggests that synchronization might underlie an analogous attentional effect observed in neurons of area V4 (Mitchell et al., 2007). However, the attentional reduction of Fano factor observed experimentally is larger than suggested by our model, and affects more significantly inhibitory neurons (Mitchell et al., 2007). Recent evidence suggests that a portion of these attentional effects comes from the attentional suppression of low-frequency (<5 Hz) fluctuating dynamics in the cortex (Mitchell et al., 2009). The presence of such slow cortical dynamics especially during the nonattention condition has not been contemplated in our model, and we therefore expect the model Fano factor in this condition to underestimate the experimental value, possibly in a cell-type-specific manner. Finally, our model also replicates the finding of additional gamma-range synchronization at the time of detection and response (Fries et al., 2008b). This might reflect the sudden increase of synchronizing top-down inputs, due to the removal of the attended item from the WM buffer in the PFC network.

In addition, our model produces specific experimentally testable predictions. On the one hand, the increase in gamma oscillations in extrastriate areas right at the time of change detection and response (Fries et al., 2008b) should be phase locked to stimulus change (Fig. 3D,F) if we assume the model of working memory erasure through synchrony (Gutkin et al., 2001). This is in contrast to attentional oscillatory enhancement in the test period before stimulus change, whose phase is not reset by test stimulus presentation (Fries et al., 2008a). In our model, this qualitative difference is due to the different dynamics of the PFC network at each of these time points. At the time of test stimulus presentation, neurons in PFC are sustaining an attentional set, which is mostly unaffected by stimulus presentation. On the contrary, detection and response is triggered through a sudden increase in PFC oscillatory activity, which resets synchronization dynamics in area MT. Second, gamma-range attentional coherence between neural firing in the sensory and executive areas occurs between neurons of similar selectivity, and only if the attended and test feature coincide with the neuronal preference. Underlying this high specificity of interareal coherent firing is the footprint of top-down synaptic projections. We propose that this experiment would help estimate the synaptic footprint of top-down attentional connections in feature space. Previous experiments have already shown such selectivity of interareal synchronization for the case of spatial attention, where attention enhanced the coherence only between neurons with shared receptive field (Gregoriou et al., 2009).

Our model has some quantitative biases in the evaluation of coherence measures, which could explain the difference with experimentally measured coherence values, typically lower (Saalmann et al., 2007; Fries et al., 2008b; Gregoriou et al., 2009). On the one hand, we are using all-to-all connectivity for simplicity. However, multiple recordings in vitro have typically reported a rate of connectivity in the order of 10% for pyramidal neurons in the neocortex (Markram et al., 1997; Song et al., 2005). Introducing a diluted random connectivity architecture in our model would make the direct connectivity between units in the MUAs unlikely, and reduce peak coherence values, especially for MUA–MUA and SUA–SUA analyses. On the other hand, based on the results by Liu and Newsome (2006), we took a weaker motion selectivity for LFPs (input currents from neurons within ±90° were averaged together) than for MUA (neurons were gathered from a window of selectivity of ±30°). The peak values of coherence measures based on LFPs and MUAs will also depend quantitatively on their precise selectivity.

By incorporating for the first time a spiking model for the source of the top-down signal, our model represents the first quantitative evaluation of the computational role of interareal synchronization for selective visual attention, recently demonstrated experimentally (Saalmann et al., 2007; Gregoriou et al., 2009). Previous models have instead focused on other synchronizing mechanisms, such as inhibitory interneurons (Tiesinga et al., 2004; Mishra et al., 2006; Börgers et al., 2008; Buia and Tiesinga, 2008), feedforward processing (Buehlmann and Deco, 2008), or neuromodulation (Börgers et al., 2005, 2008), and have assumed a rate-based top-down signal. These modeling studies have found that oscillations may have more impact in sensory activity than the 10% modulation reported here. However, our study is the first in finding explicitly a network regime that reconciles strong attentional modulations in LFP oscillations with weak attentional modulations of irregular neuronal spiking. Such constraint might be important in evaluating the functional impact of attentional synchronization on cortical processing.

Modulations of both synchrony and firing rate characterize attentional selection. It is not clear how these two types of attentional modulations are related. On the one hand, they can represent independent mechanisms by which information processing is enhanced by attention. For instance, regardless of rate modulations gamma-range synchronization could facilitate information transmission between neuronal groups selectively (Womelsdorf and Fries, 2007; Fries, 2009), it could enhance the impact of neural activity on downstream targets (Salinas and Sejnowski, 2001) (see also supplemental Fig. 7, available at www.jneurosci.org as supplemental material), or it could reduce the latencies of neural and behavioral responses (Womelsdorf et al., 2006; Buehlmann and Deco, 2008) (but see supplemental Fig. 4, available at www.jneurosci.org as supplemental material). Alternatively, rhythmic activity and rate modulations could be causally related concomitant effects of attention. Thus, rate increases might entail concomitant synchronization enhancement, or the enhancement of rhythmic firing might cause biased competition rate modulations (Tiesinga et al., 2004; Börgers et al., 2005, 2008; Mishra et al., 2006). Along this line, we find that interareal synchronization contributes at most a small fraction of firing rate modulations in extrastriate cortex. From this point of view, synchronization is just an energy-efficient substitute of rate increases in top-down afferent neurons (Fig. 7B,C). Because interareal synchronization not only modulates modestly firing rates, but it makes those rates more able to drive downstream neurons, our model shows that interareal synchronization incrementally helps in routing communication along behaviorally relevant neural populations (Womelsdorf and Fries, 2007), through the incremental added effects of modest rate increases and enhanced downstream impact. Such a role of synchronization is however only secondary to the primary role of afferent rate changes. However, we also found that the coherence between activity in distant areas encoded selectively and robustly the detection of the attended item (Fig. 5). Thus, an appropriate mechanism for the readout of interareal gamma-range coherence would extract a robust detection signal that is masked in the weak attentional rate effects of area MT. Further research should address whether such readout mechanism exists and whether this may be the primary functional role of interareal synchronization in selective attention.