Learning Not to Generalize: Modular Adaptation of Visuomotor Gain

Abstract

When a new sensorimotor mapping is learned through practice, learning commonly transfers to unpracticed regions of task space, that is, generalization ensues. Does generalization reflect fixed properties of movement representations in the nervous system and thereby limit what visuomotor mappings can and cannot be learned? Or does what needs to be learned determine the shape of generalization? We used the broad generalization properties of visuomotor gain adaptation to address these questions. Adaptation to a single gain for reaching movements is known to generalize broadly across movement directions. By training subjects on two different gains in two directions, we set up a potential conflict between generalization patterns: if generalization of gain adaptation indicates fixed properties of movement amplitude encoding, then learning two different gains in different directions should not be possible. Conversely, if generalization is flexible, then it should be possible to learn two gains. We found that subjects were able to learn two gains simultaneously, although more slowly than when they adapted to a single gain. Analysis of the resulting double-gain generalization patterns, however, unexpectedly revealed that generalization around each training direction did not arise de novo, but could be explained by a weighted combination of single-gain generalization patterns, in which the weighting takes into account the relative angular separation between training directions. Our findings therefore demonstrate that the mappings to each training target can be fully learned through reweighting of single-gain generalization patterns and not through a categorical alteration of these functions. These results are consistent with a modular decomposition approach to visuomotor adaptation, in which a complex mapping results from a combination of simpler mappings in a “mixture-of-experts” architecture.

INTRODUCTION

Generalization, the transfer of learning to novel conditions, is a common property of both perceptual and motor learning (Poggio and Bizzi 2004). When subjects learn a new sensorimotor transformation by making reaching or pointing movements to a set of training targets under altered visual feedback, movements to untrained directions or in a different region of the workspace may be affected by training. Generalization can be measured for specific task parameters, such as movement amplitude or direction, and may be narrowly or broadly tuned to those parameters. Narrow generalization is seen in adaptation to visuomotor rotation, in which subjects guide a computer screen cursor to a visual target and adapt to a rotation of the cursor's direction relative to hand direction: training in one direction generalizes to a limited range of neighboring directions (Krakauer et al. 2000; Pine et al. 1996). Similarly, adaptation to perpendicular perturbing forces transfers to a limited range of adjacent directions (Donchin et al. 2003; Gandolfo et al. 1996; Mattar and Ostry 2007). Other types of adaptation, on the other hand, exhibit broad generalization (Bedford 1989; Ghilardi et al. 1995; Krakauer et al. 2000; Vetter et al. 1999). Adaptation of visuomotor amplitude gain, which requires learning a new ratio between visually perceived and actual movement amplitude under altered visual feedback, generalizes broadly across movement direction: at least 60% of adaptation in the trained direction transfers to movements in all other directions (Bock 1992; Krakauer et al. 2000; Pine et al. 1996; Vindras and Viviani 2002).

Generalization can provide insight into the structure of representations, such as sensorimotor maps, in the nervous system (Donchin et al. 2003; Poggio and Bizzi 2004; Shadmehr 2004). A common approach is to record movements not experienced during learning and construct a generalization pattern (GP), also referred to as a generalization function. This pattern is taken to inform about stable aspects of representations, separate from learning. The difference in GP between rotation and gain adaptation, for example, has been interpreted as evidence of polar vector coding of movement (amplitude separately from direction) in the motor system (Bock 1992; Krakauer et al. 2000; Vindras and Viviani 2002): if movement amplitude and direction show different patterns of generalization, they must be encoded separately. Similarly, GPs in force field learning suggest a specific form of representation for an internal model of arm dynamics that maps a desired arm configuration to the forces necessary to achieve that configuration (Shadmehr 2004). This interpretation attributes to GPs properties of how movements are represented in the nervous system and suggests that generalization may guide learning. For example, in adaptation to force perturbations that are perpendicular to the movement, generalization of adaptation in one direction to neighboring directions is thought to facilitate learning in other directions (Donchin et al. 2003).

Generalization, however, may also reflect the learning process itself. The observed GP may be determined by the specific training set used to practice and by specific features of the adaptation process. Indeed, generalization may be a by-product of function approximation, which could be the nervous system's approach in learning certain mappings (Poggio 1990; Schaal and Atkeson 1998). In this framework, practicing movements in closely spaced directions would be expected to result in narrow generalization, whereas widely spaced training directions would yield wide generalization, simply as a reflection of the learning process and differences in the set of training movements. The resulting GP would then reflect environmental complexity (Mattar and Ostry 2007; Thoroughman and Taylor 2005) and it would be difficult to make inferences about stable representations based on GPs.

Whether generalization aids or hinders learning remains unclear. In previous studies, broad generalization was typically associated with difficulty in learning complex mappings (Bedford 1993; Bock 1992). However, several studies also demonstrated that it is possible to learn mappings of greater complexity than generalization would seemingly allow (Ghahramani and Wolpert 1997; Hwang et al. 2003; Thoroughman and Taylor 2005). We therefore set out to investigate the relationship between generalization and learning by studying visuomotor adaptation for a mapping known to have very broad generalization, i.e., visuomotor amplitude gain for reaching movements. We imposed different gain adaptation requirements in different directions. Due to the broad nature of gain generalization across directions, the task imposed a potential conflict between adaptation requirements and generalization. If generalization of gain adaptation reflects the structure of movement amplitude representation, then broad generalization may indicate a limit on how finely amplitude can be encoded across directions. It may thus not be possible to adapt to two gains in different directions. Training in one direction would be accompanied by generalization to all other directions, which would be expected to interfere with learning a different gain in another direction. If generalization is a consequence of learning, on the other hand, it should be possible to fully learn different gains in different directions. A new GP would be expected to emerge, as dictated by the specific training directions and their associated gain values.

METHODS

Subjects

We tested 60 healthy adult subjects without known neurologic abnormalities or depression. Six individuals were excluded before any formal analysis because of idiosyncratic motor behavior: when the gain perturbation was applied, they verbally expressed concern that “something was wrong” with the experiment, and the variance of their movement speed and amplitude immediately increased to values greater than triple those at baseline. Due to this large increase in movement variability across all directions, we considered their data not interpretable. All results and analyses in this report were obtained from the remaining 54 subjects (33 female, 49 right-handed; mean age ± SD: 26.6 ± 5.6 yr). All subjects provided written informed consent. Testing was performed in accordance with the Declaration of Helsinki and with the approval of Columbia University's Institutional Review Board.

Apparatus

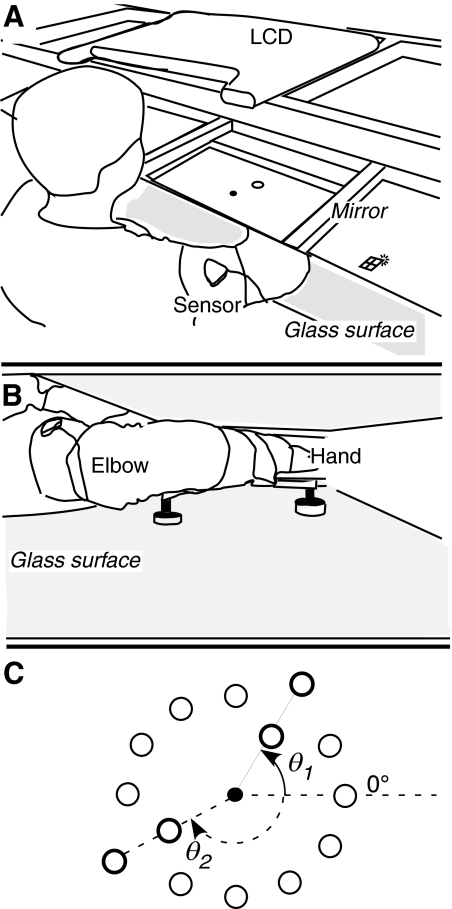
Figure 1 illustrates the experimental setup. Subjects sat at a glass-surface table (Fig. 1A) with their dominant arm strapped onto a light-weight supporting sled that hovered on three air cushions created by compressed-air jets. This apparatus allowed frictionless planar motion of the upper arm and forearm (Fig. 1B). The wrist was immobilized with a splint. A magnetic system (“Flock of Birds”; Ascension Technology, Burlington, VT) recorded position of hand, elbow, and shoulder at 120 Hz using two 6-degree-of-freedom sensors. Subjects viewed the reflection of a computer's liquid crystal display (LCD) in a mirror suspended halfway between the subject's hand and the LCD, so that the virtual image of the display in the mirror was in the plane of arm motion. The mirror blocked the subjects' view of their arm and hand. Custom software collected hand position data and controlled the computer display and could display current hand position as a screen cursor (filled black circle, 0.5 cm diameter) either to match the hand's true location or at an altered location based on experimental conditions.

Fig. 1.

Experimental apparatus. A: subject sits with right arm supported over glass surface and looks in the mirror, which reflects the computer display (LCD). The upper arm magnetic sensor is visible. B: side view of apparatus. Arm is strapped to sled, which glides on air jets. Not visible: hand (wrapped in splint to prevent wrist motion); forearm sensor (attached to bottom of air-sled); magnetic transmitter (below table). C: task workspace, showing start circle (filled circle) and target locations (open circles) in experiment 1. Thick circles, targets in training directions (θ₁, θ₂), for which endpoint feedback was provided. Thin circles, probe targets (no feedback). Target diameter, 2 cm; distance from start circle to probe targets, 10 cm.

Task

The reaching-like task was to make planar arm reversal movements (Schmidt et al. 1988) from a center position to a circular target placed along one of 12 directions separated by 30° in a circular arrangement (Fig. 1C). Before each trial, subjects positioned the screen cursor into a “start” circle (1 cm diameter). The origin of the workspace was defined as the center of the start circle. Each trial started after the subject had maintained the cursor inside the start circle for 750 ms, at which point a target (2 cm diameter) appeared. Subjects were instructed to move the hand, when ready, to the target and back in a single motion, without corrections. No requirement was imposed for reaction time: after target appearance, the computer allowed subjects to take as long as they wanted to start and complete each movement. Subjects were first familiarized with the task by making four movements to each of the 12 possible targets under continuous visual guidance, i.e., with the cursor always on. For all subsequent movements, the cursor disappeared as soon as the hand exited the start circle and subjects received no visual feedback during the movement. For movements in a training direction (θ₁, θ₂; Fig. 1C), subjects received endpoint feedback in the form of a white square (screen endpoint, S) that appeared, without delay, when the hand reversed direction at the end of the outgoing portion of the movement. S remained visible for 2 s.

The screen endpoint's location was always along the same direction as the hand's actual direction. The screen endpoint's distance R_S from the origin was manipulated relative to the distance of the hand's endpoint on the workspace R_H, by setting an imposed gain G_i. This was defined as the ratio between the screen endpoint's and the hand's distances from the origin or how far the endpoint appeared for a given hand movement

$$G_i=R_S/R_H$$ (1)

Values of G_i >1 amplified the cursor's motion on the screen, which caused the cursor to overshoot the target, whereas values of G_i <1 reduced the amplitude of cursor movement, leading to undershoot. No endpoint feedback was given after movements to any of the other targets (probe directions). There were either one or two training directions, depending on the specific group and experiment (Table 1). Each training direction had two targets at distances 8 and 12 cm from the start circle, whereas the probe directions each had one target, at a distance of 10 cm (Table 1, Fig. 1C). For left-handed subjects, the arrangement of start circle and targets was flipped about the y-axis.

Table 1.

Subject groups and testing conditions

				Training Direction, deg		Gain Value		Target Distance, cm
Group	Experiment(s)	Gain Condition	n	1	2	1	2	Training	Probe
S8	1, 2, 3	Single	7	60 (−150)	—	0.8	—	8, 12	10
S15	1, 3	Single	7	−150 (60)	—	1.5	—	8, 12	10
D815	1	Double	12	60 (−150)	−150 (60)	0.8	1.5	8, 12	10
S6	2	Single	7	−150 (60)	—	0.6	—	5, 9	7
D86	2	Double	11	60 (−150)	−150 (60)	0.8	0.6	5, 9	7
D815-nea	3	Double	10	60 (120)	120 (60)	0.8	1.5	8, 12	10

n, number of subjects. Training direction: first value used for half the subjects in a given group, indicating standardized direction (see methods); second value (in parentheses) used for the remaining subjects.

After initial familiarization, each testing session for a given subject consisted of the following three blocks of movements, with roughly 4–5 min of rest between each block.

Baseline (BL): movements to targets in the training and probe directions. For movements to training targets, endpoint feedback was veridical, i.e., with imposed gain G_i = 1. No visual feedback was provided for probe targets. The target presentation sequence was crafted to maintain visuomotor calibration and prevent the possibility of drift that might result from the absence of visual feedback. To accomplish this, probe targets were presented only one at a time, every one, two, or three trials to training targets. This resulted in twice as many movements to training directions as there were to probe directions (50 probe + 100 training in double-gain conditions; 55 probe + 110 training in single-gain conditions). Over the course of the block of trials, each probe target was preceded by all possible training targets at least once and with equal probability. The training targets themselves were also balanced so that they appeared in equal numbers across the block. There were no consecutive presentations of the same target.

Training (TRN): movements to training directions only. After eight movements with G_i = 1, the imposed gain was changed to a new value for the remainder of the block. This perturbation changed the relationship between movement amplitude and endpoint location on the display and varied depending on the group being tested (Table 1). Subjects made 60 movements in each training direction (total: 60 for single-gain conditions; 120 for double-gain conditions). For double-gain subjects, movements to the two targets in each of the two directions were interleaved in a balanced design, covering each permutation of the four targets. Therefore every four movements, all possible targets were covered (two amplitudes for each of two directions). This design was intended to minimize the possibility that a movement's position in a sequence might serve as a cue for its amplitude.

Testing (TEST): the sequence of movements was identical to that in the baseline block, but with the newly learned gain(s) imposed on feedback to training targets. Specifically, endpoint feedback was provided only for targets in the training directions. Movements to probe directions were performed with no visual feedback. Due to the absence of visual feedback, the gain observed for the probe directions necessarily reflected generalization, that is, the effect of learning new gains in the training directions.

In all subject groups, assignment of each gain to one of the two possible training directions was evenly balanced across subjects (Table 1). Two distances were used for training targets to emphasize the nature of gain changes as changes in amplitude relationships. The distance of the probe target was chosen as halfway between the two training distances to minimize possible idiosyncratic effects of seeing endpoint feedback at a specific location. Distances for groups S6, D86 were shorter than those for the other groups, to avoid the possibility of the required movements approaching the mechanical limit of arm extension in the 0.6 gain condition.

Experiments

Table 1 summarizes the subject groups and conditions for each experiment. In experiment 1 we tested whether the motor system can adapt to two different gains in different directions. Two single-gain subject groups adapted to either 0.8 or 1.5 in a single training direction. A third group of subjects simultaneously learned the two gains in two different directions. Experiments 2 and 3 were designed to test specific hypotheses generated by the results of experiment 1. In experiment 2 we trained a new group of subjects to learn two gains that were both <1. A new single-gain comparison group was also tested. The training directions in experiment 2 were the same as those in experiment 1. In experiment 3, another group of double-gain subjects adapted to a double-gain with less separation between training directions. The gains were the same as those in experiment 1, but the training targets in experiment 3 were separated by 60°, compared with 150° in experiment 1. The testing protocol was the same in all experiments (see Task). Further details are described later in results.

Gain values were assigned to training directions as follows (Table 1). The general principle was to counterbalance the assignment of training directions within each group, to avoid possible direction-specific confounding effects (e.g., idiosyncrasies of movement amplitude control for specific directions). For example, in the single-gain conditions of experiment 1, the training direction was −150° for half the subjects in each group and 60° for the remaining subjects. Similarly, in the double-gain condition of experiment 1, half the subjects were assigned training directions −150° for gain 1.5 and 60° for gain 0.8 and the other half 60° for gain 1.5 and −150° for gain 0.8.

Because gain-direction pairings differed between two halves of each subject group, we prepared data for analysis by reassigning training directions for half the subjects in each group as follows. One set of gain-direction pairs was chosen as standard in each experiment (numbers outside parentheses in the Training Direction column of Table 1): −150° for gain 1.5, 60° for gain 0.8 in experiment 1; −150° for gain 0.6, 60° for gain 0.8 in experiment 2; 120° for gain 1.5, 60° for gain 0.8 in experiment 3. For half the subjects in each group, the true gain-direction assignments were already the same as the standard directions. For the other half of subjects in each group (those whose assigned directions are listed in parentheses in Table 1), directions were reassigned to a standardized direction so that directions for a given imposed gain were the same for all subjects in the group. This standardized direction was calculated as θ = −1·θ′ + b, where θ is the reassigned direction, θ′ is the actual direction, and b = −90° for experiments 1 and 2 and 180° for experiment 3. Similar reassignments were made for single-gain conditions. For example, if a double-gain subject in experiment 1 was in the half-group that was trained with gain 0.8 at −150° and 1.5 at 60°, the preceding transformation yielded a direction of −150° for gain 1.5 and 60° for gain 0.8, which matched the gain-direction pairs for the other half of the group's subjects. Gain values could thus be analyzed and plotted against a standard set of directions for all subjects in each experiment. In the remainder of this article, including all figures, θ refers to these standardized directions.

Data analysis

Hand position was stored and filtered off-line with a zero-phase-lag Butterworth low-pass filter (cutoff frequency: 8 Hz). Movement amplitude was measured as the distance from the start circle to the reversal point (where radial velocity changed sign from positive to negative).

The main measure of interest in our study is the visuomotor gain used by the brain to control movement amplitude when planning a movement to a target of a certain distance. This can be inferred from the amplitude of a movement to a visual target whose relationship defines the movement gain G_m. For a movement with amplitude R_H to a target at distance R_T, the movement gain is defined as G_m = R_T/R_H. Note that the imposed gain G_i is the relationship imposed by the computer between how far the hand moves and how far the screen endpoint S appears on the display. The movement gain G_m reflects the nervous system's estimate of this relationship. The imposed gain answers the question “How far did the endpoint appear for a given hand movement?” whereas the movement gain answers the question “For a given target distance, how far did the hand move?” At baseline, the imposed gain is 1. If a target appears at 10 cm and the subject makes a 10-cm movement, then the screen endpoint appears at 10 cm (G_m = 1). If the imposed gain suddenly changes to 0.8, a 10-cm target still elicits a 10-cm hand movement (G_m still equals 1 before adaptation), but this 10-cm movement now places the screen endpoint at 8 cm (G_i = 0.8). After successful adaptation, the hand would move 12.5 cm when aiming to a 10-cm target, which means that movement gain has changed to 0.8, matching the imposed gain of 0.8.

We calculated an adjusted version of movement gain to remove baseline differences between imposed and movement gain. In the BL block, values of G_m exhibited slight systematic deviations from 1 across directions and across subjects. These reflect small, subject-specific direction-dependent amplitude biases in baseline movement execution. In the present study we were interested in measuring subjects' ability to adjust to a change in imposed gain relative to their own baseline, regardless of these individual and directional biases. Therefore we adjusted movement gain by subtracting any direction-dependent offset between target and movement amplitude that might be present at baseline and defined this quantity as the observed gain G_o

$$G_o=G_m-K$$ (2)

where K = (G_m − G_i)_BL is the difference between imposed and movement gains in the baseline block. This removes any baseline overshoot or undershoot associated with specific subjects or movement directions. G_o thus purely records the quantity of interest in our study, that is, the amount of visuomotor adaptation, as the change in amplitude gain from baseline.

For each gain learned in a training direction, percentage adaptation was calculated as the fraction of change from baseline (i.e., 1) for the observed gain compared with the imposed gain: percent adaptation = [(G_o − 1)/(G_i − 1)] × 100. Percent adaptation served as a measure of adaptation to each individual gain in all conditions. Note that percent adaptation can assume negative values. This would occur if the observed gain were to change in the opposite manner of the imposed change, e.g., observed gain decreasing to <1 when the imposed change is 1.5. In the double-gain condition, we were also interested in recording how well subjects learned to disambiguate two gains. For double-gain subjects, we therefore calculated percent separation as the ratio of the difference between the observed gains and the difference between the imposed gains: percent separation = [(G_o2 − G_o1)/(G_i2 − G_i1)] × 100. This was calculated for each subject by pairing successive trials to different directions. A trial in one direction was paired with the next trial, which was always in the other direction.

Statistical comparisons were performed using two-sample t-test with unequal variance. Significance level was set at α = 0.05.

MODELS.

We developed mathematical models for five possible mechanisms through which observed patterns of generalization in double-gain conditions can arise. These are introduced in the results and are described in detail in the appendix.

RESULTS

Subjects were able to learn two gains in two directions

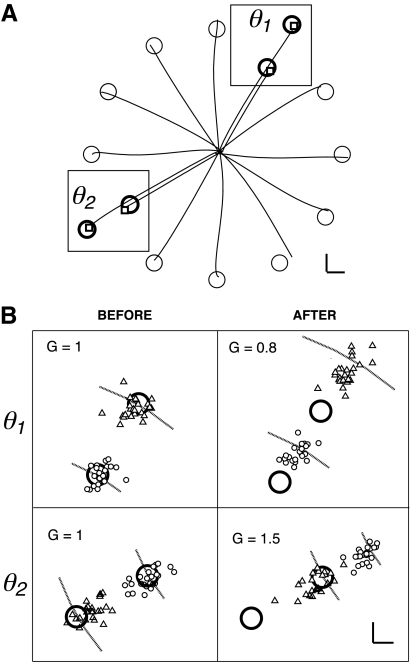
In experiment 1 we tested whether the motor system can adapt to two different gains in different directions. Subjects were able to accomplish this task (Fig. 2). The outgoing portions of sample trajectories for a single subject are shown in Fig. 2A. Trajectories were out-and-back, as instructed, and had double-peaked velocity profiles and no clear evidence of submovements, as is characteristic of reversal movements (Gottlieb 1998). Figure 2B shows movement endpoints of an individual subject for targets in the two directions for which endpoint feedback was given (FB directions) before and after training. In the baseline condition (Fig. 2B, “Before”) endpoints were clustered near the centers of the targets. In the test condition (Fig. 2B, “After”) endpoints were clustered beyond the original targets in the 0.8 gain direction and short of the original targets in the 1.5 gain direction. This reflects successful learning of the two different gains.

Fig. 2.

Example of double-gain learning. A: sample movement trajectories (outgoing portion only) to each target for a single subject. Small squares indicate endpoint shown on display for movements in training directions. Large squares indicate areas that are magnified in B. B: endpoints for a single subject's movements in training directions (θ₁, θ₂), before and after training in double-gain condition of experiment 1. Left panels refer to baseline (BL) condition (imposed gain = 1); right panels refer to testing (TEST) condition, in which imposed gain was 0.8 for direction θ₁ (top right) and 1.5 for direction θ₂ (bottom right). Circles, endpoints for movements to 8-cm targets; triangles, endpoints for 12-cm targets. Arcs indicate distance where actual hand endpoint must be for screen endpoint feedback to appear inside the target. Calibration bars in A and B: 1 cm.

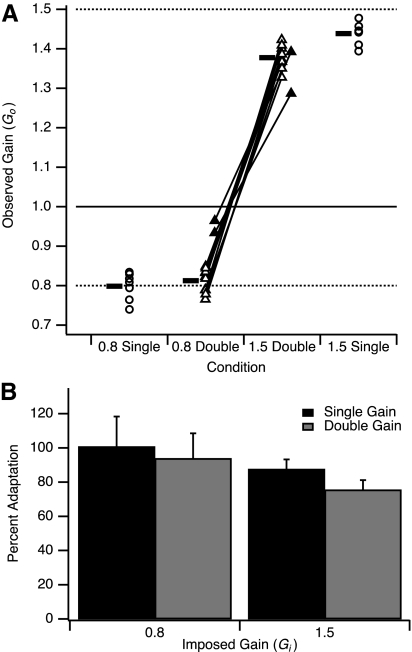
We compared the amount of adaptation in both single- and double-gain conditions (Fig. 3). Most double-gain subjects clearly learned different gains for different directions (Fig. 3A, open triangles). Results for two double-gain subjects differed considerably from those of the rest of the group: one subject had poor adaptation to both gains and the other adapted well to the 1.5 gain but had minimal adaptation to the 0.8 gain (Fig. 3A, filled triangles). We excluded these two subjects from further analysis because their learning results for the 0.8 gain in the double-gain condition were clear outliers (Mahalanobis distance >2SD from remainder of group). Moreover, these subjects' data suggested a qualitatively different type of learning, in that they adapted to one gain rather than two. Most of the remainder of the analysis was aimed at examining the mechanism by which two different gains are learned concurrently and thus was performed without these two subjects' data.

Fig. 3.

Adaptation in single- and double-gain conditions in experiment 1. A: observed gain (G_o) in TEST condition, after adaptation to imposed gain of 1.5 or 0.8. Plotted are individual subject values for single-gain (circles) and double-gain (triangles) conditions and mean group values (horizontal bars). Solid line, baseline value of imposed gain (G_i); dashed lines, imposed gain during training in respective conditions. B: percent adaptation in single- and double-gain conditions (group mean ± SD). Categories indicate gain imposed during training G_i.

Figure 3B expresses amount of learning as percent adaptation. For the 0.8 gain percent adaptation was not significantly different between single- and double-gain groups (double-gain, 94 ± 15%, mean ± SD; single-gain, 101 ± 18%; P = 0.39; two-sample t-test with unequal variances). Percent adaptation to the 1.5 gain was slightly less in the double-gain than that in the single-gain condition (double-gain, 76 ± 6%; single-gain, 88 ± 6%; P < 0.001).

Learning was slower in the double-gain condition

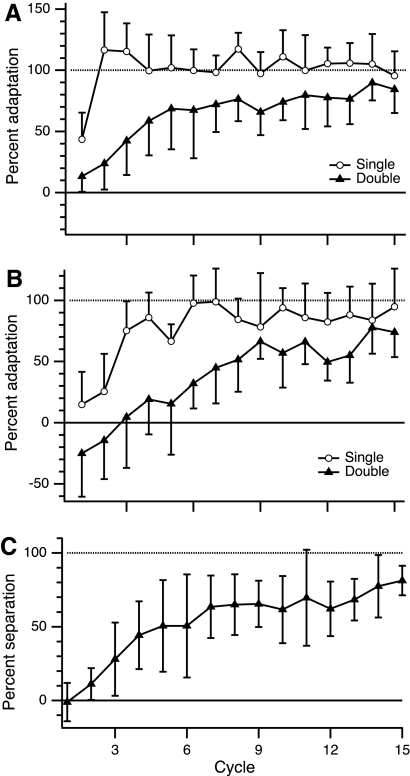
Adaptation followed a time course with a gradual, monotonic progression (aside from trial-by-trial noise) from the baseline gain to the imposed gain, in both single- and double-gain conditions (Fig. 4). At the beginning of training, the newly imposed gain induced visual errors (undershoot for the 0.8 gain; overshoot for the 1.5 gain), which led to a gradual change of the subjects' own gain. Adaptation was considerably slower in the double-gain condition than that in the single-gain condition (Fig. 4, A and B). Single-gain subjects, on average, adapted fully to the new gain within 8–12 movements (Fig. 4, A and B, open circles). Double-gain subjects, on the other hand, required the full training session of 60 movements to reach nearly full adaptation (Fig. 4, A–C, closed triangles). Mean percent adaptation, averaged over the first 12 trials of the TRN block, was 92 ± 7% (mean ± SD) in the group learning the 1.5 single gain versus 27 ± 6% in the group learning the 1.5 gain in the double-gain condition (P < 0.0001; two-sample t-test with unequal variance) (Fig. 4A). For the 0.8 gain, mean percent adaptation in the first 12 trials was 38 ± 12% for single gain and −19 ± 10% for double gain (P < 0.001). The negative value resulted because, on average, gain for the 0.8 direction increased to a value >1 in the first few movements of double-gain training (Fig. 4B). A single-plot view of double-gain learning can be obtained by calculating percent separation between the two gains (see methods) for double-gain conditions (Fig. 4C). This quantity captures the relative disambiguation of the two gains, regardless of whether adaptation was greater to one gain or the other.

Fig. 4.

Progression of adaptation in training (TRN) condition of experiment 1. A: percent adaptation to imposed gain G_i = 1.5 is plotted against training cycle (group mean ± SD; 1 cycle = 4 trials). B: percent adaptation to imposed gain G_i = 0.8. C: percent separation in double-gain condition, i.e., ratio of difference between observed gains in training directions and difference between values of G_i (1.5, 0.8) in double-gain condition, ×100%. In all panels: open circles, single-gain condition; filled triangles, double-gain condition. Note that cycles in A and B are not composed of consecutive movements, but instead indicate 4 movements with a specific gain, 0.8 or 1.5.

Learning single and double gains resulted in direction-dependent generalization

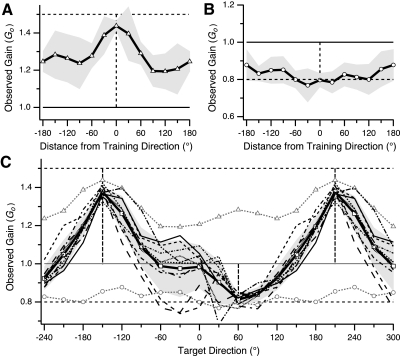
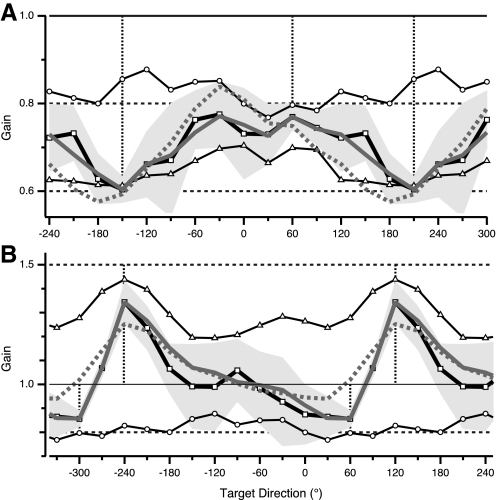
As observed in previous studies (Bock 1992; Krakauer et al. 2000; Pine et al. 1996; Vindras and Viviani 2002), adaptation to a single gain resulted in broad generalization across directions. However, as also reported in previous studies, transfer to other directions was not 100% and instead exhibited some dependence on direction. The GP associated with the 1.5 gain (Fig. 5A) had a broad peak (value 1.44) with symmetric decrement on each side of the training direction. Gain was >1.2 for all directions, which indicates that ≥45% of the learned gain, as a deviation from baseline (1.0), was transferred to all directions. The GP for the single 0.8 gain (Fig. 5B) was broader than that for the 1.5 gain, with an inverted peak (value 0.8) surrounding the training direction and gradual drop-off to 0.88 in the opposite direction. Thus in spite of this dependence of generalization on direction, ≥60% of the learned gain (deviation from 1.0) was transferred to all directions and thus there was considerable generalization to all directions in both single-gain conditions.

Fig. 5.

Patterns of generalization after single- and double-gain training in experiment 1. Plotted is gain in TEST block as a function of target direction (generalization pattern [GP]). A: observed gain (G_o) vs. target direction (relative to training direction) in adaptation to single imposed gain of 1.5. B: observed gain vs. relative target direction after adaptation to single gain of 0.8. C: observed gain vs. standardized target direction (see methods) in double-gain condition (solid black trace with squares) imposed gain 1.5 in direction −150° and 0.8 in direction 60°. Horizontal axis range is >360° to better illustrate shape of double-gain GP. Thin traces indicate double-gain GPs for individual subjects. Dashed traces with triangles and circles show single-gain GPs for gains 1.5 and 0.8, respectively (same traces as in A and B, replotted against standardized target direction). In all panels: vertical dashed lines, training directions; gray shading, ±1SD.

The GP associated with learning two gains simultaneously was characterized by a peak and a trough in the training directions (Fig. 5C), which were narrower than those in the original single-gain GPs. These could also be regarded as two peaks, one deviating upward and the other downward from baseline gain values. Our choice of training directions yielded two regions of angular separation between training directions, one smaller (210° − 60° = 150°) and one larger [60° − (−150°) = 210°; Fig. 5C]. In the region of smaller separation, the GP made a steep monotonic transition between the 0.8 and 1.5 gain directions. In the larger region, there were three directions where the gain was close to 1 and where there was greater intersubject variability (Fig. 5C). From this flat region, the GP gradually changed toward its value at the respective trained direction. These features gave the GP the appearance of two peaks, one positive and one inverted, roughly centered at the training directions. The peaks appeared approximately symmetric (at least in the group average values, although not in their variability), falling off to 1 (i.e., the baseline value) at a distance of 60–90° from the trained direction. Visual inspection of individual traces shows that the average GP reflects the general shape of individual subjects' GPs. The region of greatest intersubject variability (directions −90 to 0°) corresponds to the angular range of greater separation between training directions. Notably, this region of variability does not reflect haphazard disruption of generalization across subjects. The general shape of two opposite peaks and a flat central region was observed in all subjects. Variability in the range −90 to 0° is explained by the fact that the flat central region of the average trace reflects gain that is greater than baseline (1) for 8 of 10 subjects and <1 for the remaining two subjects.

Note that a change of gain in the probe directions (all directions except the training directions; Fig. 5) between baseline and test conditions could reflect only the effects of generalization. No visual feedback to the probe targets was provided during baseline or testing and no movements to the probe targets were made during training. Therefore our “null hypothesis” is that gain for the probe targets should remain at baseline values throughout the study. Any change of gain values in the probe direction could only reflect transfer of learning of the new gains in the training directions.

The results of experiment 1 demonstrate that broad generalization is not an impediment to learning. If single-gain GPs had been fixed and had successfully interfered with each other, then, given the interleaving of equal numbers of trials in each training direction, gain would be expected to reflect the average of the two single-gain GPs. This is not what happened.

Did double-gain adaptation reflect de novo generalization?

The double-gain GP observed in experiment 1 (Fig. 5C) suggested that there may be no special relationship between single-gain and double-gain generalization. We refer to this possibility as de novo generalization, in the sense that the motor system adopts a strategy dictated by the training set, which may or may not be the same for single and double gain. We considered two types of processes that might give rise to de novo generalization and developed models to test whether double-gain generalization is compatible with these possible processes. Details of these models are given in the appendix.

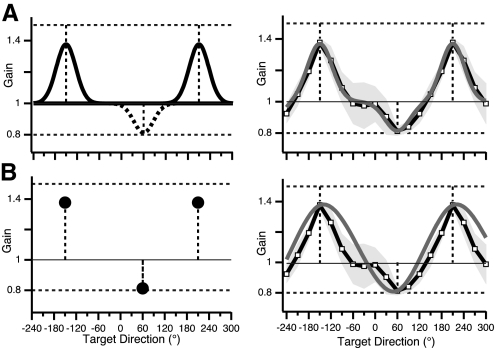
LOCAL LEARNING MODEL.

First we considered a principle of minimal change: when faced with two different gains in different directions, the nervous system adopts a strategy of local learning. The baseline gain (value = 1 in all directions) changes for those directions in which error is detected (the training directions) and for closely neighboring directions. In other words, a narrow-peaked function (Gaussian shape) develops in the training directions due to local modification of baseline gain (Fig. 6A, left). The neurophysiological motivation is that movement amplitude may be represented as a population code by neurons with narrow directional tuning. The width of the Gaussian is a preexisting property of movement representation, determined by local wiring of neurons encoding movements in the training direction. We estimated the width of this Gaussian by fitting Gaussian functions to each peak of the double-gain data (Fig. 5C). Their values were very similar (45° for the 1.5 gain and 50° for the 0.8 gain) and we chose their average (47.5°) as the SD of the Gaussian for this model. The resulting predicted GP showed a good fit with the observed double-gain GP (Fig. 6A, right, gray trace).

Fig. 6.

De novo models hypothesized to account for double-gain GP observed in experiment 1. Predicted and observed gain is plotted against standardized target direction in the double-gain condition with imposed gain values 1.5 (−150°) and 0.8 (60°). Vertical dashed lines, training directions. A: local learning model. Left: model Gaussian functions centered on training direction. Right: gain observed in double-gain condition of experiment 1 (black trace with squares; same trace as in Fig. 5C) and predicted by model (solid gray trace). Gray shading, ±1SD. B: global learning model. Left: constraining points (“knots”) for the smoothing spline function, set at values of observed gain in training direction in double-gain condition. Right: GP predicted by model. For detailed descriptions, see results and appendix.

GLOBAL LEARNING MODEL.

A second process through which double-gain generalization could emerge de novo is through smooth interpolation of gain values between those learned in the training directions (Fig. 6B, left). This model is motivated by the possibility that generalization reflects an assumption, made by the nervous system, of regularity in spatial relationships. The model assumes that the nervous system extracts regularities (global features) from environmental signals and exploits these regularities for efficient neural representations. In the case of amplitude gain, everyday experience is dominated by situations in which gain does not change with direction: when reaching for an object, for example, the distance that the hand must travel is the same as the visually perceived distance (in a three-dimensional, visually based representation of space) between the hand and the object, and this relationship is independent of direction. Such a regularity may be salient enough to lead the nervous system to encode gain as independent of direction. A principle of maximal smoothness (“allow gain to change minimally across directions”) is one way to obtain this type of coding. When faced with a second gain, the principle would cause a “reluctance” to allow gain to change with direction, leading to maximally smooth transitions from one gain to the other. Neurophysiologically, a smooth representation could arise from parsimony of neuron number. If we hypothesize amplitude-tuned neurons with broad direction tuning, then it would take more neurons to encode gain that varies greatly with direction than to encode gain that varies little with direction. Therefore a simpler network of such neurons would be required if direction dependence of gain is smoother. The model predicts gain values, for untrained directions, that produce a smooth transition between the two different gains. This can be mathematically implemented by smoothing spline interpolation, a curve-fitting procedure that minimizes curvature. The resulting trace captures some features of the double-gain GP (Fig. 6B, right). It does not predict the flat region in the range of angles most remote from the training directions, but the model trace still falls within the observed variability.

Both de novo models appeared able to explain results of experiment 1. Although the local learning model yielded an excellent fit, the global learning model could not be excluded. Furthermore, although gain in directions away from the trained ones remained at baseline, at least at the group level (directions: −60, −30, and 0°; Fig. 5C), gain in these directions also exhibited greater intersubject variability. We therefore tested these models in two further conditions.

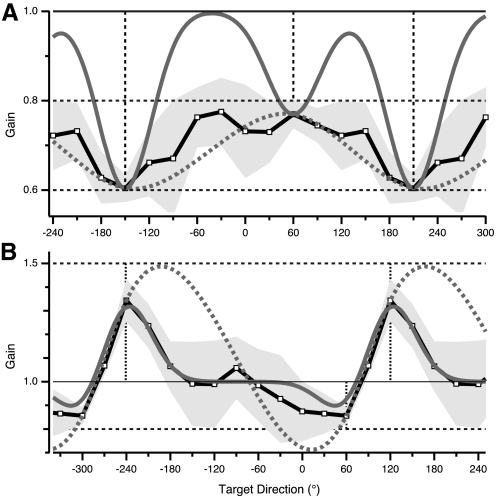
Experiment 2 was designed to test the validity of the local learning model. We trained subjects to learn two gains that were both <1 (group D86, Table 1), in the same two training directions as in experiment 1. Although in experiment 1 each gain had opposite effects on cursor movement amplitude (one reducing, the other magnifying), in experiment 2 both gains reduced cursor amplitude. The local learning model predicted that gain should remain around 1.0 at directions remote from the training directions: the essence of this model is local learning and there is no reason for gain to change from baseline in directions that are outside the width of the local Gaussian functions.

The double-gain GP for the D86 group shows full adaptation to the 0.6 gain and slight overadaptation to the 0.8 gain, in their respective training directions (Fig. 7A, squares). The observed gain for all intervening directions was between 0.6 and 0.8. Notably, gain was never between 0.8 and 1.0, in contrast to the prediction of the local learning model (Fig. 7A, solid gray trace). The other de novo model (global learning) predicted a pattern more similar to the observed data, that is, intermediate values between 0.6 and 0.8 throughout the double-gain GP (Fig. 7A, dotted gray trace).

Fig. 7.

Predicted and observed GPs for de novo models in experiments 2 and 3. A: observed gain (black trace with squares; gray shading, ±1SD) in double-gain condition with gain values 0.8, 0.6 (experiment 2); gain predicted by local learning model (solid gray trace); gain predicted by global learning model (dotted gray trace). Vertical dashed lines, training directions. Note deviation of local model's prediction from observed gain in regions between training directions. B: observed gain (black trace with squares) in double-gain condition with gain values 1.5, 0.8 and training directions separated by 60° (experiment 3); gain predicted by local learning model (solid gray trace); gain predicted by global learning model (dotted gray trace). Note hypergeneralization pattern predicted by global model.

The results of experiment 2 exclude the local learning model as an explanation of double-gain generalization. In experiment 3 we tested the validity of the global learning model. We designed experiment 3 similarly to experiment 1, but with training directions in closer angular proximity. Subjects were trained in a double-gain condition with gains 0.8 and 1.5, as in experiment 1, but the training directions were separated by only 60°, compared with the 150° separation in experiment 1.

The global model made two predictions in this condition. First, the resulting GP (Fig. 7B, dotted gray trace) should show some amount of hypergeneralization. Bringing the training directions closer increases the steepness of the transition between gain values at the training directions. The model predicted that the gain in directions on one side of each training directions (on the side of greater separation between these) would take on values further from baseline (1.0) than those learned at the training directions, to maximize smoothness of the GP (Fig. 7B). Second, the model predicted that the peaks of the GP would shift away from the training directions. Indeed, the model makes both of these predictions for any asymmetric arrangement of training directions, i.e., for any pair of training directions that are not 180° apart. However, for the specific angular separation of training directions in experiment 3, the model predicted hypergeneralization and shifting of peaks to an extent well beyond the observed variability. Note that these predictions are not affected by relaxing the smoothing spline's “rigidity” requirement: reducing the value of the smoothing factor to <0.001 did not result in any appreciable change in the predicted GP (lowest value tested: 0.00001).

Neither prediction of the global learning model was observed. The double-gain GP observed in experiment 3 was similar to that observed in experiment 1, but had asymmetric peaks (Fig. 7B, squares). There was no hypergeneralization and the peaks remained aligned with the training directions. Therefore the data of experiment 3 strongly argue against the global learning model.

The local learning model predicted that the local Gaussians, whose width was estimated in experiment 1, would partially blend into each other due to the closer separation between training directions (Fig. 7B, solid gray trace). The prediction error here is relatively small. However, an important deviation from the data is the prediction of incomplete learning in one of the training directions. Note that this model's prediction is shown here only for completeness' sake because the local learning model was already invalidated by the results of experiment 2.

Does spatial weighting of single-gain GPs better predict double-gain generalization?

The de novo generalization models we considered failed to explain the double-gain GPs in experiments 2 and 3. We therefore considered the possibility that double-gain generalization arises from combinations of single-gain GPs. Although successful learning is incompatible with averaging of the two single-gain GPs (the simplest type of combination), we considered other possible combinations of single-gain GPs with weighting coefficients that are functions of direction. The hypothesis behind these models (weighted combination models) was that single-gain GPs may represent special mappings: the single-gain condition reveals a nonrandom mapping that is, for whatever reason, selected by the sensorimotor system. If such a mapping is somehow privileged, we asked whether it might be preserved in the double-gain condition. A simple way to achieve this would be through a weighted combination of single-gain GPs. We analyzed two models of single-gain GP combinations. Details are given in the appendix.

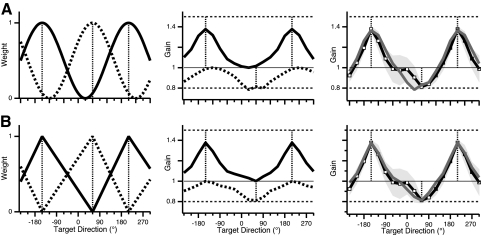
INDEPENDENT SPATIAL WEIGHTING MODEL.

Given that different gains are learned in different directions, one possible strategy is to modulate the single-gain GPs by direction. In the presence of conflicting influences on gain in intermediate directions by single-gain GPs, a weighting process could assign decreasing importance to each GP for directions increasingly removed from the trained direction. We thus hypothesized that single-gain GPs could be combined after being spatially weighted across directions. We refer to this model as “independent” spatial weighting because each weighting function is assigned to a specific single-gain GP, without regard to the training direction for the other gain. We chose cosine as the form of the weighting functions because cosine is a simple form of gradual change between maximum and minimum values across directions. Cosine tuning of neuronal activity is encountered in several cortical areas and thus is a plausible computation for the brain to perform. We hypothesized two cosine weighting functions with peaks in the 1.5 and the 0.8 gain directions (Fig. 8A, left) and multiplied these by the single-gain GPs (see appendix). The result was weighted versions of each single-gain GP (Fig. 8A, middle), which maintained the original functions' values around the respective training directions and which decayed to baseline (value 1.0) at 180° from the training directions. The model predicted a double-gain GP that is the sum of these weighted functions (Fig. 8A, right). The predicted curve qualitatively fit the double-gain GP observed in experiment 1, although it did not capture the flat region between directions −60 and 0°.

Fig. 8.

Weighted combination models hypothesized to account for the double-gain GP observed in experiment 1. Gain (predicted or observed) is plotted against standardized target direction in double-gain condition with imposed gain values 1.5 (−150°) and 0.8 (60°). Vertical dashed lines, training directions. A: independent spatial weighting model. Left: cosine weighting functions, ranging from 0 to 1, with peaks at respective training directions for each gain. Solid trace, gain 1.5; dotted trace, gain 0.8. Middle: weighted versions of single-gain GPs, obtained by multiplying single-gain GPs (traces in Fig. 5, A and B) by the weighting functions (left), after transforming single-gain GPs to deviations from baseline gain of 1. Right: double-gain GP predicted by model (gray) and observed (black). B: relative spatial weighting model. Left: linear weighting functions, ranging from 1 at the training direction for a given gain to 0 at the training direction for the other gain. Slope of each segment is determined by angular separation between training directions. Middle: weighted versions of single-gain GPs, obtained by multiplying single-gain GPs by the weighting functions. Right: double-gain GP predicted by model (gray) and observed (black).

RELATIVE SPATIAL WEIGHTING MODEL.

Given the inadequate fit of the independent spatial weighting model, we considered a method for combining two single-gain GPs that takes into account the angular distance between the two training directions. In this model, the influence of each GP on an intermediate direction is weighted by that direction's relative position between the two training directions (Fig. 8B). We hypothesized piecewise linear weighting functions (that is, functions that are linear but with different slopes and intercepts for different ranges of direction) that ranged from 1 at the training direction for each gain to 0 at the training direction for the other gain (Fig. 8B, left). We then multiplied the single-gain GPs by these weighting functions. The result was weighted versions of each single-gain GP (Fig. 8B, middle), which maintained the original functions' values at their respective training directions and decayed to baseline (value 1.0) at the other training direction. We refer to this model as “relative” spatial weighting because the slope of each linear segment of the weighting functions depends on the angular distance between the training directions. A linear combination of these weighted functions (see appendix) is the predicted double-gain GP, which shows a good fit to the data of experiment 1 (Fig. 8B, right).

We next compared the predictions of the weighted combination models to the results of experiments 2 and 3. For experiment 2, an additional group of subjects (S6, Table 1) were trained in the single-gain 0.6 condition and adapted fully at the training direction, with broad generalization (>50% adaptation) across all directions (Fig. 9A, triangles). Both weighted combination models predicted, based on these single-gain GPs, the observed double-gain data within experimental variability (Fig. 9A). The relative spatial weighting model showed closer correspondence with the data than the independent spatial weighting model.

Fig. 9.

Predicted and observed GPs for weighted combination models in experiments 2 and 3. A: observed gain in single-gain (black trace with circles, gain 0.8; black trace with triangles, gain 0.6) and double-gain (black trace with squares; gray shading, ±1SD) conditions in experiment 2; gain predicted by independent spatial weighting model (dotted gray trace); gain predicted by relative spatial weighting model (solid gray trace). Vertical dashed lines, training directions. B: observed gain in single-gain (black trace with circles, gain 0.8; black trace with triangles, gain 1.5) and double-gain (black trace with squares; gray shading, ±1SD) conditions in experiment 3; gain predicted by independent spatial weighting model (dotted gray trace); gain predicted by relative spatial weighting model (solid gray trace).

The predictions of the weighted combination models in experiment 3 are shown in Fig. 9B. The striking prediction of the independent spatial weighting model was incomplete learning of the 1.5 gain and absent learning of the 0.8 gain (Fig. 9B, dotted gray trace), as a direct consequence of the weighting functions' direction independence: bringing the training directions closer together resulted in greater interference, at the training directions, between the two cosine weighting functions. The relative spatial weighting model maintained a good fit with the data (Fig. 9B, solid gray trace). This model can successfully predict the data in experiment 3 because it explicitly takes into account the angular separation between training directions and therefore can appropriately handle a reduction of this separation.

Note that in the two weighted combination models we first scaled each single-gain GP to account for the amount of learning observed at the training directions in the double-gain condition (see appendix). We did this to remove potential confounding effects of incomplete learning. The models were designed to explain the shape of the GP, regardless of possible scaling effects due to incomplete learning of a given gain.

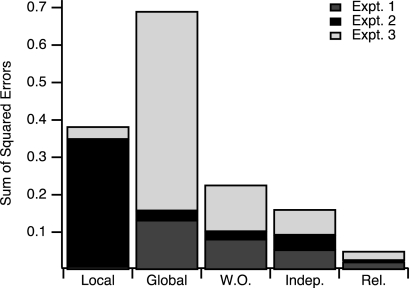
The preceding analysis revealed that only the relative spatial weighting model accurately predicted the double-gain GPs observed in all three experiments. The de novo models failed to explain double-gain generalization in experiments 2 and 3. The independent spatial weighting model was incompatible with the results of experiment 3. To quantitatively compare all models' validity across the three experiments, we calculated the deviation of each model's predictions from the observed double-gain GPs as the sum of squared residuals. This was calculated by first averaging individual subjects' double-gain GPs, then subtracting this average from each model's predicted gain, and then adding the square of these differences across all directions. This is a measure of prediction error that can be compared across models (Fig. 10). The relative spatial weighting model had the smallest error. Note that this analysis is sufficient to establish a statistically valid rank order of the models' performance because the models were based either on experimental conditions (the training directions for the de novo models) or on single-gain data obtained from separate groups of subjects (for the combination models); their predictions were then compared with independently obtained double-gain GP curves.

Fig. 10.

Goodness of fit between predictions of 5 models and data from experiments 1–3. Bar graph indicates sum of squared residuals (model prediction − observed gain at each of 12 tested target directions, averaged across subjects). Shading indicates component of error specific to each experiment (dark gray, experiment 1; black; experiment 2; light gray, experiment 3). Bars indicate errors for local learning (“Local”), global learning (“Global”), weighting-only (“W.O.”), independent spatial weighting (“Indep.”), and relative spatial weighting (“Rel.”) models.

We also calculated error for an additional model, which we refer to as the weighting-only model. We wanted to address the possibility that the good fit of the relative spatial weighting model might derive mostly from the linear weighting functions, rather than from the combination of single-gain GPs. In other words, are the weighting functions of the relative spatial weighting model effectively encoding the double-gain generalization pattern and are single-gain GPs therefore unnecessary in that model? The weighting-only model consisted of piecewise linear functions that connected the learned gains in each training direction for the double-gain conditions (see appendix for details). As Fig. 10 shows, this model's prediction error is much larger than that of the relative spatial model, which demonstrates that linear interpolation, without single-gain GPs, is inferior as a model of double-gain generalization to either of the combination models.

Learning rates

As noted earlier, the learning rate in experiment 1 was clearly slower in the double-gain than in single-gain condition. The models we developed to explain the double-gain GP do not make strong predictions about learning rates when learning two gains rather than one. Factors that could slow learning include: interference between learning in two training directions; the need to adopt a new strategy to solve a more complex sensorimotor problem; increased working memory demands; and recruiting or learning weighting functions. Slowing of learning could be explained by the local model as stemming from increased working memory demands, due to the need to learn two gains rather than one. It could be explained by the global learning model due to competition between two opposing tendencies to generalize across all directions. The combination models are compatible with slower or unchanged learning, depending on whether additional practice is required to recruit and/or learn appropriate weighting functions. Thus the reduction of learning rate when learning two gains rather than one (experiment 1) does not help to distinguish the different models' validity.

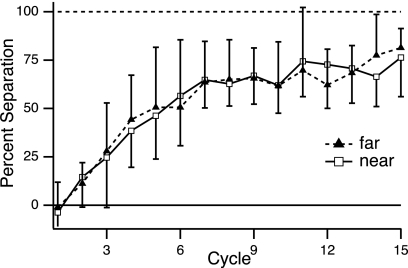
One specific prediction about learning rate, however, can be made for the global learning model. The tendency to generalize broadly leads to interference between the two gains. If this is the basis for the rate reduction in experiment 1 and if generalization is not uniform across directions (as indicated by the single-gain GP), then moving the training directions closer together predicts stronger interference and thus predicts further slowing of learning. In contrast to this prediction, the learning rates in experiments 1 and 3 were indistinguishable. Learning curves for the near and far separation of training directions showed complete overlap (Fig. 11). There was no statistical difference between the two conditions in percent separation between the two gains during early or overall learning (early: average of first 12 trials, P = 0.77; overall: average of 60 trials, P = 0.99; two-sample t-test for unequal variances). The power to detect a percent separation difference of 20 in this experiment, at the α = 0.05 level, was 0.87 for early learning and 0.95 for overall learning. This result is further evidence against the global learning model.

Fig. 11.

Progression of adaptation in training condition (TRN) of double-gain learning with greater (experiment 1) vs. smaller (experiment 3) separation between training directions. Plot shows percent separation (group mean ± SD; see Fig. 4C) between the 2 gains with training directions spaced either 150° from each other (“far”; filled triangles, dashed trace) or 60° from each other (“near”; open squares; solid trace). One cycle = 4 trials.

DISCUSSION

The present study demonstrated that broad generalization does not preclude adaptation to complex sensorimotor environments. Subjects were able to adapt to two different movement amplitude gains in two directions, even though gain adaptation to a single target direction generalized broadly across direction. The resulting double-gain generalization patterns (GPs) could not be explained as an average combination of fixed single-gain GPs, nor were they compatible with locally or globally changing GPs. Instead, the observed double-gain GPs were accurately predicted by a simple weighted combination of single-gain GP, with weighting based on relative angular separation between training directions.

We focused on the relationship between generalization and learning. The main question was whether generalization properties of gain adaptation reflect fixed coding of movement amplitude across direction (fixed-GP hypothesis) or whether they are a consequence of complexity of the mapping being learned (changing-GP hypothesis). The first possibility predicted that learning two gains in two different directions should not be possible, due to interference between competing patterns of generalization. The second possibility predicted that double-gain learning should be possible and that the resulting double-gain GP need not bear any specific relationship to single-gain GPs. Our findings were unexpected because neither prediction was borne out. Instead, subjects successfully adapted to two gains in two directions, and the resulting GP could be explained as a combination of single-gain GPs. The observed learning could not be explained as de novo formation of local or global generalization functions, but was most consistent with direction-dependent modulation of single-gain GPs. Although double-gain subjects never experienced single-gain training, their double-gain GP was consistent with learning each gain as if it were presented in isolation and modulating this learning in a direction-dependent manner.

Modular decomposition of visuomotor maps

Although our results are not consistent with the fixed-GP hypothesis, our analysis established that a major feature of this hypothesis can be preserved if it is considered a special case of a larger framework for neural representations in which multiple fixed mappings can be combined through gating modules to solve complex problems.

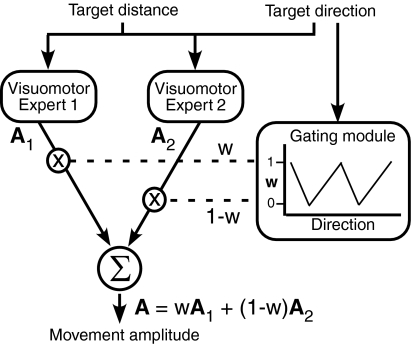
The observed double-gain GPs were well explained as combinations of single-gain GPs, modulated by weighting functions based on task variables (angular separation between training directions). Such a combination constitutes a type of “modular decomposition” (Fig. 12), previously described by Ghahramani and Wolpert (1997) for visuomotor adaptation and originally introduced as the solution achieved by artificial neural networks known as “mixtures of experts” (Jacobs 1999; Jacobs et al. 1991; Jordan and Jacobs 1994). In this network architecture, a complex problem is solved by developing “expert” modules that solve simpler components of the problem, and then combining these through appropriate “gating” modules. Mixture-of-experts architectures have been proposed as neural models of visuomotor adaptation (Ghahramani and Wolpert 1997), phoneme classification (Waterhouse and Cook 1997), object recognition (Gomi and Kawato 1993), number representation (Casey and Ahmad 2006), and control of grasping (Moussa 2004). Brain activity in visuomotor adaptation supports the existence of such architectures as a solution to certain visuomotor adaptation problems (Imamizu et al. 2004). This architecture also bears functional analogies with movement representation based on motor primitives that are combined through appropriate weighting to produce a large variety of motor behavior (Mussa-Ivaldi and Bizzi 2000; Mussa-Ivaldi et al. 1994; Polyakov et al. 2009; Thoroughman and Shadmehr 2000).

Fig. 12.

Modular decomposition model of sensorimotor transformation that computes, for a given target distance, movement amplitudes for given target directions. The model is the same as the mixture-of-experts model introduced by Ghahramani and Wolpert (1997), but with input and output quantities and gating function specific to the relative spatial weighting model of the present study. The model takes target distance and direction and computes movement amplitude based on the weighted combined output of 2 visuomotor experts, each encoding a single-gain GP. [Adapted by permission from Macmillan Publishers Ltd: Nature 386: 392–395, © 1997.]

In the study reported by Ghahramani and Wolpert (1997), when subjects learned to move to a single visual target from two different starting hand locations, the generalization pattern was consistent with decomposition of the solution into separate modules. The expert modules were two (hypothesized) simple visuomotor maps with uniform generalization across the workspace. They were combined through a sigmoidal weighting function (gating module) that encoded the relative distance between initial hand positions. In our study, the expert modules are single-gain GPs and the gating module is the function that assigns relative weight to each single-gain GP based on relative separation between training directions. Note that, although the relative spatial weighting model uses two functions, these (unlike those of the independent spatial weighting model) are related to each other, in that their sum equals one. Therefore a single gating module can compute weighting for both single-gain GPs (Fig. 12).

While Ghahramani and Wolpert (1997) measured generalization only for the complex mapping and showed that it was consistent with the weighted output of hypothesized simple mappings, we directly measured both simple and complex mappings and showed that they can be related by linear weighting. Our study thus provides, to our knowledge, the first direct demonstration of a “mixture-of-experts” solution to a complex visuomotor mapping in which the expert modules were independently measured. Given the irregular shapes of the single-gain GPs and the specificity of their shapes to the particular values of gain being learned, it is remarkable that a simple piecewise linear weighting function yielded a good fit to the observed double-gain GP in each of this study's three experiments.

The question of whether generalization interferes with learning was directly addressed in a study of force-field adaptation, in which subjects adapted to two different force fields in separate regions of the arm workspace (Hwang et al. 2003). When movements were made in untrained workspace regions, generalization was consistent with linear weighting of each force field by arm position. Although linear weighting bears analogies with the relative spatial weighting model, a crucial difference is that, in the case of force fields, weighting was not relative: it reflected arm position and its slope did not vary with separation between training workspace regions. As a consequence, when training positions were brought closer together so that single-force-field GPs overlapped, learning became slower and incomplete, suggesting that generalization imposed a constraint on learning. Because weighting in this case was encoded by a fixed parameter, learning could not adjust to increasing task complexity. In the relative spatial weighting model, in contrast, the slope of the linear gating segment was adjusted when the training directions were moved closer together. This eliminated the increase in interference that would otherwise result and made it possible to fully learn the two gains, regardless of angular separation between training directions. In support of this advantage of modular decomposition, subjects in experiment 3 learned the two gains as well, and at the same rate, as in experiment 1. It is possible that force-field adaptation engages different strategies, compared with gain adaptation, when complex mappings are to be learned, due to differences between the generalization patterns associated with these perturbations (narrow for force field, broad for gain).

Direction-dependent selection of a mapping was observed when subjects adapted to different force fields in different directions (Wainscott et al. 2005). In this case generalization was consistent with a multiplicative effect of direction on mapping selection. Because different combinations of directions and force fields were not tested, it is unknown whether the multiplicative effect was fixed by direction, analogously to Hwang et al. (2003), or flexible according to relative direction differences, as in our study.

Modular decomposition, as a solution to visuomotor adaptation, incorporates elements of the fixed-GP and changing-GP hypotheses. The single-gain GPs remain fixed, as predicted by the fixed-GP hypothesis, and a separate computation is performed so that the solution can handle increased environmental complexity. Given that the form of the weighting functions used by the gating module in a mixture of experts is not constrained by data in our experiment, how can one disprove the modular decomposition hypothesis? In principle, weighting functions can be crafted with enough complexity to transform combinations of simple GPs into complex GPs of almost any desired shape (Schaal and Atkeson 1998). If the gating module were allowed to incorporate increasing complexity, the expert modules would contribute little to the representation. Indeed, a gating module could learn the double-gain mapping itself and obviate entirely the need for single-gain experts. In this case the solution would have nothing to do with modular architecture, but would instead represent an arbitrary new solution to the double-gain mapping, as predicted by the changing-GP hypothesis. The poorer fit of the weighting-only model to the double-gain data provided experimental confirmation that the good fit of the relative spatial weighting model was not principally attributable to the weighting function.

It must be noted that a weighted combination of single-gain GPs is not the only possible interpretation of double-gain GPs observed in this study. Indeed, if our goal were to reproduce the data with a combination model, then more complex weighting functions would surely provide a better fit to the data, simply by having more adjustable parameters. The reason we find the relative spatial weighting model of interest is that it provides a reasonable fit to the data (within the bounds of measurement error) by combining single-gain GPs through a relatively simple and plausible weighting function whose parameters are set by the task structure rather than obtained through a curve-fitting procedure. The weighting function is simple in the sense that it directly reflects the relative angular separation between training directions, which is a quantity that can be obtained from the environment, given that angles have a natural value (360°) to serve as scale. It is plausible in the sense that the nervous system could compute it by linearly encoding two readily available task parameters (training directions), a computation that the nervous system could readily achieve. Indeed, linear encoding of position exists in several nervous system structures (Andersen et al. 1997; Masino and Knudsen 1990; Prud'homme and Kalaska 1994; Tillery et al. 1996). Among the linear combination models we considered, two simpler ones were not consistent with the data: averaging the two single-gain GPs should have prevented double-gain learning, and the independent spatial weighting model failed for closely spaced directions.

Although our analysis identified a simple model that accounts for the data, it does not establish whether the brain actually implements modular decomposition. The success of the relative spatial weighting model in explaining the double-gain GP does not prove that the brain learns the double-gain mapping through modular decomposition, but it establishes that this is a possible solution. We consider the model attractive for its parsimony compared with arbitrary curve fitting, but whether it is correct depends on other factors, such as the nature of the expert modules. If these happen to be well-established modules that are readily available, then it may be computationally advantageous to use them, along with an appropriate gating module, in the solution of a complex problem. This would favor the development of a mixture-of-experts representation.

A notable feature of our results is that they did not provide an account of the shape of single-gain GPs. Modular decomposition does not specify the form of representations at individual experts' level. Both combination models simply use single-gain GPs as determined by experimental data. One of the de novo models not only embodied an instance of the changing-GP hypothesis, but also had the potential to explain single- and double-gain learning within one framework. The global learning model is based on the principle that visuomotor gain is considered as uniform as possible across directions and deviates from uniformity only as imposed by the environment (e.g., different gains in different directions) and in the smoothest possible manner. In the case of single gain, this principle would produce a broad GP across directions that, to a large extent, fits our and previous observations of generalization in single-gain learning. The global learning model, however, could not account for the double-gain GPs in our three experiments.

Generalization and internal models

Generalization patterns have been used in some studies to infer the structure of internal models, that is, internal representations of mappings used by the nervous system to control movement. This is possible for representations that are presumed to be based, as seems the case for many types of representations in the cerebral cortex, on a population code, in which a perceptual feature or movement parameter is encoded in the pooled activity of a population of neurons (Poggio 1990; Poggio and Bizzi 2004; Pouget et al. 2000; Schaal and Atkeson 1998). In such models, individual neurons are assumed to respond to their inputs in a graded fashion, for example, according to “basis functions” with Gaussian shape. Adaptation in a population code of a mapping is naturally accompanied by generalization because a change in a neuron's response to a given input necessarily leads to a change in response to neighboring inputs. If a sensorimotor mapping is assumed to be encoded by a population of neurons with Gaussian response functions (referred to as basis functions because they span the space of the mapping) and, if GPs are inferred through trial-by-trial analysis of a state-space model (Thoroughman and Shadmehr 2000), then the width of the basis functions can be inferred from the GP. This approach makes it possible, for example, to use generalization data to estimate the width of tuning curves of neurons that relate direction of a visual target to the direction of hand movement required to reach it (Tanaka et al. 2009) and of neurons that relate joint torque to a desired joint angle and velocity (Shadmehr 2004).

Whether basis functions have a constant shape or whether they change with learning remains unclear. A fixed shape offers computational advantages because it allows individual neurons' tuning curves to act as building blocks that encode rules about neighboring relationships for task-relevant variables. However, a recent study identified instances of generalization that suggest that the width of presumed basis functions changes with learning and is determined by the complexity of the mapping to be learned (Thoroughman and Taylor 2005).

It is important to note that model neuronal basis functions, which model individual neurons' response properties, are distinct from what we refer to as GPs (and others have referred to as generalization functions), which indicate macroscopic properties of perceptual or sensorimotor representations. Our study does not directly inform on whether underlying neuronal basis functions are fixed or change with learning because our data are not amenable to the state-space analysis required to infer the properties of model basis functions. However, by demonstrating that double-gain generalization can be explained as a weighted combination of single-gain GPs, our study does establish that fixed basis functions are compatible with sensorimotor representations of movement amplitude. This is because, if single-gain representations can be combined, unchanged, through a weighting function, then neuronal representations of gain can also remain unchanged.

A natural question that emerges from our findings concerns the limits of modular decomposition. What is the range of complex mappings that can be generated through weighted combinations of simple generalization functions? This translates to the question of how complex a gating module can be learned. An example of a limit on this type of learning concerns adaptation to different visuomotor gains for different coordinate axes (Bock 1992). When different gains were imposed for the vertical and horizontal components of movements, gain adaptation was intermediate with only minimal direction dependence. Having different gains for horizontal and vertical components of direction results in gain that varies as a sinusoidal function of direction. In Bock's experiment, there were seven different values of gain, associated with seven different target directions. If learning multiple gains occurs through modular decomposition, it is possible that the mapping imposed in Bock's study may have been too difficult to learn by a mixture of experts. The observed difficulty in learning this mapping may indicate an inability of the gating module to learn nonlinear weighting functions. Additional experiments would be needed to directly test whether, when faced with a sufficiently complex mapping, the nervous system forsakes fixed patterns of generalization and adopts a curve-fitting strategy, or whether performance is limited to what can be learned with available patterns of generalization and gating modules.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant NS-007155-26 to T. S. Pearson, National Institutes of Health Research Project Grant R01-050824 to J. W. Krakauer and P. Mazzoni, and a Parkinson's Disease Foundation research grant to P. Mazzoni.

DISCLOSURES

No conflicts of interest are declared by the authors.

APPENDIX

The models used to examine the nature of the observed generalization functions in double-gain conditions were defined as follows. We use “gain 1” and “gain 2” to generically refer to each gain in double-gain conditions. For all models, direction θ, with range [−180°, 180°], refers to standardized target direction (see methods). The models express gain as a function of movement direction: G = f(θ). There are two training directions (θ₁, θ₂), each associated with a different imposed gain.

Local learning model

Gain in the double-gain condition was modeled as a function of direction, G_d(θ), which consists of the sum of two Gaussians, each centered at the respective training directions, with amplitudes A₁, A₂, SD σ, and bias 1

$$G_d(\theta )=1+A_1{e}^{-[{(\theta -{\theta }_1)}^2/2{\sigma }^2]}+A_2{e}^{-[{(\theta -{\theta }_2)}^2/2{\sigma }^2]}$$ (A1)

where G_d is the double-gain generalization pattern (GP), θ is target direction, 1 is the value of gain at baseline, and θ₁ and θ₂ are training directions in the double-gain condition. Each Gaussian represents the deviation of gain from baseline. Amplitudes A₁ and A₂ were set to the deviation from baseline gain (i.e., deviation from 1) of the value of gain observed at the training directions after training in the double-gain conditions. We chose observed double-gain GP values as the peaks of the Gaussians because the models were developed to explain the shape of the double-gain GP, regardless of the amount of learning achieved in each training direction. (We also examined alternative versions of this model in which amplitudes A₁, A₂ were set to the imposed gain for a given training direction. The results were qualitatively similar.) We estimated the SD σ of the model's Gaussian functions by first fitting Gaussian functions to each peak of the double-gain data (Fig. 5C). We used five data points centered on each peak to fit each Gaussian and obtained widths of 45° for the peak around gain 1.5 and 50° for the peak around gain 0.8. Given the similarity of these values, we used their average (47.5°) as the model Gaussian's width σ. The bias of the function was set at 1 (i.e., the function modeled deviations of gain from its baseline value of 1). Note that the value of σ was calculated as just described based on data obtained in experiment 1 and was kept at this value (47.5°) when modeling data from experiments 2 and 3. The reason for this is that σ in this model is hypothesized to represent the width of local tuning of movement amplitude across direction and should not be influenced by the choice of training directions.

Global learning model

This model was devised to maximize smoothness of the transition between gains in two directions. Gain was modeled as a smoothing spline: G(θ) = S(θ), where S(θ) was calculated as the (periodic) smoothing spline interpolation for the points (“knots”) G(θ₁) = G₁ and G(θ₂) = G₂, where θ₁, θ₂ indicate training directions in the double-gain condition. As in the local model, values of G₁ and G₂ were set to the gains achieved by subjects in the double-gain condition at the two training directions, that is, the deviation from baseline gain of the value of gain observed at the training directions after training in the double-gain conditions. The spline's smoothing factor r was chosen to be maximally relaxed, i.e., the smallest value (0.001) below which the fit did not further improve (on visual inspection). Smoothing splines were calculated using the built-in function “Interpolate2” in the Igor software package (WaveMetrics, Lake Oswego, OR), which implements the method in Reinsch (1967).

Independent spatial weighting model

For the weighted combination models, we introduced a function, G_s(θ), to represent GPs in single-gain conditions. This was calculated from the raw data as follows. The group mean values of a single-gain GP (SGGP; Fig. 5B) were transformed into deviation from baseline gain by subtracting 1. The SGGP was scaled by a ratio R, between the gain in a given training direction in the double- and single-gain conditions. This ratio had the effect of matching values of gain in the training directions between single- and double-gain conditions because our model was aimed at explaining the shape of double-gain GP (DGGP) and not the amount of learning in the training directions. For the 0.8 GP, this scaling resulted in no observable difference because the 0.8 gain learned was nearly identical in single- and double-gain conditions. For the 1.5 GP, this scaling amounted to a 14% reduction of the single-gain GP because the observed gain in the single- and double-gain conditions was 1.43 and 1.37, respectively. The single-gain function was thus defined as G_s = R(SGGP − 1). For gains associated with training direction θ₁, θ₂, the single-gain model functions were, respectively

$$\begin{array}{c}{G}_{s1}\left(\theta \right)=R_1\left(SGG{P}_1-1\right)\\ R_1=DGGP\left({\theta }_1\right)/SGG{P}_1\left({\theta }_1\right)\end{array}$$ (A2)

$$\begin{array}{c}{G}_{s2}\left(\theta \right)=R_2\left(SGG{P}_2-1\right)\\ R_2=DGGP\left({\theta }_2\right)/SGG{P}_2\left({\theta }_2\right)\end{array}$$ (A3)

The independent spatial weighting model used weighting functions W₁, W₂ that were cosine functions of target direction relative to training direction, adjusted to range from 0 to 1

$$\begin{array}{c}{W}_1\left(\theta \right)=2\cos \left({\theta }_1-{\theta }_2\right)-1\\ W_2\left(\theta \right)=2\cos \left({\theta }_1-{\theta }_2\right)-1\end{array}$$ (A4)

The model double-gain function G_d was defined as

$$G_d(\theta )=1+W_1(\theta )G_{s1}(\theta )+W_2(\theta )G_{s2}(\theta )$$ (A5)

Relative spatial weighting model

The functions G_s1(θ), G_s2(θ), which represent single-gain GPs, were defined as for the independent spatial weighting model. The weighting functions W₁, W₂ were linear functions of the separation between target direction and training direction, relative to the separation between training directions

$$\begin{array}{c}{W}_1\left(\theta \right)=\left(\theta -{\theta }_1\right)/\left|{\theta }_2-{\theta }_1\right|\\ W_2\left(\theta \right)=\left(\theta -{\theta }_2\right)/\left|{\theta }_2-{\theta }_1\right|\end{array}$$ (A6)

The model double-gain function G_d was defined as

$$G_d(\theta )=1+W_1(\theta )G_{s1}(\theta )+W_2(\theta )G_{s2}(\theta )$$ (A7)

Weighting-only model

This model assigned gain values to the training directions equal to the observed training-direction values in the double-gain condition. Values between training directions were computed through linear interpolation between these values. Formally, if the training directions are θ₁, θ₂ and the observed values of gain in these directions are, respectively, G₁ and G₂, then the model double-gain function is

$$G_d(\theta )=m(\theta -{\theta }_0)K$$

where m and K assume one of two possible sets of values

$$\begin{array}{c}m=\left(G_2-G_1\right)/\left({\theta }_2-{\theta }_1\right)\\ K=G_1\hspace{0.17em}\text{for}\hspace{0.17em}{\theta }_1\le \theta <{\theta }_2\end{array}$$ (A8)

$$\begin{array}{c}m=\left(G_1-G_2\right)/\left({\theta }_1+2\pi -{\theta }_2\right)\\ K=G_2\hspace{0.17em}\text{for}\hspace{0.17em}{\theta }_1\le \theta <{\theta }_2\end{array}$$ (A9)

This yields an asymmetric sawtooth function that ranges in linear segments between the values of learned gains in each training direction.