The Role of V1 Surround Suppression in MT Motion Integration

Abstract

Neurons in the primate extrastriate cortex are highly selective for complex stimulus features such as faces, objects, and motion patterns. One explanation for this selectivity is that neurons in these areas carry out sophisticated computations on the outputs of lower-level areas such as primary visual cortex (V1), where neuronal selectivity is often modeled in terms of linear spatiotemporal filters. However, it has long been known that such simple V1 models are incomplete because they fail to capture important nonlinearities that can substantially alter neuronal selectivity for specific stimulus features. Thus a key step in understanding the function of higher cortical areas is the development of realistic models of their V1 inputs. We have addressed this issue by constructing a computational model of the V1 neurons that provide the strongest input to extrastriate cortical middle temporal (MT) area. We find that a modest elaboration to the standard model of V1 direction selectivity generates model neurons with strong end-stopping, a property that is also found in the V1 layers that provide input to MT. With this computational feature in place, the seemingly complex properties of MT neurons can be simulated by assuming that they perform a simple nonlinear summation of their inputs. The resulting model, which has a very small number of free parameters, can simulate many of the diverse properties of MT neurons. In particular, we simulate the invariance of MT tuning curves to the orientation and length of tilted bar stimuli, as well as the accompanying temporal dynamics. We also show how this property relates to the continuum from component to pattern selectivity observed when MT neurons are tested with plaids. Finally, we confirm several key predictions of the model by recording from MT neurons in the alert macaque monkey. Overall our results demonstrate that many of the seemingly complex computations carried out by high-level cortical neurons can in principle be understood by examining the properties of their inputs.

INTRODUCTION

A striking feature of the primate visual system is the increase in the complexity of stimulus selectivity as one ascends the hierarchy of extrastriate cortical regions. Whereas most neurons in the primary visual cortex (V1) respond well to oriented edges at a particular point in space, neurons in the temporal and parietal processing streams respond well to specific faces or complex motion patterns. This is often thought to reflect an increase in the complexity of the computations performed by the higher-level areas, but another possibility is that important computations are performed in the neurons that provide input to the extrastriate cortex. In this study we examine this latter possibility in the context of a simple model of motion processing in the dorsal visual pathway of the macaque monkey.

The earliest stage of the primate dorsal visual stream is the V1, where receptive fields are generally <1° in diameter. Neurons in the middle temporal (MT) area have receptive fields tenfold this size and receptive fields in the medial superior temporal (MST) area are larger still. Because most of the visual input in these higher areas comes directly or indirectly from V1, receptive fields in MT and MST are presumably derived by spatially integrating the outputs of many neurons with smaller receptive fields.

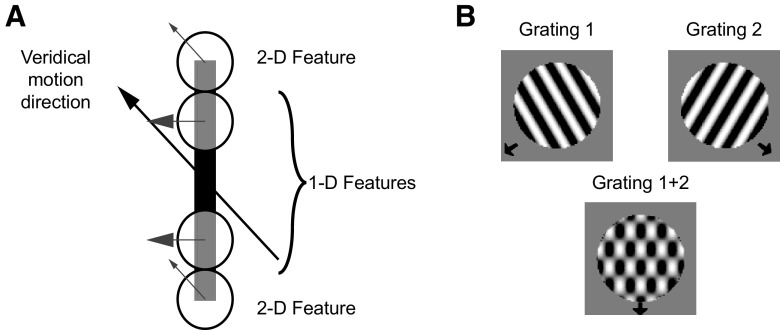
Spatial integration may serve many purposes, but in the domain of motion processing it is likely to be of crucial importance for overcoming a class of computational challenges that can collectively be described as correspondence problems (Ullman 1979). One example is the aperture problem (Fig. 1A), in which the measurement of the velocity of a moving edge is rendered ambiguous by the fact that any point along the edge can be associated with any other point at a subsequent instant in time (Wallach 1939). Consequently, there exists a family of local velocity measurements that are consistent with the global motion of the edge.

Fig. 1.

Stimuli used in the simulations. A: tilted bar stimulus. The orientation of the bar is rotated 45° counterclockwise with respect to its direction of motion. The direction of motion measured at the endpoints contains 2-dimensional features corresponding to the veridical motion direction. The edge of the bar contains only one-dimensional features that correspond to the direction of motion perpendicular to stimulus orientation. The ambiguity of these signals results from the aperture problem. B: plaid stimulus. The plaid stimulus is composed of 2 gratings drifting in different directions of motion (top). When the gratings are superimposed (bottom) the perceived direction of the resulting pattern corresponds to the motion of neither component.

Physiological studies of the aperture problem have made use of various kinds of visual stimuli. One of the best-known examples is the plaid stimulus (Adelson and Movshon 1982), which is composed of two gratings that are combined to form a single motion pattern (Fig. 1B). In general the perceived motion of the plaid corresponds to the motion of neither grating, even though most neurons in V1 respond to the motion of these components. However, many neurons in MT respond to the motion of the pattern (Movshon et al. 1986) and this has been interpreted as evidence that these neurons solve the aperture problem. Other MT neurons have responses similar to those of V1 cells, in that they respond to the motion of the plaid components. Studies using additive, sinusoidal plaids have generally reported roughly equal numbers of component-selective and pattern-selective neurons in MT (Movshon et al. 1986).

A second class of stimuli used in physiological studies of the aperture problem contains moving features that provide locally unambiguous motion signals. One example is a tilted bar stimulus (Li et al. 2001; Lorenceau et al. 1993; Pack and Born 2001), the endpoints of which provide velocity signals that can in principle be extracted by very small receptive fields (Fig. 1A). For these stimuli one finds that the vast majority of macaque MT cells accurately signal motion direction, in the sense that their responses to motion depend very little on the orientation of the bars that comprise the stimulus (Pack and Born 2001). In these experiments the neurons were not classified as pattern- or component-selective, so the relationship between the responses to the two types of stimuli is not entirely clear.

Component cells are typically modeled using a simple motion energy detector (Adelson and Bergen 1985), which has been highly successful in accounting for a variety of physiological and psychophysical findings. A key feature of the motion energy model is that its receptive field is a linear filter that effectively responds to only one plaid component at any point in time (thus the component selectivity). The responses of such a model to the tilted bar stimuli described earlier have not been examined, but as we show in the following text, motion energy models, in contrast to MT neurons, make large errors in signaling the motion of the tilted bar (see Fig. 3).

Fig. 3.

Model MT responses without V1 end-stopping. The tuning curve at the center shows the response of a model MT cell preferring leftward motion to a tilted bar moving in various directions, with an orientation that is tilted by 45° with respect to the direction of motion (bar/arrow icons). The angular deviation from the preferred direction of motion of the MT cell is 33.4°. Each peripheral panel shows the population responses, wherein each pixel corresponds to the activity of a single model V1 cell that prefers leftward motion.

Numerous models have been designed to simulate pattern selectivity by combining the outputs of motion energy detectors in various ways. A common feature of these models is the existence of nonlinear interactions among V1 neurons (Simoncelli and Heeger 1998), the result of which is sometimes described as normalization (Heeger 1992). Indeed recent modeling work has suggested that such interactions are necessary for pattern selectivity in MT (Rust et al. 2006), although in that work the spatial form of the normalization was not specified.

In this work we suggest that all of the above-mentioned results on motion integration in MT can be accommodated by a model that incorporates a spatially specific type of normalization at the level of V1. The model is composed of a number of motion energy detectors that are connected to each other in such a way as to provide normalization that is stronger along each cell's preferred orientation axis. This property is often called end-stopping in the physiological literature (Hubel and Wiesel 1965) and end-stopped V1 neurons have been shown to be capable of responding exclusively to the motion of the endpoints of bars (Pack et al. 2003). Moreover, cells with these properties are extremely common in the MT-projecting layers of V1 (Sceniak et al. 2001), suggesting that they may play a key role in motion integration (Noest and van den Berg 1993; van den Berg and Noest 1993).

The model provides a straightforward means of connecting the various results on motion integration in MT. We find that motion energy detectors combined with end-stopping can solve the aperture problem for tilted bar stimuli, but that the same model neurons are component-selective when tested with plaid stimuli. Pattern selectivity can be generated in the model by combining the outputs of model units tuned to different motion directions, so as to generate broad direction tuning. Thus end-stopping is necessary to model MT responses to tilted bars, but not sufficient for pattern selectivity, and this explains the differences in motion integration seen with the two classes of stimuli. Our results suggest that V1 end-stopping is crucial to the function of all MT cells and that the continuum from component to pattern selectivity simply reflects the variation in direction tuning bandwidth observed in this area. These results thus demonstrate that complex properties found in the extrastriate cortex can in principle be attributed to computations that are already present in the inputs from V1.

METHODS

Modeling methods

MT receptive fields are composed of multiple, nearly identical subunits (Livingstone et al. 2001) (Supplemental Fig. S1) whose responses can be approximated as motion energy detectors (Pack et al. 2006).¹ We have therefore constructed a model of a single MT receptive field consisting of a population of identical motion energy subunits tiled across space (Fig. 2B). We have extended this basic model by incorporating suppressive input from neighboring detectors arranged along the length of the excitatory receptive field, to simulate in a straightforward way the effects of end-stopping (Supplemental Fig. S2A). This suppressive influence is modeled with standard divisive normalization (Heeger 1992). The outputs of these end-stopped neurons are then fed into a model MT neuron, which sums them over space and time. The entire MT model was implemented in MATLAB (The MathWorks).

Fig. 2.

Model. A: motion energy model (adapted from Adelson and Bergen 1985). The stimulus is processed by 2 spatial filters and the resulting outputs are convolved with several temporal filters, recombined, squared, summed, and passed through a square root operation prior to the computation of an opponent stage. See methods for details. The end-stopped stage is added at the initial stage (dotted box, top right). B: middle temporal (MT) model. The MT cell receives input from a population of primary visual cortex (V1) cells with spatially shifted receptive fields. The output is determined by summing over these inputs with SoftMax weighting.

ENERGY MODEL.

Figure 2A shows the standard motion energy detector (Adelson and Bergen 1985), which we describe here briefly for completeness. Each V1 receptive field was modeled with a pair of phase-shifted Gabor filters and a pair of temporal filters. The Gabor filters had a spatial frequency of 2 cycles/° and SD of 0.25°, which yielded a receptive field size of about 1° in diameter. In our simulations the spatial resolution was 20 pixels/°. The temporal filters took the form suggested by Adelson and Bergen (1985)

$$f(t)={(gt)}^n{e}^{-gt}\left[\frac{1}{n!}-\frac{{(gt)}^2}{(n+2)!}\right]$$ (1)

where n is 3 for one filter and 5 for the other, g is 100, and the sample time is 8 ms. The filters were shifted in time so that the peak response of the fast filter occurred at 48 ms and that of the slow filters occurred at 64 ms.

The response of the energy model was computed by taking the dot product of the spatial filters and the stimulus and convolving the resulting outputs with the temporal filters. The result of this operation was then combined and squared in such a way to produce direction selectivity that was invariant to the spatial phase of the stimulus. As suggested by Adelson and Bergen (1985), we added a square root operation after the sum-of-squares to keep the output within a reasonable range.

END-STOPPING.

We elaborated on the basic motion energy model by adding a nonlinear, suppressive component, which appears at the separable response stage (Fig. 2A, box in the top right). The effects of end-stopping were modeled as an interaction between a center unit and six surround units, with three units above and three units below a vertically oriented cell; all units were identical motion energy detectors as defined earlier. The center and surround units were spaced 1° apart and aligned either obliquely or along the length of the center cell (Supplemental Fig. S2A).

For each stimulus presentation the model summed the outputs of the surround units placed on either end (up or down for a vertically oriented cell) of the center unit. Rather than summing the raw output of each unit we used the envelope of the temporal responses, defined according to

$$h{r}_{up}(t)={\displaystyle \sum _{i=1}^3\parallel H[r_{u{p}_i}(t)]}\parallel$$ (2)

$$h{r}_{down}(t)={\displaystyle \sum _{i=1}^3\parallel H[r_{dow{n}_i}(t)]}\parallel$$ (3)

where r_upi(t) and r_downi(t) are the outputs of the separable responses of the top ith and bottom ith cells in the case of a vertically oriented center cell (other orientations were generated by rotating the septuplet of center and surround cells by the appropriate angle). The envelopes of the responses in Eqs. 2 and 3 were computed via the Hilbert transform and this was done primarily to reduce the number of units in the model (and thus to speed up the simulations), but an equivalent result could be obtained by using a collection of surround units with different temporal impulse response functions.

The total surround response was then given by the following function

$$r_{surround}(t)=\sqrt{h{r}_{up}(t)·h{r}_{down}(t)}$$ (4)

The use of a multiplicative interaction in the equation ensured that the center cell was maximally inhibited when surround cells above and below the center unit were active. This allowed the model end-stopped unit to simulate two properties of real end-stopped cells: It was strongly suppressed by a long bar centered on its receptive field, but responded well to the endpoints of the same stimulus (Hubel and Wiesel 1965; Pack et al. 2003). As we show in the following text this type of interaction generated end-stopping that was similar in strength to that found in V1 (see Fig. 7). The square root operation, similar to that of the motion energy model, helped to maintain the inhibition strength within a reasonable range.

Fig. 7.

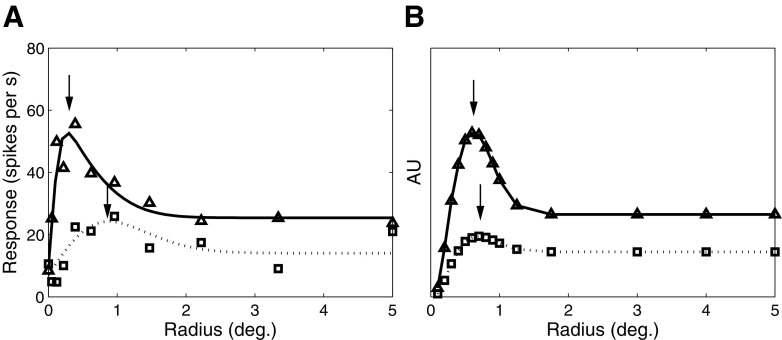
Effect of contrast on spatial summation in V1. A: size tuning for a complex cell from layer 4B for high (triangles) and low (squares) contrasts (adapted from Sceniak et al. 1999). B: model end-stopped responses as a function of stimulus size. The solid and dotted traces correspond to the responses elicited by high- and low-contrast drifting gratings. For both the model and real V1 cells, the optimal size (black arrows) increases and the suppression strength decreases as contrast decreases.

The final output of the end-stopped unit was then given by

$$R_{end-stopped}(t)=\frac{r_{in}(t)}{\epsilon +r_{in}(t)+k{r}_{surround}(t-d)}$$ (5)

where r_in(t) is the response of the center cell; r_surround(t − d) is the total surround response, which influences the output of the model neuron at a delay d; and k is a gain parameter that is one of the two free parameters that were manipulated to obtain the results described in the following text. The constant ε (set to 1 for all simulations) prevented the model output from becoming too large in the presence of weak inputs, but as we show later it also played an important role in accounting for some of the temporal dynamics observed in MT. Another advantage of modeling suppressive input as divisive (rather than subtractive) is that divisive inhibition better accounts for the observed interactions between contrast and surround suppression (Cavanaugh et al. 2002). This equation is similar to that used in standard normalization models (Heeger 1992), with the crucial difference being the spatial specificity implicit in the end-stopped model. This formulation allows us to explore the role of this spatial specificity in accounting for data from MT.

MT INTEGRATION.

For all simulations the input to the model MT cell came from the outputs of 22,801 identical end-stopped V1 units. Integration at the MT stage of the model was achieved by applying a “Soft-Maximum” (hereafter referred to as SoftMax) operation to the outputs of a population of end-stopped cells tiled 0.1° apart from each other. SoftMax is a simple way of combining inputs over space and time, while capturing a variety of nonlinearities that are observed in real neuronal responses, with a minimal number of free parameters (Lampl et al. 2004; Riesenhuber and Poggio 1999). The SoftMax equation is as follows

$$MT(t)={\displaystyle \sum _{i=1}^n\frac{{\displaystyle {\sum }_{\sigma =t-\tau }^t{R}_i(\sigma ){\displaystyle {\sum }_{\sigma =t-\tau }^t{e}^{p{R}_i(\sigma )}}}}{{\displaystyle {\sum }_{j=1}^n{\displaystyle {\sum }_{\sigma =t-\tau }^t{e}^{p{R}_j(\sigma )}}}}}$$ (6)

Here R_i(t) and R_j(t) are the responses of the ith and jth end-stopped cells, τ is the integration time constant, and p is a parameter that determines the degree of nonlinearity at the summation stage. Small values of p cause the model to perform a vector average of the inputs, whereas very large values of p correspond to a winner-take-all strategy. Previous work has suggested that a vector average is a reasonable approximation to the operation performed in MT neurons on their inputs (Pack et al. 2004; Snowden et al. 1992), so we set p = 2.5, which represents a vector average with an amplification of larger inputs relative to smaller ones. This manipulation is conceptually (and mathematically) quite similar to the introduction of an accelerating static nonlinearity at the V1 stage (Simoncelli and Heeger 1998). We found empirically that the value of τ had little effect on the simulations, so we set it to 16 ms, which conferred a low-pass characteristic on the temporal responses of the neurons.

MT OUTPUT NONLINEARITY.

For the plaid simulations, the output of MT neurons included a static nonlinear component, which we modeled with a sigmoid function of the form

$$r_{\mathrm{snl}}=\frac{r_{\max }}{1+e^{l(r_{\text{mid}}-r_{\text{bw}})}}+r_o$$ (7)

Here, r_snl is the nonlinear output of MT. The free parameters r_max = 1.1, l = 11, r_mid = 1, and r_o = 0.1 correspond to the maximum response, the degree of the slope, the half-maximum response, and the minimum response of the sigmoid function, respectively.

Neurophysiology methods

ELECTROPHYSIOLOGICAL RECORDINGS.

For the plaid experiments, we prepared two rhesus macaque monkeys for experiments by performing a sterile surgical procedure to implant a headpost and a recording cylinder. The recording chamber was positioned to allow for a posterior approach of the microelectrode through the occipital lobe to MT, which was subsequently identified based on anatomical magnetic resonance imaging scans, the clustering of direction-selective neurons, and the depth of the electrode penetration. Following recovery, the monkeys were trained to fixate a small red dot on a computer monitor. Eye position was monitored at 200 Hz with an infrared camera (SR Research) and was required to be in a fixation window of 2°. We performed single-unit recordings using tungsten microelectrodes. Waveforms were first sorted on-line and subsequently re-sorted off-line using spike-sorting software (Plexon).

The data for the bar field experiments consisted of unpublished results related to a prior set of experiments (Pack and Born 2001). Electrophysiological methods were identical to those described in the previous publication (Pack and Born 2001) and identical to those used to collect the plaid data, with the exception that eye position in these experiments was monitored with an eye coil.

PROCEDURE AND VISUAL STIMULI.

On each trial a fixation point appeared and the monkeys were required to fixate for 300 ms before the appearance of the stimulus. For each neuron, we first characterized direction selectivity with a drifting sinusoidal grating of optimal size, position, and spatial and temporal frequency on a gray background (luminance of 70.3 cd/m²). Prior to the onset of motion the grating remained stationary for 200 ms, after which it began moving in one of 12 randomly interleaved directions spaced around the circle at 30° intervals. The plaid stimuli were constructed by superimposing two gratings at half the grating contrast oriented 120° apart. Stimuli were displayed at 60 Hz at a resolution of 1,920 × 1,200 pixels and the viewing area subtended 70 × 42° of visual angle at a distance of 42 cm. All neurons were tested with high (100%) and low (10 or 5%) contrast stimuli.

The bar field stimuli were identical to those used in Pack and Born (2001). The size of the stimuli was chosen to match the size of the receptive field, which was estimated by hand-mapping with a small bar stimulus. Although this method underestimates the extent of the receptive field, it also ensures that the bar field stimuli used did not extend into the surrounds of the MT cells. Each bar subtended 3° on a grid spacing of 5°, except in the experiment on bar length, where we used lengths of 2, 4, 6, and 8°. In this case the spacing between bars was adjusted to keep the total luminance of the stimulus constant across bar lengths. On each trial the stimulus appeared on the screen and was stationary for 250 ms before moving in one of 8 directions (45° spacing) or one of 12 directions (30° spacing). A subset of neurons was tested with a bar length of 3° at high- (61.9 cd/m²) and low-luminance stimuli, with the latter being defined in this case subjectively as the lowest contrast that would reliably drive each cell. The resulting bar luminances ranged from 0.28 to 0.54 cd/m² in experiments involving a black background (0.024 cd/m²) and 16 to 20.0 cd/m² for those involving a gray (15.49 cd/m²) background. Since there were no obvious differences between the results in the two background luminance conditions, data were combined across them. All directions and contrasts were randomly interleaved.

Data analysis

Unless otherwise noted, spikes were averaged over a time period that spanned from 150 ms after the onset of stimulus motion until the end of the stimulus. This time period was chosen to exclude the early response period, during which the selectivity of MT neurons often changes substantially (Pack and Born 2001; Pack et al. 2001). Neurons were considered direction-selective if their tuning curves could be fit to a von Mises function (P < 0.05 for an F-ratio test). Recordings that did not meet these criteria were not included in the analysis. Bandwidth was calculated as the full width at half-maximum of the von Mises function.

The responses to plaids were classified according to the Z-transformed partial correlation coefficients between the data and the component and pattern predictions (Smith et al. 2005; Tinsley et al. 2003) using the following equations (shown for the Z-transformed pattern correlation)

$$Z_p=0.5\left[\frac{\ln \mathrm{\left(}\frac{1+P{C}_p}{1+P{C}_c}\right)}{\sqrt{1/(n-3)}}\right]$$ (8)

where n corresponds to the number of motion directions (12 in our experiments) and PC_p is defined as follows

$$P{C}_p=\frac{R_p-R_c{R}_{cp}}{\sqrt{(1-R_c^2)(1-R_{cp}^2)}}$$ (9)

where R_p and R_c are the raw correlations between the data and the pattern prediction and component predictions, respectively, and R_cp is the raw correlation between the two predictions. The Z-transformed component correlation (Z_c) can be obtained by exchanging PC_p and PC_c and the partial correlation (PC_c) between the component prediction and the data can be obtained by replacing R_p with R_c in the preceding equations. The pattern index was defined for each cell as Z_p − Z_c.

RESULTS

Our goal in this study was to develop a simple computational model that accounts for the data on two types of stimuli that probe the ability of MT neurons to overcome the aperture problem. In this section we present the results of the model, along with MT data that provide a test of one of the main model assumptions.

Tilted bar stimulus

As shown in Fig. 1A, a tilted bar stimulus provides a direct way to assess the effects of the aperture problem on the responses of neurons in the visual cortex. The majority of local motion measurements are limited to the component of motion perpendicular to the orientation of the bar, with the correct velocity signals being available only near the endpoints, which comprise a small fraction of the stimulus area. Nevertheless, the vast majority of MT cells respond to the motion of this stimulus in a way that does not depend on bar orientation. A role for the endpoints in driving MT responses was subsequently confirmed in both MT and V1 end-stopped neurons (Pack et al. 2003, 2004). To assess the role of end-stopping, the response of the model to tilted bar stimuli was evaluated both with and without end-stopping.

MODEL MT RESPONSES WITHOUT V1 END-STOPPING.

Figure 3 shows the responses of the V1 population to a bar subtending 3°, moving at a speed of about 6°/s after remaining stationary for 240 ms, in 16 different directions spaced evenly around the circle. Bar orientation was always rotated 45° clockwise with respect to the direction of motion. Each pixel in the population activity map corresponds to the time-averaged response of a V1 neuron that prefers leftward motion. The MT response is obtained by integrating the output responses of the population of V1 neurons (Fig. 2B). For these simulations we disabled end-stopping by setting the gain of the divisive normalization in Eq. 5 to k = 0. Thus the output of the MT model is simply the normalized motion energy outputs described in methods filtered through the nonlinear SoftMax operation; this output is shown as the tuning curve in the center of the figure.

A few points are evident in the simulation. First, the peak of the population activity clearly occurs for upward and leftward motion (135°), even though the model neuron's preferred direction of motion is leftward. This is a direct consequence of the aperture problem: a vertically oriented bar moving upward and leftward generates local motion signals that correspond to the leftward component of motion, irrespective of the vertical component (Fig. 1A), leading to an error of >30° in the direction tuning curve. We refer to this rotation of the tuning curve from the neuron's actual preferred direction as the angular deviation. In contrast to the results shown in Fig. 3, real MT neurons tested with the same stimuli showed an average angular deviation of about 5° (Pack and Born 2001). Second, the tuning curve is narrow despite the compressive nonlinearity (square root) at the oriented energy stage, normalization, and the SoftMax integration. In other words the response in the upward-leftward direction far exceeds the responses in other directions, which yields a tuning curve that is narrower than those typically observed in MT (Albright 1984). Finally, the moving bar stimulus clearly contains a small amount of motion energy in the neuron's preferred direction (180°), as shown by the two activity blobs in the population output. These responses correspond to model V1 neurons that are stimulated by the endpoints of the moving bar and their modest amplitude reflects the need for a nonlinear operation to calculate the correct direction of bar motion.

MODEL MT RESPONSES WITH V1 END-STOPPING ENABLED.

End-stopping offers a natural solution to the problem illustrated in Fig. 3, since it attenuates the ambiguous responses to the bar stimulus, while having little effect on the responses to the endpoints (Hubel and Wiesel 1965; Pack et al. 2003). Figure 4 shows the tuning curve and the population activity map for the same tilted bar stimulus, but with end-stopping turned on by setting the gain term in Eq. 5 to k = 5.

Fig. 4.

MT responses with end-stopping. Conventions are the same as those in Fig. 3. The peripheral panels show that the endpoints evoke stronger responses than the edges of the bar and the central panel shows the tuning curve, which has a preferred direction that now deviates by only 3.5° from leftward.

From Fig. 4 it can be seen that the V1 population now responds primarily to the endpoints of the bar, while remaining strongly selective for leftward motion. Moreover, the MT tuning curve now has a reasonably broad bandwidth, which is consistent with the physiological responses of real MT neurons (Albright 1984), resulting from the compressive nonlinearity inherent in the divisive inhibition of the end-stopping model, which attenuates the amplitude of the responses to the one-dimensional motion signals that otherwise far exceed the responses to the endpoints. End-stopping thus allows the model neuron to overcome the aperture problem by eliminating ambiguous signals found along the length of the bar. The preferred direction of the tuning curve found in the center of the figure is now 3.5° away from the correct motion direction, which is similar to what was found in MT (Pack and Born 2001). Thus the addition of a straightforward mechanism for end-stopping substantially improves the correspondence of the model output to MT physiology.

IMPORTANCE OF SPATIALLY SPECIFIC SUPPRESSION.

Several previous models of MT motion integration have also made use of divisive normalization at the V1 stage and this has been shown to be particularly important for capturing the responses to plaid stimuli (Rust et al. 2006). However, these models do not specify the spatial structure of the normalization pool, whereas we have claimed that the arrangement of inhibitory units can be important for modeling the responses to the tilted bar stimulus. To further test this idea, we reran the simulation depicted in Fig. 4 with different surround configurations (Supplemental Fig. S2).

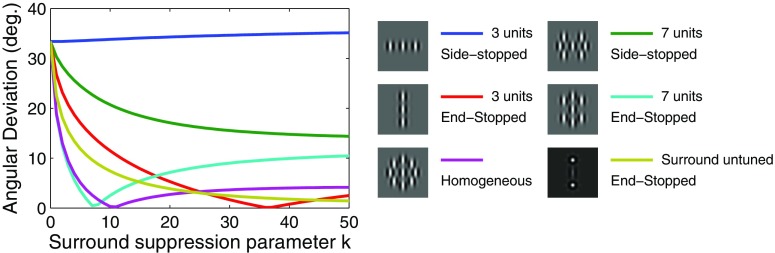
Figure 5 shows the results of the tilted bar simulation for various values of the parameter k, which controls the strength of the inhibitory contribution from the surround units. When the model surround consisted of only two inhibitory units located on either side along an axis perpendicular to the center unit's preferred orientation (side-stopping), the residual error in the preferred motion direction did not change for any value of the gain parameter k (blue line). Inclusion of the oblique inhibitory units (green line) somewhat decreased the angular deviation, but the residual error never dropped to <15°. We then tested the model with two inhibitory units located along the center unit preferred orientation axis only (end-stopping) and found that the model was able to achieve nearly perfect performance for reasonable values of the suppression parameter k (red line). The performance further increased when we included inhibitory units along the oblique axes (cyan line), whereas the extension of the end-stopped model to include a homogeneous surround (Supplemental Fig. S2E) did not appreciably improve the result (magenta line). Taken together, these results suggest that end-stopping is both necessary and sufficient to account for the MT data on tilted bar stimuli. This bears on many empirical findings on V1 surrounds because they are not typically distributed homogeneously in space at the level of single cells. Moreover, the surround asymmetries vary across V1 layers with end-stopped cells congregating in MT-projecting layer 4B (Sceniak et al. 2001).

Fig. 5.

Angular deviation as a function of the surround suppression strength. Angular deviation is the rotation of the tuning curve introduced by tilting the bar stimulus by 45°. The figure shows this value for the model with surrounds consisting of 3 side-stopped units (blue line), 7 side-stopped units (green line), 3 end-stopped units (red line), 7 end-stopped units (cyan line), homogeneous inhibition (magenta line), and end-stopped units with multiple preferred orientations (brown line). The surround suppression strength was manipulated by varying the parameter k that controls the strength of inhibition (see methods). The configurations with end-stopping units lead to small errors.

Thus far the results suggest that a spatial surround that includes end-stopping is important for motion integration and that this property is robust to the addition of surround units at other spatial locations. A related question is whether the performance of the model is similarly robust to the addition of surround units with tuning for different motion directions. To address this issue we tested an end-stopped surround that also included inhibitory units tuned to different orientations (horizontal, vertical, oblique left, and oblique right), above and below the center unit. Again, performance does not appreciably change (brown line), suggesting that the end-stopped model is both useful for motion integration and robust to the addition of other types of surround units.

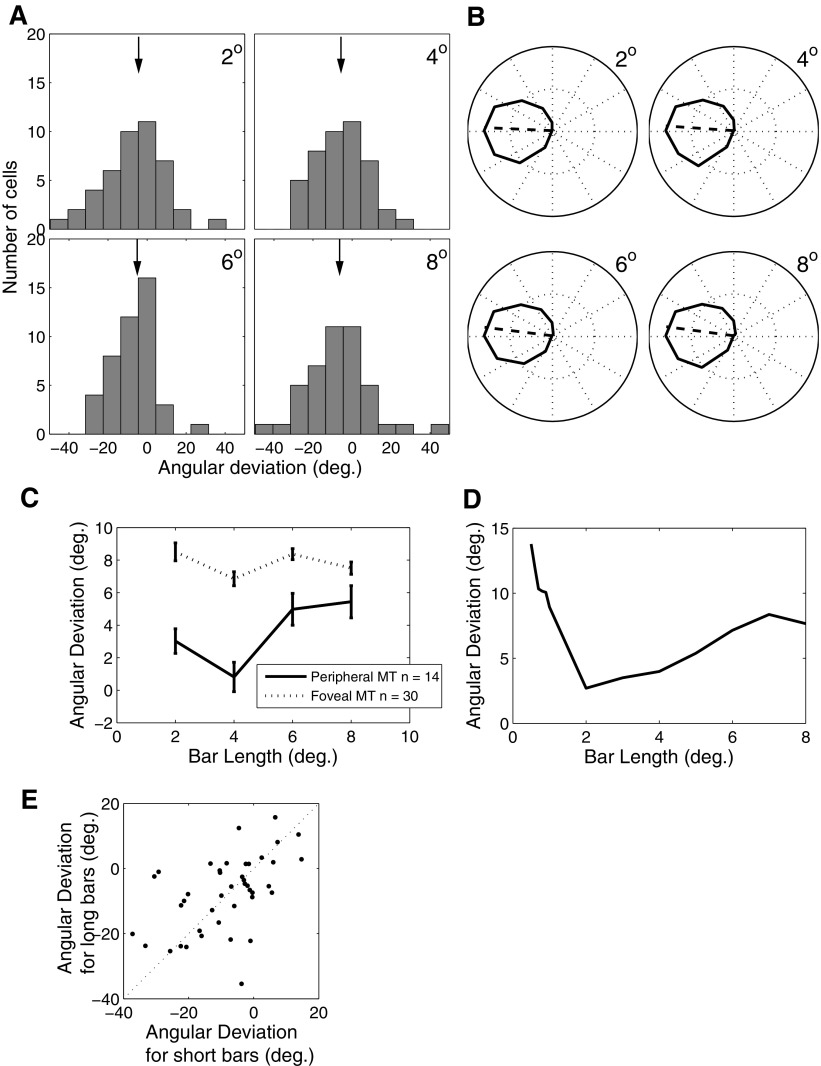
BAR LENGTH INVARIANCE IN REAL MT CELLS AND IN THE MODEL.

The previous sections have shown that an MT model that receives end-stopped V1 input can calculate the motion direction for tilted bar stimuli by preferentially responding to the two-dimensional (2D) motion signals present in the stimulus. A direct prediction of this line of reasoning is that increasing the length of the bars will have little or no effect on the responses of MT neurons because this manipulation does not affect the stimulus features to which end-stopped neurons are sensitive. We tested this prediction by recording from 44 MT neurons while presenting stimuli of varying direction, tilt angle, and length. As in the previous sections, we quantified the ability of MT neurons to accurately compute motion direction in terms of changes in the preferred motion direction with the tilt of the bars relative to their motion direction.

Figure 6A summarizes the results of this experiment for the MT data. Each panel shows the distribution of preferred directions relative to those measured during the control condition (no tilt) for a given bar length. In each case there is a distribution of angular deviations, but the mean of this distribution does not significantly change with bar length (ANOVA, P > 0.9). Figure 6B shows that the model MT neuron is similarly insensitive to bar length, with the angular deviations increasing only slightly with bar length from a value of 2.7° for a bar length of 2 to 7.66° for a bar length of 8°. The mean angular deviations for the same set of bar lengths in MT ranged from 4.8 to 7.3°. We also did not observe an effect of bar length on firing rate in the MT population (ANOVA, P > 0.5) or in the model.

Fig. 6.

Angular deviation as a function of bar length. A: distribution of angular deviations in a population of 44 MT cells for tilted bars of different lengths. The black arrows in each panel indicate the median angular deviation values (4.8, 6.6, 5.8, and 7.3° for 2, 4, 6, and 8° bar lengths, respectively). B: tuning curves from the model for different bar lengths. The correspondent angular deviation values are 2.7, 4.0, 7.2, and 7.7°. C: angular deviation as a function of bar length for central (dotted) and peripheral (solid) cells. Cells were considered peripheral if they had an eccentricity of >10°. D: same as C for the model. E: cell-by-cell correlation of angular deviation values for long (8°) vs. short (2°) bars.

Although there was no statistically significant effect of bar length on the angular deviations of the MT population, there was substantial variability across individual neurons. This raises the possibility that individual neurons might exhibit strong effects of bar length but that this relationship might be obscured by the population analysis. To examine this possibility more closely, we plotted the angular deviation for short versus long bars for each of the 44 MT cells in Fig. 6E. These values were strongly correlated (P < 0.001), suggesting that the angular deviations for small bars were predictive of those for long bars on a cell by cell basis. Importantly, there was no evidence for a subpopulation of cells that had small errors for short bars and large errors for long bars. Thus the responses of MT cells were generally immune to large changes in the strength of one-dimensional motion signals, except for a modest and nonsignificant tendency for angular deviation to increase with increasing bar length. Similar results were found in the model for changes in bar width as well (results not shown).

Although bar length might be expected to affect local motion measurements, a more relevant quantity is the bar length relative to the size of the receptive fields that process the stimulus. Receptive field size in early visual areas is strongly linked to retinal eccentricity; thus a straightforward prediction of this line of reasoning is that the angular deviations observed in MT might depend on eccentricity and that this dependence may interact with bar length (Lorenceau et al. 1993). Figure 6C shows the angular deviations for the tilted bar stimuli of different lengths for cells with receptive fields within 10° eccentricity (top; and for those >10°, bottom). In general, angular deviations at all bar lengths are smaller for the more eccentric cells, suggesting that large receptive fields are less affected by the aperture problem for a given bar length. We have previously found a similar trend in data from experiments involving smooth pursuit eye movements (Born et al. 2006).

This analysis yielded another interesting finding related to the interaction of receptive field size and bar length. From Fig. 6C it is apparent that the angular deviation actually decreases for the peripheral cells as bar length is increased from 2 to 4°. This tendency is also present in our model (Fig. 6D) because the endpoints of very short bars fail to activate the surround of V1 neurons.

EFFECTS OF STIMULUS CONTRAST ON END-STOPPING.

Our MT model is consistent with the findings of Sceniak et al. (2001) who showed that V1 neurons in the layer that has the strongest MT projection are strongly surround-suppressed and that their length suppression is stronger than their side suppression. In a related study (Sceniak et al. 1999), it was shown that surround suppression is highly dependent on stimulus contrast, such that suppression is reduced or eliminated as contrast decreases (Fig. 7A). In our model one might expect similar behavior, given that the suppression term in the denominator of Eq. 5 depends on both the normalization strength r_in + kr_surround and an offset value that we have set to ε = 1. For low contrasts the value of r_in + kr_surround ≪ ε, so the response depends primarily on activity of the center unit, with the inhibitory input being negligible. For higher contrasts r_in + kr_surround ≫ ε, so the response is suppressed for large stimulus sizes.

To verify that our model exhibits behavior similar to that of the neurons reported in the previous studies, we tested the responses of a single end-stopped unit in our model to a drifting grating of varying contrast. In the Sceniak et al. (1999) study, the contrast levels for each neuron were chosen to be on the low and high ends of the linear region of the cell's contrast response function. We performed an analogous test by first calculating a contrast response function for the model neuron and then choosing contrasts that yielded responses that were, respectively, 60 and 30% of the saturation response. The results (Fig. 7B) show contrast-dependent effects that are qualitatively similar to the physiological data, with receptive field size increasing and surround suppression strength decreasing at low contrast (dotted line) compared with high contrast (solid line). Recordings from V1 cells have shown somewhat greater effects of contrast on receptive field size and these effects can be modeled with the addition of a separate contrast gain parameter for the inhibitory units (Cavanaugh et al. 2002). We have not incorporated this property into our model because it would involve additional free parameters.

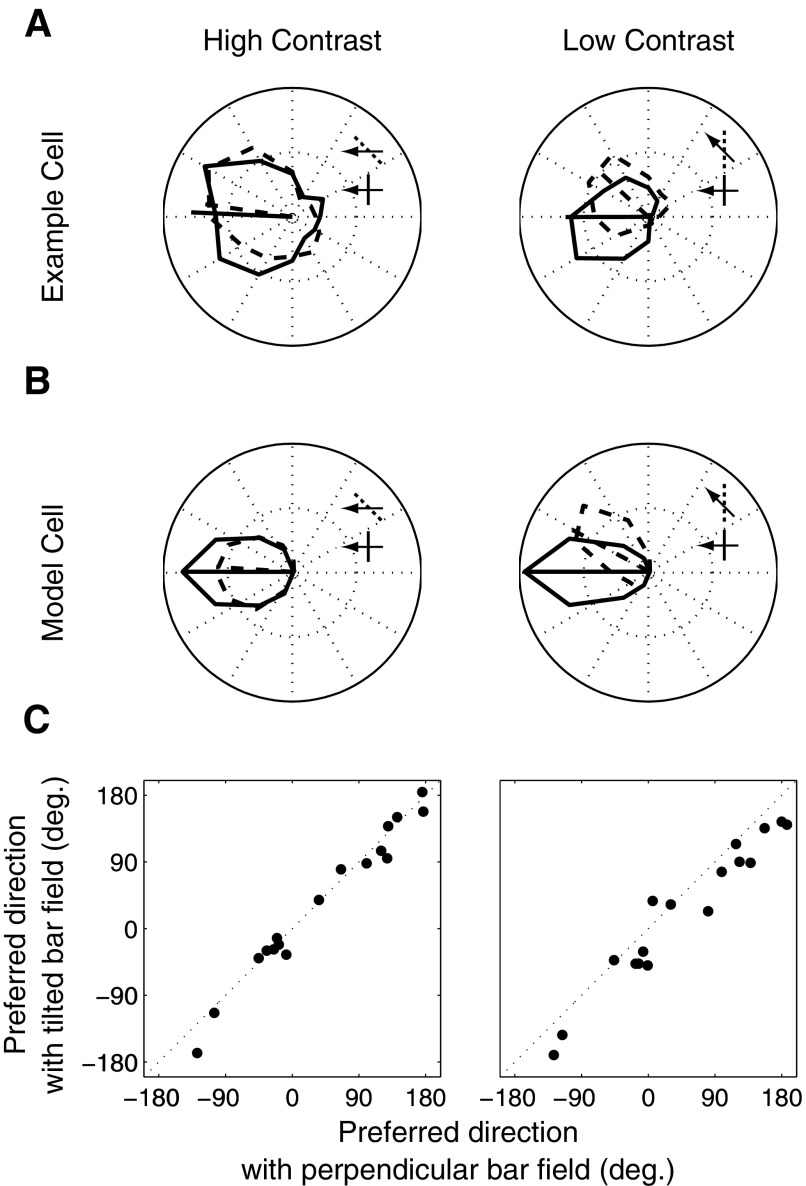
The contrast dependence of end-stopping provides us with a straightforward means of testing the key model hypothesis that end-stopping is responsible for many of the complex response properties found in MT. Specifically, if MT solves the aperture problem by virtue of end-stopped inputs, then it follows from the results shown in Fig. 7 that motion integration should be less accurate for low-contrast tilted bar stimuli. We tested this idea using data related to a previously published study (Pack and Born 2001). Figure 8A shows the responses of an example MT cell for bars with orientation perpendicular to the motion direction (solid curves) and for those rotated 45° (dotted curves) clockwise. As contrast decreases, the preferred direction for the perpendicular condition changes very little, whereas that for the tilted bars rotates by >30°. Thus the neuron is more affected by the aperture problem for low-contrast bars than for high-contrast bars. For comparison, Fig. 8B shows the contrast dependence of our model for the same stimuli. As contrast level decreases, the ratio of inhibitory strength relative to the excitatory strength decreases and one-dimensional motion signals have a stronger effect on the output of MT.

Fig. 8.

Effect of contrast on angular deviation. A: an example MT cell. The solid and dotted traces correspond to the tuning curves for bar field stimuli with no tilt and a 45° tilt at high (left) and low (right) contrasts. The bar/arrow icons show the configuration of a stimulus moving at the cell's preferred direction for the 2 tilt conditions. The arrows and bars illustrate the configurations that evoked the strongest responses. B: responses of the model MT cell under the same conditions. C: preferred directions for the tilted bar at high (left) and low (right) contrasts for 17 MT cells. At low contrast, the points lie below unity line, indicating an increase in angular deviation.

The rotation of the tuning curves can be used as a measure of the influence of contrast on motion integration in MT. We calculated this measure for 17 MT cells, by taking the vector average of the tuning curves under the two orientation conditions; the results are plotted in Fig. 8C for both high and low contrasts. Here each point corresponds to a single neuron's preferred direction and it is clear that this direction changes for nearly all of the neurons tested at low contrast. Specifically, at low contrast the preferred direction rotates toward that predicted by the component of motion perpendicular to the orientation of the bars. Although the sample size was not terribly large, the effect was quite consistent across cells and highly significant for the population (P < 0.001). A similar effect of contrast on perceived motion direction has been observed psychophysically (Lorenceau et al. 1993).

TEMPORAL DYNAMICS IN REAL MT CELLS AND IN THE MODEL.

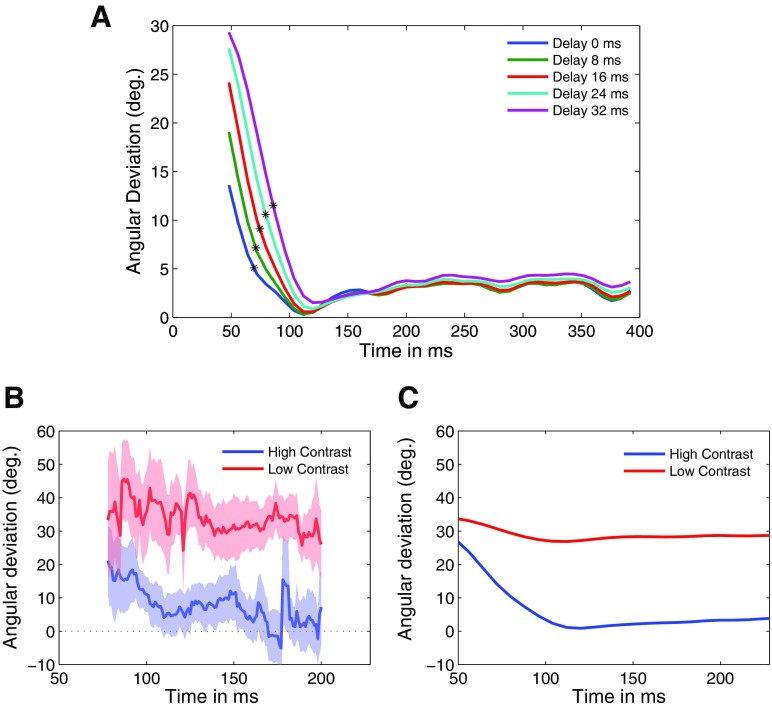
For the bar-field stimuli used in the previous study, Pack and Born (2001) showed that MT initially responds strongly to one-dimensional motion signals and subsequently encodes the true direction of motion after a delay of about 60 ms. We examined this result in more detail to determine whether our model could produce similar results. Figure 9A shows the angular deviation plotted against time for different delays, which was achieved by changing the delay parameter d in Eq. 5. We began measuring the angular deviation at the peak of the temporal impulse response of the motion energy model (48 ms). Surprisingly, even when no explicit temporal delay was incorporated into any stage of the model (i.e., when d was 0), the temporal transition (blue line) was qualitatively similar to that observed in real MT cells (Pack and Born 2001).

Fig. 9.

A: the temporal dynamics of angular deviation for different values of the delay parameter d (blue: d = 0; green: d = 8 ms, red: d = 16 ms, cyan: d = 24 ms; and magenta: d = 32 ms). B: mean responses of 17 MT cells as a function of time for high-contrast (blue) and low-contrast (red) bar stimuli. C: model response to the high- (blue) and low-contrast (red) bar stimuli.

The model explanation for these intrinsic temporal dynamics is quite similar to that outlined previously for the effects of contrast on end-stopping. Specifically, immediately following the onset of stimulus motion the outputs of both the center and the surround units are near zero. For such small responses the influence of the surround is negligible, so that the surround plays only a minor role early in the temporal response, just as it plays a very minor role for low-contrast stimuli. Specifically, for the initial response of the model, the value of r_in + kr_surround ≪ ε in Eq. 5, so the output of the model is essentially proportional to the raw motion energy in the numerator of Eq. 5. As shown in Fig. 3, this output is heavily influenced by one-dimensional motion signals. Once the responses of the motion energy units increase so that r_in + kr_surround ≫ ε, the surround influence substantially reduces the response to the preferred orientation, while preserving the response to the preferred motion direction, as shown in Fig. 4. A similar explanation for other temporal effects in V1 has been previously proposed (Carandini et al. 1997).

The match between the temporal dynamics observed in the model and that observed in real MT cells could be improved through the introduction of explicit delays in the surround response. Figure 9A shows the effects on the temporal response of changing the parameter d in Eq. 5 to various values. Not surprisingly, larger values of d simply delayed the transition from one- to 2D motion responses (green: d = 8 ms, red: d = 16 ms, cyan: d = 24 ms; and magenta: d = 32 ms) in Fig. 9A. Based on these transitions we computed the time constant, defined as the time when the angular deviation reached 1/e times the difference between the maximum and minimum angular deviations for each curve in Fig. 9A. Under this analysis the value of d that best matched the physiological time constant of 30 ms (Born et al. 2006) was a delay of d = 24 ms. We thus fixed d = 24 for the remaining simulations in this study.

Figure 9B shows the temporal dynamics for the 17 cells that were tested with both high- and low-contrast stimuli. Although these data are naturally somewhat noisy, the temporal transition seen in the high-contrast data is not apparent in the low-contrast response because the mean angular deviation remains nearly constant for the duration of the stimulus presentation. Similar effects are seen in the model (Fig. 9C).

Plaid stimulus

The previous sections showed that end-stopping of the type found in V1, in combination with a set of motion energy detectors, is sufficient to account for the responses of MT neurons to tilted bar stimuli. This suggests that the aperture problem can be overcome by appropriate spatial filtering at the level of V1, although it is not clear how such a mechanism would be effective for stimuli that lack 2D features of the kind found in tilted bar stimuli. In particular, whereas most MT neurons accurately encode the motion of tilted bars (Pack and Born 2001), previous studies have found that as many as 40% of MT neurons fail to integrate the motion of certain kinds of plaid stimuli (Movshon et al. 1986) (Fig. 1B). This would seem to be at odds with the previous findings (Pack and Born 2001) (Fig. 8C) that the vast majority of MT neurons are capable of integrating the motion of tilted bar stimuli. This latter result requires substantial nonlinearities, as indicated by Fig. 3, and so we were interested to investigate to what extent the same mechanisms could account for the data on plaid stimuli. We therefore tested our model with a plaid stimulus composed of two superimposed gratings that were oriented 120° apart. For these simulations we added a static nonlinearity (see methods) to the MT output, in that pattern selectivity cannot be computed for linear combinations of inputs (this follows from the definition of the pattern index in Eq. 9). The parameters of the nonlinearity were fixed for all simulations.

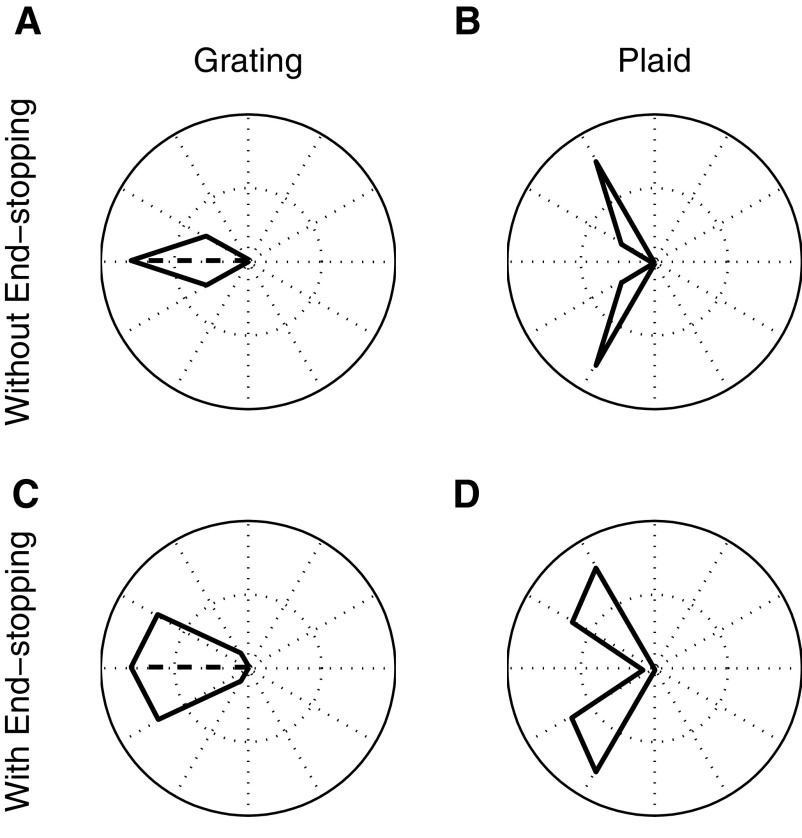
MODEL MT RESPONSES WITHOUT END-STOPPING.

We first tested the model with end-stopping disabled, by setting the value of k in Eq. 5 to 0. Figure 10, A and B shows the tuning curves corresponding to the model response to the grating and plaid stimuli. Not surprisingly, the output is clearly component-selective, as indicated by the bilobed tuning curve in response to the plaid stimulus (Fig. 10B).

Fig. 10.

Tuning curves for grating (left) and plaid (right) stimuli. A and B: MT model responses to the grating and plaid stimuli with end-stopping turned off. The bilobed tuning curve for the plaid stimulus is consistent with component selectivity. C and D: same as A and B with end-stopping turned on. Again, the model is strongly component-selective.

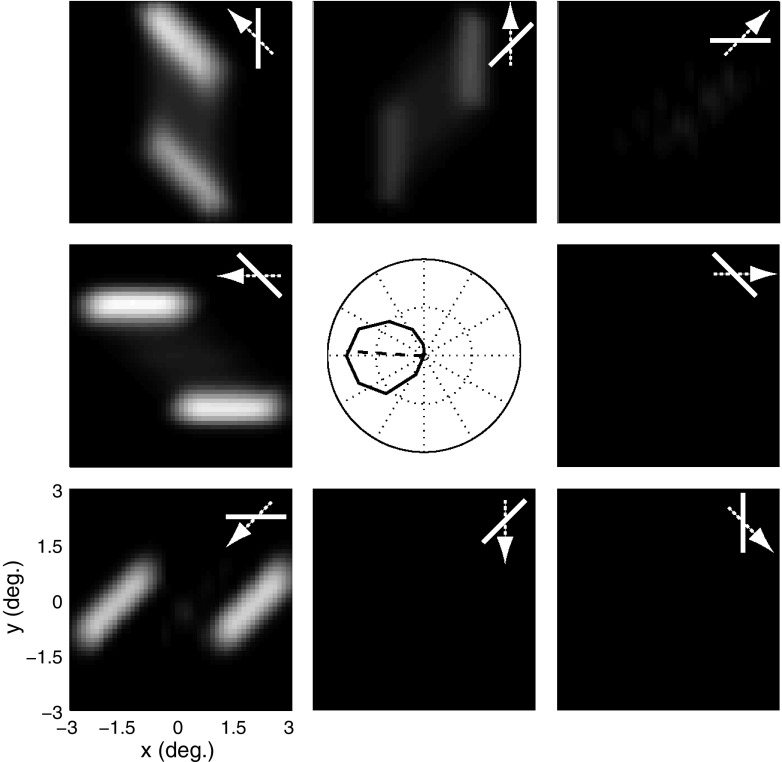
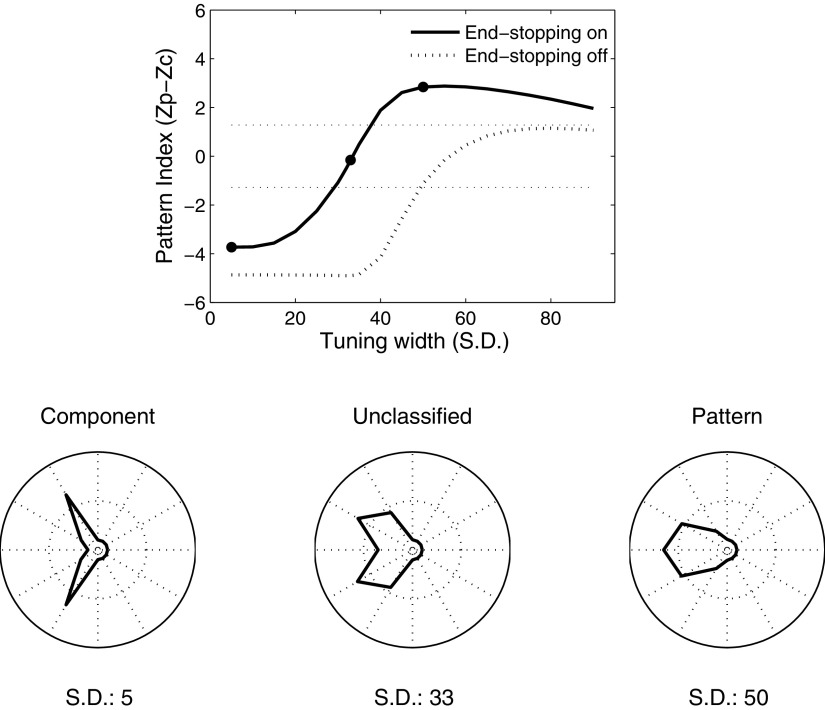
Previous work has suggested that pattern selectivity should depend in part on the width of direction tuning curves in response to gratings (Rust et al. 2006; Tinsley et al. 2003). In particular, one might expect neurons with broader direction tuning to be more pattern-selective, since broad tuning would allow them to simultaneously respond to both grating components. In our model the input to MT comes from V1 neurons that share a single preferred direction and so the direction tuning of the input from the V1 motion energy detectors is quite narrow (Fig. 3). To examine the importance of direction tuning bandwidth on pattern selectivity, we extended the model to include input from V1 neurons tuned to 12 different directions of motion, spaced evenly around a circle. The outputs of each V1 cell were then weighted with a Gaussian profile centered on the preferred direction of the MT neuron, with the integration stage of the model being identical to that used in the previous simulations. Figure 11 (dotted line) shows the resulting pattern index as the SD of the Gaussian weighting function is varied from 5 to 85°. Larger values of the pattern index correspond to tuning curves that are more similar to the prediction of pattern selectivity; lower values are more consistent with component selectivity. Although this index increases with increasing bandwidth, the model neuron fails to be pattern-selective at the criterion level of 1.28 (dashed line) for any bandwidth.

Fig. 11.

Pattern index for varying integration bandwidths. The solid and dotted traces show the pattern index when end-stopping is turned on and off, respectively. As the bandwidth of integration increases, pattern selectivity increases gradually. However, the model does not achieve statistically significant pattern selectivity (top dashed horizontal line) without end-stopping. For narrow bandwidths the model is component-selective (bottom dashed horizontal line), irrespective of the presence or absence of end-stopping. The polar plots at the bottom of the figure correspond to the tuning curves for the model with bandwidths given by the solid dots in the top panel. These example model responses from left to right are characterized as component, unclassified, and pattern.

MODEL MT RESPONSES WITH END-STOPPING.

We next performed the same simulations with end-stopping activated and the pattern index (solid line) as well as the corresponding tunings curves for a component and both an unclassified and a pattern cell are shown in Fig. 11. For narrow bandwidths of the V1 input (Fig. 10D), the model neuron is component-selective, suggesting that, in contrast to the results with tilted bars (Fig. 4), end-stopping in combination with SoftMax and the static nonlinearity is not sufficient to account for motion integration for plaid stimuli. However, when the bandwidth is increased, pattern selectivity increases, indicating that the MT neurons that receive strong end-stopped input can be component-selective or pattern-selective, depending on the range over which they integrate direction-selective inputs.

This improved pattern selectivity is explained primarily by the fact that end-stopping broadens the direction tuning at the level of V1. Indeed the idea that broad direction tuning bandwidth (Rust et al. 2006; Tinsley et al. 2003) and nonlinear normalization at the V1 stage (Rust et al. 2006) are important for pattern selectivity has been suggested before. However, a surprising finding of the current work is that these two response properties can result from a single mechanism. As shown in Fig. 4, end-stopping increases the bandwidth of direction tuning in V1 and our results in Figs. 10 and 11 suggest that this effect is necessary but not sufficient to generate pattern selectivity in MT. Thus a parsimonious account of the results presented thus far is that all MT neurons receive input from strongly end-stopped V1 neurons (thus accounting for the responses to tilted bars) and that the continuum from component to pattern selectivity reflects that variation in direction tuning bandwidth in the convergent projections from V1 to MT.

NEUROPHYSIOLOGY: MT RESPONSES AT LOW- AND HIGH-STIMULUS CONTRAST.

In the model, pattern selectivity arises through broad direction tuning in both V1 outputs and MT inputs, with neither being sufficient on its own to account for the range of selectivity observed in MT. Whereas the latter property (tuning bandwidth of the V1 to MT projection) is fixed in the instantiation of the model, the former (tuning bandwidth of V1 responses) varies according to the parameters of the stimulus. In particular, increased end-stopping leads to increased tuning bandwidth (Fig. 4) and end-stopping varies with stimulus contrast (Fig. 7). Thus a straightforward model prediction is that changes in stimulus contrast should lead to quantitative changes in pattern selectivity in both component- and pattern-selective MT neurons.

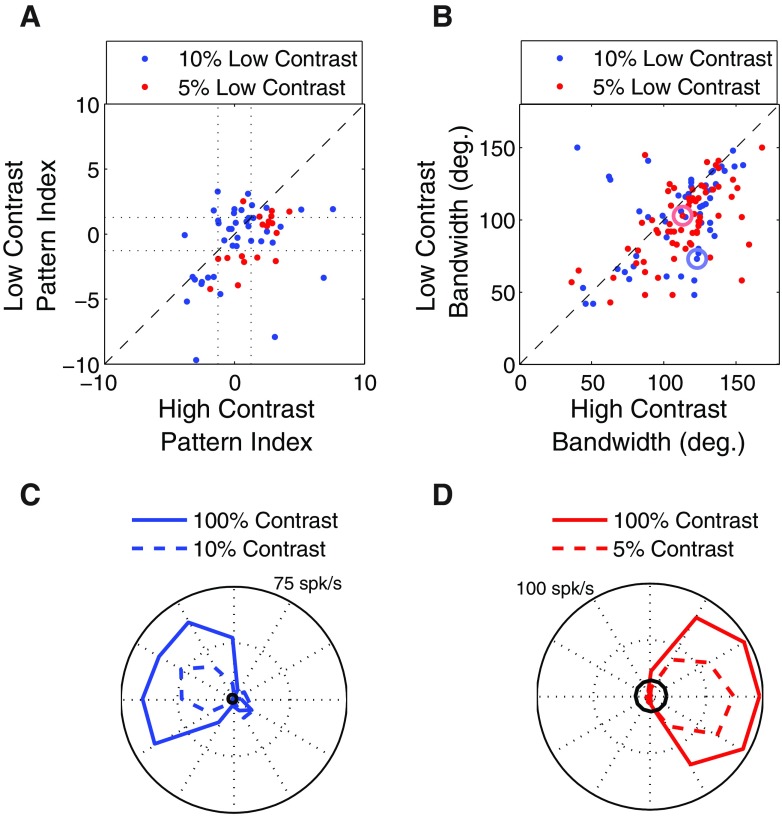
We tested this idea by comparing the responses of 58 MT neurons to plaid stimuli at high (100%) and low (5%, n = 18 or 10%, n = 40) contrast. Figure 12A shows the pattern index (defined in methods) for the population of MT cells that were tested at the two contrasts (blue: 10% low contrast; red: 5% low contrast). Each point in the figure corresponds to a single MT neuron and the shift of the population of points below the main diagonal indicates a general tendency for MT neurons to become more component-selective at lower stimulus contrasts. Across the population there was a significant effect of contrast (two-way ANOVA, no significant interaction, main effect of contrast P < 0.001) and there is no obvious difference in the effects of contrast on component- and pattern-selective neurons, suggesting that the reduction in contrast affects a mechanism common to all cell types.

Fig. 12.

Effect of contrast on pattern index and tuning bandwidth. A: pattern index for 58 MT cells at high and low contrasts. The points lying below the unity line indicate a tendency to become more component-selective at low contrast. B: tuning bandwidth for 133 MT cells in response to a grating stimulus. The points lying below the unity line indicate a tendency to become more narrowly tuned at low contrast. The circled dots correspond to the example neurons in C and D. C: direction tuning curves at high (solid line) and low (dashed line) contrast for the example neuron indicated by the large blue circle in B. Black circle indicates 2SDs above the mean of the baseline firing rate. D: as in C, but for the neuron indicated by the large red circle in B.

The model explanation for the results in Fig. 12A is that low stimulus contrast leads to reduced surround suppression in V1, which leads to narrower direction tuning. This is perhaps a counterintuitive prediction, since tuning for stimulus features is often thought to be invariant with contrast (Finn et al. 2007; but for exceptions see Krekelberg et al. 2006; Pack et al. 2005) or else to become narrower at high contrast due to the recruitment of inhibitory mechanisms (Sceniak et al. 1999). However, as shown in Fig. 12B, tuning bandwidth in MT responses to grating stimuli does indeed increase with contrast (blue: 10% low contrast; red: 5% low contrast). Here each dot corresponds to a single MT neuron and the results were significant (two-way ANOVA, no significant interaction, main effect of contrast P < 0.001). Figure 12, C and D shows two example neurons.

An alternative explanation for the results shown in Fig. 12 is the “iceberg effect,” whereby tuning bandwidth decreases more sharply with contrast in those cells that have high spiking thresholds. To examine this possibility we subtracted the tuning bandwidth measured at low contrast from that obtained at high contrast for each cell. One prediction of the “iceberg” model is that tuning bandwidth will decrease more sharply with decreasing contrast in those cells that have low spontaneous firing rate because these cells might be assumed to have a high spiking threshold and thus a minimal iceberg effect. More generally, the hypothesis predicts a negative correlation between the bandwidth differences and the spontaneous firing rates. Our analysis shows that the results are not correlated (P = 0.35 for 10%, P = 0.26 for 5%), suggesting that the narrowing of tuning curves is not due in any straightforward way to the iceberg effect. This result did not change when we included only those cells whose responses at nonpreferred directions (≤60° from preferred) were ≥2SDs above the mean of the baseline firing rate.

TEMPORAL DYNAMICS IN REAL MT CELLS AND IN THE MODEL.

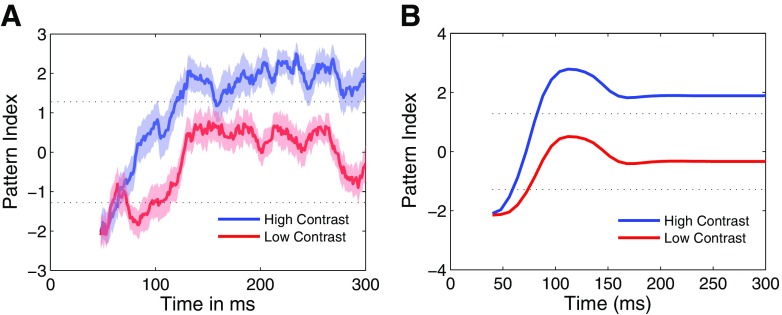
The temporal dynamics of pattern selectivity is similar to the timing of the responses observed with titled bar stimuli. That is, pattern selectivity in MT emerges roughly 60 ms after the initial component response (Pack et al. 2001; Smith et al. 2005). Figure 13A shows mean temporal dynamics of the plaid response for the 44 pattern cells depicted in Fig. 12. As in the previous studies the pattern index for the high-contrast stimulus increases during the early phases of the response before saturating at around 150 ms. For the low-contrast condition, the pattern index shows a similar time course, although it fails to reach statistical significance, as expected from Fig. 12A. Figure 13B shows similar temporal dynamics obtained from the model. In our model, such dynamic responses are to be expected because the computation of pattern selectivity relies on end-stopping, for which we hypothesize a delay at the level of V1 (Pack et al. 2003).

Fig. 13.

A: the average plaid temporal dynamics of 23 MT pattern cells from Fig. 12A. The pattern index (see methods) was computed in 24 ms time bins. At high contrast (blue), the pattern index switches gradually from an early, component-selective response to a later pattern-selective response over a period of roughly 75 ms. The pattern index transition at low contrast occurs on a similar timescale, but fails to reach statistical significance. B: same as A for the model.

DISCUSSION

Models of neuronal responses in MT have traditionally assumed an input stage that approximates the motion energy in local regions of visual space, velocity space, or frequency space (Perrone 2004; Rust et al. 2006; Simoncelli and Heeger 1998). The output of this stage is typically normalized and then summed by a second stage, which weights each input according to its selectivity for stimulus features such as spatial position and spatiotemporal frequency. Our model does not depart from this basic framework—the main novelty is a constraint on the way in which the outputs of V1 cells are normalized. Although this entails a minor structural change to previous models, we have shown that it allows our model to account for a wide range of neurophysiological data.

Our approach is similar to that taken by various psychophysical models of motion perception, which often rely heavily on the unambiguous motion of 2D features (Liden and Pack 1999; Lorenceau et al. 1993; McDermott et al. 2001; Rubin and Hochstein 1993; Weiss et al. 2002). In these models the mechanism by which such features are detected is not specified, but in the present work we implement this computation via a straightforward elaboration to the standard motion energy detector (Adelson and Bergen 1985). Our end-stopped model is qualitatively consistent with observations on real V1 neurons (Fig. 7).

Beyond representing a proof of concept for the computational utility of end-stopping, our model illustrates the more general point that complex response properties found in the higher-level visual cortex may in principle be attributable to computations carried out as early as V1, although it would clearly have to be elaborated on to account for other receptive field properties, such as surround suppression in MT. Indeed previous work has shown that neurons in ventral stream areas such as V4 are responsive to stimulus features that may be derived from nonlinear combinations of the features detected by V1 neurons (Cadieu et al. 2007), suggesting that our approach may be of general utility in modeling higher-level visual cortex.

Comparison with other models

The idea that end-stopped V1 neurons provide a key source of input to MT comes from a combination of physiological and anatomical studies. Physiologically, most macaque V1 cells exhibit end-stopping to some degree (Jones et al. 2001; Sceniak et al. 2001), with the strongest end-stopping being found in layer 4B (Sceniak et al. 2001), suggesting that the ensemble of these neurons provides very little information about the motion of extended edges (see Fig. 4). Understanding the ramifications of end-stopping for motion processing is thus particularly important because layer 4B provides roughly 90% of the input from V1 to MT (Maunsell and van Essen 1983).

In our model we have implemented end-stopping by simply introducing inhibitory inputs at the ends of the receptive fields of standard motion energy detectors. We chose this approach because the motion energy model has been tested quite thoroughly and shown to be generally consistent with the behavior of direction-selective V1 neurons (Emerson et al. 1992; Pack et al. 2006). Other models of end-stopping rely on the detection of conjunctions of orientations (Skottun 1998; Zetzsche and Barth 1990) or curvature (Dobbins et al. 1989). As in our model end-stopping is instantiated by the multiplication of oriented filters, although in the previous models the filters differed in orientation rather than in spatial position. The model of Noest and van den Berg (1993) used a similar multiplicative mechanism to account for the perception of plaid stimuli. Despite the various differences in implementation, we expect that these other formulations of end-stopping could provide a suitable front end for our MT model, given that all of them permit the detection of 2D features (Hubel and Wiesel 1965; Pack et al. 2003).

Our end-stopping model also shares some properties with a recent model of motion integration in MT (Rust et al. 2006). In this model the outputs of V1 neurons are normalized based on the combined output of the V1 population. Importantly, a “tuned” component of the normalization pool effectively inhibits the responses of individual cells in proportion to their own responses to a given stimulus. This has an effect similar to that of a compressive nonlinearity, with the resulting increase in direction-tuning bandwidth leading to greater pattern selectivity. The end-stopping in our model also has tuned normalization because it entails suppressive interactions among cells tuned to the same stimulus parameters. Indeed end-stopping increases pattern selectivity in our model simply by broadening direction-tuning curves at the level of V1 (Fig. 4). However, to account for the responses of MT neurons to tilted bar stimuli, we found it necessary to impose the condition that the normalization pool samples preferentially from neurons with specific receptive field locations. This approach is thus similar to that typically used in studies of the ventral stream of the visual cortex (Brincat and Connor 2006), in which the spatial arrangement of receptive field subunits is critically important for understanding the responses of the neurons to complex stimuli.

A different approach for isolating 2D features comes from the psychophysical model of Weiss et al. (2002). Here local velocity measurements are treated as probability distributions, so that the distribution of velocities associated with a moving edge is broad relative to that associated with a moving endpoint. Narrow velocity tuning leads to a prominent influence of 2D features in the model's second stage, which finds the single velocity consistent with all local measurements (and a prior that favors low speeds).

A similar velocity-domain approach is the model of Simoncelli and Heeger (1998), which proposes a weighted summation at the level of MT, followed by normalization, subtractive inhibition, and an output nonlinearity. In this scenario each MT neuron integrates over V1 neurons whose selectivities collectively tile the Fourier-domain representation of a particular velocity. As a result the model neurons are tuned for velocity in a manner that is invariant with the composition of the stimulus, provided that the input contains multiple orientations. This mechanism is compatible with our model and, in fact, given that end-stopping is essentially a spatial filter that passes features that contain multiple orientations, the two mechanisms would be expected to work synergistically (Born and Bradley 2005; Bradley and Goyal 2008). Indeed a selective integration of one-dimensional features would appear to be necessary for MT neurons to derive pattern selectivity from the outputs of neurons, such as those in layer 6 of V1, that lack strong surround suppression (Sceniak et al. 2001).

The idea that motion detection occurs in parallel with a stage that is selective to the spatial structure of the input is the basis of many “feature-tracking” models (e.g., Del Viva and Morrone 1998). Although feature-tracking is often associated with long-range processes that involve more cognitive aspects of visual perception (Lu and Sperling 1995), the end-stopping model performs a similar function using only mechanisms that are known to exist in V1 (see also Baloch and Grossberg 1997). Thus it would be quite interesting to examine MT responses in the context of stimuli whose perception has been attributed to feature-tracking mechanisms (e.g., Beutter et al. 1996; Bowns 1996; Scott-Samuel and Georgeson 1999). For these stimuli observers appear to determine motion direction by matching local features across space and time rather than by calculating velocity or motion energy.

Effects of contrast

We have hypothesized that end-stopping in V1 plays an important role in shaping the response properties of neurons in MT and perhaps elsewhere in the extrastriate cortex. Ideally one would test this idea by silencing intracortical inhibition in V1 while recording simultaneously in MT. However, this is a technically demanding experiment that would likely yield equivocal results (Sillito 1975) and so we have opted for a much simpler method of manipulating end-stopping. Because previous studies have shown that reducing contrast reduces surround suppression in general in V1 (Kapadia et al. 1999; Sceniak et al. 1999), we were able to use the model to make predictions about the effects of contrast on motion integration in MT. Consistent with the model hypothesis, low-contrast stimuli yielded less motion integration in MT, as manifested by larger errors in the bar-field experiment (Fig. 8) and reduced pattern selectivity in the plaid experiment (Fig. 12A).

Of course, manipulating contrast might be expected to alter other features of neuronal responses throughout the cortex and thus we cannot say conclusively that our experimental results must be due to a manipulation of the strength of end-stopping. However, most of the previously reported effects of contrast on orientation tuning can be modeled as changes in response gain, with little effect on stimulus selectivity (Finn et al. 2007). In our model stimulus contrast can affect both the peak and the width of tuning curves (Fig. 8) and we have shown that similar contrast-dependent changes occur in single MT neurons.

Temporal dynamics

In our model the earliest responses to moving stimuli are similar to those obtained at very low contrast: the responses of MT neurons are component-selective and heavily biased by stimulus orientation for tilted bar stimuli. A similar temporal profile has been observed in real MT neurons, such that the earliest responses to a moving stimulus fail to signal the motion of the pattern, with the correct global motion direction being signaled after a delay of only about 60 ms (Pack and Born 2001). In the case of the tilted bar stimulus, the response dynamics have been the subject of some debate. Majaj et al. (2002) suggested that the delay resulted from the longer latencies that are often associated with weaker stimuli in the responses of neurons in the early visual system (Albrecht 1995). An alternative explanation invokes delays in inhibitory responses necessary for computations such as normalization and end-stopping (Lorenceau et al. 1993; Pack et al. 2003). These delays have been estimated at roughly 10–30 ms (Pack et al. 2003).

Our model exhibits temporal dynamics that are similar to those observed in MT (Figs. 9 and 13). This temporal transition occurs even without any explicit delay in either the latency of excitatory responses or the inhibitory input responsible for end-stopping, although a more prolonged and physiologically accurate transition occurs when an explicit delay is included (Fig. 9). In our model the delay related to the computation of motion direction arises partially from the formulation of the normalization model, which represents the output of a single neuron as the ratio of its feedforward input to the summed input of many other neurons plus a constant. The constant can be thought of as a threshold below which the response of the normalization pool is ineffective. Thus after the onset of the stimulus, the excitatory input rises more quickly than the inhibitory contribution, so that end-stopping is absent in the earliest part of the response. The same reasoning also explains why surround effects are ineffective at low contrasts throughout the visual system (Sceniak et al. 1999; Solomon et al. 2002) and are typically associated with longer latencies than are responses in the classical receptive field centers (Cai et al. 1997; Perge et al. 2005).

The delayed inhibition hypothesized in the model may be a feature of the circuits that generate surround suppression in V1. In particular, Angelucci et al. (2002) showed that inhibitory inputs from within V1 are likely driven indirectly by feedback from extrastriate cortical areas. Although these feedback projections act on their V1 targets at very short latencies (Girard et al. 2001; Hupe et al. 2001), they activate slower, horizontal connections within V1. This interaction between feedback and horizontal connections may account for the propagation of surround signals within V1 (Bair et al. 2003).

Conclusion: MT cells and motion integration

In this work we have implemented a model in which MT neurons integrate the output of V1 motion energy detectors that are strongly suppressed by oriented inputs that extend outside their classical receptive fields. One consequence of this end-stopping property is that the resulting MT model is insensitive to one-dimensional motion signals that would otherwise lead to large biases in tuning curves measured in response to tilted bar stimuli. More surprisingly, perhaps, the same model can account not only for a number of effects of stimulus contrast, but also for the temporal dynamics observed in real MT cells.

We also tested our model with plaid stimuli and one interesting conclusion of these simulations is that the model can be made to span most of the component-pattern continuum through variations of a single model parameter. Thus there is not necessarily any functional sense in which pattern cells are more nonlinear than other types of MT cells and, in our model, the only important difference between the two was in the bandwidth of direction tuning at the MT stage. Functionally one can think of MT direction tuning as a type of smoothing operation, in which each cell averages the optic flow field locally over some bandwidth (Qian et al. 1994). Thus pattern cells smooth the flow field over a broader range of local motion directions, whereas other MT cells respond more to local motion vectors, although neither cell type is essential for solving correspondence problems like the aperture problem. Indeed in our simulations (Fig. 4) and recordings (Fig. 6), MT neurons were on average nearly perfect at solving the aperture problem, provided that local 2D features were present in the stimulus.

GRANTS

This work was supported by Canadian Institutes of Health Research Grant MOP-79352 to C. C. Pack, National Eye Institute Grant EY-11379 to R. T. Born, and National Science and Engineering Research Council Fellowship PGS D3-362469-2008 to J.M.G. Tsui.

DISCLOSURES

No conflicts of interest are declared by the authors.