Abstract
Many social animals including songbirds use communication vocalizations for individual recognition. The perception of vocalizations depends on the encoding of complex sounds by neurons in the ascending auditory system, each of which is tuned to a particular subset of acoustic features. Here, we examined how well the responses of single auditory neurons could be used to discriminate among bird songs and we compared discriminability to spectrotemporal tuning. We then used biologically realistic models of pooled neural responses to test whether the responses of groups of neurons discriminated among songs better than the responses of single neurons and whether discrimination by groups of neurons was related to spectrotemporal tuning and trial-to-trial response variability. The responses of single auditory midbrain neurons could be used to discriminate among vocalizations with a wide range of abilities, ranging from chance to 100%. The ability to discriminate among songs using single neuron responses was not correlated with spectrotemporal tuning. Pooling the responses of pairs of neurons generally led to better discrimination than the average of the two inputs and the most discriminating input. Pooling the responses of three to five single neurons continued to improve neural discrimination. The increase in discriminability was largest for groups of neurons with similar spectrotemporal tuning. Further, we found that groups of neurons with correlated spike trains achieved the largest gains in discriminability. We simulated neurons with varying levels of temporal precision and measured the discriminability of responses from single simulated neurons and groups of simulated neurons. Simulated neurons with biologically observed levels of temporal precision benefited more from pooling correlated inputs than did neurons with highly precise or imprecise spike trains. These findings suggest that pooling correlated neural responses with the levels of precision observed in the auditory midbrain increases neural discrimination of complex vocalizations.
INTRODUCTION
Vocal communicators such as humans and songbirds recognize and discriminate among complex sounds, like speech and song. As with behaving animals, the spiking responses of single neurons can also be used to discriminate among sensory signals. This ability, called neural discrimination, describes how well sensory stimuli can be classified based on a neuron's spiking response. In the visual, somatosensory, and auditory systems, the responses of individual neurons can be used to accurately discriminate among stationary stimuli based on differences in firing rate because different stimuli elicit different rates of action potentials (APs) (Britten et al. 1992; Hernandez et al. 2000; Relkin and Pelli 1987). However, time-varying stimuli such as communication vocalizations are often poorly discriminated based on firing rate alone (Schnupp et al. 2006) and, even when considering AP timing, the discriminability calculated from responses of most auditory neurons is worse than that of behaving animals (Engineer et al. 2008; Wang et al. 2007).
The failure of many individual auditory neurons to produce spike trains that can be used to accurately discriminate among complex sounds is due in part to the temporal imprecision of neural responses, which can be observed in the trial-to-trial variability in spiking responses to repeated presentations of the same sound (Kara et al. 2000). Neural mechanisms that compensate for the temporal imprecision of individual spike trains may facilitate neural and behavioral discrimination of complex sensory cues. For example, the combined activity of groups of neurons, rather than single cells, may compensate for spike train imprecision and may be important for sensory discrimination (Cohen and Newsome 2009; Geffen et al. 2009).
One approach to studying whether the combined responses of multiple neurons facilitates discrimination among complex sensory signals is to pool the responses of multiple neurons using simple models of neural integration. This approach corresponds to the fundamental circuit mechanism by which sensory neurons process information: convergence of feedforward input via synaptic integration. Testing the effects of input convergence on output responses has typically been used to measure neural discriminability among stationary cues (Gold and Shadlen 2001; Jazayeri and Movshon 2006; Miller and Recanzone 2009; Seung and Sompolinsky 1993; Zhang and Reid 2005). Pooling the responses of individual neurons can also be used to test how input convergence affects population discrimination of complex sensory signals such as birdsong.
Pooling spike trains from multiple neurons could facilitate neural discriminability in two ways. For neurons with imprecise firing, pooling responses from inputs with strong signal correlations could increase the signal-to-noise ratio, thus facilitating discrimination. For highly precise neurons, pooling spike trains from neurons with weak signal correlations could facilitate discrimination by providing independent information encoded by multiple neurons. Here, we asked whether, and to what degree, the pooled activity of groups of auditory neurons facilitated the discrimination of complex, time-varying sounds. Further, we asked whether neural discrimination depended on the strength of the signal correlations among inputs.
We recorded from neurons in the auditory midbrain nucleus mesencephalicus lateralis dorsalis (MLd), which is homologous to the inferior colliculus in mammals. MLd receives converging input from multiple pathways that originate in the cochlear nuclei and it sends auditory information to the primary auditory forebrain areas via the thalamus. Neurons in MLd typically have stimulus-locked responses to complex natural and artificial sounds (Woolley and Casseday 2004, 2005; Woolley et al. 2006) and their responses may be able to reliably discriminate among complex sounds.
We measured the degree to which single neuron responses could be used to discriminate among multiple conspecific songs based on spike train patterns. For single neurons, we measured the degree to which discriminability depended on spectral and temporal tuning properties. We then created a simple integration model that pooled the spiking responses of groups of neurons and tested whether small groups of cells discriminated better than did single neurons. For these groups of neurons, we compared neural discriminability with the tuning similarity of the input neurons and with the correlation between the input spike trains. Last, we simulated populations of neurons with varying degrees of spike train precision to investigate the conditions under which pooling responses from correlated inputs facilitated neural discrimination.
METHODS
All procedures were done in accordance with the National Institutes of Health and Columbia University Animal Care and Use Policy. Adult male zebra finches (Taeniopygia guttata) were used in this study. All birds were either purchased from a local bird farm (Canary Bird Farm, Old Bridge, NJ) or were bred and raised on site. Prior to electrophysiology, the birds lived in a large aviary with other male zebra finches, where they received food and water without restriction, as well as vegetables, eggs, grit, and calcium supplements.
Surgery
Two days prior to recording, male zebra finches were anesthetized with a single intramuscular injection of 0.04 ml Equithesin (0.85 g chloral hydrate, 0.21 g pentobarbital, 0.42 g MgSO4, 8.6 ml propylene glycol, and 2.2 ml of 100% ethanol to a total volume of 20 ml with H2O). Following lidocaine application, feathers and skin were removed from the skull and the bird was placed in a custom-designed stereotaxic holder with its beak pointed 45° downward. Small openings were made in the outer layer of the skull, directly over the electrode entrance locations. To guide electrode placement during recordings, ink dots were applied to the skull at stereotaxic coordinates (2.7 mm lateral and 2.0 mm anterior from the bifurcation of the sagittal sinus). A small metal post was then affixed to the skull using dental acrylic. After surgery, the bird recovered for 2 days.
Stimuli
Stimuli were the songs of 20 different adult male zebra finches sampled at 48,828 Hz and the frequency was filtered between 250 and 8,000 Hz. Songs were played at an average intensity of 72 dB SPL and presented in pseudorandom order, for a total of 10 trials each. All songs were balanced for root mean square (RMS) intensity. Songs ranged in duration between 1.62 and 2.46 s and a silent period of 1.2 to 1.6 s separated the playback of subsequent songs. All songs were unfamiliar to the bird from which electrophysiological recordings were made.
Electrophysiology
In preparation for electrophysiological recording, the bird was given three intramuscular injections of 0.03 ml of 20% urethane, separated by 20 min. The bird was wrapped in a blanket and placed in a custom holder using the head post. The bird's body temperature was monitored by placing a thermometer underneath the wing and was maintained between 38 and 40°C using an electric heating pad (FHC). The experiments were performed in a sound-attenuating booth (IAC). The bird was on a table near the center of the room and a single speaker was located 23 cm directly in front of the bird.
We recorded from single auditory neurons in the midbrain auditory nucleus mesencephalicus lateralis, pars dorsalis (MLd), using either tungsten microelectrodes (FHC) or glass pipettes filled with 1 M NaCl (Sutter Instrument). For both glass and tungsten recordings, electrode resistance was between 3 and 10 MΩ (measured at 1,000 Hz). Electrode signals were amplified (×1,000) and filtered (300–5,000 Hz; A-M Systems). During recording, voltage traces and APs were visualized using an oscilloscope (Tektronix) and custom software (Python; Matlab, The MathWorks). Spike times were detected using a threshold discriminator and spike waveforms were saved for off-line sorting and analysis. For off-line sorting, spike waveforms were upsampled four times using a cubic spline function (Joshua et al. 2007). Action potentials were separated from nonspike events by waveform analyses and cluster sorting using the first three principal components of the AP waveforms (custom software, Matlab).
Neurons were recorded bilaterally and were sampled throughout the extent of MLd, which is located about 5.5 mm ventral to the dorsal surface of the brain (Fig. 1A). We recorded from all neurons within MLd that were driven (or inhibited) by any of the search sounds (one rendition each of song and noise). Isolation was ensured by calculating the signal-to-noise ratio of AP and non-AP events and by monitoring baseline firing rate throughout the recording session. Although neurons were recorded bilaterally, we typically recorded from only one neuron at a time (96 of 122 neurons). When we recorded the activity of two neurons simultaneously (n = 13 pairs), they were always located in opposite hemispheres. For the 13 pairs of simultaneously recorded neurons, we measured the strength of signal and noise correlations and compared these to the strength of correlations observed in nonsimultaneously recorded neurons (Lee et al. 1998). We binned spike trains using 200 ms bins, overlapping by 150 ms. We found no differences in the signal or noise correlations during baseline or driven activity between simultaneously and nonsimultaneously recorded neurons (all comparisons, P > 0.68; Wilcoxon rank-sum test).
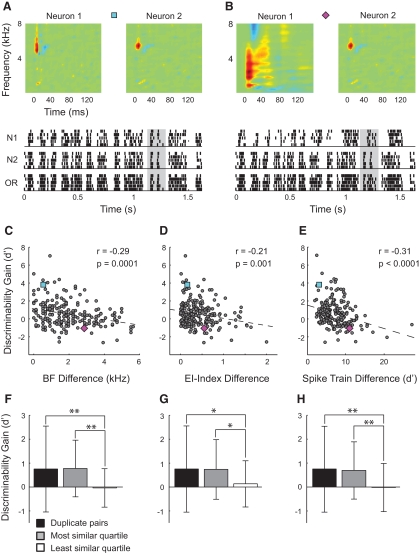
Fig. 1.
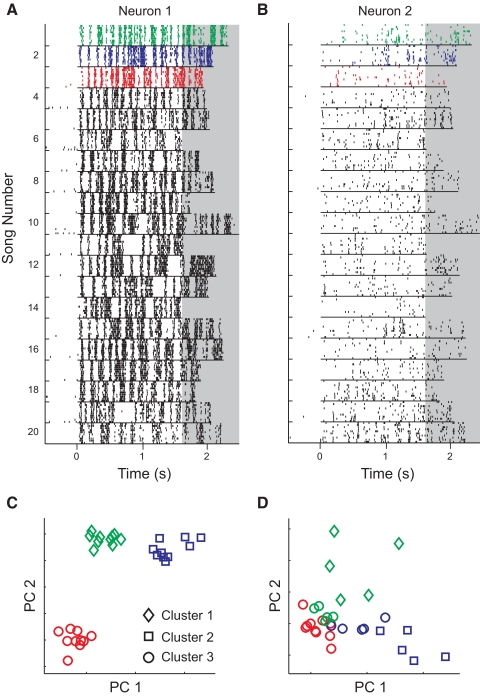
Single neurons in zebra finch mesencephalicus lateralis dorsalis (MLd) showed a range of responses to song. A: diagram of the zebra finch ascending auditory system and electrode placement. B: the waveform (top) and spectrogram (middle) of a single zebra finch song. Below the spectrogram, raster plots show spike trains collected from 8 neurons in response to multiple presentations of the song. Each line shows a single spike train and each tick represents the timing of a single action potential (AP). Each group of 10 spike trains shows the responses of a single neuron to 10 presentations of the song. For the song spectrogram, red represents high intensity and blue represents low intensity.
Single neuron neurometrics
We used four neurometrics to quantify the ability of single neuron responses to discriminate among 20 songs based on single spike train responses to individual songs. The Victor–Purpura (VP) metric calculates the “cost” of converting one spike train into another through a series of elementary steps (Victor and Purpura 1996): the insertion of a missing spike, the deletion of an extra spike, and the shifting of a common spike that is misaligned in time. The cost of inserting or deleting a spike is 1 (a unitless quantity). The cost of shifting a spike in time is equal to the size of the shift (in milliseconds) multiplied by a shifting cost q (in units 1/ms). For each neuron, we tested multiple values of q (range: 0.002–0.5/ms). For single MLd neurons, the optimal value of q ranged from 0.5 to 0.002/ms. The average neural discriminability across the population was maximized for q = 0.05/ms and this value was used for every neuron in all subsequent analyses. For a pair of spike trains and a shifting cost q, the algorithm finds the cheapest set of steps to convert one spike train into the other. The less it costs to make the two spike trains identical, the more similar they were to begin with. To calculate percentage correct, we randomly selected one spike train from each song to be used as templates (i.e., 20 of the 200 spike trains were templates). The remaining 180 spike trains were then classified as being evoked by the song associated with the lowest cost transformation. Percentage correct was calculated as the fraction of spike trains that were correctly classified (Machens et al. 2003).
The van Rossum (VR) distance metric quantifies the dissimilarity between a pair of spike trains by calculating the distance between the spike trains in high-dimensional space (van Rossum 2001). Each spike train was discretized into 1 ms bins, creating a point process of zeros and ones that was filtered with an exponential function with a short decay constant τ
where H(t) is the Heaviside step function, M is the total number of spikes in the spike train, and N is the resulting smoothed spike train. For every neuron, we varied the value of τ between 5 and 500 ms and we measured neural discriminability for each decay constant. For single neurons, the optimal decay constant spanned the range tested (5 to 500 ms). The average discriminability for the population of neurons was maximized for τ = 20 ms and all subsequent analyses used this decay constant for every neuron.
We then calculated the squared Euclidean distances between pairs of smoothed spike trains. Distance represents the dissimilarity between two spike trains; spike trains that are similar to one another have a smaller distance between them than spike trains that are dissimilar
where Dij is the distance between spike trains Ni and Nj and τ is the decay constant used to smooth the spike trains. Percentage correct was calculated by randomly selecting one spike train from each of the 20 stimuli as a template. The remaining 180 spike trains were then classified as being evoked by the song whose template was most similar.
The firing rate (FR) metric used the response strength (calculated as the driven firing rate minus the baseline firing rate) in response to each stimulus to calculate neural discriminability. As with the VR and VP metrics, a template spike train was chosen for each song and the remaining 180 spike trains were classified as being evoked by whichever song had a more similar firing rate.
The K-means algorithm classified spike trains into K clusters based on their proximity to one another in high-dimensional space (Fig. 2). As with the VR metric, the K-means metric used squared Euclidean distance as a measure of spike train similarity. However, unlike the VR metric, the K-means metric used an iterative clustering algorithm to optimally separate the spike trains into K groups (Duda et al. 2001). The spike trains were first smoothed with an exponential decay that optimized the average discriminability across the population (τ = 10 ms). The number of clusters (K) was equal to the number of stimuli used to generate the set of spike trains. The algorithm first randomly selected K spike trains as the initial cluster centers and grouped with each of these centers all the spike trains that were nearer that center than any other. Once all of the spike trains were grouped, the center of each cluster was recalculated as the geometric center of the spike trains belonging to each group. Cluster membership was recalculated using the new center positions and the algorithm was iterated until it converged on a set of K clusters, each of which contained spike trains that were closer to one cluster center than to any other. We did not force each cluster to contain 10 trials, which was the number of repetitions per stimulus. By allowing the cluster size to vary, the spike trains naturally segregated into 20 optimal clusters. Enforcing a cluster size would have decreased discriminability by associating distant spike trains with nonoptimal clusters.
Fig. 2.
MLd neural responses discriminated among songs with a wide range of abilities. A: spike trains from a single neuron in response to 10 repetitions of 20 unique zebra finch songs. Each group of 10 lines shows the responses to 10 presentations of a single song. The songs were pseudorandomly interleaved during the experiment and the responses were organized here for visualization. For analysis, the spike trains were truncated to the duration of the shortest song (1.62 s; nonshaded region). B: spike trains from a second neuron in response to the same stimuli as in A. C: in the K-means and van Rossum metrics, spike trains were represented as points in a 1,620-dimensional space (one dimension for each millisecond of activity). For illustration, here the spikes in response to the first 3 songs were projected onto 2 dimensions (the first 2 principal components). Spike trains from song 1 are shown in green, song 2 in blue, and song 3 in red. The K-means algorithm was used to classify the spike trains into clusters based on spike train dissimilarity. The shape of the marker corresponds to cluster membership. For Neuron 1, spike trains evoked by each song belong to their own cluster, indicating high discriminability. D: for Neuron 2, cluster 3 contains spike trains from songs 1, 2, and 3, indicating that the spike trains produced by this neuron cannot perfectly discriminate among the 3 songs. Color and shape labels are the same as in C.
Percentage correct was measured by analyzing the spike trains that belonged to each of the K clusters. We assigned a song label to each cluster using a “voting” scheme, in which each spike train in a cluster cast a vote for the song that evoked it. Each cluster was assigned to the song that cast the most votes. If more than one cluster had the same number of votes for a particular song (e.g., two clusters contained five spike trains from song 1), the cluster that contained the fewest spike trains from any other song was assigned to the original song (e.g., song 1), and the other cluster was assigned to the song that cast the second largest number of votes. In this way, discriminability for a particular set of 20 clusters was optimized. If each cluster contained spike trains evoked by only one song, the neuron performed with 100% discriminability. If one or more spike trains were misclassified, percentage correct dropped toward chance, which was (100/K) = 5%.
We calculated d′ as another measure of neural discriminability. Unlike percentage correct, d′ is not bounded between 0 and 100% and can therefore resolve differences in discriminability for neurons performing at 100%. To calculate d′, we first smoothed each spike train with an exponential decay (τ = 10 ms) and projected the spike trains from two stimuli onto a single vector that connected the average neural response for each group; the average neural response for a particular song was the average smoothed spike train in response to that song. We then fit a normal distribution to each of the clusters and measured the separability between the clusters, which is the distance between the cluster means (in Euclidean space) normalized by the variance of the clusters
where ui is the mean value of the ith cluster, vi is the variance of the ith cluster, and ni is the number of spike trains belonging to the ith cluster. For each neuron, we calculated d′ for every pair of clusters (190 pairs) and we averaged across all cluster pairs.
Each neurometric was iterated 100 times and, on each iteration, the neurometrics were seeded with a different set of randomly selected template spike trains. The resulting discrimination values are the mean performance across all 100 iterations. On a given iteration, if a spike train was equally similar to two or more templates, that spike train was scored as misclassified even if one of the templates represented the appropriate song category. We used this assignment criterion because ambiguity suggests poor neural discriminability. Because of this criterion, neural performance could be worse than chance, which was 5%.
Analysis of tuning
Spectrotemporal receptive fields (STRFs) were computed using the songs of 20 zebra finches and the neural responses to those songs (Theunissen et al. 2000). To estimate the best linear STRFs, we implemented a normalized reverse correlation technique using the STRFpak toolbox for Matlab (http://strfpak.berkeley.edu). To estimate the validity of the STRFs, we measured the correlation coefficient between predicted responses to novel songs (those not used in the STRF calculation) and the neuron's actual response to those songs. STRF predictions were computed by convolving the time-reversed STRF with the song spectrogram and half-wave rectifying. The correlation coefficients reported here are the mean correlation coefficients across 20 predictions.
From each STRF, we made multiple measures of auditory tuning and compared these values with the neural discrimination performance for each cell. To measure tuning, we projected the STRF onto the spectral and temporal axes. STRFs of MLd neurons are highly separable in frequency and time (Woolley et al. 2009). Therefore projecting the STRF onto the spectral and temporal axes results in very little information loss. Two measures of spectral tuning were used: best frequency (BF) and excitatory bandwidth (BW). Best frequency was determined by projecting the STRF onto the frequency axis and calculating the peak of this vector. The bandwidth of each STRF was measured at the time corresponding to the peak in excitation (i.e., response latency: 8.48 ± 2.85 ms, mean ± SD; range: 4 to 23 ms) and was calculated by computing the width of STRF pixels that were 3SDs above the average pixel value. To measure temporal tuning, we projected the STRF onto the time axis. Using this vector, we calculated the temporal modulation period, which was the difference in time between the peak in excitation and the peak in inhibition. We also calculated the Excitatory–Inhibitory (EI) index, which is the difference between the areas of excitation and inhibition divided by the sum of the areas (range: −1 to 1)
where STRF is the two-dimensional spectrotemporal receptive field. STRFE is the excitatory portion of the STRF, for which pixels less than zero were set to zero, and STRFI is the inhibitory portion of the STRF, for which pixels greater than zero were set to zero. This definition of the EI index is equivalent to the integral of the STRF divided by the integral of the absolute value of the STRF, shown on the far right-hand side. The EI index corresponds to traditionally defined temporal response patterns of auditory neurons to pure tones (e.g., onset, primary-like, sustained; Woolley and Casseday 2004; Schneider and Woolley, unpublished data).
We compared the tuning properties of pairs and triplets of neurons. For pairs of neurons, we took the absolute value of the difference between the tuning parameter of each neuron. For comparing responses among three neurons, we measured the absolute value of the difference in tuning for each pair in the triplet and calculated the average similarity of all three pairs. For an arbitrary tuning parameter p and neurons i, j, and k
Analysis of within-stimulus spike train similarity
For each neuron, we calculated the shuffled autocorrelogram (SAC), as described in Joris et al. (2006). To compute the SAC, we first binned spike times into 1 ms bins. For each spike train evoked by a single song, we measured every cross-spike train interspike interval. The histogram of the cross-spike train intervals provided a measure of the tendency for neurons to fire at similar times to repeated playback of the same song. To account for the increased number of trial-to-trial coincident spikes due to firing rate and the number of times a song was repeated, we normalized the SAC by a normalization constant (Christianson and Pena 2007; Joris et al. 2006)
where N is the number of times the song was presented (typically 10), R is the average firing rate across all N presentations of the song, ω is the duration of the coincidence window (1 ms), and D is the duration of the song (1.621 s). For each neuron, we averaged the SAC calculated independently from responses to each of the 20 songs.
From the SACs, we made two measures of spike train reliability. First, we computed the coincidence index (CI), which was the normalized number of coincident spikes at 0 ms lag (i.e., the normalized rate with which spikes were stimulus-locked with 1 ms resolution). We also calculated the half-width at half-height for each SAC, which provided an estimate of the trial-to-trial spike-timing jitter in response to a single song. In general, the CI is largest for neurons with a high degree of trial-to-trial temporal precision and decreases with temporal imprecision, whereas half-width increases with temporal imprecision. To quantify temporal precision as a single value, we calculated the CI to half-width ratio, which is largest for neurons with high temporal precision and decreases as the temporal precision decreases.
Last, we measured the spike train similarity across pairs of neurons using an extension of the d′ metric. For a pair of neurons, we first convolved each spike train with an exponential decay with a time constant of 10 ms. Using spike trains from the two neurons that were evoked by a single song, we then calculated the squared Euclidean distance between every pair of cross-neuron spike trains and the variance among the spike trains produced by each of the single neurons. For each song, we calculated d′, which was the average distance between the spike trains of the two neurons normalized by the average variance of the responses. For each pair of neurons, we calculated d′ for every song and here we report the average value across all songs.
Modeling readout neurons
We analyzed the pooled responses of groups of MLd neurons ranging in size from two to five neurons, which were selected at random from our set of MLd neurons (Parker and Newsome 1998). The models were simulations of a readout neuron that integrated information from multiple input neurons using three methods that simulated well-established physiological processes. The SUM model simulated subthreshold changes in membrane potential by integrating the responses from all input neurons and producing a graded output. The OR model simulated postsynaptic spiking activity and fired a single AP when one or more input neurons fired an AP. The AND model simulated coincidence detection, in which the readout neuron fired only when concurrent input arrived from each of the input neurons
In the previous three equations, R is the output of the readout model and N is the input from a single MLd neuron. Depending on the number of input neurons, n ranged from 2 to 5.
For each readout neuron, we simulated 200 trials: 10 trials for each of the 20 songs used in the electrophysiology experiments. On each trial, one spike train (corresponding to the appropriate song) from each input neuron was randomly selected. For the AND model, an AP was triggered at the readout neuron when every input neuron fired an AP within 5 ms of each other. We chose the integration time of 5 ms based on the observed integration time of midbrain auditory neurons (Andoni et al. 2007) and the time course of excitatory and inhibitory synaptic currents (Covey et al. 1996; Pedemonte et al. 1997). As the integration window for the AND model increased in duration, the output of the AND model approached that of the OR model. The output of each readout neuron was filtered with an exponential kernel of 10 ms and discriminability of the resultant spike trains was measured using d′.
To approximate the maximum discriminability that groups of neurons could achieve, we measured the discriminability of groups of neurons for which the spike trains were concatenated, rather than pooled. For this model, the dimensionality of the spike trains used as inputs to the discrimination algorithm was (1,621 × n).
Simulating pairs of neurons with varying temporal precision and response similarity
To test how tuning similarity and reliability affected the neural discrimination achieved by pairs of neurons, we simulated pairs of neurons that varied in the similarity of their responses and in their trial-to-trial spike train variability. For each neuron in a simulated pair, we generated 10 spike trains to each of 20 songs using a Poisson distribution with a time-varying mean that determined the probability of spiking. The functions describing the time-varying distributions were spike trains from actual MLd neurons that were convolved with a smoothing window and that served as “templates” for generating simulated spike trains. On each simulated trial, we generated a set of APs from the time-varying distribution. The degree of trial-to-trial spike train variability was controlled by smoothing each template with Hanning windows of varying widths, ranging from 1 to 100 ms. Differences in the similarity of the spike trains produced by each of the simulated neurons were introduced by allowing each spike in the template of one of the neurons to move ±n ms, where n was a random number between 0 and N. We systematically varied N between values of 0 and 125 ms. Thus using a single set of spike trains as templates, we simulated two neurons and systemically varied their across-neuron response similarity and within-neuron trial-to-trial variability. We simulated 122 different pairs of neurons (each generated from the spike trains of a single MLd neuron) at each level of response similarity and reliability. Using the simulated spike trains, we calculated single-neuron discriminability using d′ and the ability of each pair of neurons to discriminate using the OR readout model.
RESULTS
We recorded spike trains from 122 extracellularly isolated auditory midbrain (MLd) neurons from 34 adult male zebra finches. From each neuron, we recorded responses to 10 presentations (trials) of 20 different adult zebra finch songs, presented pseudorandomly (Fig. 1). Responses were generally stimulus-locked but ranged widely in spike rate and reliability (Fig. 1B). To measure how well the responses of single MLd neurons could be used to discriminate among songs and how discrimination was related to other response features, we measured neural discrimination from single neuron responses to the 20 songs and compared discriminability to spike rate and spectrotemporal tuning.
Midbrain neurons show a wide range of neural discrimination performance
The ability of single neuron responses to discriminate among songs is maximized when spike trains evoked by repeated presentations of the same song are highly similar, indicating response reliability within a stimulus, and when spike trains evoked by the presentation of different songs are dissimilar, indicating response diversity across stimuli. We asked how well the responses of single neurons could be used to discriminate among 20 different zebra finch songs using four neurometric algorithms. Because the songs varied in duration (range: 1.62 to 2.46 s), we truncated each spike train to the length of the shortest song. Figure 2, A and B shows the spike trains from two example neurons in response to 10 playback trials of 20 songs.
The Victor–Purpura (VP), van Rossum (VR), and firing rate (FR) metrics have previously been applied to neural responses in the auditory and visual systems (Victor and Purpura 1996; Wang et al. 2007). The VP and VR metrics calculate the dissimilarity between pairs of spike trains using information encoded by the timing of APs (methods). The FR metric measures the dissimilarity among neural responses based on the mean firing rate of each spike train. The K-means metric classifies spike trains into clusters based on the information conveyed by the timing of APs. Here, the algorithm was used to separate spike trains into 20 groups (because there were 20 songs) by finding 20 spike train clusters that maximized the within-group similarity and across-group diversity. Figure 2, C and D shows how the spike trains from the neurons in Fig. 2, A and B cluster using the K-means metric.
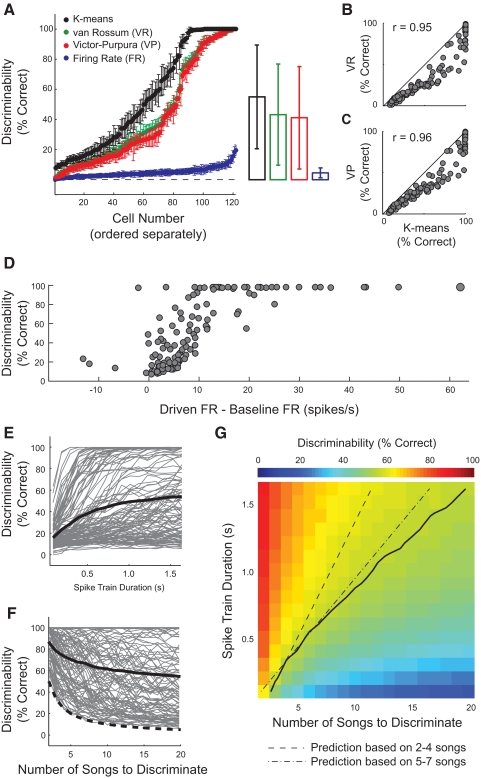
For neural discrimination of the 20 songs, the K-means metric significantly outperformed the VR, VP, and FR metrics (Fig. 3A). Average performances for the four metrics were 55.83 ± 34.5% (K-means), 43.31 ± 33.7% (VR), 41.27.0 ± 34.1% (VP), and 4.55 ± 3.3% (FR). For the K-means, VR, and VP metrics, and percentage correct performance ranged from chance (5%) to perfect (100%) discriminability, indicating that some neurons fired with significantly higher fidelity than did others (see Figs. 1B and 2, A and B). The three neurometrics that used information conveyed by the timing of APs (K-means, VR, and VP) performed significantly better than the FR metric (which did not perform significantly better than chance; P = 0.13, Student's t-test), indicating that spike timing was important for the neural discrimination of these complex sounds (Fig. 3A, right).
Fig. 3.
Four neurometrics were used to measure neural discriminability. A: within each metric, each dot represents the discriminability of a single neuron. Neurons were ordered independently for each neurometric, from lowest to highest performance. Error bars show the SD across 100 repetitions of each neurometric. The right panel shows the mean discrimination performance using each neurometric. Error bars are ±1SD. B: discriminability measured with the K-means and van Rossum metrics showed a strong correspondence (r = 0.95). C: discrimination using the K-means and Victor–Purpura metrics were also highly correlated at the single neuron level (r = 0.96). In B and C, solid lines are unity. D: discriminability measured with the K-means metric was correlated with response strengths (driven firing rate minus baseline firing rate) between 0 and 13 spikes/s (r = 0.69, P < 0.0001). E: K-means discriminability increased with spike train duration. Each gray line shows the discriminability of a single neuron; the black line shows the average for the population. F: discriminability decreased as the number of songs to discriminate increased. The solid black line shows the average discriminability for the population and the dashed line shows chance performance at each set size. G: as the number of songs to discriminate increased, the spike train duration necessary to maintain discriminability increased sublinearly. Performance is represented as color, ranging from 0 to 100% correct. The abscissa shows the number of songs to discriminate and the ordinate shows the spike train duration used in the K-means neurometric. The solid line represents the isodiscriminabiltiy contour of 56% correct, which was the average discriminability. The dashed line shows the linear prediction of spike train duration necessary to maintain this level of discriminabitliy, based on set sizes of 2–4 songs. The dotted-dashed line shows the linear prediction based on set sizes of 5–7 songs.
The average discriminability using the K-means metric was significantly higher than that of any of the other metrics (P < 1e-10, all comparisons, Wilcoxon signed-rank test) and 31 of the 122 (25.4%) neurons performed with nearly perfect discriminability (>99%) using the K-means metric. Although the VR and VP metrics predicted substantially lower estimates of discriminability than did the K-means metric, discriminability measured with the three metrics was highly correlated at the single neuron level (Fig. 3, B and C). In addition to estimating higher discriminability for MLd neurons, the K-means algorithm avoids the direct comparison of spike train pairs, but instead groups all spike trains simultaneously based on their similarity to one another (methods). Further analyses of single neuron discriminability used only the K-means neurometric.
Discriminability increases with firing rate and spike train duration
Because the midbrain neurons from which we recorded produced spike trains that exhibited a wide range of discriminability, we asked what aspects of their responses to songs were correlated with discrimination performance. Discriminability was significantly correlated with response strength (Fig. 3D), increasing linearly between response strengths of 0 and 13 Hz (n = 84, y = 8.50x + 5.67; r = 0.69), and saturating at 100% for nearly every neuron that fired >13 spikes/s above baseline (n = 31; 95.6 ± 10.4%, mean ± SD). Neurons that were inhibited (defined as mean driven firing rates that were lower than baseline firing rates) during stimulus presentation tended to be poor discriminators (n = 7; 36.8 ± 31.2%, mean ± SD).
Discriminability also increased as a function of spike train duration (Fig. 3E). We systematically shortened the spike trains used in the neural discrimination analysis, restricting the number of spikes accessible to the neurometric algorithm. On average, discriminability increased with spike train duration without reaching a plateau at 1.62 s, which was the longest duration tested. However, the responses of some neurons could be used to perfectly discriminate among the 20 songs within as little as 300 ms and the average time to plateau for neurons that reached a discrimination performance of 95% was 726.8 ms (±323.7, 1SD). Together with the positive correlation observed between discriminability and firing rate, these data suggest that increased numbers of APs lead to increased neural discrimination among songs.
We next asked how discriminability changed with the number of stimuli. For each neuron, we measured discriminability for stimulus set sizes ranging from 2 to 20 songs. At each set size, we ran the K-means metric 100 times, each time using a random subset of the 20 songs. Sixty-five of 122 neurons discriminated between two songs at 95% or better and 33 cells maintained this level of discriminability for 20 songs (Fig. 3F). As the number of stimuli increased from 2 to 20 songs, the population average dropped from 86.9 to 55.8% correct.
Last, we more closely analyzed the relationships among discriminability, spike train duration, and set size. In particular, we tested whether the spike train duration necessary for discrimination increased linearly as the number of stimuli to be discriminated increased. We systematically adjusted stimulus set size and stimulus–response duration and calculated the average neural discrimination achieved for each combination of set size and duration (Fig. 3G). From these data, we measured the spike train duration necessary for 56% discrimination performance at each set size. The performance criterion of 56% was chosen because it was the average discriminability across the population of neurons using 1.62 s spike trains (Fig. 3A). Neurons required 176 and 337 ms to discriminate among 3 and 4 songs at 56% discriminability, respectively. Extrapolating from these values predicted very long durations for discriminating among 20 songs. However, only 1,620 ms were needed, showing a sublinear relationship between the number of stimuli to discriminate and the duration necessary to maintain performance.
Neural discriminability is not correlated with auditory tuning
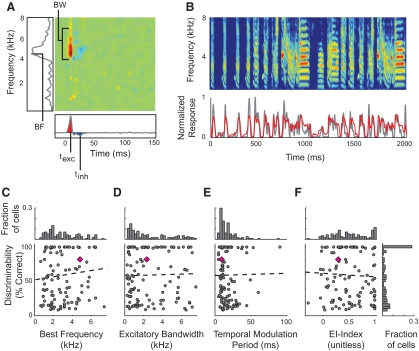
The ability of single neuron responses to discriminate among songs varied widely across the population. We next asked whether discrimination was correlated with the specific spectral and/or temporal features to which midbrain auditory neurons were tuned. To determine how the discrimination performance of a single neuron was related to its tuning properties, we estimated the spectrotemporal receptive field (STRF) for each neuron (methods; Theunissen et al. 2000). We used a normalized reverse correlation technique to obtain STRFs, which describe the joint frequency and temporal tuning of auditory neurons (Fig. 4A). STRFs provide multiple measures of frequency tuning (BF and excitatory BW) and temporal tuning (temporal modulation period and EI index).
Fig. 4.
Neural discriminability was not correlated with spectral or temporal tuning. A: spectrotemporal receptive fields (STRFs) were calculated from neural responses to zebra finch song and estimates of the spectral and temporal tuning properties were computed from the STRF. The left panel shows the spectral projection of the STRF, from which we measured the best frequency (BF). Excitatory bandwidth (BW) was measured at the time of maximum excitation. The bottom panel shows the STRF's temporal projection, from which we measured the temporal modulation period (delay between the peaks of excitation and inhibition) and Excitatory–Inhibitory (EI) index, which was the normalized balance between excitation (shown in red) and inhibition (shown in blue). Positive values indicate stronger excitation than inhibition; negative values indicate stronger inhibition (range: −1 to 1). B: an example in which the STRF predicts the neural response to a novel sound (cc = 0.8; gray trace is the poststimulus time histogram (PSTH) of actual response; red trace is predicted response). C and D: discriminability is not correlated with best frequency (r = 0.11) or spectral bandwidth (r = 0.03). The top histograms in each panel show the distribution of BFs and BWs. E and F: discriminability is not correlated with the temporal modulation period (r = 0.01) or the EI index (r = −0.01). The right histogram shows the distribution of K-means discriminability, and corresponds to C–F. Dashed lines show the linear regression and the pink diamond represents the neuron from A.
For each neuron, we measured the validity of the STRF as a model of spectrotemporal tuning by calculating how well the STRF predicted the responses to novel songs (those not used in the calculation of the STRF). For this validation, predicted poststimulus time histograms (PSTHs) were generated by convolving the STRF with the spectrograms of songs and the predicted PSTHs were compared with PSTHs of the actual neural response (Fig. 4B). Including all of the neurons from which we recorded, the average correlation between the STRF-predicted response and neural response was 0.59 ± 0.16 (cc). For the STRF in Fig. 4, the correlation coefficient between the predicted and actual PSTH was 0.80. For all analyses of spectrotemporal tuning, we limited our data set to neurons with STRFs that predicted responses with a correlation coefficient ≥0.3 (116 of 122 neurons).
The STRF in Fig. 4A shows the spectrotemporal tuning of a neuron that is maximally responsive to 5 kHz and is excited by a range of frequencies spanning about 3 kHz. The best frequency was calculated by projecting the STRF onto the frequency axis (Fig. 4A, left of STRF) and the excitatory bandwidth was measured at the time corresponding to the peak of excitation in the STRF (Fig. 4A). Temporal tuning was measured by projecting the STRF onto the time axis (Fig. 4A, below STRF). The EI index is the summed area under the primary excitatory and inhibitory regions of the curve, normalized by the overall area (range: −1 to 1). The EI index determines the degree to which neurons fire with either an onset or a sustained pattern. For the STRF in Fig. 4A, the excitatory and inhibitory regions are temporally contiguous and excitation is greater than inhibition (EI index = 0.29); neurons with this EI index have an onset response followed by a smaller sustained response. We also measured the temporal modulation period by calculating the time between the peaks of the excitatory and inhibitory regions of the STRFs. Previous analyses suggested that neurons with balanced excitation and inhibition (measured as EI index near zero) and sharp temporal tuning (measured as small temporal modulation periods) would discriminate better than neurons with slow modulation rates and those that were primarily excitatory (Narayan et al. 2005).
Comparison of K-means discriminability and STRFs showed no correlation between discriminability and either spectral or temporal tuning (Fig. 4). Best frequency and frequency tuning bandwidth were positively correlated with one another (r = 0.57; data not shown), but both were uncorrelated with discriminability (Fig. 4, C and D). Temporal modulation period and EI index were also uncorrelated with discriminability (Fig. 4, E and F). These findings show that neurons encoding a wide range of acoustic features have similar abilities to discriminate among songs.
Combined responses of multiple neurons improve discrimination
Behavioral discrimination of complex sounds such as songs is likely achieved through the combined activity of multiple neurons. We asked two questions regarding how combining the responses of multiple neurons affected the neural discrimination of songs. First, can the combined responses of multiple neurons be used to discriminate among songs better than the responses of single neurons? Second, are the combined responses of neurons with similar spectrotemporal tuning better at discriminating among songs than the combined responses of neurons with dissimilar tuning?
From the responses of single midbrain neurons, we simulated 800 readout neurons that received feedforward input from two to five cells selected at random from our set of MLd neurons (200 populations for each number of inputs). Although the MLd neurons were not typically recorded simultaneously, we found that pairs of nonsimultaneously and simultaneously recorded neurons had similar signal and noise correlations (P > 0.6, Wilcoxon rank-sum test) and we therefore assumed that their responses were primarily stimulus-driven (Lee et al. 1998; Reich et al. 2001). We modeled the readout neurons in three different ways to examine how the integration of activity from groups of neurons affected the group's capacity to discriminate (Fig. 5). The SUM model of the readout neuron integrated the responses from all input neurons and produced a graded response proportional to the concurrent input from the group. The OR model fired a single AP when one or more input neurons fired an AP. The AND model fired only when concurrent input arrived from each of the input neurons. The SUM, OR, and AND readout models simulate well-established physiological processes; subthreshold changes in membrane potential, suprathreshold spiking activity, and coincidence detection, respectively. For each model, the responses of every input neuron contributed to the response of the readout neuron with equal weight; inputs from highly discriminating neurons were not preferentially weighted compared with inputs from poorly discriminating neurons. Figure 5, A and B depicts these three methods for combining the responses of groups of neurons. For analyzing group responses, we used d′ to estimate neural discrimination. To calculate d′, we measured the squared Euclidean distance between the average neural response to a pair of songs, normalized by the average variability in the responses to each pair of songs (methods).
Fig. 5.
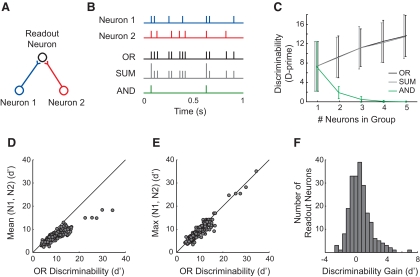
Readout neurons that received input from 2 to 5 MLd neurons were simulated. A: a diagram of a readout neuron with 2 inputs (Neuron 1 and Neuron 2). B: the readout response was modeled using 3 different models. Example responses from each model are shown for the input spike trains labeled Neuron 1 and Neuron 2. C: average discriminability across the population of readout neurons as a function of the number of input neurons. D: discriminability of OR readout neurons with 2 inputs compared with the average discriminability of the 2 inputs. Solid line is the unity line. E: discriminability of OR readout neurons with 2 inputs compared with the input neuron that discriminated best. F: histogram showing the number of OR readout neurons that achieved gains in discriminability relative to the input neuron that discriminated best (P = 1.21 × 10−4, Wilcoxon signed-rank test).
Using the SUM and OR models, the combined responses of groups of neurons could be used to discriminate among songs significantly better than the responses of single neurons (Fig. 5C). For both of these models, performance increased only gradually with three or more inputs and did not increase significantly between four and five inputs. The SUM and OR models performed almost identically, which is predicted when the inputs have few coincident spikes. Performance using the AND model decreased as the number of inputs increased, and saturated with three or more inputs. The AND model suffered with increasing numbers of inputs because the criterion for coincidence became stricter (e.g., three neurons must spike simultaneously to make the readout fire) and therefore an output spike became less likely.
At each group size, we also calculated discriminability by concatenating spike trains rather than pooling them. This provided an approximation of the degree to which neural responses could be used to discriminate without pooling. For this model, the discriminability was larger than that of any of the other models and it increased significantly for group sizes of two to five (mean d′ was 10.60, 14.18, 16.67, 18.16; for group sizes of two, three, four, and five, respectively; data not shown). The following analyses use only the OR readout model, but the results are similar for the SUM model (data not shown).
We next measured how well the readout neurons performed compared with the individual input neurons. Nearly every two-input readout model performed better than the average discriminability of the input neurons (Fig. 5D). For many readout neurons, discriminability was also better than that of the best individual neuron in the pair (Fig. 5E). We calculated the gain in discriminability as the difference between the discriminability of the readout neuron and the discriminability of the best-performing input neuron in each pair. Across the population of readout neurons, pairs discriminated significantly better than did either of the input neurons (Fig. 5F), showing that combined information from multiple neurons provided increased neural discriminability compared with that of single neurons.
Groups of similarly tuned neurons have the largest gains in discriminability
The degree to which readout neurons outperformed their best-performing input varied considerably. To create the group models, neurons were paired at random from the population of MLd neurons and some pairs had more similar tuning properties than others. We next asked whether the similarity of spectral and temporal tuning properties could account for differences in the gain in discriminability between readout neurons and their inputs.
Figure 6A shows two neurons with similar spectral and temporal tuning. Both cells fired APs at similar times throughout a song and the spike trains produced by the readout neuron shared the temporal pattern of the inputs. Figure 6B shows two neurons with different tuning. These neurons fired APs at different times throughout a song and the responses of the readout neuron reflected the combined input from both neurons, resulting in spike trains with only coarse temporal patterning.
Fig. 6.
Pairs of neurons with similar tuning properties obtained the largest gains in discriminability. A: 2 neurons with highly similar STRFs. Below the STRFs are 5 spike trains evoked by a single song for each of the neurons, as well as the output of the OR readout neuron. The rasters are highly similar for the two input neurons, which is reflected in the readout neuron. The gray bar shows qualitatively the increased signal strength obtained by the readout neuron. B: pair of neurons with dissimilar STRFs. Neuron 2 is the same as in A, but Neuron 1 has different tuning. For this pair, misaligned spike trains do not reinforce one another (gray bar). C: the gain in discriminability is correlated with the similarity of frequency tuning. The pairs in A and B are shown as a blue square and purple diamond, respectively. D: similar temporal tuning is correlated with gains in discriminability. E: pairs of neurons that produce similar spike train patterns have larger gains in discriminability than pairs of neurons with dissimilar spike train patterns. For C–E, the dashed lines show the linear regression. F–H: for the 3 parameters plotted in C–E, the gain in discriminability for the quartile of neurons with the most similar tuning (gray) and least similar tuning (white). Black bars show the gain in discriminability for readout neurons that receive input from identically tuned neurons. Error bars are ±1SD (*P ≤ 0. 01, Kruskal–Wallis test; **P ≤ 0.0002, Kruskal–Wallis test).
Across the population of readout neurons, we measured the best frequency and EI index for each input neuron and calculated the similarity of these tuning parameters for each pair. Pairs of neurons with similar best frequencies had greater increases in discriminability than did pairs of neurons with dissimilar best frequencies (Fig. 6C). Pairs of neurons with similar EI indices also had larger gains in neural discriminability (Fig. 6D). Although the linear relationships between the gain in discriminability and STRF similarity were both significant (P < 0.002 for both BF and EI correlations), the correlations were not particularly strong (r = −0.29 for BF; r = −0.21 for EI index). We next divided the neurons into quartiles based on the similarity of their tuning properties and found that the quartile with the most similar tuning properties had a significantly larger gain than the quartile with the least similar tuning (Fig. 6, F and G). The similarities between frequency bandwidth and temporal modulation rate were not correlated with gains in discriminability (data not shown).
To test the maximum extent to which tuning similarity can facilitate neural discrimination by groups of neurons, we simulated readout neurons that received inputs from duplicate copies of the same neuron. For readout neurons with these perfectly cotuned inputs, the gain in discriminability was similar to that of the most similarly tuned quartile of the randomized groups (Fig. 6, F and G). This supports the finding that tuning similarity facilitates discrimination and suggests that perfectly cotuned inputs are not necessary for increased discriminability.
Readout neurons with inputs from similarly tuned and dissimilarly tuned neurons had similar firing rates, dispelling the possibility that similarly tuned pairs produced more spikes, leading to greater discriminability (r = 0.12, readout firing rate vs. BF similarity; r = 0.045, readout firing rate vs. EI index similarity). We next asked whether the gain in discriminability for the readout neurons depended on the difference in the discriminability of the inputs. If one input was a good discriminator and the other was a poor discriminator, the poor discriminator would be unlikely to add to the pair's ability to discriminate. However, the gain in discriminability for readout neurons was not correlated with differences in discriminability between the two input neurons (r = −0.06; data not shown). Furthermore, although readout discriminability was correlated with mean input discriminability, readout gain was not (r = −0.141), suggesting that the largest gains in discriminability were not necessarily achieved by pairs of neurons with precise inputs. Last, we found no significant interactions among the gains in discriminability and BF similarity, input discriminability difference, and input discriminability mean (P > 0.1 for all interaction terms of the full model). These results suggest that readout neurons with the largest gains in discriminability have inputs that show similar spectrotemporal tuning but are not necessarily matched in individual discrimination performance or have a high average disciminability.
Correlated inputs facilitate discrimination by groups of neurons
Neurons with similar best frequencies are likely to fire APs in response to similar portions of spectrally rich, time-varying sounds such as zebra finch songs. Neurons with the same EI indices will produce APs with similar temporal patterns (e.g., bursts of APs at syllable onset). In response to complex sounds, neurons that are similarly tuned in both frequency and time should produce spike trains that are similar to one another. We calculated the similarity between the individual spike trains from each input pair using an extension of the d′ metric. Spike train similarity was significantly correlated with STRF similarity (r = 0.44, spike train similarity vs. BF and EI index similarities; data not shown). Spike train similarity was also significantly but moderately correlated with enhanced discriminability (r = −0.33; Fig. 6E), indicating that pairs of neurons with similar spike trains had larger gains in discriminability than gains of pairs with dissimilar spike trains. Separating the neurons into quartiles based on spike train similarity, we found that neurons with the most similar spike trains achieved significantly larger gains in discriminability relative to those with the least similar spike trains (Fig. 6H).
Because readout neurons with three inputs discriminated significantly better than those with two inputs (Fig. 5C), we measured the gain in discriminability for three-input readout neurons and calculated the average similarity among the best frequencies, EI indices, and the spike trains of the three input neurons. Readout neurons receiving input from three neurons with similar best frequencies and EI indices had larger gains in discriminability than those with dissimilar inputs (r = −0.35, BF similarity; r = −0.28, EI index similarity) and discriminability was correlated with spike train similarity among the three inputs (r = −0.31; data not shown).
Pooling correlated inputs facilitates discrimination by compensating for imprecise neural responses
We found that readout neurons receiving pooled input from similarly tuned cells were better discriminators than those receiving input from dissimilarly tuned cells, and that the gain in discriminability was strongest when input neurons produced correlated spike trains (Fig. 6, E and H), in agreement with previous work using pooling models (Zhang and Reid 2005). To more closely examine the conditions under which correlated inputs lead to increased gains in readout discriminability, we simulated pairs of neurons with varying levels of temporal precision in their spiking output—covering the range of precision observed in MLd neurons, as well as higher and lower precision—and varying levels of correlation between their responses (Fig. 7).
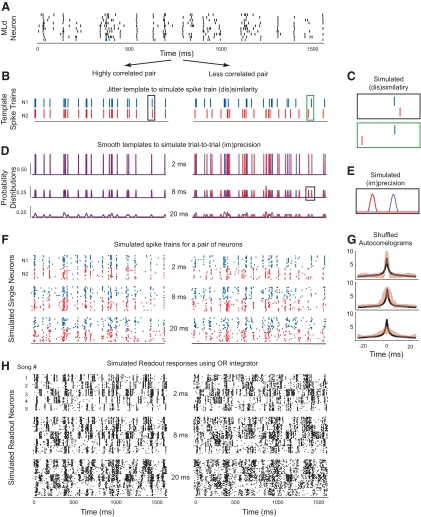
Fig. 7.
Simulating pairs of neurons with varying degrees of temporal precision and spike train similarity. A: a spike train from a real MLd neuron was used as a template from which simulated spike trains were generated. Each row shows the spiking response to one presentation of a single song; the bottom row (colored blue) was used as the template for the first simulated neuron in each pair (N1). B, D, F, and H: the left column in each panel shows a pair of neurons with highly correlated responses and the right column shows a pair of neurons with less correlated responses. B: temporal jitter was added to each “spike” in the N1 template to create a template for the second simulated neuron (N2). C: close-up of the amount of jitter introduced to the template in the left and right panels of B. D: the templates for N1 and N2 were smoothed with Hanning windows that ranged in width from 1 to 100 ms, resulting in continuous probability distributions. The blue distributions correspond to N1 and the red distributions to N2. The top, bottom, and middle panels show smoothing widths of 2, 8, and 20 ms. E: close-up of the amount of smoothing applied to the templates for N1 and N2. F: 10 spike trains were generated from each of the probability distributions. The top, middle, and bottom panels show spike trains for N1 and N2, generated from the respective distributions in D. G: the average shuffled autocorrelogram (SAC) of real MLd neurons (mean shown in black) compared with the SACs of simulated neurons (±1SD shown in red) with 2, 8, and 20 ms smoothing windows (from top to bottom). H: responses from an OR readout neurons that received simulated spike trains from N1 and N2 as inputs. From top to bottom, the readout neurons received input with progressively coarser temporal precision. Each panel shows 10 simulated responses to each of 5 songs.
We generated spike trains for a pair of simulated neurons using the spiking response from a single MLd neuron (Fig. 7A), which served as a time-varying probability distribution from which spike trains were sampled. To manipulate the correlations in the responses of the pair, we jittered the timing of each “spike” in the template of one of the simulated neurons (Fig. 7, B and C). We introduced jitter ranging from ±1 to ±125 ms, with smaller jitter resulting in more correlated inputs. For Fig. 7, B, D, F, and H, the left panels represent a pair of neurons with strong spike train correlations and the right panels represent a pair of neurons with less correlated spike trains.
To control the temporal precision of the simulated spike trains, we smoothed the point processes with a Hanning window with widths ranging from 1 to 100 ms (Fig. 7, D and E): wider smoothing windows created spike trains with greater trial-to-trial variability. The probability distributions in Fig. 7D were smoothed with Hanning widths of 2, 8, and 20 ms (top to bottom).
The blue and red spike trains in Fig. 7F were generated from the distributions in Fig. 7D. The shuffled autocorrelograms (SACs) in Fig. 7G show the temporal precision of real MLd neurons (black trace) compared with the temporal precision of simulated neurons (mean ± 1SD are shown in red). Simulated neurons with intermediate levels of precision (e.g., 8 ms) have SACs that most closely match the peak (correlation index) and width of real MLd neurons.
Using the simulated single neurons shown in Fig. 7F, we simulated readout neurons using the OR readout model (Fig. 5, A and B). The black spike trains in Fig. 7H are the output of an OR readout neuron that received the red and blue spike trains as inputs. As the temporal precision of the input neurons decreased, the readout neuron became worse at discriminating among different songs and this effect was strongest for readout neurons that received less correlated input (shown qualitatively in the bottom row of Fig. 7H).
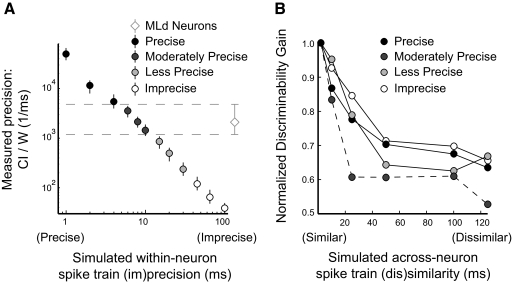
For each MLd neuron that we recorded (n = 122), we simulated a pair of neurons that varied in correlation and temporal precision. As the size of the window with which we smoothed the template widened, the precision of the simulated neurons decreased (Fig. 8A). The measured precision of a subset of simulated neurons matched closely with real MLd neurons and we used this criterion to segregate the simulated neurons into groups that had better (Precise), similar (Moderately Precise), worse (Less Precise), and poor (Imprecise) precision, relative to real MLd neurons. Simulated neurons with all levels of temporal precision fell within the range of discriminability observed in real MLd neurons, measured as d′ (data not shown).
Fig. 8.
Gain in discriminability for pairs of simulated neurons depended on spike train precision and response similarity. A: at each level of simulated precision, we measured the temporal precision as the peak of the SAC (coincidence index [CI]) normalized by the SAC half-width at half-height (W) (error bars are median with upper and lower quartiles). The diamond and dashed lines show the precision of real MLd neurons. Simulated neurons were grouped according to their observed temporal precision relative to real MLd neurons. B: within each group, the gain in discriminability was normalized to the gain achieved with highly similar inputs. The normalized gain was plotted against the similarity of the inputs.
For each readout neuron, we calculated the discriminability gain. The gain in discriminability depended on both the precision and the similarity of the inputs. Readout neurons with highly precise inputs had the largest gains in discriminability. Regardless of the temporal precision of the inputs, readout neurons achieved the largest gains if the inputs had similar spike trains.
To determine the degree to which input dissimilarity affected readout gain, we normalized the gain in discriminability for each level of temporal precision, such that for highly similar inputs, the readout neurons in each group performed equally well (Fig. 8B). Although the gain in discriminabiltiy always decreased as the inputs became dissimiliar, this decrease was the most pronounced for readout neurons that received inputs with MLd-like (Moderate) levels of precision, which quickly dropped to roughly 60% of maximum when the inputs became dissimilar. For these readout neurons, discriminability was highly dependent on input similarity. The gain of readout neurons with Highly Precise and Imprecise inputs decreased slowly when the inputs became less correlated, and plateaued at roughly 70% of their maximum gain. For these readout neurons, discriminability was less dependent on input similarity. These simulations suggest that the advantages of pooling correlated inputs are most pronounced for neurons that have biological levels of temporal precision.
DISCUSSION
We examined how well the responses of single auditory midbrain neurons could be used to discriminate among vocalizations and the relationship between neural discriminability and spectrotemporal tuning. We also investigated how well the combined responses of groups of neurons could be used to discriminate among songs. We found that single neuron responses could be used to discriminate among songs with a wide range of accuracy. For single neurons, neural discrimination performance was not related to tuning properties such as best frequency or EI index. By calculating the pooled responses of multiple neurons, we found that groups of auditory neurons discriminated among songs significantly better than did single neurons, particularly when the neurons in the group were similarly tuned. Last, we showed through simulations that the pooling of redundant spike trains was particularly advantageous for neurons with biological levels of spike train reliability.
Discrimination and spectrotemporal tuning
We found that the spectral features to which neurons were tuned did not correlate with how well the neurons' spike trains could be used to discriminate among songs. A previous theoretical study suggested that auditory neurons with temporally delayed inhibition (i.e., EI index ≅ 0) should produce spike trains that discriminate better than neurons that are purely excitatory (i.e., EI index ≅ 1) (Narayan et al. 2005). Delayed inhibition occurs in the same frequency range as excitation (see STRF in Fig. 4A) and is a potential mechanism for producing reliable and temporally precise responses (see Fig. 1B). Here, we found that the EI index of a neuron did not correlate with the neuron's ability to discriminate; neurons that performed with 100% correct neural discrimination ranged from 0 to 1 in EI index. However, the majority of the neurons from which we recorded had at least some delayed inhibition (Fig. 4F), which appears to be a typical tuning property of auditory midbrain neurons (Woolley et al. 2006, 2009). This limited our analysis of how delayed inhibition may influence neural discrimination in midbrain neurons. Further, zebra finch songs consist of syllables separated by silent epochs and the temporal pattern of every song is different. Neurons without delayed inhibition will fire during syllables and not during silent epochs, resulting in spike trains that mirror the temporal pattern of each song. This temporal pattern alone may be sufficient for neural discrimination.
Although the ability of single neuron responses to discriminate was not correlated with spectrotemporal tuning, it was highly correlated with firing rate. In general, increased numbers of APs do not necessarily provide more information about stimulus identity. For instance, although higher firing rates lead to a larger probability of coincident spikes over multiple presentations of a single song, higher firing rates also increase the probability of coincident spikes during different songs. However, because the baseline firing rates of MLd neurons were near zero, spikes that occurred during song playback were generally driven by the acoustic features of the song rather than randomly scattered throughout the spike train and were therefore useful in discrimination.
Pooling models of neural integration
We investigated the degree to which neural discrimination was facilitated by groups of neurons compared with single neurons. For this study, we used a pooling model of feedforward neural integration, in which spike trains from multiple neurons were combined to produce a single output spike train. Pooling models have been used to investigate motor planning (Georgopoulos et al. 1986) and neural responses to somatosensory (Arabzadeh et al. 2004), visual (Chen et al. 2006), olfactory (Geffen et al. 2009), and auditory stimuli (Fitzpatrick et al. 1997; Woolley et al. 2005). In previous implementations of pooling models, the neural response that was pooled was typically the average firing rate to a stimulus that varied along one or two dimensions. Rather than firing rate, we pooled the spike trains produced by multiple neurons in response to single presentations of a complex sound. Although the neurons that were pooled were not recorded simultaneously, the noise correlations observed in simultaneously and nonsimultaneously recorded neurons did not differ. This type of pooling mimics the synaptic connectivity with which neurons share information in vivo, but uses a more complex response property than firing rate alone. In agreement with previous studies using pooling models, we found significant gains in discriminability in readout neurons compared with single neurons (Figs. 5 and 6).
Our pooling model considered only excitatory feedforward connections, in which every input was equally weighted. Other pooling rules could be considered (Chen et al. 2006). For instance, we could have assigned weights to maximize the discriminability of the readout neuron, using both positive and negative weights. Alternatively, the weights could have been determined based on the discriminability of the inputs: highly discriminating inputs would be assigned larger weights than poorly discriminating inputs. Assigning positive and negative weights to input neurons can facilitate discrimination by canceling correlated noise among input signals (Chen et al. 2006), whereas assigning weights based on discriminability can facilitate discrimination by supplying primarily reliable inputs to the readout neurons.
Further studies could also examine how pooling may be optimized using the known organization of auditory circuits. In particular, auditory neurons are excited by sounds at a specific range of frequencies and are often inhibited by frequencies above or below this excitatory range (known as lateral inhibition) and similarly tuned neurons are often located near one another (Lee et al. 2004; Lim and Anderson 2007). These observations provide known biases in the probability with which auditory neurons converge and suggest the weights (e.g., excitatory or inhibitory) with which the inputs to a readout neuron should be scaled. Observing these principles of connectivity could produce feedforward models that further facilitate neural discrimination.
Although pooling models of population coding measure neural discriminability in a way that mimics synaptic connectivity, they are not the only way to measure population discriminability; also, they do not necessarily measure the optimal discriminability of a group of neurons. A previously described class of models uses the joint information contained in the responses of two or more neurons by expanding on the VP (Aronov et al. 2003) and VR metrics (Houghton and Sen 2008). For these models, retaining at least some information regarding which input neuron fired each spike significantly improved discriminability. Our pooling implementation is similar to the summed population code described in Aronov et al. (2003).
Another common approach is to predict the stimulus that evoked a set of responses from a group of neurons, without pooling the responses. This approach typically uses techniques such as mutual information (MI) or maximum likelihood (ML) inference (Rieke et al. 1999). As opposed to pooling models that integrate multiple inputs into a single spike train, optimal coding models such as these assume that the observer—the experimenter or the experimental subject—has access to all of the individual spike trains from each neuron in the group (Deneve et al. 1999; Petersen et al. 2001; Warland et al. 1997). If the responses of multiple neurons are kept separate, such as with optimal coding models, independent inputs maximize information transmission and facilitate discrimination, whereas redundant inputs provide little if any increased information (Barlow 1972; Machens et al. 2004). The difference between optimal coding models and pooling models is accounted for by the way in which spiking information is conserved in each model; in a pooling model, the identity of a single output spike cannot be traced back to a particular input neuron, whereas for optimal coding models, the APs belonging to each spike train remain segregated. For the optimal coding models, removing the information about which input neuron produced each spike significantly reduces the amount of information encoded by groups of neurons, more closely matching the results observed in pooling models (Montani et al. 2007).
Redundant coding facilitates discrimination
For the readout neurons that we simulated, discriminability was largest when the spike trains from small groups of neurons were correlated with one another. This suggests that for complex, time-varying stimuli, redundant coding may be useful for neural discrimination. One explanation for the usefulness of redundancy is to compensate for the trial-to-trial spike train variability of neurons with imprecise spike trains and to counteract the tendency for spike-timing variability to increase between the sensory epithelium and the cortex (Kara et al. 2000). Variability in spike timing limits the amount of information that can be conveyed by single neurons (Herz et al. 2005) and redundant coding is thought to increase the signal-to-noise ratio of sensory information for neurons with biological levels of spike-timing precision (Woolley et al. 2006). Previous theoretical (Salinas and Sejnowski 2000) and in vitro (Reyes 2003; Stevens and Zador 1998; Zador 1998) studies using similar models of neural integration found that input correlations increased the reliability of a readout neuron relative to the reliability of the inputs. Our model suggests that a similar phenomenon could occur in vivo.
The fact that reliability actually does decrease as sensory information propagates (Kara et al. 2000) suggests that this pooling mechanism is not fully compensatory. For instance, previous measures of neural discriminability in the auditory forebrain of zebra finches, at least two synapses removed from MLd, showed less reliable discrimination than that in the midbrain (Wang et al. 2007). Our model used a simple method of neural integration that reliably relayed spikes from input neurons to the readout neuron. In vivo, synaptic transmission is less reliable (Allen and Stevens 1994) and many presynaptic events may be necessary to trigger postsynaptic events. Furthermore, fluctuations in membrane potential at the readout neuron may cause spontaneous, nonsynaptically driven spikes to occur, further decreasing reliability. For example, MLd neurons show lower spontaneous rates than do field L neurons, which are less reliable than MLd neurons (Wang et al. 2007; Woolley and Casseday 2004). Our model aimed to capture the capacity of groups of neurons to discriminate using a simple model of synaptic integration. Extending our model to include stochastic noise and imperfect integration should decrease the capacity of readout neurons to discriminate.
A previous experiment that recorded from auditory neurons in the midbrain, thalamus, and cortex showed that redundancy decreased along the ascending auditory system, particularly between the inferior colliculus (the mammalian homologue of MLd) and the thalamus (Chechik et al. 2006). Our observation that pooling the spike trains of similarly tuned neurons maximized discriminability may support this finding. Our model encompasses the idea that MLd neurons with similar tuning synapse on the same readout (thalamic) neurons. It is unclear whether convergence such as this is the primary type of connectivity between the midbrain and thalamus, or whether divergence is also prevalent. However, the tonotopic organization of auditory information suggests that some degree of convergence is maintained along the auditory pathway (see following text for discussion). This convergence of similarly tuned MLd neurons onto a small population of thalamic neurons could reduce the redundancy of thalamic neurons by the ratio of readout (thalamic) to input (midbrain) neurons.
Topographical organization and neural discrimination
In mammals and birds, auditory neurons are organized tonotopically (Merzenich et al. 1975; Muller and Leppelsack 1985; Reale and Imig 1980; Ryan et al. 1982). Ascending and descending projections to the thalamus and midbrain are also organized tonotopically, as are locally projecting neurons within the telencephelon (Lee et al. 2004; Lim and Anderson 2007). The likelihood of auditory neurons synapsing onto a downstream neuron or with one another is therefore biased toward neurons with similar tuning properties.
The current findings, along with previous work showing that pooling spike trains from correlated neurons improves the discriminability and spike train precision of the readout neurons (Reyes 2003), provide a theoretical framework for how the auditory system should be wired for optimal discrimination: similarly tuned neurons should synapse onto the same downstream neurons or with one another. Importantly, the architecture that produces optimal discrimination matches the anatomically and electrophysiologically observed frequency organization of the auditory system (Schreiner and Winer 2007). Furthermore, we observed a gain in discriminability for neurons that had similar temporal tuning. Electrophysiology experiments suggest that the temporal response properties of midbrain auditory neurons are also organized systematically (Rodriguez et al. 2010) and that temporal information is conserved between the thalamus and cortex (Miller et al. 2001). It will be important to uncover the degree to which temporal information is topographically mapped throughout the auditory system.
The current finding that discrimination of complex stimuli is optimized via redundant coding may be important in other sensory modalities such as vision and somatosensation, where neural information is also organized topographically (Powell and Mountcastle 1959; Tootell et al. 1982; Woolsey and Van der Loos 1970). Topographic maps are thought to aid in behavioral and perceptual tasks such as sensory learning (Harris et al. 1999), pitch perception (Oxenham et al. 2004), and figure–ground segregation (Roelfsema et al. 2002). Our current findings, coupled with the known topographic organization of neural information in multiple sensory modalities, suggest further studies that could investigate whether the topographic organization of sensory information is useful in discriminating among complex sensory cues.
GRANTS
This work was supported by a Searle Scholars Program grant to S.M.N. Woolley, Gatsby Initiative in Brain Circuitry grants to S.M.N. Woolley and D. M. Schneider, and National Institute on Deafness and Other Communication Disorders Grant F31-DC-010301 to D. M. Schneider.
DISCLOSURES
No conflicts of interest are declared by the authors.
ACKNOWLEDGMENTS
We thank B. Warren for developing the software used to collect electrophysiological data and for technical support; and J. Schumacher, A. Vyas, and A. Calabrese for comments on and discussions regarding the manuscript.
REFERENCES
- Allen C, Stevens CF. An evaluation of causes for unreliability of synaptic transmission. Proc Natl Acad Sci USA 91: 10380–10383, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andoni S, Li N, Pollak GD. Spectrotemporal receptive fields in the inferior colliculus revealing selectivity for spectral motion in conspecific vocalizations. J Neurosci 27: 4882–4893, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arabzadeh E, Panzeri S, Diamond ME. Whisker vibration information carried by rat barrel cortex neurons. J Neurosci 24: 6011–6020, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aronov D, Reich DS, Mechler F, Victor JD. Neural coding of spatial phase in V1 of the macaque monkey. J Neurophysiol 89: 3304–3327, 2003 [DOI] [PubMed] [Google Scholar]
- Barlow HB. Single units and sensation: a neuron doctrine for perceptual psychology? Perception 1: 371–394, 1972 [DOI] [PubMed] [Google Scholar]
- Britten KH, Shadlen MN, Newsome WT, Movshon JA. The analysis of visual motion: a comparison of neuronal and psychophysical performance. J Neurosci 12: 4745–4765, 1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chechik G, Anderson MJ, Bar-Yosef O, Young ED, Tishby N, Nelken I. Reduction of information redundancy in the ascending auditory pathway. Neuron 51: 359–368, 2006 [DOI] [PubMed] [Google Scholar]
- Chen Y, Geisler WS, Seidemann E. Optimal decoding of correlated neural population responses in the primate visual cortex. Nat Neurosci 9: 1412–1420, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christianson GB, Pena JL. Preservation of spectrotemporal tuning between the nucleus laminaris and the inferior colliculus of the barn owl. J Neurophysiol 97: 3544–3553, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Newsome WT. Estimates of the contribution of single neurons to perception depend on timescale and noise correlation. J Neurosci 29: 6635–6648, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covey E, Kauer JA, Casseday JH. Whole-cell patch-clamp recording reveals subthreshold sound-evoked postsynaptic currents in the inferior colliculus of awake bats. J Neurosci 16: 3009–3018, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deneve S, Latham PE, Pouget A. Reading population codes: a neural implementation of ideal observers. Nat Neurosci 2: 740–745, 1999 [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern Classification. New York: Wiley, 2001 [Google Scholar]
- Engineer CT, Perez CA, Chen YH, Carraway RS, Reed AC, Shetake JA, Jakkamsetti V, Chang KQ, Kilgard MP. Cortical activity patterns predict speech discrimination ability. Nat Neurosci 11: 603–608, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzpatrick DC, Batra R, Stanford TR, Kuwada S. A neuronal population code for sound localization. Nature 388: 871–874, 1997 [DOI] [PubMed] [Google Scholar]
- Geffen MN, Broome BM, Laurent G, Meister M. Neural encoding of rapidly fluctuating odors. Neuron 61: 570–586, 2009 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science 233: 1416–1419, 1986 [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Neural computations that underlie decisions about sensory stimuli. Trends Cogn Sci 5: 10–16, 2001 [DOI] [PubMed] [Google Scholar]
- Harris JA, Petersen RS, Diamond ME. Distribution of tactile learning and its neural basis. Proc Natl Acad Sci USA 96: 7587–7591, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez A, Zainos A, Romo R. Neuronal correlates of sensory discrimination in the somatosensory cortex. Proc Natl Acad Sci USA 97: 6191–6196, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herz AVM, Benda J, Gollisch T, Machens CK, Schaette R, Schütze H, Stemmler MB. Auditory processing of acoustic communication signals: sensory biophysics, neural coding, and discrimination of conspecific songs. In: Methods in Insect Sensory Neuroscience, edited by Christensen TA.Boca Raton, FL: CRC Press, 2005, p. 129–156 [Google Scholar]
- Houghton C, Sen K. A new multineuron spike train metric. Neural Comput 20: 1495–1511, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jazayeri M, Movshon JA. Optimal representation of sensory information by neural populations. Nat Neurosci 9: 690–696, 2006 [DOI] [PubMed] [Google Scholar]
- Joris PX, Louage DH, Cardoen L, van der Heijden M. Correlation index: a new metric to quantify temporal coding. Hear Res 216–217: 19–30, 2006 [DOI] [PubMed] [Google Scholar]
- Joshua M, Elias S, Levine O, Bergman H. Quantifying the isolation quality of extracellularly recorded action potentials. J Neurosci Methods 163: 267–282, 2007 [DOI] [PubMed] [Google Scholar]
- Kara P, Reinagel P, Reid RC. Low response variability in simultaneously recorded retinal, thalamic, and cortical neurons. Neuron 27: 635–646, 2000 [DOI] [PubMed] [Google Scholar]
- Lee CC, Schreiner CE, Imaizumi K, Winer JA. Tonotopic and heterotopic projection systems in physiologically defined auditory cortex. Neuroscience 128: 871–887, 2004 [DOI] [PubMed] [Google Scholar]
- Lee D, Port NL, Kruse W, Georgopoulos AP. Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. J Neurosci 18: 1161–1170, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim HH, Anderson DJ. Antidromic activation reveals tonotopically organized projections from primary auditory cortex to the central nucleus of the inferior colliculus in guinea pig. J Neurophysiol 97: 1413–1427, 2007 [DOI] [PubMed] [Google Scholar]
- Machens CK, Schutze H, Franz A, Kolesnikova O, Stemmler MB, Ronacher B, Herz AV. Single auditory neurons rapidly discriminate conspecific communication signals. Nat Neurosci 6: 341–342, 2003 [DOI] [PubMed] [Google Scholar]
- Machens CK, Wehr MS, Zador AM. Linearity of cortical receptive fields measured with natural sounds. J Neurosci 24: 1089–1100, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merzenich MM, Knight PL, Roth GL. Representation of cochlea within primary auditory cortex in the cat. J Neurophysiol 38: 231–249, 1975 [DOI] [PubMed] [Google Scholar]
- Miller LM, Escabi MA, Read HL, Schreiner CE. Functional convergence of response properties in the auditory thalamocortical system. Neuron 32: 151–160, 2001 [DOI] [PubMed] [Google Scholar]
- Miller LM, Recanzone GH. Populations of auditory cortical neurons can accurately encode acoustic space across stimulus intensity. Proc Natl Acad Sci USA 106: 5931–5935, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montani F, Kohn A, Smith MA, Schultz SR. The role of correlations in direction and contrast coding in the primary visual cortex. J Neurosci 27: 2338–2348, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller CM, Leppelsack HJ. Feature extraction and tonotopic organization in the avian auditory forebrain. Exp Brain Res 59: 587–599, 1985 [DOI] [PubMed] [Google Scholar]
- Narayan R, Ergun A, Sen K. Delayed inhibition in cortical receptive fields and the discrimination of complex stimuli. J Neurophysiol 94: 2970–2975, 2005 [DOI] [PubMed] [Google Scholar]
- Oxenham AJ, Bernstein JG, Penagos H. Correct tonotopic representation is necessary for complex pitch perception. Proc Natl Acad Sci USA 101: 1421–1425, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker AJ, Newsome WT. Sense and the single neuron: probing the physiology of perception. Annu Rev Neurosci 21: 227–277, 1998 [DOI] [PubMed] [Google Scholar]
- Pedemonte M, Torterolo P, Velluti RA. In vivo intracellular characteristics of inferior colliculus neurons in guinea pigs. Brain Res 759: 24–31, 1997 [DOI] [PubMed] [Google Scholar]
- Petersen RS, Panzeri S, Diamond ME. Population coding of stimulus location in rat somatosensory cortex. Neuron 32: 503–514, 2001 [DOI] [PubMed] [Google Scholar]
- Powell TPS, Mountcastle VB. Some aspects of the functional organization of the cortex of the postcentral gyrus of the monkey: a correlation of findings obtained in a single unit analysis with cytoarchitecture. Bull Johns Hopkins Hosp 105: 133–162, 1959 [PubMed] [Google Scholar]
- Reale RA, Imig TJ. Tonotopic organization in auditory cortex of the cat. J Comp Neurol 192: 265–291, 1980 [DOI] [PubMed] [Google Scholar]
- Reich DS, Mechler F, Victor JD. Independent and redundant information in nearby cortical neurons. Science 294: 2566–2568, 2001 [DOI] [PubMed] [Google Scholar]
- Relkin EM, Pelli DG. Probe tone thresholds in the auditory nerve measured by two-interval forced-choice procedures. J Acoust Soc Am 82: 1679–1691, 1987 [DOI] [PubMed] [Google Scholar]
- Reyes AD. Synchrony-dependent propagation of firing rate in iteratively constructed networks in vitro. Nat Neurosci 6: 593–599, 2003 [DOI] [PubMed] [Google Scholar]
- Rieke F, Warland DK, de Ruyter van Steveninck RR, Bialek W. Spikes: Exploring the Neural Code Cambridge, MA: MIT Press, 1999 [Google Scholar]
- Rodriguez FA, Read HL, Escabi MA. Spectral and temporal modulation tradeoff in the inferior colliculus. J Neurophysiol 103: 887–903, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roelfsema PR, Lamme VA, Spekreijse H, Bosch H. Figure–ground segregation in a recurrent network architecture. J Cogn Neurosci 14: 525–537, 2002 [DOI] [PubMed] [Google Scholar]
- Ryan AF, Woolf NK, Sharp FR. Tonotopic organization in the central auditory pathway of the Mongolian gerbil: a 2-deoxyglucose study. J Comp Neurol 207: 369–380, 1982 [DOI] [PubMed] [Google Scholar]
- Salinas E, Sejnowski TJ. Impact of correlated synaptic input on output firing rate and variability in simple neuronal models. J Neurosci 20: 6193–6209, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnupp JW, Hall TM, Kokelaar RF, Ahmed B. Plasticity of temporal pattern codes for vocalization stimuli in primary auditory cortex. J Neurosci 26: 4785–4795, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiner CE, Winer JA. Auditory cortex mapmaking: principles, projections, and plasticity. Neuron 56: 356–365, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seung HS, Sompolinsky H. Simple models for reading neuronal population codes. Proc Natl Acad Sci USA 90: 10749–10753, 1993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens CF, Zador AM. Input synchrony and the irregular firing of cortical neurons. Nat Neurosci 1: 210–217, 1998 [DOI] [PubMed] [Google Scholar]
- Theunissen FE, Sen K, Doupe AJ. Spectral-temporal receptive fields of nonlinear auditory neurons obtained using natural sounds. J Neurosci 20: 2315–2331, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RB, Silverman MS, Switkes E, De Valois RL. Deoxyglucose analysis of retinotopic organization in primate striate cortex. Science 218: 902–904, 1982 [DOI] [PubMed] [Google Scholar]
- van Rossum MC. A novel spike distance. Neural Comput 13: 751–763, 2001 [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol 76: 1310–1326, 1996 [DOI] [PubMed] [Google Scholar]
- Wang L, Narayan R, Grana G, Shamir M, Sen K. Cortical discrimination of complex natural stimuli: can single neurons match behavior? J Neurosci 27: 582–589, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warland DK, Reinagel P, Meister M. Decoding visual information from a population of retinal ganglion cells. J Neurophysiol 78: 2336–2350, 1997 [DOI] [PubMed] [Google Scholar]
- Woolley SM, Casseday JH. Response properties of single neurons in the zebra finch auditory midbrain: response patterns, frequency coding, intensity coding, and spike latencies. J Neurophysiol 91: 136–151, 2004 [DOI] [PubMed] [Google Scholar]
- Woolley SM, Casseday JH. Processing of modulated sounds in the zebra finch auditory midbrain: responses to noise, frequency sweeps, and sinusoidal amplitude modulations. J Neurophysiol 94: 1143–1157, 2005 [DOI] [PubMed] [Google Scholar]
- Woolley SM, Fremouw TE, Hsu A, Theunissen FE. Tuning for spectro-temporal modulations as a mechanism for auditory discrimination of natural sounds. Nat Neurosci 8: 1371–1379, 2005 [DOI] [PubMed] [Google Scholar]
- Woolley SM, Gill PR, Fremouw T, Theunissen FE. Functional groups in the avian auditory system. J Neurosci 29: 2780–2793, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolley SM, Gill PR, Theunissen FE. Stimulus-dependent auditory tuning results in synchronous population coding of vocalizations in the songbird midbrain. J Neurosci 26: 2499–2512, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolsey TA, Van der Loos H. The structural organization of layer IV in the somatosensory region (SI) of mouse cerebral cortex. The description of a cortical field composed of discrete cytoarchitectonic units. Brain Res 17: 205–242, 1970 [DOI] [PubMed] [Google Scholar]
- Zador A. Impact of synaptic unreliability on the information transmitted by spiking neurons. J Neurophysiol 79: 1219–1229, 1998 [DOI] [PubMed] [Google Scholar]
- Zhang Y, Reid RC. Single-neuron responses and neuronal decisions in a vernier task. Proc Natl Acad Sci USA 102: 3507–3512, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]