Abstract
Repeating object images produces stimulus-specific repetition suppression referred to as functional magnetic resonance imaging-adaptation (fMRI-A) in ventral temporal cortex (VTC). However, the effects of stimulus repetition on functional selectivity are largely unknown. We investigated the effects of short-lagged (SL, immediate) and long-lagged (LL, many intervening stimuli) repetitions on category selectivity in VTC using high-resolution fMRI. We asked whether repetition produces scaling or sharpening of fMRI responses both within category-selective regions as well as in the distributed response pattern across VTC. Results illustrate that repetition effects across time scales vary quantitatively along an anterior-posterior axis and qualitatively along a lateral-medial axis. In lateral VTC, both SL and LL repetitions produce proportional fMRI-A with no change in either selectivity or distributed responses as predicted by a scaling model. Further, there is larger fMRI-A in anterior subregions irrespective of category selectivity. Medial VTC exhibits similar scaling effects during SL repetitions. However, for LL repetitions, both the selectivity and distributed pattern of responses vary with category in medial VTC as predicted by a sharpening model. Specifically, there is larger fMRI-A for nonpreferred categories compared with the preferred category, and category selectivity does not predict fMRI-A across the pattern of distributed response. Finally, simulations indicate that different neural mechanisms likely underlie fMRI-A in medial compared to lateral VTC. These results have important implications for future fMRI-A experiments because they suggest that fMRI-A does not reflect a universal neural mechanism and that results of fMRI-A experiments will likely be paradigm independent in lateral VTC but paradigm dependent in medial VTC.
INTRODUCTION
When stimuli are repeated, cortical responses in high-level visual cortex generally decrease. This reduction has been observed in many spatial scales from repetition effects in single neurons (De Baene and Vogels 2009; Li et al. 1993; McMahon and Olson 2007; Ringo 1996; Sawamura et al. 2006; Verhoef et al. 2008; Woloszyn and Sheinberg 2009) to population effects measured with functional magnetic resonance imaging (fMRI-adaptation, fMRI-A) (Grill-Spector and Malach 2001; Henson 2003; Sawamura et al. 2005; Schacter and Buckner 1998) and is thought to be a marker of experience-dependent changes in high-level visual cortex. fMRI-A occurs in several time scales, from immediate repetitions of sequentially presented images (Grill-Spector et al. 1999; Kourtzi and Kanwisher 2001; Sawamura et al. 2005) to repetition of the same images with many intervening stimuli occurring tens of seconds apart (Henson et al. 2003; Sayres and Grill-Spector 2006; Simons et al. 2003; Vuilleumier et al. 2002) or even days apart (van Turennout et al. 2000). Although fMRI-A occurs in multiple brain regions and across an impressively large number of experimental conditions, the relation between stimulus selectivity and fMRI-A is unknown. Further, it is unknown whether this relationship is consistent across brain regions and time scales (for review, see Grill-Spector et al. 2006). Understanding this relationship is important for interpreting results of fMRI-A experiments that are used to characterize functional properties of neural populations and for understanding the role of implicit experience in modifying neural representations. Consequently, the current study seeks to examine: 1) how stimulus repetition affects selectivity across the ventral stream, 2) whether repetition effects vary across time scales, 3) whether the fMRI-A profile varies across ventral stream subregions, and 4) whether repetition changes the distributed response patterns across the human ventral stream.
To address these questions, we examined the effects of repetition on category selectivity as it is a well-characterized form of stimulus selectivity in ventral occipito-temporal cortex. Category selectivity is manifested by both a regional preference to particular object categories, such as faces (Kanwisher et al. 1997), places (Epstein and Kanwisher 1998), and body parts (Peelen and Downing 2005; Pinsk et al. 2009; Schwarzlose et al. 2005), as well as in specific distributed response patterns across the ventral stream for different object categories (Cox and Savoy 2003; Haxby et al. 2001). Further, these ventral stream regions display fMRI-A. Although previous studies have examined whether category-selective regions illustrate fMRI-A to nonpreferred categories with variable findings (Avidan et al. 2002; Epstein et al. 2008; Ewbank et al. 2005; Fang et al. 2007; Grill-Spector et al. 1999; Mahon et al. 2007; Pourtois et al. 2009), the effects of fMRI-A on category selectivity have not been quantitatively examined according to the predictions of theoretical models that have been proposed to explain the reduction of fMRI responses.
Specifically, repetition may reduce fMRI responses in the following ways: by a proportional scaling factor that maintains a similar profile of selectivity across categories (De Baene and Vogels 2009; Grill-Spector et al. 2006; McMahon and Olson 2007) or nonlinearly, thus sharpening the selectivity to the preferred category (Desimone 1996; Wiggs and Martin 1998). Each hypothesis makes separate predictions for the amount of fMRI-A as a function of stimulus preference as well as the ratio between nonrepeated and repeated responses. Scaling suggests that fMRI responses to repeated stimuli are reduced by a constant fraction relative to responses to nonrepeated stimuli. In other words, there is a linear relation between the amplitude of response to repeated and nonrepeated stimuli in which the slope is the scaling factor. Because this is a multiplicative effect, the largest amount of fMRI-A will occur for stimuli that elicit the strongest response. Sharpening suggests that repetition changes cortical selectivity in that responses become more selective (more highly tuned around the preferred stimulus) after repetition. Consequently, there will be little or no fMRI-A to the preferred stimulus and the largest amount of fMRI-A to intermediate (nonpreferred) stimuli. It is currently unknown whether different models are relevant in different ventral stream regions and time scales (Grill-Spector et al. 2006).
To examine the relationship between fMRI-A and category selectivity, we conducted two high-resolution fMRI experiments varying in the time between image repeats during which subjects viewed repeated and nonrepeated images of objects from several categories (Fig. 1 and methods). To our knowledge, this is the first study that quantitatively relates category selectivity and fMRI-A, examines the effect of repetition on distributed responses in ventral occipito-temporal cortex, and uses simulations to relate fMRI-A effects to the underlying neural responses as predicted by theoretical models.
Fig. 1.
Experimental design. A: short-lagged (block) design. Each block lasted 12 s where each image was presented for 1,000 ms followed by a 500-ms blank. There was a block of scrambled images (gray) in between each intact stimulus block. In nonrepeated blocks (red), subjects saw 6–8 different images of a category. During the repeated blocks (blue), subjects saw 6–8 repeats of the same image. Nonrepeated and repeated blocks, as well as categories, were counterbalanced within each run. In each block, 0–2 randomly presented scrambled images served as foil trials. Examples of stimuli are on the right. B: long-lagged (event-related) design. Each trial lasted 2 s where each image was presented for 1,000 ms followed by a 1,000 ms blank. Nonrepeated images were shown once during the experiment. Repeated images were shown six times within a run. On average, 20 intervening stimuli occurred between repetitions of an image. Nonrepeated, repeated, and blank trials were counterbalanced within each run. Within each of the nonrepeated and repeated conditions, categories were also counterbalanced. Example of stimuli on the right. F, faces; L, limbs; FL, flowers; C, cars; G, guitars; H, houses.
METHODS
Subjects
Nine subjects (3 female, ages 24–39) participated in experiment 1 (short-lagged block fMRI-A; SL), experiment 2 (long-lagged event-related fMRI-A; LL), and a functional localizer experiment within each session to identify category-selective regions. Experiments 1 and 2 were conducted on separate days (on average 5 mo apart). The same functional localizer experiment was conducted within each of the scanning sessions, in addition to an experiment intended to localize human motion-selective cortex (hMT+). All subjects also participated in separate sessions in which we acquired a whole brain anatomical volume as well as retinotopic scans. Written consent was obtained for each subject, and the procedures were approved by the Stanford Internal Review Board on Human Subjects Research.
Experiment 1: short-lagged block adaptation
Subjects viewed blocks of gray level images of faces, limbs, flowers, cars, guitars, and houses (intact blocks), which alternated with blocks of scrambled images (scrambled blocks) of these categories (Fig. 1A). Stimuli extended 7.125° from the fovea and were programmed in MATLAB (version 7.3, The Mathworks, Natick, MA) using the Psychophysics Toolbox (Brainard 1997). There were eight runs of 27 blocks with a 12-s blank period at the start and end of each run. Half of the intact blocks contained six to eight different object images (nonrepeated), and half of the intact blocks contained six to eight repetitions of the same object image (repeated). In each intact object block, zero to two stimuli were scrambled images functioning as catch trials that occurred randomly in the block. Each image was presented for 1,000-ms with a 500-ms blank between each image. We refer to experiment 1 as “short-lagged” (SL) because in a repeated block, there were only 500-ms separating each repeated image if no catch trial occurred, and a maximum of 3 s if two catch trials occurred in succession. Subjects were instructed to fixate and to categorize images into: faces, limbs, flowers, cars, guitars, houses, or scrambled by button press on a scanner compatible response box. The order of repeated and nonrepeated conditions was counterbalanced for each scan and images were not repeated across scans.
Experiment 2: long-lagged event-related adaptation
Subjects viewed gray level images of faces, limbs, cars, and houses in eight runs of 156 trials (Fig. 1B). Each run started and ended with a 12-s blank period. Each trial lasted 2 s, where each image was presented for 1,000 ms followed by a 1,000-ms blank. For each category and within a given run, 12 images were seen once (nonrepeated) and 2 images were repeated six times (repeated). We refer to experiment 2 as “long-lagged” (LL) because there were on average 20.44 trials between repeats of the same object image with a minimum of one trial (1,000 ms) and a maximum of 87 trials (174 s). Nonrepeated, repeated, and blank trials were counterbalanced for the n−1 trial within each run, and the categories were counterbalanced within each of the repeated and nonrepeated trials. Images were not repeated across scans. Subjects were instructed to categorize each image into face, limb, house, car, or blank using a separate button press while maintaining fixation.
Block-design localizer scans
At the end of each session, subjects participated in two to four functional localizer runs to identify regions in the ventral stream selective for faces, limbs, objects, and houses. Images of faces, limbs, flowers, houses, cars, guitars, and scrambled objects appeared in blocks. Each run consisted of 32 blocks (4 of each condition and 4 blank blocks), as well as a 12-s blank period at the start and end of each run. Blocks were 12-s long and consisted of a 750-ms image presentation followed by a 250-ms blank period. Subjects performed a one-back task (that is, they responded when two consecutive images were identical) by button press while maintaining fixation.
Retinotopic mapping scans
We defined retinotopic visual areas (Fig. 2; Supplemental Fig. S11) using separate retinotopic mapping scans with standard resolution fMRI (3 mm voxels). All subjects participated in at least two polar angle scans using a rotating checkerboard wedge and two eccentricity scans using an expanding checkerboard ring (see Sayres and Grill-Spector 2008 for details). The purpose of defining retinotopic visual regions was threefold: to examine if fMRI-A occurs in V1 and human ventral visual field map V4 (hV4), to assure that the category-selective ROIs were beyond area hV4, and to use the anterior boundary of hV4 as the posterior boundary of the anatomical ROI used in the multivoxel pattern analysis.
Fig. 2.
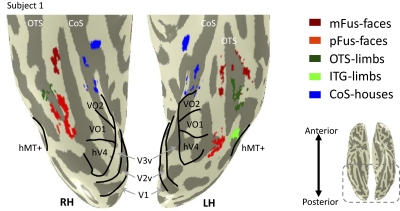
High-resolution category-selective regions of interest (ROIs). Inflated brain of a representative subject zoomed on the ventral aspect (see inset indicating the zoomed region) showing regions of interest from 3 different statistical comparisons: face-selective (red: faces > limbs, flowers, cars, guitars, and houses), limb-selective (green: limbs > faces, flowers, cars, guitars, and houses), and house-selective (blue: houses > faces, limbs, flowers, cars, and guitars). All ROIs were defined using a threshold of t > 3, voxel level. The outline of retinotopic areas V1-hV4, VO-1/2, as well as hMT+ are illustrated in black and defined from retinotopy scans and a separate hMT+ localizer scan, respectively. CoS, collateral sulcus; OTS, occipito-temporal sulcus; pFus, posterior fusiform; mFus, mid fusiform; ITG, inferotemporal gyrus.
hMT+ localizer
All subjects also participated in a scan aimed to define hMT+ in each scanning session. We defined hMT+ as a region in the posterior inferior temporal sulcus (ITS) that responded more strongly to low contrast expanding and contracting concentric gratings versus identical stationary gratings (Dumoulin et al. 2000).
fMRI data collection
SCANNING.
Subjects were scanned on a research-only GE 3-Tesla Signa scanner at the Lucas Imaging Center at Stanford University using a custom-built phased-array, eight-channel surface coil (Nova Medical, Wilmington, MA).
SL (EXPERIMENT 1).
We acquired 26 1.5-mm-thick oblique slices, using a two-shot T2*-sensitive spiral acquisition sequence (Glover 1999) (FOV = 192 mm, TE = 30 ms, TR = 2,000 ms, flip angle = 77°, and bandwidth = 125 kHz; effective resolution of 1.5 × 1.5 × 1.5 mm). We also acquired in-plane anatomical images using the same prescription as the functional scans and a standard two-dimensional RF-spoiled GRASS (SPGR, TE = 1.9 ms, flip angle = 15°, bandwidth = 15.63 kHz). The anatomical inplanes were used to co-register each subject's data to the subject's whole brain anatomy collected in a separate session.
LL (EXPERIMENT 2).
We acquired 12 slices at a voxel resolution of 1.5 × 1.5 × 3 mm and TR = 1,000 ms using a two-shot T2*-sensitive spiral acquisition sequence (FOV = 192 mm, TE = 30 ms, flip angle = 77°, and bandwidth = 125 kHz) and in-plane anatomical images using the same prescription as the functional scans.
THREE-DIMENSIONAL VOLUME ANATOMICALS.
A high-resolution anatomical volume of the whole brain was acquired with a head-coil using a T1-weighted SPGR pulse sequence (TR = 1,000 ms, flip angle = 45°, 2 NEX, FOV = 200 mm, resolution of 0.78 × 0.78 × 1.2 mm).
Data analysis
Data were analyzed with MATLAB (version 7.3) using the mrVista toolbox (http://white.stanford.edu/software).
ANATOMICAL DATA.
Anatomical volumes were segmented into gray and white volumes and from this segmentation we reconstructed the cortical surface for each subject. Data were aligned to the high-resolution anatomical volume, which enabled us to compare regions of interest across scans and to visualize activations on the volume and on the inflated cortical surface.
REGION OF INTEREST SELECTION.
We defined each region of interest (ROI) on a subject-by-subject basis and separately for each session to minimize alignment issues between the localizer and experimental data (Fig. 2 shows ROIs from a representative subject from the LL scanning session, and Supplemental Fig. S1 depicts three additional subjects). Due to the higher resolution of our scans, ROIs are typically smaller and patchier than standard fMRI (see Weiner and Grill-Spector 2010 for further elaboration on this organization). Consequently, we will not use the common acronyms (e.g., FBA, FFA, PPA) labeling these neighboring areas of cortex. Instead, we will refer to them with their category preference and their anatomical landmarks. In particular, two limb-selective clusters were defined with a contrast of limbs > faces, flowers, cars, guitars, and houses, t >3, voxel level: 1) occipitotemporal sulcus, OTS (n = 8 in experiment 1 and n = 9 in experiment 2), extending to the lateral fusiform gyrus, and 2) inferotemporal gyrus, ITG (n = 9 in experiment 1 and n = 8 in experiment 2), located lateral to hV4 and inferior to hMT+. These clusters are separate from the extrastriate body area (EBA) (Downing et al. 2001) and most likely correspond to the recently reported FBA-1/2 (Pinsk et al. 2009). Two face-selective clusters were defined with a contrast of faces > limbs, flowers, cars, guitars, and houses, t > 3, voxel level: 1) middle fusiform, mFus (n = 8 in experiment 1 and n = 9 in experiment 2) located anterior and medial to the limb-selective OTS, and 2) posterior fusiform, pFus (n = 7 in both experiments 1 and 2) located posterior and medial to the limb-selective OTS and anterior and lateral to hV4. The face-selective pFus does not overlap with the occipital face area (OFA), which is more posterior and lateral on the inferior occipital gyrus. Prior studies typically combined the mFus and pFus together to form the traditional fusiform face area (FFA) or have attempted to divide them into separate FFA clusters (e.g., FFA-1/2) (Pinsk et al. 2009). We also localized a house-selective cluster (houses > faces, limbs, flowers, cars, guitars, t >3, voxel level) in all subjects in both experiments along the collateral sulcus (CoS) and parahippocampal gyrus. The house-selective CoS is likely to be similar to the parahippocampal place area, PPA (Aguirre et al. 1998; Epstein and Kanwisher 1998).
ANATOMICAL ROIs.
We defined for each subject three anatomical ROIs on their gray matter to provide an independent and unbiased way to select voxels for our multivoxel pattern (MVP) analyses. The first ROI covered the OTS, fusiform gyrus (FG), and CoS. The posterior edge of this ROI was the anterior boundary of hV4 and the anterior edge of this ROI was the middle of the FG (along the anterior-posterior axis) and is referred to as whole VTC (Fig. 8). The second and third ROIs were created by dividing the whole VTC ROI down the anterior-posterior axis along the mid-fusiform sulcus to generate lateral (lateral VTC) and medial (medial VTC) partitions (Fig. 9).
Fig. 8.
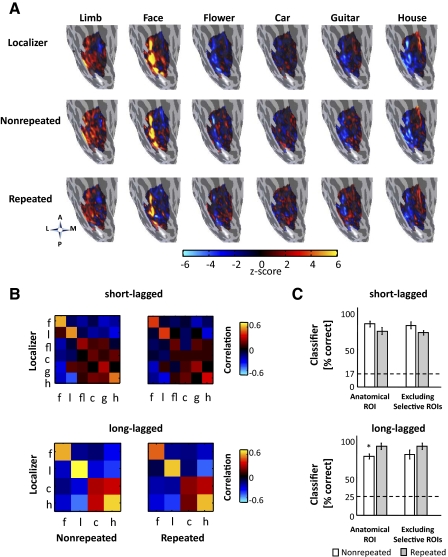
Multivoxel pattern (MVP) analysis of distributed responses to object categories in ventral temporal cortex (VTC). A: distributed responses to six object categories in the localizer scan, nonrepeated conditions in the short-lagged (SL) experiment, and repeated conditions in the SL experiment. Each panel shows the right hemisphere ventral inflated surface of a representative subject (S5) zoomed on the fusiform gyrus. (A, anterior; P, posterior; L, lateral; M, medial). The projected activation is an unthresholded z-score map across an anatomically defined VTC ROI (see methods). B: mean cross-correlation matrices between responses in the localizer scans and nonrepeated (left) or repeated (right) conditions in the short-lagged (top) and long-lagged experiment (bottom). Data are concatenated across hemispheres and averaged across subjects. Left: each element in the matrix represents the correlation coefficient between the distributed response to categories in the localizer and the nonrepeated conditions. Right: each element in the matrix represents the correlation coefficient between the distributed response to categories in the localizer and the repeated data. High on-diagonal values (orange and red) show reproducibility of the pattern of response for that category across the localizer and nonrepeated or repeated conditions. Low (or negative) off-diagonal values (blue and black) indicate that the distributed pattern of response differs across categories. F, faces; l, limbs; fl, flowers; c, cars; g, guitars; h, houses. C: winner-take-all classifier performance averaged across subjects and categories. The dotted line indicates chance level performance. Error bars: between subjects SEs. White: training with localizer data, testing with nonrepeated conditions. Gray: training with localizer data, testing with repeated conditions. Left: full anatomical VTC ROI. Right: anatomical VTC ROI excluding category-selective ROIs. Asterisks indicate classifier performance is significantly different for repeated compared with nonrepeated trials (P < 0.05).
Fig. 9.
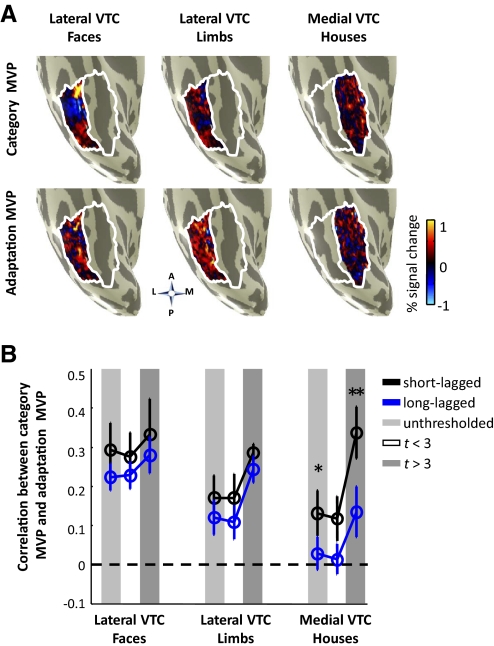
MVP analysis of category preference and category adaptation. A: MVPs showing the magnitude of responses to each of three object categories minus other categories in the localizer scans (top), and adaptation MVP (nonrepeated – repeated responses for a category) from the long-lagged experiment (bottom). Each panel illustrates the right hemisphere ventral inflated surface of a representative subject (S6) zoomed on the fusiform gyrus. (A, anterior; P, posterior; L, lateral; M, medial). The projected activation is an unthresholded map of percentage signal change across an anatomically defined lateral VTC ROI (white outline) for faces (left) and limbs (middle) and a medial VTC ROI (white outline) for houses (right; see methods for details). B: Correlation between category MVP and adaptation MVP for faces (left), limbs (middle), and houses (right). Light gray: entire anatomical region (unthresholded maps). Dark gray: Category-selective voxels determined from out of session localizer scans as voxels that show significant (t > 3) preference for a category vs. others. White: All voxels excluding category-selective voxels. Black: short-lagged paradigm. Blue: long-lagged paradigm. Asterisks indicate that the correlation for the short-lagged paradigm is significantly higher than the long-lagged paradigm (t-test, asterisk, P < 0.05; double asterisk P < 0.01).
TIME COURSE PROCESSING.
Functional data were motion corrected using an affine transformation (Nestares and Heeger 2000). Seven of 99 scans from experiment 1 and 6 of 104 scans from experiment 2 were excluded because of motion >1.5 voxels or scanner artifacts. Data were then detrended using a temporal high-pass filter with a 1/20 Hz cutoff. The times series of each voxel was converted to percent signal change by dividing the time course of each voxel by its mean intensity.
For all experiments (SL and LL experiments and localizers from both sessions), standard general linear model (GLM) analyses were applied to spatially unsmoothed data using mrVista software. We used the hemodynamic impulse response function (HRF) used in SPM2 (//www.fil.ion.ucl.ac.uk/spm/) to estimate BOLD response amplitudes for each stimulus category by computing the beta coefficients from a GLM applied to the preprocessed time courses. For the LL paradigm, we excluded the first presentation of the image that was later repeated resulting in 12 trials per category for nonrepeated trials and 10 trials per category for repeated trials per run.
Comparison of fMRI-A in early visual areas compared with category-selective regions
For V1, hV4, and each of the category-selective regions, we calculated the mean fMRI-A. fMRI-A was measured as the difference in response between nonrepeated and repeated responses for each voxel and category and then averaged across the ROI to generate one fMRI-A value for each subject. We used a t-test across subjects to determine whether there was significant fMRI-A (compared to 0) for each ROI and paradigm (Fig. 3).
Fig. 3.
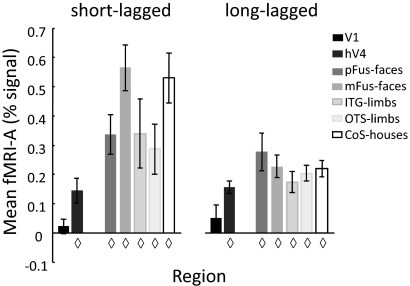
Functional magnetic resonance imaging adaptation (fMRI-A) across human ventral cortex. The y axis represents the mean voxel fMRI-A (nonrepeated-repeated measured in percentage signal change) in a region averaged across voxels, categories, and subjects. Diamonds: significant fMRI-A (as compared with 0; P < 0.005). Left: short-lagged; Right: long-lagged. Error bars reflect SE across subjects.
DISTRIBUTION OF FMRI-A LEVELS WITHIN ROIs.
We examined the distribution of fMRI-A levels for each category across voxels (Figs. 4 and 6). fMRI-A was measured as the difference in response amplitude between the nonrepeated and repeated response for each voxel and category. Distributions in Figs. 4 and 6 reflect the aggregated distribution across voxels and subjects. We used a Kolmogorov-Smirnov (K-S) nonparametric test to determine whether the distribution of fMRI-A to the preferred category in an ROI was shifted more positively than nonpreferred categories. We also conducted this analysis within each subject (Supplemental Table S1), as well as illustrate the average of the individual subject distributions in Supplemental Fig. S2.
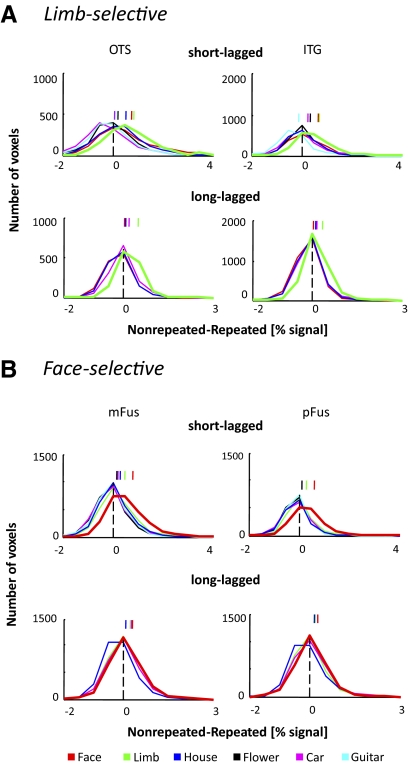
Fig. 4.
Distribution of fMRI-A magnitudes in face- and limb-selective ROIs: largest fMRI-A for preferred category. A and B: distribution of fMRI-A values across voxels and subjects. The y axis represents the number of voxels and the x axis represents the magnitude of fMRI-A (nonrepeated-repeated measured in percentage signal change). Each curve represents the distribution of fMRI-A values for a category (see legend). In each ROI, the thick line indicates the category illustrating the most fMRI-A. The vertical dashed line indicates no fMRI-A, and short vertical lines above the distributions indicate the mean fMRI-A magnitude for each category. Positive values indicate lower responses for repeated than nonrepeated conditions. Top: short-lagged paradigm; bottom: long-lagged paradigm. A: limb-selective ROIs. Note that limbs (green) elicit the most fMRI-A across paradigms. B: face-selective ROIs. Note that faces (red) elicit the most fMRI-A across paradigms.
Fig. 6.
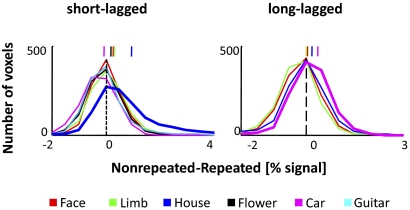
Different distribution of fMRI-A magnitudes in the house-selective CoS across paradigms. Same convention as Fig. 4. The y axis represents the number of voxels, and the x axis represents the magnitude of fMRI-A. Each curve represents the distribution of fMRI-A values for a category. The short vertical lines above the distributions indicate the mean fMRI-A magnitude for each category across voxels and subjects.
REGRESSION ANALYSES.
To quantify the relation between response amplitudes of repeated versus nonrepeated stimuli, we performed regression analyses. These analyses were conducted for each subject across voxels in an ROI (Figs. 5 and 7 and Supplemental Figs. S3 and S4) and separately for each category to examine whether the slopes of the regressions (fMRI-A ratio) and the variance explained differ across preferred and nonpreferred categories. We also conducted a polynomial regression to test whether a nonlinear model provides a better fit than a linear model but found no advantage of a nonlinear fit (Supplemental Fig. S4).
Fig. 5.
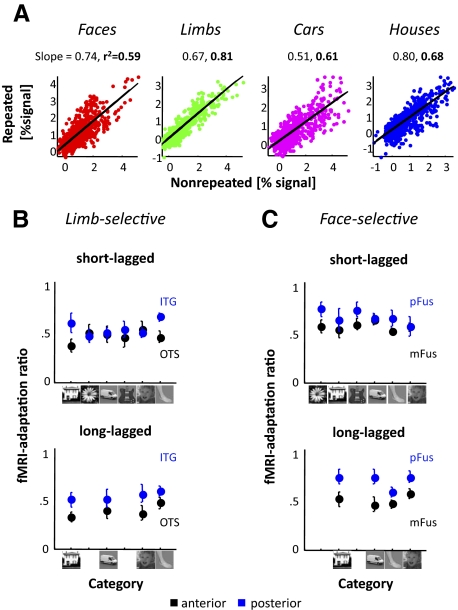
Constant fMRI-A ratios in face- and limb-selective ROIs: Repeated responses are proportional to nonrepeated responses. A: regressions of responses to repeated vs. nonrepeated stimuli in the pFus of a representative subject (S1). In each panel, each point represents a voxel's response for repeated and nonrepeated stimuli from a category in the long-lagged experiment. Each column represents data from a different category. From left to right: faces (red), limbs (green), cars (magenta), and houses (blue). The solid black line is the regression line. The slope of this regression line, which we refer to as the fMRI-A ratio, is the 1st number listed above each plot. The 2nd number listed above each plot is the R2 value of the regression, which is bolded as all regressions were significant (P < 10−20). All subjects' data for the pFus ROI are shown in Supplemental Fig. S1. B and C: fMRI-A ratio as a function of category preference. Ratios <1 illustrate fMRI-A and ratios >1 illustrate enhancement. All ratios are significantly <1 (Ps < 0.006, t-test 1-sided). Categories on the x axis are ranked on an ordinal scale generated from the independent localizer scans. B: limb-selective ROIs. C: face-selective ROIs.
Fig. 7.
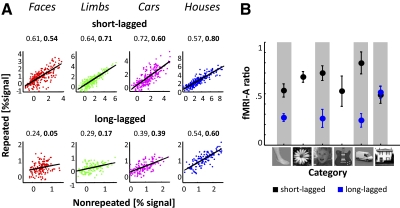
fMRI-A ratios in the house-selective CoS: qualitative difference across paradigms. A: Same convention as Fig. 5A. Regressions of responses to repeated vs. nonrepeated stimuli in the CoS of a representative subject (S8) in the short-lagged (top) and long-lagged (bottom) paradigms. Each column represents data from a different category: faces (red), limbs (green), cars (magenta), and houses (blue). The solid black line is the regression line. The slope of this regression line, which we refer to as the fMRI-A ratio, is the 1st number listed above each plot. The 2nd number listed is the R2 value of the regression, which is bolded as all regressions were significant (P < 0.01). B: same convention as Fig. 5, B and C. There are differences in fMRI-A ratios across categories and paradigms. Houses show a larger fMRI-A ratio than other categories (indicative of less fMRI-A) in the long-lagged paradigm (blue) and an opposite trend occurs in the short-lagged paradigm. Black: short-lagged; blue: long-lagged; shaded gray bars: overlapping categories across paradigms.
Comparison of mean fMRI-A and split-half ratios in each category-selective ROI
In the regression analyses, a slope equal to one indicates no fMRI-A, a slope less than one indicates fMRI-A, and a slope more than one indicates response enhancement. However, noise can produce a bias in the slope estimation, making it lower (Frost and Thompson 2000). Therefore we conducted a second measurement of the fMRI-A ratio at the ROI level that is more robust to noise as averaging across voxels reduces independent noise. To test if one is an appropriate number to use as a comparison for the fMRI-A ratios, we conducted a split-half analysis on nonrepeated responses within each category-selective ROI. Response amplitudes were estimated for each voxel, and then averaged across the ROI. We calculated two ratios for each category, separately for each subject and experiment: 1) fMRI-A ratio = repeated/nonrepeated based on data from all runs; 2) split-half ratio = nonrepeated even runs/nonrepeated odd runs calculated separately for odd/even runs.
Ratios were then averaged across subjects and categories to calculate one fMRI-A ratio and one split-half ratio for each ROI in each experiment. We used a t-test across subjects to determine if the split-half and fMRI-A ratios were significantly less than one.
Time series signal-to-noise analyses
To examine whether differences among ROIs and time scales were due to signal-to-noise differences according to anatomical location or experiment, we examined the time series signal-to-noise ratio (tSNR) (Kruger and Glover 2001) in each of the SL and LL paradigms. For each subject, we created three disk ROIs with a 5-mm radius on a lateral-medial axis along the OTS, FG, and CoS bilaterally (see Supplemental Fig. S5 for the disk locations in an example subject). Within these disks, we extracted the mean raw time series across voxels for the nonrepeated trials and computed the tSNR for each experimental run as: tSNR = 20log[mean(time series)]/[SD(time series)]. We found no significant differences in tSNR across disk locations [F(2,48) = 0.71, P = 0.50], no effect of experiment [F(1,48) = 0.49, P = 0.49], and no interaction between these factors [F(2,48) = 0.40, P = 0.67].
PATTERN ANALYSES OF REPETITION EFFECTS ACROSS THE VENTRAL STREAM.
To complement our ROI-based analyses, we conducted MVP analyses to examine whether the distributed patterns of activity across ventral cortex changed following repetition. These analyses were done for the whole anatomical ROI (described in region of interest selection), which provides an independent and unbiased way to select voxels for this analysis. MVP for each category was represented as a vector of length n (where n is the number of voxels in the ROI). For each voxel, we calculated the amplitude (GLM beta) for each condition relative to the mean beta across categories and divided this by the square root of the residual variance of the voxel GLM to convert data into z-scores and remove between-voxel effects. We visualized activations by projecting MVPs onto the first layer of gray matter (Fig. 8).
We measured the correlation between the MVP to each category from the independent localizer scans to that of the nonrepeated and repeated trials separately for each experiment. We computed the cross-correlation matrix of these coefficients across all stimulus pairings separately for each subject across both hemispheres and then computed the mean matrix across subjects (Fig. 8B). We repeated this analysis separately for the anatomical ROI excluding the category-selective regions (Fig. 8C) and for odd and even subsets of our nonrepeated and repeated data (split-half analysis; see supplemental materials and Supplemental Fig. S6).
We assessed the stability of MVPs by applying a winner-take-all (WTA) classifier. For each subject, the training data were the localizer dataset, and we separately tested classification performance on the nonrepeated and repeated conditions from each of the adaptation experiments, respectively. The WTA determines the category based on the highest correlation between the training and testing set. Classifier performance was measured for each subject and then averaged across subjects using the full anatomical ROIs, as well as the full anatomical ROIs excluding category-selective ROIs (Fig. 8C).
RELATIONSHIP BETWEEN CATEGORY MVP AND ADAPTATION MVP.
To link MVP analyses to the previous voxel-based ROI analyses, we calculated the correlation between the adaptation MVP (that is, for each voxel, we calculated the difference in response between nonrepeated and repeated trials for a specific category and measured the distributed response across voxels) to the category MVP as determined from the within session localizer data (that is, for each voxel, we calculated the difference in response to one category compared with the other five categories and examined the distributed pattern across voxels). We compared the correlation between the two MVPs across the entire lateral ROI (unthresholded condition for faces and limbs) or the entire medial ROI (unthresholded condition for houses) as well as for a subset of voxels in each of these respective ROIs that showed significant selectivity to either faces, limbs, or houses (t > 3, Fig. 9B) as well as those voxels outside of these category-selective voxels (t <3, Fig. 9B). The selectivity of voxels was determined from an independent dataset using the other session's localizer scans as activation for a category > other categories, using a threshold of t > 3, voxel level.
RESULTS
Definition of category-selective regions
We focused on ventral occipitotemporal regions because these regions are thought to be in a similar level of the visual processing hierarchy and differential category preference occurs in anatomically adjacent regions (Grill-Spector and Malach 2004; Haxby et al. 2001; Levy et al. 2001; Schwarzlose et al. 2008). Category-selective regions for faces, places, and limbs are also found in the lateral and dorsal occipitotemporal cortex, but analysis of these regions is beyond the scope of the present study.
We defined category-selective ROIs in each subject using independent block-design localizer scans (see methods). Figure 2 illustrates the location and extent of each category-selective ROI (defined as the activation of the category of interest vs. all other categories thresholded at t > 3, voxel level) relative to retinotopic areas V1-hV4 and VO-1/2 in one representative subject (see Supplemental Fig. S1 for three additional subjects). In each subject, we localized five ventral stream regions: a face-selective region on the mid-FG (face-selective mFus), a limb-selective region on the OTS extending to the lateral aspect of the FG (limb-selective OTS), a face-selective region on the posterior FG (face-selective pFus), a limb-selective region on the ITG (limb-selective ITG), and a house-selective region overlapping the collateral sulcus and sometimes extending into the parahippocampal gyrus (house-selective CoS) (see Weiner and Grill-Spector 2010 for reproducibility of the face- and limb-selective activations). As there were no significant interactions of repetition or category effects across hemispheres, our results are collapsed across the two hemispheres.
More fMRI-A in SL compared with LL paradigm in category-selective regions but not hV4 and V1
We first tested whether category-selective ROIs, hV4, and V1 illustrate significant fMRI-A. In both paradigms, each of the category-selective ROIs showed significant fMRI-A [nonrepeated–repeated (% signal) as compared with 0] averaged across voxels and categories (Fig. 3, SL: all ts > 3.57, Ps < 0.005; LL: ts >4.62, Ps < 0.002) as did hV4 [SL: t(7) = 3.66, P < 0.004; LL: t(7) = 7.87, P < 10−5]. In contrast, we did not find significant fMRI-A in V1 [SL: t(8) = 0.92, P = 0.19; LL; t(8) = 1.23, P = 0.13, Fig. 3], which is consistent with prior results (Ewbank et al. 2005; Grill-Spector et al. 1999; Sayres and Grill-Spector 2006). The magnitude of fMRI-A was larger in the SL than LL paradigm for the category-selective ROIs [2-way ANOVA using as factors region and paradigm for the 4 overlapping categories between experiments: main effect of paradigm: F(1,73) = 22.02, P < 10−5; no effect of region: F(4,73) = 2.25, P = 0.07, and no interaction: F(4,73) = 0.88, P = 0.48]. Conversely, there were no paradigm differences across V1 and hV4 [F(1,30) = 0.01, P = 0.92]. Therefore, differential fMRI-A effects in the category-selective ROIs are not merely a reflection of fMRI-A within hV4 or driven by a specific pattern of hV4 inputs into VTC.
Distribution of fMRI-adaptation values: larger fMRI-A magnitude for the preferred category in face- and limb-selective ROIs
Within each face- and limb-selective ROI, we quantified the amount of fMRI-A for each category to examine: 1) if a category-selective ROI exhibits significant fMRI-A to both preferred and nonpreferred categories, 2) if there is a difference in the amount of fMRI-A across categories, and 3) if these effects are similar or dissimilar across repetition paradigms (SL vs. LL).
We measured the magnitude of fMRI-A in each voxel and generated the distribution of fMRI-A values [nonrepeated – repeated (% signal)] for each category across voxels and subjects (Fig. 4). We found significant fMRI-A for most categories in face- and limb-selective regions in both paradigms (SL: all categories, P < 10−6, mean greater than 0, 1-sided t-test, except for cars in the limb-selective OTS and guitars in the limb-selective ITG; LL: all categories, P < 10−4, 1-sided t-test). This indicates that category-selective regions show significant fMRI-A for both the preferred category and nonpreferred categories. In the SL experiment, there was significantly larger fMRI-A (that is, the distribution of fMRI-A magnitudes was shifted to the right, see Fig. 4) for the preferred category relative to each of the other categories in face- and limb-selective ROIs (pairwise comparisons using a K-S test, Bonferroni corrected for multiple comparisons, 2-tailed, P < 10−11). Individual subject fMRI-A distributions in each ROI were similar to the aggregate distribution (see Supplemental Fig. S2 for the average distribution across subjects), and a majority of subjects showed these same effects within each of these ROIs (Supplemental Table S1 for a summary of within subjects effects). Similar results were observed in the LL paradigm (Fig. 4) where the distribution of voxel fMRI-A magnitudes was shifted more positively for the preferred category relative to each of the nonpreferred categories (K-S test, Bonferroni corrected for multiple comparisons, 2-tailed, P < 10−3). Thus face- and limb-selective regions illustrate significant fMRI-A for both preferred and nonpreferred categories in both paradigms and the largest fMRI-A magnitude occurs for the preferred category.
Constant fMRI-adaptation ratio between responses to repeated and nonrepeated stimuli within face- and limb-selective regions
To quantify the relationship between responses to repeated versus nonrepeated stimuli, we examined whether responses to repeated images are proportional to the responses to nonrepeated images and whether this relation is similar across categories (resulting in similar slopes). Note that a proportional fMRI-A effect would result in the largest fMRI-A magnitude for stimuli that generate the strongest responses in nonrepeated trials (that is, the preferred stimulus in each ROI) as illustrated in our distribution analyses. Consequently, we conducted linear regressions between responses to repeated and nonrepeated stimuli (Fig. 5A and Supplemental Fig. S3). Each point in the regression is one voxel's data for one stimulus category. We conducted these regressions across voxels within a given ROI separately for each subject and category. We refer to the slope resulting from these regressions as the fMRI-A ratio because it describes the relationship between repeated and nonrepeated responses, where a slope less than one illustrates fMRI-A (smaller slopes indicate stronger adaptation) and a slope greater than one illustrates enhancement of responses. For each ROI and category, the average fMRI-A ratio across subjects was significantly less than one in both experiments (all Ps < 0.006, t-test, 1-sided; Fig. 5 and Supplemental Fig. S3). While a split-half analysis comparing the ratio of the mean responses of nonrepeated odd trials to the mean of nonrepeated even trials verified that one is an appropriate number to use as a comparison for the fMRI-A ratios (Supplemental Table S2), the regression slopes may underestimate the fMRI-A ratio due to regression dilution (Frost and Thompson 2000). Nevertheless, a nonlinear fit (polynomial regression) does not explain significantly more variance than the linear fit in any of the ROIs and paradigms [2-way ANOVA using as factors fit type (linear/nonlinear) and category (no main effect of fit type: SL: Fs < 0.29, Ps >.59, LL: Fs < 0.14, Ps > 0.71; Supplemental Fig. S4)].
We tested whether fMRI-A ratios differed across categories and paradigms by conducting a two-way ANOVA separately for each ROI examining the effects of category (face/limb/car/house) and paradigm (SL and LL). We found no differences in fMRI-A ratios across categories in all face- and limb-selective ROIs (Fig. 5, B and C, no main effect of category, Fs < 1.44, Ps > 0.24), or category by paradigm interactions (all Fs < 0.94, all Ps > 0.43). Furthermore, in both face- and limb-selective ROIs, fMRI-A ratios did not vary by paradigm (all Fs <2.94, all Ps > 0.09). Thus within face- and limb-selective ROIs, there is a linear relationship between repeated and nonrepeated responses where repeated responses are a proportional decrease compared with nonrepeated responses and the fMRI-A ratio is largely consistent across categories and experiments within a region.
Stronger adaptation in anterior relative to posterior face- and limb-selective regions in the LL paradigm
Next we examined whether there is a difference in fMRI-A effects across posterior and anterior regions with the same category preference. Our category-selective activations show a distinct organization of face- and limb-selective regions with a posterior cluster containing two adjacent and minimally overlapping face-selective and limb-selective regions (face-selective pFus and limb-selective ITG; Fig. 2 and Supplemental Fig. S1) and a more anterior cluster with a complementary organization (face-selective mFus and limb-selective OTS).
An ANOVA of fMRI-A ratios across face-selective clusters, examining the effects of region (mFus/ pFus), paradigm (SL/LL), and overlapping categories across paradigms (face/limb/car/house) revealed differential adaptation across these regions [main effect of region F(1,108) = 18.44, P < 10−5], which also varied by paradigm [region × paradigm interaction F(1,108) = 4.33, P < 0.04]. Likewise, the two limb-selective regions exhibited differential adaptation effects [main effect of region F(1,120) = 14.69, P < 10−4] but did not differ by paradigm [no region by paradigm interaction F(1,120) = 0.59, P = 0.44 and no main effect of paradigm F(1,120) = 2.68, P = 0.10].
These regional differences are more pronounced in the LL time scales (blue in Fig. 5, B and C) and occur due to lesser fMRI-A in the more posterior regions. Specifically, in the LL experiment, the mean fMRI-A ratio across categories in the pFus was 0.69 ± 0.04 compared with 0.49 ± 0.05 in the mFus [t(14) = 3.31, P < 0.005; LL: main effect of region, F(1,56) = 22.89, P < 10−5; SL: main effect of region, F(1,78) = 7.08, P < 0.01; Fig. 5C]. Likewise, in the limb-selective regions, the fMRI-A ratio in the LL experiment was significantly larger in the posterior ITG region (0.53 ± 0.06) compared with the more anterior OTS region, which was 0.38 ± 0.03 [t(15) = 2.41, P < 0.03; LL: main effect of region, F(1,60) = 9.85, P < 0.003; SL: marginally significant main effect of region, F(1,90) = 3.63, P = 0.06; Fig. 5B]. Differences between posterior and anterior regions are also evident in the goodness of fit of the linear model (variance explained, R2, of the regression analysis, Supplemental Fig. S4, right, black conditions for faces and limbs). Specifically, in the LL experiment, the variance explained by the linear relationship between repeated and nonrepeated responses in the posterior regions is greater than the anterior regions (pFus vs. mFus and ITG vs. OTS, main effect of region, F's >12.65, P's <10−4).
Taken together, we find a linear relationship between repeated and nonrepeated responses in face- and limb-selective regions, and there are regional differences across timescales where the fMRI-A ratio varies across the posterior and anterior regions with a greater difference between regions during LL repetitions. This suggests the possibility that the fMRI-A ratio is a characteristic of these face- and limb-selective regions, and this value increases from anterior to posterior regions.
Qualitative differences in fMRI-A characteristics across time scales in the house-selective CoS
We repeated our voxel-based analyses in the house-selective CoS and observed two key findings indicative of a functional difference in this region compared with the face- and limb-selective regions. First, similar to the face- and limb-selective ROIs, there was significant fMRI-A for most categories in the house-selective CoS in both paradigms (Fig. 6, all categories SL: P < 10−6, mean >0, 1-sided t-test, except for cars; all categories LL: P < 10−5, 1-sided t-test, except for limbs). Unlike the face- and limb-selective regions, we found differences in the distribution of fMRI-A magnitudes across paradigms in the house-selective CoS (Fig. 6 and Supplemental Fig. S2). In the SL experiment, the preferred stimulus produced the strongest adaptation, where the house fMRI-A magnitude was significantly greater than the other categories (K-S test, Bonferroni corrected for multiple comparisons, P < 10−6). In contrast, in the LL experiment, the preferred category did not produce the strongest adaptation. In fact, in 5/9 subjects, cars produced the most fMRI-A, and in 2/9 subjects, faces produced the largest fMRI-A in the house-selective CoS (Supplemental Table S1). Across subjects, the largest fMRI-A magnitude was for a nonpreferred stimulus, cars (K-S test, Bonferroni corrected for multiple comparisons, P < 10−10; Fig. 6 and Supplemental Fig. S2), thus illustrating increased selectivity for houses during LL repetitions.
Second, in the SL experiment, linear regressions between responses to repeated and nonrepeated stimuli in the CoS show a similar pattern as the limb- and face-selective ROIs, whereby a linear model produces similar slopes across categories (Fig. 7A, top). In contrast, in the LL experiment, linear regressions between responses to repeated and nonrepeated stimuli in the CoS illustrate that the linear fit produces consistently shallower slopes for the nonpreferred stimuli than for houses (Fig. 7A, bottom). That is, the fMRI-A ratio for houses was larger than the fMRI-A ratio to nonpreferred categories in the LL paradigm while the reverse pattern is illustrated in the SL paradigm (Fig. 7B). A two-way ANOVA on the fMRI-A ratios, examining the effects of category (face/limb/car/house) and paradigm (SL/LL), showed a significant category effect [F(1,64) = 38.29, P < 10−5] and a significant category by paradigm interaction [F(3,64) = 6.54, P < 10−4], indicative of differential fMRI-A across the LL and SL paradigms. Furthermore, the goodness of fit of the linear model relating repeated versus nonrepeated responses was similar across categories for the SL experiment and was not different from a nonlinear model (Supplemental Fig. S4, bottom left). However, the linear model explained significantly less of the variance in the CoS responses in the LL paradigm [2-way ANOVA, main effect of paradigm: F(1,64) = 34.15, P < 10−5] and the goodness of fit varied by category [paradigm × category interaction: F(3,64) = 3.34, P < 0.02]. Thus for the LL data, the linear model only provided a reasonable fit for the CoS response to houses and explained significantly more variance for houses compared with nonpreferred categories [1-way ANOVA, main effect of category, F(3,32) = 6.19, P < 0.002; Supplemental Fig. S4, bottom right]. Finally, tSNR analyses indicate that qualitative differences in fMRI-A in the CoS compared with the face- and limb-selective regions are not due to the presence of more noise within the CoS during the LL experiment as compared with either the lateral VTC category-selective regions or to the SL experiment (Supplemental Fig. S5).
These findings support a qualitative difference in the relationship between category selectivity and fMRI-A in the house-selective CoS across paradigms, suggesting differential repetition effects across time scales in this region. In the SL paradigm, a linear model largely explains the relationship between nonrepeated and repeated responses across all categories, whereas in the LL paradigm, the fMRI-A ratios for nonpreferred categories are substantially smaller, and a linear model is only adequate for explaining repetition effects for the preferred category.
Distributed activation patterns across the ventral stream for object categories remain consistent following repetition
ROI-based analyses inform us about repetition effects within a cortical region. However, they do not examine in what way repetition affects the distributed response across the ventral stream. Because different categories also generate distinct distributed responses across VTC, we asked: do distributed responses to object categories across the VTC change with repetition? There are three possible outcomes. First, repetition may not change the distributed neural response to object categories; thus, responses to both nonrepeated and repeated images of a category may be the same. This would be predicted by a linear model of fMRI-A where responses to repeated stimuli reflect a proportional decrease relative to responses to nonrepeated stimuli. Accordingly, both nonrepeated and repeated response patterns would correlate well to localizer responses, but there may be a slight decrease in within-category correlation for repeated images due to decreased signal-to-noise resulting from adaptation. Second, distributed responses may become more distinctive with repetition as predicted by a nonlinear model of fMRI-A due to sharpening of neural responses on repetition. This would result in high within-category correlations and decreased between-category correlations among repeated responses. Finally, we may observe an extensive change in distributed response patterns with repetition (as has been observed after prolonged visual exposure to novel categories) (see Op de Beeck et al. 2006). In this case, the distributed response patterns from our localizer experiment should correlate well with responses to nonrepeated images but not with repeated image presentations.
Figure 8 presents the distributed response patterns to each of the six object categories within the anatomical VTC ROI in a representative subject from the SL experiment (similar patterns were observed for the 4 overlapping categories used in the LL experiment). The first row represents the localizer data, the second row represents the nonrepeated data, and the third row represents the repeated data. As evident in Fig. 8A, MVPs of response to different categories within an experiment are dissimilar. However, the pattern of response for a given category is similar across conditions.
Correlations between distributed response patterns during the localizer experiment and each of the nonrepeated and repeated conditions from the SL and LL experiments revealed consistent category information (see methods). In both SL and LL experiments, there was significant positive within-category correlation between localizer MVP and nonrepeated MVP (diagonal in Fig. 8B, left, all ts > 11.60, all Ps < 10−6, 1-sided), which was also significantly higher than the mean between-category correlation (off-diagonal in Fig. 8B, left, all ts > 12.99, all Ps < 10−6, paired, 2-tailed). Further, for both experiments, we found significant positive within-category correlation between localizer MVP and repeated MVP (all ts > 10.20, all Ps <10−6, 1-sided), and the mean within-category correlation was significantly higher than the mean between-category correlation (all ts > 10.77, all Ps < 10−6, paired, 2-tailed). Comparing within-category correlations across localizer and repeated MVP versus localizer and nonrepeated MVP showed that the former correlations were lower. However, a split-half analysis of repeated and nonrepeated MVP indicates that this is because of lower reproducibility of repeated MVP rather than a change in the distributed activations following repetition (supplemental results and Supplemental Fig. S6).
We used a WTA classifier to determine whether training on localizer data predicts the category subjects viewed for nonrepeated or repeated stimuli in each of the experiments (see methods, Fig. 8C). In the SL experiment, the classifier successfully determined the category that subjects viewed for both repeated and nonrepeated conditions (mean correct nonrepeated = 83% ± 0.04, repeated = 74% ± 0.04, all ts > 14.22, all Ps < 10−7, one-sided, performance >17% chance level) and the performance for nonrepeated conditions was not significantly higher than repeated conditions [Fig. 8C; t(8) = 1.34, P = 0.21, paired, 2-tailed]. In the LL experiment, the classifier showed robust performance when training on localizer data and testing on either repeated or nonrepeated trials (mean correct nonrepeated = 78% ± 0.02, repeated = 92% ± 0.04, all ts > 19.00, Ps < 10−8, 1-sided, performance >25% chance level). Here there was improved classification performance for repeated compared with nonrepeated images [Fig. 8C; t(8) = 2.29, P < 0.05, paired, 2-tailed], which was largely driven by decreased between-category correlation of cars and houses for repeated trials (Fig. 8B, bottom left).
We repeated the MVP analysis excluding the category-selective ROIs from the anatomical ROI (Haxby et al. 2001). Notably, classification performance for either nonrepeated or repeated conditions in each experiment largely did not change (Fig. 8C, right). A two-way ANOVA using as factors ROI (full anatomical ROI/anatomical ROI excluding category-selective ROIs) and repetition (nonrepeated/repeated), showed a main effect of repetition [all Fs (1, 32) >5.88; all Ps < 0.02] and no main effect of ROI and no ROI by repetition interaction (all Fs (1, 32) < 0.11; all Ps > 0.75) in either experiment. This suggests that the distributed patterns across the ventral stream largely remain the same for repeated objects even outside the category-selective ROIs.
Linking ROI and MVP analyses: category MVP predicts adaptation MVP for faces and limbs in lateral VTC but not for houses in medial VTC in the LL paradigm
Our previous analyses show that category MVP for repeated stimuli from the adaptation experiments correlates well with category MVP from the localizer experiments. However, an open question remains: does category selectivity predict the level of adaptation for that category? Thus we compared the adaptation MVP (the difference between distributed responses to nonrepeated and repeated trials) for a specific category to the category MVP (the difference between distributed responses to a category and other categories) as determined from the within session localizer data.
We divided the whole VTC ROIs along the mid-fusiform sulcus to create lateral and medial anatomical partitions (Fig. 9A). The lateral VTC contains voxels with a range of preference to faces and limbs (from strong preference in functional ROIs to weak preference in voxels outside these ROIs), whereas the medial ROI contains voxels with a range of preferences to houses. This analysis was performed in three ways: using all voxels within these anatomical ROIs (unthresholded, Fig. 9B), using only voxels that showed significant selectivity to particular categories (thresholded at t > 3, Fig. 9B), or using only those voxels outside of the selective voxels (thresholded at t < 3, Fig. 9B). Importantly, thresholding was done on the other session's localizer data to prevent circularity in the analysis (see methods).
Results reveal three separate effects for each of the preferred categories: faces and limbs in lateral VTC and houses in medial VTC. First, all correlations between face MVP and face adaptation MVP in lateral VTC are significantly positive across the three threshold conditions and paradigms [ts(8) > 3.87, Ps < 0.002]. That is, voxels with higher face preference show a larger magnitude of face adaptation (Fig. 9B, left). Effects did not differ across threshold [F(2,48) = 0.54, P = 0.58, 2-way ANOVA] or paradigm [F(1,48) = 1.5, P = 0.23], and there was no significant interaction [F(2,48) = 0.02, P = 0.98]. Thus the positive correlation between face MVP and face adaptation MVP is stable across paradigms and independent of threshold. Consequently, face preference predicts face fMRI-A magnitude across lateral VTC more generally rather than just in the face-selective mFus and pFus clusters. Put simply, stronger preference to faces predicts stronger fMRI-A to faces.
Second, correlations between limb MVP and limb adaptation MVP are also significantly positive across both threshold and paradigm [ts(8) > 2.67, Ps < 0.01]. There are no differences across paradigms [F(1,48) = 2.20, P = 0.14], but this correlation is higher for the thresholded voxels with stronger limb preference [F(2,48) = 5.48, P < 0.007; Fig. 9B, middle], and there is no interaction [F(2,48) = 0.03, P = 0.97]. Thus, these effects indicate that limb preference predicts adaptation magnitude better within the limb-selective clusters than across the lateral VTC more generally.
Third, while the correlations in medial VTC between house MVP and house adaptation MVP are higher for thresholded than unthresholded data [main effect of threshold: F(2,48) = 6.56, P < 0.003], they are consistently lower in the LL than SL paradigm [main effect of paradigm, F(1,48) = 10.23, P < 0.002, 2-way ANOVA, Fig. 9B, right]. Notably, for the LL paradigm, the correlation between the unthresholded house adaptation MVP and house MVP across the medial VTC is not significant for the unthresholded data or those voxels outside of the house-selective voxels [unthresholded: r = 0.03 ± 0.04, t(8) = 0.72, P = 0.25; t <3: r = 0.01 ± 0.04, t(8) = 0.37, P = 0.36], but this relationship is significantly positive during the SL experiment [unthresholded, r = 0.13 ± 0.06, t(8) = 2.44, P < 0.02; t <3: r = 0.12 ± 0.06, t(8) = 2.15, P < 0.03]. These results extend our findings of a different profile of fMRI-A across paradigms within the functional house-selective CoS (Fig. 7B), and indicate that this difference across paradigms extends to the anatomical medial VTC more generally. House preference predicts the magnitude of house fMRI-A in the medial VTC in the SL experiment, but not in the LL experiment, and changing the amount of time between image repeats significantly affects the response profile in house-selective functional ROIs as well as across the greater anatomical extent of the medial VTC.
Linking fMRI measurements to neural mechanisms: what inferences can we make from fMRI responses about neural mechanisms of repetition?
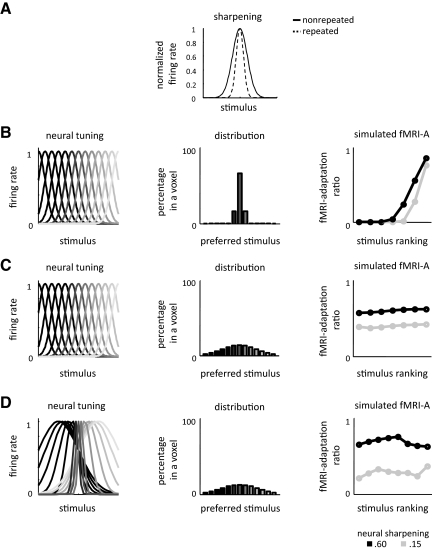
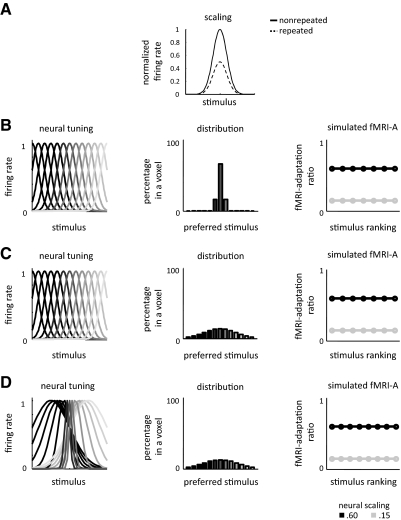
Neural sharpening is a common interpretation of the decreased responses that characterize fMRI-A (Desimone 1996; Wiggs and Martin 1998). This interpretation assumes that each neuron narrows its tuning width on repetition of a stimulus (Fig. 11A) and as a consequence of the narrower tuning curves, the neural representation within a voxel (and across voxels) decreases in size as the nonselective neurons are pruned out (due to the fact that they do not respond to repeated stimuli) and only the selective neurons remain. Although this interpretation is widely cited, there is no empirical evidence to support such a mechanism in high-level visual cortex. Rather than a change in neural tuning, an alternative neural scaling hypothesis argues that repeating stimuli induces a scaled version of neural responses to nonrepeated stimuli (Fig. 10A) (De Baene and Vogels 2009; Grill-Spector et al. 2006; McMahon and Olson 2007). Note that either neural repetition effect could also be determined by the inputs, where sharpening may result from neural inhibition (Norman and O'Reilly 2003), and scaling may result from the degree of overlapping neuronal inputs (De Baene and Vogels 2009; Sawamura et al. 2006). The neural scaling model is consistent with the fMRI-A profile in lateral VTC across time scales. Of course, this interpretation is valid only if scaling at the neural level produces proportional fMRI-A. Thus we simulated the predicted fMRI responses according to both the neural sharpening and neural scaling hypotheses to link potential neural mechanisms of repetition effects to the fMRI-A observed here (see appendix, Figs. 10 and 11). We modeled fMRI voxels to contain a range of neural populations tuned to different stimuli along a stimulus axis. This tuning can be thought of as selectivity to specific stimuli in which different neurons are tuned to particular exemplars spanning a range of selectivities within and across categories. Category selectivity was generated in one of two ways: creating voxels with a majority neural population tuned to the same stimulus as suggested by recent reports (Freiwald et al. 2009; Tsao et al. 2006) (Figs. 10B and 11B) or generating voxels containing neural populations that are more narrowly tuned to some stimuli compared with other stimuli (Figs. 10D and 11D). Specifically, we asked do proportional fMRI-A effects imply scaling of neural responses or can neural sharpening produce these effects?
Fig. 11.
Linking fMRI-A to neural mechanisms: Neural sharpening effects can generate differential fMRI-A effects. A: illustration of the neural sharpening model in a single neuron. Upon repetition, there is no effect at the peak response of the neuron. B–D: predicted fMRI-A ratio according to the sharpening model. In each row, the left panel illustrates neural tuning, the middle illustrates distribution of neural populations in a voxel color coded by their preferred stimulus, and the right panel illustrates the predicted fMRI-A ratio. We show results for two neural sharpening factors, 0.6 (black) and 0.15 (gray). A smaller number indicates more neural sharpening. B: all populations have a σ = 1 and are spaced 1 σ apart with 66% of the neurons preferring the same stimulus. As the neural responses sharpen on repetition, the predicted fMRI responses also sharpen in this voxel resulting in a higher fMRI-A ratio for the preferred category (right). C: results of the sharpening model for an example (nonselective) voxel in which the tuning is the same as B, but the distribution of neural populations is close to uniform, where the percentage of the “preferred” neural population in a voxel is 14%. Although the neural responses sharpen upon repetition, predicted fMRI-A in this voxel now resembles proportional fMRI-A effects where the fMRI-A ratio is similar across categories (right). D: same distribution of neural populations as C, but differential neural tuning varying from σ = 1 for the preferred stimulus up to σ = 8 for the least preferred stimulus; centers of neural tuning functions are spaced 1.3σ apart. Upon repetition, the predicted fMRI responses resemble our house-selective CoS data (Fig. 7B), where the preferred category has a smaller fMRI-A ratio compared with the nonpreferred categories when the neural sharpening is large (0.15) and an opposite pattern for less neural sharpening (0.6).
Fig. 10.
Linking fMRI-A to neural mechanisms: Neural scaling effects generate fMRI-A scaling effects. Results of simulating a neural scaling model of repetition suppression. A: illustration of neural scaling in a single neuron, where repetition decreases neural firing by a constant factor. B–D: predicted fMRI-A results of the neural scaling model. In each row, the left panel illustrates neural tuning, while the middle illustrates distribution of neural populations in a voxel color coded by their preferred stimulus, and the right panel illustrates the predicted fMRI-A ratio. We show results for two neural scaling factors: 0.6 (black) and 0.15 (gray). In all simulations, neural scaling produces fMRI-A scaling effects, which manifest as a constant fMRI-adaptation ratio across categories. The rows vary in the neural tunings and distribution of neural populations in a voxel. B: 66% of the neurons prefer the same stimulus, σ = 1, and spacing between neural tuning is one σ apart. C: same neural tunings as B but close to uniform distribution of neural populations, where the percentage of the preferred neural population in a voxel is 14% of the total number of neurons. D: same distribution of neural populations as C, but differential neural tuning varying from σ = 1 for the preferred stimulus up to σ = 8 for the least preferred stimulus, and centers of neural tuning functions are spaced 1.3σ apart.
Simulations show that scaling effects at the neural level produce proportional fMRI-A (that is, a constant fMRI-A ratio across stimuli) even when voxels contain heterogeneous neural populations with different stimulus preferences (Fig. 10). Specifically, neural scaling due to repetition manifests as a linear relationship between the fMRI response amplitudes to repeated versus nonrepeated stimuli in which the slope is the fMRI-A ratio. Results remain similar for different amounts of neural scaling in voxels containing a close to uniform distribution of neuronal populations (Fig. 10C) and in voxels with populations of neurons with varying tuning widths (D).
We next simulated the effects of neural sharpening in fMRI voxels (Fig. 11). All sharpening scenarios predict fMRI-A for the preferred voxel stimulus even when the preferred neural population does not adapt because of the reduced responses of neurons in the voxel tuned to nonpreferred stimuli. When there is a majority (>50%) of neurons in a voxel that are similarly tuned along the stimulus axis (Fig. 11B), our simulations show that neural sharpening effects produce a nonlinear relationship between fMRI responses to repeated and nonrepeated stimuli in which there is lesser fMRI-A (manifested as a larger fMRI-A ratio) to the best stimulus as compared with a range of intermediate nonoptimal stimuli (Fig. 11B). Thus sharpening is consistent with our house-selective CoS and medial VTC data in the LL paradigm: there is significant fMRI-A for the preferred category (houses), but the predicted fMRI-A ratio is larger (indicative of less fMRI-A) than fMRI-A ratios for the nonpreferred categories which show stronger fMRI-A.
For voxels that do not have a majority neural population (Fig. 11, C and D), simulation results illustrate deviations between neural sharpening effects and fMRI-A effects. Notably, the predicted fMRI-A varies considerably depending on specific model parameters, including the distribution of neural populations in a voxel, their tuning and overlap (Fig. 11, C and D). In voxels of low-stimulus selectivity modeled with a close-to-uniform distribution of neural selectivities with similar tuning widths (Fig. 11C), sharpening at the neural level can manifest as a proportional fMRI-A effect with constant fMRI-A ratios across stimuli (C). However, if selectivity in a voxel is produced by narrower neuronal tuning to the preferred as compared with the nonpreferred stimuli, fMRI-A effects depend on the degree of neural sharpening as well as the overlap of neural tuning functions. While in most cases neural sharpening will produce fMRI-A sharpening effects, the predicted fMRI-A to different stimuli depends on the degree of neural sharpening: larger neural sharpening produces less fMRI-A for preferred stimuli (Fig. 11D, blue) and lesser neural sharpening produces more fMRI-A for preferred stimuli (D, black). These predicted fMRI-A effects resemble our house-selective CoS data (Fig. 7b).
Overall, our simulations illustrate that when interpreting fMRI-A effects in regions that show strong selectivity for a particular stimulus, fMRI-A scaling effects are likely driven by respective neural scaling effects and neural scaling cannot produce the differential effects across time scales observed in the house-selective CoS. However, if category-selective regions do not contain a majority of neurons preferring a particular category, fMRI-A scaling results cannot differentiate between neural sharpening and neural scaling. Finally, our findings of differential fMRI-A effects across time scales in the CoS can be explained by one of two alternatives: 1) if house-selective CoS voxels contain a majority neural population tuned to houses, differential fMRI-A effects across SL and LL paradigms likely result from two separate mechanisms across timing parameters, specifically, neural scaling effects in SL repetitions (Fig. 10B) and neural sharpening effects in LL repetitions (Fig. 11B); or 2) if house-selective CoS voxels contain a minority neural population broadly tuned to houses, albeit with narrower tuning for houses than other categories, differential fMRI-A effects across timing parameters can be explained by a neural sharpening mechanism with different amounts of neural sharpening across time scales (Figs. 6, 7 and 11D).
DISCUSSION
Our data show for the first time that repetition effects in lateral ventral temporal cortex (VTC) consistently produce proportional fMRI-A across categories with similar results across repetition timing parameters, and a quantitative difference in fMRI-A ratios along a posterior-anterior axis. Posterior face- and limb-selective regions (pFus and ITG, respectively) have larger fMRI-A ratios compared with their anterior counterparts (mFus and OTS, respectively) especially during LL repetitions, suggesting differential fMRI-A scaling factors in posterior relative to anterior regions depending on timing parameters. In contrast, repetition effects in medial VTC vary qualitatively across time scales. For SL repetitions, there are similar fMRI-A effects in medial VTC as in lateral VTC. However, for LL repetitions, there is a different fMRI-A profile in medial VTC, where selectivity for the preferred stimulus increases with repetition as indicated by greater fMRI-A to a nonpreferred stimulus in our ROI analyses as well as indicated by a potential change in the distributed response patterns during repeated trials in our MVP analyses. In particular, during LL repetitions, we found larger fMRI-A magnitudes for nonpreferred categories than the preferred category (Fig. 6), different fMRI-A ratios across categories, where the preferred category has a larger fMRI-A ratio than nonpreferred categories (Fig. 7), and a weak correlation between category MVP and adaptation MVP for houses (Fig. 9B). These results suggest that different mechanisms may underlie repetition effects in medial VTC as compared with lateral VTC, especially during LL repetitions.
fMRI-A scaling effects in lateral VTC
Our evidence for proportional fMRI-A effects is consistent with previous neuroimaging and neurophysiology studies. fMRI-A studies of ventral stream regions have reported larger fMRI-A magnitudes for stimuli that elicit stronger responses than others such as high versus low contrast stimuli (Avidan et al. 2002) or upright versus inverted faces (Mazard et al. 2006). A proportional relationship between repeated and nonrepeated responses can explain decreasing fMRI-A magnitudes as a function of dissimilarity from the adapting stimulus found in several regions: the intraparietal sulcus (Piazza et al. 2004), fusiform gyrus (Drucker and Aguirre 2009; Fang et al. 2007), LO (Andresen et al. 2009), and V1 (Fang et al. 2005). Single-cell recordings also illustrate that firing of monkey inferotemporal (IT) neurons is suppressed by a constant scaling factor for repetitions of shapes (McMahon and Olson 2007) without general habituation (Li et al. 1993; Lueschow et al. 1994) and that neuronal selectivity does not change with repetition (De Baene and Vogels 2009; Woloszyn and Sheinberg 2009). Furthermore, a recent study examining how image repetition affects single-cell responses and local field potentials (LFPs) in monkey IT cortex illustrates that both spiking activity and gamma power reduce by a scaled factor upon repetition where the similarity between two images is a better predictor for the resulting adaptation than the neural response itself (De Baene and Vogels 2009). Therefore, scaling does not seem to be a specific mechanism applicable only to the relationship between category selectivity and fMRI-A in the ventral stream but is also relevant for other forms of selectivity, other regions of the brain, and varying spatial resolutions (both single units and population level responses measured with LFPs and fMRI).
fMRI-A to nonpreferred categories
One prediction of the scaling model is larger fMRI-A for the preferred stimulus compared with nonpreferred stimuli. Previous studies consistently find fMRI-A for the preferred category in category-selective regions (Andresen et al. 2009; Avidan et al. 2002; Ewbank et al. 2005; Pourtois et al. 2009) but not always for nonpreferred categories (Ewbank et al. 2005; Pourtois et al. 2009). As previously shown, the magnitude of fMRI-A is also sensitive to repetition parameters such as the number of stimulus repetitions as well as the amount of time and number of stimuli between repetitions (Henson et al. 2003; Sayres and Grill-Spector 2006). Because nonpreferred stimuli induce lower responses than preferred stimuli, the magnitude of fMRI-A to nonpreferred stimuli is lower and the detectability of fMRI-A to nonpreferred stimuli becomes more sensitive to these parameters as well as analysis methods. For example, high-resolution data increase the detection of these fMRI-A effects for nonpreferred categories by isolating the signals to a fine spatial scale, while spatial smoothing and group analyses may dilute these effects (Mahon et al. 2007; Pourtois et al. 2009). Finally, repetition suppression effects for nonpreferred stimuli have been found in electrophysiological recordings (De Baene and Vogels 2009; McMahon and Olson 2007) and follow a similar scaling pattern, suggesting that repetition scaling effects are occurring at the neuronal level. These findings underscore the utility of the fMRI-A method for probing the sensitivities of neural populations to both optimal and nonoptimal stimuli contrary to recent claims (Mur et al. 2010).
Larger fMRI-adaptation ratios for posterior compared with anterior face- and limb-selective regions for long-lagged repetitions
Our present results indicate a new general principle—that fMRI-A is anatomically-specific and time scale dependent. Such a concept is in agreement with results from fMRI-A studies in early visual cortex concluding that fMRI-A is sensitive to timing parameters in the stimulus presentation, as fMRI-A in V1 is highly contingent on timing parameters and prolonged adaptation compared with extrastriate regions (Boynton and Finney 2003; Fang et al. 2005). Further, recent neurophysiology evidence indicates different neural adaptation effects in IT cortex compared with prefrontal cortex (Verhoef et al. 2008). Our results show that even VTC regions with the same category preference illustrate differences in the amount of adaptation during LL repetitions, where fMRI-A ratios in the posterior regions—face-selective pFus and limb-selective ITG—are ∼1.5 times larger than more anterior face-selective mFus and limb-selective OTS. Notably, our findings suggest that the fMRI-A ratio is a characteristic of these ventral regions and indicates a hierarchy among VTC regions whereby higher levels of this hierarchy exhibit stronger fMRI-A. Overall, our finding suggests that anatomical location rather than stimulus preference is a better indicator of the resulting amount of fMRI-A. As fMRI studies in monkeys have also located several face-selective patches along a posterior to anterior axis in monkey STS (Moeller et al. 2008), this posterior-anterior differentiation can be tested in future monkey fMRI measurements paired with neurophysiological recordings.
Differential fMRI-A across ventral stream regions: regional differences across time scales
The difference in the profile of fMRI-A across paradigms in the house-selective CoS is consistent with a recent report suggesting differential fMRI-A effects across paradigms examining scene view sensitivity in the CoS/parahippocampal gyrus (Epstein et al. 2008). However, because paradigm differences were not evident in any of our lateral VTC regions, our results indicate regional differences in fMRI-A effects rather than paradigm differences. These findings concur with evidence showing different fMRI-A dynamics in the CoS compared with the fusiform gyrus (Gilaie-Dotan et al. 2008). It is possible that SL repetition effects reflect perceptual mechanisms and LL repetition effects reflect memory-related mechanisms as the CoS is at the intersection between visual cortex and regions involved in both perception and memory such as perirhinal cortex (see Baxter 2009; Suzuki 2009 for reviews).
Electrophysiological recordings provide additional clues for a potential medial/lateral differentiation of repetition effects. Although there is no direct empirical evidence for sharpening effects in single IT neurons, this concept was proposed following recordings in perirhinal cortex rationalizing two effects of repetition: suppression of responses in ∼2/3 of visually responsive neurons and enhancement in ∼1/3 of visually responsive neurons (Desimone 1996; Li et al. 1993; Miller and Desimone 1994). However, recent converging evidence indicates significant neural repetition suppression consistent with neural scaling effects in area TE (De Baene and Vogels 2009; McMahon and Olson 2007; Sawamura et al. 2006; Verhoef et al. 2008), which is lateral to the perirhinal recordings from which the sharpening hypothesis was based. Thus, we speculate sharpening effects may be more appropriate for medial temporal regions especially during long-lagged repetition. However, neurophysiological evidence is needed to directly test this prediction.
Stimulus repetition changes the pattern of response in medial not lateral VTC
Pattern analyses have shown that category and object identity information can be recovered from the distributed response across the ventral stream (Cox and Savoy 2003; Edelman et al. 1998; Eger et al. 2008; Haxby et al. 2001; Sayres and Grill-Spector 2008). Here we show that the patterns of responses for object categories remain largely unchanged when stimuli are repeated (Fig. 8). That is, experience-dependent changes from stimulus repetition during the course of an fMRI scan largely do not create a significant change in the distributed response to object categories across an anatomical ROI covering the OTS, Fus, and CoS. Further, there is a correspondence between the distributed response to a category (category MVP) and the distributed magnitude of adaptation to that category (adaptation MVP) for faces and limbs across paradigms in the lateral VTC. This relationship was found for houses in the medial VTC for SL repetitions but not for LL repetitions (Fig. 9). Our results have important implications for plasticity in the ventral stream because they suggest that fMRI-A does not produce robust changes in category representation in the lateral aspects of the ventral stream. However, LL repetitions change the distributed responses in medial aspects of the ventral stream along the CoS indicating that such a change in the pattern of response can occur even without extensive training (Op de Beeck et al. 2006).
Implications for fMRI-A experiments
Taken together, our results show that neural scaling best explains repetition effects observed with fMRI in lateral regions within ventral temporal cortex. In contrast, different neural mechanisms likely underlie repetition effects within medial VTC. Our simulations offer two neural explanations to these differential repetition effects across time scales observed with fMRI in the medial VTC: SL-repetitions produce neural scaling and LL-repetitions produce neural sharpening or repetition produces neural sharpening but at different levels across time scales.
HOW DO THESE RESULTS AFFECT INTERPRETATION OF fMRI-A EXPERIMENTS?
First, we present clear evidence that at the population level as measured with fMRI, repetition largely does not change the selectivity of voxels or the pattern of distributed responses across the ventral stream for immediate repetitions. While many studies that find fMRI-A interpret this as evidence for a sparsening, or sharpening, of neural responses as proposed by Wiggs and Martin (1998), our results suggest that at least at the macroscopic level this interpretation is unlikely for regions within the lateral portions of ventral temporal cortex irrespective of time between repeats. Second, our simulations suggest that in voxels with a majority neural population with similar tuning along a stimulus dimension, proportional fMRI-A effects are likely due to neural scaling. However, in voxels with a close to uniform distribution of neural populations, the interpretation is more complex as fMRI scaling may be an outcome of either neural scaling or neural sharpening (Figs. 10C and 11C). Third, the robustness of these effects across analyses (voxel-based and MVP analyses) and across paradigms (SL and LL) especially within fusiform and occipito temporal regions suggests that results of fMRI-A experiments examining sensitivity to stimulus changes will be largely independent of paradigm and analysis approach. However, in regions along the CoS, fMRI-A characteristics are more sensitive to paradigm and analysis approach, and consequently interpretation of fMRI-A effects is more complex as it may reflect different mechanisms across time scales as indicated by our simulations. Adding to this complexity, whether or not fMRI-A is an accurate reflection of the underlying neural properties within a given region or is actually a result of inputs to that region is also currently debated (Bartels et al. 2008; De Baene and Vogels 2009; Liu et al. 2009; Sawamura et al. 2006).
While the present study focuses on stimulus driven fMRI-A, top-down effects such as attention (Murray and Wojciulik 2004; Yi and Chun 2005), emotion (Ishai et al. 2004), context (Summerfield et al. 2008), and task (Henson et al. 2002; Race et al. 2009) can also modulate the level of fMRI-A. Future studies of top-down effects on fMRI-A should examine whether top-down and bottom-up effects are independent or interact and incorporate the models and simulations introduced here for stimulus-driven (bottom-up) effects with models such as prediction error (Friston 2005; Henson 2003; Henson and Rugg 2003; Summerfield et al. 2008) for explaining top-down effects.
Consequently, though the concept of neural sharpening is appealing, fMRI researchers should take caution when interpreting that reduced responses to repeated stimuli in the ventral stream are a result of “sharpening.” In fact, for the majority of regions and paradigms, there is little to no evidence from neurophysiology or fMRI (aside from the medial VTC data presented here) to support such a claim without directly testing the relationship between the selectivity of interest and the resulting fMRI-A. Future experiments measuring repetition effects with fMRI and electrophysiology in the same animal could simultaneously test if these anterior-posterior quantitative differences and lateral-medial qualitative differences extend to monkey IT cortex as well as test the predictions of our simulations to provide a critical link between repetition effects across levels: from the single neuron to the population response.
GRANTS
This work was supported by National Eye Institute Grants 5 R21 EY-016199 and RO1EY-019279 and Whitehall Foundation Grant 2005-05-111-RES to K. Grill-Spector and NEI Grant EY-03164 to B. Wardell.
DISCLOSURES
No conflicts of interest are declared by the authors.
Supplementary Material
ACKNOWLEDGMENTS
We thank N. Witthoft, D. Remus, N. Davidenko, J. Winawer, A. Wagner, B. Wandell, and T. Moore for fruitful discussions as well as J. Chen for technical assistance.
APPENDIX
Simulations relating fMRI-A to neural mechanisms
We used simulations to examine how scaling and sharpening effects at the neural level may manifest at the level of fMRI voxels. The goal of the simulations is to provide a proof of concept because we cannot noninvasively measure responses of single neurons in our subjects.
Simulating neural responses
Neural responses were modeled with Gaussian receptive fields (RF) as used in previous studies (Andresen et al. 2009; Logothetis et al. 1995; Poggio and Edelman 1990; Riesenhuber and Poggio 1999)
| (1) |
Where G is a Gaussian with mean μi and tuning width σ; and x is the stimulus dimension. Different neural populations (fi) have different means reflecting different preferred stimuli. n is the number of neural populations in a voxel. All neurons in a voxel had the same tuning width. Gaussian centers were spaced on regular intervals and neural firings were normalized to have a maximum of 1.
Neural firing rates to repeated objects were simulated using one of two models, 1) neural scaling: firing rates to repeated stimuli are a scaled version of the firing to nonrepeated objects; c is the scaling factor
| (2) |
2) neural sharpening: neural tuning width to repeated stimuli narrows around the preferred stimulus, where σ decreases by the sharpening factor c
| (3) |
Simulating fMRI voxels
fMRI voxel responses were estimated as the weighted sum of neural responses. The response of each neural population was weighted by its percentage in the voxel. pi is the percentage neurons in a voxel tuned around a particular stimulus, μi.
| (4) |
In the simulations, we first modeled category-selective voxels that respond more strongly for one category over other categories. Therefore pi are not distributed uniformly, and we used a normal probability density function for the pi (Figs. 10B and 11B). At the limit, voxels will contain one neural population in which all neurons prefer the same stimulus (Tsao et al. 2006). A narrow normal distribution will produce a majority of neurons in a voxel that prefer one stimulus, while a wide normal distribution will produce a close to uniform distribution of neural populations in a voxel (Figs. 10B and 11B). A second way to simulate category selectivity is by varying the neural tuning and the density of tuning functions. That is, category selectivity can be generated by narrower and denser tuning around the preferred category and broader and sparser tuning for nonpreferred categories (Figs. 10D and 11D). For example, CoS house-selective voxels may contain neurons with narrow tuning to houses, and neurons with broad tuning to both nonhouses and houses.
Calculating the fMRI-adaptation ratio
For each of our stimuli along the stimulus axis, we calculated the ratio between predicted fMRI responses to nonrepeated versus repeated stimuli, which is illustrated in the right column in Figs. 10 and 11.
Effects of model parameters
We estimated voxel (fMRI) responses according to each of the two models and examined the effects of several parameters: the level of neural adaptation, the neural tuning width and overlap, and the distribution of neurons in a voxel. For the scaling model, neural scaling always produces a constant fMRI-A ratio across all stimuli, and changing these parameters only produces a quantitative change in the predicted fMRI-A ratio. For the sharpening model, when there is a majority neural population in the voxel, neural sharpening effects manifest as fMRI-A sharpening effects with less fMRI-A for the preferred category than the nonpreferred category. For voxels with a close to uniform distribution of neural populations (e.g., Fig. 11, C and D), neural sharpening effects produce variable fMRI-A effects depending on model parameters of neural tuning width, overlap between neural tunings, and the degree of neural sharpening.
Footnotes
The online version of this article contains supplemental data.
REFERENCES
- Aguirre GK, Zarahn E, D'Esposito M. An area within human ventral cortex sensitive to “building” stimuli: evidence and implications. Neuron 21: 373–383, 1998 [DOI] [PubMed] [Google Scholar]
- Andresen DR, Vinberg J, Grill-Spector K. The representation of object viewpoint in human visual cortex. Neuroimage 45: 522–536, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avidan G, Hasson U, Hendler T, Zohary E, Malach R. Analysis of the neuronal selectivity underlying low fMRI signals. Curr Biol 12: 964–972, 2002 [DOI] [PubMed] [Google Scholar]
- Bartels A, Logothetis NK, Moutoussis K. fMRI and its interpretations: an illustration on directional selectivity in area V5/MT. Trends Neurosci 31: 444–453, 2008 [DOI] [PubMed] [Google Scholar]
- Baxter MG. Involvement of medial temporal lobe structures in memory and perception. Neuron 61: 667–677, 2009 [DOI] [PubMed] [Google Scholar]
- Boynton GM, Finney EM. Orientation-specific adaptation in human visual cortex. J Neurosci 23: 8781–8787, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis 10: 433–436, 1997 [PubMed] [Google Scholar]
- Cox DD, Savoy RL. Functional magnetic resonance imaging (fMRI) “brain reading”: detecting and classifying distributed patterns of fMRI activity in human visual cortex. Neuroimage 19: 261–270, 2003 [DOI] [PubMed] [Google Scholar]
- De Baene W, Vogels R. Effects of adaptation on the stimulus selectivity of macaque inferior temporal spiking activity and local field potentials. Cereb Cortex In press [DOI] [PubMed] [Google Scholar]
- Desimone R. Neural mechanisms for visual memory and their role in attention. Proc Natl Acad Sci USA 93: 13494–13499, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downing PE, Jiang Y, Shuman M, Kanwisher N. A cortical area selective for visual processing of the human body. Science 293: 2470–2473, 2001 [DOI] [PubMed] [Google Scholar]
- Drucker DM, Aguirre GK. Different spatial scales of shape similarity representation in lateral and ventral LOC. Cereb Cortex 19: 2269–2280, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin SO, Bittar RG, Kabani NJ, Baker CL, Jr, Le Goualher G, Bruce Pike G, Evans AC. A new anatomical landmark for reliable identification of human area V5/MT: a quantitative analysis of sulcal patterning. Cereb Cortex 10: 454–463, 2000 [DOI] [PubMed] [Google Scholar]
- Edelman S, Grill-Spector K, Kusnir T, Malach R. Towards direct visualization of the internal shape space by fMRI. Psychobiology 26: 309–321, 1998 [Google Scholar]
- Eger E, Ashburner J, Haynes JD, Dolan RJ, Rees G. fMRI activity patterns in human LOC carry information about object exemplars within category. J Cogn Neurosci 20: 356–370, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein R, Kanwisher N. A cortical representation of the local visual environment. Nature 392: 598–601, 1998 [DOI] [PubMed] [Google Scholar]
- Epstein RA, Parker WE, Feiler AM. Two kinds of FMRI repetition suppression? Evidence for dissociable neural mechanisms. J Neurophysiol 99: 2877–2886, 2008 [DOI] [PubMed] [Google Scholar]
- Ewbank MP, Schluppeck D, Andrews TJ. fMR-adaptation reveals a distributed representation of inanimate objects and places in human visual cortex. Neuroimage 28: 268–279, 2005 [DOI] [PubMed] [Google Scholar]
- Fang F, Murray SO, He S. Duration-dependent FMRI adaptation and distributed viewer-centered face representation in human visual cortex. Cereb Cortex 17: 1402–1411, 2007 [DOI] [PubMed] [Google Scholar]
- Fang F, Murray SO, Kersten D, He S. Orientation-tuned FMRI adaptation in human visual cortex. J Neurophysiol 94: 4188–4195, 2005 [DOI] [PubMed] [Google Scholar]
- Freiwald WA, Tsao DY, Livingstone MS. A face feature space in the macaque temporal lobe. Nat Neurosci 12: 1187–1196, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K. A theory of cortical responses. Philos Trans R Soc Lond B Biol Sci 360: 815–836, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frost C, Thompson S. Correcting for regression dilution bias: comparison of methods for a single predictor variable. J Rl Stat Soc A 163: 173–190, 2000 [Google Scholar]
- Gilaie-Dotan S, Nir Y, Malach R. Regionally-specific adaptation dynamics in human object areas. Neuroimage 39: 1926–1937, 2008 [DOI] [PubMed] [Google Scholar]
- Glover GH. Simple analytic spiral K-space algorithm. Magn Reson Med 42: 412–415, 1999 [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Henson R, Martin A. Repetition and the brain: neural models of stimulus-specific effects. Trends Cogn Sci 10: 14–23, 2006 [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Kushnir T, Edelman S, Avidan G, Itzchak Y, Malach R. Differential processing of objects under various viewing conditions in the human lateral occipital complex. Neuron 24: 187–203, 1999 [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Malach R. fMR-adaptation: a tool for studying the functional properties of human cortical neurons. Acta Psychol 107: 293–321, 2001 [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Malach R. The human visual cortex. Annu Rev Neurosci 27: 649–677, 2004 [DOI] [PubMed] [Google Scholar]
- Haxby JV, Gobbini MI, Furey ML, Ishai A, Schouten JL, Pietrini P. Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science 293: 2425–2430, 2001 [DOI] [PubMed] [Google Scholar]
- Henson RN. Neuroimaging studies of priming. Prog Neurobiol 70: 53–81, 2003 [DOI] [PubMed] [Google Scholar]
- Henson RN, Goshen-Gottstein Y, Ganel T, Otten LJ, Quayle A, Rugg MD. Electrophysiological and haemodynamic correlates of face perception, recognition and priming. Cereb Cortex 13: 793–805, 2003 [DOI] [PubMed] [Google Scholar]
- Henson RN, Rugg MD. Neural response suppression, hemodynamic repetition effects, and behavioral priming. Neuropsychologia 41: 263–270, 2003 [DOI] [PubMed] [Google Scholar]
- Henson RN, Shallice T, Gorno-Tempini ML, Dolan RJ. Face repetition effects in implicit and explicit memory tests as measured by fMRI. Cereb Cortex 12: 178–186, 2002 [DOI] [PubMed] [Google Scholar]
- Ishai A, Pessoa L, Bikle PC, Ungerleider LG. Repetition suppression of faces is modulated by emotion. Proc Natl Acad Sci USA 101: 9827–9832, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanwisher N, McDermott J, Chun MM. The fusiform face area: a module in human extrastriate cortex specialized for face perception. J Neurosci 17: 4302–4311, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kourtzi Z, Kanwisher N. Representation of perceived object shape by the human lateral occipital complex. Science 293: 1506–1509, 2001 [DOI] [PubMed] [Google Scholar]
- Kruger G, Glover GH. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magn Reson Med 46: 631–637, 2001 [DOI] [PubMed] [Google Scholar]
- Levy I, Hasson U, Avidan G, Hendler T, Malach R. Center-periphery organization of human object areas. Nat Neurosci 4: 533–539, 2001 [DOI] [PubMed] [Google Scholar]
- Li L, Miller EK, Desimone R. The representation of stimulus familiarity in anterior inferior temporal cortex. J Neurophysiol 69: 1918–1929, 1993 [DOI] [PubMed] [Google Scholar]
- Liu Y, Murray SO, Jagadeesh B. Time course and stimulus dependence of repetition-induced response suppression in inferotemporal cortex. J Neurophysiol 101: 418–436, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Poggio T. Shape representation in the inferior temporal cortex of monkeys. Curr Biol 5: 552–563, 1995 [DOI] [PubMed] [Google Scholar]
- Lueschow A, Miller EK, Desimone R. Inferior temporal mechanisms for invariant object recognition. Cereb Cortex 4: 523–531, 1994 [DOI] [PubMed] [Google Scholar]
- Mahon BZ, Milleville SC, Negri GA, Rumiati RI, Caramazza A, Martin A. Action-related properties shape object representations in the ventral stream. Neuron 55: 507–520, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazard A, Schiltz C, Rossion B. Recovery from adaptation to facial identity is larger for upright than inverted faces in the human occipito-temporal cortex. Neuropsychologia 44: 912–922, 2006 [DOI] [PubMed] [Google Scholar]
- McMahon DB, Olson CR. Repetition suppression in monkey inferotemporal cortex: relation to behavioral priming. J Neurophysiol 97: 3532–3543, 2007 [DOI] [PubMed] [Google Scholar]
- Miller EK, Desimone R. Parallel neuronal mechanisms for short-term memory. Science 263: 520–522, 1994 [DOI] [PubMed] [Google Scholar]
- Moeller S, Freiwald WA, Tsao DY. Patches with links: a unified system for processing faces in the macaque temporal lobe. Science 320: 1355–1359, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mur M, Ruff DA, Bodurka J, Bandettini PA, Kriegeskorte N. Face-identity change activation outside the face system: “release from adaptation” may not always indicate neuronal selectivity. Cereb Cortex In press [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray SO, Wojciulik E. Attention increases neural selectivity in the human lateral occipital complex. Nat Neurosci 7: 70–74, 2004 [DOI] [PubMed] [Google Scholar]
- Nestares O, Heeger DJ. Robust multiresolution alignment of MRI brain volumes. Magn Reson Med 43: 705–715, 2000 [DOI] [PubMed] [Google Scholar]
- Norman KA, O'Reilly RC. Modeling hippocampal and neocortical contributions to recognition memory: a complementary-learning-systems approach. Psychol Rev 110: 611–646, 2003 [DOI] [PubMed] [Google Scholar]
- Op de Beeck HP, Baker CI, DiCarlo JJ, Kanwisher NG. Discrimination training alters object representations in human extrastriate cortex. J Neurosci 26: 13025–13036, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peelen MV, Downing PE. Selectivity for the human body in the fusiform gyrus. J Neurophysiol 93: 603–608, 2005 [DOI] [PubMed] [Google Scholar]
- Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron 44: 547–555, 2004 [DOI] [PubMed] [Google Scholar]
- Pinsk MA, Arcaro M, Weiner KS, Kalkus JF, Inati SJ, Gross CG, Kastner S. Neural representations of faces and body parts in macaque and human cortex: a comparative FMRI study. J Neurophysiol 101: 2581–2600, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poggio T, Edelman S. A network that learns to recognize three-dimensional objects. Nature 343: 263–266, 1990 [DOI] [PubMed] [Google Scholar]
- Pourtois G, Schwartz S, Spiridon M, Martuzzi R, Vuilleumier P. Object representations for multiple visual categories overlap in lateral occipital and medial fusiform cortex. Cereb Cortex 19: 1806–1819, 2009 [DOI] [PubMed] [Google Scholar]
- Race EA, Shanker S, Wagner AD. Neural priming in human frontal cortex: multiple forms of learning reduce demands on the prefrontal executive system. J Cogn Neurosci 21: 1766–1781, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nat Neurosci 2: 1019–1025, 1999 [DOI] [PubMed] [Google Scholar]
- Ringo JL. Stimulus specific adaptation in inferior temporal and medial temporal cortex of the monkey. Behav Brain Res 76: 191–197, 1996 [DOI] [PubMed] [Google Scholar]
- Sawamura H, Georgieva S, Vogels R, Vanduffel W, Orban GA. Using functional magnetic resonance imaging to assess adaptation and size invariance of shape processing by humans and monkeys. J Neurosci 25: 4294–4306, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawamura H, Orban GA, Vogels R. Selectivity of neuronal adaptation does not match response selectivity: a single-cell study of the FMRI adaptation paradigm. Neuron 49: 307–318, 2006 [DOI] [PubMed] [Google Scholar]
- Sayres R, Grill-Spector K. Object-selective cortex exhibits performance-independent repetition suppression. J Neurophysiol 95: 995–1007, 2006. 16236787 [Google Scholar]
- Sayres R, Grill-Spector K. Relating retinotopic and object-selective responses in human lateral occipital cortex. J Neurophysiol 100: 249–267, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schacter DL, Buckner RL. Priming and the brain. Neuron 20: 185–195, 1998 [DOI] [PubMed] [Google Scholar]
- Schwarzlose RF, Baker CI, Kanwisher N. Separate face and body selectivity on the fusiform gyrus. J Neurosci 25: 11055–11059, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarzlose RF, Swisher JD, Dang S, Kanwisher N. The distribution of category and location information across object-selective regions in human visual cortex. Proc Natl Acad Sci USA 105: 4447–4452, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons JS, Koutstaal W, Prince S, Wagner AD, Schacter DL. Neural mechanisms of visual object priming: evidence for perceptual and semantic distinctions in fusiform cortex. Neuroimage 19: 613–626, 2003 [DOI] [PubMed] [Google Scholar]
- Summerfield C, Trittschuh EH, Monti JM, Mesulam MM, Egner T. Neural repetition suppression reflects fulfilled perceptual expectations. Nat Neurosci 11: 1104–1106, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki WA. Perception and the medial temporal lobe: evaluating the current evidence. Neuron 61: 657–666, 2009 [DOI] [PubMed] [Google Scholar]
- Tsao DY, Freiwald WA, Tootell RB, Livingstone MS. A cortical region consisting entirely of face-selective cells. Science 311: 670–674, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Turennout M, Ellmore T, Martin A. Long-lasting cortical plasticity in the object naming system. Nat Neurosci 3: 1329–1334, 2000 [DOI] [PubMed] [Google Scholar]
- Verhoef BE, Kayaert G, Franko E, Vangeneugden J, Vogels R. Stimulus similarity-contingent neural adaptation can be time and cortical area dependent. J Neurosci 28: 10631–10640, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vuilleumier P, Henson RN, Driver J, Dolan RJ. Multiple levels of visual object constancy revealed by event-related fMRI of repetition priming. Nat Neurosci 5: 491–499, 2002 [DOI] [PubMed] [Google Scholar]
- Weiner KS, Grill-Spector K. Sparsely-distributed organization of face and limb activations in human ventral temporal cortex. Neuroimage In press [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiggs CL, Martin A. Properties and mechanisms of perceptual priming. Curr Opin Neurobiol 8: 227–233, 1998 [DOI] [PubMed] [Google Scholar]
- Woloszyn L, Sheinberg DL. Neural dynamics in inferior temporal cortex during a visual working memory task. J Neurosci 29: 5494–5507, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi DJ, Chun MM. Attentional modulation of learning-related repetition attenuation effects in human parahippocampal cortex. J Neurosci 25: 3593–3600, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.