Neural Substrates of Graphomotor Sequence Learning: A Combined fMRI and Kinematic Study

Abstract

The goal of this study was to characterize the dynamics and functional connectivity of brain networks associated with fast (short-term) learning of handwriting using functional magnetic resonance imaging. Participants (n = 12) performed a graphomotor sequence learning task (naïve subjects learning to draw simple, 3-stroke Chinese word characters), which focused the learning process on the kinematic aspects of sequence learning instead of on the production of the line segments. Learning of the graphomotor sequence was demonstrated by a progressive improvement in movement smoothness as assessed by normalized jerk scores. Examination of the patterns of regional neural activity and functional connectivity during sequence learning demonstrated that cortical regions, which may support visuomotor mapping components of the task, were active prior to subcortical areas that may play a role in encoding and refining the novel sequences. Importantly, differences in the time course of recruitment of basal ganglia and cerebellar networks suggest distinct but integrated roles in the encoding and refining of the handwritten sequences. This implies multiple kinematic representations of graphomotor trajectories may be encoded at various spatiotemporal scales.

INTRODUCTION

The brain's ability to automate almost any task—whether cognitive, linguistic, or motoric—is fundamental to all human thought, communication, and activity (Lashley 1951). Sets of complex, multiple-stage movements become so well packaged that little or no thought is needed to initiate or complete them (consider opening a door, typing, or dancing). While learning a new sequence (of thoughts, words, or movements) can be time and attentionally demanding, after the sequence has been automated, it becomes a part of the person's routine behavioral repertoire.

Understanding how the brain encodes sequences is important both for uncovering basic neural mechanisms for sequence learning in healthy persons as well as for learning how neuropathological alterations in these processes relate to deficits in sequence learning. For example, persons with loss of nigrostriatal dopamine production due to Parkinson's disease have demonstrated impaired sequence learning (Mentis et al. 2003a,b; Nakamura et al. 2001; Smith and McDowall 2006). Degraded sequence learning may also constitute a part of the pathophysiology of Huntington's chorea (Brown et al. 2001), stuttering (Webster 1989), and stroke/traumatic brain injury (Pohl et al. 2001). Uncovering how the brain encodes novel sequences may shed light both on the neural computational processes needed for sequence learning as well as how neuropathology degrades those processes.

Motor sequence learning has been characterized as having an explicit component (learning the sequence order) as well as implicitly learning how to produce the movements accurately (Ghilardi et al. 2009; Moisello et al. 2009). The current study focuses on the implicit component of motor sequence learning, which can be captured by kinematic measures. Specifically, we have chosen to study how the brain learns to accurately produce a novel sequence of hand stroke movements to write ideomotor characters. This task is ideal to study motor learning because the individual stroke components are well learned, and many potential artifacts due to muscle strength limitations, gravity, inertia, amount of movements are negligible (Teulings et al. 1997).

Prior neuroimaging studies on the short-term learning of handwriting have revealed multiple representations of graphomotor trajectories in parietal cortex (Seitz et al. 1997) as well as a successive role of the cerebellum and the premotor cortices in trajectorial learning using PET (Seitz et al. 1994). These results are consistent with functional magnetic resonance imaging (fMRI) data obtained during the performance of Japanese kanji ideograms, which has been shown to activate left fronto-parietal networks, including the middle and inferior frontal gyri and pre- and postcentral gyri. Moreover, bilateral activations were found in the medial frontal gyrus, cingulate cortex, superior temporal gyrus, superior parietal lobe, inferior parietal sulcus, basal ganglia, and cerebellum (Nakamura et al. 2002). The Seitz et al. studies, however, included movements with varying coordination complexity requirements as the authors used handwriting patterns that required a combination of cursive, oblique, and straight vertical and horizontal strokes of varying sizes and performed with varying task demands (e.g., emphasizing accuracy or speed). Thus it is not clear whether their reports of the dynamics of relative regional brain activity changes during the short-term motor skill acquisition were related to the learning of the sequential structure of the ideogram, its coordination complexity, or both.

To examine the neural changes that occur during graphomotor sequence learning, we developed a novel behavioral task: having subjects with no prior knowledge of written Chinese learn to draw simple Chinese word characters (see Fig. 1B). Drawing short, straight lines is a highly overlearned task (used often in written English). Learning to draw Chinese word characters involves learning a novel sequence of these lines or strokes. In this manner, the task focuses the learning process on the novel sequence (the Chinese word characters), rather than learning the individual segments of the sequence (the individual lines), while keeping constant the degree of coordination complexity. This behavioral task is both naturalistic (common to everyday human experience), and complex enough to yield rich measurements of learning. Because we are employing a novel learning task, we chose to initially focus on explicit sequence learning, providing the subjects with real-time feedback of the subject's pen position, so that on-line error correction was possible. In addition, the subjects were given feedback of the quality of their performance after every Chinese character was completed (knowledge of results or KR).

Fig. 1.

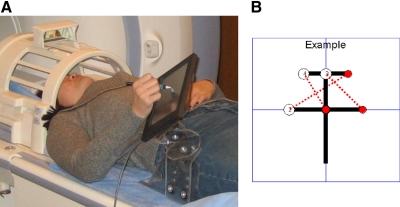
Experimental setup and task. A: position of the subject in the scanner—the nonferromagnetic, digitizing tablet is mounted on the tablet holder and arm support. Example of a Chinese character (B) that the subjects learned to draw (starts from the center).

As mentioned earlier, there were several advantages of using handwriting as the task for measuring the neural processes of motor sequence learning. Moreover, as handwriting involves minimal movement, potential movement artifacts can be minimized during neuroimaging. Also, because our interest was in how the brain encodes novel sequences of overlearned motor primitives, and not basic visual and motor processing (movement of the hand, eye movements, eye-hand coordination, etc.), the current study reduced the contribution of these processes by including them in the baseline condition (see fMRI BOLD analysis).

To assess the learning of the graphomotor sequences, Normalized jerk (Njerk) was chosen to quantify changes in movement smoothness, as it provides a kinematic measure of movement performance (Kitazawa et al. 1993) and implicit motor sequence learning (Ghilardi et al. 2009). Jerk is the change of acceleration per time, and its normalization allows for differences in the size and speed of drawing the Chinese word characters, producing a measure of movement smoothness that has been related to learning in prior studies (Contreras-Vidal and Buch 2003; Contreras-Vidal et al. 1998,. 1999; Kitazawa et al. 1993; Teulings et al. 1997). Because the focus is to examine the participation of neural regions related to sequence learning, apart from neural changes related to speed or size of drawing, Njerk was used to normalize out the individual differences between subjects in both movement time and movement length (size).

METHODS

Design

A mixed (event-block) fMRI design was used, in which the subjects repeatedly drew four ideographic characters (3 sets of line-pairs each), while they were scanned in a GE 3 Tesla MRI scanner at the National Institutes of Health, Bethesda, MD (see Fig. 1A). The graphomotor task was externally cued but was self-paced with a maximum time within each trial. The maximum time was determined by pilot testing of the behavioral task. The characters were randomly drawn from a pool of 10 characters (see Fig. 1B for an example) and randomly presented, using custom Matlab (Mathworks, Natick, MA) software. Kinematic data were acquired using a nonferromagnetic, digitizing tablet (TouchScreen, MagConcepts, Sunnyvale, CA); at a rate of 66 Hz (see Fig. 1A). In addition to the kinematic measure of learning, time stamps synchronized with the fMRI scans were recorded for each line-pair response that the subject produced.

Subjects

Twelve right-handed healthy subjects [4 female, 8 male; average age = 34.08 ± 6.69 (SD) yr], who demonstrated sequence learning on the kinematic measure employed (Njerk) were included in the study. Seven additional subjects did not have overall decreases in Njerk and were excluded. All subjects had Mini-Mental Status Examination (MMSE) scores >27 (mean 29.58 ± 0.79), and were prescreened for absence of neurological disorders, neurological injuries, chronic substance abuse, and chronic mental illness as well as for MRI safety. Subjects gave informed consent, according to National Institutes of Health and University of Maryland Institutional Review Board requirements and were screened for MRI safety according to the National Institutes of Health Nuclear Magnetic Resonance Center Policy. Subjects were paid $100 for the scan session.

Behavioral task

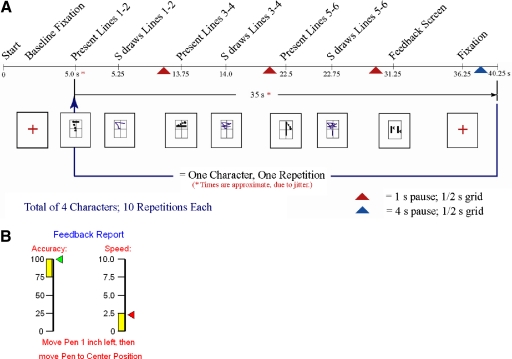
The behavioral task consisted of subjects learning to draw novel graphomotor sequences (Chinese characters) with contemporaneous collection of neuroimaging data, using fMRI. Each character consisted of six straight lines (3 line-pair sets), which were presented and drawn one line pair at a time and could be written within a 3 × 3-in space on the digitizing tablet. After each character was completed, knowledge of results was given to the subject, presenting their speed and spatial accuracy on that character (error feedback learning). The characters were randomly selected and randomly presented, to avoid positional effects. Figure 2 presents the elements of the behavioral task required to complete one character. The timing of the elements were jittered to maximize the detection of the hemodynamic responses to the task.

Fig. 2.

A and B: elements of the behavioral task A: subjects viewed a fixation cross until the character segments were presented, 2 lines at a time. After drawing the 1st pair, the 2nd line pair was given and drawn; then the final pair. A feedback screen (B) was then presented to give feedback to the subject and to have the subject recenter his/her hand on the tablet.

Each of the four characters was repeated nine times for 36 total iterations (the 1st 30 during the fMRI scanning period). Subjects learned to draw the characters on an MRI-compatible digitizing tablet, which allowed for the collection of kinematic data. Importantly, it was assumed that the motor programs for the sequence segments (drawing short, straight strokes) were highly automated, while the sequence (the character) was new to the subject, isolating the sequence learning process. As the Njerk scores were not normally distributed, learning was measured by testing for significant differences in Njerk using Friedman's nonparametric methods with Tukey's honestly significant difference criterion for the post hoc comparisons between drawing iterations (see Procedures for details).

Procedures

Each subject was given the MMSE to screen for basic orientation and cognitive functioning and completed a prescan training on drawing stars (36 times, in 2 positions on the page) to acclimate the subjects to drawing holding the pen tip down continuously. In the scanner, the subjects had a 1 min practice session of drawing random, straight lines on the tablet and then performed the same stars task (6 repetitions). The use of the stars drawing task in the scanner was to familiarize the subjects with visuomotor mapping of the task in an unfamiliar position (lying supine, with the writing tablet near the subject's hip). The scans associated with the stars drawing task were not used in either the baseline or task portions of the study. Having the subjects perform an overlearned task in the scanner was to minimize capturing learning effects from novel tool use.

Due to the length of the single continuous scan during the sequence learning task, multiple measures were taken to ensure that postural stability was maintained throughout the scan period: subjects' heads were stabilized using a vacuum pillow; foam pads were placed under the writing arm; and a wedge-shaped foam pad was placed underneath the knees of the subject. Subjects also had their right arm supported by a custom designed, Plexiglas support to constrain motion (see Fig. 1A); the writing tablet and holder were positioned for greatest subject comfort and ease of writing.

A mirror on the head coil allowed the subject to see a screen, on which instructions and the experimental tasks were presented (see Fig. 1A). The subject was instructed to focus on three important things during the entire experiment: keeping their head still, keeping the stylus tip on the tablet, and copying the examples as quickly and accurately as possible. The start of the behavioral task was synchronized with the first TTL pulse from the GE MRI scanner, using a data acquisition card (NI-DAQ 6062e PCMCIA board, National Instruments, Austin, TX), and the Matlab data acquisition toolbox (Mathworks). This allowed for the time-stamping of each instruction presented, each response made by the subject, each feedback screen, and the fixation times, all relative to the first MRI TTL pulse, synchronizing the kinematic and fMRI datasets.

The experiment provided both real-time visual feedback of the pen's position on the digitizing tablet (with a line trace) during each line-pair and KR after each ideographic character was completed. In this task, subjects were shown an example of how to draw the line pair in an example area on the left side of the screen and then copied the example on a separate writing area on the right side of the screen while the exemplar remained on the screen. The viewing angle between corresponding points on the example and writing areas was ∼6.4° to minimize the effects of eye movements. Ideographic characters were randomly chosen from the pool of 10 characters and were presented in three, two-pair line segments, in order, and with direction cues given in the example window. The sample of characters was constrained to include only characters with three straight lines and three straight transitions. Learning occurred through repeated iterations of drawing each character's line-pairs with a performance feedback screen (giving speed and accuracy) presented to the subject after each character's completion (KR).

fMRI acquisition

The echo-planar imaging (EPI) scan parameters for the functional neuroimages were: repetition time (TR) = 2,000 ms; echo time (TE) = 30.0 ms; field of view (FOV) = 240 mm; slice thickness = 5.0 mm; number of slices per volume = 30; number of volumes = 585; matrix = 64 × 64; flip angle = 90°; with a voxel size of 3.75 × 3.75 × 5 mm. EPI images were acquired in the axial plane. A high-resolution, fast spoiled gradient echo (FSPGR) anatomical scan (TR = 6.944 s.; echo number = 1, number of rows, columns = 256,256; slice thickness = 1 mm; slice spacing = 1 mm; pixel size, = 0.9375, 0.9375 mm; FOV {x,y} = 240,240; number of images = 150) was collected for each subject and was registered with the functional scans using AFNI. The final, statistical results were presented over the anatomical scan of one subject at the same settings.

Kinematic data analysis

To confirm if learning had occurred during the repetitions of the characters, the kinematic data were examined using Njerk, a measure of movement smoothness that normalizes for differences in size and speed of the line drawings (see Eq. 1). Differences in Njerk were examined for significant change using Friedman's nonparametric test as the Njerk data were not normally distributed. Post hoc comparisons between Njerk scores for each of the drawing iterations (compared with all other drawing iterations) were accomplished by using Tukey's honestly significant difference criterion (Conover 1999). Both analyses were run using the Matlab Statistics Toolbox (Mathworks). Before Njerk was computed, the kinematic data were low-pass filtered (Butterworth filter; dual-direction, filtfilt function; filter order = 4; cutoff frequency = 5 Hz). Njerk was computed using the following equation (Contreras-Vidal et al. 1998; Teulings et al. 1997)

$$\text{Njerk=}\sqrt{0.5{\displaystyle \int \text{d}t{\text{ jerk}}^2\left(t\right)\times {\text{duration}}^5/{\text{length}}^2}}$$ (1)

where duration is the time to complete the stroke, length is the stroke distance, and jerk is the third time derivative of the pen position at a given time point, t. The Njerk scores were fitted to a double exponential function (Nelder-Mead simplex algorithm as implemented in the function fminsearch of MATLAB; Mathworks) and plotted as a function of trial.

Further evidence for learning of the graphomotor sequences was obtained through the evaluation of changes in movement speed during the drawing iterations. Differences in movement speed were examined for significant change using Friedman's nonparametric test, with post hoc comparisons between iterations being analyzed using Tukey's honestly significant difference criterion; both computed with the Matlab Statistics Toolbox.

fMRI BOLD analysis

The neuroimaging data were preprocessed in AFNI (National Institute of Mental Health, National Institutes of Health, Bethesda, MD; http://afni.nimh.nih.gov) with motion correction, binary masking of the brain, and 8 mm Gaussian blurring. Binary masking was accomplished using AFNI's 3DAutomask, which calls the 3DClipLevel function. 3DClipLevel finds the median of all positive values and then sets the clip value (threshold) to 0.50 of the median through an iterative process.

To reduce the effects of lower-level visual and motor control (such as eye movements), elements of basic visual processing and hand movement were included in the baseline of the task (see Fig. 2). The composition of the baseline included the fixation screen (a plus sign), complex visual stimuli (performance feedback screen), and a simple hand motion (1 in to the left, then back to the center position). After each character was completed, the subject was instructed to perform a simple hand motion to recenter the subject's hand on the drawing tablet. This motion was after the feedback screen for speed and accuracy was presented. All three of these elements were grouped in the baseline condition.

Because the fMRI data needed to be acquired in one scan (to avoid primacy and recency effects), the total scan time (with stars task and sequence learning task) lasted almost 20 min. Long fMRI scans present additional challenges for data analysis as the effects of scanner baseline drift have to be addressed. Due to the length of the scan, the baseline (instrumental) drift was nonlinear and could not be effectively modeled using standard AFNI methods. The use of per-volume global averages or white matter normalization would have increased the risk of removing signal changes related to the learning task (due to partial volume issues). Thus to remove spurious global blood-oxygen-level-dependent (BOLD) signal drift effects, without removing signal related to the task, each subject's fMRI dataset was normalized by the grand mean (mean over all volumes and voxels) and average ventricle signal (as any signal present will be nonphysiological). The average value for eight 2 mm spherical ventricular locations (anterior and posterior ventricle locations, bilateral, at 2 different z levels, per individual neuroanatomy) was collected for each subject (Fox et al. 2006). This average (dividing on a per-volume basis) was used to remove the proportional instrumental drift over time. In addition, the same per volume ventricle values were included in the baseline model of the deconvolution, along with removal of each subject's mean, to remove additive instrumental effects.

The entire learning period was analyzed as a whole (Global analysis) and was subdivided in two ways. First, the transition point between the first and second exponents of the Njerk learning curve was used to divide the data into early and late sequence learning periods. In addition, the second exponential period was further segmented into three subsections, to examine the temporal dynamics occurring during that period. There weren't enough volumes to subdivide the early period and detect the hemodynamic response function (HRF), and three was the maximum number of bins possible in the second (late) sequence learning period. To create the subdivisions, the predicted HRF was multiplied by a binary square wave function corresponding to the time bin segment to produce a predicted HRF for that time bin. The predicted HRF was compared with each voxel, and the resulting beta coefficients for each subject were entered into a mixed-effects ANOVA (bin × subject) after transforming the results into a common (Talairach) space. A Monte Carlo simulation was performed to determine the minimum cluster size needed to avoid increased type I error due to repeated measurements. The mean for each time bin was computed (t-test maps) and was smoothed with a 3 mm Gaussian filter for presentation purposes. Neuroimaging figures present the t maps of significant BOLD activity during the given time period. The P value threshold (along with the corresponding t value) is presented on each figure.

The predicted HRF for the Global analysis was created by using the average Njerk values for the group and identifying voxels that followed the pattern of the learning curve. As the double exponential fit for Njerk was characterized by a large initial exponential decrease followed by an exponential decay with a rate that was >45 times smaller (λ1 = −0.75964 vs. λ2 = −0.016749; see Fig. 3); the predicted HRF for the binned analyses was created by convolving the duration of each line-pair movement (i.e., stroke duration) with a gamma function to allow for a more detailed analysis of the microstructure of the characters, using AFNI's waver program. Drawing stroke duration was computed using the time stamps captured using the nonferromagnetic, digitizing tablet, and the gamma function is an ideal HRF (Cohen 1997). Given the different kinematic parameters (Njerk vs. stroke duration) of the HRF for the Global analysis and for the binned analyses, they cannot be compared directly, as they reflect kinematic parameters of different time scales (i.e., macrostructure vs. microstructure of the characters).

Fig. 3.

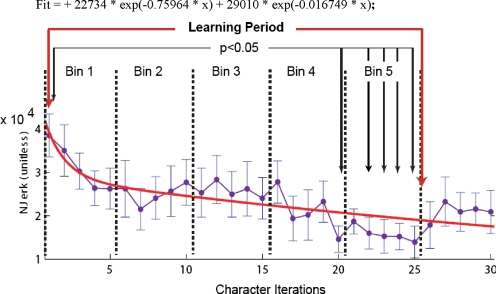
Changes in performance as sequences are learned. Average normalized jerk (Njerk) scores and double exponential fit. Significant differences between character iterations 1 and iterations 20 and 23–25 (Friedman's test; P < 0.05) define an average learning period between iterations 1 and 25. Error bars are 1 SE; fit is double exponential (adjusted r² = 0.66). The learning period is divided into 2 exponential periods (divided where the 1st and 2nd exponentials cross; early and late sequence learning periods). Bin 1 is the 1st exponential period; bins 3–5 are in the 2nd exponential period and are subdivided into bins 2A–C.

fMRI functional connectivity analysis

The connectivity analysis was data-driven with the regions of interest (ROIs) selected from the prior BOLD time bin analysis instead of a priori. Three ROIs were selected for the seed voxel cross-correlation analysis: left primary motor cortex (M1 [43 13 50]); left superior parietal lobule (SPL [18 62 55]); and the left anterior putamen (aPUT [28 −53 4]). The locations of these voxels represent the local maxima of each region (percent signal change) and were cross-correlated with all other voxels in the brain (with the effect of the hemodynamic response deconvolved out). Functional connectivity analyses included neural connections with multiple-synaptic connections as well as those with direct, anatomical connectivity. For presentation purposes, only left hemispheric cross-correlations are depicted (right hemisphere for cerebellar regions) as subjects were all right-handed.

Functional connectivity was measured using seed voxel cross-correlation with deconvolution (see AFNI website: http://afni.nimh.nih.gov/sscc/gangc/CD-CorrAna.html). Each subject's EPI dataset was transformed into common (Talairach) space; then the brain was masked with a group average, binary mask; the time series for the region of interest (M1) was extracted and deconvolved with a canonical gamma function (to remove the effect of the hemodynamic response). This modified time series was then compared with the fMRI data. The same mean removal and ventricle baseline correction methods were used as in the sequence learning analysis. The same preprocessing was also used (grand mean and ventricle normalization) as in the sequence learning study. The beta values for each subject were converted to z scores for comparison across subjects. A paired t-test across all subjects tested for differences between regions on interest across subjects for each voxel. Voxels with a P < 0.05 from this group analysis were reported in the form of a t-map overlaid on a single subject's high resolution anatomical scan. To determine the direction of the statistically significant differences between the early (1st exponential) and late (2nd exponential) sequence learning periods, conjunction maps (using step functions to produce binary masks) were created. Due to the computational demands of the seed voxel cross-correlation method, this study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health. (http://biowulf.nih.gov).

RESULTS

Behavioral results: subjects learned the novel graphomotor trajectories

Figure 3 shows the average Njerk for the 30 character iterations that occurred during the fMRI scanning. Friedman's nonparametric ANOVA testing for significant changes across all character drawing iterations was significant (P = 2.5045e−06, see Table 1). The Tukey's honestly different criterion post hoc analysis of the difference in Njerk between all drawing iterations indicated a significant difference between the first character drawing iteration and iterations 20 and 22–25 (P < 0.05). All other pairings of the iterations were not significantly different. The difference in performance between the first character and the 20th and 22nd through 25th character iterations indicates that the subjects learned aspects of the graphomotor trajectories within this time period. This improvement in task performance was important in that it confirmed both that (on average) sequence learning had occurred and that short-term learning occurred during the functional neuroimaging scan period. Njerk values for character iterations 26–30 rose above the lowest level found between iterations 20–25, but the differences were not significant and may reflect attentional shifts from the task.

Table 1.

Friedman's ANOVA for normalized jerk

Source	SS	df	MS	χ2	Prob > χ2
Columns	6021.5	29	207.638	77.7	2.50447e−06
Error	20948.5	319	65.669
Total	26970.0	359

Analysis of variance for the change in average normalized jerk scores across the sequence learning period.

SS, sum of squares; MS, mean squares.

Movement speed increased significantly during sequence learning (P = 0.0028, see Table 2) with significant differences between trials 1 and 25, using Tukey's honestly significant difference criterion (P < 0.05). This provides additional evidence that the subjects learned the graphomotor sequences during the scan period.

Table 2.

Friedman's ANOVA for movement speed

Source	SS	df	MS	χ2	Prob > χ2
Columns	4.2277e+03	29	145.7816	54.5505	0.0028
Error	2.2742e+04	319	71.2926
Total	2.6970e+04	359

Analysis of variance for the change in average movement time across the sequence learning period.

A double exponential curve [fit = 22734 * exp(−0.75964 * x) +29010 * exp(-0.016749*x); x = character iterations] best explained the Njerk data (corrected r² = 0.66) and suggested that there were two processes involved in graphomotor sequence learning as reported previously in the case of implicit learning of spatial sequences (of center-out hand movements) by trial and error (Ghilardi et al. 2000). The first was an early, fast process (1st exponential period—“early”); and the second, a slower process (2nd exponential period—“late”). The timing of the transition from the first exponential to the second exponential was therefore used to segment the fMRI data into two periods (fast/early and slow/later learning) for further analysis (see methods).

In the early (first exponential) period (the fast phase of graphomotor sequence learning), the steepest decreases in Njerk (see Fig. 3) occurred. In this time period (duration of ∼3 min and 50 s that comprised 7 characters), the subjects were making the least smooth characters (as measured by Njerk). The second exponential period (late learning) data are indicative of a slower, more gradual (or progressive) learning process. The time frame of the second exponential period was from ∼3 min, 50 s into the task (after the 1st exponential period) to the end of the scanning period, 9 min and 54 s later (timing varied per subject due to randomized jitter to maximize signal detection). During late learning, the subjects' average performance in drawing the novel characters improved gradually until around the 20th character iteration (see Fig. 3). From the 20th character iteration until the end of the scan period, the subjects' performance was at its highest level.

Neuroimaging results: global analysis

To ascertain if any patterns of neural activation were related to the entire learning period, apart from the exponential analysis and the subdivision of the second exponential period, an analysis of the entire learning period was performed without segmentation. Because the global analysis identified voxels that were significantly related to the double exponential Njerk learning curve from the behavioral task, the areas depicted as positive were those regions that covaried significantly in the same direction as learning measured by Njerk (decreased as Njerk decreased). Regions with significant negative changes were those that increased in BOLD signal as learning (Njerk) decreased. The percent signal change values of the global analysis cannot be related directly to the analyses of the first and second exponential period or the analysis of the three time bins of the second exponential period as a different predicted HRF was employed.

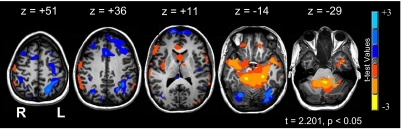
Figure 4 shows the changes in BOLD signal of ROIs during sequence learning, relative to the Njerk learning curve (see Table 3 for percent signal change and levels of significance for selected regions of interest). The dorsal visual stream (SPL, lateralized in magnitude to the left), covaried positively with the Njerk learning curve. Bilateral dorsolateral premotor cortex (dlPMC), and M1 hand area were also significantly positively related to learning. The bilateral frontal pole (FP) and bilateral visual area visual area 5/medial temporal lobe (V5/MT) were positively related to the Njerk learning curve. Medial anterior cingulate cortex (ACC) and bilateral head of the caudate nucleus (hCN) were significantly negatively related to the Njerk learning curve. Right anterior vermis (aVER) and the right dentate nucleus (DN) were also significantly negatively related to the Njerk learning curve during sequence learning. Remarkably, basal ganglia involvement did not reached statistical significance in the global analysis attesting to their potential transient role in the learning.

Fig. 4.

Learning period without segmentation. Significant positive t-test values (dark blue to light) are those areas that decreased as sequence learning progressed (started highly active; became less active). Significant negative t-test values (orange to yellow) are those areas that increased as sequence learning progressed (from less active to more active). See Table 3 for percent signal change and significance for selected regions of interest.

Table 3.

Selected regions of interest for the entire learning period

LEFT			MEDIAL			RIGHT
Region of Interest	Talairach Location	Signal Change	Region of Interest	Talairach Location	Signal Change	Region of Interest	Talairach Location	Signal Change
FP	[11 −60 2]	5.6282***	dACC	[−4 −20 36]	3.4971**	FP	[−6 −64 2]	2.7404*
PFC	[25 −35 36]	3.4690**	vACC	[0 −33 11]	−2.8287*	PFC	[−6 −35 36]	2.2940*
dlPFC	[24 −23 51]	2.3046*	pSMA	[5 −9 57]	—	dlPFC	[−32 −19 51]	4.1424**
dlPMC	[26 5 50]	0.2530*				dlPMC	[−24 4 50]	—
M1	[43 13 50]	—				MI	[−43 13 50]	—
SPL	[18 62 50]	3.3689**				SPL	[−30 54 50]	2.2468*
FCS LING	[33 81 −14]	3.2466**				FUS LING	[−31 82 −14]	3.1359**
MT/VS	[40 68 2]	2.2273*				MT/V5	[−46 64 2]	—
hCN	[7 −15 2]	−3.5063**				hCN	[−7 −15 2]	—
aPUT	[30 −4 2]	—				aPUT	[−21 −5 2]	—
TH	[8 6 10]	−2.3486*				TH	[−8 6 10]	—
aVER	[8 35 −18]	−3.0715*				aVER	[−8 35 −18]	−3.5034**
						DN	[−25 45 −29]	−3.6031**

—, P > 0.05;

^*P < 0.05;

^**P < 0.01;

^***P < 0.001;

****, P < 0.0001.

All coordinates are in Talairach space. The analysis of the entire learning period. Each voxel was compared with the average jerk (Njerk) learning curve from the kinematic analysis. Significant positive values (in bold) are those areas that fit this curve, being high early and decreasing in a double exponential manner as graphomotor sequence learning progressed. Significant negative values were the inverse: low early, with progressively higher activity later in learning.

FP, frontal pole; PFC, prefrontal cortex; dlPFC, dorsolateral PFC; dlPMC, dorsolateral premotor cortex; M1, primary motor cortex; SPL, superior parietal lobule; FUS/LING, fusiform gyrus/lingual gyrus; MT/V5, medial temporal lobe/visual area 5; hCN, head of the caudate nucleus; a PUT, anterior putamen; TH, thalamus; aVER, anterior vermis; dACC and vACC, dorsal and ventral anterior cingulate cortex; pSMA, presupplementary motor cortex; DN, deatate nucleus.

Early, fast learning period

The neuroimaging data for the two hypothesized learning periods are presented in Fig. 5. In the first, early period, significant activations were seen in bilateral dorsal visual stream areas, lateralized to the left (SPL, see Table 4A for percent signal change and level of significance for all ROIs) based on spatial extent of activation, as well as in bilateral ventral visual stream areas (fusiform/lingual gyri, FUS/LING). Medial area V5/MT was also active bilaterally in early learning as were the FPs bilaterally. The dorsal lateral premotor cortices (dlPMC) were also activated in both hemispheres. In contrast, medial ACC was significantly less active than baseline in this period. Subcortically, the aVER was significantly less active than baseline as was the right DN.

Fig. 5.

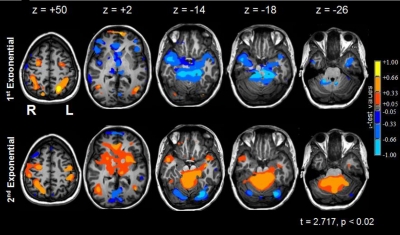
Changes in neural activity during sequence learning. Column 1 (z = +50): the significant activations during learning occurred within the left dorsal visual stream (i.e., left superior parietal lobule, L SPL) were confined to the 1st exponential period; bilateral dorsolateral premotor cortices (dlPMC) were active in both periods; primary motor cortex—hand area (L M1) was primarily active during the second exponential period. Column 2 (z = +2): the left medial head of the caudate nucleus (hCN) was below baseline in early learning and above baseline in late sequence learning; the bilateral frontal poles (FPs) were active in early learning and were below baseline in late sequence learning. Bilateral visual area 5/middle temporal areas (V5/MT) were active in both periods. Column 3 (z = −14): bilateral fusiform and lingual gyri (FUS/LING) were active in early learning and were below baseline in late sequence learning. Column 4 (z = −18): bilateral anterior vermis (aVER) was less active than baseline during early learning and more active than baseline in the 2nd exponential period. Column 5 (z = −26): the right dentate nucleus (DN) was less active in the 1st exponential period, relative to baseline, and was more active than baseline during late learning. See Table 4A for the percent signal changes and significance levels of selected regions of interest.

Table 4.

Percent signal changes for selected regions of interest

						B
	Talairach Location			A		Second Exponential
Region of Interest	R	A	I	First Exponential	Second Exponential	Bin 2A	Bin 2B	Bin 2C
Left
FP	11	−60	2	0.3679***	−0.1388*	—	−0.3184*	−0.3335**
PFC	25	−35	36	—	—	—	—	—
dlPFC	24	−23	51	—	—	—	—	−0.1789*
dlPMC	26	5	50	0.1967**	0.1529*	0.1662*	—	—
M1	43	13	50	—	0.1888**	0.2212**	0.2785*	—
SPL	18	62	50	0.4932***	—	—	—	—
FUS/LING	33	81	−14	0.2161*	−0.1334**	−0.1246*	−0.1886*	—
MT/V5	40	68	2	0.2193***	0.0974*	0.1685*	—	—
hCN	7	−15	2	−0.2123**	0.0798**	0.0623*	0.1773**	0.1483*
aPUT	30	−4	2	—	0.1431***	0.1440**	0.1858**	0.1765*
TH	8	6	10	−0.1579**	—	—	0.0869*	—
aVER	8	35	−18	−0.5063*	0.1888***	—	0.3109**	0.5409**
Medial
dACC	−4	−20	36	0.1414*	—	—	—	−0.1549*
vACC	0	−33	11	−0.1667*	0.0970*	—	0.2071*	0.1742*
pSMA	5	−9	57	—	—	—	—	—
Right
FP	−6	64	2	0.3209*	−0.2039**	—	−0.3236*	−0.3818*
PFC	−6	−35	36	—	—	—	—	—
dlPFC	−32	−19	51	—	−0.0968**	—	—	—
dlPMC	−24	4	50	0.2075**	0.1464*	0.1689**	—	—
M1	−43	13	50	—	—	—	—	—
SPL	−30	54	50	0.1993***	0.1489**	0.1486*	0.1761*	—
FUS/LING	−31	82	−14	0.1304**	—	—	—	—
MT/V5	−46	64	2	0.1694**	0.1435***	0.1488*	0.1681*	—
hCN	−7	−15	2	−0.1813*	0.0630*	—	0.1583*	—
aPUT	−21	−5	2	−0.1451*	0.1336***	0.1194*	0.1865**	0.2049***
TH	−8	6	10	—	—	0.0613*	—	—
aVER	−8	35	−18	−0.4863**	0.2014****	—	0.3403**	0.6211****
DN	−25	45	−29	−0.2806**	0.1701***	—	0.0266**	0.3741***

Column A, percent signal change for the first and second exponential learning periods. Column B, the subdivision of the second exponential period into three bins (bin 2A, bin 2B, and bin 2C) to examine the temporal dynamics of graphomotor sequence learning. All coordinates are in RAI format; numbers in bold are positive. —, P > 0.05;

^*P < 0.05;

^**P < 0.01;

^***P < 0.001;

^****P < 0.0001.

Slow, late learning period

In this hypothesized period, the left SPL was statistically indistinguishable from baseline as was the left FUS/LING region (see Fig. 5 and Table 4A). The FP was now significantly deactivated, relative to baseline, in the second exponential period. The ventral lateral PMC (vlPMC) was activated bilaterally in the late learning period. The left M1–hand area was also active during late sequence learning as were the medial ACC. Basal ganglia and cerebellar regions—specifically, left and right aPUT, thalamus, aVER, and DN (lateralized to the right)—all became significantly active during this learning phase (the 2nd exponential period).

A direct contrast between the two learning periods showed that the activity in the left SPL, and, bilaterally, in V5/MT, bilateral FUS/LING gyri, and FP was significantly higher in early as compared with late learning. In contrast, left and right PUT and hCN, ventral ACC, aVER, and right DN were all significantly more active during late as compared with early learning. A significance threshold of P < 0.02 was chosen for display purposes (see Fig. 5).

Successive recruitment of basal ganglia and cerebellar networks during the slow learning period

In time bin 2A of learning, there was a marked change in participating networks from the early fast learning period (see Fig. 6 and Table 4B). In the SPL, activation became lateralized to the right (Fig. 6A, bin 2A), whereas the basal ganglia (aPUT bilaterally; right head of caudate nucleus -hCN) and cerebellar (medial VER) regions became significantly active for the first time. The FP was no longer significantly active in bin 2A, whereas ACC became significantly active as did the M1 hand area in both hemispheres. Area MT/V5 bilaterally remained significantly active in bin 2A.

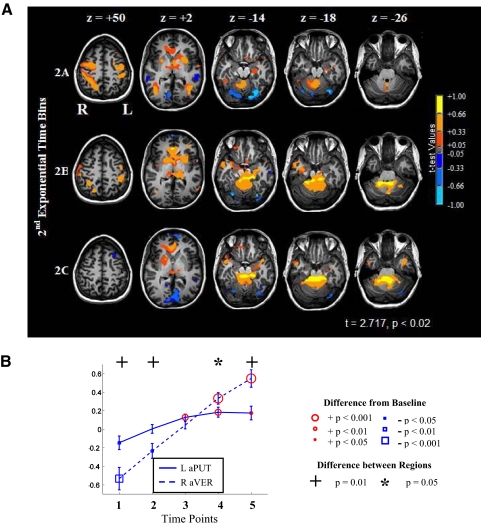
Fig. 6.

Temporal dynamics of 2nd exponential period. A: patterns of neural activity. Column 1 (z = +50): note changes in the left vlPMC and M1. Column 2 (z = +2): progression of left anterior putamen (aPUT) and bilateral V5/MT activity during sequence learning. Column 3 (z = −14): bilateral FUS/LING were significantly deactivated in bin 2A but became progressively less deactivated in bins 2B and 2C. Column 4 (z = −18): right aVER activation patterns as sequence learning progressed. Column 5 (z = −26): changes in right DN activity during sequence learning. B: changes in blood-oxygen-level-dependent (BOLD) signal during sequence learning for the left aPUT and the right aVER. Note the divergent trajectories at time-points four and five. See Table 4B for the percent signal changes and significance levels of selected regions of interest.

Cerebellar activation, especially in the region of the right DN and aVER, increased in spatial extent in bin 2B (see Fig. 6A, bin 2B). During this period of gradually increasing performance (increased smoothness measured by decreasing Njerk scores), the ACC remained significantly active as did the left M1 hand area. Also during bin 2B, activity in the striatum (aPUT and hCN) increased in extent of activation on the right side. Interestingly, the FP became significantly deactivated in bin 2B. Activity in the dlPMC and vlPMC regions, FUS/LING, and area MT/V5 was no longer significant in bin 2B.

The activation in the right aVER increased from bin 2B to bin 2C, and the ACC activation persisted (see Fig. 6A, bin 2C), whereas the dorsal visual stream (SPL), ventral visual stream (FUS/LING), M1, premotor (dlPMC and vlPMC), and left aPUT were all not significant. The anterior basal ganglia activity was exclusively right lateralized at this threshold in bin 2C. The medial FP deactivations from bin 2B increased in spatial extent in bin 2C. Left dlPFC deactivation was also present in bin 2C.

The left medial PFC was significantly more active in bin 2A than in 2B. The ventral ACC, aVER, and right DN were more active in bin 2B than 2A. The left FP, left dlPFC, and left LING/FUS gyri were more active in bin 2B than 2C, whereas the right aVER was significantly more active in bin 2C than in 2B.

Figure 6B presents a comparison of the basal ganglia and cerebellum patterns of activity during the graphomotor learning. The aPUT became active earlier than the right aVER (time point 3) but peaked in participation at time point 4. In contrast, the aVER was subthreshold at time point 3 but became progressively activated at time points 4 and 5, peaking at the latter time point. The differences between the left aPUT and the right aVER were significant at time points 4 and 5 (paired t-test; P < 0.05, time point 4; P < 0.01, time point 5).

Functional connectivity analysis

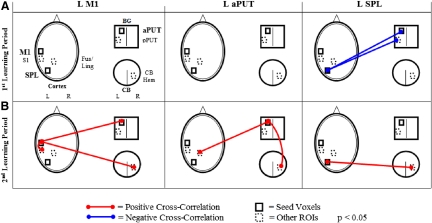
Figure 7 depicts the functional connectivity (cross-correlation) for each of the three selected seed voxels (left M1, left aPUT, and SPL; see methods for details) during the first (A) and second (B) learning periods (P < 0.05).

Fig. 7.

Seed voxel cross-correlation for selected regions of interest. Seed voxels chosen were: left M1 [43 13 50]; left aPUT [28 −5 3]; and left SPL [18 62 55]. A: cross-correlations during the 1st exponential period. Note that there were no correlations between L M1 and cortical, basal ganglia, or cerebellar regions during the 1st exponential period. There were negative correlations between the L SPL and both aPUT and posterior PUT (pPUT) in the 1st exponential period. B: cross-correlations during the 2nd exponential period. The negative cross-correlations from the 1st exponential period were not evident. L M1 was functionally connected to aPUT and to the right cerebellar hemisphere as well as to L S1. Interestingly, L aPUT was also functionally connected to the right cerebellar hemisphere, as well as to the L FUS/LING (ventral visual) areas.

In the early learning period, there were no correlations between left M1 and cortical, basal ganglia, or cerebellar regions. There were negative correlations between the left SPL and both aPUT and posterior PUT (pPUT) during this period.

In the late learning period, there was a shift in the pattern of functional connectivity between these selected regions. The left M1 became functionally connected with both basal ganglia (aPUT) and cerebellum (right cerebellar hemisphere, CB), as well as with left S1. Interestingly, the left aPUT became connected with ventral visual areas (left FUS/LING) and with the right cerebellum (right cerebellar hemisphere). Moreover, the left SPL had no significant functional connectivity with the left aPUT or pPUT but was positively connected with the right cerebellar hemisphere and with right CB.

DISCUSSION

We have identified two stages of short-term learning of a graphomotor sequence, namely, a fast, early learning stage characterized by a visuomotor network most likely involved in sensorimotor transformations, and a second, slower and prolonged learning stage that showed a successive recruitment of basal ganglia and cerebellar-cortical structures that may be involved in the encoding and retrieval of the handwriting sequences.

In the examination of the graphomotor sequence learning process, the statistical analysis of a selected kinematic measure of learning (Njerk) resulted in corroboration that learning had occurred during fMRI scanning. The Njerk allowed for normalization of the kinematic data for differences in handwriting speed and size during learning so that comparisons in the quality of movement could be made throughout the learning periods. The kinematic data also guided the division of the neuroimaging data into two segments, which were related to the first and second exponentials of a double exponential learning curve, which best characterized the kinematic data. The double exponential fit indicated that an early, fast learning process merged with a second, slower process. Double exponential fits have been reported in other visuomotor tasks that require adaptation learning (Contreras-Vidal and Buch 2003; Krakauer et al. 2000) and implicit learning of spatial sequences (Ghilardi et al. 2000) that may prove to be generalizable to other tasks including the graphomotor sequence learning task investigated in this paper. Examining the changes in BOLD activity over the time course of sequence learning has led to an abstract model of how the brain may encode graphomotor sequences.

Successive recruitment of cortical, basal ganglia and cerebellar structures during graphomotor sequence learning—early and late learning periods

Graphomotor sequence learning involved the interplay of numerous cortical and subcortical neural regions as the novel sequences were learned. The early learning period was associated with activation of the dorsal and ventral visual streams and the dorsal premotor cortex (Burnod et al. 1999; Caminiti and Johnson 1992; Caminiti et al. 1996, 1998, 1999; Lacquaniti et al. 1995), and it may reflect the tuning of sensorimotor transformations that map, for example, visuospatial signals into motor commands. The important role of the superior parietal lobule in this graphomotor sequence task is consonant with earlier studies involving graphomotor learning (Seitz et al. 1994, 1997).

In the second period of learning, the visual regions became less active, and an array of cortical and subcortical brain regions that may play a role in encoding were activated, comparable to the findings of the Floyer-Lea et al. and Muller et al. studies (Floyer-Lea and Matthews 2004; Muller et al. 2002). While the increased participation of the cerebellum might be indicative of increased eye movement as learning progressed, the concomitant increases in the fusiform gyrus (Dieterich et al. 2009) were not found as these regions became significantly deactivated during later sequence learning. Taken together, this suggests a shift from a predominantly visuomotor emphasis in the first learning phase to a motor encoding emphasis during the second, slower phase of sequence learning. This shift was also evident in the seed voxel cross-correlations, where the left primary motor cortex was uncoupled from PUT and right cerebellar hemisphere in the first period but coupled with both in the second exponential period, while significant correlations with visual areas persisted throughout both learning periods.

The persistent role of the visual areas may be related to the ventral stream regions participation in processing the Chinese word characters as visual objects; while the dorsal stream may contribute to the visually guided movements involved in drawing the characters. It was interesting that the SPL activity was initially lateralized to the left in the first exponential period, and then the SPL activation decreased in the left hemisphere, while increasing on the right side. This shift in dorsal stream lateralization as learning progressed may be related to bimanual transfer of learning or to progressive refinement of spatial representations of the movements needed in drawing the sequences.

Surprisingly, subcortical deactivation (of associative basal ganglia and cerebellum) occurred during the early phase of sequence learning. The BOLD activation patterns were supported by the lack of functional connections in the first exponential period. This novel finding suggests that during the visuomotor mapping process, when the subjects were making the most errors, the neural regions that are expected to be involved in encoding and refining the representations for the novel sequences may have been functionally “off-line.” Taken together, these findings suggest a specific neural recruitment sequence for the encoding of novel graphomotor sequences: mapping the sequence first (e.g., tuning of visuomotor transformations for movement), then encoding and refining the internal graphomotor representations for the sequence of movements.

Bridging the two learning periods

The dorsal lateral premotor cortex was active in both of the two learning processes. This dual participation (in periods that should be related to visuomotor mapping as well as encoding/refining of the internal representations for the sequence motor plans) may indicate its function as a bridge between the two processes. Rich anatomical projections to both the posterior parietal cortex and the basal ganglia places the dPMC in an ideal position to play such a role, as the kinematic motor plans are transformed into dynamic plans, to be relayed through the M1 to the periphery (Wise et al. 1997). This finding is consistent with prior studies relating the dPMC with “bottom-up” visuomotor planning (Abe and Hanakawa 2009). As sequence learning progresses, the movements organized by the dlPMC move from being visually guided initially to depending less on visual stimuli and more on proprioceptive feedback later in learning (Hikosaka et al. 1998, 1999, 2002; Sakai et al. 2000).

Interestingly, the dACC cortex's role in motor sequence learning was also only evident when the entire learning period was examined without segmentation. dACC was more active when subjects had high error levels (early in learning) and became less active as performance improved. This finding is consistent with prior research on the ACC's role in error detection (Badgaiyan and Posner 1998; Carter et al. 1998, 1999; van Veen and Carter 2002a,b).

Encoding and refining the graphomotor representations of the novel sequence

Within the second learning stage, there was a difference between the basal ganglia and cerebellar patterns of activity. Significant activation of the left aPUT began earlier than in the right aVER and diverged from the cerebellum as the subjects neared peak performance. While often related to postural control, imaging studies have also found aVER to be activated during the learning of novel motor sequences (Jueptner et al. 1997; Rauch et al. 1995; van Mier and Petersen 2006). While the aPUT and aVER are overlapping processes, the relative timing of the activation of the basal ganglia and cerebellum indicate that encoding began prior to refining and that refining appeared to continue after the encoding process had leveled-off. When the subjects were at their highest level of performance (bin 2C), activity in the left basal ganglia asymptoted at the same level as in bin 2B, while activity in the medial cerebellum continued to increase, yielding a significant difference in activation level between the two regions in bin 2B.

This suggests that the basal ganglia and cerebellum may be participating in different but complementary processes or at different scales, perhaps related to encoding the novel characters using knowledge of results (aPUT, HCN) and the refinement of the motor plans for the individual line pairs (aVER). It is interesting that the left aPUT and the right aVER were functionally connected throughout the second exponential period, suggesting ongoing coordination between basal ganglia and cerebellum during the encoding and refinement periods. Although the early cerebellar activity seen in the Seitz et al. study was not evident, the activation patterns of the left aPUT was comparable to the Seitz et al.'s studies of graphomotor sequence learning.

In summary, we were able to capture dynamic patterns of neural activity on-line during graphomotor sequence learning using fMRI. However, it could be argued that the generalizability of the results of the current study may be limited by the use of movement smoothness (Njerk) as the kinematic measure of learning. However, the Njerk scores were necessary to accurately measure learning across graphomotor production of varying speed and size. Moreover, as only straight strokes were required, potential effects of coordination complexity (e.g., due to curved or looping characters) were minimized. Individual differences in the size and speed of the drawing movements were not examined in the current study and may account for variations in neural activity during sequence learning. Similarly, the role of attention was not systematically addressed in the current study, but was controlled by the use of complex visual baseline stimuli (the feedback screen).

Conclusions

Graphomotor sequence learning involves multiple, interacting networks of neural regions that contribute successively to the formation of multiple representations for graphomotor trajectories (Seitz et al. 1994, 1997). First, the novel sequence of movements is initially mapped to form an internal representation of the sequence, involving cortical processes (including the dorsal and ventral visual streams). This representation may be then progressively refined and recoded subcortically (in the basal ganglia and the cerebellum) as performance improves. Premotor cortical regions play a role during the early, fast visuomotor mapping, and the later, slower encoding and refinement processes. Interestingly, the basal ganglia appeared to be recruited transiently early in the slower stage of graphomotor sequence learning, whereas the cerebellar network appeared to be recruited progressively.

DISCLOSURES

No conflicts of interest are declared by the authors.