CHARMM General Force Field (CGenFF): A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields

Abstract

The widely used CHARMM additive all-atom force field includes parameters for proteins, nucleic acids, lipids and carbohydrates. In the present paper an extension of the CHARMM force field to drug-like molecules is presented. The resulting CHARMM General Force Field (CGenFF) covers a wide range of chemical groups present in biomolecules and drug-like molecules, including a large number of heterocyclic scaffolds. The parametrization philosophy behind the force field focuses on quality at the expense of transferability, with the implementation concentrating on an extensible force field. Statistics related to the quality of the parametrization with a focus on experimental validation are presented. Additionally, the parametrization procedure, described fully in the present paper in the context of the model systems, pyrrolidine, and 3-phenoxymethylpyrrolidine will allow users to readily extend the force field to chemical groups that are not explicitly covered in the force field as well as add functional groups to and link together molecules already available in the force field. CGenFF thus makes it possible to perform “all-CHARMM” simulations on drug-target interactions thereby extending the utility of CHARMM force fields to medicinally relevant systems.

Introduction

Background

Computational biochemistry and biophysics is an ever growing field that is being applied to a wide range of heterogeneous systems of increasing size and complexity. Recent examples include simulations of the nucleosome,¹ ion channels² and the ribosome.³ While greater computational resources, including massively parallel architectures, and efficient codes such as NAMD⁴ and Desmond⁵ have made important contributions to these advances, the quality of the force fields that act as the framework of computational biochemistry and biophysics have improved to the point that stable simulations of these systems are possible. Towards this goal the CHARMM additive, all-atom force field⁶ has made an important contribution. Apart from proteins,⁷ it supports nucleic acids^8–10 and lipids,^11,12 and has limited support for carbohydrates,^13–15 with a more complete carbohydrate extension in preparation,¹⁶ allowing simulations on all commonly encountered motifs in biological systems. However, its coverage of the wide range of chemical space required for the field of computational medicinal chemistry is limited.

To date, a number of force fields with wide coverage of drug-like molecules are available. Here, we will limit our discussion to force fields that were parametrized to reproduce condensed phase properties. Indeed, as classical additive force fields do not account for polarizability, a given additive force field will only perform well in a given dielectric medium. As a special case, Allinger’s most recent MM4 force field accurately predicts gas-phase conformational energetics of organic molecules and includes terms that account for polarizability in an approximate way.¹⁷ Nevertheless, this force field has not been evaluated in a condensed phase, high-dielectric medium, and may be assumed to be unsuitable for condensed phase studies of, for example, drug-protein interactions. The Merck Molecular Force Field (MMFF94), on the other hand, was developed with the explicit goal of performing MD simulations on pharmaceutically relevant systems in the condensed phase. Indeed, it was originally conceived as “a combined organic/protein force field that is equally applicable to proteins and other systems of biological significance”.¹⁸ One drawback of this approach is that the general nature of the force field inherently compromises its accuracy in representing classes of molecules in a well-defined chemical space, such as proteins. To overcome this problem, efforts were started to create general force fields that are meant to be used with existing, highly optimized and tested biomolecular force fields. As a result of this effort, Amber^19,20 now includes the General Amber Force Field (GAFF)²¹ and the Antechamber toolkit,²² which allow the user to generate an Amber force field model for an arbitrary input molecule. Another example is OPLS-AA, whose optimizations emphasized condensed phase properties of small molecules and has been extended to cover a diverse set of small molecule model compounds.^23,24 However, none of these force fields is expected to be applicable in combination with the CHARMM force field, as interactions between molecules are dominated by a delicate balance of parameters. Indeed, while it is tempting to combine a biomolecular force field (like CHARMM) for a system’s biological part with an organic force field (such as MMFF94) for its drug-like part, it is unlikely that this will yield properly balanced intermolecular interactions, because the nonbonded parameters are developed using different strategies for different force fields.²⁵ To cure this problem, the CHARMM General Force Field (CGenFF) was created. CGenFF is an organic force field explicitly aimed at simulating drug-like molecules in a biological environment represented by the CHARMM additive biomolecular force fields. Consequently, CGenFF uses the same class I potential energy function as the other CHARMM force fields,⁶ and more generally, all the conventions and recommendations for usage of the biomolecular CHARMM force fields apply to CGenFF as well. The form of the CHARMM potential energy function used to calculate the energy, V(r), were r represents the Cartesian coordinates of the system, is shown in equation 1.

$$\begin{array}{l}\text{Intramolecular}(\text{internal},\text{bonded}\text{terms})\\ \sum _{\mathit{bonds}}{K}_b{(b-b_0)}^2+\sum _{\mathit{angles}}{K}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{\mathit{dihedrals}}{K}_{\phi }(1+cos(n\phi -\delta ))+\sum _{\begin{array}{l}\mathit{improper}\\ \mathit{dihedrals}\end{array}}K\varphi {(\varphi -{\varphi }_0)}^2+\sum _{\mathit{Urey}-\mathit{Bradley}}{K}_{UB}{\left(r_{1,3}-r_{1,3;0}\right)}^2\\ \text{Intermolecular}(\text{external},\text{nonbonded}\text{terms})\\ \sum _{\mathit{nonbonded}}\frac{q_i{q}_j}{4\pi D{r}_{ij}}+{\epsilon }_{ij}\left[{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^6\right]\end{array}$$ (1)

The intramolecular portion of the potential energy function includes terms for the bonds, valence angles, torsion or dihedral angles, improper dihedral angles and a Urey-Bradley 1,3-term, where b_o, θ_o, ψ_o and r_1,3,o are the bond, angle, improper and Urey-Bradley equilibrium terms, respectively, n and δ are the dihedral multiplicity and phase and the K’s are the respective force constants. The intermolecular terms include electrostatic and van der Waals (vdW) interactions, where q_i and q_j is the partial atomic charge of atom i and j, respectively, ε_ij is the well depth, R_min,ij is the radius in the Lennard-Jones (LJ) 6–12 term used to treat the vdW interactions, and r_ij is the distance between i and j. In addition, the energy function in equation 1 has been extended to include a 2D dihedral energy correction map, referred to as CMAP, which has been used to improve the treatment of the conformational properties of the φ, ψ terms in the peptide backbone,^26,27 though it may be applied to other systems. More details of the CHARMM potential energy function may be obtained from reference ²⁵.

Parametrization Philosophy

The main challenge in creating a general force field is to cover enough of the vast chemical space occupied by drug-like molecules to make the model of utility. To attain this, a systematic optimization protocol is required that is 1) of a level of accuracy appropriate for the proposed application of the force field, 2) fast enough to parametrize large numbers of model compounds and 3) simple enough to enable CHARMM users to easily extend the force field to chemical groups of their interest. For these reasons, the standard CHARMM optimization procedure for biomolecular force fields has been simplified for the purpose of creating CGenFF, with a stronger emphasis on quantum mechanical (QM) calculations than with the biomolecular CHARMM force fields. Nevertheless, those simplifications are designed to maintain the consistency of the force field required for computational studies of heterogeneous systems. Indeed, improvements in computer power and QM methodology allow for QM calculations of a sufficiently high level of theory to attain the required accuracy to be performed in a timely fashion.

In order to build a successful force field for drug-like molecules, it is essential to select appropriate model compounds. For CGenFF, two classes of model compounds were targeted. The first class comprises a wide range of heterocycles. As this class of compounds acts as the scaffold for the majority of pharmaceuticals, a comprehensive set of heterocycles would act as building blocks for a diverse range of compounds. Accordingly, emphasis was placed on accurate optimization of the intermolecular parameters in these molecules as well as reproduction of target geometries, vibrational spectra and conformational properties. The second class consists of simple functional groups. A wide variety of chemical groups occur in drug-like compounds, fulfilling roles that range from linking different parts of the molecule to being substituents on aromatic and heterocyclic groups, often in orientations that involve direct interactions with the biomacromolecular binding partner. Accordingly, a large number of functional groups were explicitly parametrized when building CGenFF.

Given the availability of a wide range of heterocycles and functional groups, it is anticipated that eventually the majority of effort to extend the force field will involve linking those groups together to create the molecule of interest. This procedure requires the selection of the appropriate fragments from the palette of molecules in CGenFF, applying standard approaches for covalently linking those rings and functional groups, followed by evaluation of the model. The force field includes a wide range of default internal parameters for many of the links, such that once the user creates the topology for their molecule, they will generally be able to perform molecular mechanics calculations. However, it is strongly suggested that the user perform a series of well-defined QM calculations to test the conformational properties of the linkers between the rings comprising their molecule, compare the molecular mechanical (MM) and QM conformational properties and perform optimization of the appropriate (typically dihedral) parameters as described below. Accordingly, this manuscript focuses on presentation of the parameter optimization methodology, a detailed description of the methods required to extend the force field, and validation of the obtained model for ring systems and functional groups. Efforts to automate many of these tasks are in progress and will be presented in future works.

Methodology

Principles

Class I additive force fields (see equation 1), which do not explicitly treat electronic polarization, have been designed for use in polar environments typically found in proteins and in solution. To achieve this, the use of experimental target data, supplemented by QM data, was strongly emphasized during optimization of the nonbonded parameters in the biomolecular CHARMM force fields, in order to ensure physical behavior in the bulk phase. However, reproducing experimental data requires molecular dynamics (MD) simulations, which have to be set up carefully and repeated multiple times in the course of the parametrization, making the usage of experimental target data non-trivial and time-consuming. In addition, for many functional groups that may occur in drug-like molecules experimental data may not be available. Due to this lack of data, and since one of the main goals of CGenFF is easy and fast extensibility, a slightly different philosophy was adapted, with more emphasis on QM results as target data for parameter optimization. This is possible due to the wide range of functionalities already available whose parameters were optimized based largely on experimental data, along with the establishment of empirical scaling factors that can be applied to QM data in order to make them relevant for the bulk phase.

The only cases where experimental data would be required are situations where novel atom types are present for which LJ parameters are not already available in CGenFF. These cases would require optimization of the LJ parameters, supplemented with Hartree-Fock (HF) model compound-water minimum interaction energies and distances (see step 2.a under “Generation of target data for parameter validation and optimization” and step 1 under “Parametrization procedure”), based on the reproduction of bulk phase properties, typically pure solvent molecular volumes and heats of vaporization or crystal lattice parameters and heats of sublimation. Descriptions of the optimization protocol have been published previously.^7,9,25 However, it should be noted that CGenFF has been designed to cover the majority of atom types in pharmaceutical compounds, such that optimization of LJ parameters is typically not required.

The remainder of this section includes 1) the procedure to add new model compounds and chemical groups to the force field, 2) the procedure for generating the QM target data, and 3) the procedure for application of the QM information to parametrize new molecules. To put these procedures in better context, example systems including pyrollidine, the addition of substituents to pyrollidine and the development of a linker between pyrollidine and benzene are presented.

Addition of model compounds

Model compounds are added in the context of a hierarchical and extensible force field. Accordingly, step one of extending CGenFF involves identifying available compounds that are chemically similar to the compound of interest. These available compounds are then used as the starting point to create an initial topology entry; information from the available compounds in CGenFF should be used to select the appropriate atom types and initial estimates of the partial atomic charges. At this stage the molecule, along with its bonded and nonbonded lists, can be generated in CHARMM,^28,29 which will return a list of missing bonded parameters as an error message. These parameters may be either 1) treated with wildcards or 2) explicitly added to the force field via their inclusion in the parameter file. In case 1, energies as well as the full array of calculations available in CHARMM may readily be performed; however, it is recommended that the user perform validation calculations to determine that the parameters are yielding satisfactory geometries and conformational energies. This involves performing the appropriate QM calculations followed by the analogous MM calculations and checking that the target properties are adequately reproduced. In case 2 the user would undertake the parameter optimization procedure on only the new parameters required for that molecule. This includes the QM calculations, followed by the analogous MM calculations and parameter optimization to minimize the difference between the MM and QM data (see below). It should be emphasized that in the context of a drug optimization project these procedures typically need to be performed only once on the parent compound as the addition of various functional groups, as required to create a congeneric series, may be performed without additional parameter optimization.

Addition of functional groups to parent compounds/linking rings

Following the assignment of parameters and their optimization for the new parent molecule, standard functional groups such as acids, amines, and alkyl moieties, may readily be added. The same approach is applicable both to adding functional groups to available compounds in CGenFF and to linking ring systems to create more complex chemical species. The first step of this procedure consists of removing hydrogen atoms from the heavy (ie. non-hydrogen) atoms between which the new covalent bond will be created. Next, taking advantage of the modular nature of the distribution of charges in CHARMM, the charges on those hydrogens are summed into their original parent heavy atoms, thereby preserving the integer charge of the molecule. In the case of adding functional groups to an existing molecule, typically, no additional parameters are required and the molecule is ready for study. However, if new parameters are required, which is often the case when more complex functional groups or linkers are being added, it will be necessary to assign wildcard or add explicit parameters followed by the appropriate level of validation and optimization.

Generation of target data for parameter validation and optimization

Central to the development of the CHARMM additive force fields was the use of a consistent optimization protocol, especially with the nonbonded parameters. To maintain this consistency, it is necessary to generate the appropriate target data. As discussed above, all the target data required for CGenFF extensions is obtained from QM calculations, with the exception of cases where explicit optimization of LJ parameters is required. Details of target data generation follow.

1. Internal parameters: Target data for the internal or bonded parameters include geometries, vibrational spectra and conformational energies. While not mutually exclusive, these may be partitioned into three aspects.

   1. Bond, valence angle, and Urey-Bradley equilibrium terms and the dihedral phase and multiplicity are based on geometries optimized at the MP2/6–31G(d) (MP2/6–31+G(d) in the case of anions) level. This level of theory has been shown to yield satisfactory agreement with experimental geometries for complex systems such as nucleic acid bases and sugars^9,30,31 while being computationally accessible.

   2. Bond, valence angle, Urey-Bradley, improper and torsion force constants are based on MP2/6–31G(d) vibrational spectra. The F matrix is scaled by a factor 0.89, which corresponds to scaling all frequencies by a factor 0.943,³² and a symbolic potential energy distribution (PED) analysis is performed in the “local internal valence coordinate” space that was first proposed by Pulay et al.³³ The PED analysis may be performed using the MOLVIB³⁴ module in CHARMM.^28,29

   3. Force constants for torsions comprised of only non-hydrogen atoms are usually optimized based on (relaxed) one-dimensional potential energy scans performed at the MP2/6–31G(d) level. This level of theory has been shown to yield energy surfaces consistent with distributions of dihedrals in oligonucleotides^9,30,31. However, for systems in which dispersion dominates the conformation properties, like alkanes,³⁵ higher levels of theory may be required. Single point calculations at the RIMP2/cc-pVTZ level based on the MP2/6–31G(d) optimized geometries are computationally accessible and have been shown to adequately treat the conformational energetics of complex systems such as carbohydrates.³⁶

2. External or nonbonded parameters. Optimization of the nonbonded parameters for CGenFF is typically limited to the partial atomic charges, though in special cases LJ parameters may be optimized.

   1. Partial atomic charges: initial estimates for the partial atomic charges may be made by analogy, or alternatively, from the MP2/6–31G(d) Merz-Kollman charges.^37,38 This charge-fitting scheme provides a good initial guess for the CGenFF partial atomic charges, especially in the case of heterocycles. The QM dipole moment is also used as a guideline for the optimization of the partial charges of compounds with zero net charge. Typically, the force field should overestimate gas phase dipole moments by 20 to 50 percent in order to be relevant for the bulk phase, though the magnitude of the charges is based on reproduction of QM interactions with water, as described below.

      Final optimization of the charges is based on QM data for the model compounds interacting with water in a variety of orientations. For all hydrogen bond donors or acceptors, a complex is built containing an idealized hydrogen bond interaction between the model compound in the MP2/6–31G(d) optimized geometry and a water molecule in the TIP3P³⁹ geometry. If the functional group can form more hydrogen bonds (eg. an alcohol that can donate as well as accept a hydrogen bond), a separate complex for each possible hydrogen bond has to be constructed. The complexes are set up with an “ideal,” typically linear, geometry and then the interaction distance is optimized at the HF/6–31G(d) level, keeping all other degrees of freedom fixed. Finally, the optimized interaction distance is measured and the interaction energy is determined (without basis set-superposition error correction). For neutral polar model compounds, this interaction energy is multiplied by a factor 1.16 to be relevant for the bulk phase; no such scaling is performed for charged compounds. Similarly, the QM hydrogen bond length is offset by −0.2 Å shorter to yield parameters appropriate for the bulk phase.^40–43 It should be emphasized that the HF/6–31G(d) level of theory along with the scaling of energies and offsetting of distances are used to maintain compatibility with the remainder of the CHARMM additive force fields. While higher levels of QM theory may lead to more accurate hydrogen bond energies and geometries,^44,45 their use as target data will lead to an imbalance between the nonbond interactions of different parts of the force field, thereby compromising the treatment of the interactions of the drug-like molecule with the target macromolecule as well as the aqueous solvent.

   2. LJ parameters. In the rare cases that the optimization of LJ parameters is required, it is necessary to obtain experimental thermodynamic data (eg. pure solvent densities and heats of vaporization) as the target data. Obtaining sufficiently accurate dispersion interactions at QM level requires high levels of theory (ideally CCSD(T) or better) and large basis sets, which carry a substantial computational cost. Moreover, gas-phase dispersion interactions may not be readily applicable to the condensed phase. However, as a supplement to the experimental target data, QM data of rare gas-model compound interactions can be used to facilitate the optimization of the relative values of the LJ parameters.^46,47 Further discussion of the LJ parameter optimization, which has been presented elsewhere,^46–48 will not be included as part of the present manuscript.

Parametrization procedure

When working with a new compound, there will usually be a number of parameters that need to be validated and optimized. Initial values for the new parameters should be based on analogous parameters for similar chemical species already available in CGenFF; simple scripts can quickly identify such similar parameters (an example can be found in the supplementary material). Obtaining the best possible guess for each parameter is very important, as this maximizes the possibility that the parameters will be adequate such that optimization is not required. If optimization is required, the extent that a parameter will change is decreased when an appropriate initial guess is used, which in turn decreases the likelihood that more than one iteration through the parametrization procedure is required (see below).

Once initial guesses are assigned to the new parameters, the user should test those parameters to determine if optimization is required. This validation is based on performing the MM calculations listed below and comparing the results with the QM data listed above. If the level of agreement is deemed satisfactory, optimization is not required, otherwise optimization must be performed. Typically, even in situations were a relatively large number of new parameters are needed, only a subset of parameters will have to be optimized. While the decision on which parameters to optimize is done by the user based on information from the validation test, in most cases only a small number of torsion parameters, associated with only non-hydrogen atoms, will need to be optimized.

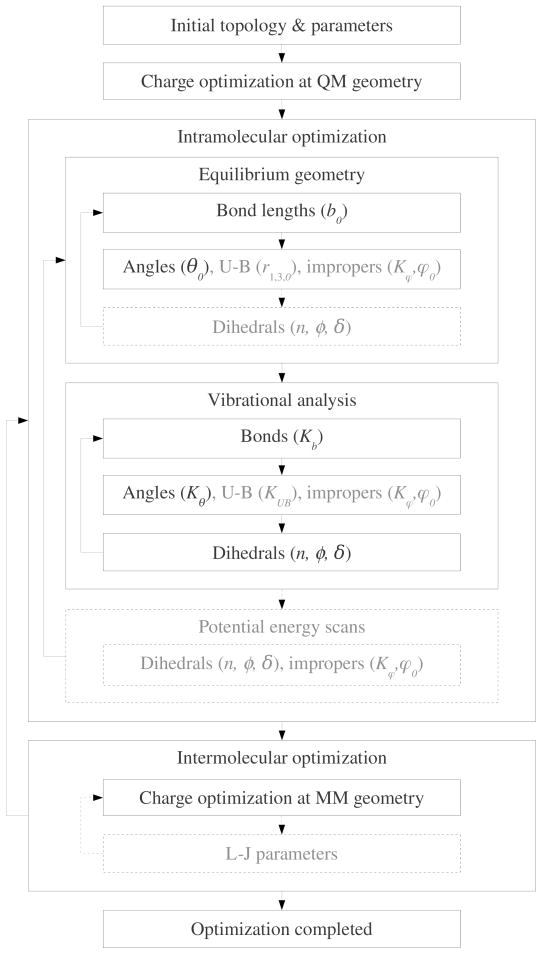
In principle as well as in practice, all parameters in a force field are interdependent and need to be optimized in a self-consistent fashion. Therefore, force field parametrization is an iterative procedure, as described previously.⁹ However, if the order in which different aspects of the force field are parametrized is chosen carefully, the parametrization usually converges in one or two iterations. Specifically, within the parametrization of a model compound, the different types of parameters are typically optimized consecutively as described in the following text and in Scheme 1.

Scheme 1.

1. Partial atomic charges: Optimization of the charges is initially performed with the model compound in its MP2/6–31G(d) optimized conformation. Once the initial charges have been determined and internal parameters optimized, the CHARMM minimized geometries are used (see step 5 below). Scaled HF/6–31(d) model compound-water interactions and the dipole moment are used as target data, with emphasis on the interactions with water. Ideally, the model compound-water interaction energies should be within 0.2 kcal/mol from the target interaction energies. For polar, neutral molecules, empirical results should overestimate the magnitude of the QM dipole moment by 20 to 50% and should reproduce its orientation. In the case of flexible molecules, more than one minimum energy conformation can be used to verify that the charges properly treat the different conformations. Several rules facilitate charge fitting. First, charges are adjusted to maintain integer charges on groups of atoms, such as rings. Aliphatic hydrogen atoms are always assigned a charge of +0.09, except when they are located on an aliphatic carbon atom directly adjacent to a positively charged nitrogen atom, where they are assigned a standard charge of +0.28. Similarly, aromatic C-H moieties not adjacent to a heteroatom are assigned charges of −0.115 and +0.115 on the C and the H atom, respectively.

2. Optimization of the equilibrium bond and valence angle parameters to reproduce the target geometries. In general, respective deviations of up to 0.03 Å and 3° from the QM geometry are acceptable.

3. Optimization of bond, valence angle, Urey-Bradley, improper and dihedral angle force constants, targeting the scaled MP2/6–31G(d) vibrational spectrum. Emphasis is placed on reproduction of both the frequencies and the PED (ie. contributions of internal degrees of freedom or “local internal valence coordinates” to the individual frequencies).³³ As the lower frequency modes generally represent larger deviations in the molecule’s geometry that occur during MD simulations, it is important to reproduce those modes more accurately. Also, in order to facilitate conformational sampling during an MD simulation, it is considered preferable to produce vibrational frequencies that are slightly lower than the target values, thereby making the molecule too flexible, rather than producing vibrational frequencies that are higher than the target values. Apart from these basic rules, it is difficult to objectively quantify the quality of the parametrization. A general target is to get the vibrational frequencies to be within, on average, 5% of their MP2 values. However, it is often difficult the unambiguously correlate the QM and MM frequencies due to multiple local internal valence coordinates contributing to each frequency. These contributions will often differ between the QM and MM spectra. In addition, the contribution of multiple local internal valence coordinates to a given frequency indicates that parameters for a number of internal coordinates contribute to that frequency. Thus, the assignment of a selected QM normal mode to an MM normal mode is often qualitative in nature, requiring an empirical decision by the user. To facilitate this decision making process, the user should follow the example frequency and PEDs in Table 4 and in the supplementary material. Finally, it should be noted that reproduction of stretching modes involving hydrogens is trivial and typically not important given the use of SHAKE⁴⁹ or related algorithms to constrain covalent bonds involving hydrogens during MD simulations.

4. Optimization of dihedral force constants using the MP2/6–31G(d) potential energy surfaces (PES). Torsion parameters are initially optimized based on the vibrational spectra in step 3 above with the final optimization of the terms associated with only non-hydrogen atoms optimized to reproduce QM PES; the only exception are dihedrals that involve a hydrogen donor such as that on an -OH or -SH moiety. This procedure may be performed manually, by systematically changing the force constants and phase for the different multiplicities in the dihedral expansion (ie. 1- through 6-fold terms).

   Alternatively, a Monte-Carlo Simulated Annealing (MCSA) protocol developed in our laboratory may be used to automatically optimize the targeted parameters.⁵⁰ In CHARMM it is possible to use any value for the phase;⁵¹ however, it is strongly suggested that values of 0 and 180° be used as the parameters are then appropriate for different stereoisomers associated with a given dihedral. When optimizing torsion parameters, it is often not possible to reproduce the entire energy surface. In such cases emphasis should be placed on accurately reproducing low energy regions and low barriers versus high-energy regions and barriers, as the latter will not be populated or crossed during a typical room temperature MD simulation.

5. In theory, the charges should be re-optimized upon completion of the internal parameters due to changes in the intramolecular geometry. However, in practice, the CGenFF equilibrium conformation at this point is usually so close to the MP2/6–31G(d) equilibrium conformation that little or no changes in the charges will occur. If the charges are re-optimized, then steps 2, 3 and 4 must be repeated, as the geometries, vibrations and PES are sensitive to the nonbond parameters. While this iterative procedure should be performed until convergence, given good initial guess parameters, at most one or two iterations should be necessary.

Table 4.

Pyrrolidine vibrational spectra for the scaled MP2 level and CGenFF. t5RNG and d5RNG are 5-membered ring torsions and deformations, respectively. s Stands for bond stretching, with the variations ss for methylene symmetrical stretching and sa for methylene asymmetrical stretching. c Stands for methylene scissoring, r for methylene rocking, i for methylene twisting and w for wagging. C25 is used for the C2 and C5 atoms’ contributions summed together; C34 is defined analogously for C3 and C4.

MP2/6–31G(d) scaled by a factor 0.943							CGenFF
freq	assignment	%	assignment	%	assignment	%	freq	assignment	%	assignment	%	assignment	%
33.0	t5RNG1	91					99.3	t5RNG1	95
289.1	t5RNG1a	88					322.9	t5RNG1a	94
580.9	d5RNG1a	30	d5RNG1	30	rC34H2	16	594.4	d5RNG1a	84
623.6	d5RNG1a	39	d5RNG1	30			629.4	d5RNG1	68
770.4	rC34H2	67					784.9	rC34H2	88
832.1	rC34H2	28	rC25H2	27	d5RNG1a	16	833.8	rC25H2	44	rC34H2	43
842.3	wN1H	37	sC-N	24			870.3	sC3-C4	36	rC25H2	17	wN1H	17
876.1	sC2-C3	49	sC3-C4	42			888.0	sC2-C3	43	wN1H	34
901.9	sC2-C3	75					961.0	sC2-C3	68
915.7	sC-N	57	rC25H2	25			990.9	sC-N	31	wN1H	21	wC25H2	15
968.3	wN1H	28	iC34H2	27			1026.6	rC25H2	28	wN1H	18
1017.3	rC25H2	31	rC34H2	27	iC25H2	19	1028.1	rC25H2	39	rC34H2	29
1020.3	sC3-C4	32	sC2-C3	16			1083.7	sC-N	36	wC25H2	18	dN1H	16
1080.2	sC-N	81					1104.9	wC34H2	23	wC25H2	20
1174.7	iC25H2	29	iC34H2	25	rC34H2	16	1164.4	iC34H2	74
1181.9	iC25H2	37					1199.7	iC34H2	82
1217.2	iC34H2	70					1209.2	iC25H2	70	iC34H2	16
1251.2	wC34H2	35	iC34H2	16	rC25H2	16	1233.8	iC25H2	70
1261.2	wC34H2	56	wC25H2	37			1303.5	wC34H2	64
1292.1	iC25H2	49	wC34H2	20			1310.7	wC25H2	45	dN1H	43
1305.2	wC34H2	35	wC25H2	25	iC25H2	18	1332.0	wC34H2	84
1328.4	wC25H2	84					1458.2	cC25H2	37	sC-N	19
1413.5	dN1H	78					1463.0	wC25H2	35	cC25H2	31	sC-N	17
1460.5	cC34H2	70	cC25H2	29			1475.5	cC34H2	86
1468.9	cC25H2	74	cC34H2	26			1495.4	cC34H2	92
1472.7	cC25H2	61	cC34H2	38			1566.1	cC25H2	66	sC-N	16	wC25H2	16
1490.0	cC34H2	65	cC25H2	35			1568.8	cC25H2	56	sC-N	24
2930.7	ssC25H2	90					2850.8	ssC25H2	99
2935.9	ssC25H2	77	ssC34H2	17			2851.2	ssC25H2	99
2937.2	ssC34H2	85					2881.2	saC25H2	98
2949.3	ssC34H2	93					2884.6	saC25H2	97
2983.1	saC34H2	76	saC25H2	17			2897.7	ssC34H2	98
2992.8	saC25H2	58	saC34H2	31			2901.8	ssC34H2	99
2999.5	saC25H2	75	saC34H2	20			2920.0	saC34H2	98
3008.1	saC34H2	67	saC25H2	31			2932.0	saC34H2	99
3300.0	sN1-H1	100					3365.0	sN1-H1	100

Computational details

All quantum chemical calculations (HF, MP2) were performed using Gaussian 03.⁵² QM optimizations were performed to default tolerances. Empirical force field calculations were performed using the program CHARMM.^28,29 It should be noted that the number of the CGenFF residues (ie. model compounds) and parameters in CGenFF exceed array limits in earlier versions of CHARMM. In addition, the number of characters in atom and residues names has been extended to six. These issues have been taken into account in version 36 of CHARMM; an in-house patch for CHARMM versions 34 and 35 is included in the supplementary material. Empirical energy minimizations were perfomed to a RMS gradient of 10⁻⁵ kcal/(mol Å) following which vibrational analyses were performed using the VIBRAN and MOLVIB³⁴ modules in CHARMM. All empirical gas phase calculations included all nonbonded interactions (ie. infinite cutoff distance). Sample input files can be found in the supplementary material and on the MacKerell lab website.⁵³

QM PES calculations were performed using the relaxed potential energy scan facility of the default redundant internal coordinate optimizer (keyword “Opt=ModRedundant”) in Gaussian 03. This facility constrains the internal coordinate(s) being scanned and minimizes all other coordinates at every scan point. MM PES were calculated by reading the QM geometries of all the scan points into CHARMM, harmonically restraining the target dihedral angle(s) with a force constant of 10000 kcal/(mol radian), and minimizing all remaining degrees of freedom. This methodology makes it more likely that the portions of the molecule that are not being scanned have the same local minimum conformation in the QM and in the MM scan.

Condensed phase pure solvent properties were calculated using a cubic cell containing 216 copies of the molecule being studied. The cell was initially constructed by placing a copy of the respective molecule on each grid point of a cubic 6×6×6 lattice, whose grid spacing was chosen to correspond to the experimental molecular volume. In the presence of periodic boundary conditions,⁵⁴ each system was minimized for 10000 steepest descent steps, gradually heated to the relevant temperature during a 10ps MD simulation, then equilibrated for 1.2 ns. This equilibration was followed by a production simulation of 400ps, during which the volume of the system was monitored to obtain the CGenFF molecular volume. The particle mesh Ewald method⁵⁵ was used for the treatment of the Coulomb interactions with a real space cutoff of 12 Å, a 4^th order cubic spline and a kappa value of 0.34. For the LJ interactions, a force-switching function⁵⁶ was applied over the range of 10–12 Å, and a long-range correction was used to account for LJ interactions beyond the cutoff distance.⁵⁴ A timestep of 1 fs was used in conjunction with the “Leapfrog” algorithm⁵⁷ to integrate the equations of motion. The SHAKE algorithm⁴⁹ was applied to constrain the length of covalent bonds to hydrogen atoms to their equilibrium values. The Nosé-Hoover thermostat^58,59 and the Langevin piston barostat⁶⁰ were used to generate the isothermal-isobaric ensemble (NPT) with continuous dynamics. Heats of vaporization were calculated using

$${\mathrm{\Delta }}_{\mathit{vap}}H=-\frac{\langle U_{\mathit{liq}}\rangle +P\langle V_{\mathit{liq}}\rangle }{N_{\mathit{mol}}}+\langle U_{\mathit{gas}}\rangle +RT\approx -\frac{\langle U_{\mathit{liq}}\rangle }{N_{\mathit{mol}}}+\langle U_{\mathit{gas}}\rangle +RT$$ (2)

where T is the temperature, R is the gas constant, <U_liq>, the potential energy of the liquid, is the average potential energy from the 400 ps production MD simulations, and <V_liq> is the average volume of the simulation box over the same period of time. As indicated by equation 2, the term P<V_liq> is negligible for practical purposes^* and was ignored during the actual calculations. Finally, U_gas, the gas phase energy, was obtained from separate 50 ps equilibration + 50 ps production vacuum MD simulations of all 216 molecules in the cubic box, with the final energy the average of the 216 average potential energies from the 50ps production simulations. These gas-phase simulations were performed using Langevin dynamics with a 1 fs integration time step, a friction coefficient of 5 ps⁻¹, and no truncation of nonbonded interactions. Out of the 112 CGenFF compounds subjected to pure solvent simulations, two (p-chlorotoluene and p-xylene) remained solid. These metastable states mandated 1.6 ns pre-equilibrations at a higher temperature (393.15 K), causing the compounds to melt. Simulations were then initiated from the final timeframe of the 393.15 K runs. Both systems remained liquid during these 1.2 ns equilibration + 0.4 ns production simulations at their respective experimental temperatures. Additionally, convergence of the bulk solvent properties of 2 other model compounds (2-butyne and acetonitrile) was problematic. For these two compounds, the simulation was performed starting from a 7×7×7 cubic lattice, and the duration of the equilibration and production runs were both set to 800ps.

Results and Discussion

CGenFF aims to be a general force field for drug-like molecules developed to be compatible with the CHARMM all-atom additive biomolecular force fields. Accordingly, the same approach as used for development of the CHARMM force fields was applied, including charge optimization based on HF/6–31G(d) model compound-water interaction data. While higher levels of theory that treat hydrogen bonding with significantly more accuracy⁴⁵ are applicable to the systems studied, the use of HF/6–31G(d) assures that a balanced, consistent force field will be obtained with respect to the nonbond interactions.²⁵ Given the importance of nonbonded interactions in the biological activity of pharmaceutical compounds, proper treatment of these terms is considered an essential feature of CGenFF.

Construction of the initial version of CGenFF was based on the numerous molecules that have been parametrized as model compounds for the CHARMM biomolecular force field.^{6–8,11–14,48,61} For instance, phenol was parametrized as a precursor for tyrosine, N-methylacetamide (NMA) as a precursor for the protein backbone, dimethyl phosphate as a precursor for the phosphodiester backbone in nucleic acids, and so on. Additionally, a substantial number of prosthetic and non-biological model compounds were parametrized in the past as part of different application studies.^{7,9,11,14,47,62–67†} Initially, all the atoms types were converted to a common nomenclature, where the second letter in each atom type is a G to indicate the General FF. The final atom types are listed in the supplementary material. All the available parameters were then converted to these new atom types and combined, yielding the starting point for CGenFF. At this stage there were numerous repeated parameters. These were each analyzed manually and the most appropriate parameter was chosen based on arguments such as the quality of the original parametrization and generalizability of the model compounds. This effort resulted in an “initial force field”, containing 301 model compounds and 3175 parameters. At this point, it should be emphasized that even the best possible choice of parameters compromises the quality of the force field for the purpose of representing the original biomolecules. Accordingly, CGenFF should only be used for drug-like molecules, with the biological macromolecules being represented by the original CHARMM additive force fields. CHARMM input scripts to combine the biomolecular CHARMM force fields with CGenFF to study, for example, protein-ligand interactions, are included in the supplementary material and on the MacKerell lab website.⁵³

To extend CGenFF to cover a wider range of drug-like molecules, a list of 68 compounds including a large number of heterocyclic scaffolds (as listed on the web site of Maybridge⁶⁸) was targeted. These comprise a large number of aromatic and saturated 5-membered and 6-membered rings, indole- and quinoline-like bicyclic species, a few common tricyclic compounds, and cage-like structures such as quinuclidine, norborane and adamantane. In addition, a number of additional classes of molecules have been included in CGenFF associated with ongoing projects in the MacKerell laboratory as well as molecules considered relevant for drug discovery. These include nitro- and halogenated benzenes, benezenesulfonate, biphenyl, aromatic amides and ethers, urea, aldehydes, ketones, nitriles, alkynes, hydrazine, sulfoxides, opioids,⁶⁹ bile acids, selected aromatic and aliphatic halogens, indolizines and amidines.⁷⁰ Notably, these comprise some novel linkers, such as urea, ketones, alkynes, hydrazines and sulfoxides. At the time of publication of this paper CGenFF has been explicitly parametrized for a total of 445 model compounds, including both CHARMM “residues” and “patches”, and includes 139 atom types and 5129 bonded parameters. The full topology and parameter files are included in the supplementary material. While the list of compounds and moieties presents a substantial extension of the CHARMM biomolecular force fields, it is by no means complete. Future efforts in our laboratory will continue to expand the coverage of CGenFF and the information presented in this manuscript will allow users to extend the force field to their own molecules of interest.

A case study: pyrrolidine

As a case study, the optimization of parameters for pyrrolidine is considered before results are presented on general trends with respect to the reproduction of target data by the full set of model compounds. A more elaborate version of this and the following section can be found in the supplementary material and on the MacKerell lab website in the form of a tutorial in HTML format.⁵³

As outlined in the parametrization philosophy section, the first step in treating the new compound is creation of the residue definition for the residue topology file (RTF) followed by identification of missing parameters. As discussed elsewhere,^28,29 the RTF includes the CGenFF chemical atom types, the partial atomic charge for each atom and the connectivity. Initial atom types and charges for pyrrolidine were obtained by analogy with previously parametrized molecules that are chemically similar to the new molecule.

At this stage, when initially generating the structure and calculating its energy, CHARMM^28,29 will present error messages for parameters that are missing. These are the parameters for which i) initial estimates must be obtained or wildcard parameters applied, ii) validation must be performed and iii) optimization may be performed if deemed necessary. It should be emphasized that the hierarchical development of CGenFF requires that only new parameters for a given molecule be optimized, thereby insuring that the integrity of previously optimized molecules is maintained. Alternatively, a user may choose to optimize selected parameters that are already available in the force field; however, this will comprise the quality of previously optimized molecules such that those new parameters should only be used for the particular molecule under study. Assignment of initial guesses to the missing parameters is again based on analogy. Scripts to facilitate this procedure may be found in the supplementary material or obtained from the MacKerell laboratory website.⁵³

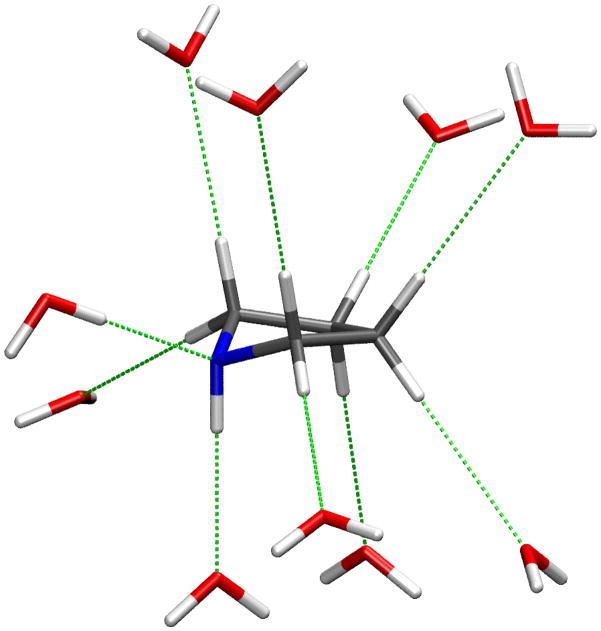
Initiation of the validation step involves generating target data. Step one is an MP2 optimization of the molecule. As pyrrolidine exhibits tetrahydrofuran-like conformational flexibility,⁷¹ and its NH group can undergo pyramidal inversion, 4 starting conformations were initially selected and subjected to the QM optimization. The absolute minimum from this simplistic conformational search is an asymmetric ¹T₂ conformation, as defined following the nomenclature of M. Sundaralingam,⁷² but using the standard atom numbering for the pyrrolidine ring as shown in Figure 1 rather than the atom numbering convention for furanose sugars. This conformation, in which the proton on the nitrogen atom is in an axial position, was used for the optimization of the charges. As discussed above, the target data for this optimization consists mainly of scaled HF minimum interaction energies and distances between the model compound and individual water molecules. In the case of pyrrolidine, 10 different monohydrates were generated, as shown in Figure 2; however, in many cases it may be better to only consider interactions with hydrogen bonding groups and non-polar moieties adjacent to a heteroatom. Once the target data for the interactions with water and the QM dipole moments are obtained, the corresponding empirical values are calculated and compared to the target values. If the level of agreement is deemed satisfactory (see criteria above), then the charges as well as the LJ parameters are considered valid and no optimization is performed. If optimization is deemed necessary, the charges are manually adjusted to improve the overall agreement between the scaled QM and the empirical values. The final set of charges that result from this procedure yield good overall agreement with the individual interaction energies and geometries with water (Table 1) and with the dipole moment (Table 2). The level of agreement for the water interactions in Table 1 may be considered a general rule for defining adequate agreement with the target data. The most favorable interaction, which is expected to dominate in aqueous solution, is well reproduced, as is the order of the interaction energies. In many cases the less favorable interactions, especially those involving nonpolar groups, are less well reproduced with respect to both interaction energies and geometries. Concerning the dipole moment, the magnitude of the CGenFF dipole moment is 22% higher than the HF dipole moment and 30% higher than the MP2 dipole moment. As discussed above, this overestimation of the dipole moment is desirable in order to correctly reproduce bulk phase properties. The Z-component of the dipole moment (Table 2) points in the opposite direction relative to the target data. As this component is relatively small, the direction of the dipole moment vector deviates only 23° and 26° from the HF and MP2 result, respectively. In accord with the iterative parameter optimization procedure (Scheme 1), once the bonded parameters are optimized, the interactions with water and dipole moment should be re-considered using the CGenFF minimized conformation for the MM calculation. If deemed necessary, additional optimization of the charges could be undertaken, though typically this is not required.

Figure 1.

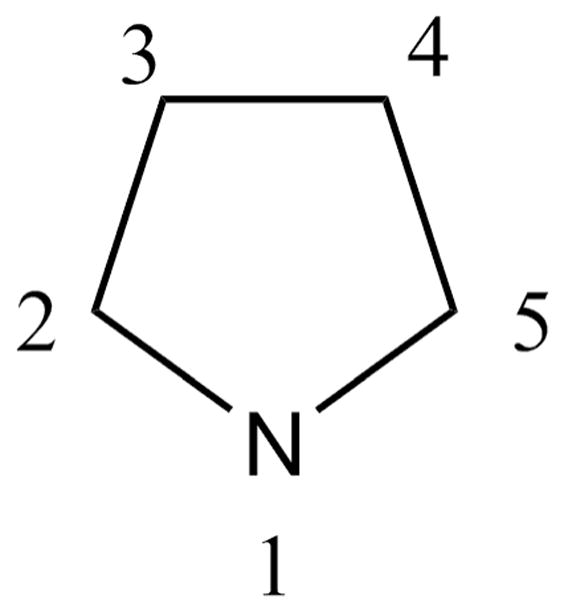
Pyrrolidine with atom numbering convention.

Figure 2.

Interaction orientations of pyrrolidine with water molecules that were used for charge optimization. Note that only a single water molecule is interacting with pyrrolidine during each calculation; all water molecules are shown simultaneously only for convenience.

Table 1.

Interaction energies (kcal/mol) and distances (Å) of pyrrolidine-water complexes in different geometries. HF/6–31G(d) interaction energies are scaled by a factor 1.16 (see “methodology”). HF interaction distances are not scaled; however, bulk phase hydrogen bonds should be roughly 0.2 Å shorter than vacuum. Results include Average Deviation (AD), Root Mean Square Deviation (RMSD) and Absolute Average Deviation (AAD).

interaction geom.	ΔE(HF)*	ΔE(CGenFF)	ΔΔE	r(HF)	r(CGenFF)	Δr
N1H…OHH	−2.86	−2.67	0.19	2.31	2.00	−0.31
N1…HOH	−7.55	−7.64	−0.09	2.07	1.90	−0.17
C2H…OHH	−0.68	−0.62	0.06	2.84	2.76	−0.08
C2H…OHH	−1.03	−0.87	0.16	2.78	2.73	−0.05
C3H…OHH	−0.93	−0.90	0.03	2.84	2.78	−0.06
C3H…OHH	−1.11	−0.85	0.26	2.85	2.79	−0.06
C4H…OHH	−0.92	−0.92	0.00	2.85	2.77	−0.08
C4H…OHH	−1.01	−0.85	0.16	2.86	2.79	−0.07
C5H…OHH	−0.62	−0.62	0.00	2.85	2.76	−0.09
C5H…OHH	−1.06	−0.87	0.19	2.78	2.73	−0.05
AD			0.10			−0.10
RMSD			0.14			0.13
AAD			0.12			0.10

Table 2.

Components of pyrrolidine’s dipole moment (Debye) at the HF level, the MP2 level, and from CGenFF. The HF dipole moment is calculated on the MP2 optimized geometry.

μ component	HF/6–31G(d)†	MP2/6–31G(d)	CGenFF
X	1.4623	1.3567	1.79132
Y	−0.4527	−0.4254	−0.47355
Z	0.2902	0.3352	−0.40192
tot	1.5581	1.4608	1.89595

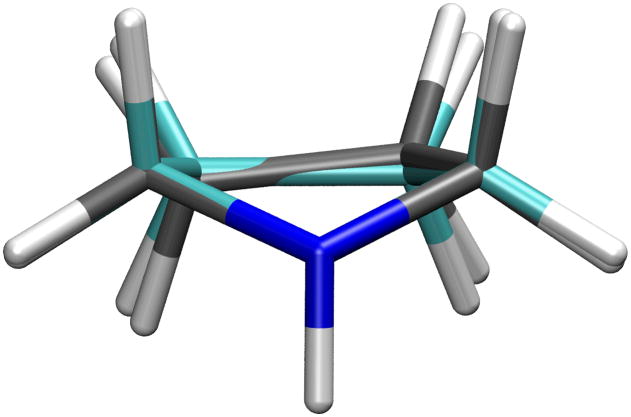
The quality of the equilibrium bond lengths and angles can be judged by the equilibrium (ie. minimum energy) geometry (Table 3). Most of the empirical values in this table are in excellent agreement with the QM target data. Differences are typically lower than 0.03 Å and 3° for the bonds and angles, respectively. In the case of pyrrolidine, the level of agreement in Table 3 was obtained following optimization of the additional bond, valence angle and dihedral angle parameters that were added for this molecule; if a similar level of agreement was obtained with the parameters directly assigned by analogy, parameter optimization would not have been required. The relatively large deviations of the dihedral angles and to a lesser extent the N-C-C angles can be explained by the fact that the CGenFF minimization, although starting from a ¹T₂ conformation, minimizes to a symmetrical ¹E conformation after optimizing the parameters. As can be seen in Figure 3, these conformations are quite similar; ¹E is an envelope conformation with the nitrogen atom at the tip, while ¹T₂ is a slightly twisted version of the same envelope conformation. Although the ¹E conformation is a first order saddle point at MP2 level, its energy is only 0.005 kcal/mol higher than the ¹T₂ conformation. In fact, this slight deviation in the pseudorotational energy profile was a deliberate trade-off to improve other parts of pyrrolidine’s potential energy surface as well as the potential energy surfaces of other molecules with which it shares parameters.

Table 3.

CGenFF equilibrium geometry of pyrrolidine compared to MP2 level.

Coordinate	MP2	CGenFF	difference	Coordinate	MP2	CGenFF	difference
bond lengths/Å				angles/°
C5-H51	1.10	1.10	0.01	C5-N1-H1	108	110	2
C5-H52	1.09	1.10	0.01	H1-N1-C2	108	110	3
N1-H1	1.02	1.02	0.00	N1-C2-H21	108	109	2
C2-H21	1.10	1.10	0.01	H21-C2-C3	110	112	2
C2-H22	1.09	1.10	0.01	N1-C2-H22	111	112	1
C3-H31	1.09	1.10	0.00	H22-C2-C3	114	113	−1
C3-H32	1.10	1.10	0.01	H21-C2-H22	108	107	0
C4-H41	1.09	1.10	0.00	C2-C3-H31	113	112	−1
C4-H42	1.09	1.10	0.01	H31-C3-C4	113	112	−1
C5-N1	1.47	1.48	0.01	C2-C3-H32	110	111	1
N1-C2	1.47	1.48	0.01	H32-C3-C4	111	111	0
C2-C3	1.54	1.52	−0.01	H31-C3-H32	107	107	−1
C3-C4	1.55	1.54	−0.01	C3-C4-H41	112	112	0
C4-C5	1.55	1.52	−0.03	H41-C4-C5	111	112	0
				C3-C4-H42	111	111	0
				H42-C4-C5	111	111	0
				H41-C4-H42	107	107	0
				C4-C5-H51	110	112	2
dihedrals/°				H51-C5-N1	108	109	2
C2-C3-C4-C5	9	0	−9	C4-C5-H52	114	113	0
N1-C2-C3-C4	−31	−28	3	H52-C5-N1	110	112	1
				H51-C5-H52	107	107	0
				C5-N1-C2	103	102	−1
				N1-C2-C3	106	103	−3
				C2-C3-C4	104	105	1
improper dihedrals/°				C3-C4-C5	104	105	0
C5-C2-H1-N1	44	42	−2	C4-C5-N1	108	103	−5

Figure 3.

The ¹T₂ (carbon atoms in black) and ¹E (carbon atoms in cyan) conformations of pyrrolidine.

Initial optimization of the bond stretching, angle bending and dihedral angle force constants was based on the reproduction of the scaled MP2 vibrational spectrum. The results of this optimization can be found in Table 4. Agreement is generally fair, although matching the individual modes is complicated because, as discussed above, mixing of the contributions from different internal degrees of freedom is different in the MP2 and the CGenFF spectra, a phenomenon that occurs in all but the simplest molecules. The considerable discrepancy in the lowest ring torsion is a consequence of the different conformations; indeed, this torsion is the sole coordinate along which the conformations differ. As non-rigid torsions cannot be accurately parametrized based on the vibrational spectrum alone, the ring torsions involving only non-hydrogen atoms were ignored during this stage of the parameter optimization process.

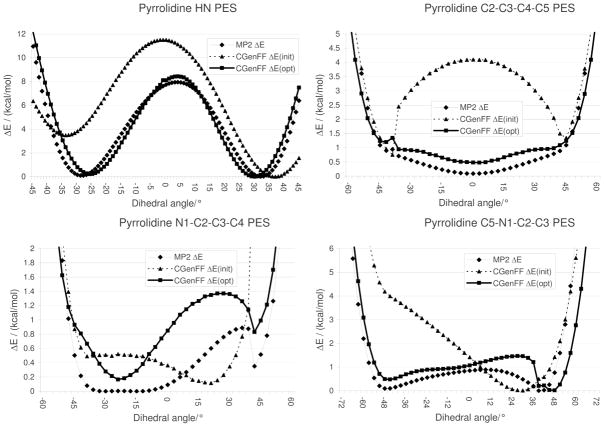
Final optimization of dihedral parameters associated with torsions involving only non-hydrogen atoms was based on adiabatic potential energy scans. Target data for these scans were obtained at the MP2 level on the improper dihedral that describes the NH pucker and for the three ring torsions that are chemically different (Figure 4). These potential energy scans were used as target data for optimization of the associated dihedral parameters. As shown in Figure 4, the initial MM parameters result in large differences in the overall shape of the PES as well as in the locations of the minima, illustrating the fact that phenomena such as ring strain vary widely for small rings containing different atoms, making parameters that apply to these rings poorly transferrable between rings. Such limitations, in part, motivated our effort to explicitly parameterize a large number of heterocycles. After optimization, the agreement between the MP2 and CGenFF surfaces becomes excellent; the minima are now in good agreement with the QM minima and the magnitude of the remaining energetic discrepancies is 0.5 kcal/mol. The evaluation considers the relative energies as well as the overall shape of the energy profiles. It is typically desirable to fit the lower energy regions of the surfaces (< 5 kcal/mol) as these are sampled to the largest extent in MD simulations. However, if conformational changes are to be studied, it is important that the barrier heights also be in satisfactory agreement with the target data. In addition, when the results from the studies to be undertaken are highly sensitive to the conformational energies, one may consider higher-level calculations for use as target data. In such situations the user should consider MP2/cc-pVTZ single point calculations on the MP2/6–31G* optimized geometry. This level of theory has shown utility in complex systems that include anomeric centers³⁶ and is particularly attractive in combination with the RIMP2 method, which saves approximately an order of magnitude in CPU over the canonical MP2 method.⁷³

Figure 4.

Potential energy scans of pyrrolidine. The HN PES was defined as N1-C1-C5-H (Figure 1).

For the majority of model compounds, there are typically one or two rotatable bonds that need to be considered when performing the final parameter optimization. In such cases, those torsions usually can be treated independently by performing potential energy scans for each dihedral while all remaining degrees of freedom on the surface are allowed to relax, then fitting the associated dihedral parameters. However, non-planar 5-membered rings as well as more complex systems require special attention. For example, with pyrrolidine, the three in-ring dihedrals as well as the amine out-of-plane surface (Figure 5) are correlated, as are their parameters. In such cases, the individual dihedrals are still scanned at the QM level with all other degrees of freedom, including other dihedrals that have to be fit allowed to relax. However, when scanning the corresponding MM surfaces for a given dihedral it is necessary that the remaining dihedrals associated with parameters that are being fit be restrained in the QM optimized structures from the QM PES. The use of these additional restraints assures that the energy contributions from those dihedrals are taken into account when performing the fitting. It should be emphasized that when performing PES on multiple dihedrals in a given molecule, the relative energies of each individual dihedral PES should be offset to the global energy minimum for all the PES, thereby assuring that the optimization of the different dihedral parameters satisfactorily reproduces the relative conformational energies of the molecule and not just of the individual dihedrals. This offset is included in Figure 4 for pyrrolidine. The MCSA fitting program developed in our laboratory⁵⁰ includes utilities to account for these issues.

Figure 5.

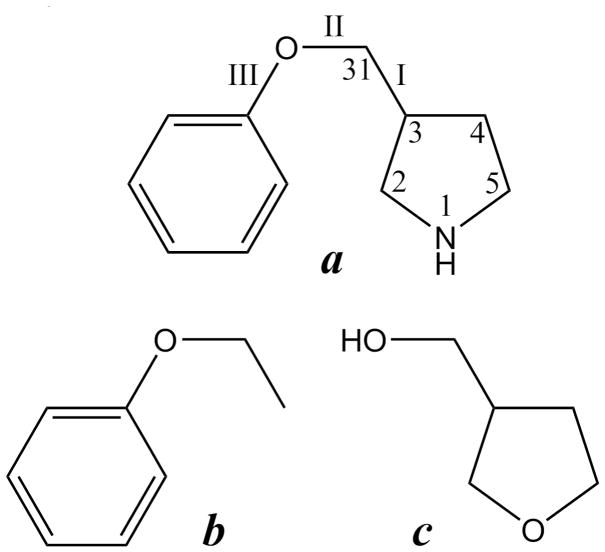
3-phenoxymethylpyrrolidine (a) and two “parent” model compounds from which it “inherited” parameters: ethoxybenzene (b) and 3-hydroxymethyltetrahydrofuran (c)

3-phenoxymethylpyrrolidine

To demonstrate how a user can build a drug-like molecule out of the functional groups and heterocycles present in CGenFF, a benzene ring will be attached to the 3-position of pyrrolidine by means of an oxymethyl linker, yielding 3-phenoxymethylpyrrolidine (Figure 5a). It should be noted that the phenoxymethyl group is treated as a separate charge group (using the “GROUP” directive in the CHARMM residue topology file) with a zero net charge. This modularity, which also applies to other chemical groups, greatly facilitates building new model compounds.

Next, as with pyrrolidine, missing parameters are identified. Most of these missing parameters are in-ring dihedrals resulting from the introduction of a tertiary carbon type in the pyrrolidine ring and thus can directly be transferred from the parent compound pyrrolidine. Additionally, even though the N1–C2–C3–C31 dihedral (using the atom numbering in Figure 5a) involves an exocyclic non-hydrogen atom, it was copied from N1-C2-C3-H in pyrrolidine in order to avoid distorting the ring’s torsional energy profile, which was carefully parametrized in the previous section. For the remainder of the missing parameters, existing parameters with excellent analogy were found.

At this point, it should be noted that with increasing system size, it becomes increasingly difficult to perform extensive parameter validation or optimization, as the computational cost of the QM calculations usually scales with the square of the system size (or worse). Moreover, vibrational analysis is rendered impractical by the extensive mixing that occurs in the vibrational spectrum of larger compounds, and the number of sites at which to perform water interactions as well as the number of dihedrals to scan become large. Therefore, it is not recommended to perform explicit parameter optimization on these larger compounds. Rather, one should focus on the regions of the molecule linking together ring systems, taking advantage of the availability of explicit parameters for a large number of ring systems already in CGenFF. Moreover, parameters for dihedrals associated with freely rotatable bonds often perform poorly when transferred to a different molecule. This is due to the dihedral parameters typically being the final term optimized, thereby accounting for the contribution of long range nonbond interactions to the PES. For example, if the charge on one of the rings on one end of a previously parametrized linker changes, the PES associated with the rotatable bonds in the linker may change, justifying validation of the PES and, if necessary, optimization of the relevant dihedral parameters.

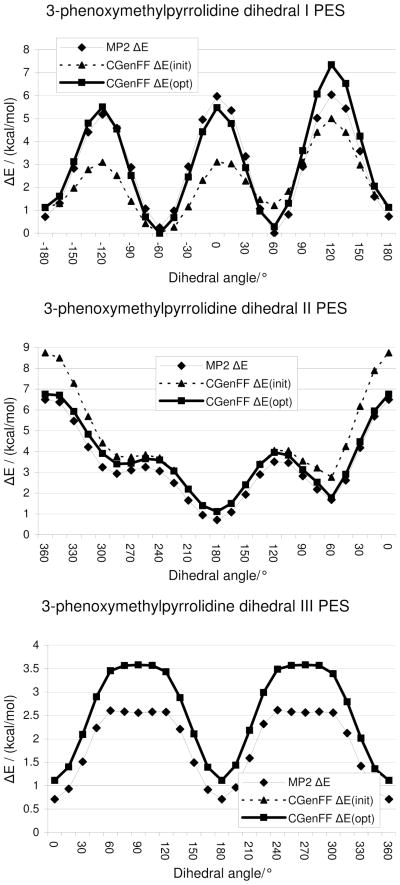
In the particular case of 3-phenoxymethylpyrrolidine, potential energy scans are performed on the three rotatable dihedrals in the linker (Figure 6a). During the initial, fully relaxed QM scans, the pyrrolidine ring underwent several conformational changes, making comparison to the MM scan points problematic. To avoid this issue, the pyrrolidine ring conformation was constrained both during the QM and the MM scan. As an initial guess, the parameters for dihedrals I and II in Figure 5a were respectively copied from 3-hydroxymethyltetrahydrofuran (Figure 5c) and ethoxybenzene (Figure 5b). Since dihedral III involves exactly the same atom types as a dihedral in ethoxybenzene, the PES on this dihedral serves as a validation rather than being aimed at optimizing the associated dihedral parameter. Should the validation indicate that this parameter is not satisfactory, re-optimization may be considered for the purpose of performing simulations on this particular model compound (ie. 3-phenoxymethylpyrrolidine). In this case, the newly optimized parameter should not be added to CGenFF as this would compromise the force field’s representation of ethoxybenzene and derivatives. Presented in Figure 6 is the MM PES for the initial and optimized parameters along with the corresponding QM PES. With the initial MM parameters, although the maxima and minima are at the right locations as compared to the QM PES, their heights show large deviations. After a few iterations of adjusting the dihedral parameters and redoing the MM calculation, the final MM PES in Figure 6 were obtained. The PES of dihedral I (figure 6a) has improved considerably. The barrier at 120° is significantly too high, but this cannot be improved without sacrificing other parts of the PES. Such compromises are common during parameter optimization, requiring decisions by the user on which aspects of the model to sacrifice. The agreement for dihedral II (figure 6b) is excellent, except for a slight, constant offset. This offset is caused by the fact that during most of this potential energy scan, dihedral I (figure 6a) was at the local minimum at 180°, the energy of which is slightly overestimated. Dihedral III displays the same constant offset. Although its barriers are overestimated, the discrepancy in barrier height is only 0.6 kcal/mol, which is more than satisfactory for a parameter that was not subject to optimization. Finally, it should be emphasized that when performing PES on multiple dihedrals in a given molecule, the relative energies of each individual dihedral PES should be offset to the global energy minimum for all the PES, thereby assuring that the optimization of the different dihedral parameters satisfactorily reproduces the relative conformational energies of the molecule and not just of the individual dihedrals.

Figure 6.

Potential energy scans on the central torsion of the oxymethyl linker in 3-phenoxymethylpyrrolidine.

Overall quality of CGenFF

A total of 111 additional compounds were parametrized as part of the present study. In the remainder of this section, an overview of the ability of CGenFF to reproduce the target data for these molecules is presented. Prior to that overview, results are presented for compounds that included unique atom types not already in the CHARMM biomolecular force fields and that, accordingly, were subjected to LJ parameter optimization.

Compounds for which LJ parameter optimization was required

LJ parameter optimization was required for a total of 21 atom types. The corresponding model compounds are listed in Table 5 along with their pure solvent properties and the atom types subjected to LJ optimization. As may be seen from the list, the compounds include atom types that are typically not encountered in biological macromolecules. For example, triple bonds are not seen in biological systems, and a series of halogenated benzenes and ethanes were studied as required for CGenFF to cover the halogens, which occur widely in pharmaceutical compounds. For all these molecules, the CGenFF parameter assignment and optimization approach was followed, as described and applied to pyrrolidine above. Once satisfactory geometries, vibrational spectra, conformational energies and interactions with water were obtained using preliminary LJ parameters, optimization of the LJ parameters on the novel atom types was undertaken based on reproduction of the experimental heats of vaporization and molecular volumes of the corresponding pure solvents. Optimization was only performed on the novel atom types, simplifying the process. Table 5 shows that the experimental properties for the series of halogenated compounds as well as acetaldehyde, acetone, hydrazine, 2-butyne and acetonitrile are reproduced well following optimization. For 3-cyanopyridine, which shares its new atom types with acetonitrile, the only density that was found in the literature was determined below its melting point, so that only the heat of vaporization could be used as target data. Its calculated heat of vaporization, which was 64% too high before optimization, is substantially improved upon introduction of the parameters that were optimized for acetonitrile. For the optimization of the 5-membered ring sp² atoms, a compromise had to be made between the properties of the different model compounds. Typically, molecular volumes are overestimated and heats of vaporization are underestimated for pyrrole and furan, while the trends are opposite for the remaining compounds. The optimized set of LJ parameters overestimates the molecular volume of furan by 9% and underestimates the molecular volume of 1,2,3-triazole by 7%; the molecular volumes of all other compounds are bracketed by these two values and satisfactorily reproduce the experimental results. Comparable trends are observed for the heats of vaporization, although the relative deviations are much larger. Such compromises are typical for force fields and may be magnified in molecules which contain π-orbitals, where treating the vdW surface as a sum of spherical atoms is expected to be a poor approximation. The inclusion of these additional atom types and their corresponding LJ parameters significantly extends the coverage of the CGenFF, thereby limiting the need for users to optimize LJ parameters in the future.

Table 5.

Parametrization of L-J parameters using experimental liquid densities and heats of vaporization as target data. The abreviations “exp” and “calc” respectively stand for “experimental” and “calculated”. For the calculated properties, data are presented using both the initial (“init”) and optimized (“opt”) parameters. Densities (ρ) are in g/ml, molecular volumes (V) are in ų and heats of vaporization (Δ_vapH) are in kcal/mol.

Model compound	new atom types	ρ(exp)	V(exp)	V(calc)	deviation	ΔvapH (exp)	ΔvapH (calc)	deviation
2-butyne	CG1T1	0.6910	130.0	131.2	1.0%	6.38	6.42	0.6%
acetonitrile	CG1N1, NG1T1	0.7860	86.7	87.6	1.0%	8.10	8.10	0.0%
3-cyanopyridine	CG1N1, NG1T1					10.76	12.25	13.9%
acetaldehyde	CG2O4	0.788	92.8	93.6	0.8%	6.60	6.39	−3.1%
acetone	CG2O5, OG2D3	0.791	121.9	124.4	2.1%	7.48	7.32	−2.1%
furan	CG2R51	0.936	120.8	131.5	8.8%	6.74	5.61	−16.7%
pyrrole	CG2R51	0.967	115.2	117.4	1.9%	10.16	9.63	−5.2%
thiophene	CG2R51	1.051	132.9	131.1	−1.4%	8.27	8.43	1.9%
imidazole	CG2R51, CG2R53	0.937	120.6	116.8	−3.2%
4-methylimidazole	CG2R51, CG2R53	0.938	145.3	144.8	−0.3%
oxazole	CG2R51, CG2R53	1.05	109.2	103.9	−4.8%	7.77	9.90	27.4%
thiazole	CG2R51, CG2R53	1.2	117.8	114.8	−2.6%	9.49	10.65	12.2%
pryrazole	CG2R51, CG2R52	0.952	118.7	116.6	−1.8%
isoxazole	CG2R51, CG2R52	1.078	106.4	108.1	1.6%	8.72	10.64	22.0%
2-pyrazoline	CG2R52	1.04	111.9	110.6	−1.2%
1,2,3-triazole	CG2R51	1.192	96.2	89.3	−7.2%
benzothiazole	CG2R53	1.238	181.3	176.2	−2.8%	14.03	16.60	18.4%
pyrimidine	CG2R64, NG2R62	1.016	130.9	128.8	−1.6%	11.90	12.21	2.6%
pyridine	NG2R60	0.978	134.3	132.5	−1.3%	9.60	10.03	4.5%
hydrazine	NG3N1	1.0036	53.0	53.1	0.2%	10.68	10.60	−0.7%
1,4-dioxane	OG3C61	1.034	141.5	143.9	1.7%	9.23	9.61	4.2%
1,3-dioxane	OG3C61	1.0286	142.2	143.6	1.0%	9.35	10.04	7.4%
chlorobenzene	CLGR1	1.106	169.0	168.0	−0.6%	9.80	9.93	1.3%
bromobenzene	BRGR1	1.491	174.9	174.5	−0.2%	10.64	10.71	0.7%
iodobenzene	IGR1	1.823	185.8	183.5	−1.3%	11.69	11.54	−1.2%
chloroethane	CLGA1	0.9214	116.3	116.6	0.3%	6.64	6.63	−0.2%
1,1-dichloroethane	CLGA1	1.1757	139.8	139.1	−0.5%	7.31	7.31	−0.1%
1,1,1-trichloroethane	CLGA3	1.339	165.4	162.6	−1.7%	7.77	7.71	−0.8%
bromoethane	BRGA1	1.4604	123.9	121.1	−2.3%	6.60	6.74	2.2%
1,1-dibromoethane	BRGA2	2.0555	151.8	149.2	−1.7%	9.46	9.71	2.6%

Nonbonded parameters

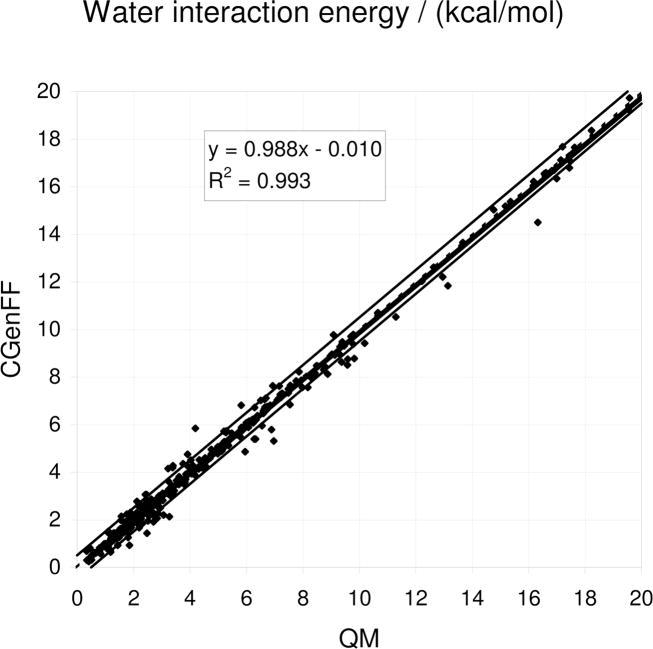
The overall quality of the nonbonded parameters may be evaluated based on the gas phase model compound-water interactions and on the bulk phase properties. As for the water minimum interaction energies, a correlation plot of the scaled HF/6–31G* target data versus the CGenFF results is presented in Figure 7.^‡ As is evident, the agreement of the empirical model with the QM data is excellent, which is supported by the statistical analysis shown in Table 6. This level of agreement is not unexpected as the partial atomic charge optimization is performed to specifically reproduce these target data. That said, it is notable that the force field is able to reproduce the wide range of interaction energies, from less than 1 kcal/mol to up to 20 kcal/mol. The ability to reproduce this range of interactions indicates that the proper balance of different hydrogen bonding interactions will be present when molecules interact with, for example, proteins.

Figure 7.

Comparison of the QM and CGenFF minimum water interaction energies for the model compound-water monohydrate interactions. The QM level of theory is MP2/6–31G(d) for model compounds containing sulfur atoms and scaled HF/6–31G(d) for all remaining compounds. The green lines represent deviations of ± 0.5 kcal/mol.

Table 6.

Statistical analysis of the differences in the interactions with water and dipole moments with respect to the relevant target data for all model compounds parametrized as part of the present study. Results include Average Deviation (AD), Root Mean Square Deviation (RMSD) and Absolute Average Deviation (AAD).

		data points	AD	RMSD	AAD
||μ||	compared to MP2	78	30%	37%	32%
	compared to HF	65	27%	35%	30%
μ direction	compared to MP2	78	5.1	8.5	5.1
	compared to HF	65	5.0	8.1	5.0
Water interaction energy (kcal/mol)		437	0.07	0.34	0.20
Water interaction distance (Å)		437	0.11	0.20	0.16
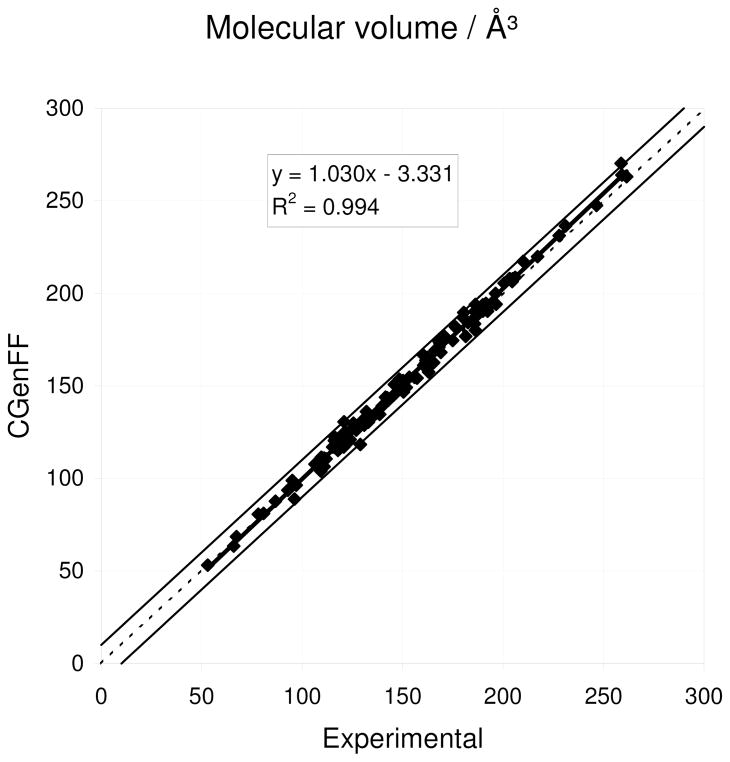
Molecular volume (Å3)		111	0.6%	2.6%	2.1%
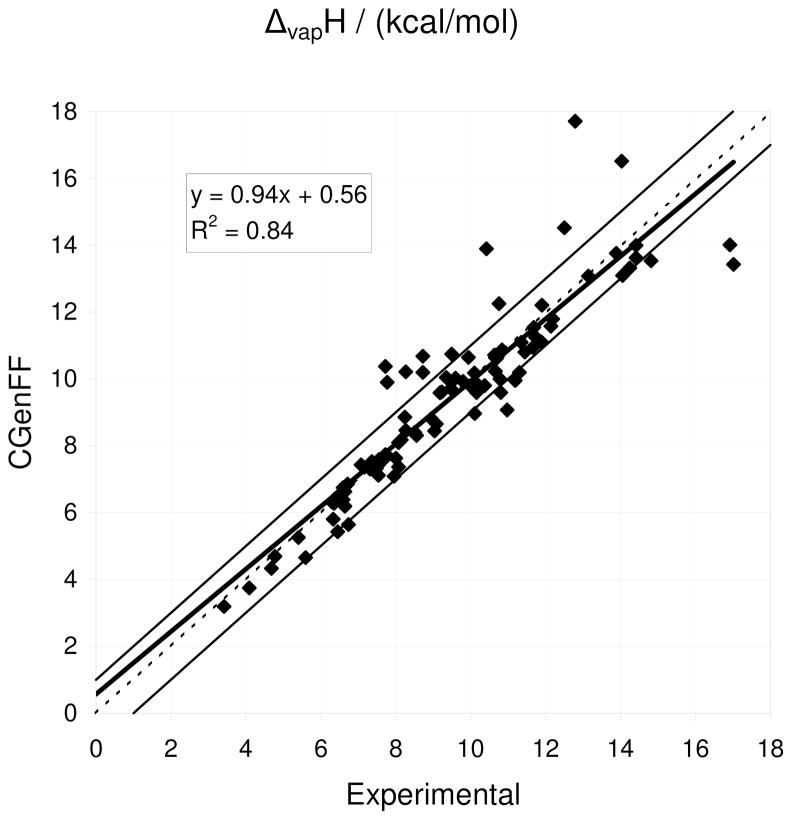
Heat of vaporization (kcal/mol)		95	−0.3%	10.6%	7.0%

As previously discussed, charge optimization involves systematically overestimating the charges, thereby implicitly polarizing the molecules. This is evidenced by the systematic overestimation of the dipole moments by 30 and 27 % with respect to the MP2/6–31G* and HF/6–31G* levels, respectively, based on the average difference (Table 6). The orientations of the dipole moments are generally satisfactory.

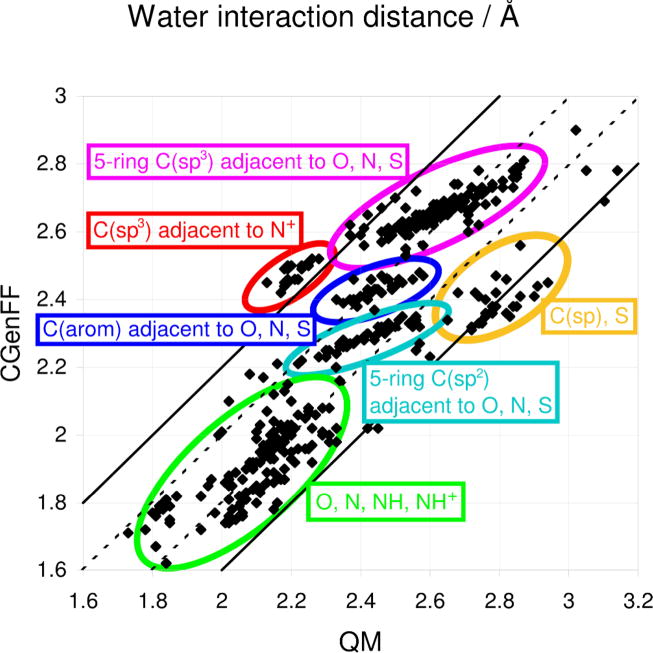
Further investigation of the nonbonded terms in the model was performed by analyzing the interaction distances of the minimized model compound-water complexes. Correlation plots of the QM and CGenFF results are presented in Figure 8. As discussed in the methodology, hydrogen bonds should be 0.2 Å shorter than the HF interaction distances to properly reproduce pure solvent properties.^40–43 In contrast to the interaction energy results in Figure 7, interesting trends associated with subsets of compounds are evident. These different subsets have been circled to identify the classes of molecules with which they are associated. Hydrogen bonds involving heteroatoms, circled in green, show good correlation between the 0.2 Å offset QM and CGenFF results, as evidenced by the fact that their data points are clustered around the lower dotted line. This is expected as both the energy scaling and distance offset for the HF/6–31G(d) level of theory were developed based on interactions dominated by moieties containing these atom types (ie. hydrogen bonding functional groups).^40–43 Interactions involving sp² carbons adjacent to heteroatoms in 5-membered rings also show good correlation with the offset QM data (cyan circle). This is due to the charges as well as the LJ parameters on these carbons typically being optimized to reproduce their interactions with water and pure solvent properties. For the interactions involving aromatic carbons and sp³ carbons adjacent to heteroatoms in 5-membered rings (ie. C-H…OHH bonds, represented by the blue and magenta series, respectively), the data points are clustered around the upper dotted line, indicating that their CGenFF interaction distances are close to the QM results. Indeed, the 0.2 Å offset may not apply for these classes of compounds due to their diminished hydrogen bonding character. Furthermore, the pure solvent properties used to optimize the LJ parameters for this class of molecules are dominated by nonpolar interactions. This effect also accounts for the fact that for sp³ carbons adjacent to nitrogen atoms carrying a positive charge (red circle), the CGenFF distances are systematically too long. Nevertheless, the interaction energies of these interactions, which are typically less favorable than standard hydrogen bonds, are adequately reproduced. Generally speaking, the lack of more ideal agreement with the target QM is due to the inherent limitation that the LJ parameters in a class I additive force field are not sensitive to the presence of adjacent electron withdrawing or positively charged functional groups. Indeed, this appears to contribute to the slopes for these classes in Figure 8 being too small. The final class of interactions, involving sulfur atoms and sp hybridized carbon and nitrogen atoms (orange circle), are systematically shorter than the target data. With the sp carbon atoms, it was found that this shortening was necessary to obtain good bulk solvent properties and, in the case of nitrogen, to reproduce QM water interaction data for the linear complex. We speculate that this is due to the fact that a diffuse electron cloud surrounds sp centers in all directions except along the bond axis. Similarly, for the sulfur atoms, the discrepancy in hydrogen bond distance is due to the increased radii and diffuse character of these atoms. When this class of functional groups was initially parametrized, it was found that the HF/6–31G(d) level of theory and its standard scaling and offset rules were not appropriate, and it was necessary to apply the MP2/6–31G(d) level of calculation for the interactions with water. Subsequently, it was found that the MM minimum interaction distances had to be significantly shorter than the corresponding QM distances at this level of theory, in order to obtain the correct pure solvent properties (A.D. MacKerell, Jr., unpublished). Overall, while many of the minimum interaction distances in CGenFF differ significantly from the QM target values, it should be emphasized that the most favorable interactions, which will make the largest contributions towards interactions of molecules with their environment, are the most accurately treated in the force field.

Figure 8.

Comparison of the QM and CGenFF minimum water interaction distances for the model compound-water monohydrate interactions. The QM level of theory is MP2/6–31G(d) for model compounds containing sulfur atoms and HF/6–31G(d) for all remaining compounds. Green: direct interaction with heteroatoms (O, N, NH, NH⁺); cyan: 5-membered ring C(sp²) adjacent to heteroatom; blue: C(aromatic) adjacent to heteroatom; magenta: 5-membered ring C(sp³) adjacent to heteroatom; red: C(sp³) adjacent to N⁺; orange: C(sp), S. The bottom dotted line represents the situation where the CGenFF distance is 0.2 Å smaller than the QM distance, as ideally would be the case for regular hydrogen bonds. The top dotted line represents CGenFF=QM, which is the ideal case for interactions that have a weak hydrogen bonding character. The top and bottom solid lines represent deviations of ± 0.2 Å.

An important metric by which to judge the quality of the nonbonded parameters is their ability to reproduce condensed phase properties. Accordingly, for the compounds that are liquids at room temperature and for which experimental data are available, molecular volumes and heats of vaporization were determined via MD simulations of the pure solvents. Results for the 111 molecular volumes are shown in Figure 9 with statistical analysis in Table 6.^§ As is evident, the force field does an excellent job at reproducing the experimental volumes. This is substantiated by the average difference being 0.6 % though the absolute average difference is 2.1 %. This small average difference is important because it indicates that the force field does not have a bias towards larger or smaller molecular volumes. Concerning the heats of vaporization, the results are shown in Figure 10 for the 95 compounds for which experimental data is available, with statistical analysis in Table 6. Although deviations for this quantity are slightly larger than for the molecular volume, overall, the agreement is satisfactory over a wide range (3–14 kcal/mol). As with the molecular volumes, the average difference for the heats of vaporization is near zero (−0.3 %) while the absolute average difference is much higher (7.0 %), again indicating that the force field has little bias towards over- or underestimating the nonbonded interactions occurring in the pure solvents. The ability of CGenFF to satisfactorily reproduce the pure solvent properties demonstrates the overall quality of the nonbonded parameters. While the partial atomic charges were optimized for the majority of molecules on which the pure solvent properties were calculated, in most cases the LJ parameters were directly transferred from other molecules. This gives confidence that transfer of LJ parameters to chemically similar molecules in the future, combined with the appropriate charges, will yield satisfactory nonbonded representations.

Figure 9.

Molecular volumes from pure solvent simulations of the model compounds that exist as liquids at room temperature. The thick line is the regression line for which the equation is shown. The dotted line represents perfect reproduction of the experimental data, while the thin parallel lines represent deviations of ± 10 ų. The experimental molecular volume of each compound was derived by dividing its molecular mass by its experimental density. Experimental densities were mostly obtained from the catalog of Sigma-Aldrich^®,⁷⁵ supplemented with data from the CAS REGISTRY^SM (accessed through the SciFinder Scholar^® interface), from the CRC Handbook of Chemistry and Physics,⁷⁶ and from the catalog of TCI America.⁷⁷

Figure 10.

Heats of vaporization from pure solvent simulations of the model compounds that exist as liquids at room temperature. The thick line is the regression line for which the equation is shown. The dotted line represents perfect reproduction of the experimental data, while the thin parallel lines represent deviations of ± 1 kcal/mol. Experimental data were mostly obtained from reference ⁷⁸, supplemented with data from Dykyi,⁷⁹,⁸⁰ Geiseler and Rauh⁸¹ (obtained through the NIST Chemistry Webbook⁸²) and the CRC Handbook of Chemistry and Physics.⁷⁶

Bonded parameters

Optimization of the bonded parameters focused on geometries, vibrational frequencies and dihedral potential energy scans calculated at the MP2/6–31G(d) level of theory. Statistical analyses of differences between the optimized QM and MM geometries and vibrational spectra for the model compounds are reported in Table 7. As is evident, the CGenFF minimized geometries are in excellent agreement with the target data. Again, this is not unexpected as the the associated force field parameters were explicitly optimized to reproduce these data. However, it should be emphasized that the majority of parameters that apply to any particular model compound were optimized previously on a different model compound. Thus, the observed level of agreement is not trivial and supports the transferability of the parameters in the context of pharmaceutical compounds. Overall, the vibrational frequencies, while somewhat less ideal than the geometries, are still well within acceptable limits (Table 7). The +4% mean deviation indicates that on average, the vibrational frequencies are slightly overestimated. This reflects the fact that the MP2 frequencies were scaled down by a factor 0.943 prior to parametrization and analysis, which proved to be less appropriate for the lower modes involving torsions. Indeed, these low frequency modes are generally parametrized targeting QM dihedral potential energy scans as described above. This process typically yields vibrational frequencies for the related torsional modes that are close to the unscaled MP2 results. It should also be noted that only frequencies lower than 2700 cm⁻¹ were considered, as fitting of higher frequencies due to hydrogen stretching is trivial and these degrees of freedom are typically being constrained by SHAKE during MD simulations. In combination, the ability of the force field to reproduce both the geometric and vibrational target data indicates the quality of the bonded parameters in CGenFF.

Table 7.

. Statistical analysis of the internal geometries and the vibrational frequencies for all model compounds parametrized as part of the present study. Average Deviation (AD), Root Mean Square Deviation (RMSD) and Absolute Deviation (AAD) are presented. Only the vibrational frequencies lower than 2700 cm⁻¹ were considered.

	data points	AD	RMSD	AAD
Bond lengths (A)	899	−0.0003	0.016	0.012
Valence angles (deg)	1420	−0.0945163	1.50627	1.07109
Dihedrals (deg)	137	−1.0	7.3	3.5
Vibrational frequencies	2619	3.6%	19.7%	6.4%

Summary

Presented is an extension of the biomolecular CHARMM all-atom additive force fields to drug-like molecules. Due to the general nature of this class of compounds, the force field is referred to as the CHARMM General Force Field, or CGenFF. While initial creation of CGenFF was based on the CHARMM biomolecular force fields, that process involved eliminating a number of overlapping parameters, thereby sacrificing the ability of CGenFF to accurately treat biological macromolecules. Therefore, when studying proteins, nucleic acids, lipids or carbohydrates in conjunction with CGenFF, the original biomolecular force fields must be used for those biomolecular parts of the system.

Emphasis in the development of the force field was placed on supplying highly optimized chemical building blocks that users can assemble into their molecules of interest. This allows for CGenFF to focus on the accuracy of both the nonbond and bonded aspects of the model. To achieve this, the force field is based on a hierarchical optimization approach where, as each new model compound is added to the force field, only those new parameters that are unique to that molecule (ie. not previously available in the force field) are optimized. This maximizes the ability of CGenFF to reproduce the target data, while maintaining the integrity of the force field. Results presented in this manuscript indicate that the model does indeed accurately reproduce geometric, vibrational and energetic data, including interactions with water, as well as satisfactorily reproducing the experimental molecular volumes for 111 pure solvents and heats of vaporization of 95 molecules.

As CGenFF is designed to act as the basis for building larger, more complex molecules, an extensive description of the parametrization approach is presented. This includes the type of target data required to either validate or optimize the force field, the procedures to extend the force field to new molecules and the procedures to optimize parameters associated with those new molecules. The latter includes procedures to link individual rings to produce larger, more complex molecules. Consequently, CGenFF can be expected to grow steadily towards a more complete coverage of chemical space. To facilitate this effort, a variety of scripts and programs are included in the supplementary material and may be obtained from the website of the MacKerell laboratory.⁵³