Cue salience and infant perseverative reaching: tests of the dynamic field theory

Abstract

Skilled behavior requires a balance between previously successful behaviors and new behaviors appropriate to the present context. We describe a dynamic field model for understanding this balance in infant perseverative reaching. The model predictions are tested with regard to the interaction of two aspects of the typical perseverative reaching task: the visual cue indicating the target and the memory demand created by the delay imposed between cueing and reaching. The memory demand was manipulated by imposing either a 0- or a 3-second delay, and the salience of the cue to reach was systematically varied. Infants demonstrated fewer perseverative errors at 0-delay versus 3-second delay based on the cue salience, such that a more salient visual cue was necessary to overcome a longer delay. These results have important implications for understanding both the basic perceptual-motor processes that produce reaching in infants and skilled flexible behavior in general.

Introduction

Stability and flexibility are hallmarks of skilled behavior. Stability depends on incorporating previous experience into the present. Flexibility requires forgoing past ways of doing things and shifting responses to meet new demands. One task that has been widely used to study the early development of flexible responding is Piaget’s (1954) A-not-B. Originally proposed as a measure of infants’ ability to represent objects independent of their own action, the task consists first of repeated hidings and findings of objects in one location (A) and then a shift trial in which the object is hidden in a new location (B). Given a delay between hiding and search, infants 8 to 12 months of age typically perseverate on the shift trial, searching at A rather than at B. This task is now generally understood as one of a class of executive control tasks that require flexibility in the face of a past stable response (e.g. Zelazo, Müller, Frye & Marcovitch, 2003; Marcovitch & Zelazo, 1999; Munakata, 1998; Diamond, 1991). The paper uses this task to explore the dynamics of stability and flexibility in infants as a function of the strength of the cue to shift to a new response.

Stability and flexibility are fundamentally about the integration of processes operating over different time scales – at minimum, processes of longer term memories of past actions and short-term memories of the more recent cue. The nested dynamics of memory processes in the A-not-B task is formally accounted for by the Dynamic Field Theory (DFT; Thelen, Schöner, Scheier & Smith, 2001). The experiments reported here test novel predictions of DFT. The plan of the paper is as follows: First, we present an overview of the DFT model. Study 1 then presents the formal simulations and Study 2 an experimental test of the model predictions. In the General discussion, we consider the implications of these ideas and results for thinking about flexibility and stability in general and also with respect to other accounts of the A-not-B error.

Dynamic processes in reaching

The variant of the A-not-B task that we consider in this paper is a cued reaching task (e.g. Clearfield, Diedrich, Smith & Thelen, 2006; Diedrich, Highlands, Spahr, Thelen & Smith, 2001; Thelen et al., 2001; Diedrich, Thelen, Smith & Corbetta, 2000; Smith, Thelen, Titzer & McLin, 1999; Munakata, 1997). Two objects are placed on the table and are continuously in the infant’s view. The experimenter cues one by waving it. The infant must remember this cue because a delay is imposed before the infant is allowed to reach. This cycle of a cue, a delay, and an allowed reach is repeated several times for a series of A trials. Typically on these trials, infants reach to the cued target. Then, on the shift trial, the experimenter cues the other target – by picking it up and waving it. Here, after the delay, infants typically reach back to A, just as in Piaget’s original task. The DFT account is derived from a general theory of the dynamics of motor planning (Erlhagen & Schöner, 2002; Thelen et al., 2001) and has been shown to account for at least some aspects of infant performance in this task. Accordingly, as an introduction to the DFT – as an effort to make its formal predictions more intuitive – we give an overview of the processes and task factors relevant to directed reaching to a target.

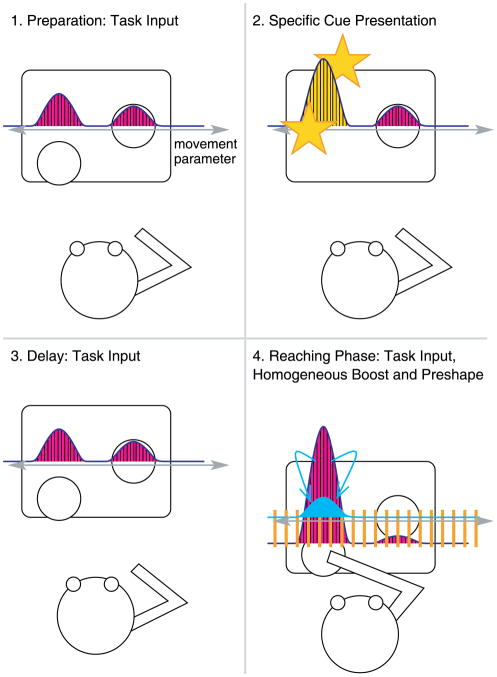
Consider, first, the task of reaching for a single target resting on a surface. Doing this requires activating a motor plan that specifies a direction in space. Many factors will impact these plans and reaching directions (Thelen et al., 2001; Smith et al., 1999) but since there is one final pathway, movement of the arm, these must be integrated into a single decision concerning the direction to reach. One such factor is the mere presence of a reachable object. If two objects are sitting near each other with all else being equal, there should be an equal probability to reach to either object. Whether any such reach occurs will depend on whether the activation generated by the object surpasses some threshold. Furthermore, the activation may be tipped in favor of one object over the other if one object is closer to the reacher than another. In the DFT, the activation of motor plans generated simply by the presence of two possible reaching targets is called the task input and is illustrated in Figure 1 by the pink curve (see also Table 1). The motor planning field (blue curve) codes for the relevant movement parameter (gray double-arrow), which for the task described here (reaching for one of two identical targets) is simply the reaching direction, that is some location in space. For each location in space, the relative amount of motor planning activation determines the tendency to reach in that particular direction.

Figure 1.

Inputs to the dynamic field in different situations. The motor planning field (blue curve) codes for the relevant movement parameter (gray double-arrow), which for this task is simply the reaching direction. The pink curve represents the task input, and the yellow curve is the specific input (the transient visual cue to one location). The turquoise curve is the preshape (motor memory), and the orange bars represent the homogeneous boost from pushing the box into infants’ reaching space.

Table 1.

Key terms of the dynamic field theory model

Term/Symbol in the model	General definition	Applied to the perseverative reaching task
Behavioral dimension φ	The behavior required to realize an action decision	A reach to a particular location
Motor planning field ump	Neural coding of movement preparation, only a sabele peak state represents a decision	Tendency to reach to some location at any given time
Task input stask	The perceptual layout of a given task	Two identical targets near each other
Specific input sspec	The transient directing of attention to an aspect of the task	Waving and calling attention to one of the targets
Homogeneous boost hboost	Increasing activation equally in the field	General motivation to execute a movement, by pushing the targets within reachable space
Preshape activation upre	Recent behavioral history	Accumulated memory for recently performed reaches

The above description concerns static potential targets sitting in view of the reacher. However, attention may also be drawn to a target by some event (second panel of Figure 1), for example, the experimenter telling the subject to pick it up, pointing at it, or picking it up and waving it. This is mapped in the model by the specific input (yellow curve) which induces a localized peak in the motor planning field at the cued location. If a brief delay is imposed between this cue and when the reach is allowed, the activation induced by the specific input is no longer available and the corresponding motor planning peak is expected to decay (third panel of Figure 1). The delay is then terminated by some event that enables reaching (the subject’s being told it’s time to reach or the targets being pushed into reachable space). The termination of the delay presumably causes a generalized excitation in the motor planning field and is modeled as a homogeneous boost (orange bars) that increases the activation equally in the entire field (last panel of Figure 1). Whenever the activation in the field reaches a certain threshold, neural interactions – local excitation and global inhibition – are set in action which in turn allow for a single localized peak to form. Its location specifies the direction in which a reach may be executed. These dynamic processes, from cue to reach, are proposed to underlie the evolution and execution of a reaching plan.

But there are other processes operating at slower time scales that are also relevant. Specifically, the execution of a reach will leave a memory trace for that movement, which is modeled as the accumulation of preshape activation (turquoise curve). This kind of motor memory build-up is possible because the reaching decision is maintained (by the neural interactions within the field) long enough to generate a consistent motor memory trace in the parameters that actively encode the reaching direction. By this mechanism, recent reaches supply input to the motor planning field on subsequent trials.

The integration of these processes can create a conflict, if the subject has reached first to one location (location A) a number of times, and then a target at a different location (location B) is cued. This should create a conflict because the previous reaches create a motor memory that potentiates the formation of a peak at the first location, whereas the specific input (the new cue to reach to the second location) potentiates activation in the field at that second location. Where the infant reaches depends on the relative strengths of these two conflicting inputs to the field at the moment the reach is allowed. This paper is specifically concerned with two factors relevant to the resolution of this conflict: the salience of the specific cue calling for a shift and the delay between the cue and when the infant is allowed to reach. The peak induced by the specific cue at the new location will decay during the delay between the cue and the reach (as it did on the initial A trials). But on the B trials this allows the preshape in the field (due to the prior reaches to A) to dominate. The goal of this paper is to understand the dynamics of the strength of the memory for previous reaches to A and the strength of the specific cue as a function of decay. We seek to understand when perseveration does or does not occur as a function of the integrative response of the field to both the immediate input and the memory from previous reaches. Altering the relative strengths of these inputs to the decision to reach should systematically alter the response of the field.

We summarize here the major claims relevant to this paper. First, this model is a general model of goal-directed behavior designed to capture the dynamic balance between stability and flexibility that produces behavior. Second, because decisions in the moment always integrate the immediate present and the just-previous past, there is always a tendency to perseveration as well as flexibility. Which outcome occurs is the product of the intrinsic dynamics of the field, the strength of the just-previous history (preshape), the strength of the immediate (specific) input, and the time delay between that specific input and the execution of a reach. Although perseveration is likely for young infants, which has been amply demonstrated in many experimental studies (e.g. Clearfield et al., 2006; Thelen et al., 2001; Smith et al., 1999; Munakata, 1998; Piaget, 1954), ‘flexibility’ should also be possible. Perseveration and flexibility – even in an ‘infant’ system with hard to achieve and rapidly decaying memory for the specific input – should be systematically related to the relative strength of the specific input and the previous reaching history and should also be systematically related to the delay over which that more immediate memory must be maintained. Study 1 shows how this is achieved by simulating the DFT model; behavioral tests are presented in Study 2.

Study 1

The specific version of the repetitive reaching task chosen as the starting point for the simulations typically induces perseveration in 80% of 8–10-month-old infants (e.g. Smith et al., 1999; Munakata, 1997). This task includes six trials to one location (A) followed by two cues to the second location (B), with identical reaching targets and a 3-second delay between the specific cue and reaching. The structure of this particular version of the A-not-B task enhances the likelihood of reaching to A on the A trials by providing (on the initial A trials) a stable task input throughout the delay that should induce a stronger peak in the field. This is done by placing the A target slightly closer to the infant on the first three A trials (see Figure 2 for the task input across all trials). This increased task input to the A location increases the likelihood of a reach to A. The reach in turn creates a preshape trace for A, thus increasing the probability of the next reach to A. Following the three A trials with this increased task input are three A trials with even task input (the objects are placed equally distant from the infant). Then, there are two B trials, where the second object is cued, and again, both objects are equidistant from the infant.

Figure 2.

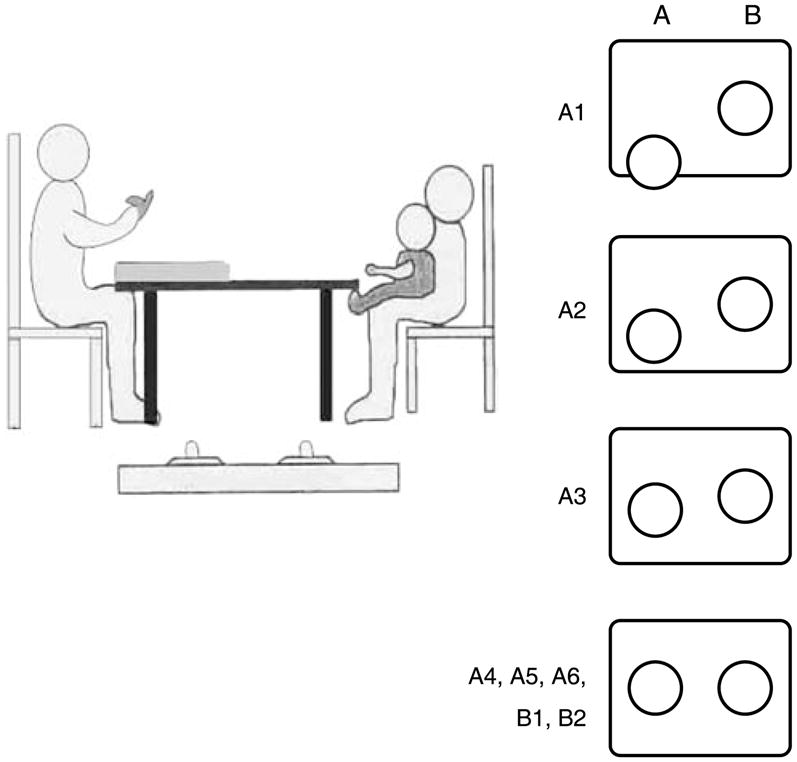
Overview of the infant reaching task. The left panel shows a side view of the set-up and materials, and the right panel illustrates the training procedure.

The model

The effect of variants in the strength of the specific cue as a function of delay is investigated in a DFT model that describes the coupled dynamics of young infant motor plans and their preshape (motor memory) under the influence of the repetitive reaching task. The model used in the present simulations is a version of the dynamic field theory proposed by Thelen et al. (2001) and extended by Dineva (2005). The model is a set of integro-differential equations (see Appendix A) that describe a tightly coupled and interactive dynamic system, where the motor planning field evolves under the influence of the internal cooperative interactions and its own recent history, while in turn both neuronal interaction and motor history also depend on the current state of the field dynamics.

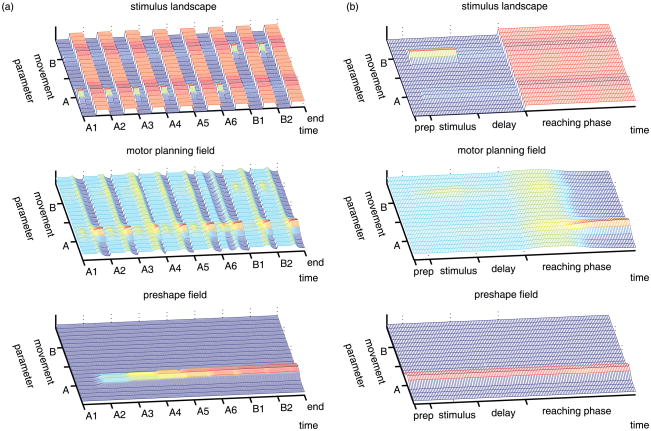
To simulate the task (see Appendix B), the DFT model is exposed to six A trials with the specific cue at A, that are followed by two B trials. Figure 3 illustrates the typical time course of this experiment. The top panel of Figure 3(a) shows the stimulus landscape over the entire session, including both A and B trials. The bottom panel shows the preshape field, which carries the history of many reaches to A. All those inputs influence the evolution of the motor planning field, which is plotted in the middle. Critically, over the six A trials, stimulation is typically stronger to the A side (due to the increased task input of the closer A target on the first A trials), which makes the motor planning field form a stable peak there. The pronounced peaks in the middle panel at the end of each trial represent reaches, which then leave a trace in the preshape field. Over the course of the trials, the preshape trace at the A location slowly grows (as seen in the bottom panel).

Figure 3.

Dynamic field model in a typical A-not-B task: plot (a) shows the simulation of the entire experiment whereas plot (b) zooms on the details of the first B trial. The top panels show the stimulus landscape, as it is given by the experimental setting, and which supplies the input to the motor planning field (plotted in the middle). The bottom panels show the preshape field, or motor memory, which is accumulated with each reach, represented by the stable above threshold peaks during the reaching phase. The preshape field is another input source for the motor planning field.

On the first B trial (zoomed in for Figure 3(b)), the motor planning field evolves under competing influences – one comes from the stimulus landscape and pulls to B, and the other is the preshape trace to A, which is the system’s own recent history. The task-related environmental influences are again pictured in the top panel. At the beginning of the trial, the presentation at the B location induces a corresponding peak in the motor planning field (due to the same mechanism as on the A trials). However, when the presentation is over, the peak in the motor planning field decays gradually during the delay. At the start of the reaching phase, the field is then boosted with increased activation across the entire field (corresponding to pushing the targets into infants’ reaching space). Now, a new peak forms at the location where the inputs are highest, which is the A location because of the preshape trace. In this example, perseveration occurs.

Predictions

One factor that impacts whether or not the preshape trace will dominate over the specific cue to the new location is when the decision to reach is made (Dineva, 2005). As shown in Figure 3(b), right after the specific input to B, there is strong activation on the B side, and weak activation on the A side from the preshape trace. It is during the delay that activation at B decays, falling below the task plus preshape activation at A. Thus, the probability of a reach actually happening to A is time-dependent: If the delay is interrupted earlier, the influence of the specific cue at B on the final reaching decision will be stronger.

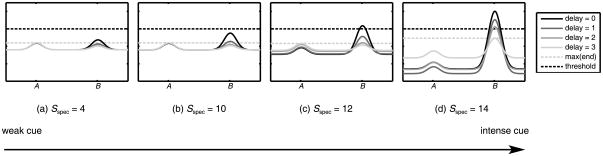
Another important factor in the evolution of where to reach to a particular location is the salience of the specific cue. Stronger cues will induce higher peaks which then will take longer to decay completely. Figure 4 shows delay phases for simulations using different cue strengths ranging from weak to strong. For a weak cue at B immediately after stimulation (black curves), the motor planning activation at B might not be sufficient to overcome the preshape trace at A. If the stimulating event is rather dull, the model (and infants) may make perseverative errors. However, if the cue is stronger, it will induce a higher activation peak at B, which will override the preshape to A. Thus the prediction is that perseverative errors should gradually decrease for increasing specific stimulation.

Figure 4.

Cue strength/delay interaction on the B trial in an ideal model without noise. The black solid line shows the impact of the specific stimulation of a different strength – weak (a), moderate (b), strong (c), or intense (d) – on the motor planning field right before the delay begins. A gray-scale code shows the gradual fading of the motor planning activation during the delay period: the lighter the curve, the more time has passed since cuing. The dark dashed line marks the threshold for neural interactions, and the light dashed line shows the maximum field activation at the end of the delay. After the delay, the impact of a cue is marked by the difference of activation between A and B (the distance of the B peak from the light dashed line).

But introducing a long delay changes the dynamic balance among the inputs. If the specific input is strong enough to persist over the delay, it should lead to B side reaches, even after a delay. The gray scale code in Figure 4 illustrates the fate of the peaks during the course of the delay. With a 3-second delay (thinnest gray curves), the model showed above-threshold activation only for the most salient cue. The difference in that case is that the cue was strong enough to pierce the threshold and engage the cooperative interactions between the excited field sites, which significantly slowed the decay of the peak.

These predictions are explored in a series of simulations where the salience of the specific input was systematically varied from S_spec = 4 to S_spec = 17 over different delays. The value of the specific input parameter reflects the strength of the perceptual input of the transient cue given at the start of the trial.

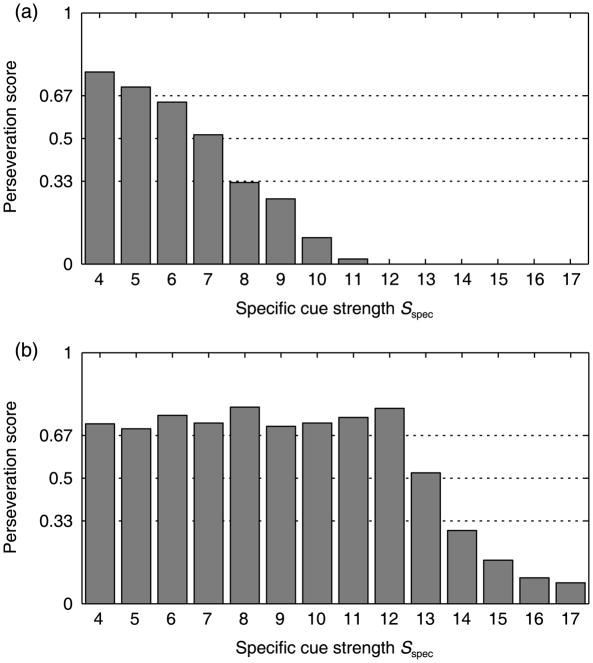
Recall that fluctuating input strengths (i.e. a non-deterministic model) are used to capture the variability inherent in any task. To generate stochastic power, each cue strength condition was realized 300 times for each of the two different delay conditions (no delay or a 3-second delay). For each simulation, a perseveration score was computed as the mean number of reaches to A on both B trials. The resulting perseveration rates per condition are plotted in Figure 5.

Figure 5.

Results of the dynamic field model in simulations without delay (a) and with delay (b). Shown are mean perseveration scores (y-axis) versus specific cue strength (x-axis).

The simulations confirmed the predicted nonlinear effects of linear changes in the specific input. Without delay (Figure 5(a)), and when the cue salience is low, the model shows a high perseveration rate. As the cue strength increases, the perseveration rate drops gradually. In this situation, the preshape trace accumulated on the A trials is quite directly matched against the very recent cue presentation – the stronger the impact of the cue, the fewer perseverative errors are made. In contrast, with a delay (Figure 5(b)), perseveration rates depend nonlinearly on the cue strength. In particular, perseveration remains high for a wide range of cue strengths, and drops fairly suddenly only at the highest salience cues. Note that this sudden drop of perseverative errors was predicted based on whether the cue is strong enough to engage the cooperative interactions among the stimulated neurons. When this happens, there is much more activation in the system than just that which comes from the stimulation.

These simulations demonstrate that perseveration is not a property of the system, but rather a potential behavior that can emerge given certain circumstances. The model demonstrates how behavior is integrated across multiple time-scales, and how the extent to which behavior is pulled to the just-recent past depends on the strength of the present cue. The crucial difference between the most intense cue and the less salient cues is that it is strong enough to engage the cooperative interactions in the motor planning field because it reaches the aforementioned threshold (detection instability is the technical term for this kind of threshold piercing, when a slight change of stimulation leads to drastic difference in how the system responds). Here, the local excitatatory interactions significantly slow down the decay of the peak.

In addition, the model emphasizes the critical influence of time in decisions to act. The decision to reach depends on the strength of the preshape compared to the strength of the specific input, but which side dominates also depends on when the decision to act occurs. If the decision occurs immediately after the specific cue, it is more likely to overpower the preshape, depending on the particular strength of the cue and the preshape.

The experiments that follow test these predictions in infants by systematically varying the salience of the specific cue across two different memory demands.

Study 2

The DFT model simulations provided key predictions about the interaction between the specific input and the delay; in particular, perseveration rates should depend on both salience of the cue and delay. Without a delay, perseveration should be high at weak specific cue strengths and should drop as the salience of the cue increases. In contrast, with a delay, perseveration should persist across a wider range of specific cue strengths, and then drop for very strong specific cue strengths. Over the course of the delay, the memory for the less-salient cues should fade, leaving only a strong preshape for A which then dominates the reaching decision. Only the strongest cue will be retained (helped by neural cooperativity) over the course of the delay, and overpower the preshape to result in incorrect reaching.

These predictions were tested by manipulating the strength of the specific cue, the signal that directs attention to one target or the other. There are several ways that one might do this. We chose to manipulate the visual properties of the cueing objects since it seems likely that these are relevant to the infants. Specifically, infants were presented with pairs of identical reaching targets. Across three between-subjects conditions, these targets varied in their intrinsic attention-getting properties. In all conditions, the targets were placed on a uniform brown presentation box from which they were picked up and cued. In all conditions, when on the presentation box, the targets were the same plain brown color (thus the task input was the same in all conditions). However, the undersides of the targets – what the infants saw when the experimenter lifted and presented the cue – differed. In the low-strength condition, the underside and thus transient display aspect of the targets were painted this same brown, in the medium-strength condition, the undersides were painted red, yellow and blue with stripes and polka dots, and in the high-salience condition, the undersides presented multi-colored flashing lights. The scale of these differences is not known and thus exactly where these different strengths fall with respect to simulations is also not known. However, the intrinsic attention-getting properties (and thus cue strength) vary considerably – and in an orderly manner – from merely a movement of a target the same color as the backdrop, to a movement that reveals colorful markings, to a movement that reveals both colorful markings and flashing lights. The key prediction was that the different cue strengths would impact infants’ rate of perseveration differently in no-delay and delay versions of the task.

Method

Participants

A total of 108 (54 males, 54 females) 9-month-old (±2 weeks) infants participated in the study. The infants were full-term, non-disabled, and primarily from white, middle-class families. An additional 15 infants were recruited but not included in the analyses due to experimenter error or fussiness (four in the low-salience conditions, four in the medium-salience conditions and seven in the high-salience conditions). Eighteen infants were randomly assigned to each of two Delay times for each of three specific cue conditions. Infants were recruited from published birth announcements, and families received a small gift for participation.

Apparatus

Infants were tested in a brightly lit room with relatively uniform walls while they sat on a parent’s lap at a table across from the experimenter. All infants were tested with round wooden objects (9.5 cm diameter, 0.7 cm height) with a knob in the center and all were painted brown except on the bottom, the non-visible underside when the objects were at rest. After cuing, the experimenter placed the objects on a brown cardboard box (30 cm × 23 cm × 5 cm) 12.5 cm apart (center to center) on the box. All sessions were videotaped.

Three levels of salience were created by painting the undersides of the objects. Only the underside of the objects was painted so that once the object was cued and placed on the surface, the pattern was no longer visible. Note that this altered only the specific input, the transient cue, and not the task input, which remained constant across conditions. The bottoms of the objects differed in the following way:

1. Low salience: plain brown bottom, matching the top of the object and the box.

2. Medium salience: red, yellow, and blue stripes with polka dots.

3. High salience: three multi-colored flashing lights attached to object bottom.

Procedure

Infants were given the opportunity to play with the objects prior to the start of the experiment. This is a typical aspect of the A-not-B procedure as infants are more likely to reach for familiar objects. Infants were cued to reach to the A side six times, followed by two cues to the B location. Which side was cued first was counterbalanced across infants. The experimenter waved and tapped the object to capture infants’ attention. For the first A trial, the object was placed so that it was hanging over the edge of the box (see Figure 2). Over the next three trials, the experimenter gradually moved it farther back until, on the fourth A trial, it was even with the B object, which remained midline on the box. The experimenter then presented the infant with two more A trials with the objects even, and then two B trials, again with the objects even. In the No-delay condition, on each trial the box was pushed into infants’ reaching space immediately after cueing the object. If an infant did not reach after approximately 30 seconds, the trial ended. If an infant failed to reach twice in a row, the experiment stopped and the infant was excluded from further analyses. The Delay condition was identical, except that on each trial the experimenter paused for 3 seconds after cueing the object and placing it on the box. Then, after the delay, the box was pushed to the infants’ reaching space.

Behavior was scored from the videotapes. The first object the infant touched was judged as the side contacted. In the event that an infant reached with both hands, the videotape was played frame by frame to determine which object he or she reached first. Two observers scored each infant: agreement on the hand contacting first was 100%.

Results and discussion

The first analyses examined infants’ reaches to A on the six A trials. Consistent with past research and as indicated in Table 2, infants mostly reached correctly to A in all three conditions both with and without delay. A 2 (Delay) by 3 (Specific cue condition) ANOVA yielded only a reliable main effect of delay with infants in the No-delay condition reaching correctly on 90% of the A trials and those in the Delay condition reaching correctly on 82% of the A trials, F(1, 102) = 5.75, p < .02. This effect of delay is not surprising since the transient signal to A may (just like the signal to B on B trials) be expected to decay. However, relevant to the key question for this study – the role of the strength of specific cue as a function of delay – there are three critical conclusions from these A trial performances. First, there should be a strong tendency to reach to A in all conditions and thus there should be a strong preshape to A on the B trials. Second, the lack of effect of Specific cue condition (and interaction with delay) suggests that any effects due to the Specific cue on the B trials cannot be due to the strength of the motor memory for prior reaches to A. Third, the relative strength of motor memories – as measured by A trial performance – works counter to the DFT’s critical predictions of the interaction between delay and specific cue on B trials. That is, motor memories for reaches to A trials are (perhaps only slightly) stronger in the No-delay than Delay condition, yet the model predicts – greater (or equal depending on the specific cue) perseveration in the Delay than No-delay condition.

Table 2.

Mean and standard error of infants’ reaches to A on the six A trials in the three Specific cue conditions under the two different delay intervals

Delay	0 delay	3-sec delay
Specific cue
Low	5.6 (.2)	5.2 (.2)
Medium	5.6 (.2)	4.9 (.3)
High	5.2 (.3)	4.7 (.3)

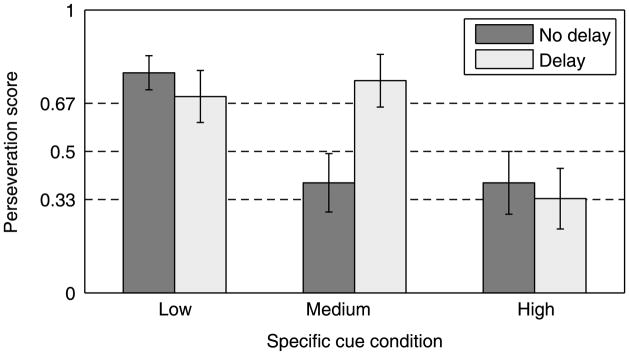
Infants’ performance on the two B trials was analyzed as follows: Each infant was assigned a perseveration score (0, .5, or 1) based on the number of reaches to A on the two B trials. A 2 (Delay) by 3 (Specific cue condition) ANOVA revealed a reliable effect of the Specific cue condition, F(2, 102) = 7.69, p < .001, and a reliable interaction between Delay and Specific cue, F(2, 102) = 3.38, p < .05. As can be seen in Figure 6, infants were more likely to perseverate given a Delay than No delay, as has been shown before (e.g. Wellman, Cross & Bartsch, 1986; Diamond, 1985). The new result is the finding that this effect of Delay depends on the salience of the specific cue. The ability to maintain the most recent cue in memory depends, as the DFT model predicts, on the strength of that stimulus cue. When there is no delay, perseveration will still occur if the transient signal that specifies the new direction is weak. This new finding is of some significance that will be discussed further in the General discussion. The results also show that even with long delay, perseveration is not inevitable; infants will shift to the new location if the specific cue calling for such a shift is salient enough. This interaction between delay and specific cue illustrates the importance of the dynamics – of the rise and fall of activations in the system as a function of sensory input and of memories – in determining the stability and flexibility in this task.

Figure 6.

Interaction plot of infants’ perseveration score in the Delay by Specific cue conditions.

These conclusions are also supported by an analysis of the performances of individual infants. Table 3 shows the number of individual infants reaching perseveratively on both, on one, or on neither of the B trials. As is apparent, in the Low-salience and High-salience conditions, the delay period seems to matter very little. When the specific cue that signals the need to shift flexibly to a different reach direction is weak, equal numbers of infants perseverate on both B trials, whether there is a delay or not. Likewise, when the specific cue that signals the need to shift the direction of response is very salient, nearly equal numbers of infants respond correctly, never reaching to A on the B trials. The effect of delay is seen only at moderate levels of cue salience. A comparison of the distributions of infants responding perseveratively on at least one B trial versus always responding correctly indicates a reliably different pattern of infant performances in the No-delay versus Delay condition for infants in the Medium-salience condition, χ²(1) = 6.36, p < .01, but not in the other two stimulus conditions.

Table 3.

Number of infants reaching to A twice, once or never on the two B trials in the three Specific cue conditions under the two different delay intervals

Number of reaches to A	0 delay			3-sec delay
	2	1	0	2	1	0
Specific cue
Low	10	8	0	10	5	3
Medium	5	4	9	13	3	2
High	6	2	10	5	2	11

This observed pattern of results fits the underlying dynamic process as conceptualized by the DFT. The addition of this delay between specific cue and reach impacts the rate of perseveration because the activation induced by the specific cue fades away during the delay. However, if the sensory cue itself is strong enough, it can engage the cooperative interaction within the motor planning system and the memory necessary for flexible responding can be maintained during the delay. Recall that in the field, interactions are nonlinear and are engaged only when activation at some sites (neurons) pierces a certain threshold; a strong specific cue – as the model predicts and the present results show – can do this. In brief, the interaction effect of cue strength and delay illustrates how both perseverative and correct responses emerge in the integration of memories operating on two time scales.

General discussion

Perseveration, by all accounts, arises because of competition between two sets of processes, one tied to more temporally distant past activity by the system and one tied to more immediate events. The competition between those two processes depends on the relative strength of the activation that drives each of them. However, these are dynamic processes operating over different time scales and the competition evolves and resolves in time. Perseveration, then, is an emergent behavior in a complex dynamic system. The goal of the dynamic field model, and the present simulations and behavioral test of it, is to understand the dynamic processes that underlie the trade-off between flexible shifting and perseveration, and in this way the tendency of immature, and potentially also compromised systems to perseverate. The present experiments provide new insights into these processes by examining the strength of the more immediate cue, the one signaling a need to shift, in this dynamic competition.

The most significant contributions – along with the general support they provide for the DFT model – are the following:

1. The strength of the specific cue (to shift) is not solely important but interacts (potentially nonlinearly) with the temporal properties of the task. This fact provides evidence for the different time scales of the two competing processes.

2. Developmentally immature systems – both simulations and babies – may perseverate even when there is no delay between the specific cue and the action. This indicates that the direction of a reach is always an integration of activation from memories for past reaches and immediate input. Perseveration is not simply a matter of not remembering the most recent specific cue; that memory must be integrated into the present task context. No other models have explicitly predicted such high rates of perseverative reaching in a standard A-not-B task with no delay.

3. Developmentally immature systems – both simulations and babies – will shift, following the specific cue, even given a delay between the cue and the signal to reach. Thus, perseveration is not an inherent trait of an immature system but instead is a potential of that system, emergent in tasks with specifiable characteristics.

4. The specific version of the DFT that predicts and explains these results implies that the processes that lead to perseveration or correct shifting by babies are fundamentally the same as those that lead to shifting in mature systems (Dineva, 2005). Moreover, the likelihood of shifting over perseveration can be increased by increasing activation in the field from the specific cue. This critical role for the amount of activation has potential implications for understanding why compromised cognitive systems (as well as immature ones) tend to perseverate.

Predictions and novel findings

The predicted findings, their explanation, and their implications derive most centrally from the theoretical requirement to stabilize activation by the neural interactions in the field; only stabilized activation can generate a response. This is what the current model adds to previous ideas of process competition that may lead under some circumstances to perseveration, as examined in the preceding DFT model by Thelen et al. (2001) and in the PDP (partially distributed processing) model by Munakata (1998). In both these models a faster process, similar to the evolving field in the current model, is understood as a working memory process. Such activation may be (as is often the case in the practical applications of these models) quickly changing and widely distributed over the entire space that is representing the final outcome. The new idea (see also Schöner & Dineva, 2007) is that such a transient ‘active process’ is not enough; instead, the key issue is the ability of the system to stabilize an activation peak that can be sustained by the neural interactions within the system without further input. This idea leads to two new predictions supported by the present results.

The first prediction concerns performance under No delay. None of the previous models has ever explicitly predicted that infants may perseverate in an otherwise standard perseverative reaching task without delay. This is because read-out is the instantaneous maximum right after stimulation. This allows for a relatively weak cue to have a direct and thus relatively strong impact, always leading to a correct response without a delay. However, a response does not happen even without a delay unless a threshold that leads to sustained internally generated activation is pierced. This competition can allow the weaker but longer lasting motor memory to win. The field interactions that then actively maintain this decision is what in this model serves as working memory supporting the behavioral response. This prediction and its empirical confirmation are a first in the infant A-not-B literature. Previous studies have shown that infants do not perseverate without a delay between the specific cue and the signal to reach (Marcovitch & Zelazo, 1999; Wellman et al., 1986; Diamond, 1985; Gratch, Appel, Evans, LeCompte & Wright, 1974; Harris, 1973). This is typically interpreted in terms of perseveration arising from the need to represent the target over a delay (Marcovitch & Zelazo, 2006; Diamond, 1985; Munakata, 1998): No delay implies no need to maintain a required representation and thus no perseveration. According to DFT, this is not precisely correct. Perseveration arises because of insufficient activation from the specific cue to the new target. This insufficient activation at the time of the signal to reach may arise either from a weak specific cue or from decay in activation over a long delay.

The second new prediction concerns performance under delay. With a delay, Thelen et al. (2001) predict a gradual decay of perseveration with an increased cue strength. Munakata (1997) has tested cue strength by increasing the salience of the cue between the A and the B trials, which resulted in fewer perseverative reaches (as the DFT would also predict). However, this finding rested on a change in cue salience during the experiment (between the A and B trials), rather than comparing different cue strengths that remained constant for each infant over the course of the experiment. But without testing this directly, it is still consistent with Munakata’s (1998) model that given a stronger cue (or more input units that one might associate with a more complex cue), one would expect more activation to specify the cuing location and thus directly reduce perseveration. However, infant perseveration is relatively frequent given a delay for all but the most salient cue. This was predicted by the DFT model, and is due to requiring an active working memory process (the formation of an activation peak that feeds back on itself) to be set in action and maintain the cue over the delay. The system is inherently nonlinear: a wide range of cues may be not sufficiently strong to pass the threshold and take advantage of the system’s cooperative interactions that can sustain activation, and thus a memory for the new cue. Even though it seems obvious that a strong cue will reduce perseveration, there is, that we know of, only one study that showed such an effect, less perseveration when the hidden object was a cookie rather than a toy (Diamond, 1997). By the present account, this is because a sufficiently intense specific cue should pierce the threshold for neural cooperativity and yield a self-sustaining peak that persists over a long delay, even in these immature systems. The finding that infants successfully shifted to the B location given the ‘intense’ lighted target – even with a 3-second delay between the cue and the reach – supports this prediction.

These predictions and findings are not inconsistent with some recent competition models, such as the cognitive capacity account (Berger, 2004) and the Hierarchical Competing Systems Model (HCSM; Marcovitch & Zelazo, 2006). The cognitive capacity account posits that with increased task demands, infants must use more cognitive resources, thus rendering them unable to inhibit a prepotent response (Berger, 2004). This account would explain the present results as perseveration increasing as the task became more difficult. But this account would not necessarily predict the salience-by-delay interaction, because it isn’t obvious what aspect of the interaction would make the task harder and the motor demands (the reach execution) did not change. Moreover, the specific factors that impact cognitive capacity are not well specified. So it is possible that the DFT might be a more specific instantiation of the mechanism that Berger (2004) calls cognitive capacity. Similarly, the HCSM proposes that a response-based system (corresponding to a motor memory) competes with a conscious representational system (which monitors that task information and the subject’s own responses to it; Marcovitch & Zelazo, 2006). Again, the present findings could be consistent with this model, in that as the delay increased, the representational system was taxed to remember the correct location, and over the delay, the memory of the response system decayed. But again, this model would not have explicitly predicted the salience-by-delay interaction because both cue salience and the delay are part of the same representational system, not necessarily part of the response system. Further, the DFT model may again be a more specific instantiation of the mechanism behind the HCSM representational system. Finally, neither of these models generalizes across different cognitive tasks (the Piagetian A-not-B task, a sandbox search task for 2–6-year-old children, a canonical spatial recall task, and a position discrimination task) and ages (from infancy through childhood and adulthood) as the DFT approach does (Simmering, Spencer & Schutte, 2008).

In total, these two findings about the A-not-B errors in infants – perseveration with weak cues and no delay but no perseveration with very strong cues and a long delay – provide strong support for the DFT account of the error.

Representations

The DFT, along with the present infant results, has implications for how one conceptualizes representation as well as developmental process. These are considered next. Within the DFT account, several potential targets can be represented simultaneously as sub-threshold peaks in the motor planning field. But actual behavior requires a decision. This decision by the field occurs when the field goes through an instability (Schöner & Dineva, 2007). More specifically, activation reaches the threshold such that cooperative interactions within the field are set to work, translating the distributed sub-threshold activations into a unique and stable peak. Such a peak represents a decision to reach, which is self-sustained as local excitation, while lateral inhibition suppresses competitive locations. This decision is forced by the signal to reach and the homogeneous boost that signal causes in the field as a whole. If the peak does not pierce the threshold, there is no reach. While the present model is specific to reaching, the same dynamics can be used to understand other behaviors, such as looking (Schöner & Thelen, 2006). Indeed, several studies have demonstrated perseverative looking, which may be explained by these same dynamics (e.g. Hofstadter & Reznick, 1996; Diamond, 1990). Evidence from cortical recordings in monkeys supports these ideas of coding that distinguishes between potential and final targets (Bastian, Schöner & Riehle, 2003). In a multi-target reaching task, directionally tuned neurons encode for several neighboring target locations with a broadly spread activation; only after a go-signal specifies the goal location does this neural activation continuously transform into a sharp peak centered at the goal location (which predicts the response).

This conceptualization sees representations (sub-threshold peaks of activation) and decisions (formation of a single supra-threshold and self-sustained peak) as continuous processes. As such the DFT account offers an alternative to thinking about internal representations and their relation to behavior, and thus development. These theoretical issues are particularly cogent in the study of the A-not-B error, because this error, as originally conceived by Piaget (1954), was indicative of the infant’s lack of an object concept. In the original Piagetian task, an object was hidden before the delay (in contrast to the continually present targets in the present experiment). In Piaget’s view, then, the task measured the infant’s representation of the hidden object. This representation was, in turn, considered to be a symbolic propositional belief in the permanence of things. Since Piaget, numerous studies have manipulated all aspects of his A-not-B task, almost all of them hiding an object, in an effort to understand infants’ representation of object permanence (for reviews, see Marcovitch & Zelazo, 1999; Smith et al., 1999; Wellman et al., 1986). More recent accounts of infants’ performance in hidden object A-not-B tasks conceptualize the relevant representations as internal activation that persists despite the occlusion of the object (Munakata, 1998).

The present procedure uses two continuously in view targets, and so may not speak directly to the representations of hidden objects (but see below). Nonetheless, the present view of representations as sub-threshold activation in the field that may yield a decision through a self-sustained peak that suppresses competitors may provide useful insights into representations, more generally, including those for occluded objects. The first point to be made about such representations with the present model is that they are processes in time. Perseveration is not about the knowledge an infant does or does not have. It is about competing activations that yield a decision, an outwardly observable behavior.

The second point is that prior to a decision (and thus implicitly), the system has competing representations or knowledge. If one were to accept and extend this analysis to the case of the hidden object, this would imply that prior to the signal to reach, the system has knowledge both about the recent hiding location and the past hiding location (in the form of motor memory of repeated reaching to that location). Thus, within this model, the field forces – through the effects of cooperativity – a single representation to emerge and to underlie behavior. Behavior demands cognitive coherence and a single representation. Behavior – the only outward signal one can have of internal processes and knowledge – is itself a single coherent outcome that resolves potentially multiple internal representations. This might be a general truth of the human cognitive system (Barsalou, 1983, 2005). If this is so, then knowing is never an all-or-none proposition, but rather always the result of competing processes (sensory information or memory of previous experiences), with the strongest process at the moment of the action winning the decision.

Within this framework, the central difference between the traditional hidden object task and the present reaching task may not lie in the nature of the underlying representations (Bremner & Bryant, 2001; Munakata, 1997, 1998) but rather in the amount of activation and thus the likelihood of passing the threshold for a decision to act. Hiding an object may be, at minimum, a very salient (and attention-getting) specific cue. It is certainly plausible that the attention-getting properties of the objects in the present study (the painted design and flashing lights on the bottom of the object) served the same role as hiding a toy, in that the visually interesting event was shown to the infant (the specific input) and then hidden from view (the task input) and the infant needed to remember the location over a delay. One interesting open question is the source of this potential extra ‘intensity’ of hiding an object – or of having lighted versus plain brown targets. The extra intensity could be conceptualized simply in terms of the visual events themselves. However, other aspects of ‘intensity’ such as general arousal level or infants’ motivation to get the target may matter and may – directly or indirectly–enhance activation levels in the field. If they do, they will also, by this model, influence the likelihood of shifting correctly versus perseveration. For example, retrieving a hidden object from under a cover may strengthen the motor memory of each reach, compared to lifting the ever-present object. This stronger motor memory would then create a stronger bias to reach to A, thus making a switch to B unlikely depite the strong cue. Previous research on the A-not-B error already tells us that a variety of task factors matter, including hiding versus not hiding objects (Munakata, 1998), the layout of the locations (Diedrich et al., 2001), distracting the infant’s attention during the delay (Smith et al., 1999), and so on. From the dynamic field point of view, since a young system requires a lot of activation to generate a stable decision, any of these factors could pull and push the system around before reaching cooperativity – and thus influence the decision.

The A-not-B task taps into a very specific and constrained behavior, a reach to a location in space, which varies only alongside a single relevant dimension. However, the framework of the DFT model can be extended to more complicated multidimensional tasks, and has been shown to be able to account for decision-making in which task aspects can independently influence parameters of a response along distinct spatial dimensions (like the direction and extent of a movement; Erlhagen & Schöner, 2002). Moreover, Faubel and Schöner (2008) use a DFT model for a robot to learn object names. Multiple perceptual feature dimensions (like color, shape and aspect-ratio) are dynamically linked via space. If an object is presented to the system then memory traces are accumulated over the feature dimensions by means of a preshape dynamics (a process that is similar to the preshape trace that is accumulated with every reach alongside the behavioral dimension in the present model). The system can use this past experience to link the properties to each other, enabling the definition of an object in terms other than space. One can think of this preshape that is accumulated alongside multiple feature dimensions as a sort of object concept formation. This example suggests that if one wants to tap into the developmental formation of categorical representations of objects, then one needs experiments that influence behavior at the level of object-relevant parameters beyond the reaching direction. The reaching variant of the A-not-B task might simply not be sufficient to reveal concept formation.

Development

The A-not-B task is informative, however, about the development of memory guided reaching. The key aspects of the developmental pattern of infant perseveration are these: 8–10-month-old infants typically perseverate in this task, under both relatively brief and long delays (Wellman et al., 1986). Infants between 10 and 12 months will also perseverate, but only as the delay increases between the hiding event and the reach (Diamond, 1985). After 12 months, infants generally do not perseverate, even after a very long delay (Wellman et al., 1986, but see Espy, Kaufmann, McDiarmid & Glisky, 1999; Wishart, 1987). The key question is what components of the system (including, but not limited to reaching skill, brain development, increased memory, experience reaching for targets, etc.) change over these months in order to produce correct reaching in place of perseveration.

In the present study, we were able to boost young infants’ behavior, making it look like that of older infants, by increasing the salience of the specific cue, such that it dominated the reaching decision even over a delay. It is worth noting that, when subjected to strong cues, the motor planning field of younger infants operates just like that used to model older infants (Dineva, 2005; Dineva, Schöner & Thelen, in preparation). Following Thelen et al. (2001), age is modeled as an increase of the resting level. The higher the resting level, the easier it is to enter the cooperative regime. Alternatively, the strong cue compensates for the resistance (low resting level), enabling activation to pass the cooperativity threshold. Importantly, what the model is doing given an immature system (low resting level) and a very strong specific cue and a mature system (high resting level) and any specific cue is fundamentally the same: Activation reaches threshold, feeds back on itself and suppresses competing activation, yielding a sustained peak and thus a behavioral decision. For the young infant, the amount of activation provided by the specific cue is more crucial in getting to a sustained regime than for an older infant because of the low resting activation level in the field. That is, in a more developed system, this regime comes more easily.

All this suggests that the key issue in overcoming perseveration is the activation of the field. The activation due to the new specific cue – the one calling for a shift in response – must reach high enough levels to enter the cooperative regime to be sustained over the delay. This can happen because of a high resting level in the field, because of a strong specific cue, or because of a brief delay, or because of some combination of these factors. These ideas help make sense of one of the more challenging aspects of the developmental data on the A-not-B error. Although the error is a robust behavioral phenomenon in 8- to 10-month-olds, it is also highly context dependent, varying with the precise nature of the task (for reviews see Marcovitch & Zelazo, 1999; Smith et al., 1999; Wellman et al., 1986). Context should matter more for the more immature system. Since cooperativity is difficult to achieve and activation decays rapidly, the environmental context will systematically push the system around by altering competing activation levels. Immature systems are input-driven as the outcome of the field dynamics will vary more with these task factors.

These ideas may also help us to understand the vulnerability of compromised systems to perseveration. In that context, perseveration is often studied under the rubric of executive function, where inflexibility (i.e. perseveration) is the repeated production of an action or thought in the absence of an appropriate stimulus (e.g. Zelazo et al., 2003; Diamond, 1991). Perseveration is a hallmark of psychopathology and brain injury, including injury to the prefrontal cortex (e.g. Luria, Pribram & Homskaya, 1964). The immaturity of the prefrontal cortex has also been implicated in young infants’ failure to reach correctly on A-not-B tasks (e.g. Diamond & Goldman-Rakic, 1989). Variants of the A-not-B task are also often used as diagnostic tools in the assessment of neurological disorders (e.g. Diamond, 2001; Gazzaniga, Ivry & Mangun, 2002). By the present analysis, the fundamental nature of both immaturity and damage may be decreased activation, making it more difficult for the system to get above the threshold for cooperativity. More generally, damage to the system may result in loss not of some specific function but rather as the result of an unspecific decrease in overall activation levels (Kimberg & Farah, 2000; Farah & McClelland, 1991). A lesion may also cut through a long-distance excitation-inhibition loop between different brain regions, reducing thus cooperative interactions within the system as a whole.

Conclusion

These insights from the present simulations and experiments derive from a focus on performance, from an attempt to understand the dynamics of the system that underlies behavior. Doing this requires the parametric examination of the performance space because behaviors are not properties of fixed representations or knowledge structures but the emergent product of a complex dynamic system in a particular task. This perspective has important consequences for how the field thinks about and studies development.

The manipulations in the present experiments elicited perseveration or correct responding by manipulating the attention-getting properties of the specific cues and by manipulating the timing of events in the task. In this way, these experiments are very much like the classic experiments by Thelen and her colleagues on walking (Thelen, Fisher & Ridley-Johnson, 1984; Thelen, 1986). These studies turned 1–7-month-old non-walkers into walkers by putting them into water and on treadmills, methods that revealed the multiple components of the system (limb mass, muscle control, posture, balance) that must come together to allow walking. In everyday parlance, it seems useful to characterize 7-month-old infants, for example, as categorically unable to walk, but in scientific terms such a characterization obscures the processes that underlie the skill of walking. Likewise, perseveration is not a trait of babies but a behavioral outcome of a complex system in a task. The present results provide new insights into the nature of that system.

Appendix A

Model equations

$${\tau }_{\text{mp}}·\frac{\partial u_{\text{mp}}}{\partial t}(\phi ,t)=-u_{\text{mp}}(\phi ,t)+g_{\text{coop}}(\phi ,t)+h_{\text{rest}}+\dots u_{\text{pre}}(\phi ,t)+s_{\text{input}}(\phi ,t)+{\eta }_{\text{noise}}(\phi ,t)$$ (1)

$$g_{\text{coop}}(\phi ,t)=\int {\omega }_{\text{coop}}(\phi -{\phi }^{\prime })·f_{\sigma }(u_{\text{mp}}({\phi }^{\prime },t))d{\phi }^{\prime }$$ (2)

$${\tau }_{\text{pre}}·\frac{\partial u_{\text{pre}}}{\partial \text{t}}(\phi ,t)=[-u_{\text{pre}}(\phi ,t)+f_{\sigma }(u_{\text{mp}}(\phi ,t))]·{\chi }_{\text{act}}(t)$$ (3)

Equation (1) says that, at any given point (φ, t) in behavioral space and in time, the way the motor planning activation u_mp will change (note the temporal derivative on the left-hand side) depends on its current level, the interactions g_coop between the field sites, the preshape dynamics u_pre, and on the current inputs to the field s_input (as given by the task!) which fluctuate somewhat η_noise.

The cooperative interactions are described in equation (2), where ω_coop is a Gaussian interaction kernel with global inhibition, and 0 ≤ f_σ ≤ 1 is a smooth sigmoidal threshold function (for details and parameters, see Thelen et al., 2001; Dineva, 2005). To put it into words, each site φ receives activations from all other field sites φ′. But, sites that have negative activation will be weighted almost zero by f_σ and thus not contribute significantly to the integral in equation (2), while positively activated sites will have up to a full effect on the other sites. This effect is captured by ω_coop, the homogeneous interaction kernel: close-by sites will mutually excite each other, and distant sites will compete by means of inhibition. Importantly, whether sites will be activated strongly enough to participate in the interactions and thus form a localized time-persistent peak depends on the relative balance of inputs to the field versus the negative resting level h_rest = − 12.

Next to the inputs s_input that come from the current task situation, activation also adds from the preshape field u_pre, as described by equation (3). The preshape field is a dynamic field that evolves under the influence of the motor planning field, but only when sites u_mp(φ, t) are sufficiently activated (parsed by the same threshold function f_σ as in equation (2)). The characteristic function χ_act makes sure that a motor planning trace is accumulated only when an action is performed (then χ_act = 1, otherwise 0). This prevents preshape activation from spontaneous decay in the here regarded time range of several minutes. Therefore, traces of recent reaches provide activation to the motor planning field. However, this activation, although very persistent, is quite weak: u_pre converges to 1 for the location of reaching after a couple of reaches to the same location, and it couples back to u_mp.

Appendix B

Simulations

To a large extent and in every task, input activation comes from the current context s_input which describes the stimulus landscape – how much activation the environment provides at any given point (φ, t). In the repetitive reaching task (recall Figure 1 and Table 1), this is some combination of the task input marking the targets s_task (equation (4)), the specific cue that transiently exhibits one of the targets over the other s_spec (equation (5)), and h_boost = 9, the homogeneous boost that adds the same amount of activation in the entire field. The localized inputs are modeled as a Gaussians 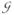_loc centered at some location ‘loc’ (this captures the idea that inputs are mediated via population coding). For instance, the task input is given as the sum of two Gaussians, one is centered at A the other at B:

(4)

with S_task = 2 being its strength, and the partially constant function F_A/B = 1.2, 0.8, 0.4 or 0 is adding some additional activation when the A location stands out somewhat over B (see staggering in Figure 2). Similarly, the specific input, when presented depends on which location is cued:

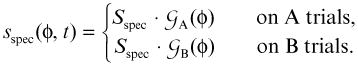(5)

The amplitude of the specific cue is set S_spec = 10 for the canonical task. In addition, this is the parameter manipulated in the present simulations. Finally, inputs are not always perceived by the same strength, which we model by adding spatially correlated noise that is centered at the relevant locations:

(6)

The ξ_A and ξ_B are two Gaussian White Noise (GWN) processes, and the strength by which they contribute is q_task = 0.1.

A simulation is realized by using the standard Euler approximation with a fixed Euler step (e.g. Kloeden & Platen, 1992) to implement the model with a Matlab program.