Abstract
We establish a general asymptotic theory for nonparametric maximum likelihood estimation in semiparametric regression models with right censored data. We identify a set of regularity conditions under which the nonparametric maximum likelihood estimators are consistent, asymptotically normal, and asymptotically efficient with a covariance matrix that can be consistently estimated by the inverse information matrix or the profile likelihood method. The general theory allows one to obtain the desired asymptotic properties of the nonparametric maximum likelihood estimators for any specific problem by verifying a set of conditions rather than by proving technical results from first principles. We demonstrate the usefulness of this powerful theory through a variety of examples.
Key words and phrases: Counting process, empirical process, multivariate failure times, nonparametric likelihood, profile likelihood, survival data
1. Introduction
Semiparametric regression models are highly useful in investigating the effects of covariates on potentially censored responses (e.g. failure times and repeated measures) in longitudinal studies. It is desirable to analyze such models by the nonparametric maximum likelihood approach, which generally yields consistent, asymptotically normal, and asymptotically efficient estimators. It is technically difficult to prove the asymptotic properties of the nonparametric maximum likelihood estimators (NPMLEs). Thus far, rigorous proofs exist only in some special cases.
In this paper, we develop a general asymptotic theory for the NPMLEs with right censored data. The theory is very encompassing in that it pertains to a generic form of likelihood rather than specific models. We prove that, under a set of mild regularity conditions, the NPMLEs are consistent, asymptotically normal, and asymptotically efficient with a limiting covariance matrix that can be consistently estimated by the inverse information matrix or the profile likelihood method.
This paper is the technical companion to Zeng and Lin (2007), in which several classes of models were proposed to unify and extend existing semiparametric regression models. The likelihoods for those models can all be written in the general form considered in this paper. For each class of models in Zeng and Lin (2007), we identify a set of conditions under which the regularity conditions for the general theory hold so that desired asymptotic properties are ensured.
2. Some Semiparametric Models
We describe briefly the three kinds of models considered in Zeng and Lin (2007). We assume that the censoring mechanism satisfies coarsening at random (Heitjan and Rubin (1991)).
2.1. Transformation Models for Counting Processes
Let N*(t) record the number of events that the subject has experienced by time t, and let Z(·) denote the corresponding covariate processes. Zeng and Lin (2007) proposed the following class of transformation models for the cumulative intensity function of N*(t)
where G is a continuously differentiable and strictly increasing function with G′(1) > 0 and G(∞) = ∞, R*(·) is an indicator process, Z̃ is a subset of Z, β and γ are regression parameters, and Λ(·) is an unspecified increasing function. The data consist of {Ni(t), Ri(t), Zi(t); t ∈ [0, τ]} (i = 1, …, n), where , Ci is the censoring time, and τ is a finite constant. The likelihood is
where dNi(t) = Ni(t) − Ni(t−).
2.2. Transformation Models With Random Effects for Dependent Failure Times
For i = 1, …, n, k = 1, …, K and l = 1, …, nik, let denote the number of the kth type of event experienced by the lth individual in the ith cluster, and Zikl(·) the corresponding covariate processes. Zeng and Lin (2007) assumed that the cumulative intensity for takes the form
where Gk, Λk, and are analogous to G, Λ, and R* of Section 2.1, Z̃ikl is a subset of Zikl plus the unit component, and bi is a vector of random effects with density f (b; γ). Let Cikl, Nikl, and Rikl be defined analogously to Ci, Ni, and Ri of Section 2.1. The likelihood is
2.3. Joint Models for Repeated Measures and Failure Times
For i = 1, …, n and j = 1, …, ni, let Yij be the response variable at time tij for the ith subject, and Xij the corresponding covariates. We assume that (Yi1, …, Yini) follows a generalized linear mixed model with density fy(y|Xij; bi), where bi is a set of random effects with density f (b; γ). We define and Zi as in Section 2.1, and assume that
where Z̃i is a subset of Zi plus the unit component, ψ is a vector of unknown constants, and v1 ◦ v2 is the component-wise product of two vectors v1 and v2. The likelihood is
For continuous measures, Zeng and Lin (2007) proposed the semiparametric linear mixed model
where H̃ is an unknown increasing function with H̃(−∞) = −∞, H̃(∞) = ∞, and H̃(0) = 0, α is a set of regression parameters, X̃ij is typically a subset of Xij, and εij (i = 1, …, n; j = 1, …, nij) are independent with density fε. Write Λ̃(y) = eH̃(y). The likelihood is
3. Nonparametric Maximum Likelihood Estimation
All the likelihood functions given in Section 2 can be expressed as
where
, θ is a d-vector of regression parameters and variance components,  = (Λ1, …, ΛK),
= (Λ1, …, ΛK),  pertains to the observation on the ith cluster, and Ψ is a functional of
pertains to the observation on the ith cluster, and Ψ is a functional of  , θ, and
, θ, and  . For nonparametric maximum likelihood estimation, we allow
. For nonparametric maximum likelihood estimation, we allow  to be discontinuous with jumps at the observed failure times and maximize the modified likelihood function
to be discontinuous with jumps at the observed failure times and maximize the modified likelihood function
where Λk{t} denotes the jump size of the monotone function Λk at t. Equivalently, we maximize the logarithm of the above function
| (1) |
We wish to establish an asymptotic theory for the resulting NPMLEs θ̂ and 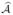 .
.
4. Regularity Conditions
We impose the following conditions on the model and data structures.
(C1) The true value θ0 lies in the interior of a compact set Θ, and the true functions Λ0k are continuously differentiable in [0, τ] with , k = 1, …, K.
(C2) With probability one, P(infs∈[0,t] Rik·(s) ≥ 1|Zikl, l = 1, …, nik) > δ0 > 0 for all t ∈ [0, τ], where .
(C3) There exist a constant c1 > 0 and a random variable r1( ) > 0 such that E[log r1(
) > 0 such that E[log r1( )] < ∞ and, for any θ ∈ Θ and any finite Λ1, …, ΛK,
)] < ∞ and, for any θ ∈ Θ and any finite Λ1, …, ΛK,
almost surely, where . In addition, for any constant c2,
where ||h||V[0,τ] is the total variation of h(·) in [0, τ], and r2( ), which may depend on c2, is a finite random variable with E[|log r2(
), which may depend on c2, is a finite random variable with E[|log r2( )|] < ∞.
)|] < ∞.
We require certain smoothness of Ψ. Let Ψ̇θ denote the derivative of Ψ( ; θ,
; θ,  ) with respect to θ, and let Ψ̇k[Hk] denote the derivative of Ψ(
) with respect to θ, and let Ψ̇k[Hk] denote the derivative of Ψ( ; θ,
; θ,  ) along the path (Λk + εHk), where Hk belongs to the set of functions in which Λk + εHk is increasing with bounded total variation.
) along the path (Λk + εHk), where Hk belongs to the set of functions in which Λk + εHk is increasing with bounded total variation.
(C4) For any (θ(1), θ(2)) ∈ Θ, and
with uniformly bounded total variations, there exist a random variable ℱ( ) ∈ L4(P) and K stochastic processes μik(t;
) ∈ L4(P) and K stochastic processes μik(t;  ) ∈ L6(P), k = 1, …, K, such that
) ∈ L6(P), k = 1, …, K, such that
In addition, μik(s;  ) is non-decreasing, and E[ℱ(
) is non-decreasing, and E[ℱ( )μik(s;
)μik(s;  )] is left-continuous with uniformly bounded left- and right-derivatives for any s ∈ [0, τ]. Here, the right-derivative for a function f(x) is defined as limh→0+(f (x + h) − f (x+))/h.
)] is left-continuous with uniformly bounded left- and right-derivatives for any s ∈ [0, τ]. Here, the right-derivative for a function f(x) is defined as limh→0+(f (x + h) − f (x+))/h.
The following condition ensures identifiability of parameters.
(C5) (First Identifiability Condition) If
almost surely, then θ* = θ0 and for t ∈ [0, τ], k = 1, …, K.
The next assumption is more technical and will be used in proving the weak convergence of the NPM-LEs. For any fixed (θ,  ) in a small neighborhood of (θ0,
) in a small neighborhood of (θ0,  ) in Rd × {BV[0, τ]}K, where BV[0, τ] denotes the space of functions with bounded total variations in [0, τ], (C4) implies that the linear functional
) in Rd × {BV[0, τ]}K, where BV[0, τ] denotes the space of functions with bounded total variations in [0, τ], (C4) implies that the linear functional
is continuous from BV[0, τ] to R. Thus, there exists a bounded function η0k(s; θ,  ) such that
) such that
(C6) There exist functions ζ0k(s; θ0,  ) ∈ BV[0, τ], k = 1, …, K, and a matrix ζ0θ(θ0,
) ∈ BV[0, τ], k = 1, …, K, and a matrix ζ0θ(θ0,  ) such that
) such that
In addition, for k = 1, …, K,
where η0km is a bounded bivariate function and η0kθ is a d-dimensional bounded function. Furthermore, there exists a constant c3 such that |η0km(s, t1; θ0,  ) − η0km(s, t2; θ0,
) − η0km(s, t2; θ0,  )| ≤ c3|t1 − t2| for any s ∈ [0, τ] and any t1, t2 ∈ [0, τ].
)| ≤ c3|t1 − t2| for any s ∈ [0, τ] and any t1, t2 ∈ [0, τ].
The final assumption ensures that the Fisher information matrix along any finite-dimensional sub-model is non-singular.
(C7) (Second Identifiability Condition) If with probability one,
for some constant vector v ∈ Rd and hk ∈ BV[0, τ], k = 1, …, K, then v = 0 and hk = 0 for k = 1, …, K.
Remark 1
(C1)–(C2) are standard assumptions in any analysis of censored data. (C3) pertains to the model structure, and (C4) and (C6) essentially impose the smoothness of this structure. Although they appear technical, these conditions are easy to verify in practice. (C5) and (C7) usually require some work to verify, but can be translated to simple conditions in specific cases.
5. Some Useful Lemmas
Lemma 1
For any constant c, the following classes of functions are P-Donsker:
Proof
We only prove that ℱ3k is P-Donsker; the proofs for the other two classes are similar. For k = 1, …, K, we define a measure μ̃k in [0, τ] such that, for any Borel set A ⊂ [0, τ],
Condition (C4) implies that μ̃k([0, τ]) ≤ ||ℱ( )||L4(P)||μik(τ;
)||L4(P)||μik(τ;  ) − μik(0;
) − μik(0;  )||L6(P). Thus, μ̃k is a finite measure. According to Theorem 2.7.5 of van der Vaart and Wellner (1996), the bracket covering number for any bounded set in BV[0, τ] is of order exp{O(1/ε)} in L2(μ̃k), k = 1, …, K. Thus, we can construct Nε ≡ (1/ε)d × exp{O(K/ε)} × exp{O(1/ε)} brackets for the set of (θ,
)||L6(P). Thus, μ̃k is a finite measure. According to Theorem 2.7.5 of van der Vaart and Wellner (1996), the bracket covering number for any bounded set in BV[0, τ] is of order exp{O(1/ε)} in L2(μ̃k), k = 1, …, K. Thus, we can construct Nε ≡ (1/ε)d × exp{O(K/ε)} × exp{O(1/ε)} brackets for the set of (θ,  , H) in ℱ3k, denoted by
, H) in ℱ3k, denoted by
such that and
Any (θ,  , H) must belong to one of these brackets. Obviously, the bracket functions
, H) must belong to one of these brackets. Obviously, the bracket functions
cover all the functions in ℱ3k. Since
where c is a constant depending on K, the L2(P)-distance within each bracket pair is O(ε). Hence, the bracket entropy integral of ℱ3k is finite, so that ℱ3k is P-Donsker.
Lemma 2
For any bounded random variable (θ, Λ) in Θ × BV[0, τ], the function g(s) ≡ |E[Ψ̇k( ; θ,
; θ,  ) [I(· ≥ s)]/Ψ (
) [I(· ≥ s)]/Ψ ( ; θ,
; θ,  )]| is left-continuous and satisfies that, for any s ∈ [0, τ], there exist δs, cs > 0 such that |g(s̃) − g(s)| ≤ cs|s̃ − s| for s̃ ∈ (s − δs, s) and |g(s̃) − g(s+)| ≤ cs|s̃ − s| for s̃ ∈ (s, s + δs).
)]| is left-continuous and satisfies that, for any s ∈ [0, τ], there exist δs, cs > 0 such that |g(s̃) − g(s)| ≤ cs|s̃ − s| for s̃ ∈ (s − δs, s) and |g(s̃) − g(s+)| ≤ cs|s̃ − s| for s̃ ∈ (s, s + δs).
Proof
Since μik(t;  ) is non-decreasing in t, it follows from (C4) that for any s1 and s2,
) is non-decreasing in t, it follows from (C4) that for any s1 and s2,
Thus, g(s) is in BV[0, τ] and is left-continuous. In addition, the left- and right-differentiability of E[ℱ( )μik(s;
)μik(s;  )] in (C4) implies that the second part of the lemma holds.
)] in (C4) implies that the second part of the lemma holds.
Lemma 3
For any h(s) ∈ BV[0, τ], the linear map is a bounded compact operator from BV[0, τ] to BV[0, τ].
Proof
It is clear from (C6) that this function maps any bounded set in BV[0, τ] into a bounded set consisting of Lipschitz-continuous functions. The result thus follows since any bounded and Lipschitz-continuous functions consist of a totally bounded set in BV[0, τ] and the linear map is continuous.
6. Consistency
The following theorem states the consistency of θ̂ and Λ̂k, k = 1, …, K.
Theorem 1
Under (C1)–(C5), .
Proof
We fix a random sample in the probability space and assume that (C1)–(C5) hold for this sample. The set of such samples has probability one. We prove the result for this fixed sample. The entire proof consists of three steps.
Step 1
We show that the NPMLEs exist or, equivalently, Λ̂k(τ) < ∞ (k = 1, …, K) for large n. By (C3), the likelihood function is bounded by
If Λk(τ) = ∞ for some k, then (C2) implies that, with probability one, inft∈[0,τ] Rik·(t) ≥ 1 for some i, so that the above function is equal to zero. Thus, the maximum of the likelihood function can only be attained for Λ̂k(τ) < ∞.
Step 2
We show that lim supn Λ̂k(τ) < ∞ almost surely, i.e., Λ̂k(τ) is bounded uniformly for all large n. By differentiating the objective function (1) with respect to Λk{Yikl} for which and Rikl(Yikl) = 1, we note that Λ̂k{Yikl} satisfies
In other words,
To prove the boundedness of Λ̂k(τ), we construct another step function Λ̃k with jumps only at the Yikl for which and Rikl(Yikl) = 1,
that is,
We show that Λ̃k uniformly converges to Λ0k. By Lemma 1,
| (2) |
uniformly in s ∈ [0, τ]. Since the score function along the path Λk = Λ0k + εI(· ≥ s) with the other parameters fixed at their true values has zero expectation,
| (3) |
where δ(t = s) is the Dirac function. The submodel is not in the parameter space; however, we can always choose a sequence of submodels in the parameter space which approximates this submodel. Thus, the uniform limit of Λ̃k(t) is
That is, Λ̃k(t) uniformly converges to Λ0k(t).
We next show that the difference between the log-likelihood functions evaluated at (θ̂, 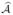 ) and (θ0,
) and (θ0, 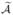 ), where
), where 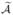 = (Λ̃1, …, Λ̃K), is negative eventually if some Λ̂k(τ) diverges, which will induce a contradiction. The key arguments are based on (C3). Clearly, n−1ℒn(θ̂,
= (Λ̃1, …, Λ̃K), is negative eventually if some Λ̂k(τ) diverges, which will induce a contradiction. The key arguments are based on (C3). Clearly, n−1ℒn(θ̂, 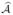 ) ≥ n−1ℒn(θ0,
) ≥ n−1ℒn(θ0, 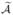 ). It follows from (2) and (3) that nΛ̃k{t} converges to
, and is thus uniformly bounded away from zero, where t is an observed failure time. Therefore,
). It follows from (2) and (3) that nΛ̃k{t} converges to
, and is thus uniformly bounded away from zero, where t is an observed failure time. Therefore,
which is bounded away from − ∞ when n is large. That is,
where O(1) denotes a finite constant. On the other hand, (C3) implies that
where . Thus,
| (4) |
We now show that the right-hand side diverges to − ∞ if Λ̂k(τ) diverges for some k. The proof is based on the partitioning idea of Murphy (1994). Specifically, we construct a sequence t0k = τ > t1k > t2k > … in the following manner. First, we define
where R̄ik·(t) = infs∈[0,t] Rik·(s). Clearly, such a t1k exists, and the above inequality becomes an equality if t1k > 0. If t1k > 0, we choose a small constant ε0 such that
and define
Such a t2k exists. If t2k > 0, the inequality is an equality, and we define
We continue this process. The sequence eventually stops at some tNk,k = 0. If this is not true, then the sequence is infinite and strictly decreases to some t* ≥ 0. Since all the inequalities are equalities, we sum all the equations except the first one to obtain
which implies that
This contradicts the choice of ε0. Thus, the sequence stops at some tNk,k = 0.
If we write Iqk = [tq+1,k, tqk), then the right-hand side of (4) can be bounded by
| (5) |
Since log x is a concave function,
Therefore, (5) can be further bounded by
By (C2),
so that
According to the construction of the tqk’s, the coefficients in front of log Λ̂k(tqk) are all negative when n is large enough. Therefore, the corresponding terms cannot diverge to ∞. However, if Λ̂k(τ) → ∞, the first term in the summation goes to −∞. We conclude that for all n large enough, Λ̂k(τ) < ∞. Thus, lim supn Λ̂k(τ) < ∞.
Step 3
We obtain the consistency result from (C5). Since Λ̂k is bounded and monotone, Λ̂k is weakly compact. Helly’s Selection Theorem implies that, for any subsequence, we can always choose a further subsequence such that Λ̂k point-wise converges to some monotone function . Without loss of generality, we also assume that θ̂ converges to some θ*. The consistency will hold if we can show that and θ* = θ0. Since Λ0k is continuous, the weak convergence of Λ̂k to Λ0k can be strengthened to the uniform convergence of Λ̂k to Λ0k in [0, τ].
Note that
| (6) |
Clearly, Λ̂k is absolutely continuous with respect to Λ̃k. By condition (C3),
since Λ̂k converges to
and is bounded and {ℱ( )μjk(t;
)μjk(t; 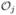 ): t ∈ [0, τ]} is a P-Glivenko-Cantelli class. By Lemma 1 and the Glivenko-Cantelli Theorem,
): t ∈ [0, τ]} is a P-Glivenko-Cantelli class. By Lemma 1 and the Glivenko-Cantelli Theorem,
The numerator and denominator in the integrand of (6) converge uniformly to deterministic functions, denoted by g1k(s) and g2k(s), respectively. It follows from (3) that is bounded away from zero. We claim that inf s∈[0,τ] g2k(s) > 0. If this is not true, then there exists some s* ∈ [0, τ] such that g2k(s*+) = 0 or g2k(s*) = 0. By Lemma 2, there exist δ* and c* such that |g2k(s)| ≤ c*|s − s*| for s ∈ (s*, s* + δ *) or s ∈ (s* − δ *, s*]. On the other hand, for any ε > 0,
Taking limits on both sides, we obtain . Let ε → 0. By the Monotone Convergence Theorem, , or . This is a contradiction since the right-hand side is infinite. The contradiction implies that the limit g2k(s) is uniformly positive. We can take limits on both sides of (6) to obtain . Thus, is also absolutely continuous with respect to Λ0k and . Since Λ0k(t) is differentiable with respect to t, so is . Write . The forgoing arguments show that dΛ̂k(t)/dΛ̃k(t) uniformly converges to , which is uniformly positive in [0, τ].
It follows from the inequality n−1ℒn(θ̂, 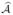 ) ≥ n−1ℒn(θ0,
) ≥ n−1ℒn(θ0, 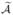 ) that
) that
In view of Lemma 1, the Glivenko-Cantelli Theorem and the uniform convergence of dΛ̂k/dΛ̃k, taking limits on both sides of the above inequality yields
The left-hand side is the negative Kullback-Leibler distance of the density indexed by (θ*, 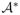 ). Thus, (C5) entails that θ* = θ0 and Λ* = Λ0.
). Thus, (C5) entails that θ* = θ0 and Λ* = Λ0.
7. Weak Convergence and Asymptotic Efficiency
Define 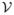 = {v ∈ Rd, |v| ≤ 1}, and
= {v ∈ Rd, |v| ≤ 1}, and 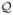 = {h(t): ||h(t)||V [0,τ] ≤ 1 }. We identify (θ̂ − θ0,
= {h(t): ||h(t)||V [0,τ] ≤ 1 }. We identify (θ̂ − θ0, 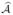 −
−  ) as a random element in l∞(
) as a random element in l∞(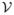 ×
× 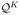 ) through the definition
.
) through the definition
.
Theorem 2
Under (C1)–(C7), n1/2(θ̂ − θ0, 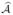 −
−  ) →d ℊ in l∞(
) →d ℊ in l∞(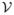 ×
× 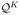 ), where ℊ is a continuous zero-mean Gaussian process. Furthermore, the limiting covariance matrix of n1/2(θ̂ − θ0) attains the semiparametric efficiency bound.
), where ℊ is a continuous zero-mean Gaussian process. Furthermore, the limiting covariance matrix of n1/2(θ̂ − θ0) attains the semiparametric efficiency bound.
Proof
The proof is based on the likelihood equation and follows the arguments of van der Vaart (1998, pp. 419–424). Let ℒ(θ,  ) be the log-likelihood function from a single cluster, ℒ̇θ(θ,
) be the log-likelihood function from a single cluster, ℒ̇θ(θ,  ) be the derivative of ℒ(θ,
) be the derivative of ℒ(θ,  ) with respect to θ, and ℒ̇k(θ,
) with respect to θ, and ℒ̇k(θ,  )[Hk] be the path-wise derivative along the path Λk + εHk. We sometimes omit the arguments in these derivatives when θ = θ0 and
)[Hk] be the path-wise derivative along the path Λk + εHk. We sometimes omit the arguments in these derivatives when θ = θ0 and  =
=  . Let
. Let 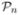 be the empirical measure based on n i.i.d. observations, and
be the empirical measure based on n i.i.d. observations, and 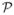 be its expectation.
be its expectation.
Let 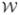 = (h1, …, hK) ∈
= (h1, …, hK) ∈ 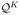 . The likelihood equation for (θ̂,
. The likelihood equation for (θ̂, 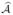 ) along the path (θ̂+εv,
) along the path (θ̂+εv, 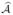 +ε∫
+ε∫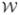 d
d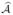 ), where v ∈ Rd and hk ∈ BV [0, τ], is given by
), where v ∈ Rd and hk ∈ BV [0, τ], is given by
To be specific,
Since (θ0,  ) maximizes
) maximizes 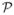 [ℒ(θ,
[ℒ(θ,  )],
)],
These equations, combined with the likelihood equation for (θ̂, 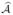 ), yield
), yield
Define
, where δ0 is a small positive constant. When n is large enough, (θ̂, 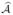 ) belongs to
) belongs to 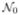 with probability one. By Lemma 1 and the Donsker Theorem,
with probability one. By Lemma 1 and the Donsker Theorem,
| (7) |
where op(1) represents some random element converging in probability to zero in l∞(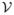 ×
× 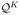 ).
).
Under (C6), the first term on the right-hand side of (7) is
The second term is . It follows from (C6) that the above expression is
Thus, the right-hand side of (7) can be written as
where (B1, B21, …, B2K) are linear operators in Rd × {BV [0, τ]}K, and
| (8) |
| (9) |
It follows from the above derivation that
| (10) |
We can write (B1, B21, …, B2K)[v, 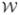 ] as
] as
We wish to prove that (B1, B21, …, B2K) is invertible. As shown at the end of this section, η0k(t; θ0,  ) < 0, so that the first term of (B1, B21, …, B2K) is an invertible operator. It follows from Lemma 3 that the second term is a compact operator. Thus, (B1, B21, …, B2K) is a Fredholm operator, and the invertibility of (B1, …, B2K) is equivalent to the operator being one-to-one (Rudin (1973, pp. 99–103)). Suppose that B1[v,
) < 0, so that the first term of (B1, B21, …, B2K) is an invertible operator. It follows from Lemma 3 that the second term is a compact operator. Thus, (B1, B21, …, B2K) is a Fredholm operator, and the invertibility of (B1, …, B2K) is equivalent to the operator being one-to-one (Rudin (1973, pp. 99–103)). Suppose that B1[v, 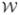 ] = 0, …, and B2K[v,
] = 0, …, and B2K[v, 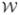 ] = 0. It is easy to see from (10) that the derivative of
along the path (θ0 + εv,
] = 0. It is easy to see from (10) that the derivative of
along the path (θ0 + εv,  + ε∫
+ ε∫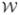 d
d ) is zero. That is, the information along this path is zero, or
almost surely. By (C7), v = 0 and
) is zero. That is, the information along this path is zero, or
almost surely. By (C7), v = 0 and 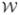 = 0, so that (B1, B21, …, B2K) is one-to-one and invertible.
= 0, so that (B1, B21, …, B2K) is one-to-one and invertible.
It follows from (7) that, for any (v, 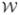 ) ∈
) ∈ 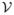 ×
× 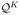 ,
,
where (ṽ, h̃1, …, h̃K) = (B1, B21, …, B2K)−1(v, h1, …, hK). Since
we have
Thus, . Consequently,
We have proved that n1/2(θ̂− θ0, 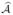 −
−  ) converges weakly to a Gaussian process in l∞(
) converges weakly to a Gaussian process in l∞(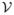 ×
× 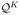 ). By choosing hk = 0 for k = 1, …, K, we see that vTθ̂ is an asymptotically linear estimator of vT θ0 with influence function
. Since the influence function lies in the space spanned by the score functions, θ̂ is an efficient estimator for θ0.
). By choosing hk = 0 for k = 1, …, K, we see that vTθ̂ is an asymptotically linear estimator of vT θ0 with influence function
. Since the influence function lies in the space spanned by the score functions, θ̂ is an efficient estimator for θ0.
It remains to verify that η0k(t; θ0,  ) < 0. Under (C6),
. The choice of Hk(s) = I(s ≥ t) yields
) < 0. Under (C6),
. The choice of Hk(s) = I(s ≥ t) yields 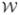 [Ψ̇k(
[Ψ̇k( ;θ0,
;θ0, )[I(· ≥ t)]/Ψ(
)[I(· ≥ t)]/Ψ( ;θ0,
;θ0, )] = η0k(t;θ0,
)] = η0k(t;θ0, ). On the other hand, the score function along the path Λ0k + εI(· ≥ t) with the other parameters fixed at their true values has zero expectation. We expand this expectation to obtain
). On the other hand, the score function along the path Λ0k + εI(· ≥ t) with the other parameters fixed at their true values has zero expectation. We expand this expectation to obtain
Thus, η0k(t; θ0,  ) < 0.
) < 0.
8. Information Matrix
Theorem 2 implies that the functional parameter  can be estimated at the same rate as the Euclidean parameter θ. Thus, we may treat (1) as a parametric log-likelihood with θ and the jump sizes of Λk, k = 1, …, K, at the observed failure times as the parameters and estimate the asymptotic covariance matrix of the NPMLEs for these parameters by inverting the information matrix. This result is formally stated in Theorem 3. We impose an additional assumption.
can be estimated at the same rate as the Euclidean parameter θ. Thus, we may treat (1) as a parametric log-likelihood with θ and the jump sizes of Λk, k = 1, …, K, at the observed failure times as the parameters and estimate the asymptotic covariance matrix of the NPMLEs for these parameters by inverting the information matrix. This result is formally stated in Theorem 3. We impose an additional assumption.
(C8) There exists a neighborhood of (θ0,  ) such that for (θ,
) such that for (θ,  ) in this neighborhood, the first and second derivatives of log Ψ(
) in this neighborhood, the first and second derivatives of log Ψ( ; θ,
; θ,  ) with respect to θ and along the path Λk + εHk with respect to ε satisfy the inequality in (C4).
) with respect to θ and along the path Λk + εHk with respect to ε satisfy the inequality in (C4).
For any v ∈ 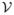 and h1, …, hK ∈
and h1, …, hK ∈ 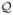 , we consider the vector
, where h⃗k is the vector consisting of the values of hk(·) at the observed failure times. Let ℐn be the negative Hessian matrix of (1) with respect to θ̂ and the jump sizes of (Λ̂1, …, Λ̂K).
, we consider the vector
, where h⃗k is the vector consisting of the values of hk(·) at the observed failure times. Let ℐn be the negative Hessian matrix of (1) with respect to θ̂ and the jump sizes of (Λ̂1, …, Λ̂K).
Theorem 3
Assume (C1)–(C8). Then ℐn is invertible for large n, and
in probability, where AVar denotes the asymptotic variance.
Proof
The proof is similar to that of Theorem 3 in Parner (1998); see also van der Vaart (1998, pp. 419–424). First, (10) implies that, for any v ∈ 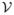 and h1, …, hK ∈
and h1, …, hK ∈ 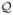 ,
,
| (11) |
where ℒ̈ pertains to the second-order derivative of the log-likelihood function.
On the right-hand side of (10), we replace 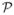 by
by 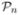 to obtain two new linear operators Bn1 and Bn2k. It is easy to show that Bn1 and Bn2k converge uniformly to B1 and B2k, respectively. Under (C8), the results of Lemma 1 apply to the second-order derivatives ℒ̈ and the operators (B1, B21, …, B2K). By replacing θ0, Λ0k and
to obtain two new linear operators Bn1 and Bn2k. It is easy to show that Bn1 and Bn2k converge uniformly to B1 and B2k, respectively. Under (C8), the results of Lemma 1 apply to the second-order derivatives ℒ̈ and the operators (B1, B21, …, B2K). By replacing θ0, Λ0k and 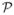 on both sides of (11) with θ̂, Λ̂0k and
on both sides of (11) with θ̂, Λ̂0k and 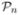 , we obtain
, we obtain
According to the proof of Theorem 2, (B1, B21, …, B2K) is invertible, and so is (Bn1, …, Bn2k) for large n. Note that can be written as for some matrix ℬn. Therefore ℬn is invertible, and so is ℐn. Furthermore,
According to Theorem 2, the asymptotic variance of is
where (ṽ, h̃1, …, h̃K) is (B1, B21, …, B2K)−1(v, h1, …, hK ), which can be approximated by (Bn1, Bn21, …, Bn2K)−1(v, h1, …, hK). Hence, the asymptotic variance can be approximated uniformly in v and hk’s by its empirical counterpart , which is further approximately by .
9. Profile Likelihood
Theorem 4
Let pln(θ) be the profile log-likelihood function for θ, and assume (C1)–(C8). For any εn = Op(n−1/2) and any vector v,
where Σ is the limiting covariance matrix of n1/2(θ̂ − θ0). Furthermore, .
Proof
We appeal to Theorem 1 of Murphy and van der Vaart (2000). Specifically, we construct the least favorable submodel for θ0 and verify all the conditions in their Theorem 1. For notational simplicity, we assume that K = 1. It is straightforward to extend to K > 1.
It follows from the proof of Theorem 2 that
where B2 stands for the operator (B21, …, B2K), and ℒ̈ΛΛ[H1, H2] denotes the second-order derivative of ℒ(θ, A) with respect to Λ along the bi-directions H1 and H2. On the other hand,
where is the dual operator of ℒΛ in L2[0, τ]. Thus, if we choose h such that , then
By definition, ∫hdΛ0 is the least favorable direction for θ0 and ℒ̇θ − ℒ̇Λ [∫hd Λ0] is the efficient score function. Such an h exists since B2(0, ·) is invertible. In addition, h ∈ BV [0, τ]. Hence, we can construct the least favorable submodel at (θ, Λ) by ε ↦ (ε, Λε) with dΛε (θ, Λ) = {1 + (ε − θ) · h} dΛ. Clearly, Λθ (θ, Λ) = Λ and
If θ̃ →p θ0 and Λ̂θ̃ maximizes the objective function with θ̂ replaced by θ̃, we can use the arguments in the proof of Theorem 1 to show that Λ̂θ̃ is consistent. In the likelihood equation for Λ̂θ̃, we can use the arguments for the linearization of (7) to show that, uniformly in h ∈ 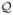 ,
,
The arguments for proving the invertibility of (B1, B2) show that h ↦ B2(0, h) is invertible. Thus,
By condition (C6), we obtain the no-bias condition, i.e.,
We have verified conditions (8)–(11) of Murphy and van der Vaart (2000).
Condition (C4), together with Lemma 1, implies that the class
is P-Donsker and that the functions in the class are continuous at (θ0, Λ0) almost surely, while condition (C8) implies that the class
is P-Glivenko-Cantelli and is bounded in L2(P). Therefore, all the conditions in Murphy and van der Vaart (2000) hold, so that the desired results follows from their Theorem 1.
10. Applications
In this section, we apply the general results to the problems described in Section 2. We identify a set of conditions for each problem under which regularity conditions (C1)–(C8) are satisfied so that the desired asymptotic properties hold. These applications not only provide the theoretical justifications for the work of Zeng and Lin (2007), but also illustrate how the general theory can be applied to specific problems.
10.1. Transformation Models With Random Effects for Dependent Failure Times
We assume the following conditions.
(D1) The parameter value belongs to the interior of a compact set Θ in Rd, and for all t ∈ [0, τ], k = 1, …, K.
(D2) With probability one, Zikl(·) and Z̃ikl(·) are in BV [0, τ] and are left-continuous with bounded left-and right-derivatives in [0, τ].
(D3) With probability one, P (Cikl ≥ τ|Zikl) > δ0 > 0 for some constant δ0.
(D4) With probability one, nik is bounded by some integer n0. In addition, E[Nik·(τ)] < ∞.
(D5) For k = 1, …, K, Gk(x) is four-times differentiable such that Gk(0) = 0, , and for any integer m ≥0 and any sequence 0 < x1 < … < xm ≤ y,
for some constants μ0k and κ0k > 0. In addition, there exists a constant ρ0k such that
(D6) For any constant a1 > 0,
and there exists a constant a2 > 0 such that for any γ,
(D7) Consider two types of events: k ∈ 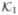 indicates that event k is recurrent and k ∈
indicates that event k is recurrent and k ∈ 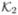 indicates that event k is survival time. For k ∈
indicates that event k is survival time. For k ∈ 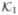 ∪
∪ 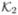 , if there exist ck(t) and v such that with probability 1, ck(t) + vTZikl(t) = 0 for k ∈
, if there exist ck(t) and v such that with probability 1, ck(t) + vTZikl(t) = 0 for k ∈ 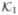 and ck(0) + vTZikl(0) = 0 for k ∈
and ck(0) + vTZikl(0) = 0 for k ∈ 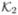 , then v = 0.
, then v = 0.
(D8) If there exist constants αk and α0k such that for any subset Lk ⊂ {1, …, nik} and for any ωkl and tkl,
then γ = γ0. In addition, if for k ∈ 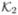 and for any t,
and for any t,
then Λ1 = Λ2. Furthermore, if for some vector v and constant αk,
then v = 0.
(D1)–(D4) are standard conditions for this type of problem. We show that (D5) holds for all commonly used transformations. We first consider the class of logarithmic transformations G(x) = ρ log(1 + rx) (ρ > 0, r > 0). Clearly,
Thus, in (D5), we can set μ0 to ρr(1 + 1/r) min(1, r)−ρ and κ0 to ρ. We can verify the polynomial bounds for G″(x)/G(x), G(3)(x)/G(x) and G(4)(x)/G(x) by direct calculations. We next consider the class of Box-Cox transformations G(x) = {(1 + x)ρ − 1}/ρ. Clearly,
Thus, we can set μ0 to 4ρ + exp(1/ρ) and κ0 to ρ. The polynomial bounds for G″ (x)/G(x), G(3)(x)/G(x) and G(4)(x)/G(x) hold naturally. Finally, we consider the linear transformation model: H(T) = β T Z + ε, where ε is standard normal. In this case, G(x) = − log{1 − Φ(log x)}, where Φ is the standard normal distribution function. We claim that there exists a constant ν0 > 0 such that φ (x) − ν0{1 − Φ(x)}(1 + |x|). If x < 0, then φ(x) ≤ (2π)−1/2 ≤ 2(2π)−1/2 {1 − Φ(x)}(1 + |x|). If x ≥ 0,
By the L’Hospital rule,
Therefore, φ(x)/[{1 − Φ(x)}(1 + x)] is bounded for x ≥ 0. Without loss of generality, assume that y > 1. Clearly,
Since (1 + x) φ(log(x))/[x{1 − Φ(log x)}] is bounded when x is close to zero and it is bounded by a multiplier of (1 + log x) when x is close to ∞, (1 + x)φ(log(x))/x{1 − Φ(log x)} ≤ ν01 + ν02 log(1 + x) for two constants ν01 and ν02. Therefore,
Since 1 − Φ(x) ≤ 21/2 exp(−x2/4) when x > 0, the above expression is bounded by
where all the ν’s are positive constants. The polynomial bounds for G″ (x)/G(x), G(3)(x)/G(x) and G(4)(x)/G(x) follow from the fact that φ(x)={1 − Φ (x)} ≤ O(1 + |x|).
Condition (D6) pertains to the tail property of the density function for the random effects f(b; γ). For survival data, , so that the first half of condition (D6) is tantamount to that the moment generating function of b exists everywhere. This condition holds naturally when b has a compact support or a Gaussian density tail. The second half of condition (D6) clearly holds for Gaussian density functions.
(D7) and (D8) are sufficient conditions to ensure parameter identifiability and non-singularity of the Fisher information matrix. In most applications, these conditions are tantamount to the linear independence of covariates and the unique parametrization of the random-effects distribution. Specifically, if Z̃ikl is time-independent, then the second condition in (D8) is not necessary; if Z̃ikl does not depend on k and l, and b has a normal distribution, then the other two conditions in (D8) hold as well provided that Z̃ikl is linearly independent with positive probability; if Z̃ikl is time-independent and 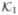 is non-empty (i.e., at least one event is recurrent), then (D8) can be replaced by the linear independence of Z̃ikl for some k ∈
is non-empty (i.e., at least one event is recurrent), then (D8) can be replaced by the linear independence of Z̃ikl for some k ∈ 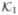 and the unique parametrization of f (b; γ).
and the unique parametrization of f (b; γ).
We wish to show that (D1)–(D8) imply (C1)–(C8), so that the desired asymptotic properties hold. Conditions (C1) and (C2) follow naturally from (D1)–(D4). To verify (C3), we note that
where
and .
If ||Λk||V [0,τ] are bounded, then
for any fixed constant B0 such that P(|b| ≤ B0) > 0. Thus, Ψ( ; θ,
; θ,  ) is bounded from below by
, so that the second half of (C3) holds. It follows from (D5) that
) is bounded from below by
, so that the second half of (C3) holds. It follows from (D5) that
Since exp{βT Zikl(s) + bT Z̃ikl(s)} ≥ exp{−O(1 + |b|)}, we have , so that
Thus, the first half of (C3) holds as well.
We now verify (C4). Under (D5),
Thus, it follows from the Mean-Value Theorem that
where the last inequality follows from integration by parts and the fact that Zikl(t) and Z̃ikl(t) have bounded variations. It then follows from (D6) that |Ψ ( ; θ(1),
; θ(1), 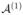 ) − Ψ (
) − Ψ ( ; θ(2),
; θ(2), 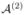 )| is bounded by the right-hand side of the inequality in (C4). By the same arguments, we can verify the bounds for the other three terms in (C4).
)| is bounded by the right-hand side of the inequality in (C4). By the same arguments, we can verify the bounds for the other three terms in (C4).
To verify (C6), we calculate that
For (θ,  ) in a neighborhood of (θ0,
) in a neighborhood of (θ0,  ),
),
Thus, for the second equation in (C6), η0km(s, t; θ0,  ) is obtained from the derivative of η0k with respect to Λm along the direction Λm − Λ0m, and η0kθ is the derivative of η0k with respect to θ. Likewise, we can obtain the first equation in (C6). It is straightforward to verify the Lipschitz continuity of η0km.
) is obtained from the derivative of η0k with respect to Λm along the direction Λm − Λ0m, and η0kθ is the derivative of η0k with respect to θ. Likewise, we can obtain the first equation in (C6). It is straightforward to verify the Lipschitz continuity of η0km.
The verification of (C8) is similar to that of (C4), relying on the explicit expressions of Ψ̈ θθ ( ; θ,
; θ,  ) and the first and second derivatives of Ψ(
) and the first and second derivatives of Ψ( ; θ,
; θ,  + εℋ) with respect to ε.
+ εℋ) with respect to ε.
It remains to verify the two identifiability conditions under (D7) and (D8). To verify (C5), suppose that (β, γ, Λ1, …, Λk) yields the same likelihood as (β0, γ0, Λ10, …, Λk0). That is,
We perform the following operations on both sides sequentially for k = 1, …, K and l = 1, …, nik.
(a) If the kth type of event pertains to survival time, for the lth subject of this type of event, the first equation is obtained with Rikl(t) = 1 and for any t ≤ τ, i.e., the subject does not experience any event in [0, τ]. The second equation is obtained by integrating t from tkl to τ on both sides under the scenario that Rikl(t) = 1 and has a jump at t, i.e, the subject experiences the event at time tkl. We then take the difference between these two equations. In the resulting equation, the terms and are replaced by and , respectively.
(b) If the kth type of event is recurrent, for the lth subject of this type of event, we let Rikl(t) = 1 and let have jumps at s1, s2, …, sm and for any arbitrary (m + m′) times in [0, τ]. We integrate s1, …, sm from 0 to tkl and integrate from 0 to τ. In the obtained equation, is replaced by {Gk(qikl(tkl))}m {Gk(qikl(τ))}m′ on both sides. Note that m and m′ are arbitrary. We then multiple both sides by {(iωkl)m/m!}/m′! and sum over m, m′ = 0, 1, … On both sides of the resulting equation, the terms associated with k and l are replaced by exp{iωklGk(qikl(tkl))}.
After these sequential operations, we obtain
For survival time, we can let any subject from the nik subjects have tkl = 0, which results in
where ξkl is any positive variable.
The above expression implies that {Gk(qikl(t)), k ∈ 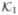 } as a function of
} as a function of
has the same distribution as {Gk(qikl0(t)), k ∈ 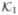 } as a function of
} as a function of
so this is true between {qikl(t)} and {qikl0(t)} because of the one-to-one mapping. Thus, the distributions of {
} and {
} should also agree and they have the same expectation. Now let tkl = 0 for k ∈ 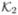 . Since E[b1] = E[b2] = 0, we obtain
for k ∈
. Since E[b1] = E[b2] = 0, we obtain
for k ∈ 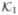 . The above arguments also yield
. The above arguments also yield
We compare the coefficients of ξkl for k ∈ 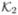 . This yields that for any subset Lk ⊂ {1, …, nik},
. This yields that for any subset Lk ⊂ {1, …, nik},
We differentiate the above expression with respect to tkl at 0 for k ∈ 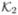 . It then follows from (D8) that log λk(0) − log λ0k(0) + (β − β0)T Zikl(0) = 0 and γ = γ0. Thus, (D7) implies that β = β0 and λk(t) = λ0k(t) for k ∈
. It then follows from (D8) that log λk(0) − log λ0k(0) + (β − β0)T Zikl(0) = 0 and γ = γ0. Thus, (D7) implies that β = β0 and λk(t) = λ0k(t) for k ∈ 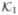 . On the other hand, for any fixed k ∈
. On the other hand, for any fixed k ∈ 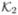 , we let tk′l′ = 0 if k′ ≠ k or l′ ≠ l. Thus, ∫b exp{− Gk(qikl(tkl))}f (b; γ0)db = ∫b exp{− Gk(q0ikl(tkl))}f (b; γ0)db. Therefore, Λk = Λ0k for k ∈
, we let tk′l′ = 0 if k′ ≠ k or l′ ≠ l. Thus, ∫b exp{− Gk(qikl(tkl))}f (b; γ0)db = ∫b exp{− Gk(q0ikl(tkl))}f (b; γ0)db. Therefore, Λk = Λ0k for k ∈ 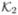 according to (D8).
according to (D8).
To verify (C7), we write v = (vβ, vγ). We perform operations (a) and (b) on the score equation in (C7). The arguments used in proving the identifiability yield
| (12) |
where
. We differentiate (12) with respect to tkl twice at 0 for k ∈ 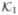 . Comparison of the coefficients for ωkl yields ∫b e2bTZ̃ikl(0) f′(b; γ0)T vγdb = 0. We also differentiate (12) with respect to tkl at 0 for k ∈
. Comparison of the coefficients for ωkl yields ∫b e2bTZ̃ikl(0) f′(b; γ0)T vγdb = 0. We also differentiate (12) with respect to tkl at 0 for k ∈ 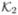 . Thus, for each k ∈
. Thus, for each k ∈ 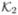 and l = 1, …, nik,
. It then follows from (D8) that vγ = 0. For fixed k0 and l0, with the fact of vγ = 0, the score equation under operations (a) and (b), where in (a) we let
for any t ≤ τ and in (b) we let m = 0 whenever k ≠ k0 or l ≠ l0, becomes a homogeneous integral equation for hk0 (t) + Zik0l0 (t)T vβ. The equation has a trivial solution, so hk0 (t) + Zik0l0 (t)T vβ= 0. Since k0 and l0 are arbitrary, (D7) implies that hk = 0 and vβ= 0.
and l = 1, …, nik,
. It then follows from (D8) that vγ = 0. For fixed k0 and l0, with the fact of vγ = 0, the score equation under operations (a) and (b), where in (a) we let
for any t ≤ τ and in (b) we let m = 0 whenever k ≠ k0 or l ≠ l0, becomes a homogeneous integral equation for hk0 (t) + Zik0l0 (t)T vβ. The equation has a trivial solution, so hk0 (t) + Zik0l0 (t)T vβ= 0. Since k0 and l0 are arbitrary, (D7) implies that hk = 0 and vβ= 0.
Remark 2
For survival time, (D5) is required to hold only for m = 0 and m = 1.
Remark 3
The above results do not apply directly to the proportional hazards model with gamma frailty because (D6) does not hold when b has a gamma distribution. It is mathematically convenient to handle this model because the marginal hazard function has an explicit form. The likelihood is a special case of ours with
in the notation of Parner (1998). Clearly, Ψ satisfies (C3) when θ > 0. The other conditions can be verified in the same manner as before.
Remark 4
Our theory does not cover the case in which the true parameter values lie on the boundary of Θ. It is delicate to deal with the boundary problem. One possible solution is to follow the idea of Parner (1998) by extending the definition of the likelihood function outside Θ and verifying (C2)–(C8) for the extended likelihood function.
Remark 5
We have assumed known transformations. We may allow Gk to belong to a parametric family of distributions, say Gk(·; φ), where φ is a parameter in a compact set. Then θ contains φ. Our results and proofs apply to this situation if (D5) holds uniformly in φ and the two identifiability conditions are satisfied.
10.2. Joint Models for Repeated Measures and Failure Times
For the (parametric) generalized linear mixed model, the likelihood can be viewed as a special case of that of Section 10.1 except that there is an additional parameter α in f(y|x; b). We assume that (D1)–(D8) hold but with (D6) replaced by the following condition.
(D6′) For any constant a1 > 0,
and there exists a constant a2 > 0 such that for any γ and α,
almost surely, where r3( ) is a random variable in L2(P).
) is a random variable in L2(P).
Under these conditions, the desired asymptotic properties follow from the arguments of Section 10.1.
Under the semiparametric linear transformation model for continuous repeated measures, the likelihood is in the form of that of Section 2.2 with K = 2 and ni2 = ni, where the time to the second type of failure is defined by Yij (assuming without loss of generality that Yij ≥ 0). Thus, if we regard Yij as a right-censored observation when it is greater than a very large value (i.e., the upper limit of detection), then the asymptotic results given in Section 10.1 hold. When such an upper limit does not exist, the estimator for Λ̃ can be unbounded when sample size goes to infinity. Then our proof of Theorem 1 does not apply.
10.3. Transformation Models for Counting Processes
We verify (C1)–(C8) under the following conditions.
(E1) The parameter value belongs to the interior of a compact set Θ in Rd, and for all t ∈ [0, τ].
(E2) With probability one, P (C ≥ τ|Z) > δ0 > 0 for some constant δ0.
(E3) Condition (D5) holds.
(E4) With probability one, Z(·) and Z̃ are in BV [0, τ] and are left-continuous with bounded left- and right-derivatives in [0, τ].
(E5) If γT Z̃ is equal to a constant with probability one, then γ = 0. In addition, if βT Z(t) = c(t) for a deterministic function c(t) with probability one, then β = 0.
In this case,
By (D5),
for some constant μ1. Thus, (C3) follows from the boundedness of γT Z̃i. We can verify the other conditions by using the arguments of Section 10.1.
To verify the first identifiability condition, we assume that has jumps at x, x1, …, xm for some integer m. After integrating both sides of the equation in (C5) over x1, …, xm from 0 to τ and integrating x from x to τ, we obtain
Multiplying both sides of this equation by 1/m! and summing over m ≥ 0, we obtain
Setting in the likelihood function yields
Thus
Then Λ* (t) is absolutely continuous with respect to t. Differentiating both sides with respect to x and letting x = 0 yield λ* (0) > 0. When x converges to zero, the left-hand side is while the right-hand side is . Thus, . By (E5), γ0 = γ *. Furthermore, . It follows from (E5) that β0 = β* and Λ0 = Λ*.
To verify (C7), we assume that the score function along (β0 + εhβ, γ0 + εhγ, dΛ0 + εhdΛ0) is zero. Equivalently, if we let , then we obtain
We multiply both sides by the likelihood function and let have jumps at times t1, t2, …, tm. We integrate t1 from 0 to t and tl, 1 < l ≤ m from 0 to τ. By multiplying the resulting equation by 1/(m − k)! and summing over m = 1, 2, …, we obtain
Differentiation with respect to t then yields
Combining the above two equations, we have
This is a homogeneous integral equation for and has zero solution. That is, . It follows from (E5) that h(t) = 0 and hβ= 0. Thus, hγ = 0.
11. Concluding Remarks
We have developed a general asymptotic theory for the NPMLEs with right censored data and shown that this theory applies to the models considered by Zeng and Lin (2007). This theory can also be used to establish the desired asymptotic properties for other existing semiparametric models, particularly the models mentioned in Sections 7.1–7.4 of Zeng and Lin (2007), as well as those that may be invented in the future. It is much simpler to verify the set of sufficient conditions identified in this paper than to prove the asymptotic results from scratch. Conditions (C1) and (C2) are standard conditions required in all censored-data regression; (C3), (C4) and (C6) are certain smoothness conditions that can be verified directly, as demonstrated in Section 10; (C5) and (C7) are two minimal identifiability conditions that need to be verified for any specific problem.
Although the basic structures of our proofs mimic those of Murphy (1994; 1995) and Parner (1998), our technical arguments are innovative and substantially more difficult because we deal with a very general form of likelihood function rather than specific problems. In all previous work, verification of the Donsker property relies on the specific expressions of the functions, whereas our Lemma 1 provides a universal way to verify this property. In verifying the invertibility of the information operator, all previous work requires an explicit expression of the information operator that is identified as the sum of an invertible operator and a compact operator, whereas we allow a very generic form of information operator obtained from the likelihood function (1). Murphy and van der Vaart (2001) stated that the consistency of NPMLEs needs to be proved on a case-by-case basis; however, we were able to prove the consistency for a very general likelihood function. Although we borrowed the partitioning idea of Murphy (1994), our technical arguments are very different because of the generic form of the likelihood.
In some applications, the failure times are subject to left truncation in addition to right censoring. To accommodate general censoring/truncation patterns, we define N(t) as the number of events observed by time t and R(t) as the at-risk indicator at time t, reflecting both left truncation and right censoring. Assume that the truncation time has positive mass at time 0, so that (C2) is satisfied. Then all the results continue to hold.
This paper is concerned with the theoretical aspect of the NPMLEs and complements the work of Zeng and Lin (2007). The interested readers are referred to the latter for the calculations of the NPMLEs and for the use of the semiparametric regression models and NPMLEs in practice. The latter also provides rationale for the kind of model considered in Sections 2 and 10 of this paper. Although the latter contains some theoretical elements, this paper presents the theory (especially the regularity conditions) in a more rigorous manner and provides all the proofs.
Contributor Information
Donglin Zeng, Email: dzeng@bios.unc.edu.
D. Y. Lin, Email: lin@bios.unc.edu.
References
- Heitjan DF, Rubin DB. Ignorability and coarse data. Ann Statist. 1991;19:2244–2253. [Google Scholar]
- Murphy SA. Consistency in a proportional hazards model incorporating a random effect. Ann Statist. 1994;22:712–731. [Google Scholar]
- Murphy SA. Asymptotic theory for the frailty model. Ann Statist. 1995;23:182–198. [Google Scholar]
- Murphy SA, van der Vaart AW. On profile likelihood. J Am Statist Assoc. 2000;95:449–485. [Google Scholar]
- Murphy SA, van der Vaart AW. Semiparametric mixtures in case-control studies. J Multi Analy. 2001;79:1–32. [Google Scholar]
- Parner E. Asymptotic theory for the correlated gamma-frailty model. Ann Statist. 1998;26:183–214. [Google Scholar]
- Rudin W. Functional Analysis. McGraw-Hill; New York: 1973. [Google Scholar]
- Van der Vaart AW. Asymptotic Statistics. Cambridge University Press; Cambridge: 1998. [Google Scholar]
- Van der Vaart AW, Wellner JA. Weak Convergence and Empirical Processes. Springer; New York: 1996. [Google Scholar]
- Zeng D, Lin DY. Maximum likelihood estimation in semiparametric regression models with censored data (with discussion) J R Statist Soc, Ser B. 2007;69:507–564. [Google Scholar]


