Abstract
Most motor tasks require the simultaneous coordination of multiple muscles. That coordination is poorly understood in part because there is no noninvasive means of isolating a single muscle's contribution to the resultant endpoint force. The contribution of a single motor unit to isometric tasks can, however, be characterized using the spike-triggered averaging (STA) technique, applied to a single motor unit's spike train. We propose that a technique analogous to STA, which we call electromyogram (EMG)-weighted averaging (EWA), can be applied to surface EMGs to extract muscle mechanical action from the natural endpoint force fluctuations generated during steady isometric contraction. We demonstrate this technique on simultaneous recordings of fingertip force and surface EMG from the first dorsal interosseous (FDI) and extensor indicis (EI) of humans. The EWA direction was approximately the same across a wide range of fingertip force directions, and the average EWA direction was consistent with mechanical action direction of these muscles estimated from cadaveric and imaging data: the EWA directions were 193 ± 2° for the FDI and 71 ± 5° for the EI (95% confidence). EWA transient behavior also appears to capture temporal characteristics of muscle force fluctuations with peak force time and general waveform shape similar to that of the associated spike-triggered averages from single motor units. The EWA may provide a means of empirically characterizing the complex transformation between muscle force and endpoint force without the need for invasive electrode recordings or complex anatomical measurements of musculoskeletal geometry.
INTRODUCTION
The goal of many motor tasks is to exert force against the environment. Understanding how the CNS coordinates muscles requires an understanding of how individual muscles exert force against the environment at an endpoint; i.e., a muscle's mechanical action. The CNS simultaneously activates many motor units from multiple muscles when coordinating almost every motor task. Simultaneous activation makes it difficult to characterize a muscle or a motor unit's individual mechanical properties, and it also makes it difficult to characterize how a motor unit contributes to a muscle's force and how the muscle's force contributes to an overall task such as application of force by the body. The mechanical contributions are a complex function of body configuration, musculoskeletal geometry, motor unit contractile properties, and activation history. Relevant data may be obtained experimentally from a approaches such as cadaveric measurements (An et al. 1983; Valero-Cuevas et al. 2000) and magnetic resonance imaging (MRI) (Fowler et al. 2001), and at the single motor unit level, from surface electrode arrays (Merletti et al. 2003), intramuscular recording (Moritz et al. 2005), and intra-neural micro stimulation (Keen and Fuglevand 2004; Thomas et al. 1990b) during isometric force production tasks. But the bulk properties of a muscle or a motor unit population are difficult to estimate noninvasively. We propose a means of characterizing a muscle's contribution to applied endpoint force using whole-muscle surface electromyogram (EMG), which may obviate the need for invasive EMG measurements.
A well-established method to extract the force associated with single motor unit contractions (SMUs) is spike-triggered averaging (STA). It averages the endpoint force following each of a motor unit's spikes (i.e., action potential onsets). If performed over a sufficient number of spikes, the effect is to cancel out the background motor unit activity (Stein et al. 1972), leaving a residual signal characterizing that unit's transient force fluctuation. Spikes required for STA of force are typically recorded using fine-wire EMG, and the resulting STA has been used to estimate the mechanical action of individual motor units (ter Haar Romeny et al. 1984; Thomas et al. 1986). It has also been used to study changes in motor unit mechanical properties in a wide variety of contexts, such as during static and dynamic contractions (Keen and Fuglevand 2004; Ogawa et al. 2006), whether muscle is activated volitionally or spontaneously firing (Chan et al. 2001). Despite some limitations that have been well characterized (Calancie and Bawa 1986; Taylor et al. 2002), STA has provided important insights into human motor systems (Gossen et al. 2003).
A drawback of the STA method for characterizing motor units is that it applies only to single motor units. The force fluctuations associated with single motor units are routinely very small when compared with the net limb force, thus requiring a large number of spikes to be used in the averaging. It may prove preferable to estimate the action of a large population of motor units or even an entire individual muscle, but this would require a large number of invasive fine-wire unitary recordings or the use of surface arrays to record sufficient data. It may thus prove helpful if transient force characteristics similar to STA, but for a whole muscle rather than a single motor unit, could be obtained noninvasively using the least amount of instrumentation.
An alternative to fine-wire intramuscular unitary recordings is surface EMG, which is not invasive and effectively surveys a large number of motor units simultaneously but has no force-averaging technique similar to STA. The key to the standard STA technique is that action potentials must be sorted into discrete spikes to which the corresponding endpoint forces may be aligned, whereas surface EMG is not considered similarly separable because of the complex conduction of motor unit electrical potentials to the skin surface (Fuglevand et al. 1992; Keenan et al. 2007). The surface EMG is nonetheless considered to be a superposition of relatively brief waveforms initiated by motor unit spikes (De Luca et al. 2006; Fuglevand et al. 1993; Keenan and Valero-Cuevas 2007; Zhou and Rymer 2004a). If the surface EMG retains information about spike times of the recorded motor units, in the form of transient increases in EMG amplitude, it may be possible to associate those increases with endpoint force to highlight the force fluctuations of the constituent motor units. Averaging over sufficient time may attenuate the contribution from motor units of other muscles and thus extract the force fluctuations associated with the muscle of interest from the total endpoint force.
We propose that an appropriate generalization of STA for characterizing muscle force generation is to cross-correlate the rectified surface EMG with endpoint force. This is because the alignment of forces according to discrete SMU spikes is equivalent to a cross-correlation, which we here apply to surface EMG in a technique we term EMG-weighted averaging (EWA). If surface EMG is indeed analogous to a superposition of SMU action potentials, its cross-correlation with endpoint force should produce the equivalent of an average spike-triggered force average across multiple motor units.
To test this concept, we applied it to the task of isometric force production by the index finger of human subjects. We performed EWA on measured fingertip forces and surface EMGs from both the first dorsal interosseous and the extensor indicis muscles. We show that the EMG-weighted averages correspond with independent data regarding spatiotemporal characteristics of STAs exhibited by motor units within each of those muscles. The proposed method is less invasive than the intramuscular recordings required for STA and provides information about a large population of motor units.
METHODS
We applied the proposed EWA technique to experimental recordings of surface EMG and isometric force measured at the fingertip. The fingertip forces were measured as human subjects produced combinations of flexion-extension/abduction-adduction joint torque. We refer to the cross-correlation between EMG and fingertip force as the EWA trajectory, which we will show yields information about the direction of muscle force fluctuations in the fingertip space. Here we develop the theoretical rationale for EWA and then describe an experimental application of the proposed technique. We then examine the relationship between the EWA trajectory and the average STA across motor units in the recording volume.
Rationale for EMG weighted averaging
The EWA is based on a cross-correlation of EMG and force. We interpret STA as a special case of the more general cross-correlation technique (see appendix). Transient increases in EMG are generally expected to reflect transient increases in muscle force. The cross-correlation of force and surface EMG may thus yield similar results to the STA. Although the surface EMG contains little information regarding individual motor units (Farina et al. 2004), it may nevertheless help produce a measure of force fluctuations induced by its constituent motor unit population.
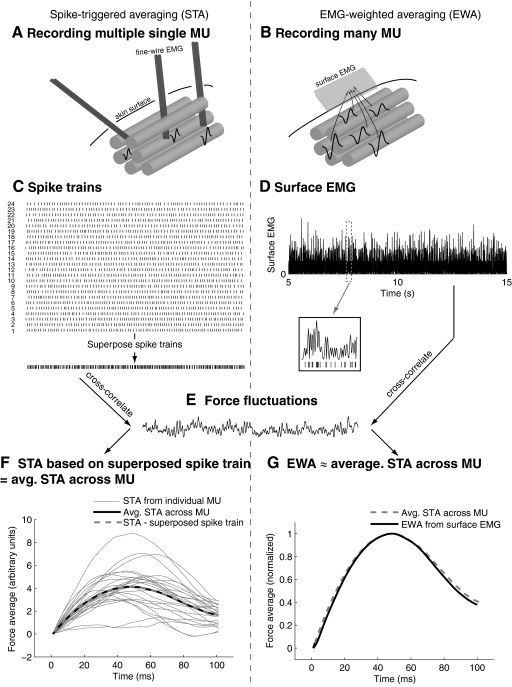
The two techniques may be conceptually compared in parallel (Fig. 1). Whereas STA requires motor unit spikes be recorded and discriminated, usually by intramuscular EMG (Fig. 1A), EWA uses the combined effect of many spikes in many motor units influencing a surface electrode (Fig. 1B) or a nonselective intramuscular electrode. The data hypothetically available from spike discrimination would be a spike train for each individual motor unit or a single spike train formed by superimposing the individual spike trains (Fig. 1C). The spikes are equivalent to mathematical impulse functions, so that the STA is equivalent to the cross-correlation of endpoint forces with a train of impulse functions (see appendix). The proposed EWA method relies on a rectified surface EMG recording that contains superimposed action potential waveforms from a population of motor units, so that increases in surface rectified surface EMG will be correlated with discharges in the superimposed spike train (Fig. 1D).
Fig.1.
Conceptual comparison of spike-triggered averaging (STA) and electromyogram (EMG)-weighted averaging (EWA). A: STA is typically performed by sorting motor unit spike trains from fine-wire EMG recordings, whereas EWA (B) is performed on a rectified surface EMG signal composed of electrical potentials from many motor units. C: STA typically uses spike trains from individual motor units as a measure of activity, and these spike trains could be combined into a single spike train representing all spikes from all motor units. D: EWA uses rectified surface EMG as a measure of activity, and increases in surface EMG will be correlated with increased activity in the superposed spike train (inset). E: both STA and EWA cross-correlate their activity measure with force fluctuations to produce STA (F) or EWA (G) waveforms. We expect a high degree of similarity between the average STA waveform and the EWA waveform because the surface EMG may be highly correlated with the superposed spike train.
We propose that the surface EMG signal may not need to be decomposed into constituent spikes because relative to the time course of force production, a surface-recorded action potential may approximate an impulse function. Assuming that rectified surface EMG is roughly equivalent to the superposition of action potentials, its cross-correlation with fluctuations in endpoint force (Fig. 1E) will theoretically yield an average STA taken across the population of motor units contributing to the surface EMG. Several different averages could be computed from the spike trains (Fig. 1F). An STA could be computed from each individual motor unit spike train. The average of the STAs from each individual motor unit could be taken (averaging across spikes, then motor units). Or the spike trains could first be superimposed and then STA performed on the superimposed spike train (“averaging” across motor units, then spikes). The latter two averages are equivalent because of the commutative property of mathematical addition (Fig. 1F). Because the surface EMG will be correlated to the superimposed spike train, we hypothesize that the EWA will be equivalent to the average of the STAs from individual motor units (Fig. 1G).
A key assumption for the impulse function approximation is that a motor unit action potential is much shorter than the resulting force twitch. As an example, the force twitch estimated from STA for the first dorsal interosseous typically rises to a peak 50–60 ms after a spike and then decays slowly (Chan et al. 2001; Thomas et al. 1986) over a time course that may be 10 times as long as a typical action potential (e.g. De Luca et al. 2006; Petersen and Kugelberg 1949; Zhou and Rymer 2004b). Surface-recorded action potentials can extend ≤20 ms (Macefield et al. 1996; Westling et al. 1990; Zijdewind and Thomas 2001), and the effect of long durations will be examined in a sensitivity analysis.
The impulse function approximation also underlies the requirement for rectification of EMG signals. Without rectification, the positive and negative fluctuations of an action potential would largely cancel each other in the cross-correlation. Rectification cannot correct for canceling interference between distinct action potentials (Day and Hulliger 2001; Keenan et al. 2005; Zhou and Rymer 2004a) prior to recording. However, as long as there are some increases in rectified EMG that are correlated with motor unit discharges within the muscle, and EWA is performed for a sufficient length of time, EWA will still estimate the mechanical action associated with any noncanceling motor unit spikes.
METHODS
We performed EWA on fingertip forces produced by the metacarpophalangeal (MCP) joint torques of the human index finger, using surface EMG recordings from the first dorsal interosseous (FDI) and extensor indicis (EI) muscles. In the posture studied, FDI produces mostly abduction with a small amount of flexion joint torque, while the EI produces mostly extension with a small amount of adduction joint torque (Fowler et al. 2001). Seven unimpaired subjects participated in the study. All subjects were right-handed and used their dominant index finger to produce isometric forces in different directions and magnitudes in the flexion-extension/abduction-adduction (FEAA) task plane. The Northwestern University Institutional Review Board approved the study protocol, and informed consent was obtained from each subject prior to participation.
Forces were recorded from the index finger, mechanically isolated from the rest of the body. As described previously (Kutch et al. 2008), subjects were seated upright in an adjustable chair with the shoulder abducted ∼15° with the elbow resting on a padded support. The elbow joint was flexed to 90°, and the forearm was casted and secured in a plastic orthosis in a pronated position with the palm facing down. The index finger was casted and placed in a fixed cylindrical tube, so that forces were exerted against the inside of the tube and about an “endpoint” just distal to the DIP joint. One Velcro strap was placed around the subject's waist, and two Velcro straps were crossed over each shoulder to restrain the subject and to minimize shoulder movement. Isometric index finger forces in the FEAA plane were measured using a sensitive 6 axis load cell (JR3, Woodland, CA, Model 20E12A-I25 9N.5), at a sampling rate of 1,000 Hz. We also recorded surface EMGs from the FDI and EI. The EMGs were recorded using miniature electrode/preamplifiers (DELSYS, Boston, MA) with two silver recording surfaces, 5 mm long and 10 mm apart, with preamplifier filters of bandwidth 20–450 Hz for surface recordings, with gains set to 100 and a sampling rate of 2,000 Hz. (EMG electrodes were placed on the skin through a small portal in the cast over the muscle of interest). While the system of restraints used in this experiment was designed to allow the subject to easily produce force with the index finger only, it should be noted that EI lies deep to extensor carpi ulnaris and extensor digitorum, and in close proximity to other muscles such as the extensor pollicis longus. Thus we expect that the recording from EI will be relatively unselective compared with the recording from the FDI.
Each trial consisted of the exertion of a fingertip force toward a target from an array of target forces, chosen in random order. The array included 24 different directions distributed equally over the FEAA plane at 15° increments, each at one of three different magnitude levels. A rest trial was first collected for each subject to establish EMG baseline levels. For subsequent trials, the subject viewed their instantaneous fingertip force as a dynamic cursor along with the target force on the visual display. The subject was instructed to gradually exert force in the target direction and then to hold the target force as precisely as possible for ∼10–20 s. The experimenter examined the time-domain force traces on-line and asked for trials to be repeated if forces were found not to be approximately constant. The force feedback display was zeroed, with the subject at rest, before each set of trials. Subjects were asked to rest for ≥10 s between each trial, and ≥1 min after each group of ten trials. The force magnitude levels were chosen to require very minimal effort for all subjects, ∼1–3 N in magnitude.
Analytical procedures
Cross-correlation was performed between surface EMG and the simultaneously recorded endpoint force. We used surface EMG recordings from a muscle EMUSCL(n) (n denotes discrete time point), along with two force components: fingertip force due to MCP flexion/extension FFE(n), and fingertip force due to MCP abduction/adduction FAA(n). The EWA trajectory was computed as follows
| (1) |
where the summation was carried out over steady-state intervals. The EWA trajectory in the FEAA plane was shifted so that it began from the origin at zero time lag. For each trial, the average abduction/adduction force F̄AA was combined with the average flexion/extension force F̄FE to characterize the direction of the task performed in that trial. Statistics of directions were analyzed using circular statistics, implemented in MATLAB as the CircStat toolbox (Berens 2009).
To define the overall level of muscle activity for a trial in a given direction, raw EMG traces were first rectified and averaged across the steady period. We fitted a cosine tuning curve as a function of task direction (Hoffman and Strick 1999; Todorov 2002) to the processed EMG data within each subject and magnitude level (24 values for each level), minimizing the sum-squared error. The EMG data for each level and subject were then normalized to the maximum of the fit, thus avoiding normalization to a spurious maximum in the data. Each EWA was quantified temporally and spatially, based on the time lag between 0 and 100 ms when the EWA trajectory reached its first peak magnitude. We used this time lag to define the EWA time to peak and used the corresponding spatial direction to define the EWA direction.
Computational models
We developed a computational model to examine the expected correspondence between STA and EWA and the sensitivity of EWA to its underlying assumptions. We employed the Fuglevand model (Fuglevand et al. 1993) to relate force fluctuations with surface EMG during steady isometric contractions. Our implementation contained 120 motor units. The model we employed had neural, muscle, and EMG models (Table 1). The neural model was used to simulate spike trains from a set of motor units for a given level of muscle excitation. The muscle model was used to convert the motor unit spike trains into time-varying muscle force. The EMG model was used to convert the motor unit spike trains into time-varying EMG. We used a simple EMG model where each motor unit spike added a brief waveform to the simulated EMG. The waveforms were modeled as first-order Hermite-Rodriguez (HR) functions (which have positive and negative phases) as has been done previously (Zhou and Rymer 2004b; Zhou et al. 2007). This the waveform of EMG initiated by a motor unit spike had the form
| (2) |
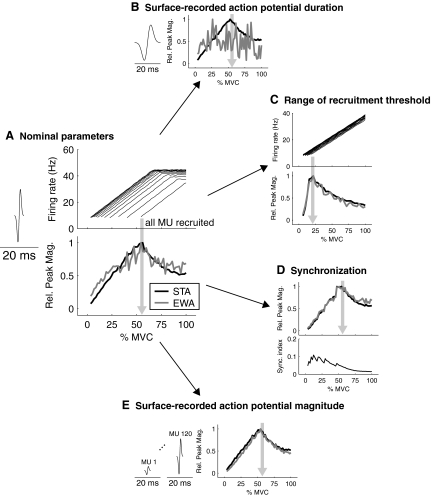
For a desired surface-recorded action potential duration of APD, we computed λ by λ = APD/(4√2). This choice of λ caused H(t) to decay to ∼0 at both +APD/2 and −APD/2, giving an entire action potential duration of APD. A spike at time S from any motor unit within the simulated muscle would cause H(t − SAPD/2) to be added to the simulated surface EMG. The sensitivity of EWA to the surface-recorded action potential was analyzed by varying the amplitude and duration of these waveforms (Table 1). The sensitivity of EWA to motor unit recruitment was analyzed by varying the range of muscle excitation levels need to recruit all motor units. Sensitivity to synchronization was tested by perturbing initially uncorrelated motor unit spike times (Yao et al. 2000). The degree of synchronization was quantified by calculating the probability that the time difference between spikes was <6 ms for all active motor unit pairs. We defined a synchronization index (sync. index) as the difference in this probability between the spike trains when initially generated with independent spike times and after the synchronization algorithm was applied (Binder and Powers 2001; De Luca et al. 1993). Each simulation was run for 60 s with a time step of 1 ms.
Table 1.
Model parameters
| Models | Parameters | Varied | Values |
|---|---|---|---|
| Neural | Range of recruitment threshold | Yes | 30, 5 |
| Minimum firing rate | No | 8 Hz | |
| Excitatory drive-firing rate gain | No | 1 | |
| Peak firing rate for first motor unit | No | 45 Hz | |
| Peak firing rate difference | No | 10 Hz | |
| Coefficient of variation in inter-spike interval | No | 0.2 | |
| Synchronization: fraction of reference spikes | Yes | 0, 0.061 | |
| Synchronization: fraction of test units | Yes | 0, 0.061 | |
| Muscle | Range of peak forces | No | 100 |
| Longest contraction time | No | 90 ms | |
| Range of contraction times | No | 3 | |
| EMG | Surface-recorded action potential duration | Yes | 5, 20 ms |
| Surface-recorded action potential magnitude | Yes | All equal, proportional to peak force |
The nominal parameter set is shown in bold. The sensitivity of the model to each of the varied parameters was examined by changing that parameter alone while keeping the other parameters at their nominal value.
RESULTS
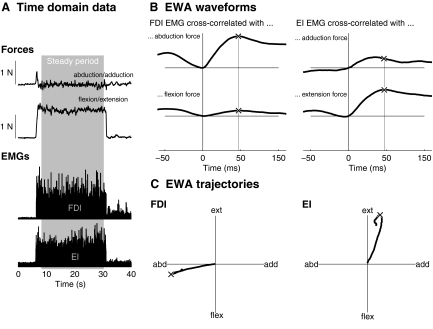
We found that EWA produced consistent force averages for both FDI and EI, revealing mechanical information embedded in fingertip forces and surface EMGs (Fig. 2). Despite the simultaneous activity of multiple muscles, EWA was shown to be able to highlight the force fluctuations of one muscle while averaging out the action of others. When viewed macroscopically, the simultaneously recorded FDI and EI surface EMG signals appeared to be noisy and minimally informative (Fig. 2A). However, when EWA was performed with the abduction/adduction-flexion/extension force components, it exhibited information about individual muscle force fluctuations along multiple axes (Fig. 2B). The EWA also exhibited spatial features in fingertip space (Fig. 2C), such as a roughly unidirectional trajectory corresponding approximately with the directions of greatest activation. Notice that the EWA waveforms are approximately periodic with increased correlation for negative time lags (EMG lags behind force). The periodicity of the cross-correlation function is a commonly observed feature of STAs (Taylor et al. 2002) and likely results from the periodic oscillation of force during an unfused tetanus (Thomas et al. 1990a).
Fig.2.
Representative EWA. A: a sample trial is shown in the time domain, where the subject exerted primarily a metacarpophalangeal (MCP) extension force, which produced EMG activity in both the 1st dorsal interosseous (FDI) and extensor indicis (EI) muscles. B: cross-correlation of rectified surface EMG and force components yielded EWA waveforms peaking at time lag (between EMG and force) of 50 ms. The EWA time to peak is shown as a vertical line. C: plots of EWA components against each other shows EWA trajectories in task space, approximately directed along the mechanical action of each muscle. ×, the point along the trajectory when the EWA magnitude peaked.
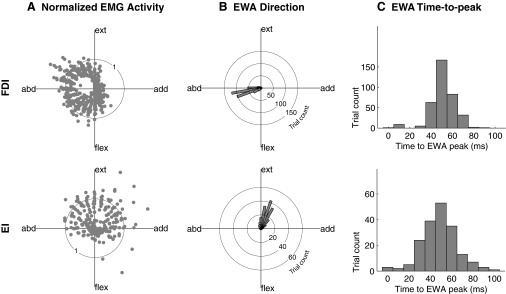
The muscle activity and the EWA directions in endpoint space were found to be consistent with data from independent sources from the literature. Both FDI and EI muscles were active across a large but directed portion of a multidimensional task space, each covering at least a 180° range of task directions, consistent with the hypothesis that muscles are activated when the dot product of the desired force vector and the muscle force vector is positive (Herrmann and Flanders 1998). The FDI was active mainly in the left half of the MCP flexion-extension/abduction-adduction plane, between extension and flexion (Fig. 3A). The EI was active mainly in the upper half of the MCP flexion-extension/abduction-adduction plane, between adduction and abduction. Across these active ranges, the EWA directions were highly focused near the direction of mechanical action (Fig. 3B), showing that EWA is relatively insensitive to task direction and that these muscles generate force in approximately the same direction across a large range of task directions. The average EWA direction for the FDI was 193 ± 2° (measured counter-clockwise from the adduction axis, 95% confidence interval for the average). The average EWA direction for the EI was 71 ± 5°.
Fig.3.
EMG activity, EWA direction, and EWA time to peak for all trials. A: polar plots of normalized EMG activity as a function of task direction for the FDI and EI with each dot representing a trial. The FDI was primarily active in the left half-plane between extension and flexion and the EI in the upper half-plane between adduction and abduction. B: polar histograms of EWA direction for the FDI and the EI for trials in the half-plane where each muscle was active, showing that regardless of task direction, the EWA direction was focused near the direction of mechanical action for both muscles. C: histograms of EWA time to peak for the FDI and EI for trials in the half-plane where each muscle was active. Data shown are for all trials and all subjects.
The mechanical action directions are similarly comparable to data drawn from previous cadaveric, electrophysiological, and imaging studies (An et al. 1983; Fowler et al. 2001; Kamper et al. 2006). The average mechanical action estimate across these studies is 207° for the FDI and 73° for the EI. The alignment of the EWA direction along the muscle mechanical action indicates that EWA effectively filtered out the force contribution of other muscles and suggests that there was relatively little correlation between motor units with distinct directions of mechanical action (Keen and Fuglevand 2004; Kutch et al. 2007).
The EWA directions presented here are also in agreement with our previous study of force covariance ellipses as an indicator of muscle activity (Kutch et al. 2008). In that study, we found that there were local peaks in the target-directed variance fraction (covariance ellipse skinniness and alignedness with the target direction) at 195° (near EWA direction estimate for FDI) and 75° (near EWA direction estimate for EI). Thus on average across the subjects studied, there was excellent agreement between the EWA-estimated direction of mechanical action and the target directions where narrow target-directed covariance ellipses were observed.
The time course of the EWA waveforms was also comparable to that expected from the superposition of multiple STAs (Fig. 3C). The EWA time-to-peak histograms for both the FDI and EI for most trials exhibited a force peak at a time lag of ∼50 ms (FDI 51.5 ± 11.5 ms and EI 51.2 ± 17.3 ms, SDs). These were similar to STA times to peak reported in the literature (Chan et al. 2001). For example, three studies of FDI report time-to-peak values of 47–61 ms (Kossev et al. 1994; Milner-Brown et al. 1973, 1974) from hundreds of single motor units. We are not aware of any studies using STA for the EI, but the related digital extensor, extensor digitorum communis, has motor units with STA time to peak of 40–70 ms (Monster and Chan 1977).
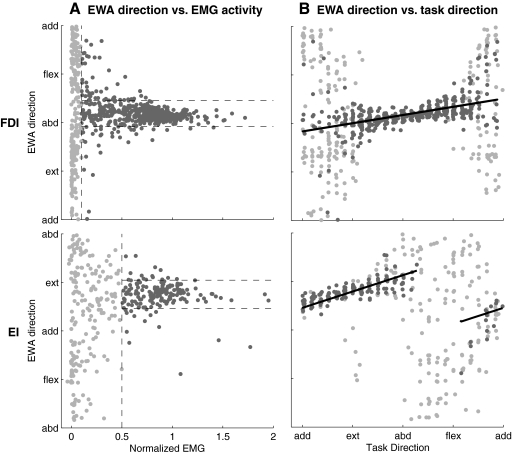
Plotting EWA direction against normalized EMG activity revealed that EWA could provide another means, independent of EMG amplitude, of identifying the set of tasks for which a particular muscle is active (Fig. 4A). When a muscle is inactive, the EWA is a cross-correlation between the endpoint force and noise, yielding a low-amplitude trajectory that is essentially random in direction. As a muscle becomes active, the EWA direction should focus near the mechanical action direction of the muscle. Grouped data are presented to show that we consistently observed EWA trajectories that were focused near the direction of mechanical action across regions of task space with high relative EMG activity (Fig. 4). When the normalized FDI EMG activity was greater than a 10% threshold, the SD of the FDI EWA direction was 24° versus 77° when normalized FDI EMG was <10%. When the normalized EI EMG activity was greater than a 50% threshold, the SD of the EI EWA direction was 26° versus 73° when normalized EI EMG was <50%. These results show that EWA can indicate when EMG activity is generating detectable force fluctuations along the direction of muscle action, which can provide evidence that the EMG is translating into measurable force.
Fig.4.
EWA-based thresholding and EWA shifts as a function of task direction. A: the EWA direction is essentially random when the muscle as little activity and becomes focused along the muscle's direction of action only when the EMG activity is greater. EMG threshold is determined so that the SD of EWA direction across above-threshold trials (●) is ∼25°. Below-threshold trials are shown as light points. B: a plot of EWA direction vs. task direction for above-threshold (●) and below-threshold ( ) trials. A linear fit (—) to the above-threshold trials illustrates small but predictable shifts in EWA direction with changes in task direction.
) trials. A linear fit (—) to the above-threshold trials illustrates small but predictable shifts in EWA direction with changes in task direction.
We also observed a slight dependence of EWA direction on task direction. Even though the EWA direction histograms were relatively focused (Fig. 3B), a plot of EWA direction against task direction (Fig. 4B) illustrates a systematic dependence. For tasks with normalized EMG activity greater than threshold, a linear regression analysis indicated a significant change in EWA direction as a function of task direction for both the FDI and the EI. The slope of the EWA direction as a function of task direction for the FDI was 0.13 (significantly >0, P < 0.00001). The slope of the EWA direction as a function of task direction for the EI was 0.34 (significantly >0, P < 0.00001). One possible interpretation of this task dependence is that different parts of the muscle may be activated differently as a function of task direction; other interpretations will be addressed in the discussion.
Since our analysis of EWA direction suggests relatively little correlation of force fluctuations among muscles, we turn our attention to computationally analyzing changes in EWA magnitude for a single muscle as the force output of that muscle increases. Computer simulations revealed a nonmonotonic dependence of EWA on muscle excitation level (Fig. 5A). Our model predicts that such dependence arises because motor unit recruitment and firing rate have different effects on EWA. We examined changes in EWA and average STA magnitude as the excitation of a muscle was increased from 0 to 100% maximum voluntary contraction (MVC). We found that if motor units were recruited up to ∼50% MVC, the average STA increased until all motor units were recruited and then decreased with greater excitation (Fig. 5A). This was the case only for short action potential durations of <20 ms, above which the upper limit of recruitment was not indicated (Fig. 5B). The correlation between the changes in average STA and EWA with % MVC (Fig. 5A) declined with increasing action potential duration from 5 to 20 ms. The correlation coefficient was 0.91 at 5 ms, 0.73 at 10 ms, 0.53 at 15 ms, and 0.30 at 20 ms. However, for all action potential durations other than 20 ms, the EWA magnitude had a clear peak at 50% MVC. The peak in EWA as a function of excitation (%MVC) may therefore serve as an indicator of the upper limit of motor unit recruitment as the %MVC at which the EWA magnitude peaks changes when the range of recruitment thresholds is compressed (Fig. 5C). To analyze the effect synchronization on changes in EWA magnitude, we selected parameters (Yao et al. 2000) that would produce an average synchronization index of 8% across all active motor unit pairs for 0–30% MVC (De Luca et al. 1993). When applied to all excitation levels 0–100% MVC, synchronization led to a gradual decline in the actual synchronization index (Fig. 5D) but had little effect on the changes in EWA magnitude with % MVC. We found that making the motor unit action potential magnitude proportional to motor unit force did not affect the % MVC at which the EWA magnitude peaked (Fig. 5E). Based on these sensitivity analyses, surface-recorded action potential duration appeared to be the most important factor governing EWA similarity to the average STA across motor units and its ability to indicate the upper limit of motor unit recruitment.
Fig.5.
Sensitivity analysis of EWA. Using the Fuglevand model of muscle force production and EMG, we examined the sensitivity of EWA to several parameters. We found that changes in EWA magnitude were very similar to changes in the magnitude of the average STA as the muscle force was increased from 0 to 100% maximum voluntary contraction (MVC). A: the surface-recorded action potential duration is shown relative to 20 ms. The firing rate of every 10th motor unit in the model is shown as a function of muscle force level with ↓ indicating the force level at which all motor units have been recruited. The EWA and average STA magnitude first increased and then decreased with the peak indicating the percentage MVC at which all motor units were recruited. B: we found that this effect disappeared when the surface-recorded motor unit action potential was lengthened to 20 ms. C: if the range of muscle force over which motor units were recruited was compressed, the peak EWA magnitude reflected this compressed recruitment. D: we found the peak in EWA magnitude as a function of percentage MVC indicated the upper limit of motor unit recruitment in the presence of physiological levels of motor unit synchronization. E: if the surface-recorded action potential durations were not assumed to be equal, but rather to be proportional to the motor unit force generating capacity, the peak EWA magnitude still indicated the upper limit of motor unit recruitment.
DISCUSSION
Our goal was to develop a noninvasive tool to estimate the mechanical action of a group of motor units. We have introduced the EWA as a means of noninvasively extracting the mechanical action of individual muscles from the endpoint force in multi-muscle tasks. We find that this technique, when applied to different muscles controlling the human index finger, generates force trajectories that are largely similar to those from STA of force based on single motor unit recordings but obtained using surface rather than fine-wire electrodes. We next discuss considerations to be made when using the EWA technique and the limitations under which it can be applied most effectively as well as possible applications.
We have shown here that EWA characterizes the direction of muscle action for the FDI and EI muscles. Although these muscles are relatively widely spaced in task space (∼90° in the abduction/flexion plane), the same technique may be able resolve actions with less separation. As an example, the biceps brachii and brachioradialis muscles have mechanical action directions estimated to be 8° apart in the flexion-extension/pronation supination plane of the elbow (Ettema et al. 1998). This is considerably greater than the 95% confidence intervals from our estimated directions, which was ∼5°, suggesting that EWA may have sufficient resolution to distinguish between the two.
The EWA method could potentially apply to other limbs and other tasks, including multijoint tasks. A requirement for any task is that the endpoint force be sensitive to the force fluctuations of constituent motor units. Long, heavily damped limbs may detract from that sensitivity. Another requirement is that the relevant degrees of freedom at the endpoint be measured along sufficient directions to resolve the degrees of freedom of the muscles. For multi-joint tasks, this will typically translate into a need to mechanically isolate the degrees of freedom of interest and to use multi-axis load cells to measure their effects at the endpoint. Although we have only tested EWA in a static task, it may be applicable to some dynamic tasks, provided that a nonstationary force baseline can be subtracted prior to cross-correlation and that sufficient trials can be collected to allow for an EWA waveform to emerge. The EWA has yet to be tested for practical applicability, but there are no fundamental limitations preventing its use in such tasks.
The similarity of EWA to STA depends on the duration of the surface-recorded action potential, which must be short relative to the duration of the motor unit force twitch (Fig. 5B). Whereas STA aligns segments of the force trace according to spikes in a particular motor unit, EWA aligns segments of the force trace according to relative peaks in EMG. The precision of that alignment requires that, relative to the force twitch, the rectified action potentials resemble discrete spikes. If the surface-recorded action potential is relatively long, the alignment will be diffuse, and the similarity between EWA and STA will be poor. Fortunately, the durations for the muscles studied here were appropriate; for example, 5 ms for FDI's motor unit action potentials (Petersen and Kugelberg 1949; Zhou and Rymer 2004b) and 50 ms for its force fluctuations (Chan et al. 2001; Thomas et al. 1986). Surface-recorded action potential durations can also be very brief for other muscles (De Luca et al. 2006). In all other applications, it is important to restrict EWA to cases where the action potentials are considerably shorter than the corresponding force twitches.
Because EWA is based on the same principles as STA, it is subject to many of the same limitations. Although STA was originally developed to characterize the forces due to single motor units (Buchthal and Schmalbruch 1970; Stein et al. 1972), its transient waveform has been found to vary with the degree of partial twitch fusion, especially when the forces overlap due to short inter-spike intervals (Calancie and Bawa 1986; Nordstrom et al. 1989). Moreover, even modest amounts of motor unit synchronization can profoundly affect the STA force transient (Keen and Fuglevand 2004; Kutch et al. 2007; Taylor et al. 2002). If the time course of a muscle's force twitch is to be characterized from EWA, the activation conditions should be similar to those appropriate for STA. Based on the findings of this study, it appears that EWA waveforms are meaningful when they rise to a single peak between 0 and 100 ms and are directed along the mechanical action direction of the muscle, which are similar to the conditions under which STA waveforms are considered meaningful (Thomas et al. 1986).
Several other factors warrant consideration when applying EWA to uncover the force fluctuations induced by a motor unit population. First, the force average of motor units that generate large surface potentials, either due to motor unit size or proximity to the recording electrode (Zhou and Rymer 2004a), will be overrepresented in the EWA. A possible compensation would be to record from additional locations, which could even include in-dwelling, fine-wire electrodes, as EWA is not restricted to surface EMG alone. Second, the EWA forces may contain overrepresentation of motor units with high relative firing rates because those units will contribute more to the average (see appendix). Third, many muscles may be composed of mechanically heterogenous motor units that may be differentially activated, for example the FDI (Masquelet et al. 1986), biceps brachii (Herrmann and Flanders 1998; ter Haar Romeny et al. 1984), and cat biceps femoris (Chanaud and Macpherson 1991; Chanaud et al. 1991). If EWA is to be used to study these phenomena, care should be taken that surface electrodes record only from the motor units of interest; otherwise, EWA will average out any mechanical heterogeneity in the motor units being recorded. Finally, we note that EWA waveforms have no interpretable units unlike STA waveforms that have units of force.
One unexplained phenomenon observed here was the roughly linear dependence of EWA direction on task direction (Fig. 4). One possible explanation is that the mechanical action and activation of different motor units within a single muscle may not be homogeneous. For example, mechanical action direction could change depending on the task direction because of differential activation of motor units (Herrmann and Flanders 1998) nonlinear force summation among muscles due to tendon network elasticity or deformation of some muscles by the forces of others (Valero-Cuevas et al. 2007), or myofascial force transmission (Huijing 1999). If motor units within a single muscle can have distinct mechanical actions, the CNS might then activate them accordingly (Kuo 1994) to produce the desired endpoint force. This could potentially explain why motor units within a muscle can be differentially activated based on the required direction of limb force (Chanaud and Macpherson 1991; Desmedt and Godaux 1981; Herrmann and Flanders 1998; ter Haar Romeny et al. 1982).
Another possible explanation is that there may be substantial correlation between motor unit discharges in muscles with different mechanical actions (Kutch et al. 2007). Synchronization among motor units in different muscles (Bremner et al. 1991a–c) could cause EWA direction to change as the balance of muscles shifted to produce endpoint force in different directions because EWA from one muscle would have no longer fully attenuated contributions from other muscles. A final possibility for the shift in EWA direction is that we did not allow sufficient time for the EWA averaging to take place. We performed EWA on steady periods of force lasting 16 s on average, and it is unknown whether longer trials would cause any differences. There is therefore currently insufficient information to resolve the cause of EWA force average direction dependence. Multi-unit recordings from more index finger muscles in the same tasks could help determine if synchronization can largely explain the observed EWA changes or if these other mechanisms contribute.
While our analysis of experimental data focused on EWA direction and time course, our computational models focused on EWA magnitude. We performed this sensitivity analysis of EWA magnitude because we believe that the application of highest immediate utility may be using EWA to indicate the upper limit of motor unit recruitment, due to its sensitivity to the level of excitation of the muscle (Fig. 5A). Based on our model simulations, we hypothesize that EWA magnitude would initially increase as the muscle began to generate force and, at some force level, would begin and continue to decrease as force approaches maximum. The decreasing correlation between force and EMG occurs when no new motor units are being recruited, and the force fluctuations of the active motor units are diminishing as these motor units discharge more rapidly (Thomas et al. 1991). In this way, EWA may provide a noninvasive marker of the neural drive required to recruit all motor units in a muscle, a quantification that may be clinically relevant (Blaschak et al. 1988; Gemperline et al. 1995) to applications such as the study of aging (Galganski et al. 1993; Keen et al. 1994; Semmler et al. 2000), spinal cord injury (Thomas 1997), and amyotrophic lateral sclerosis (Dengler et al. 1990). Determining if EWA can indicate the upper limit of motor unit recruitment remains to be determined experimentally. But our computational analyses provide a basis for such experimental studies as EWA appears to identify the upper limit of motor unit recruitment under all conditions simulated except when the surface-detected motor unit action potentials were ≥20 ms.
This study suggests that the EWA technique may be useful for at least three purposes. First, as experimentally demonstrated, EWA can characterize the spatial direction and temporal fluctuation of magnitude of muscle action at the endpoint. This is significant because there are no other noninvasive means to estimate muscle mechanical action, and mechanical action is an important parameter in studying the biomechanical basis for the neural control of motor behavior (Kuo 1994; Kurtzer et al. 2006; Lawrence et al. 1993). Second, the directionality of EWA becomes focused on the direction of muscle mechanical action when EMG is elevated and that may prove useful for determining when EMG activity is producing measurable force. Third, EWA may provide a window into recruitment and rate modulation during force production and may enable muscle-specific estimates of the upper limit of motor unit recruitment, important for both scientific and clinical questions. All of these uses for EWA may facilitate the understanding of how multiple muscles cooperate to produce coordinated motor action.
GRANTS
This work was supported by National Institutes of Health NRSA Training Grant 1F31NS-057855-01 to J. J. Kutch and W. Z. Rymer and Midwest Regional Rehabilitation Network Grant NICHD R24 HD-039627 to A. D. Kuo. J. J. Kutch made revisions to this manuscript while supported as a postdoctoral research associate by National Science Foundation Grants EFRI-COPN 0836042 and National Institutes of Health Grants AR-050520 and AR-052345 to Dr. Francisco J. Valero-Cuevas.
DISCLOSURES
No conflicts of interest are declared by the authors.
ACKNOWLEDGMENTS
We thank B. Sinder, S. Chikando, and Dr. N. Suresh for technical assistance and helpful discussions.
Present address of J. Kutch: Dept. of Biomedical Engineering, University of Southern California, 3710 S. McClintock Ave., RTH 421, Los Angeles, CA 90089.
APPENDIX
Spike-triggered averaging is a special case of cross-correlation
The cross-correlation of two signals f(n) and u(n), where n refers to discrete samples in time, is given by
| (3) |
Suppose that f(n) represents force and u(n) a series of spikes, where the jth spike occurs at time Sj. Then u(n) is 1 if n = Sj and 0 otherwise. The cross-correlation becomes
| (4) |
Thus up to a constant normalizing by the number of spikes, cross-correlation and the STA are equivalent.
EWA over-represents motor units with higher firing rate
Suppose that there is a population of M motor units discharging spikes. Let Sij represent the time of the jth spike in motor unit i. Consider superimposing all spikes from all motor units into a single spike train. We define Ni as the total number of spikes in motor unit i, and N as the total number of spikes across all motor units. Similarly, STAi(n) refers to the STA trajectory for motor unit i, and STA(n) to the summed trajectory across all units. The STA force transient based on the superposed spike train is
| (5) |
This sum can also be written as
| (6) |
The individual terms in this sum are the force transients of the individual motor units, STAi(n). Therefore the STA force transient from the merged spike train, which we have argued will be similar to the EWA based on surface EMG, is
| (7) |
Therefore the STA force transient based on the merged spike train is actually a weighted sum of the STA force transients from the individual motor units, the weighting factors being the relative number of spikes contributed by each motor unit.
REFERENCES
- An KN, Ueba Y, Chao EY, Cooney WP, Linscheid RL. Tendon excursion and moment arm of index finger muscles. J Biomechan 16: 419–425, 1983 [DOI] [PubMed] [Google Scholar]
- Berens P. Circstat: a matlab toolbox for circular statistics. J Stat Software 31: 1–21, 2009 [Google Scholar]
- Binder MD, Powers RK. Relationship between simulated common synaptic input and discharge synchrony in cat spinal motoneurons. J Neurophysiol 86: 2266–2275, 2001 [DOI] [PubMed] [Google Scholar]
- Blaschak MJ, Powers RK, Rymer WZ. Disturbances of motor output in a cat hindlimb muscle after acute dorsal spinal hemisection. Exp Brain Res 71: 377–387, 1988 [DOI] [PubMed] [Google Scholar]
- Bremner FD, Baker JR, Stephens JA. Correlation between the discharges of motor units recorded from the same and from different finger muscles in man. J Physiol 432: 355–380, 1991a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremner FD, Baker JR, Stephens JA. Effect of task on the degree of synchronization of intrinsic hand muscle motor units in man. J Neurophysiol 66: 2072–2083, 1991b [DOI] [PubMed] [Google Scholar]
- Bremner FD, Baker JR, Stephens JA. Variation in the degree of synchronization exhibited by motor units lying in different finger muscles in man. J Physiol 432: 381–399, 1991c [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchthal F, Schmalbruch H. Contraction times and fiber types in intact human muscle. Acta Physiol Scand 79: 435–452, 1970 [DOI] [PubMed] [Google Scholar]
- Calancie B, Bawa P. Limitations of the spike-triggered averaging technique. Muscle Nerve 9: 78–83, 1986 [DOI] [PubMed] [Google Scholar]
- Chan KM, Doherty TJ, Brown WF. Contractile properties of human motor units in health, aging, and disease. Muscle Nerve 24: 1113–1133, 2001 [DOI] [PubMed] [Google Scholar]
- Chanaud CM, Macpherson JM. Functionally complex muscles of the cat hindlimb. III. Differential activation within biceps-femoris during postural perturbations. Exp Brain Res 85: 271–280, 1991 [DOI] [PubMed] [Google Scholar]
- Chanaud CM, Pratt CA, Loeb GE. Functionally complex muscles of the cat hindlimb. II. Mechanical and architectural heterogenity within the biceps-femoris. Exp Brain Res 85: 257–270, 1991 [DOI] [PubMed] [Google Scholar]
- Day SJ, Hulliger M. Experimental simulation of cat electromyogram: evidence for algebraic summation of motor-unit action-potential trains. J Neurophysiol 86: 2144, 2001 [DOI] [PubMed] [Google Scholar]
- De Luca CJ, Adam A, Wotiz R, Gilmore LD, Nawab SH. Decomposition of surface EMG signals. J Neurophysiol 96: 1646, 2006 [DOI] [PubMed] [Google Scholar]
- De Luca CJ, Roy AM, Erim Z. Synchronization of motor-unit firings in several human muscles. J Neurophysiol 70: 2010–2023, 1993 [DOI] [PubMed] [Google Scholar]
- Dengler R, Konstanzer A, Kuther G, Hesse S, Wolf W, Struppler A. Amyotrophic lateral sclerosis: macro-EMG and twitch forces of single motor units. Muscle Nerve 13: 545–550, 1990 [DOI] [PubMed] [Google Scholar]
- Desmedt JE, Godaux E. Spinal moto-neuron recruitment in man-rank deordering with direction but not with speed of voluntary movement. Science 214: 933–936, 1981 [DOI] [PubMed] [Google Scholar]
- Ettema GJC, Styles G, Kippers V. The moment arms of 23 muscle segments of the upper limb with varying elbow and forearm positions: implications for motor control. Hum Move Sci 17: 201–220, 1998 [Google Scholar]
- Farina D, Merletti R, Enoka RM. The extraction of neural strategies from the surface EMG. J Appl Physiol 96: 1486–1495, 2004. [DOI] [PubMed] [Google Scholar]
- Fowler NK, Nicol AC, Condon B, Hadley D. Method of determination of three dimensional index finger moment arms and tendon lines of action using high resolution MRI scans. J Biomechan 34: 791–797, 2001 [DOI] [PubMed] [Google Scholar]
- Fuglevand AJ, Winter DA, Patla AE. Models of recruitment and rate coding organization in motor-unit pools. J Neurophysiol 70: 2470–2488, 1993 [DOI] [PubMed] [Google Scholar]
- Fuglevand AJ, Winter DA, Patla AE, Stashuk D. Detection of motor unit action-potentials with surface electrodes—influence of electrode size and spacing. Biol Cybern 67: 143–153, 1992 [DOI] [PubMed] [Google Scholar]
- Galganski ME, Fuglevand AJ, Enoka RM. Reduced control of motor output in a human hand muscle of ederly subjects during submaximal contractions. J Neurophysiol 69: 2108–2115, 1993 [DOI] [PubMed] [Google Scholar]
- Gemperline JJ, Allen S, Walk D, Rymer WZ. Characteristics of motor unit discharge in subjects with hemiparesis. Muscle Nerve 18: 1101–1114, 1995 [DOI] [PubMed] [Google Scholar]
- Gossen ER, Ivanova TD, Garland SJ. Factors affecting the stability of the spike-triggered averaged force in the human first dorsal interosseus muscle. J Neurosci Methods 126: 155–164, 2003 [DOI] [PubMed] [Google Scholar]
- Herrmann U, Flanders M. Directional tuning of single motor units. J Neurosci 18: 8402–8416, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman DS, Strick PL. Step-tracking movements of the wrist. IV. Muscle activity associated with movements in different directions. J Neurophysiol 81: 319–333, 1999 [DOI] [PubMed] [Google Scholar]
- Huijing PA. Muscular force transmission: a unified, dual or multiple system? A review and some explorative experimental results. Arch Physiol Biochem 107: 292–311, 1999 [DOI] [PubMed] [Google Scholar]
- Kamper DG, Fischer HC, Cruz EG. Impact of finger posture on mapping from muscle activation to joint torque. Clin Biomech 21: 361–369, 2006 [DOI] [PubMed] [Google Scholar]
- Keen DA, Fuglevand AJ. Distribution of motor unit force in human extensor digitorum assessed by spike-triggered averaging and intraneural microstimulation. J Neurophysiol 91: 2515–2523, 2004 [DOI] [PubMed] [Google Scholar]
- Keen DA, Yue GH, Enoka RM. Training-related enhancement in the control of motor output in elderly humans. J Appl Physiol 77: 2648–2658, 1994 [DOI] [PubMed] [Google Scholar]
- Keenan KG, Farina D, Maluf KS, Merletti R, Enoka RM. Influence of amplitude cancellation on the simulated surface electromyogram. J Appl Physiol 98: 120–131, 2005. [DOI] [PubMed] [Google Scholar]
- Keenan KG, Farina D, Meyer FG, Merletti R, Enoka RM. Sensitivity of the cross-correlation between simulated surface emgs for two muscles to detect motor unit synchronization. J Appl Physiol 102: 1193–1201, 2007 [DOI] [PubMed] [Google Scholar]
- Keenan KG, Valero-Cuevas FJ. Experimentally valid predictions of muscle force and EMG in models of motor-unit function are most sensitive to neural properties. J Neurophysiol 98: 1581–1590, 2007 [DOI] [PubMed] [Google Scholar]
- Kossev A, Elek JM, Wohlfarth K, Schubert M, Dengler R, Wolf W. Assessment of human motor unit twitches—a comparison of spike-triggered averaging and intramuscular microstimulation. Electroencephalogr Clin Neurophysiol 93: 100–105, 1994 [DOI] [PubMed] [Google Scholar]
- Kuo AD. A mechanical analysis of force distribution between redundant, multiple degree-of-freedom actuators in the human—implications for the central-nervous-system. Hum Move Sci 13: 635–663, 1994 [Google Scholar]
- Kurtzer I, Pruszynski JA, Herter TM, Scott SH. Primate upper limb muscles exhibit activity patterns that differ from their anatomical action during a postural task. J Neurophysiol 95: 493–504, 2006 [DOI] [PubMed] [Google Scholar]
- Kutch JJ, Kuo AD, Bloch AM, Rymer WZ. Endpoint force fluctuations reveal flexible rather than synergistic patterns of muscle cooperation. J Neurophysiol 100: 2455–2471, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutch JJ, Suresh NL, Bloch AM, Rymer WZ. Analysis of the effects of firing rate and synchronization on spike-triggered averaging of multidirectional motor unit torque. J Comput Neurosci 22: 347–361, 2007 [DOI] [PubMed] [Google Scholar]
- Lawrence JH, Nichols TR, English AW. Cat hindlimb muscles exert substantial torques outside the sagittal plane. J Neurophysiol 69: 282–285, 1993 [DOI] [PubMed] [Google Scholar]
- Macefield VG, Fuglevand AJ, Bigland-Ritchie B. Contractile properties of single motor units in human toe extensors assessed by intraneural motor axon stimulation. J Neurophysiol 75: 2509–2519, 1996 [DOI] [PubMed] [Google Scholar]
- Masquelet AC, Salama J, Outrequin G, Serrault M, Chevrel JP. Morphology and functional-anatomy of the 1st dorsal interosseous muscle of the hand. Surg Radiol Anat 8: 19–28, 1986 [DOI] [PubMed] [Google Scholar]
- Merletti R, Farina D, Gazzoni M. The linear electrode array: a useful tool with many applications. J Electromyogr Kinesiol 13: 37–47, 2003 [DOI] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB, Lee RG. Contractile and electrical properties of human motor units in neuropathies and motor neurone disease. J Neurol Neurosurg Psychiatry 37: 670–676, 1974 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB, Yemm R. Contractile properties of human motor units during voluntary isometric contractions. J Physiol 228: 285–306, 1973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monster AW, Chan H. Isometric force production by motor units of extensor digitorum communis muscle in man. J Neurophysiol 40: 1432–1443, 1977 [DOI] [PubMed] [Google Scholar]
- Moritz CT, Barry BK, Pascoe MA, Enoka RM. Discharge rate variability influences the variation in force fluctuations across the working range of a hand muscle. J Neurophysiol 93: 2449–2459, 2005 [DOI] [PubMed] [Google Scholar]
- Nordstrom MA, Miles TS, Veale JL. Effect of motor unit firing pattern on twitches obtained by spike-triggered averaging. Muscle Nerve 12: 556–567, 1989 [DOI] [PubMed] [Google Scholar]
- Ogawa T, Kawata T, Tsuboi A, Hattori Y, Watanabe M, Sasaki K. Functional properties and regional differences of human masseter motor units related to three-dimensional bite force. J Oral Rehabil 33: 729–740, 2006. [DOI] [PubMed] [Google Scholar]
- Petersen I, Kugelberg E. Duration and form of action potential in the normal human muscle. Br Med J 12: 124, 1949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semmler JG, Steege JW, Kornatz KW, Enoka RM. Motor-unit synchronization is not responsible for larger motor-unit forces in old adults. J Neurophysiol 84: 358–366, 2000 [DOI] [PubMed] [Google Scholar]
- Stein RB, Yemm R, French AS, Mannard A. New methods for analyzing motor function in man and animals. Brain Res 40: 187–192, 1972 [DOI] [PubMed] [Google Scholar]
- Taylor AM, Steege JW, Enoka RM. Motor-unit synchronization alters spike-triggered average force in simulated contractions. J Neurophysiol 88: 265–276, 2002 [DOI] [PubMed] [Google Scholar]
- ter Haar Romeny BM, Denier van der Gon JJ, Gielen CCAM. Changes in recruitment order of motor units in the human biceps muscle. Experimental. Neurology 78: 360–368, 1982 [DOI] [PubMed] [Google Scholar]
- ter Haar Romeny BM, Denier van der Gon JJ, Gielen CCAM. Relation between location of a motor unit in the human biceps brachii and its critical firing levels for different tasks. Exp Neurol 85: 631–650, 1984 [DOI] [PubMed] [Google Scholar]
- Thomas CK. Contractile properties of human thenar muscles paralyzed by spinal cord injury. Muscle Nerve 20: 788–799, 1997 [DOI] [PubMed] [Google Scholar]
- Thomas CK, Bigland-Richie B, Johansson RS. Force-frequency relationships of human thenar motor units. J Neurophysiol 65: 1509–1516, 1991 [DOI] [PubMed] [Google Scholar]
- Thomas CK, Bigland-Ritchie B, Westling G, Johansson RS. A comparison of human thenar motor-unit properties studied by intraneural motor-axon stimulation and spike-triggered averaging. J Neurophysiol 64: 1347–1351, 1990a [DOI] [PubMed] [Google Scholar]
- Thomas CK, Johansson RS, Westling G, Bigland-Ritchie B. Twitch properties of human thenar motor units measured in response to intraneural motor-axon stimulation. J Neurophysiol 64: 1339–1346, 1990b [DOI] [PubMed] [Google Scholar]
- Thomas CK, Ross BH, Stein RB. Motor-unit recruitment in human first dorsal interosseous muscle for static contractions in three different directions. J Neurophysiol 55: 1017–1029, 1986 [DOI] [PubMed] [Google Scholar]
- Todorov E. Cosine tuning minimizes motor errors. Neural Comput 14: 1233–1260, 2002 [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Towles JD, Hentz VR. Quantification of fingertip force reduction in the forefinger following simulated paralysis of extensor and intrinsic muscles. J Biomech 33: 1601–1609, 2000 [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Yi JW, Brown D, McNamara RV, Paul C, Lipson H. The tendon network of the fingers performs anatomical computation at a macroscopic scale. IEEE Trans Biomed Eng 54: 1161–1166, 2007 [DOI] [PubMed] [Google Scholar]
- Westling G, Johansson RS, Thomas CK, Bigland-Ritchie B. Measurement of contractile and electrical properties of single human thenar motor units in response to intraneural motor-axon stimulation. J Neurophysiol 64: 1331–1338, 1990 [DOI] [PubMed] [Google Scholar]
- Yao W, Fuglevand RJ, Enoka RM. Motor-unit synchronization increases emg amplitude and decreases force steadiness of simulated contractions. J Neurophysiol 83: 441–452, 2000 [DOI] [PubMed] [Google Scholar]
- Zhou P, Rymer WZ. Factors governing the form of the relation between muscle force and the EMG: a simulation study. J Neurophysiol 92: 2878–2886, 2004a [DOI] [PubMed] [Google Scholar]
- Zhou P, Rymer WZ. Muap number estimates in surface EMG: template-matching methods and their performance boundaries. Ann Biomed Eng 32: 1007–1015, 2004b [DOI] [PubMed] [Google Scholar]
- Zhou P, Suresh NL, Rymer WZ. Model based sensitivity analysis of EMG-force relation with respect to motor unit properties: applications to muscle paresis in stroke. Ann Biomed Eng 35: 1521–1531, 2007 [DOI] [PubMed] [Google Scholar]
- Zijdewind I, Thomas CK. Spontaneous motor unit behavior in human thenar muscles after spinal cord injury. Muscle Nerve 24: 952–962, 2001 [DOI] [PubMed] [Google Scholar]