Abstract
The origin of cooperation is a central challenge to our understanding of evolution1–3. Microbial interactions can be manipulated in ways that animal interactions cannot, thus leading to growing interest in microbial models of cooperation4–10 and competition11,12. In order for the budding yeast S. cerevisiae to grow on sucrose, the disaccharide must first be hydrolyzed by the enzyme invertase13,14. This hydrolysis reaction is performed outside of the cytoplasm in the periplasmic space between the plasma membrane and the cell wall. Here we demonstrate that the vast majority (~99%) of the monosaccharides created by sucrose hydrolysis diffuse away before they can be imported into the cell, thus making invertase production and secretion a cooperative behavior15,16. A mutant cheater strain that does not produce invertase is able to take advantage of and invade a population of wildtype cooperator cells. However, over a wide range of conditions, the wildtype cooperator can also invade a population of cheater cells. Therefore, we observe coexistence between the two strains in well-mixed culture at steady state resulting from the fact that rare strategies outperform common strategies—the defining features of what game theorists call the snowdrift game17. A model of the cooperative interaction incorporating nonlinear benefits explains the origin of this coexistence. We are able to alter the outcome of the competition by varying either the cost of cooperation or the glucose concentration in the media. Finally, we note that glucose repression of invertase expression in wildtype cells produces a strategy which is optimal for the snowdrift game—wildtype cells cooperate only when competing against cheater cells.
Yeast prefer to use the monosaccharides glucose and fructose as carbon sources. However, when these sugars are not available, yeast can metabolize alternative carbon sources such as the disaccharide sucrose18. After sucrose is hydrolyzed by invertase, the resulting monosaccharides are imported13,14, yet some of the glucose and fructose may diffuse away from the cell before it is able to import them into the cytoplasm (Supp. Fig 1). If such sugar loss by diffusion is significant then we might expect that high-density cultures would grow more quickly than low-density cultures, since cells at high density benefit from their hydrolysis products and those of their abundant neighbors. Indeed, we find that cells grown in media supplemented with sucrose—but not glucose—grow much faster at high cell density than at low cell density. The growth rate at high cell density in 5% sucrose is similar to the growth rate at saturating (2%) glucose concentrations. However, the growth rate at low cell density is ~40% slower, equivalent to the growth rate in only 0.003% glucose (Supp. Fig. 2). The fraction of invertase-created glucose that is captured can be estimated by dividing the rate of glucose uptake of cells growing in 0.003% glucose by the measured rate of invertase activity, yielding an estimated glucose capture efficiency of only ~1% (Supp. Fig. 3). Analytic calculations of glucose diffusion suggest that this low capture efficiency is an expected consequence of diffusion and the known properties of the sugar importers (Supp. Fig. 4).
Given that 99% of glucose created by a cell is lost to neighboring cells, it may be possible for a “cheater” strain to take advantage of the cooperators by not secreting invertase and instead simply consuming the glucose created by other cells15. If cooperative cells shared all of the glucose that they created (i.e., if 100% of hydrolyzed glucose and fructose diffused away from the hydrolyzing cell), then both the cooperators and cheaters would have the same access to sugar, yet only the cooperators would bear the metabolic cost of invertase production and secretion. In this case, the cheaters would always outgrow the cooperators, and the interaction would be what is called a "prisoner’s dilemma", in which cooperation is not sustainable in a well-mixed environment1,17. However, we found that yeast retain a small fraction of the glucose created by sucrose hydrolysis, which may be sufficient to allow cooperative strategies to survive.
To explore this problem, we performed a set of competition experiments between the wildtype strain ("cooperator") and a mutant strain lacking the invertase gene ("cheater" or “defector”, see Supp. Fig 1). Consistent with a metabolic cost associated with invertase production, we find that in glucose-supplemented media cooperators grow more slowly than cheaters only when invertase is being expressed (Supp. Fig. 5)15. In addition, the cooperator strain in our experiments is a histidine auxotroph; therefore, limiting the histidine concentration in the media slows the growth of the cooperator relative to the cheater, allowing us to experimentally increase the “cost of cooperation” (Supp. Fig 6). We can measure the relative abundance ("fractions") of the two strains in a mixed culture by flow cytometry because they are expressing different fluorescent proteins (Supp. Fig. 7).
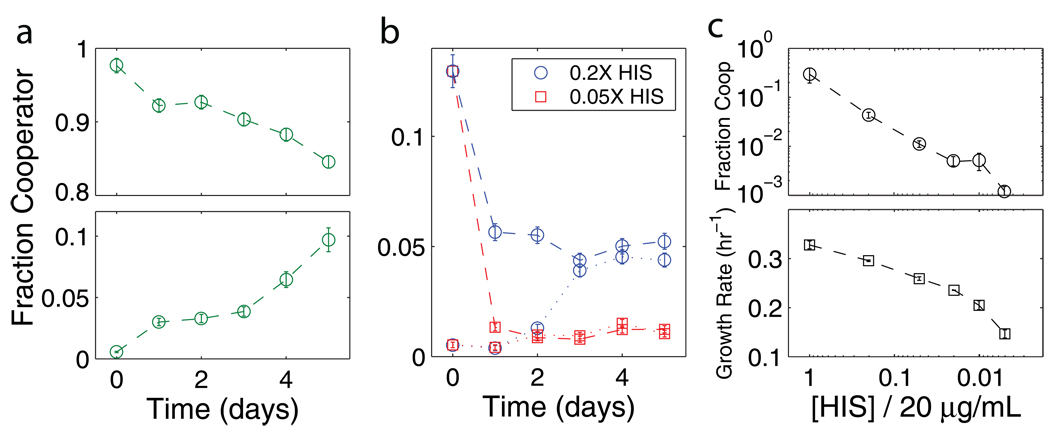
We began by monitoring the change over time in the fractions of cooperators and cheaters cocultured in sucrose media. Each coculture started from a different initial fraction of cooperators, and each day we performed serial dilutions into fresh media and measured the cell density and relative abundance of the two strains. In cultures starting with a small fraction of cheaters, the cheaters increased in frequency, consistent with the cheaters "taking advantage" of the cooperators (Fig. 1a). However, when the initial fraction of cooperators was low, we found that the frequency of cooperators increased, suggesting that at steady state there will be coexistence between the two strains. Indeed, the equilibrium fraction is independent of the starting fraction but depends upon the histidine concentration (Fig. 1b; the equilibrium fraction in saturating histidine was f ~ 0.3). As the cost of cooperation increased, we observed a decrease in both the equilibrium fraction of cooperators and the mean growth rate of the culture at equilibrium (Fig. 1c). A large cost of cooperation therefore allows the cheaters to dominate the population but also results in a low growth rate of both strains. Coexistence was also observed in continuous culture, meaning that the “seasonality” imposed by serial dilution in batch culture is not necessary for coexistence11 (Supp. Fig. 8). If the cooperators are initially only a small fraction of the population, then there will be little glucose available in the media. In this case the cooperators have an advantage because they are able to capture at least some small fraction of the glucose that they create. As the fraction of cooperative cells increases, the glucose concentration also increases, and eventually the growth rate of the two strains becomes equal. Similarly, if the initial fraction of cooperative cells is above the equilibrium level, then their fraction will decrease; as this occurs we find that the growth rate of the culture also decreases (Supp. Fig. 9). Such a decrease in mean population fitness caused by evolutionary dynamics is a defining feature of the challenges posed by cooperation.
Figure 1. Competition between the wildtype cooperator and mutant cheater strains.
a, In sucrose culture a small fraction of cheaters can invade a population of cooperators (top), and a small fraction of cooperators can also invade a population of cheaters (bottom), together implying coexistence between the two strains at steady state ([histidine] = 20 µg/mL ≡ 1X, no imposed cost of cooperation). b, As the histidine concentration becomes limiting we find that equilibrium between the two strains is reached within experimental timescales regardless of starting fractions. The fraction of cooperators at equilibrium does not depend upon the starting fraction but does depend upon the histidine concentration. Panels a and b show typical data, with error bars showing an estimate of the error (see Supp. Fig. 7). c, Both the equilibrium fraction of cooperators (circles) and the mean growth rate (squares) decrease as the cost of cooperation increases (lower histidine concentrations). Error bars are the s.e.m., n = 3.
Our experimental observation of coexistence between the cooperator and cheater strains implies that the interaction is governed by what game theorists call the "snowdrift game" (also known as the hawk-dove game or the game of chicken)3,17. The snowdrift game derives its name from the potentially cooperative interaction present when two drivers are stuck behind a large pile of snow, and each driver must decide whether to clear a path by shoveling. In this model of cooperation the optimal strategy is the opposite of one’s opponent (cooperate when your opponent defects and defect when your opponent cooperates). The snowdrift game is therefore qualitatively distinct from the prisoner’s dilemma, in which all players have the incentive to cheat regardless of the strategies being followed by others. Coexistence between cooperation and defection arises in a snowdrift game because rare strategies, which will often interact with the opposite strategy, do comparatively well.
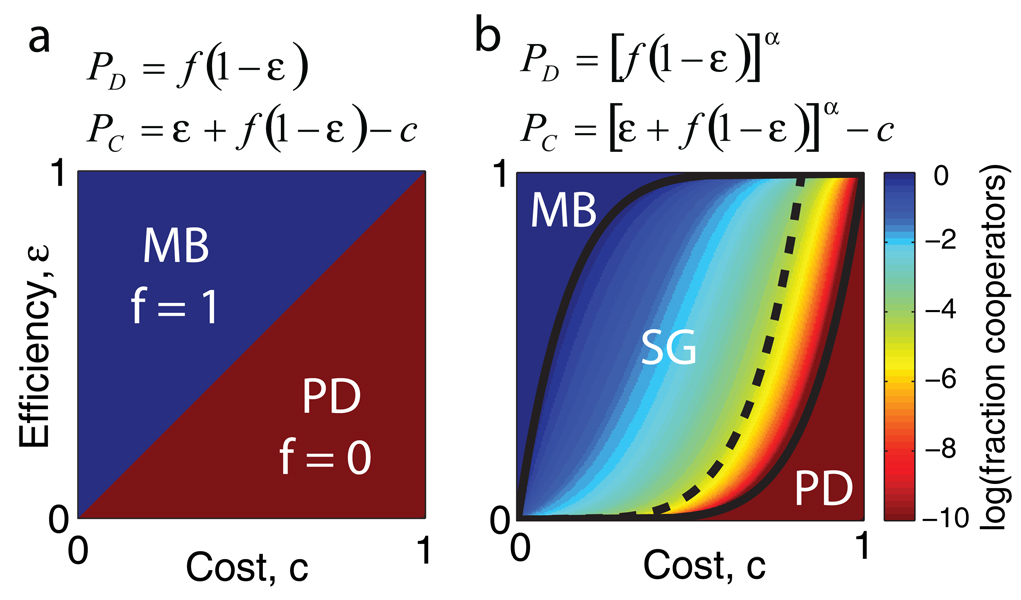
In order to understand why sucrose metabolism is a snowdrift game, we constructed a simple phenomenological game-theory model of the interaction. We assume that invertase expression costs c and generates total benefits of unity that are captured with efficiency ε. In this scheme, for large capture efficiencies and/or small costs of cooperation (ε > c), the cooperators always outgrow the defectors and therefore take over the population (Fig. 2a). However, for small capture efficiencies and/or large costs (ε < c), the interaction is a prisoner’s dilemma (PD) in which the defectors always do better, thus leading to extinction of the cooperators. However, in our experiments we observed coexistence between the two strains, an outcome that never occurs in the simple model of Fig. 2a. The ability to capture a sufficiently large fraction of the benefits of cooperation can indeed allow cooperators to take over a population, but does not on its own lead to coexistence between cooperators and cheaters.
Figure 2. Game theory models of cooperation in sucrose metabolism.
a, Payouts P and resulting phase diagram of the cooperative fraction f at equilibrium in a simple linear model in which cooperation costs c and leads to total benefits of unity which are captured with an efficiency ε. This model leads to fixation of cooperators (f = 1) at low cost and/or high efficiency of capture (ε > c ⇒ MB: Mutually Beneficial Game5) but fixation of defectors (f = 0) for high cost and/or low efficiency of capture (ε < c ⇒ PD: Prisoner’s Dilemma). b, Model of cooperation with experimentally measured concave benefits yields a central region of parameter space that is a snowdrift game (SG), thus explaining the coexistence that is observed experimentally (α = 0.15 in figure, see Supp. Fig. 10). Adding glucose makes the cheaters less reliant on the cooperators, thus reducing the range of parameters in which cooperation can survive (solid to dashed line, see Supp. Fig. 11).
Coexistence of the two opposing strategies requires that the strains are mutually invasible. In particular, a lone cooperator must outperform a population composed entirely of defectors17. Indeed, we have already found experimentally that wildtype yeast in dilute cellular conditions are able to grow at a significant rate despite capturing only ~ 1% of the glucose created (Supp. Fig. 2). This is because growth as a function of glucose is highly concave; doubling the glucose concentration therefore does not double the growth rate. By measuring the growth rate as a function of glucose concentration we conclude that all benefit terms in our model should be raised to the power α = 0.15 ± 0.01 (Supp. Fig. 10 and Fig. 3c). Including this non-linear effect alters the phase diagram and creates a large region of parameter space that is a snowdrift game in which there is coexistence between the two strategies19 (Fig. 2b; a > 1 leads to bistability19,20, see Supp. Table 1). The saturating nature of growth on glucose means that a small number of cooperators can supply the glucose for many cells, thus providing a natural explanation for the small fraction of cooperators often observed in our competition experiments (Fig. 1c and 3a,b).
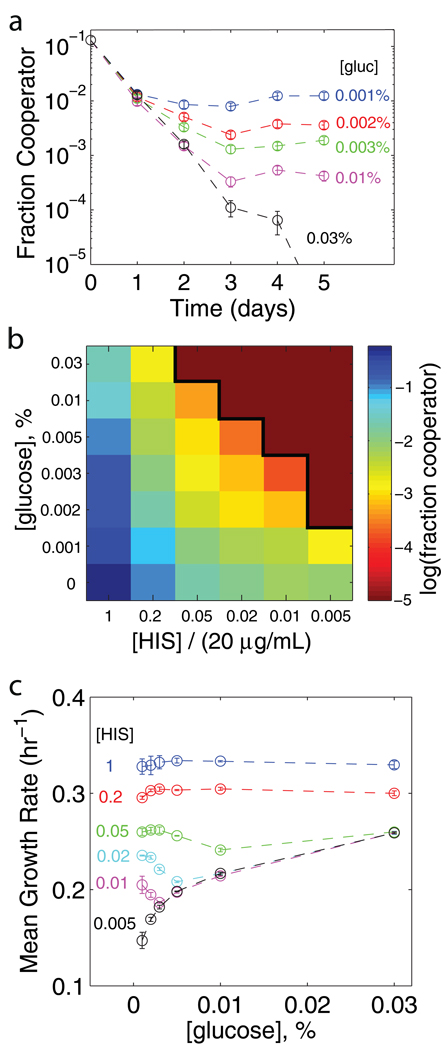
Figure 3. Varying the glucose concentration can transform the outcome of competition.
a, As the glucose concentration in the media increases, the equilibrium fraction of cooperators decreases ([histidine] = 0.05X = 1 µg/mL). Typical data shown, error bars are an estimate of the error in measurement of the fraction (see Supp. Fig 7). b, Fraction of cooperators at equilibrium as a function of the glucose and histidine concentration (all cultures have 5% sucrose, mean of two or three independent experiments, see Supp. Fig. 12 for error). The cooperators can be driven extinct by either increasing the “cost of cooperation” or by adding glucose to the media (solid black line denotes the extinction boundary). c, Mean growth rate of co-culture at equilibrium as a function of glucose concentration (Error bars correspond to s.e.m., n = 3). Adding glucose can decrease the growth rate at equilibrium because there are fewer cooperators to hydrolyze sucrose. As expected, if there are no cooperators at equilibrium then the growth rate is not a function of the histidine concentration. The nonlinear relationship between growth rate and glucose concentration is visible in the 0.005X histidine data (black).
The sub-linear relationship between growth rate and glucose suggests that the glucose concentration in the media may be an important parameter governing the cooperative interaction. As the glucose concentration increases, the cheaters become less reliant on the cooperators, and cooperation becomes more difficult to maintain (dashed line in Fig. 2b and Supp. Fig. 11). Therefore, we expect that adding glucose will decrease the fraction of cooperators at equilibrium, eventually transforming the game into a prisoner’s dilemma and driving the cooperators extinct. The glucose concentration necessary to transform the game into a prisoner’s dilemma is expected to be a decreasing function of the cost of cooperation. Remarkably, these predictions and the associated phase diagram can be confirmed experimentally (Fig. 3a,b and Supp. Fig. 12).
Increasing the glucose available in the media decreases the fraction of cooperators at equilibrium and can even drive the cooperators extinct. As the cooperators decrease in frequency, the amount of sucrose being hydrolyzed also decreases. Indeed, we find that for some costs of cooperation this effect is so severe that the equilibrium growth rate of the mixed culture actually decreases as we add glucose to the media (Fig. 3c). This non-intuitive decrease in the coculture growth rate is a striking result of the cooperative interaction since the growth rate of each strain cultured alone increases as glucose levels increase in the media.
Similar to many other alternative modes of carbon metabolism, invertase expression is repressed at high concentrations of glucose18. Given this genetically encoded strategy, how does a wildtype cell respond when placed in competition against cells that either always cooperate or always defect? Competition against always-defecting cells leads to low glucose concentrations, resulting in wildtype cells cooperating by expressing invertase (as in our competition experiments). In contrast, a wildtype cell competing against an always-cooperating strain would result in the glucose concentration rising to the point (> 0.1%) where invertase expression is repressed, thus causing the wildtype cell to cheat18,21 (see Supp. Fig. 5a). We therefore see that the wildtype invertase production strategy is exactly what might be expected in a snowdrift game—wildtype cells pursue the strategy opposite that of their opponents. It is possible that glucose repression of invertase is partly determined by these social considerations, helping to make a population of wildtype cells relatively immune to invasion by strains with alternative strategies22.
Our results are consistent with a recent study which found that a cheater strain was more fit than the wildtype cooperator strain when growing at high density on a sucrose plate15. In this paper Greig and Travisano classify sucrose metabolism as a prisoner’s dilemma, although their experimental results are also consistent with the cooperative interaction being a snowdrift game. Distinguishing between these two games requires observation of competition at low starting fraction of cooperator. In addition, the competition must be performed in a well-mixed environment because spatial structure, such as the agar plate used by Greig and Travisano, can drastically affect the outcome of competition16,23.
The experimental observation of coexistence between cooperator and cheater strains in a well-mixed environment makes sucrose metabolism in yeast a particularly clear example of the snowdrift game24, and may explain the existence in wild yeast populations of copy number variation in the SUC2 gene, including the presence of cheaters25. Coexistence between cooperator and cheater strains in our experiments provide a concrete example of how interactions between alternative alleles can promote biological diversity11,24,26. Similar cooperative interactions may be present in other enzymatic processes that occur in the periplasmic space of yeast such as phosphate scavenging, starch degradation, and phospholipase activity. It would be interesting to study the outcome of competition between the cooperator and cheater strains in spatially structured environments9,15,16,23,27–29, particularly given a recent theoretical prediction that spatial structure often inhibits cooperation in a snowdrift game27.
METHODS SUMMARY
Strains
All strains were derived from haploid cells BY4741 (mating type a, EUROSCARF). The “wildtype” cooperator strain has an intact SUC2 gene, defective HIS3 gene (his3Δ1), and YFP expressed constitutively by the ADH1 promoter (inserted using plasmid pRS401 containing MET15). The mutant cheater strain lacks the SUC2 gene (EUROSCARF Y02321, YIL162w::kanMX4), has an intact HIS3 gene, and has tdtomato expressed constitutively by the PGK1 promoter (inserted using plasmid pRS301 containing HIS3). Growth rate and invertase expression experiments in Supp. Fig. 2 and 5a were done using a strain containing YFP driven by the SUC2 promoter (inserted using plasmid pRS306 containing URA3).
Competition Experiments
Co-culture experiments were performed in 5mL batch culture at 30C using synthetic media (minus histidine) supplemented with 5% sucrose and variable concentrations of glucose and histidine. Cultures were maintained in a “well-mixed” condition by growing in an incubator shaker at 225 rpm. The 20% sucrose stock solution was filter-sterilized and stored with 1 mM Tris pH 8.0 to prevent acid-catalyzed autohydrolysis. Nevertheless, 5% sucrose media typically had a monosaccharide concentration of ~0.0001%. Experiments in Figure 1 have 0.001% glucose added manually. Serial dilutions were performed daily (23 hours of growth) such that the starting optical density was 0.0025, corresponding to ~150,000 cells. Fractions were determined using a BD FACScan flow cytometer (Supp. Fig. 7) and periodically confirmed by selective plating. Equilibrium data in Figures 1c and 3b,c were recorded after five days of competition between the two strains.
Supplementary Material
Acknowledgments
The authors would like to thank D. Kim, A. Raj, K. Gora, D. Muzzey, and B. Pando for helpful discussions and/or experimental help. This work was supported by grants from the NIH and NSF to AvO. JG is supported through a Pappalardo Postdoctoral Fellowship and an NIH K99 Pathways to Independence Award.
Footnotes
Supp. Information is linked to the online version of the paper at www.nature.com/nature
References
- 1.Axelrod R, Hamilton WD. The Evolution of Cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- 2.Nowak MA. Five rules for the evolution of cooperation. Science. 2006;314:1560–1563. doi: 10.1126/science.1133755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Smith JM. Evolution and the Theory of Games. Cambridge: Cambridge University Press; 1982. [Google Scholar]
- 4.Velicer GJ. Social strife in the microbial world. Trends in Microbiology. 2003;11:330–337. doi: 10.1016/s0966-842x(03)00152-5. [DOI] [PubMed] [Google Scholar]
- 5.West SA, Griffin AS, Gardner A, Diggle SP. Social evolution theory for microorganisms. Nature Reviews Microbiology. 2006;4:597–607. doi: 10.1038/nrmicro1461. [DOI] [PubMed] [Google Scholar]
- 6.Griffin AS, West SA, Buckling A. Cooperation and competition in pathogenic bacteria. Nature. 2004;430:1024–1027. doi: 10.1038/nature02744. [DOI] [PubMed] [Google Scholar]
- 7.Shou WY, Ram S, Vilar JMG. Synthetic cooperation in engineered yeast populations. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:1877–1882. doi: 10.1073/pnas.0610575104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Diggle SP, Griffin AS, Campbell GS, West SA. Cooperation and conflict in quorum-sensing bacterial populations. Nature. 2007;450:411-U7. doi: 10.1038/nature06279. [DOI] [PubMed] [Google Scholar]
- 9.Rainey PB, Rainey K. Evolution of cooperation and conflict in experimental bacterial populations. Nature. 2003;425:72–74. doi: 10.1038/nature01906. [DOI] [PubMed] [Google Scholar]
- 10.Smukalla S, et al. FLO1 Is a Variable Green Beard Gene that Drives Biofilm-like Cooperation in Budding Yeast. Cell. 2008;135:726–737. doi: 10.1016/j.cell.2008.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.MacLean RC, Gudelj I. Resource competition and social conflict in experimental populations of yeast. Nature. 2006;441:498–501. doi: 10.1038/nature04624. [DOI] [PubMed] [Google Scholar]
- 12.Chao L, Levin BR, et al. Structured Habitats and the Evolution of Anticompetitor Toxins in Bacteria. Proceedings of the National Academy of Sciences of the United States of America-Biological Sciences. 1981;78:6324–6328. doi: 10.1073/pnas.78.10.6324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carlson M, Botstein D. 2 Differentially Regulated Messenger-Rnas with Different 5' Ends Encode Secreted and Intracellular Forms of Yeast Invertase. Cell. 1982;28:145–154. doi: 10.1016/0092-8674(82)90384-1. [DOI] [PubMed] [Google Scholar]
- 14.Dickinson JR, Schweizer M. The Metabolism and Molecular Physiology of Saccharomyces cerevisiae. Boca Raton, FL: CRC Press; 2004. [Google Scholar]
- 15.Greig D, Travisano M. The Prisoner's Dilemma and polymorphism in yeast SUC genes. Proceedings of the Royal Society of London Series B-Biological Sciences. 2004;271:S25–S26. doi: 10.1098/rsbl.2003.0083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.MacLean RC, Brandon C. Stable public goods cooperation and dynamic social interactions in yeast. J. Evol. Biol. 2008;21:1836–1843. doi: 10.1111/j.1420-9101.2008.01579.x. [DOI] [PubMed] [Google Scholar]
- 17.Doebeli M, Hauert C. Models of cooperation based on the Prisoner's Dilemma and the Snowdrift game. Ecology Letters. 2005;8:748–766. [Google Scholar]
- 18.Gancedo JM. Yeast carbon catabolite repression. Microbiology and Molecular Biology Reviews. 1998;62:334–361. doi: 10.1128/mmbr.62.2.334-361.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Motro U. Cooperation and Defection - Playing the Field and the Ess. Journal of Theoretical Biology. 1991;151:145–154. doi: 10.1016/s0022-5193(05)80358-3. [DOI] [PubMed] [Google Scholar]
- 20.Skyrms B. The Stag Hunt and Evolution of Social Structure. Cambridge: Cambridge University Press; 2004. [Google Scholar]
- 21.Ozcan S, Vallier LG, Flick JS, Carlson M, Johnston M. Expression of the SUC2 gene of Saccharomyces cerevisiae is induced by low levels of glucose. Yeast. 1997;13:127–137. doi: 10.1002/(SICI)1097-0061(199702)13:2<127::AID-YEA68>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 22.Santorelli LA, et al. Facultative cheater mutants reveal the genetic complexity of cooperation in social amoebae. Nature. 2008;451:1107-U7. doi: 10.1038/nature06558. [DOI] [PubMed] [Google Scholar]
- 23.Nowak MA, May RM. Evolutionary Games and Spatial Chaos. Nature. 1992;359:826–829. [Google Scholar]
- 24.Fiegna F, Velicer GJ. Competitive fates of bacterial social parasites: persistence and self-induced extinction of Myxococcus xanthus cheaters. Proceedings of the Royal Society of London Series B-Biological Sciences. 2003;270:1527–1534. doi: 10.1098/rspb.2003.2387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Naumov GI, Naumova ES, Sancho ED, Korhola MP. Polymeric SUC genes in natural populations of Saccharomyces cerevisiae. Fems Microbiology Letters. 1996;135:31–35. doi: 10.1111/j.1574-6968.1996.tb07962.x. [DOI] [PubMed] [Google Scholar]
- 26.Kerr B, Riley MA, Feldman MW, Bohannan BJM. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature. 2002;418:171–174. doi: 10.1038/nature00823. [DOI] [PubMed] [Google Scholar]
- 27.Hauert C, Doebeli M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature. 2004;428:643–646. doi: 10.1038/nature02360. [DOI] [PubMed] [Google Scholar]
- 28.Keymer JE, Galajda P, Muldoon C, Park S, Austin RH. Bacterial metapopulations in nanofabricated landscapes. Proc Natl Acad Sci U S A. 2006;103:17290–17295. doi: 10.1073/pnas.0607971103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nadell CD, Xavier JB, Foster KR. The sociobiology of biofilms. FEMS Microbiology Reviews. 2009;33:206–224. doi: 10.1111/j.1574-6976.2008.00150.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.