Model-Based Quality Assessment and Base-Calling for Second-Generation Sequencing Data

SUMMARY

Second-generation sequencing (sec-gen) technology can sequence millions of short fragments of DNA in parallel, and is capable of assembling complex genomes for a small fraction of the price and time of previous technologies. In fact, a recently formed international consortium, the 1,000 Genomes Project, plans to fully sequence the genomes of approximately 1,200 people. The prospect of comparative analysis at the sequence level of a large number of samples across multiple populations may be achieved within the next five years. These data present unprecedented challenges in statistical analysis. For instance, analysis operates on millions of short nucleotide sequences, or reads—strings of A,C,G, or T’s, between 30–100 characters long—which are the result of complex processing of noisy continuous fluorescence intensity measurements known as base-calling. The complexity of the base-calling discretization process results in reads of widely varying quality within and across sequence samples. This variation in processing quality results in infrequent but systematic errors that we have found to mislead downstream analysis of the discretized sequence read data. For instance, a central goal of the 1000 Genomes Project is to quantify across-sample variation at the single nucleotide level. At this resolution, small error rates in sequencing prove significant, especially for rare variants. Sec-gen sequencing is a relatively new technology for which potential biases and sources of obscuring variation are not yet fully understood. Therefore, modeling and quantifying the uncertainty inherent in the generation of sequence reads is of utmost importance. In this paper we present a simple model to capture uncertainty arising in the base-calling procedure of the Illumina/Solexa GA platform. Model parameters have a straightforward interpretation in terms of the chemistry of base-calling allowing for informative and easily interpretable metrics that capture the variability in sequencing quality. Our model provides these informative estimates readily usable in quality assessment tools while significantly improving base-calling performance.

1. Introduction

Over the past four years, commercialization of second-generation (sec-gen), also known as high-throughput, DNA sequencing technologies has increased rapidly, with the most cost-effective platforms currently producing megabases of sequence per day. Massively parallel sequencing is poised to become one of the most widely used tools in genomics research. Some are predicting it will overtake microarrays in the near future (Ledford, 2008) as the technology of choice for high-throughput genomics. Currently, the major manufacturers are Illumina (formerly Solexa) (Bennett et al., 2005), 454/Roche (Margulies et al., 2005) and ABI/SOLID (Shendure et al., 2005). For each of these sequencing platforms, a complex data analysis pipeline is required to generate the measurements and statistics analysts need in their biological or clinical applications.

Current data analysis tools operate on millions of short nucleotide sequences, referred to as reads, which are strings of A,C,G or T’s between 30–100 characters long. However, as with microarrays, these reads are generated by processing raw data in the form of fluorescence intensity measurements reported by the instrument. Converting these raw intensities into discretized reads requires complicated statistical manipulation of noisy continuous data, a process known as base-calling. Software provided by the manufacturers typically provide a quality score for each reported base. These millions of sequence reads, and their associated quality scores are then analyzed down-stream according to the biological or clinical application.

In this paper, we show that the base-calling procedure of generating reads from intensity measurements results in relatively infrequent but systematic errors that can mislead downstream analysis of the discretized sequence reads. Variability in these errors is large, where some of the intensity measurements can be easily turned into base-calls while others show a large amount of errors. The implication is that not all sequence reads are created equal, showing a large variation in quality. Furthermore, this variation in quality is also related to position along the sequence read, further expanding the space in which variation in quality must be explained. To complicate things further, variability in quality differs between samples.

In order to properly gauge the results of downstream analyses it is imperative that a measure of uncertainty is attached to each statistic arising from analysis of the discretized sequence reads. Furthermore, a method that models this uncertainty throughout the entire base-calling pipeline will be the most useful for those carrying out these analyses. This need has been recognized by other groups which have developed alternative base-calling methods for the Illumina/Solexa platform. For example, Alta-Cyclic (Erlich et al., 2008) uses a training set to train a convolution filter and a support vector machine to make much more accurate base calls. However, this setting is complex enough that succinct and clear quality metrics are difficult to obtain. On the other hand, Rougemont et al. (2008) define a well-designed probabilistic model for base-calling similar in spirit to the work we present here. Although this method also improves base calling, the level at which modeling of technical features of the data is done is too coarse to provide read-level quality metrics. The work in this paper addresses the need for simple yet informative quality assessment at the read-level while retaining the advantages of a probabilistic model as that defined by Rougemont et al. (2008) and improved base-calling performance.

The importance of properly characterizing uncertainty is best exemplified by the task of searching for new single nucleotide polymorphisms (SNPs); one of the major tasks of the 1,000 Genomes Project (Hayden, 2008). One of the goals of this project is to use the sequence of at least 1,000 individuals to list SNPs that occur with at least 1% frequency in the human population genome-wide, and down to 0.5% frequency within genes. The error rates we have observed in some data sets are high enough, and biased enough, i.e. not all sequencing errors are equally likely, that the nucleotide composition of the mapped reads is corrupted to the point that variants in samples are falsely reported, even when using base-calling qualities to weigh mapping mismatches.

In this paper we provide a model for short read fluorescence intensity data to provide more reliable and informative quality assessment metrics as part of a unified framework that captures sequencing uncertainty from base-calling to mapping. The paper is organized as follows: in Section 2 we review and summarize the data generation process for the Illumina/Solexa second-generation sequencing technology; in Section 3 we discuss some exploratory data analysis on short read sequencing errors and quality measures to motivate the intensity-based uncertainty model we introduce in Section 4 we introduce the intensity model; quality metrics derived from the intensity model are given in Section 5; we conclude with results in Section 6 and a discussion in Section 7.

2. Technology Review

In this paper we will concentrate on Illumina/Solexa sec-gen sequencing technology (Bennett et al., 2005). However, data from other technologies have similar characteristics and we expect models similar to the one presented here to apply to these technologies. This technology generates millions of reads of short DNA sequences by measuring in parallel the fluorescence intensity of millions of PCR amplified and labeled fragments of DNA from a sample of interest. The DNA fragments attach to a glass surface where it is then PCR-amplified in-situ to create a cluster of DNA fragments with identical nucleotide composition. A sequence read is generated from these DNA clusters in parallel using a clever biochemical procedure called sequencing-by-synthesis. The procedure is done by cycles where a single nucleotide is sequenced from all DNA clusters in parallel, with subsequent cycles sequencing nucleotides along the fragment one at a time.

Sequencing in each cycle is done by adding labeled nucleotides which incorporate to their complementary nucleotide synthesizing DNA fragments complementary to the fragments in each cluster as sequencing progresses. At each cycle a set of four images are created measuring the fluorescence intensity along four channels. Each of the four images corresponds to one of the four nucleotides. Fluorescence intensity measurements are obtained from these images and the sequence of each DNA fragment, or read, is then inferred from these measurements.

For example, in the GA I Illumina/Solexa platform reads of 36 base pairs are produced. This implies that there are 36 quadruplets of images for a set of reads. Each quadruplet is associated with a position for each read (the first quadruplet would be the first base in each read) and a read is associated with a physical location on the image. These images are then processed to produce fluorescence intensity measurements from which sequences are then inferred. After further post-processing the highest intensity in each quadruplet of intensity measurements determines the base at the corresponding position of the corresponding read. For Illumina/Solexa technologies, a typical run can produce 1.5 gigabases per sample, or nearly 50 million reads.

Illumina/Solexa provides software that take as input the intensities measured from the images and return sequence reads and a quality measure for each position of each read. They also provide the ELAND software that maps the generated sequencing reads to a reference genome. However, programs developed elsewhere are now used as frequently as those provided by manufacturers. For instance, the current most time and space efficient mapper is the BOWTIE (Langmead et al., 2009) program while MAQ (Li et al., 2008) is used extensively in the 1,000 Genomes Project. Both use manufacturer-supplied qualities in their mapping protocols, where mismatches between reads and the reference are weighted by the reported quality of the mismatched base. It bears repeating that in the most commonly used analysis pipelines, base-calling qualities are reported and mapping is done using these qualities. However, we will show that the reported base-calling qualities are not good enough indicators of error-rate, and are too coarse a measure to quantify bias in sequencing error. Therefore, the current protocol of mapping using qualities is not sufficient to guard against these problems.

In most applications, other than re-sequencing, or de novo sequencing, the statistics used by analysis result from matching these millions of reads to a reference genome. For example, in quantitative applications such as ChIP-seq (Mikkelsen et al., 2007; Ji et al., 2008; Jothi et al., 2008; Valouev et al., 2008; Zhang et al., 2008) or RNA-seq (Marioni et al., 2008; Mortazavi et al., 2008), statistics used in downstream analysis are derived from the number of reads mapping to genomic regions of interest, while in applications such as SNP discovery, statistics are derived from the nucleotide composition of the reads mapping to the reference genome.

3. Exploratory analysis of sequencing errors and quality measures

To calibrate a sequencing instrument we can process DNA from monoploid organisms for which the genome is known and small, e.g. bacteriophage ϕX174. Sequencing runs generated by Illumina GA sequencers usually include one lane containing a sample of ϕX174 as a control. This paper reports on data from the control lane of an Illumina ChIP-seq experiment, and is available upon request. We note, however, that we have observed similar behavior in data from other Illumina control runs.

3.1 Exploring sequencing errors

Reads produced from these control runs should match the phage’s genome exactly. However, we find that for a typical run, only 25–50% of the reads match perfectly. In particular, for our example Illumina data only 37% of the reads were perfect matches. This suggests an overall base-call error rate of at least 2%. Among high quality reads, as defined by the manufacturer and described above, the percent of perfect matches increased only to 45%. Close examination of these qualities revealed that lower values were more common near the end of the reads (positions 30 and higher in reads of length 36). We therefore investigated the relationship between error rate and position on the read. To do this we took a random sample of 25,000 reads and matched each to the genome permitting up to 4 mismatches. We then assumed the mismatches were due to errors in the reads, i.e. if the best match of a particular read contained 2 mismatches we assumed read errors at the location of these mismatches. We made three important observations listed below.

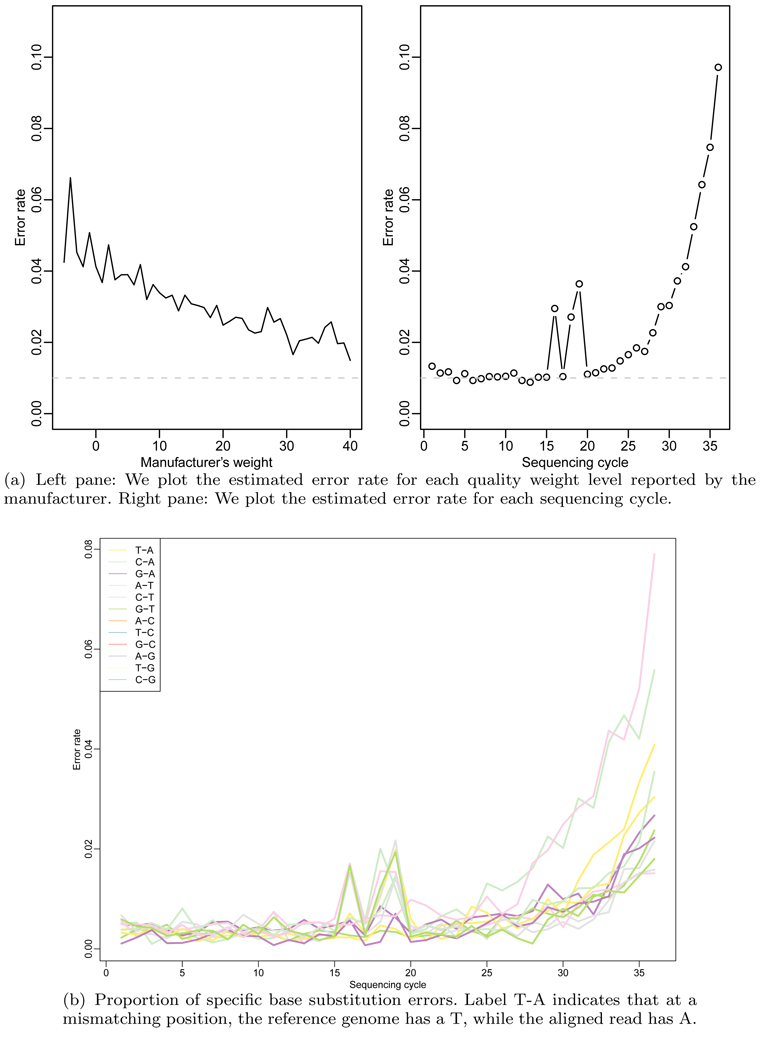
A first observation was that the weight provided by the manufacturer was a poor predictor of the observed error rate (Figure 1(a)) The error rate change between the best and worst quality scores was only 0.02 to 0.05. This implies that the best improvement we can hope for by ignoring the low weight reads is a 0.02 error rate. A second observation was that position within the read had a large effect on error rate (Figure 1(a)). This confirmed results published by other groups (Dohm et al., 2008). The error rate changed from 0.01 to 0.10 when comparing positions 1–12 to the last position (Figure 1(a)). This implies that the overall error rate can be greatly improved by down-weighting the last 10 locations of the read. The third observation was that, in this dataset, high error rates occurred at positions 16 and 18. The likely explanation for this is that a problem occurred with the images corresponding to the bases at these positions resulting on more errors. We have observed this type of artifact in multiple datasets, which underscores the need for informative quality metrics. Further data exploration reveled that certain types of errors were more common than others. For example, calling an A a T was the most frequent miscall (Figure 1(b)). These observations are, again, consistent with previously published results (Dohm et al., 2008).

Figure 1.

Exploration of sequencing errors. The top two plots show how the quality weight reported by the manufacturer is not a very good predictor of errors compared to sequencing cycle. We see also that the number of errors increases considerably as sequencing cycles progress. The bottom plot shows that certain erroneous base substitutions are more prevalent that others, that is, there is technical bias in sequencing errors. We see later how these technical biases influence downstream analysis.

3.2 Implications for genotyping

The core goal of genotyping is determining the nucleotide variation in each genomic position across populations. The initial step is determining if an individual sample shows variants at specific sites. To find SNPs using MAQ, the software currently used by the 1000 Genomes Project, the sample is sequenced and mapped to the reference genome, allowing for a small number of mismatches. Then the nucleotide composition of the reads mapping to each site, along with qualities reported by the manufacturer, is used to determine if a SNP exists at that site. Errors in sequencing can lead to obfuscation in the computation using nucleotide composition if there are systematic biases in these errors. This obfuscation results in a number of false positive SNPs reported, and require ad-hoc filtering methods.

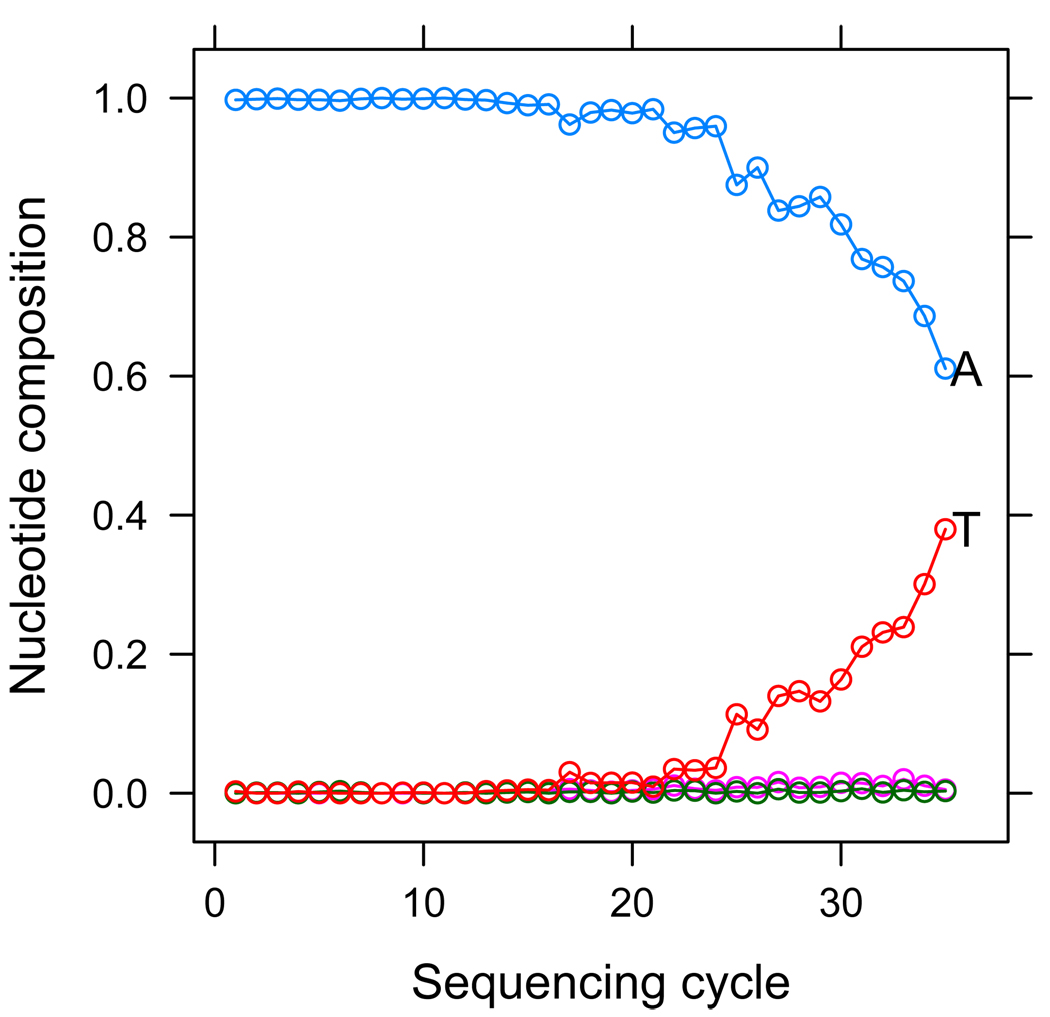
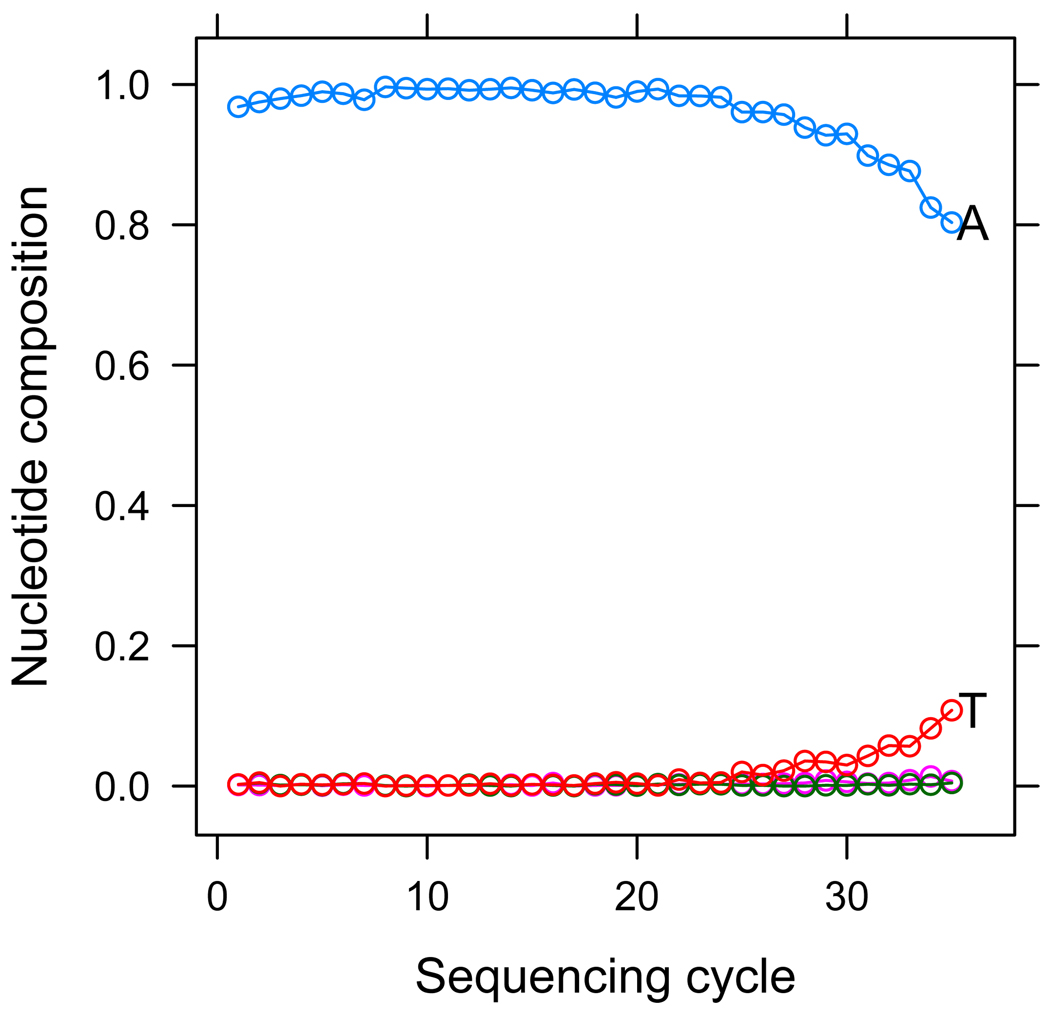
As an example, we processed data obtained from a bacteriophage ϕX174 sample using this pipeline. In this case, no heterozygous SNPs should be reported as this is a monoploid organism, but MAQ reports 45 spurious SNPs out of almost 5000 genomic sites. Looking further at one of these positions we can see the source of error in this case. We plot in Figure 2 the nucleotide composition of reads at that specific site, stratified by sequencing cycle. We can see that the incorrect base-calls, T calls, occur much more frequently in the latter positions of reads. This systematic bias in the base-calling errors that make MAQ falsely report this position as a SNP.

Figure 2.

We plot the base composition of reads aligning to a specific genomic position falsely reported by MAQ as a SNP. We stratify base composition by cycle, that is, at tick 1 of the x-axis we plot the base composition of the first cycle in reads which align to the SNP site in the first cycle, and so on. We can see a trend whereupon T’s become much more frequent only in reads that align to the SNP site at later sequencing cycles, indicating a technical bias in base-calls at this position.

Next, we asked if by looking at intensity data we can see what causes the biased base miscalls that leads to this falsely discovered SNP. In Web Figure W1 we plot the intensity measurements from the A and T channels for those reads and cycles which map to the corresponding genomic position. We saw that most of the T calls are made in later sequencing cycles, that average intensity is low for those calls, and that the difference to the A intensity is small. That is, the intensity data indicates that these T calls are not very certain. However, the quality filter used by MAQ was not enough to clarify these calls. A quality score that only gives the uncertainty in the measurement of the reported base is too coarse to capture this problem. On the other hand, representing uncertainty with respect to all four intensity measurements can guard against this problem if the technical bias present in this case, e.g. the bias towards incorrectly calling T instead of A in later sequencing cycles is properly captured.

4. Modeling fluorescence intensity

In the previous Section we saw that sequencing errors, even at low overall error rates, that are systematically biased can result in incorrect downstream analysis. Our goal in this paper is to define a framework that captures uncertainty in the sequencing pipeline in a way that allows downstream analysis to guard against these systematic errors. The core of our methodology is to model this uncertainty starting from measurements of fluorescence intensity all the way through read mapping. In this Section we motivate and develop our model to capture uncertainty from fluorescence intensity. The purpose of this model is to generate a short-read nucleotide probability profile for each read by drawing information not only from the intensities of each individual read as sequencing cycles progress, but also from other reads, making use of the large numbers of samples provided by these technologies. In the next Section, we describe quality metrics derived from these intensity model estimates that capture base-calling uncertainty.

For each read i we observe over N sequencing cycles, a 4-by-N matrix of measured fluorescence intensities. We denote this matrix as y_i, and specify measurements further as, for example y_ijA, indicating the measured intensity for read i, cycle j in the A channel. The intensity quadruplet of all four channels for read i and cycle j is denoted as y_ij. We plot in Figure W2 an example of intensity data. In an optimal setting, one would expect that each panel in Figure W2 shows three clusters of points: one along the x-axis, corresponding to reads where the nucleotide at the current cycle corresponds to that axis, another group for the y-axis respectively, and another group around the origin, corresponding to clusters where the nucleotide at the current cycle corresponds to neither of the two bases plotted. The actual data, however, showed some salient features that deviate from this expectation: (a) scatter, instead of high and low clusters, the intensity measurements for each channel are scattered across the intensity spectrum, (b) signal loss and corruption across cycles, where overall intensity decays and there is more overlap between intensity clusters as cycles progress and, (c) cross-talk, where intensity clusters for pairs of channels are highly correlated, e.g. A and C measurements.

The started log transform

We saw previously that fluorescence intensity in each fragment cluster is measured in cycles, as fragments complementary to those in the cluster are synthesized. However, at each cycle nucleotide incorporation might fail for a strand, terminating synthesis for subsequent cycles. Therefore, as incorporation fails, one would expect an exponential loss of measured signal from each cluster. To model this type of exponential process in the signal, and to control the variance in measurements, we preprocess the intensity measurements using a started log₂ transform. Since the intensity measurements given by Illumina have been background-corrected during image processing—unfortunately there is no way to recover the uncorrected signal without going back to the image data — some of the measured intensity values are negative, and thus a logarithmic transform is not defined. In the following, we show transformed observed intensities, denoted as h(y) = log₂(y + c). Constant c is chosen depending on the smallest intensity value s in the first cycle of a random sample of fragment clusters; if this value is positive we set c = 0, otherwise, we set c = |s|. If any of the unsampled intensities is lower than c, it is set to c before taking the log transform.

4.1 Effects observed in intensity data

The read-cycle effect

We can explain scatter in the intensity data by what we denote a read effect. Each fragment undergoes an in situ PCR reaction to amplify the corresponding sequence fragment and create a fragment cluster. The amount of amplification varies drastically between fragments. Since the fluorescence intensity of each cluster depends on the amount of amplification, the overall intensity, that is, measured across channels and cycles, varies significantly between clusters. We can clearly see this from the data, e.g. in Web Figure W3 where boxplots of all the intensity measurements for a random sample of reads show the wide variation in intensity across reads.

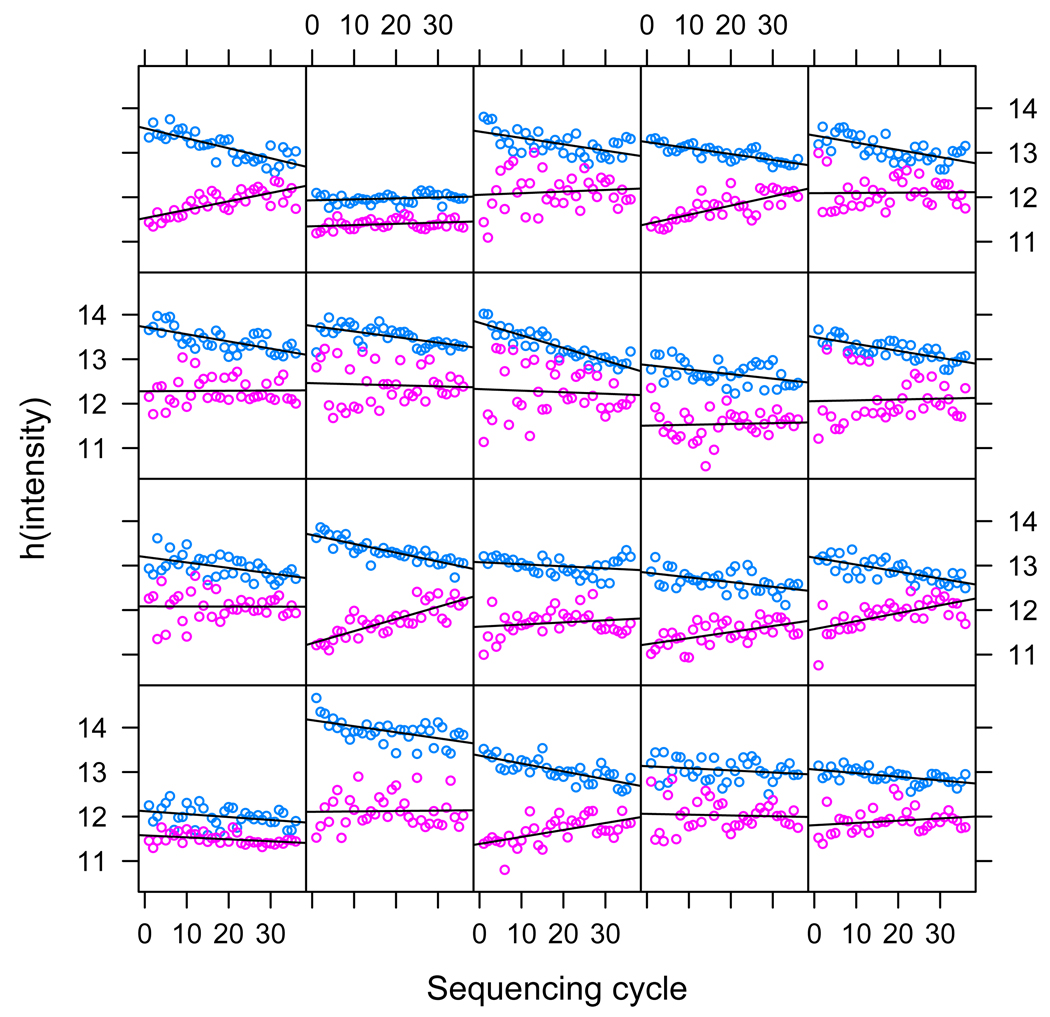
Similarly, there is a cycle effect in the measured intensities of each read, where intensity in the upper range drops as sequencing progresses, while it increases in the lower range. Figure 3 shows this effect for a few reads. Each panel in this figure shows two groups of points for each read: the upper group is the maximum intensity over the four channels at the corresponding cycle — this is the signal we are trying to capture — while the lower group is the median of the other three channels — this is noise. Due to the started log transform described above, these two groups can be modeled as linear functions of cycle. The intercepts of the two least-square lines model the overall intensity measurements of the cluster. The slope of the upper line models signal loss, while the slope of the lower line models signal corruption.

Figure 3.

The read-cycle effect. Each panel corresponds to measured intensities for a single read. The upper (blue) points are the maximum intensity at each sequencing cycle, the lower (pink) points are the median of the remaining intensities. We can observe the cycle effect: signal (upper line) drops and background (lower line) rises. Observe that due to the started log transform, using a linear model for this effect is appropriate. The intercept of the signal model (upper line) captures the read effect, while the slope captures the cycle effect, and similarly for the background model (lower line).

The base-cycle effect

Finally, we describe a global effect observed across reads. In this case, we noticed that overall intensity measurements vary between channels differently as sequencing cycles progress. Web Figure W4 illustrates this. We see how the median of intensity measurements change differently across channels as sequencing cycles progress. For instance, the median intensity in the G channel drops much faster than the other channels as sequencing progresses.

4.2 The intensity model

Our proposed intensity model for read i cycle j is h(y_ij) = Mu_ij where M is a matrix that models the cross-talk effect and h is the started log transform discussed above. We assume M is a matrix with unit diagonal so that the measured log transformed intensities are linear combinations of the underlying log intensities u_ij. This linear combination assumption is consistent with the cross-talk model of Li and Speed (1999). In fact, we estimate M using their procedures as is also used in the Illumina platform.

We model u_ijc, the underlying log intensity of read i, cycle j, channel c, as follows:

$$u_{\mathit{\text{ijc}}}={\mathrm{\Delta }}_{\mathit{\text{ijc}}}[{\mu }_{\mathit{\text{cj}}\alpha }+{\alpha }_{0i}+(j-1){\alpha }_{1i}+{\mathrm{∊}}_{\mathit{\text{ijc}}}^{\alpha }]+(1-{\mathrm{\Delta }}_{\mathit{\text{ijc}}}) [{\mu }_{\mathit{\text{cj}}\beta }+{\beta }_{0i}+(j-1){\beta }_{1i}+{\mathrm{∊}}_{\mathit{\text{ijc}}}^{\beta }] ,$$ (1)

where ${\mathrm{∊}}_{\mathit{\text{ijc}}}^{\alpha }~N(0,{\sigma }_{\alpha i}^2) \text{and} {\mathrm{∊}}_{\mathit{\text{ijc}}}^{\beta }~N(0,{\sigma }_{\beta i}^2)$ for all i, j, c, and Δ_ijc is an indicator of the true, unobserved, nucleotide being measured for read i in cycle j. That is,

$${\mathrm{\Delta }}_{\mathit{\text{ijc}}}=\{\begin{array}{cc}1\hfill & \text{if}c\text{is the nucleotide in read}i\text{position}j\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array},$$

and ∑_c Δ_ijc = 1 for all i, j.

This model is motivated by Figure W2 and 3 and is best understood by referring to those two plots. Parameters α_i = [α_0i α_1i] and β = [β_0i β_1i] correspond to the intercepts and slopes of the two read-specific linear models shown in Figure 3: α_i to the upper linear model, or the “signal loss model”, and β_i to the lower linear model, i.e., the “signal-corruption” model. Parameters μ_cjα and μ_cjα are used to capture base-cycle effects, that is, how the median intensity in each channel varies as sequencing cycles occur (Web Figure W4). These two parameters are shared by reads in each tile. Thus, given N reads and M cycles, there are N sets of α_i and β_i parameters, each estimated from 4 *M observations, and a set of base-cycle parameters μ_cjα and μ_cjβ, each estimated from N *M observations. In the Illumina data we use in this paper, N ≈ 30, 000 and M ≈ 40.

Parameter estimates are computed using the EM framework (Dempster et al., 1977), with details on how we derive them given in Web Appendix A. A result of estimating using the EM framework is an estimate of z_ijc:= E{Δ_ijc = 1|u_ij} = P(Δ_ijc = 1|u_ij), e.g., the posterior probability that the true nucleotide for read i in cycle j is c.

We reiterate that the effects included in the model are there as a result of an exploratory analysis of Illumina intensity data. They capture features of the data explainable by the chemistry of the sequencing process. For example, signal loss is due to the decreasing ability of nucleotide incorporation to occur as sequencing progresses, while signal corruption is due to residual fluorescence measured from previous sequencing cycles. Along with the cross-talk effect, these are inherent in the sequencing-by synthesis process. While better chemistry can diminish the strength of these effects, one might not expect their disappearance, especially, as more sequencing cycles are carried out in newer technologies. The model proposed here can be easily modified to accommodate changes in these effects or effects that arise as technology changes.

5. Quality assessment from the intensity model

An immediate consequence of using our model is access to meaningful, informative, and easily computable quality metrics. Recall that the model parameters have straightforward interpretation in terms of the technical characteristics of each read. To capture quality of each read we define the SNR metric, which measures how easily distinguishable are the signal and noise models for each read. We define it as

$${\mathit{\text{SNR}}}_i=\frac{1/N{\Vert X{\alpha }_i-X{\beta }_i\Vert }_2^2}{1/2({\sigma }_{\alpha i}^2+{\sigma }_{\beta i}^2)}$$

where Xα_i and Xβ_i are the means of the signal and background linear models. Thus, this signal-to-noise ratio compares, for each read, the average squared distance between the two estimated means and the average estimated variance. This metric is extremely efficient to compute once parameters are estimated and easily interpretable.

We can also define metrics from the probability profiles z_ijc described in the previous Section to indicate a measure of quality for each read with respect to nucleotide identity uncertainty. A simple metric is the entropy of the nucleotide distribution for each position in the sequencing read. For instance, for read i, cycle j, the entropy quality metric would be H_ij = −∑_c z_ijc log₂ z_ijc, while for read i the entropy metric is H_i = −∑_jc z_ijc log₂ z_ijc. These are equivalent to the quality metrics defined by Rougemont et al. (2008). In addition to using these metrics to automatically filter reads in downstream analysis, we can use aggregated results to provide quality reports at coarser resolutions, e.g. tile, lane or sample quality. Furthermore, the entropy metric can be used as a quality weight for each position in each read when mapping to the genome using quality-aware mappers such as BOWTIE and MAQ.

6. Results

6.1 Parameter estimates

Web Figure W5 shows histograms of estimated parameters for the linear effects models for tile worth of reads (~ 25,000 reads). We see bigger spread in the distribution of the signal parameters (α) compared to the background parameters (β). That is, the “read effect” has a stronger influence on signal rather than background. Also, there is less spread in the signal loss estimates α₁ compared to the read effect α₀ estimates. That is, while PCR amplification induces high variability in overall signal strength, signal loss is very similar across reads. The distributions of the standard deviation estimates are similar for both the signal and background models, indicating that the model may support a single error distribution for both the signal and background models in each read. Web Figure W6 shows estimated base-cycle effects for these reads. We consistently see correction for high signal in the T channel, which increases in later sequencing cycles. This is consistent with the bias we observed in base-calls and intensities (Sections 3 and 4). It is worth noting that this type of analysis is made possible from the interpretability of the model we have developed for intensities.

6.2 Quality metrics

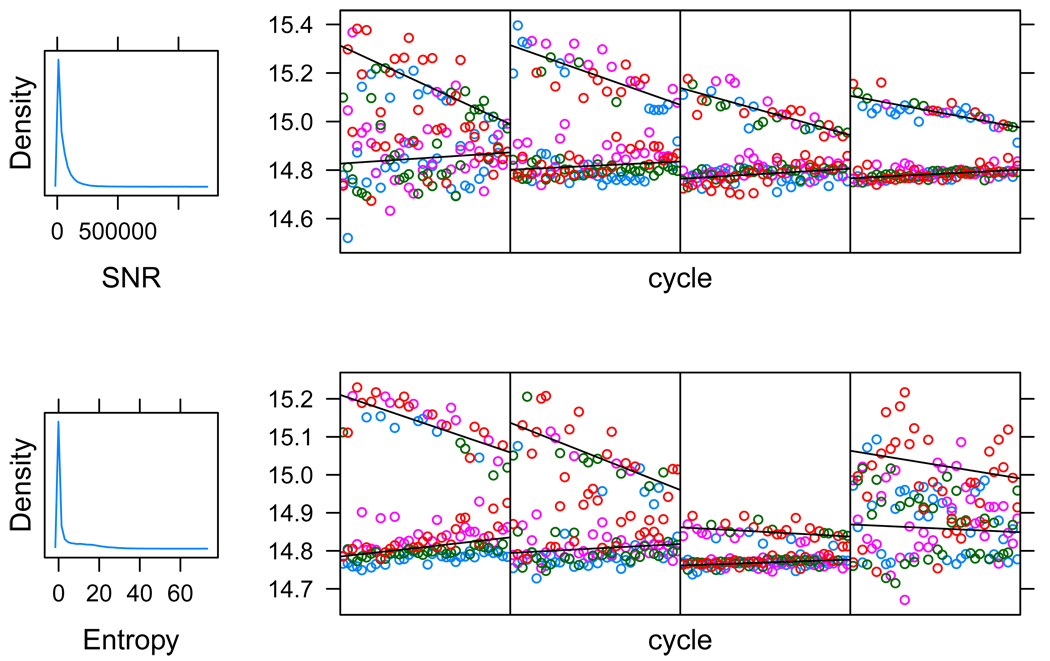
In Figure 4 we plot histograms of estimates of the two quality metrics defined in Section 5 along with intensity data of representative reads across each quality metric range. The first plot in each row gives a histogram of the metric for the same sample of reads. The plots that follow in each row give exemplary data from reads across the quality metric spectrum. The leftmost is a read with very low metric value, the rightmost is a read with a very high value, the two middle reads have close to median quality metric values. For SNR, low values are poor quality reads, while for Entropy, high values are poor quality reads.

Figure 4.

Four read quality metrics. The first plot in each row gives a histogram of the metric for a sample of reads. The plots that follow in each row give exemplary data from reads across the quality metric spectrum. The leftmost is a read with very low metric value, the rightmost is a read with a very high value, the two middle reads have close to median quality metric values.

We see that reads with high SNR values have well separated signal and noise mean lines and that the actual intensity data has low variability around the means. In contrast, reads with low SNR values are usually highly variable or have mean lines that are close together. On the other hand, the Entropy metric, which is based on the probability profiles z_ijc, provides a better picture of overall variability within measurements in a single read. This allows for reads that appear to have high variation around the signal and background linear means, to still be identified as high quality reads.

Figure 5 shows that the two metrics we have defined are significantly better predictors of read mappability than the quality values provided by the manufacturer. The plot was created as follows: we mapped 10 tiles of data (~ 290,000 reads) allowing for a maximum of 3 mismatches anywhere on the read; if a read mapped under this policy (either by our, or Solexa base-calls) it was labeled as mappable, and labeled as unmappable otherwise. We then plot an ROC curve (Fawcett, 2004) using each quality metric as a predictor of mappability. We see that both metrics outperform the manufacturer’s, with Entropy being the better of the two. Again, this is not surprising, since Entropy is a function of the probability profiles, which, due to the base-cycle effects, are not a simple function of the linear read-specific models. One interpretation of this plot is that if a filtering policy is defined using an allowable mismatch rate of 10%, then the Solexa metric will only recover 60% of the matching reads, while SNR would recover 80%, and Entropy 90%.

Figure 5.

Quality metrics as predictors of mappability. We took reads from 10 tiles (~ 290,000 reads) and mapped to the reference genome allowing up to 3 mismatches. If a read maps to the genome under this policy with either the base-calls from Bustard or our method we tag it as mappable, and as unmappable otherwise. We then plot an ROC curve using each quality metric as a predictor of mappability. The Solexa quality metric for a read is the mean quality weight reported for that read. Points in the x-axis correspond to filtering policies where, e.g., “allow 10% of the unfiltered data to not match the genome”, the corresponding point in the y-axis is the percentage of the mappable reads unfiltered by the policy.

6.3 Improved yield and accuracy

In this section we report on improved yield and accuracy resulting from using our model for base-calling and quality assessment. We took the entire set of reads in our sample dataset (one lane of data with ~ 12 M 26 base-pair reads) and created files in the same format as those produced by Solexa, consisting of a base-call and quality value for each base. We use the Entropy metric as the quality value to each base, rescaled to the Phred (Ewing et al., 1998) scale of quality values. This allows us to use existing mapping software, BOWTIE, in this case, to map reads we produce to the genome. We also used Entropy to filter out reads that have too many uncertain base-calls. Web Table W1 compares the mapping of our reads to those produced by Solexa using the same mapping policy (at most two mismatches in the first 24 positions). In summary, our base-caller yields an increase of more than 11% in the number of reads mapped, and a 7% increase in the number of perfectly mapped reads. We note that using the procedure discussed in the supplementary material, fitting our model for base-calling takes roughly 1 minute per tile on a cluster node with a 3 GHz processor. Using a 15 node cluster, we carried out the analysis of this full lane of data—both base-calling and mapping with BOWTIE—in less than two hours.

6.4 Improved SNP calling

We processed the mapping from the previous Section using the MAQ SNP calling pipeline to ascertain how our base-calling and quality metrics improves downstream analysis. Using the Solexa pipeline, MAQ reported 37 high quality SNPs (Phred score ≥ 100), while using our base-calls and Entropy-based quality metric results in MAQ reporting only 10 SNPs, a reduction of nearly 70% in false positives. As illustration, we replot Figure 2 using our basecalls in Figure 6. While there is still some of the bias towards T in the tail of reads, it is much less pronounced, enough for MAQ to avoid falsely calling this position a SNP.

Figure 6.

We redo Figure 2 using our own base-calls. Notice the reduced bias in T calls at the tail of reads aligning to the SNP position. MAQ does not report this position as a SNP using our base-calls.

7. Discussion

In this paper, we have presented some of the statistical and computational challenges presented by the analysis of second-generation sequencing data. In particular, we have shown how infrequent but systematic errors arise in these data and how it can mislead downstream analysis. In addition, the large variation in sequencing read quality must be captured in meaningful and informative metrics and used judiciously in downstream analysis.

We have presented a model-based approach for quality assurance and base-calling of data from the Illumina/Solexa second-generation sequencing platform that addresses these shortcomings. Using a probabilistic model that properly captures technical features of the raw continuous intensity data, yields simple but informative quality metrics. Furthermore, it draws information across reads and sequencing cycles, and is able to quantify the global variability inherent in the base-calling procedure. We have shown that our base-calling model can improve on the manufacturer’s method in both yield and accuracy, leading to improved genotyping down-stream analysis. The model attempts to capture effects in the intensity data, in particular, read-cycle and base-cycle effects that lead to the technical biases we have observed. While improvement is seen, there is still room for further improvement— better capturing the base-cycle effect being the most immediate. We currently add a shift in the intensity distribution according to base and cycle. However, these distributions vary beyond shifts implying that a global strategy to model this variation might be required. We are investigating further normalization strategies to address this (Bolstad et al., 2003).

Beyond improved performance, the model allows for easily interpretable metrics. In situations where there is a deluge of measurements to contend with, models that strive for simplicity and interpretability are paramount. In addition, we implement a very efficient method for parameter estimation that allows for analysis to be performed in hours rather than weeks. Again, these types of concessions are required in data-intensive situations like this one.

Our ultimate motivation for this work is to allow downstream analysis in clinical and biological research using second-generation sequencing that appropriately quantifies and captures the uncertainty inherent in the sequencing process. Along with collaborators, we are applying our methods in multiple projects. One example is microRNA profiling and discovery (Morin et al., 2008). In this case, the DNA fragments to sequence are short and require that DNA strands, called adapters, be attached to each fragment of interest. An initial step in analysis is finding this adapter within each resulting read, which can start at any position along the read. Furthermore, the discovery of mutations in microRNA experiments have attracted recent interest. We are developing a probabilistic framework that uses our nucleotide probability profiles to incorporate robust adapter finding and variant discovery. Another application of interest is variant discovery in pooled samples, where the frequency of true genetic variants is close to the biased error rates we discussed above. Again, our methods allow for a sound framework in which to carry out this type of analysis.