Estimating the personal cure rate of cancer patients using population-based grouped cancer survival data

Abstract

Cancer patients are subject to multiple competing risks of death and may die from causes other than the cancer diagnosed. The probability of not dying from the cancer diagnosed, which is one of the patients’ main concerns, is sometimes called the “personal cure” rate. Two approaches of modeling competing-risk survival data, namely the cause-specific hazards approach and the mixture model approach, have been used to model competing-risk survival data. In this article, we first show the connection and differences between crude cause-specific survival in the presence of other causes and net survival in the absence of other causes. The mixture survival model is extended to population-based grouped survival data to estimate the personal cure rate. Using the colorectal cancer survival data from the Surveillance, Epidemiology and End Results (SEER) Program, we estimate the probabilities of dying from colorectal cancer, heart disease, and other causes by age at diagnosis, race and American Joint Committee on Cancer (AJCC) stage.

1 Introduction

Net survival, i.e., survival in the absence of other causes, is a measure of excess mortality due to cancer. This is a hypothetical measure of survival if all causes of death other than cancer of interest were to be eliminated. Net survival is a desirable measure to evaluate the progress of cancer treatment and control efforts since the interpretation as excess mortality due to cancer is not a ected by changes in mortality due to other diseases.¹ However, net survival does not represent the actual survival patterns observed in a cohort of cancer patients. Comorbidity for cancer patients may limit treatment options and increase the risk of death from other causes. Usually comorbidity from competing causes increases with advancing age and is greater for patients in poor health. Thus, net survival may not be an ideal measure for assessing the impact of a cancer diagnosis in the presence of multiple competing risks. From another perspective, crude cause-specific probabilities of death provide measures of cause-specific mortality in the presence of causes of death in addition to cancer and reflect mortality patterns actually observed among patients.² Thus, they are appropriate measures when the focus is on inference and comparison of cause-specific failures under a variety of conditions. Such probabilities can be used to weigh the risks and benefits of various treatment options, particularly for patients diagnosed at older ages when comorbidity is high.

There has been considerable progress against cancer due to improvements in treatment, and the dissemination of early diagnosis and screening. Thus, successfully treated cancer patients may die from a cause other than the diagnosed cancer, which is called “personal cure.” The corresponding proportion of dying from causes other than the diagnosed cancer is defined as the personal cure rate. Gordon³ originally applied the mixture model to estimate the personal cure rate using breast cancer data from a clinical trial. To assess mortality from cancer at the population level, we extend the mixture model for competing-risk survival to population-based cancer survival data in order to calculate crude probabilities of dying from cancer and other competing risks. The rest of the paper is organized as follows: In Section 2, we first describe survival data with competing risks and review the mixture model for continuous survival data. Next, we extend the mixture model to grouped survival data, describe the estimation method and discuss the connection between net survival and crude survival. In Section 3, we apply the mixture model to colorectal cancer survival data to calculate the probabilities of dying from three competing causes of death. We discuss the potential use and limitations of the mixture model in the Discussion section.

2 The mixture model for grouped survival data with competing risks

We consider a patient subject to K mutually exclusive competing risks of death and assume that the primary outcome is a random pair (D, T), where D takes a value from the set {1, 2, ..., K} indicating cause of death and T is a non-negative random variable representing time to death. Let z denote a vector of covariates. The cause-specific hazard rate, defined as the probability of dying from cause k alone in [t, t + dt) in the presence of all acting risks, given T ≥ t,⁴ is given by

$$h_k(t∕z)=\underset{dt\to 0}{\lim }\frac{P(t\le T<t+dt,D=k\mid T\ge t,z)}{dt},k=1,\dots ,K.$$

Let $h(t\mid z)={\sum }_{k=1}^K{h}_k(t\mid z)$ and $S_k(t\mid z)=\exp \{-{\int }_0^t{h}_k(u\mid z)du\}$. The survival function for T is

$$S_T(t\mid z)=P(T>t)=\exp \left\{-{\int }_0^{t}h(u\mid z)du\right\}=\prod _{k=1}^K{S}_k(t\mid z).$$

David and Moescheberger⁵ consider the observed death time T as the minimum of K latent death times, i.e., T = min(T₁,···, T_K). When the competing risks T₁, . . . , T_K, are independent, S_k(t|z) can be interpreted as the net survival function from cause k in the absence of other causes and h_k(t|z) is the net hazard.⁶ Net survival can be estimated by the Kaplan-Meier method or the actuarial method by treating the other causes of deaths as censored.

The crude cumulative probability or cumulative incidence function (CIF) of dying from cause k in the presence of other causes is

$$F_k^{\ast }(t\mid z)=P(T\le t,D=k\mid z)={\int }_0^t{h}_k(u\mid z)S(u\mid z)du.$$ (1)

The functions $F_k^{\ast }(t\mid z)$ is also called sub-distribution function for cause k, k = 1, ..., K. Let π_k(z) = P(D = k|z) be the probability of dying from cause k and Q_k(t|z) = P(T > t|D = k, z) be the conditional crude survival function. Then $F_k^{\ast }\left(t\right)={\pi }_k\left(z\right)\{1-Q_k(t\mid z)\}$.

2.1 Review of mixture model for competing risk data

The mixture model⁷ specifies the death probabilities π_k(z) and the crude survival P(T > t|D = k, z), k = 1, ..., K. It does not require the independence assumption among competing risks. The cause of death D follows a multinomial distribution with probabilities P₁(z), ..., P_K(z) with

$${\pi }_k\left(z\right)=P(D=k\mid z)=\frac{\exp ({\mu }_k+{\gamma }_k^{T}z)}{\sum _{l=1}^K\exp ({\mu }_l+{\gamma }_l^{T}z)},$$ (2)

where μ_k is a scalar constant and γ_k is a vector of regression coefficients. Because ${\sum }_k{P}_k\left(z\right)=1$, we set μ_K = 0 and γ_K = 0 for identifiability purpose. We also assume cause D = 1 is death due to cancer of interest. The personal cure rate is then calculated as 1 − P₁(z).

The functions Q_k(t|z) = P(T > t|D = k, z), k = 1, ..., K are called crude cause-specific survival functions.¹ Larson and Dinse⁷ use a proportional hazards (PH) model for Q_k(t|z):

$$Q_k(t\mid z)=\exp \left\{-{\int }_0^t{q}_k(u\mid z)du\right\},$$ (3)

where $q_k(t\mid z)=q_k\left(t\right)\exp \left({\beta }_k^{T}z\right)$, q_k(t) is the baseline hazard function and β_k is a vector of regression coefficients. The overall survival function can also be expressed as

$$S_T(t\mid z)=\sum _{k=1}^K{\pi }_k\left(z\right)Q_k(t\mid z).$$ (4)

It can be shown that S_k(t|z) ≥ Q_k(t|z) (see Appendix I) for all t unless P_j(z) = 0 for j ≠ k. The inequality implies that, under the independent competing-risks assumption, the net survival function in the absence of other causes is always greater than the crude cause-specific survival function in the presence of other causes. Hence, the Kaplan-Meier and actuarial estimates always overestimate the conditional crude cause-specific survival probability.

2.2 The mixture model for grouped survival data

Survival times from population-based cancer registries are usually grouped into annual or monthly intervals, I_j = (t_j−1, t_j] for j = 1, ..., J, where t₀ = 0 and t_J = τ denote the beginning and end of follow-up, respectively. For the cohort with covariates z, let n_jz be the number of people alive at the beginning of interval I_j, d_kjz be the number of people who die from cause k, k = 1, ..., K and let l_jz be the number of people lost to follow-up in the interval. For simplicity of notation, we omit the subscript z and denote the observed data as $\mathcal{D}=(n_j,l_j,d_{kj},k=1,\dots ,K;j=1,\dots ,J)$. The total number of people who die during interval I_j is $d_j={\sum }_{k=1}^K{d}_{kj}$.

The probability of dying from cause k during the interval I_j is

$$P(t_{j-1}<T\le t_j\mid D=k,z)=Q_k(t_{j-1}\mid z)-Q_k(t_j\mid z).$$ (5)

Because some people are lost to follow-up during the interval, a widely used technique is to adjust the person-years at risk as $n_j^{\ast }=n_j-0.5\ast l_j{,}^{6,8,9}$ and the resulting estimate is called the actuarial estimate. Gail⁶ showed that the actuarial estimate is a good approximation of the maximum likelihood estimate (MLE) of S(t) under the assumption that time when lost to follow-up and time of death from competing risks are independent. The actuarial estimate can also be justified by assuming that time when lost to follow-up is uniform in interval I_j. Then the number of people who are censored at time t_j, i.e., T > t_j, is

$$c_j=\{\begin{array}{cc}{n}_j^{\ast }-d_j-n_{j+1}^{\ast }\hfill & \text{when}j<J,\hfill \\ n_J^{\ast }-d_J\hfill & \text{when}j=J.\hfill \end{array}\phantom{\}}$$

Let θ₀ = (μ_k, γ_k, k = 1, ..., K) be the parameters in the logistic model (2) for the cause of death and let θ_k be the parameters for the crude survival functions Q_k(t), k = 1, ..., K. The likelihood function for observed competing-risk survival data $\mathcal{D}$ is

$$L(\theta \mid \mathcal{D})=\prod _{j=1}^J\left[S{(t_j\mid z)}^{c_j}\prod _{k=1}^K{\left\{{\pi }_k\left(z\right)\left(Q_k(t_{j-1}\mid z)-Q_k(t_j\mid z)\right)\right\}}^{d_{kj}}\right],$$

where θ = (θ₀, θ₁, ..., θ_K). As the Newton-Raphson method requires the calculation of a complex Hessian matrix, the Expectation-Maximization (EM) algorithm is used to find the MLEs of θ.

The complete data are ($n_j^{\ast }$, d_kj, c_kj, k = 1, ..., K, j = 1, ..., J), where c_kj is the number of people censored at time t_j who would ultimately die from cause k. Using Equation (4), the loglikelihood for the complete data is log $L\left(\theta \right)=\ell \left(\pi \right)+{\sum }_{k=1}^K{\ell }_k\left(Q\right)$, where

$$\begin{array}{cc}\hfill \ell \left(\pi \right)& =\sum _{k=1}^K\sum _{j=1}^J\left(d_{kj}+c_{kj}\right)\log {\pi }_k\left(z\right)\hfill \\ \hfill {\ell }_k\left(Q\right)& =\sum _{j=1}^J\left[d_{kj}\log \left\{Q_k(t_{j-1}\mid z)-Q_k(t_j\mid z)\right\}+c_{kj}\log Q_k(t_j\mid z)\right]\hfill \end{array}$$

The E-step assigns the censored observations, i.e., the people who are lost to follow-up or who are still alive at the end of the study, into one of the K causes of death according to their conditional probabilities P(D = k|z, t > t_j). The expected number of deaths due to causes k in interval I_j for those censored people is

$$c_{kj}=c_{j}P(D=k\mid z,T>t_j)=c_j\frac{{\pi }_k\left(z\right)Q_k(t_j\mid z)}{S_T(t_j\mid z)}.$$ (6)

The M-step involves maximizing the loglikelihood functions $\ell \left(\pi \right)$ and ${\ell }_k\left(Q\right)$, k = 1, ..., K.

The MLEs of the parameters in π_k(z) can be obtained by multinomial logistic regression, and the estimation of the parameters in Q_k(t|z) depends on the model specifications for Q_k(t|z). The popular models include the Weibull and Gompertz models and the semi-parametric proportional hazards model. For arbitrary interval-censored survival data, various methods are proposed by Finkelstein¹⁰, Pan and Chappell¹¹ and Goetghebeur and Ryan¹². For grouped survival data, we follow Prentice and Gloeckler¹³ and write the loglikelihood ${\ell }_k\left(Q\right)$ as

$$\ell \left(Q_k\right)=\sum _{j=1}^J\left[d_{kj}\log \{1-p_{kj}\left(z\right)\}+(r_{kj}-d_{kj})\log p_{kj}\left(z\right)\right]$$

where p_kj(z) = Q_k(t_j|z)/Q_k(t_j−1|z) and $r_{kj}={\sum }_{l=j}^J(d_{kl}+c_{kl})$. Let ${\alpha }_{kj}=\log \left\{{\int }_{t_{j-1}}^{t_j}{h}_k\left(u\right)du\right\}$, j = 1, ..., J. Then,

$$p_{kj}\left(z\right)=\exp \{-\exp ({\alpha }_{kj}+{\beta }_{k}z)\}.$$ (7)

The estimates of θ_k = (α_k1, . . . , α_kJ, β_k) can be obtained by SAS PROC LOGISTIC.

Several factors complicate variance estimation for the parameter estimates. First the dimension of parameters is large for the semiparametric model. Second variance estimates do not come from the EM algorithm as a byproduct. Several approaches to calculate the observed information matrix in an EM context have been proposed.^14,15 But, these approaches involve tedious algebra and are analytically intractable. Another variance estimator, which is simple to compute and also turns out to have good small sample properties, is based on multiple imputation.^12,16 First the expected numbers of deaths due to cause k in interval I_j, c_kj, j = 1, ..., J, are imputed M times using a multinomial distribution with conditional probabilities given in (6), after the final step of the EM algorithm is completed. Then for each imputed “complete” data set, a point estimate $\widehat{\theta }\left(m\right)$ and a variance estimate v_m of θ are calculated, m = 1, ..., M. Let $\stackrel{‒}{\theta }={\sum }_{m=1}^M{\widehat{\theta }}_{\left(m\right)}∕M$. The variance estimate for the MLE $\widehat{\theta }$ is given by

$$V\left(\widehat{\theta }\right)=(1+1∕M)\frac{\sum _{m=1}^M{({\widehat{\theta }}_{\left(m\right)}-\stackrel{‒}{\theta })}^2}{M-1}+\sum _{m=1}^M{v}_m∕M.$$ (8)

This is a weighted sum of the within-imputation variance and the between-imputation variance.

2.3 Estimating net survival from the mixture model

The direct output from the mixture model consists of death probabilities from different causes and the conditional crude survival function. Under the assumption of independent competing risks, the net survival S_k(t|z) can be derived from output from the mixture model. We assume that h_k(t|z) = w_kj(z)h(t|z) for t ∈ I_j, where the weights w_kj(z) are constants for each interval I_j and covariate z. From (1), we have

$$\begin{array}{cc}\hfill F_k^{\ast }\left(t_j\right)-F_k^{\ast }\left(t_{j-1}\right)& ={\int }_{t_{j-1}}^{t_j}{h}_k(u\mid z)S_T(u\mid z)du=w_{kj}\left(z\right){\int }_{t_{j-1}}^{t_j}h(u\mid z)S_T(u\mid z)du\hfill \\ \hfill & =w_{kj}\left(z\right)\left\{S_T(t_{j-1}\mid z)-S_T(t_j\mid z)\right\},\hfill \end{array}$$

hence

$$w_{kj}\left(z\right)=\frac{F_k^{\ast }(t_j\mid z)-F_k^{\ast }(t_{j-1}\mid z)}{S_T(t_{j-1}\mid z)-S_T(t_j\mid z)}.$$ (9)

Because

$$\frac{S_k(t_j\mid z)}{S_k(t_{j-1}\mid z)}=\exp \left\{-{\int }_{t_{j-1}}^{t_j}{h}_k(u\mid z)du\right\}={\left\{\frac{S_T(t_j\mid z)}{S_T(t_{j-1}\mid z)}\right\}}^{w_{kj}\left(z\right)},$$

the net survival function S_k(t_j|z) can be estimated by

$$S_k(t_j\mid z)=\prod _{l=1}^j{\left\{\frac{S_T(t_l\mid z)}{S_T(t_{l-1}\mid z)}\right\}}^{w_{kl}\left(z\right)},$$ (10)

where w_kl is given by (9). The variance estimates for crude survival Q_k(t|z) and net survival S_k(t_j|z) are given in Appendix II. The relationship between S_k(t|z) and S_T (t|z) and $F_k^{\ast }(t\mid z)$ implies that the net survival functions can be calculated as a by-product of the mixture survival model under the independent competing risk assumption.

3 Application

The Surveillance, Epidemiology, and End Results (SEER) Program of the National Cancer Institute is an authoritative source of information on cancer incidence and survival in the United States (http://www.seer.cancer.gov). SEER currently collects and publishes cancer incidence and survival data from population-based cancer registries covering approximately 26 percent of the US population. SEER coverage includes 23 percent of African Americans, 40 percent of Hispanics, 42 percent of American Indians and Alaska Natives, 53 percent of Asians, and 70 percent of Hawaiian/Pacific Islanders. The SEER Program began collecting data on cancer cases in 1973 in the states of Connecticut, Iowa, New Mexico, Utah, and Hawaii and the metropolitan areas of Detroit and San Francisco-Oakland. In 1974-1975, the metropolitan area of Atlanta and the 13-county Seattle-Puget Sound area were added. These original 9 regions are referred to as the SEER 9 registries, covering 10% of the US population.

Colorectal cancer is the third most common cancer and the third leading cause of cancer-related mortality in the United States. Over the past decade, colorectal cancer incidence and mortality rates have modestly decreased or remained level. The most recent estimates from the American Cancer Society show that there are 106,100 new cases of colon cancer, 40,870 new cases of rectal cancer and 49,920 deaths from colorectal cancer for the year 2009. If diagnosed early and treated successfully, colorectal cancer can be cured. In fact, many colorectal cancer patients live long enough to die ultimately from other causes, most commonly from heart disease.

Because of the long history of the SEER 9 registries, we use the colorectal cancer survival data for illustration. We consider three competing risks (K = 3), namely, colorectal cancer death (D = 1), heart disease death (D = 2) and death due to other causes (D = 3). Here, we use the mixture model to estimate probabilities of dying from different causes given a patient's age at diagnosis, race and the American Joint Committee on Cancer (AJCC) stage. There are remarkable differences between racial and ethnic groups in both incidence and mortality. The mortality rate from colorectal cancer for African Americans is higher than that for whites (American Cancer Society, 2008). To confirm this conclusion, we also test the difference in probabilities of dying from multiple causes between whites and African Americans.

The SEER data we consider consist of 199,715 colorectal cancer cases diagnosed from 1975 to 2002. The end of followup is December, 2003 and the maximum followup time is 28 years. The survival data are then stratified by single age (50, 51,...,99, 100+), race (white, black) and AJCC stage (I, II, III, IV). The average age at diagnosis is 64, and 92% are whites and 8% are African Americans. The percentages of cancer stages I-IV are 20%, 33%, 25% and 22%, respectively.

In the first analysis, we fit separate mixture models for each combination of race and AJCC stage in order to estimate the probabilities of dying from different causes. Age at diagnosis is used as a covariate in equations (2) and (7). To account for the possible quadratic effect of age, the square of age is also included as a covariate. Figure 1 plots the observed and modeled probabilities of dying from colorectal cancer with respect to age at diagnosis. The observed probabilities are calculated as the proportion dying from colorectal cancer for each single age group ${\tilde{\pi }}_1={\sum }_{j=1}^J{d}_{1j}∕{\sum }_{j=1}^J{d}_j$. The modeled probabilities are the estimates ${\widehat{\pi }}_1$ in Equation (2). For example, less than 40% of the patients diagnosed with Stage I colorectal cancer actually die from colorectal cancer. We see that the modeled probabilities fit the observed probabilities reasonably well. The probabilities of colorectal cancer death increase with AJCC stage. This makes sense as a diagnosis of more advanced colorectal cancer implies higher probability of death. Overall, the probability of colorectal cancer death decreases in older patients except for very old ages. Figure 1 also shows that the probabilities of dying from colorectal cancer are much lower for whites than blacks in the same cancer stage.

Figure 1.

Observed and modeled probabilities of dying from colorectal cancer by age at diagnosis *

Figure 2 plots the nonparametric and modeled cumulative probabilities of death due to colorectal cancer within 5 years of cancer diagnosis by age at diagnosis. The nonparametric estimate¹⁷ is calculated as

$${\tilde{F}}_1^{\ast }(t\mid z)=\sum _{t_j\le t}\frac{d_{1j}}{n_j}\tilde{S}(t_{j-1}\mid z),$$

where $\tilde{S}(t_{j-1}\mid z)={\prod }_{l=1}^{j-1}(1-d_l∕n_l^{\ast })$ is the actuarial survival. The modeled probabilities are the estimates of ${\widehat{F}}_1^{\ast }(t\mid z)$. We see that the 5-year probabilities of colorectal cancer death do not change much with age at diagnosis for stage I, and the corresponding probabilities increase slightly with age at diagnosis for Stage III and IV. This shows that patients with more severe diagnosis are more likely to die from cancer.

Figure 2.

Nonparametric and modeled cumulative probabilities of death due to colorectal cancer within 5 years of diagnosis *

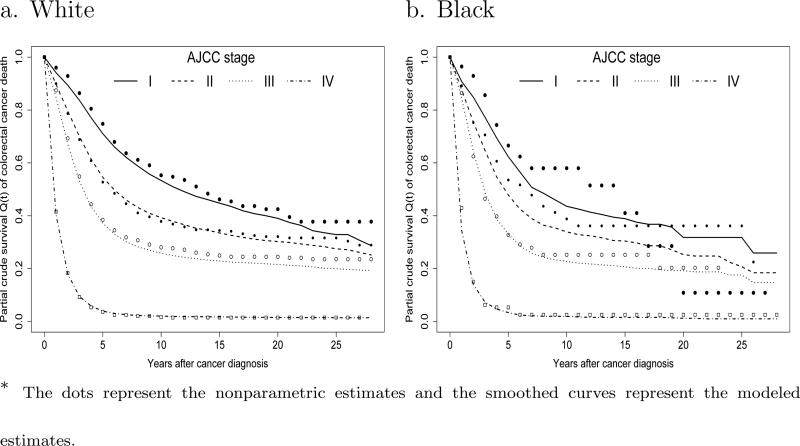
One may be interested in the actual survival pattern after diagnosis. As an example, we show the nonparametric and modeled conditional crude cause-specific survival estimates in the presence of competing risks for patients diagnosed at age 70 in Figure 3. We see that white patients have slightly higher crude survival rates than blacks. Figure 3 also shows that for stage IV cancer the conditional cause-specific survival rates are all less than 5% after 5 years of diagnosis. This implies that for patients diagnosed with stage IV cancer at age 70, 95% of cancer deaths would occur within 5 years after diagnosis.

Figure 3.

Conditional crude survival estimates Q₁(t) of colorectal cancer death in the presence of competing risks for patients diagnosed at age 70 *

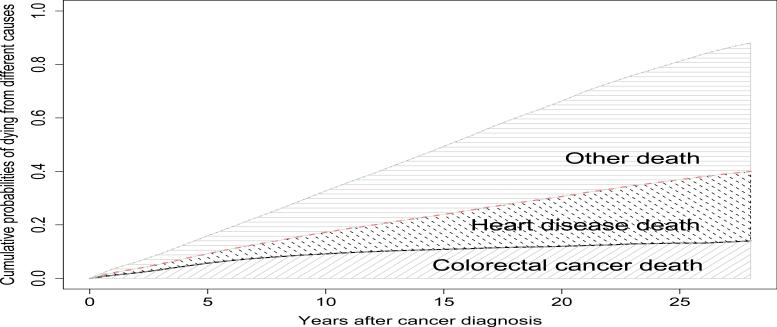
The unconditional cumulative probability of death due to cancer versus other causes is useful to describe the experience of individual patients. For example, Figure 4 shows the cumulative probabilities of death due to three causes for white patients diagnosed with stage I cancer at age 70. The personal cure rate is about 90%. The cumulative colorectal cancer death probability levels off after about 10 years from diagnosis, but the probability of death due to other causes still increases. So if a patient does not die from colorectal cancer within 10 years, it is very likely that he will die from another cause.

Figure 4.

Cumulative cause-specific probabilities of death for white patients diagnosed at age 70 with Stage I colorectal cancer

The analysis above can be used to describe the survival patterns experienced by cancer patients. In contrast, a statistical model presents a great advantage when some form of inference is required. As we see from Figures 1 and 2, differences exist in survival patterns between racial and ethnic groups. In the second analysis, we perform a formal test to examine the effect of race on probabilities of dying from different causes for each cancer stage. The covariate z of interest is the indicator of being black. In logistic model (2), the parameters exp(γ₁) and exp(γ₂) represent the odds ratios of being blacks on the probabilities of dying from cancer and heart disease, respectively. For example, exp(γ₁) > 1 means that blacks have higher probability of dying from colorectal cancer than whites. The estimates of odds ratio and the 95% confidence intervals (CI) are shown in Table 1. For stages I and II, blacks have a significantly higher risk of dying from colorectal cancer than whites. For Stage III, whites and blacks have similar cause-specific probabilities. For Stage IV, blacks have a lower probability of dying from cancer, but a higher probability of dying from heart disease.

Table 1.

Odds ratios of race on the probabilities of dying from different causes

Stage	Parameter	Cause of death	Estimate	95% CI	p-value
I	exp(γ1)	Cancer	1.322	(1.187, 1.472)	<0.001
	exp(γ2)	Heart Disease	1.202	(1.047, 1.381)	0.009
II	exp(γ1)	Cancer	1.229	(1.138, 1.328)	<0.001
	exp(γ2)	Heart Disease	1.046	(0.954, 1.147)	0.335
III	exp(γ1)	Cancer	1.060	(0.968, 1.161)	0.212
	exp(γ2)	Heart Disease	1.017	(0.896, 1.154)	0.797
IV	exp(γ1)	Cancer	0.807	(0.729, 0.894)	<0.001
	exp(γ2)	Heart Disease	1.223	(1.037, 1.441)	0.017

By using a logistic model for probabilities of dying from different causes, the mixture model implicitly assumes that hazards from different causes are constant after the end of the follow-up. Usually, hazards due to causes other than cancer will increase remarkably as people get older, while the hazard due to cancer death may remain similar with respect to age. Misspecification of the logistic model might yield biased estimates. It is also necessary to have a sufficiently long follow-up time to observe most deaths and their corresponding causes, so that death probabilities can be modeled reliably.

As shown in Figures 1 and 2, the mixture model provides a reasonably good fit to the observed data. However, one can argue that most of the patterns and probabilities can be easily obtained by smoothing the raw data. For example, a multinomial logistic model with splines can be used to estimate π_k, the probabilities of dying from different causes. Here, we are trying to model the probabilities π_k and crude survival functions Q_k(t) simultaneously. This provides a complete picture of survival patterns after cancer diagnosis.

4 Discussion

In this article, we apply the mixture model to grouped survival data with competing risks from population-based cancer registries. This model can be used to estimate probabilities of death due to different competing causes. The personal cure rate is helpful to describe the survival experience after cancer diagnosis. This model can also be applied to data from clinical trials. For example, one can compare the probabilities of different types of failures to evaluate the risk and benefit of two treatment options. Physicians can determine the appropriate treatments for cancer patients based on their comorbidities and prognosis.

An alternative approach to competing-risk data is to model the net survival functions^5,13. To ensure identifiability, the competing risks are assumed to be independent. The cancer patients, especially in their old ages, have higher comorbidity problems than the general cancer-free population. The mixture model assumes that the process of loss to follow-up is independent of the competing risks of death, but it does not require independence among the K competing risks. Another advantage of using the mixture model is that the net survival function can be derived as a by-product.

Appendix I. Proof of S_k(t|z)≥Q_k(t|z)

Based on equation (3), we have $q_k(t\mid z)=-\frac{d{Q}_k(t\mid z)}{dt}∕Q_k(t\mid z)$. Because $Q_k(t\mid z)=1-F_k^{\ast }(t\mid z)∕{\pi }_k\left(z\right)$ and from (1),

$$q_k(t\mid z)=\frac{\frac{d{F}_k^{\ast }(t\mid z)}{dt}}{{\pi }_k\left(z\right)Q_k(t\mid z)}=\frac{h_k(t\mid z)S_T(t\mid z)}{{\pi }_k\left(z\right)Q_k(t\mid z)}\ge h_k(t\mid z).$$

Thus

$$S_k(t\mid z)=\exp \left(-{\int }_0^t{h}_k(r\mid z)dr\right)\ge \exp \left(-{\int }_0^t{q}_k(r\mid z)dr\right)=Q_k(t\mid z).$$

Appendix II. Variances for Q_k(t|z) and S_k(t|z)

The variances of Q_k(t|z) and S_k(t|z) can be derived from the covariance matrix of θ in (8) using the delta method. Let θ_k = (α_k1, ..., α_kJ, β_k) be the parameters in θ_k(t|z) and V(θ_k) be the covariance matrix of θ_k. Because

$$\log Q_k(t_j\mid z)=\sum _{l=1}^j\log p_{kl}\left(z\right)=-\sum _{l=1}^j\exp ({\alpha }_{kj}+{\beta }_{k}z),$$

the variance of Q_k(t_j|z) can be calculated as

$$\widehat{Var}\left[Q_k(t_j\mid z)\right]=\frac{1}{Q_k{(t_j\mid z)}^2}{\phantom{\mid }{\Gamma }_{kj}V\left({\theta }_k\right){\Gamma }_{kj}^{\prime }\mid }_{\theta =\widehat{\theta }},$$

where γ_kj = (log p_k1(z), ..., log p_kj(z), z log Q_k(t_j|z)).

Let $S_k^{\ast }(t\mid z)={\pi }_k\left(z\right)Q_k(t\mid z)$. Then $S_T(t\mid z)={\sum }_{k=1}^K{S}_k^{\ast }(t\mid z)$. Assuming the parameters (θ_k, μ_k, γ_k), k = 1, ..., K, are functionally independent, we have

$$\frac{\partial S_T(t\mid z)}{\partial {\theta }_k}=\frac{\partial S_k^{\ast }(t\mid z)}{\partial {\theta }_k},k=1,\dots ,K,$$ (11)

where the partial derivatives of $S_k^{\ast }(t_j\mid z)$ are:

$$\begin{array}{cc}\hfill \frac{\partial S_k^{\ast }(t_j\mid z)}{\partial {\mu }_k}& =\frac{Q_k(t_j\mid z)}{{\pi }_k\left(z\right)\{1-{\pi }_k\left(z\right)\}},\hfill \\ \hfill \frac{\partial S_k^{\ast }(t_j\mid z)}{\partial {\gamma }_k}& =\frac{z{Q}_k(t_j\mid z)}{{\pi }_k\left(z\right)\{1-{\pi }_k\left(z\right)\}},\hfill \\ \hfill \frac{\partial S_k^{\ast }(t_j\mid z)}{\partial {\alpha }_{kl}}& ={\pi }_k\left(z\right)Q_k(t_j\mid z)\log p_{kl}\left(z\right),l=1,\dots ,J\hfill \\ \hfill \frac{\partial S_k^{\ast }(t_j\mid z)}{\partial {\beta }_k}& =z{\pi }_k\left(z\right)Q_k(t_j\mid z)\log Q_k(t_j\mid z).\hfill \end{array}$$

The variance of S_T(t_j|z) can be calculated as:

$$\widehat{Var}\left[{\widehat{S}}_T(t_j\mid z)\right]={\phantom{\mid }\left(\frac{\partial S_T(t_j\mid z)}{\partial \theta }\right)V\left(\theta \right){\left(\frac{\partial S_T(t_j\mid z)}{\partial \theta }\right)}^{\prime }\mid }_{\theta =\widehat{\theta }},$$

where V(θ) is the variance of $\widehat{\theta }$.

The variance of S_k(t_j|z) is given by $\widehat{Var}\left[{\widehat{S}}_k(t_j\mid z)\right]=\widehat{Var}\left[\log S_k(t_j\mid z)\right]∕S_k{(t_j\mid z)}^2$, where

$$\widehat{Var}\left[\log {\widehat{S}}_k(t_j\mid z)\right]={\phantom{\mid }\left(\frac{\partial \log S_k(t_j\mid z)}{\partial \theta }\right)V\left(\theta \right){\left(\frac{\partial \log S_k(t_j\mid z)}{\partial \theta }\right)}^{\prime }\mid }_{\theta =\widehat{\theta }}.$$

Based on Equation (10), $\log S_k(t_j\mid z)={\sum }_{l=1}^j{w}_{kl}\left(z\right)[\log S_T(t_l\mid z)-\log S_T(t_{l-1}\mid z)]$. We have

$$\begin{array}{cc}\hfill \frac{\partial \log S_k(t_j\mid z)}{\partial \theta }=& \sum _{l=1}^j\{\frac{\partial w_{kl}\left(z\right)}{\partial \theta }[\log S_T(t_l\mid z)-\log S_T(t_{l-1}\mid z)]\phantom{\}}\hfill \\ \hfill & \phantom{\{}+w_{kl}\left(z\right)\left[\frac{1}{S_T(t_l\mid z)}\frac{\partial S_T(t_l\mid z)}{\partial \theta }-\frac{1}{S_T(t_{l-1}\mid z)}\frac{\partial S_T(t_{l-1}\mid z)}{\partial \theta }\right]\},\hfill \end{array}$$

where $\frac{\partial S_T(t_j\mid z)}{\partial \theta }$ is given in (11) and

$$\frac{\partial w_{kj}\left(z\right)}{\partial \theta }=\frac{\frac{\partial S_k^{\ast }(t_{j-1}\mid z)}{\partial \theta }-\frac{\partial S_k^{\ast }(t_j\mid z)}{\partial \theta }}{S_T(t_{j-1}\mid z)-S_T(t_j\mid z)}-\frac{S_k^{\ast }(t_{j-1}\mid z)-S_k^{\ast }(t_j\mid z)}{{[S_T(t_{j-1}\mid z)-S_T(t_j\mid z)]}^2}\left[\frac{\partial S_T(t_{j-1}\mid z)}{\partial \theta }-\frac{\partial S_T(t_j\mid z)}{\partial \theta }\right].$$

Note that $\frac{\partial S_k^{\ast }(t_{j-1}\mid z)}{\partial {\theta }_i}=0$ for i ≠ k.