Genetics of microstructure of cerebral white matter using diffusion tensor imaging

Abstract

We analyzed the degree of genetic control over intersubject variability in the microstructure of cerebral white matter (WM) using diffusion tensor imaging (DTI). We performed heritability, genetic correlation and quantitative trait loci (QTL) analyses for the whole-brain and 10 major cerebral WM tracts. Average measurements for fractional anisotropy (FA), radial (L_⊥) and axial (L_||) diffusivities served as quantitative traits. These analyses were done in 467 healthy individuals (182 males/285 females; average age 47.9±13.5 years; age range:19–85 years), recruited from randomly-ascertained pedigrees of extended families. Significant heritability was observed for FA (h²=.52±.11;p=10⁻⁷) and L_⊥(h²=.37±.14; p=0.001), while L_|| measurements were not significantly heritable (h²=.09±.12; p=.20). Genetic correlation analysis indicated that the FA and L_⊥ shared 46% of the genetic variance. Tract-wise analysis revealed a regionally diverse pattern of genetic control, which was unrelated to ontogenic factors, such as tract-wise age-of-peak FA values and rates of age-related change in FA. QTL analysis indicated linkages for whole-brain average FA (LOD=2.36) at the marker D15S816on chromosome 15q25, and for L_⊥(LOD=2.24) near the marker D3S1754 on the chromosome 3q27. These sites have been reported to have significant co-inheritance with two psychiatric disorders (major depression and obsessive-compulsive disorder) in which patients show characteristic alterations in cerebral WM. Our findings suggest that the microstructure of cerebral white matter is under a strong genetic control and further studies in healthy as well as patients with brain-related illnesses are imperative to identify the genes that may influence cerebral white matter.

Introduction

Cerebral white matter (WM) consists of axonal bundles that connect proximal and distal brain regions and create large-scale neural networks facilitating complex behaviors (Le Bihan, 2003). Although an appreciation of the genetic mechanisms that control intersubject variability in these networks is critical for understanding normal and pathological function, the lack of noninvasive methodologies to study WM had held back discoveries in this field (Crick and Jones, 1993). Recent developments in magnetic resonance diffusion tensor imaging (DTI) have enabled in vivo measurement of WM microstructure (Basser, 1995; Basser et al., 1994). In parallel, methods of statistical genomics have been developed to measure the degree of genetic control over intersubject variability in a trait and to localize chromosomal regions that control this variability. These advances lead to several recent studies that demonstrated evidence for genetic control over variability in cerebral WM through analysis of fractional anisotropy (Chiang et al., 2009b) and regional WM density (Hulshoff Pol et al., 2006) in twins. Additionally, genetically-linked aberrations in the WM integrity were reported in the Williams syndrome (Hoeft et al., 2007; Marenco et al., 2007) and schizophrenia (Konrad et al., 2009; McIntosh et al., 2008; Winterer et al., 2008). In this manuscript, we synergistically combined these methodological advances in neuroimaging and statistical genomics to study the genetic causes of the intersubject variability in the microstructure of the cerebral WM.

The first objective of this study was to test the hypothesis that intersubject variability in the WM microstructure, measured using DTI, is under a high degree of genetic control. The DTI technique provides direct quantification of the tensor describing translational motion of water molecules within WM axons. In myelinated axons, this motion is enhanced along the axial direction and constrained in the direction perpendicular to it. Therefore, DTI-extracted parameters are highly sensitive to the degree of axonal myelination, average axonal diameter and axonal density (Song et al., 2003; Song et al., 2005). To this end, we used three DTI measurements: diffusivity in the axial (along the longitudinal axis L_||) and radial (across the axonal wall, L_⊥) directions and fractional anisotropy (FA) of water diffusion. The axial and radial diffusivities provide direct and quantitative measurements of regional water diffusion in mm²/sec (Basser, 1995; Basser et al., 1994). Additionally, axial and radial diffusivities are commonly combined into a unitless parameter, FA, that measures the difference in the magnitudes of the water diffusion between axial and radial directions. FA values are high (maximum theoretical value is 1.0) in heavily myelinated WM tracts, low (0.05–0.2) in gray matter and near zero in cerebrospinal fluid (Basser, 1994; Conturo et al., 1996; Pierpaoli and Basser, 1996; Ulug et al., 1995).

The second objective was to analyze the regional pattern of genetic control over intersubject differences in the microstructure of the major cerebral WM tracts. Specifically, we hypothesized that the degree of the regional genetic control was modulated by several ontogenic and senescence factors. Prior studies of the genetics of intersubject variations in regional brain morphology indicated a possible connection between ontogenic factors such as variability in the prenatal neurohormonal environment and the degree of genetic contribution to variability of brain structures. For instance, a progressively lower degree of genetic contribution was found for cortical structures that appeared later in cerebral development (Brun et al., 2008; Cheverud et al., 1990; Lohmann et al., 1999).

These findings imply that intersubject variability in the later developing structures may have higher contributions from environmental factors. To test these regional-control hypotheses, we used findings from our recent study of heterogeneity and heterochronicity of cerebral myelination trends in a large group of healthy subjects (N=820) aged 10 to 90 years(Kochunov et al., 2010). There, we showed that cerebral myelination, measured by FA, followed a quadratic trajectory with age, with peak myelination levels observed between 2^nd and 4^th decades of life. We carefully mapped by-tract myelination rates, age-of-peak and senescence rates in ten major cerebral WM. Here, we used the results of this study to specifically test whether the earlier developing WM tracts, that carry sensory and motor information, were under higher genetic control than later-developing associative tracts.

The third objective was to localize specific chromosomal regions that influence intersubject variability in DTI parameters using quantitative trait linkage (QTL) analysis. QTL analysis identifies chromosomal regions that control phenotypic variability by calculating the degree of co-inheritance between a phenotype and a set of specific genetic markers distributed homogenously across all chromosomes. Additionally, QTL analysis was used to study whether the genetic influences in different DTI parameters would map to the same or different chromosomal regions thereby providing a direct estimate of the degree of shared genetic control among DTI parameters. Successful genetic linkage analyses were recently performed on a neuroimaging phenotype, volume of hyperintense WM lesions (DeStefano et al., 2006; Kochunov et al., 2009b; Turner et al., 2005) providing chromosomal targets that are responsible for variability in this trait and explicating genetic relationships between hypertension and the volume of hyperintense WM. More recently, candidate gene analysis of DTI scans (Chiang et al., 2009a) revealed that polymorphism in the brain-derived neurotrophic factor (BDNF) gene influence fiber integrity in normal subjects. In a study of 258 twins, the BDNF polymorphism significantly contributed to the variation in FA in the posterior cingulate gyrus, where it accounted for around 90–95% of the total variance in FA, suggesting that common genetic variants may strongly determine white matter integrity.

Recently, an analytic method, tract-based spatial statistics (TBSS), was developed to quantify voxel-level variation in DTI parameters among subjects along the major WM tracts (Smith et al., 2006a; Smith et al., 2007). TBSS was developed to overcome the shortcomings of voxel-based analysis of DTI data. Hardware of MR scanners limits the spatial resolution of DTI data, therefore making intersubject voxel-based analysis susceptible to misalignment and partial-volume effects necessitating specialized processing (Chiang et al., 2008; Smith et al., 2006b). TBSS processing addresses this by extracting the spatial course of major WM tracts, and then analyzing diffusion parameters values that correspond to the middle of the tract. Applying this technique to DTI data collected from randomly selected individuals from large extended pedigrees allowed us to investigate the specific hypotheses proposed in aims 1 to 3 and to study the extent to which intersubject variation in DTI parameters is under genetic control.

Materials and Methods

Subjects

467 (182 males/285 females) active members of the San Antonio Family Study were analyzed here (Mitchell et al., 1996). Subjects ranged in age from 19 to 85 years of age (average age=47.9±13.5 years) and were members of 49 families with an average family size of 9.4±8.5 individuals (range 2–38). Subjects were excluded for MRI contraindications, history of neurological illnesses, or reports of a major neurological event (e.g., stroke). All participants provided written informed consent on forms approved by the University of Texas Health Science Center San Antonio (UTHSCSA).

Diffusion tensor imaging

Diffusion tensor imaging was performed at the Research Imaging Center, UTHSCSA, on a Siemens 3T Trio scanner using an eight-channel phased array head coil. A single-shot single refocusing spin-echo, echo-planar imaging sequence was used to acquire diffusion-weighted data with a spatial resolution of 1.7×1.7×3.0mm. The sequence parameters were: TE/TR=87/8000ms, FOV=200mm, 55 isotropically distributed diffusion weighted directions, two diffusion weighting values, b=0 and 700 s/mm² and three b=0 (non-diffusion-weighted) images. The number of diffusion directions, number of b=0 images and the magnitude of the b values were calculated using an optimization technique that accounts for the diffusivity of the cerebral WM and the T2 relaxation times (Jones et al., 1999).

Diffusion tensor processing

DTI images were processed using the diffusion tensor analysis toolkit (FDT) distributed with FSL (http://fsl.fmrib.ox.ac.uk/fsl/fdt/) (Behrens et al., 2003). First, DTI images were corrected for spatial misalignments and distortions due to eddy currents produced by simple head motion and large diffusion gradients. Next, multivariate regression was used to estimate the six components of diffusion tensor: three eigenvectors (V_1,2,3) and three eigenvalues (L_1,2,3) for every voxel in a DTI image. The 3D maps of three eigenvalues were converted to voxel-wise maps of axial (L_||), radial, (L_⊥), and fractional anisotropy (FA) using equations: 1–3.

$${\text{L}}_{\left|\right|}={\text{L}}_1$$ Eq. 1

$${\text{L}}_{\perp }=\frac{L_2+L_3}{2}$$ Eq. 2

$$FA=\sqrt{\frac{3·[{(L_1-1/3{\displaystyle \sum _{i=1..3}}{L}_i)}^2+{(L_2-1/3{\displaystyle \sum _{i=1..3}}{L}_i)}^2+{(L_3-1/3{\displaystyle \sum _{i=1..3}}{L}_i)}^2]}{2·(L_1^2+L_2^2+L_3^2)}}$$ Eq. 3

TBSS processing

A tract-based spatial statistics (TBSS) method, distributed as a part of FSL package, was employed for tract-based analysis of diffusion parameters (Smith et al., 2006a). TBSS is used for intersubject analysis of FA and other diffusion parameters and consists of the following steps: First, 3D images of DTI parameters (L_||, L_⊥ and FA) were calculated by fitting the diffusion tensor to the raw diffusion data using FMRIB Diffusion Toolbox (FDT) (Smith SM, 2002). During FDT processing, spatial distortions produced by eddy currents were corrected using 12-parameter affine registration to the b=0 image and a diffusion tensor model is fit for every voxel (Smith SM, 2002). Then, FA images are nonlinearly aligned to a group-wise, minimal-deformation target (MDT) brain. Nonlinear alignment is achieved by a one-to-one non-linear transformation with 30,000 degrees of freedom, using a coarse-to-fine multi-scale approach, to register homologous spatial features of two images performed using FMRIB’s Non-Linear Image Registration Tool (FNIRT)(Klein et al., 2009; Smith et al., 2004). The group’s MDT brain is identified by warping all individual brain images in the group to each (Kochunov et al., 2001). The MDT brain is selected as the brain image that minimizes the deformation from other brain images in the group. Once, FA images are non-linearly aligned to the MDT brain, images of other diffusion parameters (L_|| and L_⊥) are transformed using the FA image’s transform. Next, individual FA images are averaged to produce a group-average anisotropy image. This image is used to create a group-wise skeleton of white matter tracts. The skeletonization procedure is a morphological operation, which extracts the medial axis of an object. This procedure is used to encode the medial trajectory of the white matter fiber-tracts with one-voxel thick sheaths.

Finally, diffusion parameters from Equations 1–3 for each image are projected onto the group-wise skeleton of white matter structures. This step accounts for residual misalignment among individual white matter tracts. This processing is performed under two constraints. A distance map is used to establish search borders for individual tracts. The borders are created by equally dividing the distance between two nearby tracts. Secondly, a multiplicative 20 mm full width at half-max (FWHM) Gaussian weighting is applied during the search to limit maximum projection distance from the skeleton.

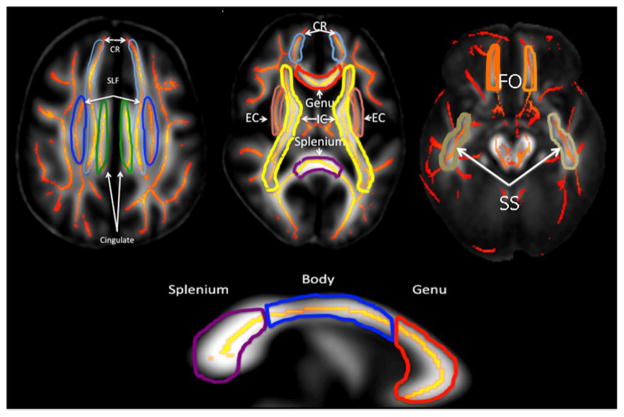
Tract-based calculation of diffusion parameter

The population-based, 3D, DTI cerebral WM tract atlas developed in John Hopkins University (JHU) and distributed with the FSL package (Wakana et al., 2004) was used to calculate population average diffusion parameter values along the spatial course of the ten, largest (volume≥ 5cm³) WM tracts (Table 1, Figure 1). The JHU atlas was nonlinearly aligned to the MDT brain and image containing labels for individual tracts was transferred to MDT space using nearest-neighbor interpolation. Per-tract average values were calculated by averaging the values along the tracts in both hemispheres. Per-tract average values were calculated by collapsing and averaging the values along the tracts in both hemispheres. The whole-brain average diffusion values were calculated by averaging values for the entire white matter skeleton.

Table 1.

White matter tracts used in the analysis (C=Commissural, P=Projection, A=Association).

Tract	Fiber Type	Connections
Genu of Corpus Callosum (GCC)	C	Cerebral Hemispheres
Body of Corpus Callosum (BCC)	C	Cerebral Hemispheres
Splenium of Corpus Callosum (SCC)	C	Cerebral Hemispheres
Cingulum	A	Cingulate Gyrus/Hippocampus
Corona Radiata (CR)	P	Cortical/Subcortical
External Capsule (EC)	A	Frontal/Temporal/Occipital
Internal Capsule (including thalamic radiation) (IC)	P	Subcortical/Brainstem/Cortex
Superior/Inferior Fronto-Occipital Fasciculi (FO)	A	Frontal/Parietal/Occipital
Superior Longitudinal Fasciculus (SLF)	A	Frontal/Temporal/Occipital
Sagittal Stratum (SS)	A/P	Subcortical/Temporal/Occipital

Figure 1.

Average DTI parameters were measured for ten major cerebral WM tracts

Genotyping

The details of the genotyping procedure can be found in (Kammerer et al., 2003). After DNA was extracted from lymphocytes, fluorescently labeled primers from the MapPairs Human Screening set (versions 6 and 8 (Research Genetics, Huntsville, AL, USA)) and PCR were used to amplify 417 specific markers spaced at approximately 10-cM intervals across 22 autosomes. An automated DNA sequencer (ABI Model 377 with Genescan and Genotyper software; Applied Biosystems, Foster City, CA, USA) was used. The average heterozygosity index for these markers was approximately 0.76. The sex-averaged marker map was confirmed by deCODE genetics (Kong et al., 2002) and markers not on this map were placed by interpolation of their physical location (Goring et al., 2007).

Genotypes were subjected to extensive data cleaning with SimWalk2 software package (Sobel and Lange, 1996). The computation was based on maximum likelihood marker allele frequencies (Boehnke, 1991). This statistical procedure is designed to detect inconsistencies and unlikely genotypes. An iterative process was followed to eliminate genotypes that are likely to be erroneous until no more inconsistencies or possible errors could be identified. Following this, the multipoint identity-by-descent matrices were estimated using the Markov chain Monte Carlo methods implemented in Loki (Heath, 1997). The probabilities of multipoint identity-by-descent allele sharing among all possible pairs of related individuals were computed using the genotypes at all linked markers jointly in the computations.

Heritability and Bivariate Genetic Correlation Analyses

Variance components methods, as implemented in the Sequential Oligogenic Linkage Analysis Routines (SOLAR) software package (http://solar.sfbrgenetics.org) (Almasy and Blangero, 1998), were used to estimate the heritability and shared genetic variance among global and regional traits. Detailed description of the methods used to calculate heritability and bivariate genetic correlations is provided in other manuscripts from this group published in this issue (Kochunov et al., 2009a; Winkler et al., 2009). In short, heritability (h²) is defined as a measurement of the proportion of total phenotypic variance that is explained by additive genetic factors and is assessed by contrasting the observed phenotypic covariance matrix with the covariance matrix predicted by kinship (Almasy and Blangero, 1998). Bivariate genetic correlation analysis is performed to calculate the proportion of common genetic variance that influences both traits. If the genetic correlation coefficient (ρ_G) is significantly different from zero, then the significant portion of the variability in two traits are considered to be influenced by shared genetic factors (Almasy et al., 1997b).

Quantitative Trait Linkage (QTL) Analysis

QTL analysis was performed to localize potential genes influencing phenotypic variation to specific chromosomal locations (Almasy and Blangero, 1998). The goal of this analysis is to identify specific chromosomal locations that co-inherit with the trait, which then suggests that genes at this location control the phenotypic variability in the trait. The hypothesis of significant linkage was assessed by comparing the likelihood of a classical additive polygenic model to that of a model allowing for both a polygenic component and a variance component due to linkage at a specific chromosomal location. The logarithm of odds (LOD) score was used to assess the significance of linkage. LOD score is the log₁₀ of the ratio of the probability of obtaining a set of observations, assuming a specified degree of linkage, to the probability of obtaining the same set of observations with independent assortment. For this exact pedigree structure and density of markers, a LOD of 1.67 is required for suggestive significance (likely to happen by chance less than once in a genome-wide scan) and a LOD of 2.88 is required for genome-wide significance at the 0.05 level.

An inverse Gaussian transformation was utilized to assure normal range for kurtosis and skewness (Almasy and Blangero, 1998). All genetic analyses were conducted with age, sex, age*sex, age², age²*sex included as covariates.

Correction for multiple comparisons

The level of statistical significance for bivariate genetic correlation was set at p ≤ .01 and at p≤.001 for the tract-based heritability measurements to reduce the probability of Type 1 errors associated with multiple (3 and 30) comparisons.

Results

Whole-brain analysis

Heritability estimates for whole-brain average diffusion parameters are shown in Table 2. Whole-brain average FA showed the highest heritability among all diffusion parameters (h²=.52) followed by heritability estimates for L_⊥ (h²=.37) (Table 2). Heritability estimate for the whole-brain average L_|| was not significant. Only ~9% of the intersubject variability in L_|| was explained by genetic factors, indicating that the variability in this phenotype was predominantly influenced by the environmental factors. Age and age² were significant covariates for all three whole brain average traits and accounted for 24–31% of phenotypic variability. However, there were no significant age by sex or age² by sex covariates.

Table 2.

Heritability (h²) estimates, significant covariates, percent of the variability explained by covariates for three whole brain average DTI parameters.

Trait	h2±SD (p)	Significant Covariates	% Variance Explained by Covariates
FA	.52±.11 (1E-7)	Age (1.5E-17), Age2 (.002)	31%
L||	.09±.12 (.2)	Age (5E-9), Age2 (.04)	24%
L⊥	.37±0.14 (0.001)	Age (1E-13), Age2 (.02)	25%

Bivariate genetic correlation analysis was used to study the portion of the shared genetic variance between the traits (Table 3). Bivariate genetic correlation analysis reported, that FA and L_⊥ shared 46% of common genetic variance (ρ_g=−.68±.13; 1E-4). The negative sign of genetic correlation indicated that shared genetic factors produce opposing changes in the magnitude of these traits. That is, the genetic factors that produced increases in the radial diffusivity were also responsible for decreases in FA. The magnitude of the genetic correlation coefficient between L_|| and L_⊥ indicated that over 90% of the variability in L_|| explained by genetic factors (h² ~9%) was shared with that in L_⊥.

Table 3.

Genetic correlation (ρ_G) estimates for whole brain average DTI parameters.

Trait	FA	L||	L⊥
FA	1	−.70±.29 (0.09)	−.68±.13 (1E-4)
L||		1	.95±.07 (0.04)
L⊥			1

^*Bolded values were significant at p p ≤ .01 level.

By-tract analysis

The results of the by-tract average heritability estimates for ten major WM bundles are shown in Table 4. The by-tract pattern of heritability for FA, L_||, and L_⊥ mirrored the results of the whole-brain values. By-tract, heritability measurements for FA had the highest tract average heritability value (h²=0.49±0.10), with significant heritability observed for every tract (Table 4). By tract, heritability measurements for the L_⊥ showed an intermediate tract average heritability value (h²=0.32±0.8) with seven of the ten by-tract measurements showing heritability significant at p ≤ .001 level. The lowest tract average heritability (h²=0.19±0.5) estimates were observed for the L_||, where there were no findings of significant (p ≤ .001). Age was a significant covariate for all regional FA and L_⊥ measurements that showed statistically significant heritability (Table 4). Sex was a significant covariate for L_⊥ measurements in the body of CC and External Capsule (Table 4). Again, there were no significant age by sex or age² by sex covariates.

Table 4.

Average within-tract FA measurements, age-of-peak, maturation and decline rates in FA values with age and heritability estimates for three DTI parameters..

Tract	Average FA	Age of Peak (AOP) (year)*	Maturation rate prior to AOP (FA units/year)*	Decline rate after AOP (FA units/year)*	FA: h2 (p)	L||: h2(p)	L⊥: h2(p)
Genu of Corpus Callosum	.59±.05	34.2±5.7	21.3±5.0 ·10−4	26.5±3.2 ·10−4	.66 (1E-9)a	.13 (.1)	.34 (1E-4) a
Body of Corpus Callosum	.62±.03	31.8±7.7	14.7±8.9 ·10−4	17.6±3.3 ·10−4	.54 (1E-7) a	.22 (.01)	.42 (1E-5) a,b
Splenium of Corpus Callosum	.75±.03	29.9±10.5	8.4±7.1 ·10−4	12.1±2.5 ·10−4	.57 (1E-7) a	.23 (.01) a,b	.41 (1E-5) a
Cingulum	.43±.02	39.4±5.8	13.6±2.6 ·10−4	12.0±1.9 ·10−4	.34 (1E-3) a	.22 (.01)	.38 (1E-11) a
Corona Radiata (CR)	.46±.02	27.9±5.7	2.5±4.0 ·10−4	12.0±1.0 ·10−4	.56 (1E-7) a	.14 (.1) a,b	.36 (1E-4) a
External Capsule (EC)	.37±0.01	25.6±7.7	0.3±5.7 ·10−4	9.7±0.9 ·10−4	.43 (1E-5) a	.20 (.01) a	.35 (1E-3) a,b
Internal Capsule (including thalamic radiation) (IC)	.55±.01	31.7 ±9.3	4.7±2.9 ·10−4	6.5±1.0 ·10−4	.43 (1E-6) a	.15 (.1) a,b,c	.18 (.1) a
Superior/Inferior Fronto- Occipital Fasciculi (FO)	.52±.02	38.9±6.6	10.9±3.0 ·10−4	14.5±2 ·10−4	.41 (1E-5) a	.20 (.1) a	.28 (.01) a
Superior Longitudinal Fasciculus (SLF)	.43±.01	28.8±7.6	6.8±4.0 ·10−4	9.4±1.1 ·10−4	.58 (1E-7) a	.22 (.01) a	.23 (.01) a
Sagittal Stratum (SS)	.42±.01	23.1±11.6	12.4±13.0 ·10−4	6.7±..8 ·10−4	.40 (1E-4) a	.25 (.01) a,b	.27 (1E-3) a

^*data taken from(Kochunov et al., 2010). Bolded values were significant at p p ≤ .001 level.

The pattern of significant (p ≤ .001) covariates was coded as age (^a), sex (^b), age²(^c).

The results of the correlation analysis between the by-tract heritability estimates for the three diffusion parameters and the by-tract age of peak and the rates of the age-related maturation and decline are shown in Table 5. There were no significant correlations between the three diffusion parameters and the age of peak and the rates of maturation and age-related declines.

Table 5.

Spearman correlation [coefficients (p-values)] between by-tracts patterns of heritability for FA, L parallel, and L perpendicular vs. and various FA measures.

Measurement	FA: h2 (p)	L||: h2(p)	L⊥: h2(p)
Average FA	.50 (.14)	.01 (.90)	.32 (0.2)
Age of Peak FA (AOP)*	−.16 (.70)	−.18 (.60)	.11 (.80)
FA maturation rate prior to AOP*	.22 (.50)	.03 (.90)	.24 (.50)
FA decline rate after AOP*	.60 (.06)	−.41 (.24)	.47 (.17)

^*Taken from (Kochunov et al., 2010)

Linkage analysis

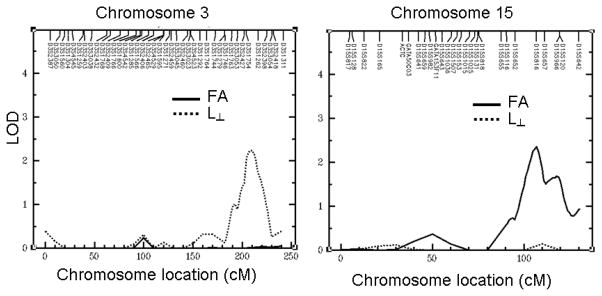
Results of the linkage analysis for three whole-brain average DTI parameters are summarized in Table 6 and the locations of the peak LOD scores are shown in Figure 2. The LOD scores for the two DTI parameters, FA and L_⊥, approached statistical significance (.05<p<.10). The maximum LOD score for the FA values (LOD = 2.36) was observed at the location 107 cM from the p terminal at the marker D15S816 (Figure 2). This region was previously reported to harbor major depressive disorder 2 (MDD2) genes (Holmans et al., 2004; McAuley et al., 2009; Park et al., 2004). The maximum LOD score for the L_⊥ values (LOD= 2.24) was observed at the location 212 cM from the p terminal located near the marker D3S1262 (Figure 2). This chromosomal region was reported as a region of a significant difference between patient with obsessive-compulsive disorder (OCD) and controls (Shugart et al., 2006). This region is also known to contain several genes important controlling the consumption of energy and metabolism (Choquette et al., 2008). The linkage results for the L_|| were not significant and the location of the maximum LOD overlapped with that of the L_⊥. There were no other suggestive linkages for any of the traits.

Table 6.

Result of the quantitative trait linkage analysis for three whole-brain average DTI measurements

Trait	LOD (p)	Marker (Location)	Previous QTL results
FA	2.36	D15S816 (15q25)	Major Depressive Disorder 2 (MDD2) gene (Mcauley et al., 2009)
L||	1.34	D3S1754( 3q27)
L⊥	2.24	D3S1754( 3q27)	Obsessive Compulsive Disorder(Shugart et al., 2006) and Genes affecting energy metabolism(Choquette et al., 2008)

Figure 2.

Suggestive LOD scores were observed for whole-brain measurements of FA at c15q25 and L_⊥ at c3q27.

Discussion

As hypothesized, we observed significant genetic control over variability in WM microstructure but were unable to demonstrate that the degree of genetic contribution is higher for earlier developing WM tracts. Finally, we found that the chromosomal regions that influence intersubject differences in the cerebral WM microstructure include genes associated with major depressive and obsessive compulsive.

Heritability of the whole-brain measurements

We observed significant differences in the heritability estimates for the radial (L_⊥) versus axial (L_||) diffusivities, with the latter being non-significant. The radial diffusivity (L_⊥) is a measurement of a restricted diffusivity across the axonal walls. Biologically, this measurement describes the permeability of axonal membranes and therefore serves as an indirect estimate of the axonal myelination level (Song et al., 2003). Studies in animal models that carefully manipulated cerebral myelination levels have unambiguously showed that the radial diffusivity was highly sensitive to regional demyelination (Song et al., 2003; Song et al., 2005). In contrast, axial diffusivity (L_||), which reflects unobstructed diffusivity along the axonal long axis, is less understood. L_|| is exclusively sensitive to changes in the axonal flow due to injuries resulting in contusions and/or transaction of fiber bundles (Budde et al., 2007). Therefore, we interpret the significant heritability estimate for L_⊥ and the lack thereof for L_|| as indications that radial diffusivity is under strong genetic control while the intersubject differences in axonal diffusivity are chiefly due to environmental factors.

The highest heritability among DTI parameters was observed for the fractional anisotropy (FA) of water diffusion, where over 50% of the intersubject variability was explained by genetic factors (Table 2). Absolute FA values are sensitive measurements of regional myelination levels, the degree of intra-voxel fiber coherence, axonal density and average axonal diameter (Beaulieu, 2002). However, intersubject differences in regional FA values are associated with differences in the local axonal myelination levels (Abe et al., 2002; Gao et al., 2009; Madler et al., 2008; Song et al., 2003). Hence, FA is thought to be a more sensitive index of changes in cerebral myelination than either L_⊥ and L_|| (Budde et al., 2007; Madler et al., 2008). The heritability estimates for FA reported here, are consistent with those reported in prior studies using voxel-based 3D mapping approaches (Chiang et al., 2009b)(Lee et al., 2009).

Next we studied the degree of shared genetic variance among the white matter measures. This occurs when the same genetic factors influence multiple traits and it can be formally demonstrated using the genetic correlation which indexes the extent to which genetic variance is shared between two traits (Almasy et al., 1997a), Genetic correlation between FA and L_⊥ was significant (ρ_G =−.68±.13; p=1E-4), suggesting that these traits have shared and unique genetic influences. In contrast, genetic correlation analysis between FA and the L_⊥/L_|| ratio suggested that these phenotypes are almost entirely influenced by the same genetic factors (ρ_G=0.90±0.05, p=1E-7).

Heritability of the by-tract measurements

By-tract genetic analysis tested whether earlier developing structures are under a higher degree of genetic control than later developing structures by correlating tract-level estimates of heritability with age of the peak for FA and FA maturation rates. Some developmental biologists have suggested that earlier developing structures may be more tightly controlled by genetic factors during development and therefore show higher heritability. Such an effect has been reported for DTI, as Lee et al., (Lee et al., 2008) found that the heritability of FA in the occipital lobes was numerically higher than that for the frontal lobes, which develop over a more protracted period (Gogtay et al., 2004). However, others have noted that the earliest developing structures are clearly evolvable through the course of the evolutionary history (Raff, 1996), and therefore may be susceptible to environmental perturbations. Previously, we directly tested the assertion that earlier developing structures are under higher genetic control(Kochunov et al., 2009a) and showed that the degree of genetic contribution to morphological variability in the primary cerebral sulci was not significantly different between early versus later developing cortical sulci (Kochunov et al., 2009a). Here, we find that tract-level heritability values were not modulated by the age at which these tracts reached maturity and that earlier developing WM tracts did not show higher degree of genetic contribution (Table 5). In fact, the study’s highest heritability estimate (h²=.66±0.11, p=10⁻⁹) was observed for the FA of the late-developing area, the genu of the CC. The genu contains thinly myelinated, pre-frontal commissural fibers myelinate later in life (age-of-peak = 34.2±5.7 years)(Aboitiz, 1992; Aboitiz et al., 1992; Kochunov et al., 2010).

The by-tract, heritability patterns for FA and L_⊥ showed positive, but not significant, correlations with the by-tract average FA values (r=.50 and .32, p=.14 and .20, respectively). A significant correlation between average FA values and heritability estimates may point toward a possible methodological bias. Fiber-tracking literature indicates that higher average FA values are an indication of high spatial coherence of fiber bundles within a region (Behrens et al., 2003). For example, the corpus callosum (CC) is composed of the fiber bundles that originate in the corona radiata (CR), but its average FA value (FA=0.61±0.05) is substantially higher than that in the CR (FA=0.46±0.02). This difference in the average FA values between structures that share axonal bundles is primarily due to differences in spatial complexity between tracts. The fiber bundles located in the CR follow a geometrically complex path (Wakana et al., 2004). Once within CC, these fibers become predominantly oriented in the L-R direction and are therefore more spatially coherent, resulting in higher average FA. However, this well-recognized methodological bias did not adversely influence our analysis as the heritability for the FA values in the CC (h²=0.57±0.11) was essentially identical to that in the CR (h²=0.56 ±0.12).

Linkage analysis

Quantitative trait linkage (QTL) analysis identified two chromosomal regions that influence the microstructure of cerebral WM. A suggestive linkage (LOD=2.36) was found for FA, in a region located at 107 cM on the chromosome 15, at the marker D15S816. This region contains the family of MDD2 genes, named for their involvement in the Major Depressive Disorder 2 disorder (Holmans et al., 2004; McAuley et al., 2009; Park et al., 2004). It contains several genes expressed in the brain that could possibly affect FA measurements including SEMA4B (semaphorinprecursor 4B) known to control the axonal extension and growth (Williams-Hogarth et al., 2000) and several other genes implicated in neuronal development (Holmans et al., 2004). In addition, a region located on the chromosome 3 at 212 cM, near the marker D3S1262, showed suggestive linkage (LOD=2.24) for L_⊥. This chromosomal region had the highest LOD score for obsessive-compulsive disorder in a recent whole-genome linkage study in 219 families (Shugart et al., 2006). This region was also reported to harbor genes that control energy intake and metabolism by a QTL study in 217 families (Choquette etal., 2008). Many other important genes, including genes that code for the human 5-HT3 serotonin receptor-like 3D and 3E (Niesler et al., 2003)and the adiponectin gene (ADIPOQ), a key hormone in energy regulation (Sutton et al., 2005)are located at this region. The only other currently published genetic study of DTI assessed the effects of a candidate gene, BDNF, on FA in the posterior cingulate gyrus (Chiang et al., 2009a).

The pattern of significant covariates

Genetic analysis reported that a significant (up to 31%) portion of the intersubject variability in the whole brain and regional DTI measurements was explained by subject’s age and gender (Tables 2 and 4). Subject’s age was expected to be a significant covariate as the DTI parameters, especially FA and L_⊥, are known to be very sensitive measures of microstructural WM integrity and therefore are commonly used to tract deterioration in normal aging and disorders (Kochunov et al., 2007; Pfefferbaum et al., 2000; Sullivan et al., 2001). Findings of significant regional gender-related differences, including the body of CC, have also been previously reported (Schmithorst et al., 2008; Westerhausen et al., 2004).

Limitations

By-tract genetic analyses in this manuscript were performed on DTI parameters that were averaged for voxels assigned to a tract. Ideally, this study would have been performed using a high-dimensional, multivariate joint analysis of voxels constituting the WM tract. A multivariate approach greatly improves the power of genetic discovery (Amos et al., 2001; Amos and Laing, 1993). Unfortunately, such a massive multivariate analysis is beyond our existing computational abilities due to the multifold increases in the dimensionality of the covariance matrices that account for non-independent structure of subjects in this family-based experimental design.

Conclusion

Our study analyzed the heritability, degree of shared genetic variance and quantitative trait loci for the three commonly used DTI-based measurements of WM microstructure. Heritability analysis of the whole-brain average axial (L_||) and radial (L_⊥) diffusivities and fractional anisotropy (FA) showed that a significant portion of variability in the later two parameters (37% and 52%, respectively) was explained by genetic factors. The latter two parameters also shared 46% of common genetic variance, suggesting that a relatively large set of genes influence white-matter microstructure and that these genes were not necessarily common to all DTI-derived traits. Intersubject variability in axial diffusivity was not hereditable and was thought to be influenced by environmental rather than genetic factors, consistent with previous finding (Budde et al., 2007). By-tract heritability measurements in the three diffusion parameters mirrored results from the whole brain analysis. By-tract heritability estimates were heterogeneous and this variation has yet to be explained. Linkage analyses identified two suggestive chromosomal regions for whole-brain FA and L_⊥ measurements. Overall, these findings imply that further research in healthy as well as patients with brain-related illnesses that combines genetics with neuroimaging methods such as DTI is necessary to study the genes that may influence white matter.