Ultraviolet Spectroscopy of Protein Backbone Transitions in Aqueous Solution: combined QM and MM Simulations

Abstract

A generalized approach combining Quantum Mechanics (QM) and Molecular Mechanics (MM) calculations is developed to simulate the n → π* and π → π* backbone transitions of proteins in aqueous solution. These transitions, which occur in the ultraviolet (UV) at 180–220 nm, provide a sensitive probe for secondary structures. The excitation Hamiltonian is constructed using high level electronic structure calculations of N-methylacetamide (NMA). Its electrostatic fluctuations are modeled using a new algorithm, EHEF, which combines a molecular dynamics (MD) trajectory obtained with a molecular mechanics forcefield, and electronic structures of sampled MD snapshots calculated by QM. The lineshapes and excitation split-tings induced by the electrostatic environment in the experimental UV linear absorption (LA) and circular dichroism (CD) spectra of several proteins in aqueous solution are reproduced by our calculations. The distinct CD features of α-helix and β-sheet protein structures are observed in the simulations and can be assigned to different backbone geometries. The fine structure of the UV spectra is accurately characterized and enables us to identify signatures of secondary structures.

Introduction

The function of proteins normally depends crucially on their secondary structure and dynamic fluctuations¹. Optical spectroscopy provides a direct probe of the conformations of biological systems and the coupling between biomolecules and their surroundings.^2,3 The investigation of these systems requires the development of simulation tools that adequately represent the fluctuations of the molecular environment. Protein motions in aqueous solution lead to fluctuations of the electrostatic environment. These, in turn, induce changes in the intra- and inter-molecular interactions, and thereby change the local Hamiltonian. Hamiltonian fluctuations shift and broaden the spectra. And a proper description is crucial for the prediction of spectral fine structure and lineshapes. To simulate the fluctuation effects, one might need to consider thousands of snapshots to reflect the conformation diversity.⁴ However, repeated quantum mechanics (QM) calculations are prohibitively expensive. QM approaches can accurately describe small molecules, where small typically means less than one hundred atoms. Molecular mechanics (MM) methods can describe large complexes, but neglect potentially important quantum mechanical effects. The combined approach of QM and MM calculations has become widely used for simulating large biological molecules.^5,6 A typical combined simulation generates geometric snapshots along the molecular dynamics (MD) trajectory based on a MM forcefield, and applies QM methods to describe the electronic structure for each snapshot. For example, accurate QM theory can be used to describe the active site of a protein, while the contribution of the rest of the system is treated more approximately.

Significant progress has been made in the simulation of vibrational infrared spectra of proteins by building a map to represent the local Hamiltonian as a function of geometric parameters or electric fields at some reference points.^4,7,8 Such “map function” methods reproduce the electrostatic environment from many MD snapshots with reasonable calculation cost. In such approaches the physical relationships between the Hamiltonian and geometrical structures are replaced by some fitting functions. The simulation results are sensitive to the number of reference points, the way they are chosen, and the type of functions used. Due to the lack of simple physical guidelines, complicated numerical analysis and expensive test calculations must be performed to establish a special map for a specific molecules. It is hard to construct a generalized map model that is transferable between different systems.

Linear absorption (LA) and circular dichroism (CD) spectroscopy of proteins in the ultraviolet (UV) region 180–220 nm are commonly used for secondary structure characterization.⁹ α-helix and β-sheet are two important types of secondary structure elements. Specific regions in the spectra reflect the electronic excitations. In CD spectra, α-helical proteins show a strong positive peak at 190 nm (52000 cm⁻¹) and a negative doublet at 208 and 222 nm (48000 and 45500 cm⁻¹). Sheet-containing proteins are less ordered and the CD spectra vary a little more. Their common features are a negative amplitude at 180 nm (55000 cm⁻¹), a positive band at around 195 nm (51000 cm⁻¹) and usually a negative peak at approximately 215 nm (44500 cm⁻¹).¹⁰ The simulation of UV spectra by the matrix method has been shown to be very successful by several groups.^11–14 Based on either empirical parameterization or ab-initio parameter sets, the Dichro-Calc package^15,16 has given good agreement between simulated and experimental CD spectra.

In previous simulations, fluctuations were added phenomenologically by convoluting the spectra with a broadening factor.^13,17 Here we develop a generalized approach combining QM and MM methods for calculating these spectra. We focus on the simulation of the n → π* and π → π* (denoted as nπ* and ππ* below) bands of the protein backbone in the 180–220 nm wavelength region. We start with high level electronic structure calculations on N-methylacetamide (NMA), which is a model system for the peptide bond. Two electronic excitations in NMA have been considered: the nπ* and ππ* transitions. Using this as a basis we constructed the exciton Hamiltonian. For the proteins, MD simulations in water were performed to create a large number of geometric snapshots. A number of these snapshots were selected as representative structures. QM calculations were carried out to compute the ground state electronic density of the protein. To combine the QM and MM simulation results, we have developed an efficient algorithm called exciton Hamiltonian with electrostatic fluctuations (EHEF). EHEF performs charge population analysis for the MD samples. Charges contributed by localized atomic orbitals are treated as atomic partial charges, and charges arising from delocalized atomic orbitals are treated with a set of grid point charges fitted from the electrostatic potential. A set of standard atom-atom charges are generated in the “internal coordinate frame”. For a given conformation, charge distributions were deduced from the standard atom-atom charges by updating atom-atom vectors of the corresponding MD geometric structure. Using the full charge distributions we calculate the interactions between the chromophore and environment. We, thus, avoid expensive repeated QM calculations and obtain the fluctuating Hamiltonian at the QM level for all MD snapshots. The present algorithm is based on physical considerations which requires no empirical parameters, and can be transferred directly to other systems. Using this algorithm, we have studied the UV LA and CD spectra for several typical proteins in aqueous solution: hemoglobin, leptin, tropomyosin, lentil lectin, monellin and FtsZ. The very distinctive features of UV spectra, which depend on the secondary structure, are reproduced in good agreement with experiment.

Theoretical methods

Exciton model for the nπ* and ππ* transitions

Protein backbone electronic transitions can be described by the Frenkel exciton model^18,19 in the Heitler-London approximation.

$$\hat{H}={\displaystyle \sum _{\mathit{\text{ma}}}{\epsilon }_{\mathit{\text{ma}}}{\hat{B}}_{\mathit{\text{ma}}}^{†}{\hat{B}}_{\mathit{\text{ma}}}+{\displaystyle \sum _{\mathit{\text{ma}},\mathit{\text{nb}}}^{m\ne n}{J}_{\mathit{\text{ma}},\mathit{\text{nb}}}{\hat{B}}_{\mathit{\text{ma}}}^{†}{\hat{B}}_{\mathit{\text{nb}}}}}$$ (1)

where ma is the a electronic transition on the peptide unit m (in our case, a = 1 for nπ* and a = 2 for ππ*). ${\hat{B}}_{\mathit{\text{ma}}}^{†}$ is the creation operator which promotes the m peptide unit into the excited state a, and B̂_ma is the corresponding annihilation operator denoting the ground state |0 >. The commutation relations of these operators are $[{\hat{B}}_{\mathit{\text{ma}}},{\hat{B}}_{\mathit{\text{nb}}}^{†}]={\delta }_{\mathit{\text{mn}}}(1-2{\hat{B}}_{\mathit{\text{mb}}}^{†}{\hat{B}}_{\mathit{\text{ma}}})$.²⁰ The ground state energy is < 0|Ĥ|0 > = 0. In the single-exciton manifold, the m-th singly-excited state energy is $<0|{\hat{B}}_{\mathit{\text{ma}}}{\hat{H}}^{(e)}{\hat{B}}_{\mathit{\text{ma}}}^{†}|0>={\epsilon }_{\mathit{\text{ma}}}$, and the resonant coupling between singly-excited states m and n is given by $<0|{\hat{B}}_{\mathit{\text{ma}}}{\hat{H}}^{(e)}{\hat{B}}_{\mathit{\text{nb}}}^{†}|0>=J_{\mathit{\text{ma}},\mathit{\text{nb}}}$.

By diagonalizing the Frenkel Hamiltonian matrix, we obtain the excitation energies and transition moments, which are then used to simulate the UV spectra. This model enables us to compute single excitations using QM calculations for each isolated chromophore of the entire protein. The resonant coupling between transition densities of two chromophores m and n is

$$J_{\mathit{\text{ma}},\mathit{\text{nb}}}=\frac{1}{4\pi \epsilon {\epsilon }_0}{\displaystyle \int {\displaystyle \int \mathrm{d}{\mathbf{r}}_{\mathbf{m}}\mathrm{d}{\mathbf{r}}_{\mathbf{n}}\frac{{\rho }_{\mathit{\text{ma}}}^{\mathit{\text{eg}}}({\mathbf{r}}_{\mathbf{m}}){\rho }_{\mathit{\text{nb}}}^{\mathit{\text{ge}}}({\mathbf{r}}_{\mathbf{n}})}{|{\mathbf{r}}_{\mathbf{m}}-{\mathbf{r}}_{\mathbf{n}}|}}}$$ (2)

where r is the spatial coordinate. ${\rho }_{\mathit{\text{ma}}}^{\mathit{\text{eg}}}({\mathbf{r}}_{\mathbf{m}})\text{and}{\rho }_{\mathit{\text{ma}}}^{\mathit{\text{ge}}}({\mathbf{r}}_{\mathbf{m}})$ are the transition charge densities. All the excitation energies and charge densities can be obtained from the QM calculations of the isolated chromophore. As there are two dominant transitions in the far-UV region for proteins, we here consider two transitions nπ* and ππ* in each amide chromophore site (i.e. peptide bond).

To compute intermolecular couplings via Eq. (2), we need to calculate the permanent and transition charge densities of each molecule. We selected N-methylacetamide (NMA) as a model for an isolated peptide unit. The electronic excited states of NMA were taken from calculations,¹⁵ using the complete-active space self-consistent-field method within a self-consistent reaction field (CASSCF/SCRF) and multi-configurational second-order perturbation theory (CASPT2), as implemented in MOLCAS.²¹ Monopoles for a given state were determined by fitting their electrostatic potential to reproduce the ab initio electrostatic potential for that state.¹⁵ An ab initio based parameter set was extracted¹⁵ to represent the transition energy, the permanent and transition charge densities of the isolated peptide unit.

Electrostatic Fluctuations

As recognized in earlier work of Kurapkat et al., interactions of a chromophore with local electrostatic fields can lead to considerable energy shifts of its transitions.²² The transition energy is affected by the fluctuating electrostatic potential coming from the rest of the protein and the surrounding solvent. These effects will be incorporated below.

To set the stage, we firstly survey some commonly used methods. In the dipole approximation, the state energy ε can be expressed as²³

$$\epsilon ={\epsilon }_0+\mu ·\mathbf{F}$$ (3)

where ε₀ represents the state energy of the isolated molecule, μ is the electric dipole moment, and F is the electric field induced by the surroundings. The transition energy ${\epsilon }_{\mathit{\text{ma}}}^F$, including electrostatic environmental fluctuations, is then computed as

$$\begin{array}{cc}{\epsilon }_{\mathit{\text{ma}}}^F\hfill & =({\epsilon }_0^m-{\epsilon }_0^g)-({\mu }_{m,a}^{\mathit{\text{ee}}}-{\mu }_m^{\mathit{\text{gg}}})·\mathbf{F}\hfill \\ \hfill & ={\epsilon }_{\mathit{\text{ma}}}-({\mu }_{m,a}^{\mathit{\text{ee}}}-{\mu }_m^{\mathit{\text{gg}}})·\mathbf{F}\hfill \end{array}$$ (4)

where |g > denotes the ground state, and ${\mu }_{\mathit{\text{ma}}}^{\mathit{\text{ee}}}\text{and}{\mu }_m^{\mathit{\text{gg}}}$ are the permanent dipoles of the excited states and ground state, respectively. Nevertheless, the above formula is not very accurate for extended systems. The main problem is that the dipole moment and electric field are not evenly distributed in space, so that a single $({\mu }_{m,a}^{\mathit{\text{ee}}}-{\mu }_m^{\mathit{\text{gg}}})·\mathbf{F}$ factor cannot account for the environment fluctuation corrections to transition energies. To account for the spatial distribution of ${\mu }_{\mathit{\text{ma}}}^{\mathit{\text{ee}}},{\mu }_m^{\mathit{\text{gg}}}$, and F one can use a set of reference points in the peptide, and build a map to represent the excitation energy as a function of the electric field at those reference points. To represent the spatial distributions better, the gradient or higher order derivatives of the electric field may be used as variables. A simple map can be expressed as

$${\epsilon }_m^F={\epsilon }_m+{\displaystyle \sum _i{\alpha }_i{\mathbf{F}}_{\mathbf{i}}+{\displaystyle \sum _i{\beta }_i\frac{\mathrm{d}{\mathbf{F}}_{\mathbf{i}}}{\mathrm{d}r}+\dots }}$$ (5)

F_i is the electric field at the i-th reference point, α_i and β_i are empirical parameters obtained by fitting to experimental data. The local geometric changes of the excited chromophore are usually the main factors that affect the local Hamiltonian. Since obtaining the transition dipole moment requires expensive QM calculations, one can consider another type of map which parameterizes the excitation energy with geometric variables at reference points.

$${\epsilon }_m^F={\epsilon }_m+{\displaystyle \sum _i{\alpha }_i^{\prime }{\mathbf{K}}_{\mathbf{i}}+{\displaystyle \sum _i{\beta }_i^{\prime }{\mathbf{K}}_{\mathbf{i}}^{\mathbf{2}}+\dots }}$$ (6)

where K_i stands for different geometric variables, such as atomic bond lengths, bond angles, dihedral angles, and so on. ${\alpha }_i^{\prime }\text{and}{\beta }_i^{\prime }$ are fitted parameters.

Such map methods avoid the expensive QM calculations for the excited chromophores under the influence of the environment. A major limitation is that the parameters can only be obtained by fitting theoretical results with experiments or high-level QM calculations. The simulations depend on the number and choice of reference points, and the functions used to describe them. It is not possible to develop a universal map that is transferable between different systems.

Here we develop an alternative approach to calculate the full-space corrections of excitation energies due to electrostatic fluctuations. Instead of using the dipole moment, we compute the product of the transition charge density and electric field. By integrating that product over space, we calculate the interactions between the excited states and environment directly. The excitation energy corrected by the environment electrostatic potential and intermolecular interactions is then expressed as

$${\epsilon }_{\mathit{\text{ma}}}^F={\epsilon }_{\mathit{\text{ma}}}-{\displaystyle \int \mathrm{d}[{\rho }_{\mathit{\text{ma}}}^{\mathit{\text{ee}}}(\mathbf{r})-{\rho }_m^{\mathit{\text{gg}}}(\mathbf{r})]·\mathbf{r}·\mathbf{F}(\mathbf{r})}$$ (7)

where ε_ma is the excitation energy of the a-th transition of the chromophore m. ${\rho }_{\mathit{\text{ma}}}^{\mathit{\text{ee}}}({\mathbf{r}}_{\mathbf{m}})\text{and}{\rho }_m^{\mathit{\text{gg}}}({\mathbf{r}}_{\mathbf{m}})$ represent the molecular charge density of the excited and ground state of the chromophore, respectively. The electric field F(r) is computed as the gradient of the Coulomb potential induced by the ground state charge density of the surrounding environment on the excited chromophore. The fluctuating excitation energy is, thus, given as

$${\epsilon }_{\mathit{\text{ma}}}^F={\epsilon }_{\mathit{\text{ma}}}+{\displaystyle \sum _l\frac{1}{4\pi \epsilon {\epsilon }_0}{\displaystyle \int {\displaystyle \int \mathrm{d}{\mathbf{r}}_{\mathbf{m}}\mathrm{d}{\mathbf{r}}_{\mathbf{l}}\frac{[{\rho }_{\mathit{\text{ma}}}^{\mathit{\text{ee}}}({\mathbf{r}}_{\mathbf{m}})-{\rho }_m^{\mathit{\text{gg}}}({\mathbf{r}}_{\mathbf{m}})]{\rho }_l^{\mathit{\text{gg}}}({\mathbf{r}}_{\mathbf{l}})}{|{\mathbf{r}}_{\mathbf{m}}-{\mathbf{r}}_{\mathbf{l}}|}}}}$$ (8)

where l runs over the molecular sites surrounding the excited excited chromophore m, and ${\rho }_l^{\mathit{\text{gg}}}({\mathbf{r}}_{\mathbf{l}})$ represents the charge density of the ground state of molecular site l.

Simulation of the full ground state charge distribution

The electronic structures of amino acid side chains in proteins and the surrounding water molecules were computed in the gas phase with density functional theory (DFT) implemented in the GAUSSIAN03 package,²⁴ at the B3LYP/6-311++G** level. The fragments considered were, for example, methane (representing the side chain of alanine), indole (representing the side chain of tryptophan), etc., and an individual water molecule. The full charge distribution is calculated from the DFT densities. In QM approaches, one can calculate charge densities by coarse-graining the electronic wavefunction in space. Krueger et al.²⁵ have employed a grid technique to compute the intermolecular couplings. In their transition density cube (TDC) method, 3-D space is divided into many small volume elements. Couplings were calculated directly from the Coulomb interactions between charges of the cubes in each molecule. This method gives high accuracy, because it is based on full QM calculations. However, it is very expensive, since it requires a large number of cubes to maintain the precision (normally ≈ 500,000 cubes for a system with ≈ 50 atoms). Madjet et al.²⁶ have developed a more efficient way for taking the charge distribution into account. In their TrEsp (transition charge from electrostatic potential) code, electrostatic potentials on sample points are computed at the QM level. Partial charges are then assigned to atomic positions by fitting to potentials. TrEsp has been successful in the study of many biological systems. However, charges distributed only at the atomic positions cannot represent the electronic cloud over the space and the corresponding electronic properties when the molecular orbitals are delocalized.

Our algorithm combines the advantages of the above methods, to obtain affordable and accurate full charge distributions. Based on DFT calculations, we decomposed the Kohn-Sham orbitals into atomic orbitals, and divided them into two groups: localized and delocalized. For the localized atomic orbitals, we adopted the TrEsp procedure, i. e., we compute the electrostatic potential and fit it to atomic partial charges. We further computed charge distributions induced by the delocalized atomic orbitals, which vary in space much more slowly than the localized ones. We then introduce a set of regular grids and assign fictitious charges on the grid points. Each grid point is divided into a large number of small cubes, in a similar way to (and of a similar size to) cubes employed in the TDC method. Sample points around each grid point are taken and the electrostatic potential induced by the charges of the small cubes inside that grid is calculated. The fictitious charge for each grid point is obtained by fitting the sample electrostatic potential. In the end the atomic partial and fictitious grid charges are used to compute the Coulomb interactions and transition dipoles. Most localized charges are included as atomic partial charges, and the spatial distribution of those delocalized charges varies slowly with the coordinates, so that the space resolution requirement is very loose. Distribution of delocalized charges can be described by a limited number of grid points (normally ≈ 10,000 cubes for a system with ≈ 50 atoms), which is much smaller than the number of cubes used in the TDC methods. Since the size of the grid points is much smaller than the interatomic distance, the resultant electrostatic interactions are as accurate as the TDC. This algorithm offers a good balance between accuracy and cost.

Atom-atom charges for individual MD snapshots

For molecules with a rigid geometry, one can define the charge distributions in a molecular frame and reuse them for any MD snapshots. However, proteins are not rigid and the interatomic distances and angles do vary during the MD simulations. Nevertheless, the conformation dynamics only lead to slight changes in atomic bond lengths and angles. For a pair of atoms, one can expect that the distribution of their electronic charges changes only slightly with their atomic positions. We, therefore, define an “internal coordinate frame” for each pair of atoms, and describe their charge distributions as atom-atom charges with respect to the atom-atom vector (vector between the atoms).

Standard QM methods compute the electronic charge density by integrating atomic orbitals over space:

$${\rho }_m^{12}(\mathbf{r})=V_{\delta }{\displaystyle {\int }_r^{r+\delta }{\displaystyle {\int }_s{\displaystyle \sum _{\eta }^{\mathit{\text{occ}}}{\displaystyle \sum _{i,j}{c}_i^{1,\eta }{c}_j^{2,\eta }{\psi }_i{\psi }_j\mathrm{d}\mathbf{s}\mathrm{d}\mathbf{r}\prime }}}}$$ (9)

where ${\rho }_m^{12}(\mathbf{r})$ represents the transition charge density between state |1 > and |2 > of molecule m. In this study, |1 > and |2 > are both limited to the ground state of amino acid side chains or water molecules, in order to calculate their permanent charge densities. In principle, Eq. (9) is a general expression for both permanent and transition charge densities. V_δ is the volume element. $c_i^{1,\eta }\text{and}{c}_j^{2,\eta }$ are the orbital coefficients of state |1 > and |2 >, respectively, in which η runs over all the occupied molecular orbitals. ψ_i(r − r_A) is one of the basis functions of atom A_i. The charge density can, therefore, be decomposed in the atomic site representation:

$$\begin{array}{cc}{\rho }_m^{12}(\mathbf{r})\hfill & ={\displaystyle \sum _{i,j}{V}_{\delta }{\displaystyle {\int }_r^{r+\delta }{\displaystyle {\int }_s{\displaystyle \sum _{\eta }^{\mathit{\text{occ}}}{c}_i^{1,\eta }{c}_j^{2,\eta }{\psi }_i(\mathbf{r}-{\mathbf{r}}_{A_i}){\psi }_j(\mathbf{r}-{\mathbf{r}}_{A_j})\mathrm{d}\mathbf{s}\mathrm{d}\mathbf{r}\prime }}}}\hfill \\ \hfill & ={\displaystyle \sum _{i,j}{\rho }_{A_i,A_j}^{12}(\mathbf{r}-{\mathbf{R}}_{ij})}\hfill \end{array}$$ (10)

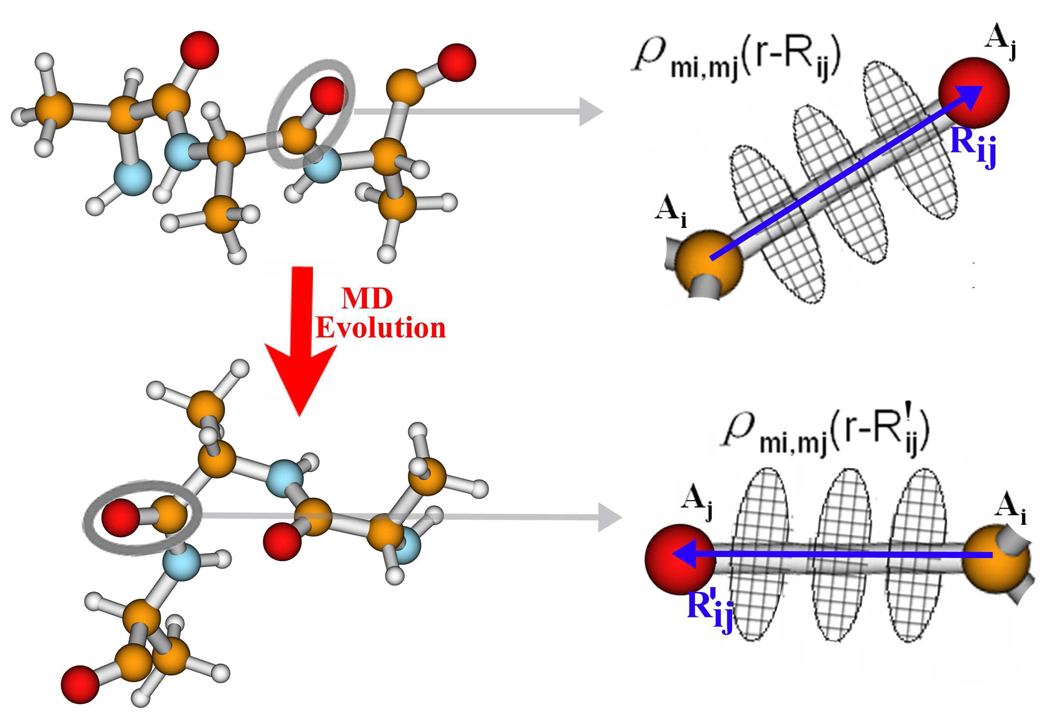
in which R_ij = r_Ai − r_Aj is the atom-atom vector, and A_i, A_j is a pair of atoms. The sum runs over all the atomic positions in the molecule. ${\rho }_{A_i,A_j}^{12}(\mathbf{r}-{\mathbf{R}}_{\mathit{\text{ij}}})$ is the density arising from the atom-atom charges. A fragment of a protein is shown in Figure 1, to illustrate how we compute atom-atom charges. For every A_i, A_j pair, we define the atom-atom vector R_ij. We also define a set of (usually ten) planar disks perpendicular to R_ij, whose centers lie on R_ij, located in the range ±1.5|R_ij|. Each disk is divided into (typically 20 to 50) small grid points. The atom-atom charge for each pair of atoms A_i and A_j is computed as ${\displaystyle \int {\rho }_{A_i,A_j}^{12}(\mathbf{r}-{\mathbf{R}}_{\mathit{\text{ij}}})\mathrm{d}\mathbf{r}}$. This was found to be stable during the MD simulations. The spatial distributions of atom-atom charges are described by their relative position with respect to the atom-atom vector R_ij.

Figure 1.

A_i and A_j have been selected to show the description of atom-atom charges based on the atom-atom vectors R_ij and ${\mathbf{R}}_{\mathit{\text{ij}}}^{\prime }$, whose atom-atom charges are described as ${\rho }_{A_i,A_j}^{12}(\mathbf{r}-{\mathbf{R}}_{\mathit{\text{ij}}})\text{and}{\rho }_{A_i,A_j}^{12}(\mathbf{r}-{\mathbf{R}}_{\mathit{\text{ij}}}^{\prime })$ respectively.

We selected ideal structures or several sampled MD snapshots as representative structures. From the QM calculations, we computed the distributions of the atom-atom charges for the representative geometry. The standard atom-atom charges are generated for a representative atom-atom vector R_ij. When the geometry is varied and the atom-atom vector changes to R′_ij, a new set of atom-atom charges ${\rho }_{A_i,A_j}^{12}(\mathbf{r}-\mathbf{R}{\prime }_{\mathit{\text{ij}}})$ are mapped out from the standard ones by reproducing the position relative to R′_ij. As long as the chemical structure does not vary strongly, the newly mapped atom-atom charges can accurately reflect the electronic properties of each MD snapshot, at the QM level. For each MD snapshot, we calculated the full atom-atom charge distributions from the standard atom-atom charges. With the full atom-atom charge distribution, we calculated the electrostatic potential over all space, thus generating the local Hamiltonian for each MD snapshot. QM accuracy is retained, with very few QM calculations.

Computational Details

MD simulations of several proteins were performed in water with the CHARMM22 force field²⁷ and the TIP3P water model²⁸ in the software package NAMD.²⁹ We considered a dilute solution. Each residue feels the electrostatic potential from the surrounding water and other residues of the same protein. Simulations were conducted in the NPT ensemble and and we employed cubic periodic boundary conditions. The particle Mesh Ewald Sum method was used to treat the long-range electrostatics. A nonbonded cutoff radius of 12 Å was used. All MD simulations started from a 5000 step minimization and 600 ps heating from 0 K to room temperature 310 K. The MD simulation time step was 1 fs. After 2 ns equilibration, we simulated 16 ns dynamics at 1 atmosphere pressure and 310 K. Structures were recorded every 400 fs. An ensemble of MD snapshots was used to compute the local excitation Hamiltonian and the UV spectra. The effect of the electrostatic potential generated by water, the peptide groups, and the amino acid side chains was investigated. The protein structures are stable during the MD simulations, with a root mean square deviation (rmsd) of backbone atoms from the initial structure of 0.7~1.5 Å and 0.7~2.4 Å for α-helix and β-sheet proteins, respectively.

QM calculations were performed using GAUSSIAN03²⁴ and MOLCAS7.²¹ Our EHEF algorithm was used to calculate the full atom-atom charge distribution from the QM calculations. The use of the exciton matrix method implemented in the DichroCalc program has been very successful in reproducing protein UV spectra.^13,14 Parameters for the transition energies of the isolated peptide units, the resonant couplings, electric and magnetic transition dipole moments are extracted from the DichroCalc package. By combining our SPECTRON code²⁰ with DichroCalc, we constructed the effective electronic excitation Hamiltonian and calculated the UV spectra. The simulated spectra reported here are based on 2000 MD snapshots, and they are compared to spectra computed with DichroCalc for a single conformation.¹³

UV Spectra of Proteins

Transition Energy Fluctuations

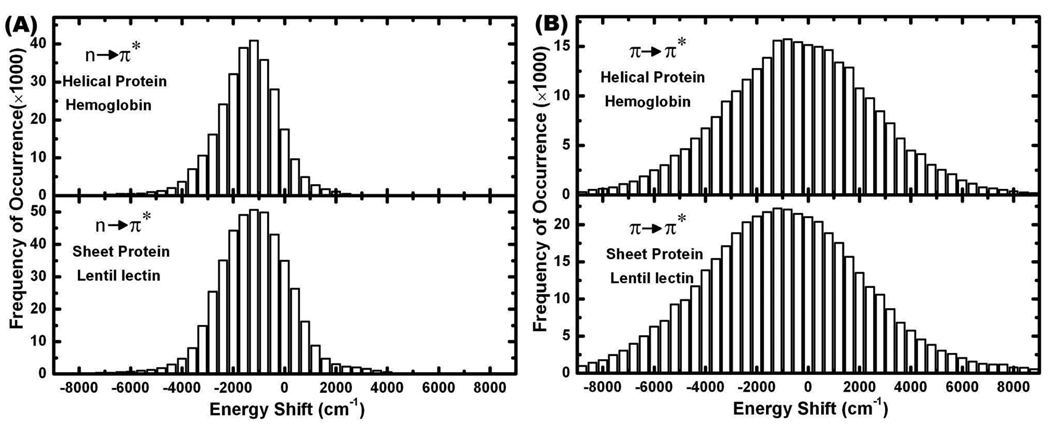
We first examine how the fluctuations of the molecular environment affect the transition energy of a individual peptide group (${\epsilon }_{\mathit{\text{ma}}}^F$ in Eq. (8)). For the helical protein hemoglobin (RSCB code 1hda.pdb) and sheet protein lentil lectin (RSCB code 1les.pdb), the distributions of excitation energy ${\epsilon }_m^F$ of many peptide groups at 310 K relative to that of an isolated NMA have been depicted in Figure 2 (A) and (B). There are no clear differences between the transition energy fluctuations of helical and sheet proteins. Both the nπ* and ππ* transitions show distinct asymmetric distributions. The nπ* and ππ* transitions have red-shifts in their excitation energies of ~ 1200 cm⁻¹ (0.15 eV) and ~ 1000 cm⁻¹ (0.12 eV), respectively, which are consistent with an earlier combined QM and MM study on the NMA molecule.³⁰ Our method is based on the full charge distributions, which are more accurate than the atomic charges obtained from Mulliken population analysis considered previously.³⁰ The distribution of nπ* excitation energy shifts is similar to that computed from NMA in water,³⁰ but that of the ππ* transition is much broader in our simulations. Different peptide groups are affected differently by the electrostatic potentials, which can vary from protein to protein. This is one reason why the bands in CD spectra of proteins can vary in their precise location.^{13,14,31–33} It corresponds to the shifts of the ππ* excitation energy of −8000 to 6000 cm⁻¹ with respect to the excitation energy of the NMA molecule at 52631 cm⁻¹.

Figure 2.

(A) and (B): Distribution of transition energy shifts due to the electrostatic environment from 310K simulations. Left column: nπ* (~45454 cm⁻¹) transitions. Right column: ππ* (~52631 cm⁻¹) transitions.

α-Helical Proteins: Hemoglobin

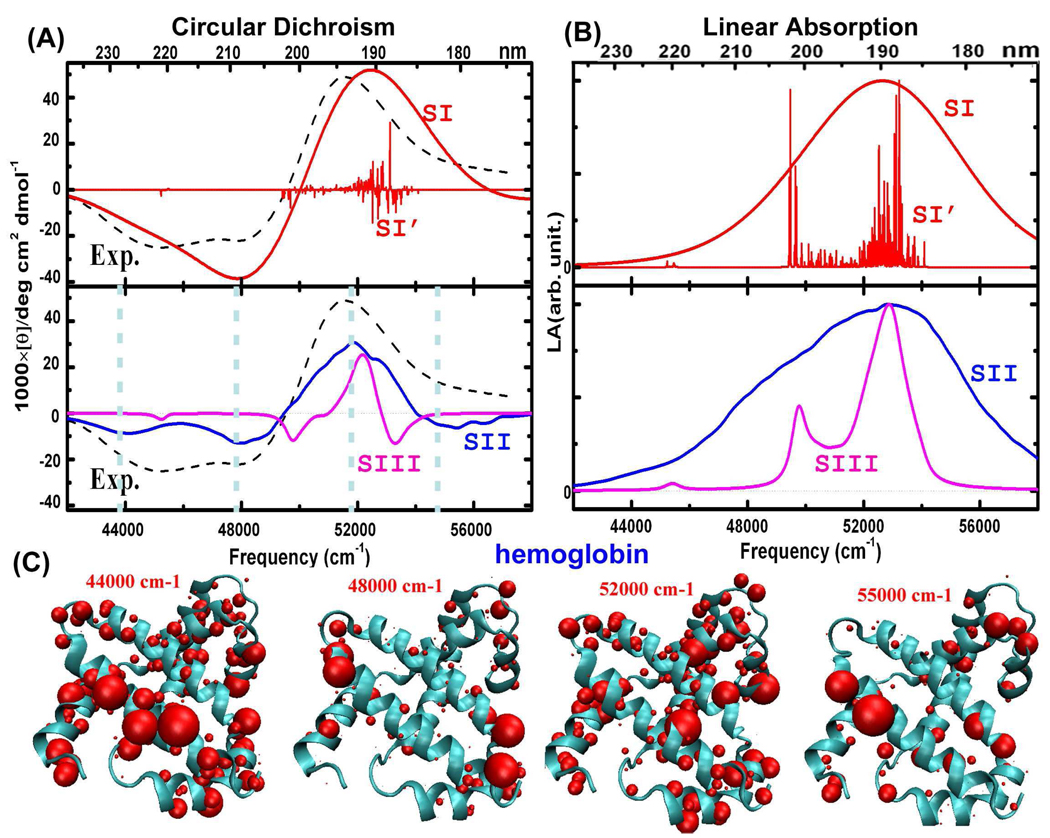
Hemoglobin is a typical α-helical protein. The structure is shown in Figure 3. Its X-ray crystal structure reported in the RSCB protein data bank (1hda.pdb) was taken as the starting geometry. MD simulations were carried out on the tetrameric hemoglobin, neglecting the heme groups. The UV spectra were calculated using a single chain geometry extracted from the MD trajectories. Firstly, CD and LA line spectra calculated based on the single X-ray structure are plotted (labeled SI’) in Figure 3 (A) and (B). Spectra convoluted with Gaussian lineshape with a full width at half maximum height (FWHM) value of 12.5 nm^13,14 for the single conformation are plotted as well (labeled SI). The SI CD spectrum reproduces the experimental peaks³¹ at 48000 and 52000 cm⁻¹, but under-estimates the intensity of the peak at around 44000 cm⁻¹. The relationship between the CD line spectra and corresponding convoluted spectra is not very straightforward. For instance, a positive (negative) peak in the line spectrum can be shifted or even canceled in the convoluted spectrum by the negative (positive) contributions of neighboring transitions. The negative CD peak at 48000 cm⁻¹ in the SI in Figure 3 (A) mainly arises from the negative CD signals at around 45000 and 50000 cm⁻¹. Moreover, in the LA spectra in Figure 3 (B), the transitions at 50000 cm⁻¹ evident in the line spectrum SI’ are buried in SI by the convoluted signals from 52000 to 54000 cm⁻¹, which are much stronger and denser in the frequency region.

Figure 3.

α-helical protein hemoglobin (protein data bank PDB code: 1hda) together with X-ray crystal structures. SI’ represent the simulated line spectra based on a single conformation (scaled by a factor 1/1000), and SI are SI’ convoluted with a Gaussian envelope. SII are simulated spectra based on 2000 MD snapshots that consider the electrostatic potential from all the surroundings, and SIII only takes account of peptide groups (scaled by a factor 1/15). The experimental CD spectrum³¹ is shown as dashed black lines. (C): Transition populations corresponding to the four CD peaks. The volume of the balls represents the amplitude of the electronic transition.

The full CD spectrum obtained by using our algorithm for 2000 MD snapshots is shown as the curve SII in Figure 3 (A). SII provides a better resolution than SI of the experimentally observed double minimum. The experimental lineshape is well described by this combined QM and MM simulation. The three main CD peaks at ~44000, 48000, and 52000 cm⁻¹ are reproduced by SII. The origin of additional CD peaks in SII compared to SI is that peptide groups are affected by different electrostatic potentials. The SII LA spectrum shown in Figure 3 (B) reproduces the bandshapes of the convoluted LA spectrum of the single conformation (SI LA).

To examine how the environment influences the electronic transitions, we have calculated spectra taking into account only the local fluctuations of peptide groups, and neglecting the electrostatic potential induced by the amino acid side chains and surrounding water molecules. The simulated spectra are labeled SIII in Figure 3 (A) and (B). The SIII bandwidths are much narrower than SII. Protein backbone fluctuations only account for about 6 nm FWHM, while the amino acid side chain fluctuations contribute ~ 10 – 12 nm. No empirical parameters were needed in generating SII to describe the inhomogeneous broadening. For the ππ* transitions at about 52000 cm⁻¹, the FWHM obtained from SII CD spectra is 10.4 nm, agreeing well with the FWHW of 12.0 nm found in the experimental spectra. In both experiment and simulation, the band of nπ* transitions at 44000 cm⁻¹ overlaps with the band at 48000 cm⁻¹ (induced by exciton splitting of the ππ* transitions), so that we have to extract their FWHM by fitting with Gaussian lineshapes separately. The FWHM of 44000 and 48000 cm⁻¹ bands in the simulated spectra are found to be 14.5 and 10.2 nm, respectively, which are close to the values of 19.4 and 9.5 nm obtained from corresponding experimental bands. Additive simulations (not shown) found that the electrostatic potential induced by water only weakly affects the UV spectra. Water has only an indirect influence on the electronic transitions, by affecting the protein geometries.

To analyze the CD spectra of hemoglobin, we display the transition populations, which are defined as the squares of exciton wave function coefficients. Transition populations of the four CD peaks at 44000, 48000, 52000, and 55000 cm⁻¹ are plotted in Figure 3 (C). CD peaks at 48000 and 52000 cm⁻¹ are known to come from exciton splitting of the ππ* transitions.³⁴ The 48000 cm⁻¹ transition has polarization parallel to the helical axis, and we see that they are very strong in the helix termini. The 52000 cm⁻¹ transition is polarized perpendicular to the helical axis, and is almost evenly distributed across the protein. The 44000 cm⁻¹ peak comes from the helical regions, while the 55000 cm⁻¹ peaks come from the turns. We can now explain the missing CD features in the SI and SIII spectra. This is mainly due to the omission of the electrostatic potential induced by surrounding peptide groups, amino acid side chains and water molecules. Transition densities of different peptide bonds are affected differently by their surroundings. A single broadening factor for all transitions misses fine structural details of the spectrum. The SII spectra carefully include the electrostatic potentials induced by surrounding molecular groups and capture these finer details.

β-Sheet Protein: Lentil Lectin

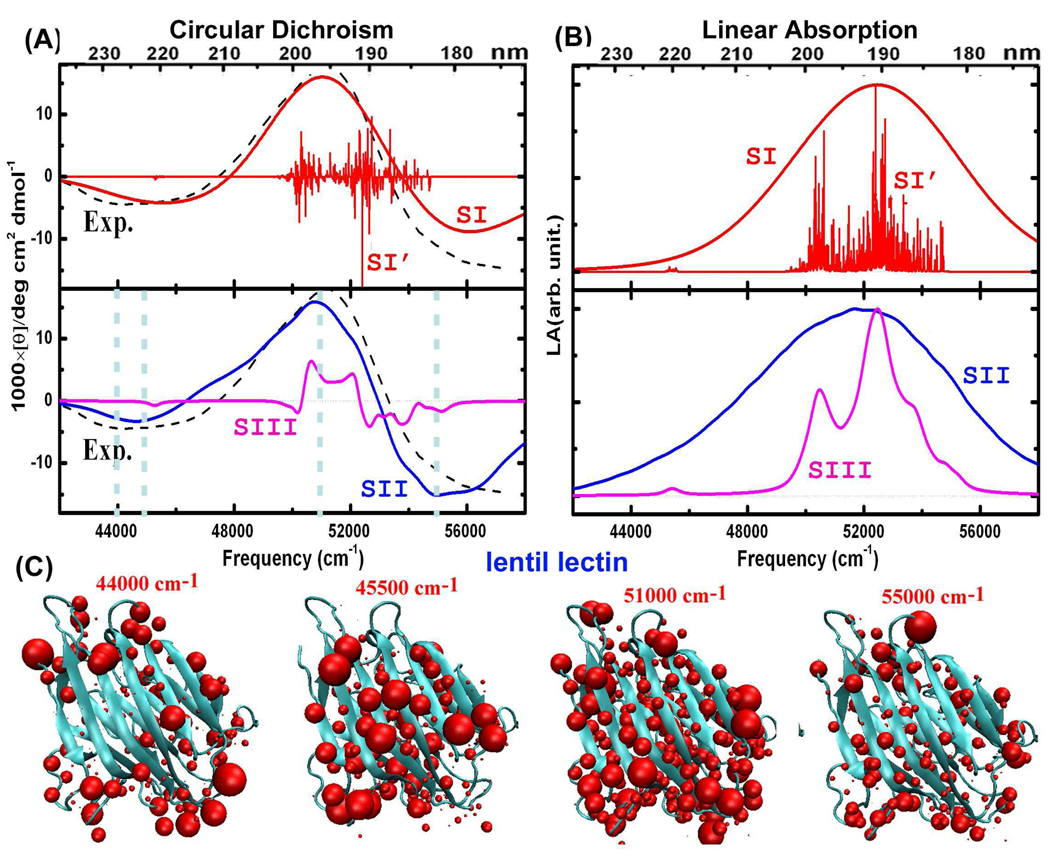
Figure 4 shows the simulated CD and LA spectra, and the corresponding X-ray crystal structure of lentil lectin (PDB code 1les), which is a typical β-sheet protein. The experimental CD peaks^31,32 at 45500, 51000, and 55000 cm⁻¹ are well reproduced by the simulated SII spectrum of the ensemble of 2000 MD snapshots. Compared to SI spectra based on single conformation, SII spectra provide more detailed fine structure. The SIII CD spectra are much narrower than SII and experiment, demonstrating the importance of the electrostatic potential due to amino acid side chains. As the ππ* exciton splitting is much weaker in sheet structures, we do not observe a CD peak at 48000 cm⁻¹. The transition populations at frequencies of 44000, 45500, 51000, and 55000 cm⁻¹ are displayed in Figure 4 (C). The 44000 cm⁻¹ transition occurs at the turn regions. CD peaks at 45500 and 55000 cm⁻¹ originate from the sheet regions, while the 52000 cm⁻¹ peak has contributions from transitions from all peptide groups.

Figure 4.

As for Figure 3, but for sheet-containing protein lentil lectin (PDB code 1les).

Comparison of Helical and Sheet Proteins

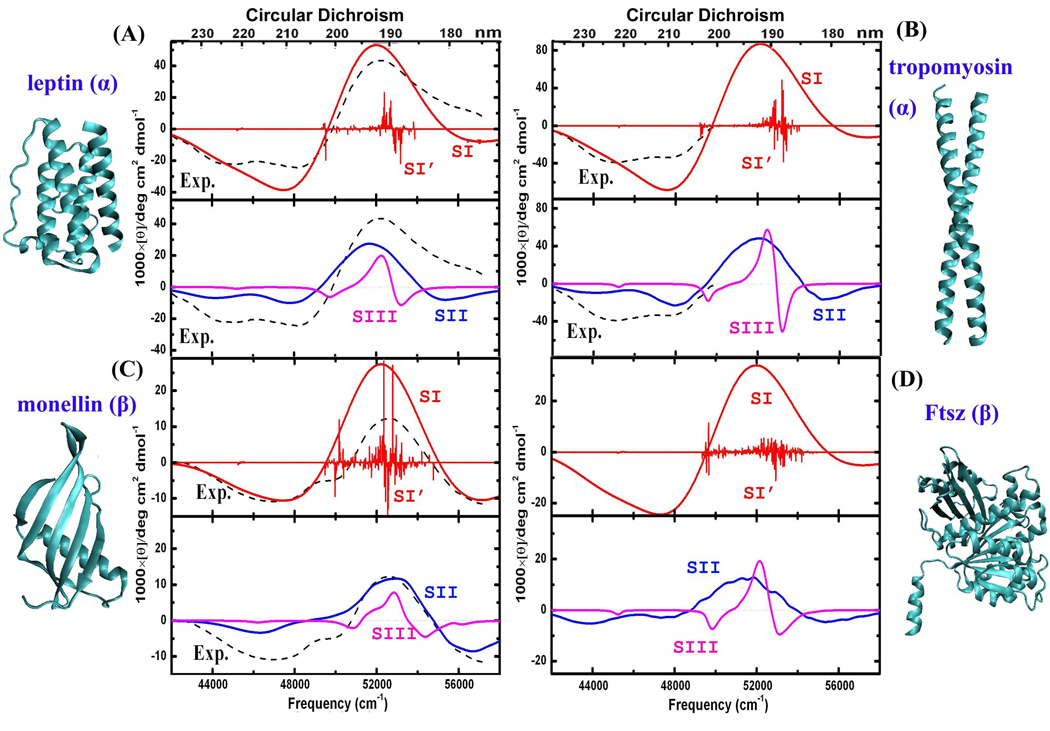
To explore the relationship between the UV spectra and secondary structures, we display in Figure 5 the simulated CD spectra and corresponding X-ray crystal structures of four more proteins: the helical proteins leptin (PDB code 1ax8) and tropomyosin (PDB code 2d3e), sheet protein monellin (PDB code 1mol), and αβ-protein FtsZ (PDB code 1fsz). In all cases the simulated SII spectra reproduce the experimental fine structure.^31,33 Compared to SI and SIII, the SII spectra computed from 2000 MD snapshots provide better agreement with experiments.

Figure 5.

CD spectra of α-helix protein: leptin (PDB code 1ax8) and tropomyosin (PDB code 2d3e), sheet-containing protein: monellin (PDB code 1mol), αβ-protein: FtsZ (PDB code 1fsz), together with X-ray crystal structures. Same labels as in Figure 3.

We now summarize the CD spectra of the three helical protein (hemoglobin, leptin and tropomyosin) and the two sheet proteins (lentil lectin and monellin). We observe two negative CD peaks at 44000 and 48000 cm⁻¹ in helical proteins, compared to a single strong negative peak at around ~45000–46000 cm⁻¹ in sheet proteins. The negative CD peak at around ~55000–56000 cm⁻¹ is more pronounced in sheet proteins. The αβ-protein FtsZ contains both helix and sheet motifs, and shows the helix feature of two negative peaks at 44000 and 48000 cm⁻¹, and the sheet feature of intense negative peaks at ~45000–46000 and ~55000–56000 cm⁻¹.

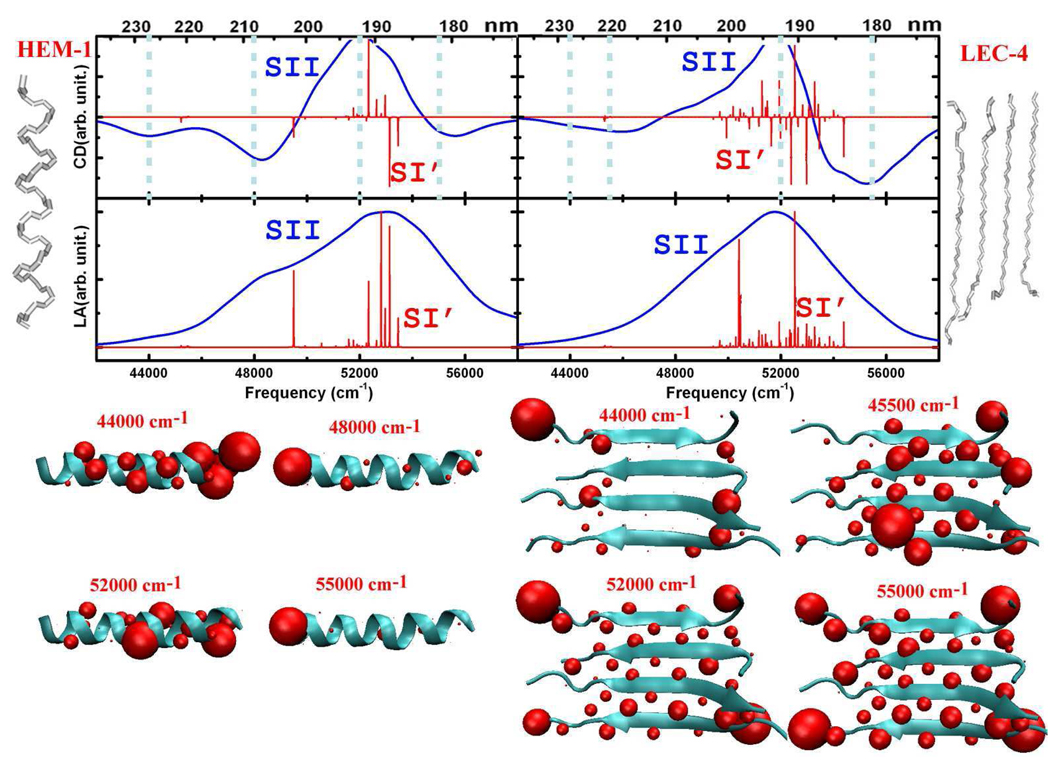
We have used some model systems to examine the relationships between CD peaks and secondary structures. A helical fragment was extracted from hemoglobin (Pro124-His143 of chain D in 1hda.pdb), and a sheet fragment containing four β strands was taken from lectin (4 strands: Thr1-Phe11 of chain C, Val37-Leu46 of chain D, Val60-Val70 of chain C, Glu158-Ala169 of chain C in 1les.pdb). The fragments are denoted as HEM-1 and LEC-4, respectively. The simulated CD and LA spectra are depicted in Figure 6. We see two negative peaks at 44000 and 48000 cm⁻¹ in the CD spectrum of HEM-1, and two strong negative peaks at around ~45000–46000 and ~55000–56000 cm⁻¹ in the CD spectrum of LEC-4. The transition populations corresponding to the CD peaks of HEM-1 and LEC-4 are displayed at the bottom of Figure 6. The 48000 cm⁻¹ peak results from the exciton splitting in helices, and is absent in the CD of sheet proteins. Transition populations at 52000 cm⁻¹ are distributed all over both fragments, consistent with the observation of intense positive CD signals in both helical and sheet proteins. The transition populations of model systems are consistent with the full proteins, as shown in Figure 3 (C) and Figure 4 (C). These CD peaks may thus be used to probe the secondary structure.

Figure 6.

CD and LA spectra of α-helix (HEM-1: fragment of 1hda.pdb) and β-sheet (LEC-4: fragment of 1les.pdb) model structure. Same labels as in Figure 3.

Conclusions

We have developed a generalized full-space approach combining QM and MM calculations to study the fluctuating effective electronic Hamiltonian in proteins. A large number of structure snapshots were created using MD simulations, some of which were chosen as representative structures of the structural ensemble and on these we performed a full charge distribution analysis. The EHEF code was used to combine the MM and QM results, and to provide a fluctuating trajectory of the excitation parameters. The transition energy fluctuations of electronic transitions can be evaluated for each selected trajectory point. This allows us to avoid expensive repeated QM calculations and obtain the fluctuating Hamiltonian at the QM level for all the snapshots. Simulations of UV spectra of proteins in water with fluctuation effects show good agreement with experiment. The bandshapes of CD and LA spectra have been reproduced by simulations without using empirical parameters. The fine structure of the UV spectra has been well described by considering the electrostatic environment.