Abstract
A model of the outer membrane of Gram-negative bacteria was created by the deposition of a monolayer of purified rough mutant lipopolysaccharides at an air/water interface. The density profiles of monovalent (K+) and divalent (Ca2+) cations normal to the lipopolysaccharides (LPS) monolayers were investigated using grazing-incidence X-ray fluorescence. In the absence of Ca2+, a K+ concentration peak was found in the negatively charged LPS headgroup region. With the addition of CaCl2, Ca2+ ions almost completely displaced K+ ions from the headgroup region. By integrating the experimentally reconstructed excess ion density profiles, we obtained an accurate measurement of the effective charge density of LPS monolayers. The experimental findings were compared to the results of Monte Carlo simulations based on a coarse-grained minimal model of LPS molecules and showed excellent agreement.
Keywords: monolayer, Monte Carlo simulation, electrostatics, biological interface
Biological surfaces expose a variety of charged macromolecules that interact with various sorts of ions under physiological conditions. However, despite the crucial role of charged macromolecules in modulating the interaction between cells and their surrounding environments, the quantitative understanding of electrostatics at such soft, complex interfaces still remains a general scientific challenge. For example, the outer membrane surface of Gram-negative bacteria is mainly composed of lipopolysaccharides (LPSs) (1), whose negatively charged saccharide head groups stabilize the structural integrity of bacteria and protect bacteria against their environment. Several in vivo studies (2, 3) demonstrated that bacteria increase their resistance against cationic antimicrobial peptides (e.g., protamine) in the presence of divalent cations (Ca2+, Mg2+). Therefore, for the development of peptide-based antibiotics (4), it is important to understand the molecular mode of action of antimicrobial peptides.
A number of theoretical models for the interactions of LPS molecules with divalent cations (5–7), suggested that the ions would bind to the charged 2-keto-3-deoxyoctonoic acid (KDO) groups (the “inner core”) thereby stabilizing the membrane. Recently, we measured grazing-incidence X-ray scattering from a monolayer of rough mutant LPS from Salmonella enterica sv. Minnesota at an air/water interface and demonstrated the Ca2+-induced increase in the electron density near the inner core (8). These observations were supported by the results of Monte Carlo (MC) simulations of a coarse-grained model (8). A further challenge would be to extend such a strategy to wild-type LPSs that possess polydisperse, specific O-polysaccharide chains (O-side chains). Pink et al. (9) carried out MC simulations of a minimal model of the more complex, wild-type LPSs from Pseudomonas aeruginosa (PAO1) and concluded that divalent cations would induce a collapse of the negatively charged O-sidechains toward the membrane surface. Because it is difficult in practice to deposit LPSs with nonuniform O-sidechains at the air/water interface, we deposited LPS monolayers on hydrophobized substrates, and performed high-energy specular X-ray reflectivity at the solid/liquid interface (10). By extending the conventional slab model representation to treat polydisperse O-sidechains, their collapse was detected from the change in the electron density profiles in the presence of Ca2+. The next challenge was to establish the depth profiles of monovalent and divalent cations that should reflect the observed O-sidechain collapse.
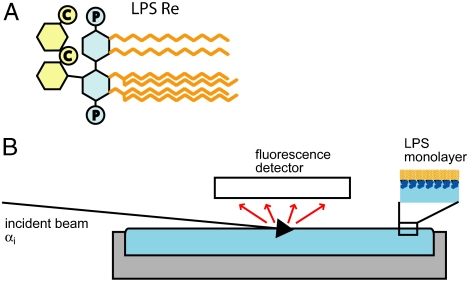
For this work, we deposited a monolayer of purified rough mutant lipopolysaccharides (LPS Re) from Salmonella enterica sv. Minnesota R595 at the air/water interface and measured grazing-incidence X-ray fluorescence (GIXF) (Fig. 1B), which permits determination of the distribution of chemical elements, identified from their emission spectra. Although this method was used to resolve the weak depletion of ions in the vicinity of the water surface (11), applications of GIXF have been limited to studies with little relevance to biological systems, such as the adsorption of proteins stabilized with lead acetates to the solid/liquid interface (12) and ion adsorption to synthetic surfactant monolayers at the air/water interface (13, 14). Our intent is to utilize GIXF to establish the distributions of monovalent and divalent cations in a realistic model of bacterial surfaces and compare the results with the predictions of our MC simulations.
Fig. 1.
Experimental system. (A) Structure of LPS Re from the strain R595 of Salmonella enterica sv. Minnesota. C and P denote carboxyl and phosphate groups, respectively. (B) Sketch of the setup used for GIXF measurements at the air/water interface. Fluorescence radiation from the ions was recorded with an energy sensitive detector at various angles of incidence αi below and above the critical angle for total reflection αC.
Results and Discussion
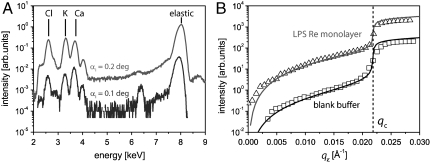
Fig. 2A shows the fluorescence spectra from LPS Re monolayers measured in Ca2+-loaded buffer at incidence angles below (αi = 0.1°, blue) and beyond (αi = 0.2°, red) the critical angle, αC = 0.16°. These spectra were fitted by multiple Gaussians to extract the total fluorescence intensity from each element. In Fig. 2B, K+ fluorescence intensities (peak position: 3.61 keV) in the absence (squares) and presence (triangles) of an LPS Re monolayer on Ca2+-free buffer are plotted as a function of qz with the two curves vertically offset for clarity. In the vicinity of the critical edge of total reflection (qc = 0.022 Å-1) the shape of the curve depends on the imaginary part β of the refractive index (n = 1 - δ + iβ) of the bulk medium for the incident X-ray beam. In our experimental system a maximum near the critical edge (13) was not observed due to the strong X-ray absorption by water at 8 keV. Instead, we observed a monotonic increase in the signal with increasing qz.
Fig. 2.
X-ray fluorescence signals. (A) Fluorescence spectra from an LPS Re monolayer on Ca2+-loaded buffer recorded at angles of incidence αi below (lower curve) and above (upper curve) the critical angle, αC = 0.16°. (B) Fluorescence intensities as a function of qz. Experimental (open symbols) and modeled (solid lines) K+ fluorescence from an LPS Re monolayer (triangles) and from a blank Ca2+-loaded buffer (squares). The two curves are shifted vertically for clarity. The qz value corresponding to the critical angle (qc) is indicated with a vertical broken line.
To model the fluorescence signals, the absorption coefficients of the bulk medium for illumination and fluorescence radiation must be considered. Solid lines in Fig. 2B are the modeled K+ fluorescence signals superimposed on the experimental data. We adjusted the β value (imaginary part of the refractive index) of pure water at 8 keV for the bulk ion concentrations, but ignored the contribution from fluorescence absorption because it is negligibly small in our experimental qz-range. One sees that the global shape of the experimental curves is well represented by the model curves over several orders of magnitude in intensity. Nevertheless, in the following discussion, we deal with the fluorescence intensities normalized by the signals from the blank buffer to eliminate undefined geometrical effects.
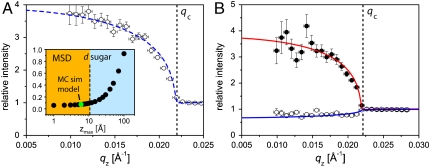
Fig. 3 shows the normalized fluorescence signals from LPS Re monolayers on (A) Ca2+-free and (B) Ca2+-loaded buffers. Open and closed circles indicate signals from K+ and Ca2+ ions, normalized by the signals from the corresponding blank buffers. On Ca2+-free buffer (A), the intensity of K+ fluorescence is significantly higher than the bulk level (corresponding to relative intensity of unity) below the critical angle (qz < qc), indicating that K+ ions are enriched near the air/water interface in the presence of an LPS monolayer. However, the intensity of K+ fluorescence at qz < qc is very weak on Ca2+-loaded buffer (B). Significantly strong fluorescence signals from Ca2+ at qz < qc imply that K+ ions near the interface are almost completely displaced by Ca2+ ions.
Fig. 3.
Normalized X-ray fluorescence intensities as a function of qz. (A) K+ fluorescence on Ca2+-free buffer. Measured data points (open circles) and best-matching model signal (dashed blue line) for fixed concentration peak position (zmax = 5 Å). (Inset) MSD of the fit as a function of zmax. The thickness of the saccharide headgroups (11 Å) is indicated by a vertical dashed line. (B) Fluorescence on Ca2+-loaded buffer (K+, open circles; Ca2+, closed circles). The best-matching model signal for Ca2+ with fixed zmax = 5 Å is indicated with a solid red line. The solid blue line superimposed on the K+ data points corresponds to a constant K+ concentration starting from the chain/sugar interface. Vertical error bars were obtained via Gaussian error propagation from the parameters used to fit the fluorescence spectra. Horizontal error bars reflect the finite angular resolution.
To gain more insight into the absolute ion concentration profiles in the z-direction, the measured fluorescence signals were modeled using the electron density profiles of LPS Re monolayers reconstructed from grazing-incidence X-ray scattering out of the specular plane (GIXOS) (15, 16). As described before (8, 17), we used a two-slab model including interfacial roughness to fit the measured GIXOS curves: the first slab represents hydrocarbon chains and the second one carbohydrate head groups. The best-matching model parameters (presented in SI Text, which also includes the fits) are in good agreement with previous structural studies on various LPS membranes (8, 18–20).
For the air/water interface in the absence of LPS monolayers (blank buffer), we assumed a constant ion concentration in the bulk (c0 = 0.1 M for K+, c0 = 0.05 M for Ca2+), because the influence of ion depletion near the air/water surface (11) was negligibly smaller than the significant accumulation of ions in the presence of LPS monolayers. The excess concentration profile of cations condensed near the charged LPS Re monolayer was parameterized as
| [1] |
with a vanishing ion density at the chain/carbohydrate interface, cex(z = 0) = 0, and the requirement 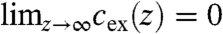 . This enabled us to model ion distributions that possess a concentration maximum with a smooth decay to the bulk concentration with only two free parameters: (i) the concentration maximum cmax and (ii) the z-position zmax of this maximum.
. This enabled us to model ion distributions that possess a concentration maximum with a smooth decay to the bulk concentration with only two free parameters: (i) the concentration maximum cmax and (ii) the z-position zmax of this maximum.
To model the normalized fluorescence signals, we varied zmax stepwise, and performed a least-squares fit of the peak concentration cmax for each step. In Fig. 3A (Inset), the mean square deviation (MSD) of the fit is plotted as a function of zmax, indicating that K+ ions should achieve a concentration maximum at zmax ≤ 10 Å. In fact, the MSD starts increasing significantly for higher zmax values*. This upper limit (zmax ≈ 10 Å) seems reasonable when one considers the thickness of the carbohydrate head groups (d = 11 Å; see SI Text) deduced from the GIXOS experiments and indicated by a dotted vertical line in Fig. 3A (Inset). Accordingly, we conclude that the maximum of the K+ concentration lies within the headgroup region of the LPS Re monolayer.
The broken line in Fig. 3A is the modeled fluorescence signal corresponding to zmax = 5 Å and cmax ≈ 3.0 M, assuming that K+ ions achieve a concentration maximum in the middle of the carbohydrate slab. If one takes the area per molecule value for Ca2+-free buffer (A = 166 Å2), then, by integrating the excess K+ concentration along z-axis, we obtain the number of K+ ions, NK ≈ 2.30, associated with one LPS Re molecule in average. Although this depends on the choice of the zmax value, the deviation in NK is only by a few percent in the experimentally determined range 0 < zmax < 10 Å.
The solid red line in Fig. 3B shows that the Ca2+ fluorescence intensity from the LPS monolayer on Ca2+-loaded buffer is well represented by a concentration profile with a maximum at zmax = 5 Å, corresponding to cmax ≈ 1.5 M. Taking the area per molecule value in Ca2+-loaded buffer (A = 140 Å2), integrating the excess Ca2+ concentration along the z-axis yields the number of Ca2+ ions per LPS Re is NCa ≈ 1.05. It should also be noted that the values of the normalized K+ fluorescence signal in Ca2+-loaded buffer at qz < qc are slightly less than unity. Although this appears to suggest the depletion of K+ near the monolayer, nonetheless the theoretically modeled fluorescence signal (blue solid line in Fig. 3B), that assumes a constant K+ concentration (c0 = 0.1 M) down to z = 0 Å, represents the experimental results very well. This indicates that in Ca2+-loaded buffer the K+ concentration is not significantly altered from the bulk value by the monolayer. The reduction in K+ fluorescence observed in the presence of the monolayer can be attributed to (i) the suppression of K+ fluorescence due to the absence of ions within the alkyl chain layer (-13 Å < z < 0 Å), and (ii) the decrease in the beam penetration depth (and thus the volume of the illuminated region) due to the higher electron density of the headgroup region compared to bulk water.
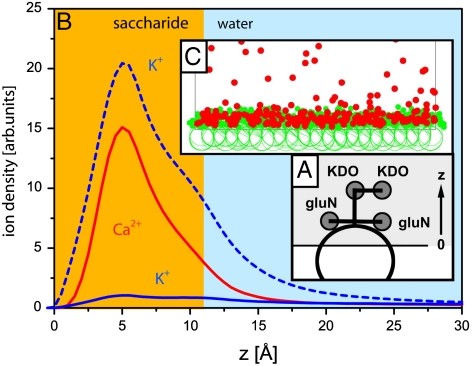
The minimal model of LPS Re used for the coarse-grained MC simulations is presented in Fig. 4A, and Fig. 4B shows the simulated ion density profiles. The broken blue line indicates the K+ density in Ca2+-free buffer, whereas the solid blue and red lines represent the K+ and Ca2+ densities in Ca2+-loaded buffer. As above with the GIXF models, z = 0 is defined as the interface between hydrocarbon chains and carbohydrate head groups. Note that the global shape of the simulated ion density profiles is similar to the function used for modeling the fluorescence signals [1]. The positions of the maxima for K+ ions in Ca2+-free buffer (broken blue line) and Ca2+ ions in Ca2+-loaded buffer predicted by the MC simulation (zmax = 5 Å) show excellent agreement with the GIXF models. The snapshot from the MC simulation (Fig. 4C) clearly shows the condensation of divalent cations in the carbohydrate head groups. Furthermore, the replacement of K+ ions (solid blue line in Fig. 4B) by Ca2+ (solid red line in Fig. 4B) in Ca2+-loaded buffer indicated by the MC simulation is fully consistent not only with the GIXF results but also with the analytical continuum description of ion distributions near charged surfaces according to Gouy–Chapman theory (21, 22). Another important conclusion that we can draw from the continuum description and MC simulations is that the net charge across the interface is completely compensated on sufficiently long length scales†. Because the contribution of Cl- to the charge compensation at the interface is negligibly small, the surface charge compensation is dominated by K+ in Ca2+-free buffer, whereas it is vastly dominated by Ca2+ in Ca2+-loaded buffer, indicating that the average charge per LPS Re is Qtot ≈ -2.3 e in Ca2+-free buffer, and Qtot ≈ -2.1 e in Ca2+-loaded buffer, respectively. If one considers the uncertainty in the area per molecule (approximately 10%), the net charge per LPS Re molecule predicted from two independent subphase conditions seem to achieve good quantitative agreement.
Fig. 4.
MC simulations. (A) Diagram of the LPS Re minimal model. (B) Calculated ion density profiles. Dashed line: K+ ions in Ca2+-free buffer. z = 0 is defined as the chain/carbohydrate interface. Solid lines: Ca2+ and K+ ions in Ca2+-loaded buffer. (C) Simulation snapshot with 50 mM divalent cations (red circles).
The charge density on LPS surfaces in physiological buffers is still under debate (23). Hagge et al. (24) deduced the average charge per LPS Re molecule, Q ≈ -3.6 e, from the molecular structure‡ assuming ionization of all chargeable groups. However, the degree of dissociation of surface-confined acids depends via the local pH on the electric potential at the surface (22). In addition, the pKa value of dissociable groups confined at a surface can be different from the solution pKa values. For instance, when also accounting for local pH, the pKa value of surface-confined carboxyl groups is reported in ref. 25 to be higher (7.7) than the pKa value (< 5.5) of carboxylic acids in solution (26). For the present system, an estimation, exemplarily performed for Ca2+-free buffer using Eq. 9 in ref. 25, results in a surface pH value of 5.25 (SI Text). Furthermore, this enables us to estimate the surface pKa values of the carboxyl groups in an LPS Re monolayer, yielding pKa = 5.5. These calculations support the dissociation state and average total charge of LPS molecules deduced from the measured ion accumulation. In summary, the strategy as presented here is suited for the precise determination of the actual charge density of biological surfaces under environmental conditions.
Conclusions
We have presented a quantitative way to measure the amount and location of ions at LPS monolayers. The results show excellent agreement with the predictions of a minimal coarse-grained model of LPS molecules studied by MC simulations. In cases of more complex LPS mutants and wild-type LPSs, this will enable us to monitor conformational changes along with ion redistribution in response to various buffer compositions. Moreover, this approach offers a unique possibility for the accurate measurement of the effective charge density of biological interfaces in general. The combination of X-ray scattering, X-ray fluorescence, and real-space computer simulation used in this study enables one to gain quantitative information about the electrostatic interactions of charged membranes and macromolecules with various ion species under physiological conditions.
Materials and Methods
Materials and Sample Preparation.
LPS Re was purified from the deep rough mutant R595 of Salmonella enterica sv. Minnesota as previously reported (27). LPS Re possesses two saccharides comprising the KDO inner core in addition to the Lipid A anchor. With two carboxyl groups in the KDO core and two phosphate groups attached to glucosamines of the Lipid A anchor, LPS Re can carry up to four negative charges. In contrast to wild-type LPSs with polydisperse O-sidechains, LPS Re has a unique saccharide head group.
All chemicals were purchased from Fluka (Taufkirchen) and used without further purification. Double deionized water (MilliQ, Molsheim) with a specific resistance of ρ > 18 MΩcm was used throughout this study. “Ca2+-free buffer” contained 100 mM KCl and 5 mM Hepes, at pH 7.4. Ca2+-loaded buffer additionally contained 50 mM CaCl2. LPS Re was dissolved in 9∶1 mixtures (v/v) of chloroform and methanol at a concentration of 1 mg/mL. To create monolayers at the air/water interface, the LPS Re solution was spread onto the buffer surface of a Langmuir film balance. Prior to compression, 20 min were allowed for the complete evaporation of the solvent. The film was compressed to a surface pressure of π = 20 mN/m at 20 °C. According to the pressure-area isotherms of LPS Re monolayers, this corresponds to molecular areas of about 166 Å2 on Ca2+-free buffer and 140 Å2 on Ca2+-loaded buffer, respectively (17).
GIXF.
Experiments were carried out at beamline ID10B at the European Synchrotron Radiation Facility (ESRF) (Grenoble). During X-ray irradiation the monolayer was kept in a helium atmosphere. A monochromatic X-ray beam (λ = 1.55 Å) hits the air/water interface at incident angles αi below and above the critical angle of water (αC = 0.16°). At each angle, the fluorescence radiation emitted by the ions was recorded with an energy sensitive detector and normalized by the detector counting efficiency. Subsequently, the intensities were normalized by the elastically scattered beam intensity at 8 keV to compensate for any systematic differences between the experiments. For direct comparison with the theoretically modeled fluorescence signals, the incident angle αi was transformed into the scattering vector component normal to the interface, qz = (4π/λ)· sin αi. In the last step, the fluorescence signals in the presence of monolayers were normalized by the signals recorded from blank buffer. This procedure avoids artifacts arising from the experimental geometry, such as the size of beam footprint and the fluorescence detector aperture. Furthermore, absorption effects are cancelled, as they apply equally to all experiments.
Simulation of Normalized Fluorescence Intensities.
The fluorescence intensity emitted by an ion species j at the air/water interface 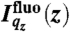 can be written as (14):
can be written as (14):
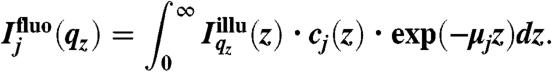 |
[2] |
cj(z) denotes the vertical concentration profile of species j, and μj the absorption coefficient of water for the fluorescence radiation. For our experimental systems, μ-1 is in the range of several tens to hundreds of micrometers. 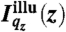 is the vertical intensity profile of the incident illumination, which depends on the incident angle αi and on the electronic structure of the monolayer. For a monolayer at the air/water interface, this electronic structure can be obtained by GIXOS and parameterized using slab models§, where each slab represents a layer of constant electron density within the monolayer (28–30). Accordingly, once the illumination profiles
is the vertical intensity profile of the incident illumination, which depends on the incident angle αi and on the electronic structure of the monolayer. For a monolayer at the air/water interface, this electronic structure can be obtained by GIXOS and parameterized using slab models§, where each slab represents a layer of constant electron density within the monolayer (28–30). Accordingly, once the illumination profiles 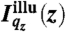 are known, the ion concentration profiles cj(z) can be reconstructed from the measured fluorescence intensities
are known, the ion concentration profiles cj(z) can be reconstructed from the measured fluorescence intensities 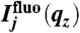 using Eq. 2.
using Eq. 2.
The vertical illumination profile in medium j (bulk media and slabs) is given by |E+(z) + E-(z)|2 where the waves E+(z) and E-(z) propagate in the positive and negative z direction, respectively. The amplitude E(z) = E+(z) + E-(z) in each slab can be calculated from all the partial waves reflected back and forth between the interfaces separating the slab from its neighboring media. Starting from the expressions given by Born and Wolf (31), we performed the summation over an infinite number of such reflections to obtain:
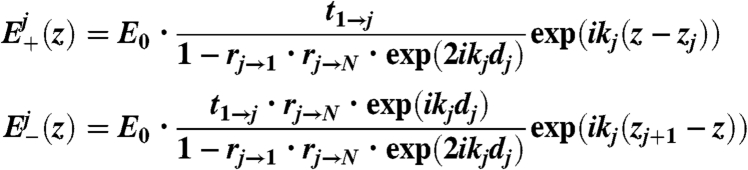 |
[3] |
Here, E0 denotes the amplitude of the incident wave, N the total number of media, kj is the z-component of the wave vector and zj the vertical position of the interface between media j and j + 1. dj is the thickness of medium j, and tx→y and rx→y the Parratt amplitude transmission and reflection coefficients (32) for a beam traveling from the medium x to the medium y. The result of Eq. 3 is fully equivalent to the illumination intensity profile calculated from a matrix formalism (33). To compute the fluorescence signal for each ion species, the integral in Eq. 2 is evaluated with a parameterized concentration profile cj(z).
Minimal Model and MC Simulations.
To simulate density profiles of different ion species near an LPS Re monolayer, we employed a “minimal model” (9) and performed MC simulations using the Metropolis algorithm (34, 35). The aqueous region of the simulation volume ranged from z = 0 to z = 200 Å. The aqueous solution (z > 0) and the hydrocarbon-chain region (z < 0) were represented as two dielectric continua with relative permittivities εw = 81 and 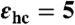 , respectively (22). We represented some (implicit) monovalent ion screening in the aqueous solution by linearized Poisson–Boltzmann theory (9, 22, 36) and represented the remaining monovalent ions and all divalent ions explicitly by charged spheres. We calculated electrostatic interactions according to expressions derived by Netz (37). A more detailed description is given elsewhere (8, 9). The membrane plane of the simulation volume possessed 100 LPS Re molecules (17). Each saccharide group of an LPS molecule was represented by a sphere of radius rsugar = 1.5 Å, connected by stretchable bonds with equilibrium lengths L0 (38). We restricted the relative angle between successive saccharide–saccharide bonds of these semiflexible molecules to be 30 ± 10° (9). Negatively charged sugars possessed charge -1 in units of e = 1.6 × 10-19 C located at their centers. The hydrocarbon-chain moieties of a molecule were represented by a portion of an anchoring sphere of radius Ranchor = 7.0 Å, centered at z0 = -4.0 Å. Molecules were allowed to move along the z-axis by ± 1.5 Å from equilibrium. Anchoring spheres were allowed to rotate around their centers but no ions or saccharide groups were allowed to move their centers into the region z < 0. Hydrated ions were represented by spheres of radius Rion = 1.8 Å, with charges located at their centers. We used an implicit monovalent ionic strength of 25 mM (yielding a Debye length κ-1 ≈ 2 nm), and added sufficient explicit monovalent ions in the “bulk” to match the experimental concentrations used. Bulk was defined as the upper half of the simulation volume, 100 Å < z < 200 Å. The resulting effective screening length was
, respectively (22). We represented some (implicit) monovalent ion screening in the aqueous solution by linearized Poisson–Boltzmann theory (9, 22, 36) and represented the remaining monovalent ions and all divalent ions explicitly by charged spheres. We calculated electrostatic interactions according to expressions derived by Netz (37). A more detailed description is given elsewhere (8, 9). The membrane plane of the simulation volume possessed 100 LPS Re molecules (17). Each saccharide group of an LPS molecule was represented by a sphere of radius rsugar = 1.5 Å, connected by stretchable bonds with equilibrium lengths L0 (38). We restricted the relative angle between successive saccharide–saccharide bonds of these semiflexible molecules to be 30 ± 10° (9). Negatively charged sugars possessed charge -1 in units of e = 1.6 × 10-19 C located at their centers. The hydrocarbon-chain moieties of a molecule were represented by a portion of an anchoring sphere of radius Ranchor = 7.0 Å, centered at z0 = -4.0 Å. Molecules were allowed to move along the z-axis by ± 1.5 Å from equilibrium. Anchoring spheres were allowed to rotate around their centers but no ions or saccharide groups were allowed to move their centers into the region z < 0. Hydrated ions were represented by spheres of radius Rion = 1.8 Å, with charges located at their centers. We used an implicit monovalent ionic strength of 25 mM (yielding a Debye length κ-1 ≈ 2 nm), and added sufficient explicit monovalent ions in the “bulk” to match the experimental concentrations used. Bulk was defined as the upper half of the simulation volume, 100 Å < z < 200 Å. The resulting effective screening length was 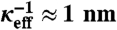 . In the “Ca2+-loaded” case the system additionally contained a number of divalent cations and twice as many monovalent anions, to yield the desired bulk concentration. The system was equilibrated at T = 300 K for > 106 MC steps, and equilibrium averages were measured for a further 106 steps.
. In the “Ca2+-loaded” case the system additionally contained a number of divalent cations and twice as many monovalent anions, to yield the desired bulk concentration. The system was equilibrated at T = 300 K for > 106 MC steps, and equilibrium averages were measured for a further 106 steps.
Supplementary Material
Acknowledgments.
M.T. is a member of the German Excellence Cluster “Cell Network,” the Center for Quantitative Analysis of Molecular and Cellular Biosystems (BIOQUANT), and Karlsruhe Institute of Technology. M.T. thanks the German Science Foundation (Ta 259/6) and the Helmholtz Society (BioInterface Program) for support. E.S. thanks the State Baden–Württemberg and the Deutscher Akademischer Austausch Dienst (DAAD) for fellowships. D.A.P. thanks the Natural Sciences and Engineering Research Council of Canada (NSERC). We thank ESRF for synchrotron beam times, the High Performance Computing Laboratory of St. Francis Xavier University (hpcLAB) and the Atlantic Computational Excellence Network (ACENET) for computing assistance, and the Advanced Foods and Materials Network of Centres of Excellence (AFMNet-NCE) for support.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.0913737107/-/DCSupplemental.
*A fluorescence signal modeled with zmax = 20 Å, which significantly deviates from the measured data points, is shown in SI Text.
†Beyond these qualitative results the continuum description is not employed in this study. Especially it should not be used for the microscopic description, as it loses its validity for the high charge densities and ion strengths here. Moreover, it does not take the z-extension of the charged sugar and the volume occupied by the headgroups into account.
‡A certain fraction of LPS Re molecules (approximately 40%) possess an extra palmitoyl chain, together with a phosphatidylethanolamine and a positively chargeable 4-amino-deoxyarabinose unit.
§For illumination at small angles (qz ≅ qc) the interfacial roughness between the slabs does not have to be considered. In the used qz-range the Névot–Croce factors 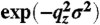 are close to unity, regarding the low roughness σ (∼3 Å) of LPS Re monolayers at the air/water interface.
are close to unity, regarding the low roughness σ (∼3 Å) of LPS Re monolayers at the air/water interface.
References
- 1.Lüderitz O, et al. Lipopolysaccharides of Gram-negative bacteria. In: Razin Shmuel, Rotem Shlomo., editors. Current Topics in Membranes and Transport. Vol 17. Amsterdam: Elsevier; 1982. pp. 79–151. [Google Scholar]
- 2.Brock TD. The effect of salmine on bacteria. Can J Microbiol. 1958;4:65–71. doi: 10.1139/m58-009. [DOI] [PubMed] [Google Scholar]
- 3.Truelstrup Hansen L, Austin JW, Gill TA. Antibacterial effect of protamine in combination with EDTA and refrigeration. Int J Food Microbiol. 2001;66:149–161. doi: 10.1016/s0168-1605(01)00428-7. [DOI] [PubMed] [Google Scholar]
- 4.Hancock REW, Chapple DS. Peptide antibiotics. Antimicrob Agents Chemother. 1999;43:1317–1323. doi: 10.1128/aac.43.6.1317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kotra LP, Golemi D, Amro NA, Liu GY, Mobashery S. Dynamics of the lipopolysaccharide assembly on the surface of Escherichia coli. J Am Chem Soc. 1999;121:8707–8711. [Google Scholar]
- 6.Lins RD, Straatsma TP. Computer simulation of the rough lipopolysaccharide membrane of Pseudomonas aeruginosa. Biophys J. 2001;81:1037–1046. doi: 10.1016/S0006-3495(01)75761-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shroll RM, Straatsma TP. Molecular structure of the outer bacterial membrane of Pseudomonas aeruginosa via classical simulation. Biopolymers. 2002;65:395–407. doi: 10.1002/bip.10279. [DOI] [PubMed] [Google Scholar]
- 8.Oliveira RG, et al. Physical mechanisms of bacterial survival revealed by combined grazing-incidence X-ray scattering and Monte Carlo simulation. CR Chimie. 2009;12:209–217. [Google Scholar]
- 9.Pink DA, et al. Ivalent calcium ions inhibit the penetration of protamine through the polysaccharide brush of the outer membrane of Gram-negative bacteria. Langmuir. 2003;19:8852–8858. [Google Scholar]
- 10.Schneck E, et al. Calcium ions induce collapse of charged O-side chains of lipopolysaccharides from Pseudomonas aeruginosa. J R Soc Interface. 2009;6:S671–S678. doi: 10.1098/rsif.2009.0190.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Padmanabhan V, Daillant J, Belloni L. Specific ion adsorption and short-range interactions at the air aqueous solution interface. Phys Rev Lett. 2007;99:086105-1–086105-4. doi: 10.1103/PhysRevLett.99.086105. [DOI] [PubMed] [Google Scholar]
- 12.Novikova NN, et al. X-ray fluorescence methods for investigations of lipid/protein membrane models. J Synchrotron Radiat. 2005;12:511–516. doi: 10.1107/S0909049505013579. [DOI] [PubMed] [Google Scholar]
- 13.Novikova NN, et al. Total reflection X-ray fluorescence study of Langmuir monolayers on water surface. J Appl Crystallogr. 2003;36:727–731. [Google Scholar]
- 14.Yun WB, Bloch JM. X-ray near total external fluorescence method: Experiment and analysis. J Appl Phys. 1990;68:1421–1428. [Google Scholar]
- 15.Mora S, Daillant J, Luzet D, Struth B. X-ray surface scattering investigation of Langmuir films: Phase transitions and elastic properties. Europhys Lett. 2004;66:694–700. [Google Scholar]
- 16.Wiegart L, Struth B, Tolan M, Terech P. Thermodynamic and structural properties of phospholipid Langmuir monolayers on hydrosol surfaces. Langmuir. 2005;21:7349–7357. doi: 10.1021/la050478m. [DOI] [PubMed] [Google Scholar]
- 17.Oliveira RG, et al. Crucial roles of charged saccharide moieties in survival of Gram-negative bacteria revealed by combination of grazing incidence X-ray structural characterizations and Monte Carlo simulations. Phys Rev E. 2010:041901-1–041901-12. doi: 10.1103/PhysRevE.81.041901. [DOI] [PubMed] [Google Scholar]
- 18.Brandenburg K, Seydel U. Physical aspects of structure and function of membranes made from lipopolysaccharides and free lipid A. Biochim Biophys Acta. 1984;775:225–238. [Google Scholar]
- 19.Seydel U, Brandenburg K, Koch MHJ, Rietschel ET. Supramolecular structure of lipopolysaccharide and free lipid A under physiological conditions as determined by synchrotron small-angle X-ray diffraction. Eur J Biochem. 1989;186:325–332. doi: 10.1111/j.1432-1033.1989.tb15212.x. [DOI] [PubMed] [Google Scholar]
- 20.Snyder S, Kim D, McIntosh TJ. Lipopolysaccharide bilayer structure: Effect of chemotype, core mutations, divalent cations, and temperature. Biochemistry. 1999;38:10758–10767. doi: 10.1021/bi990867d. [DOI] [PubMed] [Google Scholar]
- 21.Grahame DC. Diffuse double layer theory for electrolytes of unsymmetrical valence types. J Chem Phys. 1953;21:1054–1060. [Google Scholar]
- 22.Israelachvili JN. Intermolecular and Surface Forces. London: Academic; 1985. [Google Scholar]
- 23.Coughlin RT, Peterson AA, Haug A, Pownall HJ, McGroarty EJ. A pH titration study on the ionic bridging within lipopolysaccharide aggregate. Biochim Biophys Acta. 1985;821:404–412. doi: 10.1016/0005-2736(85)90044-6. [DOI] [PubMed] [Google Scholar]
- 24.Hagge SO, Hammer MU, Wiese A, Seydel U, Gutsmann T. Calcium adsorption and displacement: Characterization of lipid monolayers and their interaction with membrane-active peptides/proteins. BMC Biochem. 2006;7:15, 1–13. doi: 10.1186/1471-2091-7-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hu K, Bard AJ. Use of atomic force microscopy for the study of surface acid-base properties of carboxylic acid-terminated self-assembled monolayers. Langmuir. 1997;13:5114–5119. [Google Scholar]
- 26.Lide DR. CRC Handbook of Chemistry and Physics. Boca Raton: CRC; 2009. [Google Scholar]
- 27.Galanos C, Lüderitz O, Westphal O. A new method for the extraction of R lipopolysaccharides. Eur J Biochem. 1969;9:245–249. doi: 10.1111/j.1432-1033.1969.tb00601.x. [DOI] [PubMed] [Google Scholar]
- 28.Doshi DA, Watkins EB, Israelachvili JN, Majewski J. Reduced water density at hydrophobic surfaces: Effect of dissolved gases. Proc Natl Acad Sci USA. 2005;102:9458–9462. doi: 10.1073/pnas.0504034102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schubert T, et al. Structure of synthetic transmembrane lipid membranes at the solid/liquid interface studied by specular X-ray reflectivity. J Phys Chem B. 2008;112:10041–10044. doi: 10.1021/jp803937m. [DOI] [PubMed] [Google Scholar]
- 30.Tidswell IM, et al. X-ray specular reflection studies of silicon coated by organic monolayers (alkylsiloxanes) Phys Rev B. 1990;41:1111–1128. doi: 10.1103/physrevb.41.1111. [DOI] [PubMed] [Google Scholar]
- 31.Born M, Wolf E. Principles of Optics. 6th Ed. Oxford: Pergamon; 1980. [Google Scholar]
- 32.Parratt LG. Surface studies of solids by total reflection of X-rays. Phys Rev. 1954;95:359–369. [Google Scholar]
- 33.Ohta K, Ishida H. Matrix formalism for calculation of the light beam intensity in stratified multilayered films, and its use in the analysis of emission spectra. Appl Optics. 1990;29:1952–1959. doi: 10.1364/AO.29.002466. [DOI] [PubMed] [Google Scholar]
- 34.Binder K. Monte Carlo Simulation in Statistical Physics: An Introduction. Berlin: Springer; 1988. [Google Scholar]
- 35.Lai PY, Binder K. Structure and dynamics of polymer brushes near the theta point: A Monte Carlo simulation. J Chem Phys. 1992;97:586–595. [Google Scholar]
- 36.Deserno M, Holm C, May S. Fraction of condensed counterions around a charged rod: Comparison of Poisson–Boltzmann theory and computer simulations. Macromolecules. 2000;33:199–206. [Google Scholar]
- 37.Netz RR. Debye–Huckel theory for interfacial geometries. Phys Rev E. 1999;60:3174–3182. doi: 10.1103/physreve.60.3174. [DOI] [PubMed] [Google Scholar]
- 38.Carmesin I, Kremer K. The bond fluctuation method—A new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules. 1988;21:2819–2823. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.