Water Dynamics and Interactions in Water-Polyether Binary Mixtures

Abstract

Poly(ethylene) oxide (PEO) is a technologically important polymer with a wide range of applications including ion-exchange membranes, protein crystallization, and medical devices. PEO’s versatility arises from its special interactions with water. Water molecules may form hydrogen bond bridges between the ether oxygens of the backbone. While steady-state measurements and theoretical studies of PEO’s interactions with water abound, experiments measuring dynamic observables are quite sparse. A major question is the nature of the interactions of water with the ether oxygens as opposed to the highly hydrophilic PEO terminal hydroxyls. Here, we examine a wide range of mixtures of water and tetraethylene glycol dimethyl ether (TEGDE), a methyl-terminated derivative of PEO with 4 repeat units (5 ether oxygens) using ultrafast infrared polarization selective pump-probe measurements on water’s hydroxyl stretching mode to determine vibrational relaxation and orientational relaxation dynamics. The experiments focus on the dynamical interactions of water with the ether backbone because TEGDE does not have the PEO terminal hydroxyls. The experiments observe two distinct subensembles of water molecules: those that are hydrogen bonded to other waters and those that are associated with TEGDE molecules. The water orientational relaxation has a fast component of a few ps (water-like) followed by much slower decay of ∼20 ps (TEGDE associated). The two decay times vary only mildly with the water concentration. The two subensembles are evident even in very low water content samples, indicating pooling of water molecules. Structural change as water content is lowered either through conformational changes in the backbone or increasing hydrophobic interactions is discussed.

I. Introduction

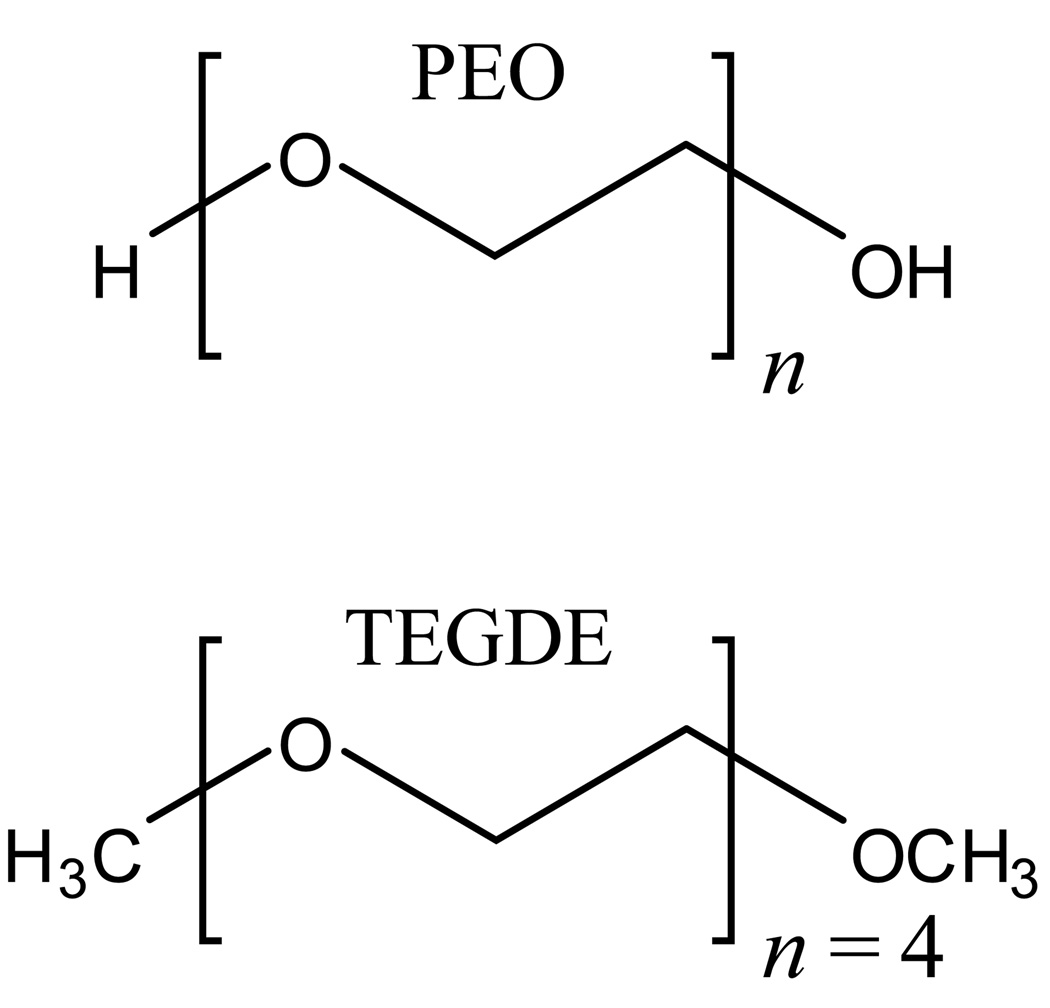
The polymer poly(ethylene oxide) (PEO, see Figure 1), a polyether compound also known as poly(ethylene glycol) or poly(oxoethylene), is important in many industrial, environmental, and biological applications because of its hydrophilic properties. PEO is soluble in both water and non-polar solvents while similar polymers, such as poly(methylene oxide) and poly(propylene oxide), exhibit different behaviors.¹ PEO-based membranes find utility in industrial applications to enhance proton conduction in fuel cells,^2,3 ion conduction in polymer electrolyte batteries,⁴ and in other situations requiring ion-exchange membranes. In biological applications, PEO aids in crystallizing macromolecules⁵ and, as a hydrated thin film, provides an antifouling coating for metal surfaces and biomedical devices.⁶ Using PEO-based surfactants is advantageous for the environment because they are more biodegradable than alkylphenol-based surfactants.⁷

Figure 1.

Molecular structures of poly(ethylene oxide) (top) and TEGDE (bottom). The n denotes the number of repeating units.

The properties of PEO change with the extent of hydration. Therefore, it is important to gain an understanding of the molecular processes governing the interactions between the polymer and water molecules. PEO is terminated with hydroxyl groups, which contribute to the compound’s hydrophilicity. However, the ether oxygens along the polymer backbone as well as hydrophobic interactions with the ethylenes must also be considered to gain insights into polymer/water interactions. To explicate the role played by the polyether backbone, we have studied tetraethylene glycol dimethyl ether (TEGDE) (see Figure 1) over a range of water concentrations from almost pure water to one water per TEGDE molecule (one water per five ether oxygens). Orientational dynamics and vibrational population relaxation of the water were explored for the TEGDE/water systems using ultrafast infrared (IR) polarization selective pump-probe spectroscopy of water’s hydroxyl stretch.

Neutron-scattering,^8–11 steady-state IR and Raman spectroscopy,^12–23 thermodynamic measurements^24–28 and simulations^7,10,29–32 have produced a substantial amount of important information about the static, and to some degree the dynamic, nature of PEO-water systems. The studies indicate that PEO chains can form helical structures in water that allow the ether oxygens to lie approximately the same distance apart as oxygens in bulk water. Specifically, the waters stabilize a gauche conformation of oxygens around the C-C bonds of the backbone, the preference for which generally increases with higher water content.^21,33 This structure can permit water molecules to form bridging hydrogen bonds between the oxygens.^21,33 The C-C bonds can also adopt a trans conformation that will occur more frequently with less water in the system.^21,33 The proposed structure of TEGDE/water suggests that water dynamics can be strongly influenced by hydrogen bonding to the ether oxygens, and dynamical information can provide insights into TEGDE structure as a function of water concentration. PEO generally has two alcohol (hydroxyl) end groups which significantly affect the dynamics for low water content solutions and for solutions with short polymer chains.³¹ With little water, the water molecules will mainly hydrogen bond to the hydroxyls. In contrast, TEGDE has terminal methyl groups which makes the molecule similar to long-chain PEO whose terminal hydroxyl groups are no longer significant.³¹ By studying TEGDE it is possible to investigate the dynamics and interactions of water with the polymeric ether chains without competition from water-alcohol interactions. The number of hydrogen bonds that an ether oxygen can accept^32,34,35 and the ability of waters to cross-link separate ether molecules have been studied.^21,32 The results indicate that hydrophobic interactions of water with TEGDE are also important.

The ultrafast IR polarization selective pump-probe experiments³⁶ on the water hydroxyl stretch enable us to measure the water dynamics in water/polyether systems on the timescale on which the water molecules are moving, providing information beyond the scope of steady-state measurements.³⁷ The experiments yield both the population relaxation (lifetimes) and the orientational relaxation. Vibrational population relaxation is sensitive to the local structural environment experienced by the water molecules while anisotropy measurements provide information on the hydrogen bond network rearrangement. Together, these experiments provide significant insights into the dynamics and interactions of the polyether/water solutions.

II. Experimental Methods

The IR pump-probe experiments are made on the OD stretch of dilute HOD in H₂O. The use of dilute HOD, as opposed to pure H₂O or D₂O, is important to eliminate vibrational excitation transfer.^38–41 Vibrational excitation transfer causes the decay of the transition dipole anisotropy induced by the pump pulse,⁴² which interferes with measurements of orientational relaxation. It also changes the location of the excitation, which impedes the use of the vibrational lifetime as a probe of the local environment. MD simulations of pure water have shown that dilute HOD in H₂O does not change the behavior of water and that observations of the OD hydroxyl stretch report on the dynamics and local environment of water.⁴³

Tetraethylene glycol dimethyl ether (99+%, Acros, Figure 1) was used as received. Mass spectral analysis verified the purity of the material. The mixtures of water and TEGDE were prepared by mass with the following molar ratios of water:TEGDE: 200:1, 100:1, 50:1, 37:1, 25:1, 15:1, 10:1, 7:1, 2.7:1, and 1:1. The corresponding mole fractions of water in these systems, in the above order, are: 0.995, 0.99, 0.98, 0.974, 0.962, 0.937, 0.89, 0.875, 0.73, and 0.50. Water content was verified for each of the solutions by Karl Fischer Titration (Mettler Toledo). Background-subtracted infrared spectra were taken with an FT-IR spectrometer. Samples for the experiment were prepared by sandwiching a portion of the water/TEGDE mixture between two CaF₂ windows separated by a Teflon spacer of various thicknesses. The thickness was chosen so that the optical density at the OD stretching frequency was between 0.3 and 0.5.

An optical parametric amplifier converts the output from a Ti:Sapphire oscillator-regenerative amplifier into ∼4µm, ∼70 fs mid-IR pulses, which are then beam-split into the probe and pump pulses. The pump is rotated 45° relative to the probe and chopped. The two beams cross in the sample, and the parallel and perpendicular components of the probe are selected by a polarizer on a computer-controlled rotation mount. The probe signal is frequency-resolved by a monochromator and detected by a 32-element mercury-cadmium-telluride array detector.

III. Results and Discussion

A. Absorption Spectroscopy

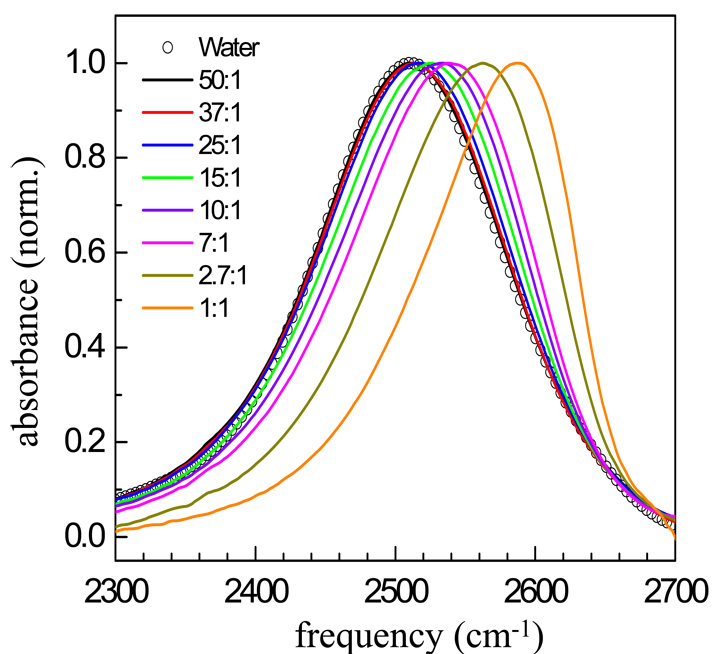
Figure 2 shows FT-IR spectra for the OD stretch of HOD in pure water and in eight mixtures, 50:1 down to 1:1. The higher water content samples (200:1 and 100:1) have spectra that are indistinguishable from pure water. The spectrum of the 50:1 sample is almost identical to that of the OD stretch of HOD in pure H₂O, peaking at 2511 cm⁻¹. The peak positions of the absorption bands shift to the blue (higher frequency) over an ∼80 cm⁻¹ range as the water content is decreased.

Figure 2.

FT-IR absorption spectra of the OD stretch of HOD in H₂O for eight water/TEGDE mixtures and water. An increasing blue shift can be seen as the water content decreases.

Recent theoretical studies with comparison to experiments of various salt/water solutions attribute a blue shift to a reduction in the electric field along the hydroxyl stretch of the water bound to a large anion compared to a hydroxyl bound to a water oxygen.⁴⁴ Hydroxyls bound to a water oxygen will have the spectrum of pure water. The largest blue shift occurs for the 1:1 mixture, in which there is only one water molecule per TEGDE molecule. In this case, the IR spectrum peaks at 2589 cm⁻¹.

As water content decreases, the spectra develop an increased asymmetry. Even for pure water, the IR spectrum of the OD stretch displays a substantial tail on the red side of the spectrum. The pronounced tail is most likely attributable to hydroxyls bound to water oxygens even in the lowest water content sample in which the spectrum is dominated by water associated with TEGDE. That the lowest water content solutions contain a significant amount of ODs still hydrogen bonded to water oxygens is supported by the analysis of our pump-probe data. A detailed analysis of the spectra is presented below.

B. Population Relaxation

As discussed in Section II, the polarization selective IR pump-probe experiments are performed on the OD stretch of dilute HOD in H₂O/TEGDE systems. The measurements yield the signal parallel, I_‖(t), and perpendicular, I_┴(t), to the pump polarization. With I_‖(t) and I_┴(t), the vibrational excited state population decay, P(t), is obtained using,³⁶

$$P(t)=I_{\parallel }(t)+2I_{\perp }(t).$$ (1)

Equation 1 holds whether there are one or several subensembles in the system. I_‖(t) and I_┴(t) are also used to determine the orientational relaxation in Section III.D, where they are discussed further. The deposition of heat following vibrational relaxation produces a constant offset in the data at long-time, an effect that has been well documented.^36,45–48 The P(t) data have been corrected for this heating contribution using procedures developed previously.^45,46

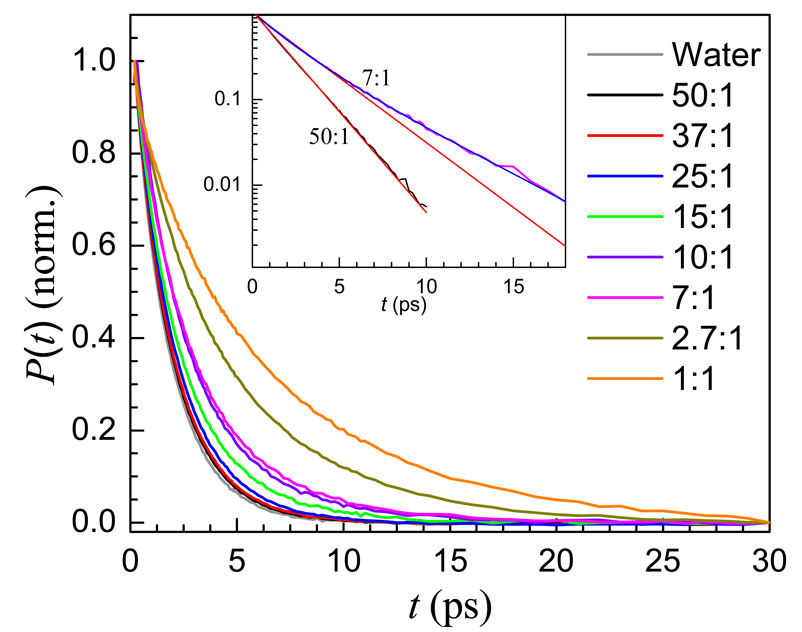
Population relaxation data, P(t), are shown in Figure 3. The decay for pure water is also shown for comparison. These data are collected at the wavelength corresponding to the peak of the IR absorption for each sample (see Figure 2). Each set of data was fit to either a single or bi-exponential decay. To obtain the wavelength-dependence of population relaxation in this system, data were also analyzed at a wavelength on the blue side of the absorption line corresponding to the quarter width point. The wavelengths and the results of the fits are given in Table 1.

Figure 3.

Population relaxation data for the OD stretch of HOD in H₂O in eight water/TEGDE mixtures and water. As water content decreases, the vibrational lifetimes increase. Inset: Semi-log plot of the 50:1 and 7:1 population relaxation decays. The 50:1 data are fit well to a single exponential decay, while the 7:1 sample is not (red lines). The 7:1 data are fit well to a bi-exponential decay (blue line).

Table 1.

Water/TEGDE population relaxation fitting parameters

sample	wavelengths (cm−1)		center			blue
	center	blue	fw	T1w (ps)	T1e (ps)	fw	T1w (ps)	T1e (ps)
water	2507		1	1.7
50:1	2510	2549	1*	1.9*		1*	2.1*
37:1	2520	2559	1*	1.9*		1*	2.2*
25:1	2520	2559	1*	2.0*		1*	2.4*
15:1	2530	2559	0.61	1.7	3.4	0.60	2.0	3.4
10:1	2534	2565	0.50	1.8	3.7	0.46	2.1	4.2
7:1	2539	2568	0.42	1.7	3.8	0.38	2.0	4.5
2.7:1	2569	2589	0.31	2.0	5.5	0.26	2.3	6.2
1:1	2589	2610	0.25	2.3	7.7	0.18	2.8	9.3

f_w is the amplitude of the T_1w water-like component. The T_1e ether associated component has amplitude 1 − f_w.

^*As discussed in the text, these are not purely water-like. Further discussion of these values is given in connection with Table 3.

Amplitude error bars: ±0.02 for single exponentials and ±0.04 for bi-exponentials.

Time constant error bars: ±0.2 ps for single exponentials and ±0.3 ps for bi-exponentials.

The OD stretch under observation has distinct structural environments that depend on the nature of the hydrogen bonding interactions. The structure will affect the process of vibrational relaxation.^36,49,50 Water molecules can either interact with other water hydroxyls (labeled as w waters), or they can interact with the polyether molecule (labeled as e waters). Molecular dynamics (MD) simulations have observed different environments of bulk-like water (free) and bound water associated with the polyether.¹⁰ In these ultrafast pump-probe experiments we excite the 0➔1 vibrational transition. This excitation will decay by pathways involving other modes in the system. Energy must be conserved. The initially excited OD stretch decays into a combination of lower frequency modes that have energies that sum to the original OD vibrational energy.⁴⁹ These pathways include high frequency modes of the excited water molecule, such as bends, high frequency modes of other molecules (water or TEGDE) and low-frequency bath modes, such as torsional and translational modes.^36,51 Because several discrete intramolecular modes are unlikely to match the energy of the initially excited mode, creation or annihilation of one or more modes of the continuum is necessary to conserve energy.⁴⁹ The OD stretch in different structural environments will have different coupled intramolecular modes and will experience different density of states of the continuum. Therefore, the lifetime is very sensitive to the local environment.³⁶

In the current experiments, if the OD stretch is hydrogen bonded to a water oxygen (w water) it will be coupled to a different set of intramolecular modes and a different continuum than if the OD is hydrogen bonded to an ether oxygen (e water). First consider the data for the center wavelengths (Table 1). The three water-rich samples, 50:1, 37:1, and 25:1, fit very well to single exponential decays. The time constants are a little longer than the time constant for OD relaxation of dilute HOD in bulk water and get longer as the water content decreases. At these high water concentrations, the sample will be composed of mostly w waters with e waters saturating the polyether molecules. If the e waters decay with a somewhat longer lifetime than the w waters, which should have a value essentially that of bulk water, then the data will appear as single exponential decays within experimental error with a lifetime that is a bit longer than that of found in bulk water. At the center wavelength most of the signal will come from water-like ODs (w) with a small contribution from ODs bound to ether oxygens (e). As the water concentration decreases, the fraction of e waters relative to w waters increases, and the vibrational relaxation will display a slower single exponential decay, as we observe. The wavelength dependence supports this interpretation (see Table 1). The data collected at bluer wavelengths for these three high water concentrations still fit quite well to single exponential decays, but in each case the decay is somewhat slower. At the bluer wavelengths the fraction of the pump-probe signal coming from e water will increase relative to w water. The slower contribution to the decay is increased, and the fit to the data yields a slower decay. Therefore, the wavelength dependence supports the idea that the apparent single exponential population decays for high water content samples arises from contributions from both w water and e water.

When the water concentration is lowered to the point where w waters stop dominating the system, ∼15:1, the population decay data no longer fit well to a single exponential function, but fit very well to a bi-exponential. The inset in Figure 3 shows the 50:1 data (black) and the 7:1 data (magenta) both with single exponential fits (red). The 50:1 data are fit well by a single exponential. The 7:1 data cannot be fit to a single exponential but fit well to a bi-exponential, shown as the blue curve through the 7:1 data.

The 15:1 solution marks a point at which the e water begins to be the dominant water species. TEGDE, with five ether oxygens, can make up to ten hydrogen bonds with water hydroxyls. A 15:1 solution has thirty hydroxyls per five ether oxygens. In addition to actual hydrogen bonding, some water molecules will have hydrophobic interactions with the methyl end groups and the ethylene segments. At 15:1 and lower water concentrations, the system's preference for gauche conformations decreases,^21,33 altering the structure of the polyether. As the water concentration is decreased further, the number of w waters becomes very small and e waters should predominate.

The fractions (f_w) in Table 1 show smaller relative populations of the w water with decreasing overall water content. However, a surprising result occurs for the 1:1 sample (one water per five ether oxygens). If the waters were distributed uniformly among the ether oxygens, there would only be e waters, which should result in a single exponential decay. For the center frequency for the 1:1 sample (Table 1), there is a very slow component, 7.7 ps, with substantial amplitude (75%). Based on the results for the high water concentration samples that yield single exponential decays, all of which are ∼2 ps, and the results for the intermediate bi-exponential decays, it is reasonable to assign this slow component to e water. However, there is a 25% component of the relaxation that occurs on a timescale consistent with w water. The observation of the bi-exponential decay for the 1:1 sample strongly suggests that the water molecules are not distributed uniformly among the ether oxygens. Even in the very low water content samples, aggregation of water occurs, resulting in w water to be present. Water cluster formation in concentrated TEGDE solutions has been suggested by several MD simulations and thermodynamic calculations.^8,10,25,32 The population decay results provide direct evidence for water clustering.

Considering only the center frequency (Table 1) as the water concentration is increased to 2.7:1, 7:1, and 10:1, the fraction of the slow component decreases with a corresponding increase in the fast component. This is consistent with the basic picture that the number of e waters decreases while the number of w waters increases as the water concentration increases. Note also that the decay time of the fast component (w) is basically unchanged within experimental error and is close to the 1.7 ps decay time of OD for dilute HOD in bulk water. In contrast, the decay time of the slow component becomes significantly faster. There is a very large change in going from the 1:1 sample to the 7:1 sample. The significant change in decay times with water concentration indicates that the local environment experienced by e water changes as the amount of water changes and that the e water should not be associated with a single unique structure. For 7:1 and higher water contents, the change of the slow component is less dramatic. The change in the decay times with wavelength at a given water concentration demonstrates that there is an inhomogeneous distribution of environments. Distinct environments that give rise to different lifetimes are correlated with the absorption wavelength.⁴⁸

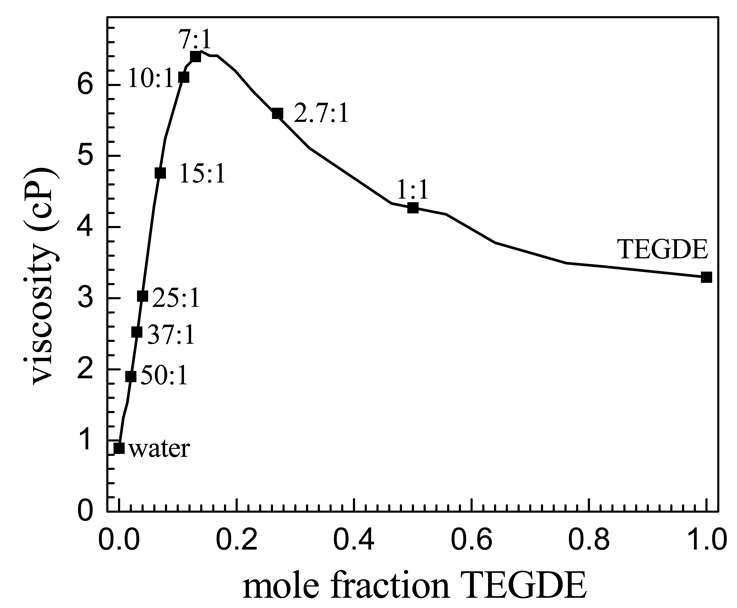
Figure 4 shows a plot of the viscosity as a function of the TEGDE mole fraction taken from the literature²⁸ with the specific water concentrations studied here indicated. The slow component of the bi-exponential decays becomes longer as the water concentration decreases from 15:1 to 1:1, but the viscosity first increases and then decreases. The density of the water/TEGDE solution series peaks at the 10:1 solution.^26,28,52 The lack of correlation of the slow population decay component with either the density or viscosity shows that local molecular structure is not directly related to the bulk density or viscosity.

Figure 4.

Viscosity data for mixtures of water and TEGDE reproduced from McGee et. al.²⁸ The positions of the eight solutions studied in this work as well as pure water and TEGDE are noted on the plot.

C. Analysis of the Spectra with the Two-Component Model

Because the pump-probe data can be rationalized well with a two-component model (w and e waters) to describe the water/polyether system, we investigated whether this model works for the FT-IR spectra. The results of a study of the OD stretch of HOD in H₂O in the AOT reverse micelle system³⁶ show that the absorption spectra of water inside different sizes of reverse micelles could be fit with a summation of the pure water spectrum and the spectrum of water in the smallest reverse micelle in which water primarily interacts with the ionic AOT head groups.³⁶ These results are consistent with the recent theoretical work on salt/water solutions.⁴⁴ Hydroxyls associated with the negatively charged AOT sulfonates would yield a blue shifted spectrum and hydroxyls not associated with the sulfonates would give a spectrum of pure water.

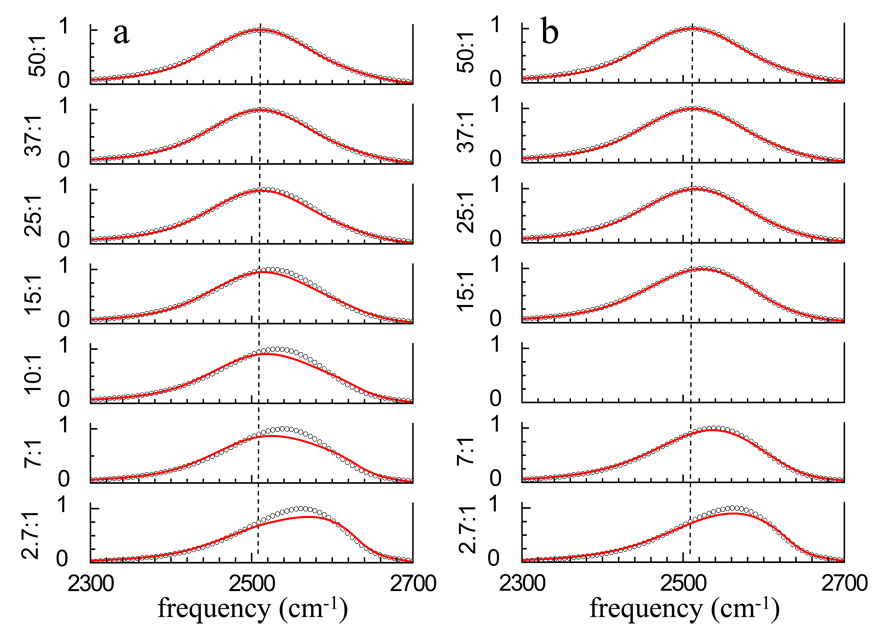
Based on the results for ions in water solutions⁴⁴ and AOT reverse micelles,³⁶ a simple two component model was tried for fitting the FT-IR spectra obtained for the eight water/TEGDE mixtures to determine if the series of spectra could be reproduced by combining the spectrum of pure water with the spectrum of the lowest concentration of water in TEGDE. We fit the FT-IR spectra of the 50:1, 37:1, 25:1, 15:1, 10:1, 7:1, and 2.7:1 mixtures with differing ratios of the pure water spectrum to the 1:1 spectrum, which is the most water-poor of the series. The results of this procedure are shown in Figure 5a and the fit parameters are listed in Table 2. The dashed line is centered at the peak of the 50:1 spectrum and is an aid to the eye. The fits are good for the highest water concentrations, but this is not surprising because the spectra are dominated by hydroxyls that are not associated with the polyether. Note that even in the 25:1 spectrum, the fit is somewhat low to the blue of the center of the spectrum. As the water concentration decreases, the fits become increasingly poor. There are substantial discrepancies in peak position, width, and overall shape.

Figure 5.

a) FT-IR spectra (circles) of the OD stretch of HOD in H₂O and fits (red curves) using a linear combination of the bulk water and 1:1 spectra. The spectra are not fit well by this model at the lower concentrations. b) Fits (red curves) to the FT-IR spectra (circles) using bulk water and the 10:1 spectra for the water-rich samples and the 10:1 and 1:1 spectra for the water-poor samples. The fits are greatly improved but still deviate from the data at the lower water concentrations.

Table 2.

Fitting parameters for spectra in Figure 5.

		50:1	37:1	25:1	15:1	10:1	7:1	2.7:1
Bulk/1:1 (Figure 5a)	Fraction bulk	1.0	0.99	0.97	0.89	0.81	0.70	0.37
	Fraction 1:1	0	0.01	0.03	0.11	0.19	0.30	0.63
Bulk/10:1/1:1 (Figure 5b)	Fraction bulk	0.99	0.92	0.75	0.38
	Fraction 10:1	0.01	0.08	0.25	0.61		0.88	0.48
	Fraction 1:1						0.12	0.52

Simulations have suggested that long PEO chains saturate with water around 0.5 weight percent.^10,30 Using this idea that the backbone becomes saturated at a certain water content, and that each ether oxygen can accept a maximum of two hydrogen bonds from water, it is possible that a structural change occurs at an intermediate concentration. The structural change could be an increasing heterogeneity amongst the conformations of the backbone in intermediate solutions, such as a greater mix of gauche and trans C-C bonds, as well as increased contact with hydrophobic groups. For PEO/water systems, it was established that both the pure polymer melt and dilute solutions contain less structural heterogeneity than in intermediate solutions of water and PEO.³⁰ After the backbone has been saturated, addition of more water will not induce further stabilization, making the environment more homogeneous.

To account for possible structural changes, another fitting procedure was used. The spectra for the samples with the higher water concentrations (50:1, 37:, 25:1, and 15:1) were fit with a combination of the pure water spectrum and the 10:1 mixture spectrum, and the spectra for the samples with the lower water concentrations (7:1 and 2.7:) were fit with a combination of the 10:1 and 1:1 spectra. Figure 5b shows the results of this fitting procedure. Again, the dashed line is centered at the peak of the 50:1 spectrum and is an aid to the eye. The higher concentration samples are fit well. The lower concentration samples are not fit as well, but there is substantial improvement compared to the fits in Figure 5a.

The two component model used in attempting to fit the spectra in Figure 5a works well for water in AOT reverse micelles because the local interactions that are responsible for the each component’s spectrum do not change with the amount of water. As more water is added to the AOT reverse micelles system, the water nanopool increases in size. The manner in which the water’s hydroxyl group interacts with the AOT head group does not change, so the spectrum as a function of water content can be reproduced by the sum of the two component spectra.

In the water/TEGDE system at high water concentrations, the polyether is saturated with water. Additional water forms a water-water network that has a spectrum like that of pure water. Hydroxyls associated with the saturated polyether have another spectrum. That the pure water spectrum and the 10:1 spectrum do a reasonable job of reproducing the higher water concentration spectra indicates that the spectrum of water associated with the saturated polyether does not change significantly when additional water is added. The 10:1 sample corresponds to two water molecules (four hydroxyls) per ether oxygen. Even for this sample, it is quite possible that not all ether oxygens accept hydrogen bonds from water hydroxyls. Reducing the concentration should result in an increased number of ether oxygen sites with either one or zero hydrogen bonded hydroxyls. The lowest concentration sample, 1:1, has one water molecule (two hydroxyls) for every five ether oxygens. If the only thing that changed when the water concentration is reduced below 10:1 is going from sites with two hydroxyls bound to each ether oxygen to one or no hydroxyls per ether oxygen, then the fitting procedure used in Figure 5b should still work to fit the low concentration spectra. Clearly it does not, which suggests structural changes occur that modify the nature of the interaction between water hydroxyls and TEGDE. A similar structural reorganization effect on the IR spectrum of water in heterogeneous systems has been observed in studies of water in Nafion fuel cell membranes.⁵³ The non-statistical mixing of the lower water content solutions (as demonstrated by the P(t) data) could in part account for a structural change.

D. Orientational Relaxation

In addition to the population relaxation, the orientational relaxation parameters of a system are extracted from polarization selective pump-probe experiments using the signals I_‖(t), and I_┴(t). For a single ensemble, I_‖(t), and I_┴(t) are given by

$$I_{\parallel }(t)=e^{-t/T_1}[1+0.8C_2(t)]$$ (2)

$$I_{\perp }(t)=e^{-t/T_1}[1-0.4C_2(t)]$$ (3)

where C₂(t) is the second Legendre polynomial orientational correlation function.⁵⁴ For a single ensemble, the anisotropy decay, r(t), is obtained from,

$$r(t)=\frac{I_{\parallel }(t)-I_{\perp }(t)}{I_{\parallel }(t)+2I_{\perp }(t)}=0.4C_2(t)$$ (4)

The denominator in equation 4 is the population relaxation (given in equation 1). In equation 4 the denominator divides out the lifetime and gives the pure orientational relaxation. As discussed in the previous section, the OD hydroxyls can be divided into two broad subensembles, those that are water-like (w), in which the HODs are hydrogen bonded to a water oxygens, and ether associated (e) with OD hydroxyls hydrogen bonded to an ether oxygen or otherwise associated with a TEGDE molecule, possibly through a hydrophobic interaction.^55,56 Included in the e subensemble are HODs with the OH associated with TEGDE and the OD hydrogen bonded to a water oxygen. Such HODs will undergo orientational relaxation that is distinct from the w subensemble. With the w and e subensembles having different orientational correlation functions and different lifetimes, r(t) is given by³⁶

$$r(t)=0.4\left(\frac{f_w{e}^{-(t/T_{1w})}{C}_2^w(t)+f_e{e}^{-(t/T_{1e})}{C}_2^e(t)}{f_w{e}^{-(t/T_{1w})}+f_e{e}^{-(t/T_{1e})}}\right),$$ (5)

where the f_i are the fractions of the signal coming from the two ensembles. The f_i depend on both the concentration of the two subensembles and their transition dipoles. T_1i are the vibrational population decay time constants as discussed in connection with Table 1. We have already seen that the lifetimes of ether associated ODs are longer than the water-like ODs. $C_2^i(t)$ are the orientational correlation functions for the i^th species. The numerator is I_‖(t) − I_╧(t) and the denominator is I_‖(t) + 2I_╧(t). In contrast to a system composed of a single ensemble, the denominator no longer divides out the population relaxation. For a system with two subensembles, the utility of using r(t) is lost.

In all samples containing water, r(t) has a very short time inertial component that decays in less than 200 fs regardless of whether equation 4 or 5 applies.^57–60 Following this ultrafast component, the orientational relaxation in pure water and other systems containing water decays much more slowly.^36,45,46,48 For example, the time constant for orientational relaxation of HOD in H₂O is 2.6 ps.⁴⁶ The inertial component is obscured in these experiments by a large non-resonant signal that tracks the IR pulse duration. Therefore, we do not obtain data for times less than 200 fs. The inertial component is manifested as an initial value for the anisotropy in equations 4 or 5 that is less than 0.4. This value is determined by extrapolating the data back 200 fs to t = 0.

For samples with very high water content, 200:1 and 100:1, following the inertial component, the r(t) decays appear to be single exponential within experimental error with time constants of 2.8ps and 3.4ps, respectively. These decays times (discussed further below) are somewhat longer than that of HOD in bulk water. Beginning with the 50:1 sample and for all of the lower water concentration samples, the anisotropy decays, r(t), are not single exponential, and they differ dramatically from pure water. Figure 6 displays the anisotropy decay (equation 4) of HOD in bulk water and in the 50:1 water/TEGDE solution. The 50:1 sample decays to what appears to be a constant off-set with a substantial fraction of the anisotropy in the off-set. Fitting the 50:1 data to a decay plus a constant off-set or to a bi-exponential decay yields a decay time constant of 1.7 ps and a constant, that is an effectively infinitely long decay. The water (HOD in H₂O) data, in contrast, fits well with a single exponential decay with a time constant of 2.6 ps. If the 50:1 is indeed composed of two subensembles of water molecules, those that are waterlike and those that are ether associated, then the w and e subensembles will have different orientational correlations functions (equation 5). NMR^55,61–63 and MD simulations^64,65 support a two component picture of water orientational dynamics near surfaces and solutes. They find that the water interacting directly with the solute or surface has slower orientational dynamics than bulk water, but the rest of the water has essentially bulk-like dynamics.

Figure 6.

Plots of orientational relaxation of water, r(t), for the 50:1 solution and bulk water. Bulk water decays to zero, while the 50:1 solution displays a plateau starting at ∼5ps.

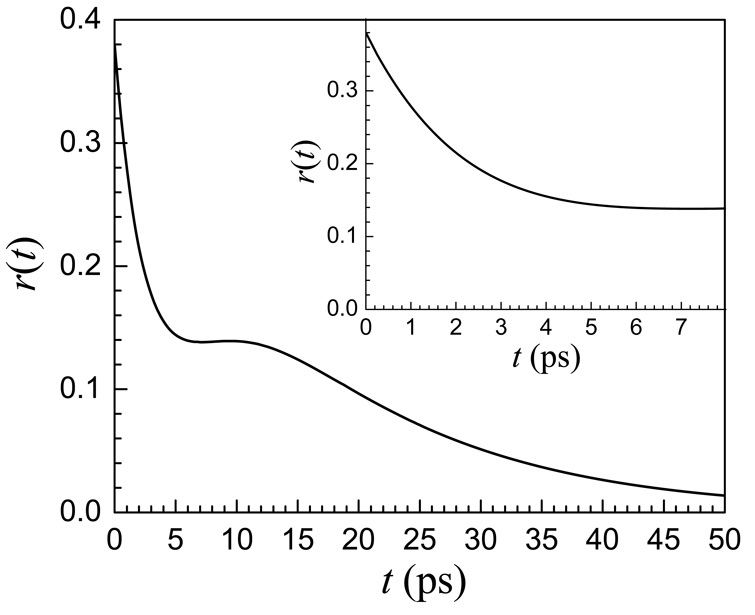
Two subensembles, each having single exponential orientational relaxation, do not produce anisotropy data, r(t), that is bi-exponential. The anisotropy decay for two subensembles each with its own vibrational lifetime and orientational correlation function is given in equation 5. Figure 7 shows the results of a calculation of r(t) using equation 5. The C_is are taken to be single exponentials with orientation relaxation decay time constants for the water-like and ether associated hydroxyls give by τ_rw and τ_re, respectively. In this example, T_w = 1.6 ps, τ_rw = 2.8 ps, f_w = 0.83 and T_e = 2.6 ps, τ_re = 15 ps, f_e = 0.17. Here the T_w and τ_rw values for the lifetime and the orientational relaxation time constants for the water-like portion match the values for OD of HOD in pure water within experimental error. The main portion of the figure shows the calculated decay to 50 ps. The curve decays rapidly, plateaus, and then continues to decay at a much slower rate. In the experiments, the vibrational lifetimes limit the time range over which the data can be observed. This is particularly true for r(t), where at long time, two small numbers are subtracted and then divided by a small number. Therefore, it is not possible to measure the data past ∼8 ps. The inset in Figure 7 shows the first 8 ps of the curve in the main portion of the figure. The calculated curve out to 8 ps is composed of a relatively fast decay to a plateau like the 50:1 data shown in Figure 6. The inset in Figure 7 reproduces the 50:1 data in Figure 6. Thus a reasonable explanation for data like that shown in Figure 6 is that the two subensembles of water molecules, w and e, give rise to the anisotropy decay like that shown in the main portion of Figure 7, but because the measurements have a limited time span, the data give the false appearance of arising from a fast decay followed by an essentially infinitely slow decay. The generated curves in Figure 7 use parameters that were obtained from fitting the 50:1 data in the manner discussed next.

Figure 7.

A calculated curve using the two-subensemble model for anisotropy (equation 5). At long time, r(t) decays to zero. At short time, the curve appears to approach a plateau. The inset is has an expanded time axis and displays the experimentally accessible time range. The inset has the same shape as the 50:1 data displayed in Figure 6.

For two subensembles, equation 5 shows that the denominator does not divide out the population relaxation. Therefore, it is better to simultaneously fit two separate curves, P(t) given in equation 1 and

$$\begin{array}{cc}R(t)=I_{\parallel }(t)-I_{\perp }(t)\hfill & =f_w{e}^{-(t/T_{1w})}{C}_2^w(t)+f_e{e}^{-(t/T_{1e}})C_2^e(t)\hfill \\ \hfill & =f_w{e}^{-(t/T_{1w})}{e}^{-(t/{\tau }_{rw})}+f_e{e}^{-(t/T_{1e})}{e}^{-(t/{\tau }_{re})}\hfill \end{array}.$$ (6)

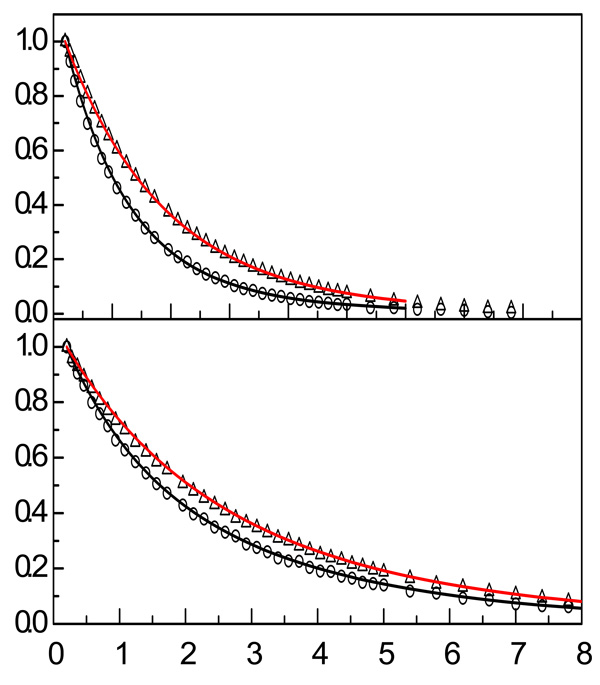
The C_is are single exponentials with orientational relaxation decay time constants τ_rw and τ_re for the water-like and ether interacting hydroxyls, respectively. The fits need to be internally consistent, reproducing both R(t), which depends on the orientational relaxation and the population decays, and P(t), which is determined only by the lifetimes. The advantage of this method is that the two curves, R(t) and P(t), have better signal-to-noise ratios than r(t), which is their ratio. Figure 8 shows two sets of R(t) and P(t) data (symbols) with the simultaneous fits (solid curves) for the 50:1 and 7:1 samples’ data. With the sum of the fractions, f_w + f_e = 1, the initial value of R(t) from equation 2 and equation 3 is 1.2. However, in the figure, R(t) has been normalized to 1. It is clear from Figure 8 that the simultaneous fits are very good.

Figure 8.

Simultaneous fits (solid curves) to R(t) and P(t) data (symbols) for the 50:1 and 7:1 solutions. The simultaneous fits yield the population relaxation and reorientational relaxation parameters.

Before discussing the lower water content samples, we will return briefly to the 200:1 and 100:1 samples. These samples have r(t)s that can be fit to single exponentials. Calculations were performed using equation 5 with the parameters used to produce the data for the 50:1 sample (see Figure 6 and Figure 7 and Table 3) except for the water-like and ether associated fractions, f_w and f_e. The fractions were changed to reflect the additional water with no adjustable parameters. The 50:1 sample has f_w = 0.83 and f_e = 0.17, which correspond to 83 and 17 hydroxyls in the two fractions. We fixed the number of hydroxyls associated with the ethers because they are saturated at 50:1 and for the 200:1 sample increased the number of hydroxyl in the water fraction to 383 and in the 100:1 sample to 183. Increasing f_w causes the fast decay seen at short times in Figure 7 to drop further before leaving off. Within the experimental window, the observable portions of the calculated curves were fit extremely well as single exponentials with decay constants of 2.9 ps and 3.4 ps for the 200:1 and 100:1 samples, respectively. These numbers are essentially identical to the measured decay times given above. Therefore, the two subensemble model reproduces the apparent single exponential decays for high water content and yields the observed decay times.

Table 3.

Parameters from simultaneous fits to the R(t) and P(t) data

Center Wavelengths
sample	wavelength (cm−1)	fw	T1w (ps)	T1e (ps)	τrw (ps)	τre (ps)
50:1	2510	0.83	1.6	2.9	2.8	15
37:1	2520	0.80	1.6	3.0	3.7	17
25:1	2520	0.77	1.7	3.1	3.6	25
15:1	2530	0.61	1.7	3.4	3.4	20
10:1	2534	0.50	1.8	3.7	3.9	19
7:1	2539	0.42	1.7	3.8	2.9	23
2.7:1	2568	0.31	2.0	5.5	2.4	16
1:1	2589	0.25	2.3	7.7	1.0*	11*
Blue Wavelengths
sample	wavelength (cm−1)	fw	T1w (ps)	T1e (ps)	τrw (ps)	τre (ps)
50:1	2549	0.75	1.8	2.8	2.4	12
37:1	2560	0.70	1.8	3.0	2.9	14
25:1	2560	0.68	1.9	3.3	2.9	23
15:1	2560	0.60	2.0	3.4	3.4	21
10:1	2565	0.46	2.1	4.2	3.0	17
7:1	2568	0.38	2.0	4.5	2.8	20
2.7:1	2589	0.26	2.3	6.2	1.8	15
1:1	2610	0.18	2.8	9.3	0.9*	9*

f_w is the amplitude of the T_1w and τ_rw water-like components. The T_1e and τ_re ether associated components have amplitude f_e = 1−f_w.

Amplitude error bars: ±0.04.

Time constant error bars: ±0.3 ps for T_1w, T_1e (ps) and τ_rw; ±3 ps for τ_re.

^*See text for revised values using wobbling-in-a-cone mechanism.

Table 3 gives the results for simultaneous fits to R(t) and P(t) for the center wavelengths and the higher frequency (blue) wavelengths for the various lower water content samples. The wavelengths are given in Table 1. As discussed in Section III.B, the high water content samples, 50:1, 37:1, and 25:1, have population decays that were fit to single exponentials. In Section III.B, we suggested and supported by the wavelength dependent results (see Table 2) that these decays actually contained two components with similar enough lifetimes that the two components could not be readily separated. The results of the simultaneous fits to R(t) and P(t) yield the two lifetimes. The T_1w values show little change with water content and for all but the lowest two water content samples are within experimental error of the 1.7 ps OD lifetime in bulk water. In contrast, T_1e displays a concentration dependence that is well outside the error bars, with the lowest two water content samples showing the largest changes. The lifetime is very sensitive to local structure. Particularly at low water concentration there are large changes in T_1e with wavelength. These changes demonstrate that there is considerable inhomogeneity in the nature of the environments experienced by ether associated water.

The rotational time constant for the water-like component, τ_rw, of the 50:1 sample is within experimental error the same as pure water (2.6 ps). For the center wavelength τ_rw increases as the water content is decreased and then decreases again. The maximum occurs for the 10:1 sample although the 7:1 sample has the maximum bulk viscosity (see Figure 4). The difference in the 10:1 and 7:1 viscosities is not large. The bluer wavelength shows the same trend although at this wavelength, the variation is virtually within the error bars except at the lowest water concentrations. The net result is that the influence of TEGDE on the water-like component is not great. Both the vibrational lifetime and the orientational relaxation time are very similar to those of bulk water except for the lowest water concentration samples, particularly the (1:1) sample. We will return to this sample below.

The rotational decay times, τ_re, for the ether associated water differ substantially from those of HOD in bulk water. The trend for the center wavelength and the bluer wavelength are the same. The error bars for τ_re are ±3 ps. Given the size of the error, the trend (Table 3) shows that the highest two water content samples and lowest two water content samples have faster orientational relaxation than the middle concentrations. The 7:1 sample seems to mark a transition point in the series of solutions. The 1:1 sample is significantly faster than the rest. The error bars for this sample are smaller than ±3 ps because the lifetimes, particularly T_1e, are longer. The longer ether component lifetime and the faster reorientation make the measurements subject to smaller error.

The amplitude of the water-like component, f_w, decreases monotonically as the water content decreases. The amplitude of the hydroxyls associated with the ether increases as f_e = 1 − f_w. For the bluer wavelength, the f_w values are all smaller than they are at the center wavelengths. This is consistent with the hydroxyls bound to ethers having spectra that are blue shifted from the water-like hydroxyls. The f_is cannot be directly associated with the concentrations of the species because they depend on both the concentration and the transition dipole to the fourth power.³⁶ As discussed above, the ether associated fraction can include both water bound to ether oxygens and water molecules that have hydrophobic interactions with the methyl and ethylene portions of TEGDE. The combination of these two effects can decrease the water-like fraction f_w. Although the fractions cannot necessarily be directly related to the concentrations, the trend is significant. As the water concentration is decreased the water-like component decreases. As discussed in Section III.B, even at the lowest water concentration, where statistically we might expect all the hydroxyls to be bound with ether oxygens, the waterlike fraction, arising from OD hydroxyls bound to water oxygens, is significant. Therefore, the non-negligible fraction of water-like hydroxyls at low water concentrations indicates the formation of water rich regions, that is, there is some clustering of waters such that even at very low water contents there are still some w waters.

The two component model fits the data well with consistent and reasonable values and trends except for the lowest water concentration sample, 1:1. The indication that the model may not be correct for the 1:1 sample is made particularly clear by the τ_rw value of ∼1 ps, which is much faster than the values found for other samples including bulk water. It is not reasonable to have orientational relaxation that is almost a factor of three faster than pure water in a sample that has almost no water in it. Complete orientational randomization requires a concerted swapping of hydrogen bonds that takes the OD hydroxyls under observation to new orientations.⁵⁸ The 1:1 sample displays a bi-exponential anisotropy decay, r(t) (equation 2), which suggests that a wobbling-in-a-cone mechanism^36,48,66,67 for orientational relaxation might be applicable for low water content solutions. With wobbling-in-a-cone, orientational relaxation occurs on two time scales. For water in restricted environments, there is a fast time scale (∼ 1 ps), there is orientational diffusion that can only sample a limited cone of angles.^36,48,67 Following the sampling of the cone of angles, orientational randomization is completed on a longer time scale by jump orientational relaxation.^48,58 The fast wobbling component is associated with fluctuations of the intact hydrogen bond network that cause the OD hydroxyl to sample a restricted range of angles.⁶⁸

The bi-exponential decay of the population, P(t), demonstrates that there are indeed two subensembles of water molecules in the 1:1 sample. Nonetheless, when the two subensembles are tightly coupled through the hydrogen bond network, it has been observed in other systems that the orientational relaxation can decay as a single ensemble even though the population decays as a bi-exponential.³⁶ Here, the basic idea is that in the 1:1 sample there are so few water molecules that the concerted jumps necessary for complete orientational randomization require participation of both hydroxyls bound to water oxygens and hydroxyls bound to ether oxygens. The orientational relaxation of the two subensembles is not independent, and the result is a single orientational correlation function. If we assume that the wobbling-in-a-cone mechanism accurately describes the dynamics of the 1:1 sample, then we obtain a wobbling time constant of 0.7 ps (τ_w) and a time of constant for complete randomization of 15 ps (τ_l). The cone semi-angle is 25°. The result is the slower decay component is almost the same as the 2.7:1 sample’s slow decay. Extraction of these parameters from anisotropy data has been described in detail previously.³⁶

All of the concentrations from 50:1 through 7:1 give either infinite or extremely long τ_l values with no consistent trend if the wobbling model is applied. The τ_rw and τ_re values obtained from the two component model for the 2.7:1 data are reasonable and consistent with the values for higher water content samples (see Table 3). A fit to the wobbling model yields time constants τ_w = 1.3 ps and τ_l = 24 ps, which are also reasonable values. Therefore, we cannot be certain whether the two component model or the wobbling model is more appropriate for this sample. The significant differences between the T_1e value for the 2.7:1 sample and the higher water concentration samples suggest that there has been a substantial change in the hydroxyl local environment, perhaps supporting the wobbling model. In either case, the 2.7:1 sample has a long orientational relaxation decay of ∼20 ps.

NMR studies of PEO have suggested that water makes hydrogen bonds between separate PEO molecules at low water contents, leading to restricted polymer motion.³⁵ It has been further proposed through simulations that single water molecules could form cross-links between different polyether molecules, although the cross-links would be most stable and abundant in long-chain hydroxyl-terminated PEO.³¹ Even if only some of the TEGDE molecules in the 7:1 solution are cross-linked, those molecules that are cross-linked could contribute to the observed high viscosity (see Figure 4). The bi-exponential population decays, P(t), observed here show that there are two types of water hydroxyls at all concentrations, those that are hydrogen bonded to water oxygens and those that are bonded to ether oxygens. There can be a small concentration of transitory unbound hydroxyls, but free hydroxyls are energetically highly unfavorable. For a water molecule to undergo reorientation, its hydroxyls will switch oxygen hydrogen bonding partners. The results shown in Table 3 demonstrate that the orientational relaxation has only a mild dependence on water content. Even at the lowest water content, 1:1, for which the wobbling-in-a-cone model was used, the orientational randomization time is very similar to the slow time components measured at higher water concentrations. There is a tendency for both the water-like and ether associated reorientation times to be slower in the region of higher viscosity, but the trend is not pronounced.

IV. Concluding Remarks

Polarization selective pump-probe experiments were used to study the vibrational population relaxation and orientational relaxation of the OD hydroxyl of dilute HOD in mixtures of H₂O and TEGDE. The ratio of water to TEGDE was varied from 200:1 to 1:1. Substantial differences from a sample of bulk water became observable in the 50:1 sample. At higher water contents (200:1 and 100:1), the population relaxation and orientational relaxation were similar to but somewhat slower than those measured in bulk water, with the orientational relaxation exhibiting single exponential decays. However, even for these samples the small increases in the orientational relaxation times relative to bulk water are consistent with the two component model.

Vibrational population relaxation (Table 1 and Table 3) is very sensitive to the local environment. Bi-exponential decays arise because there are two distinctly different environments for the water hydroxyls. Differences in the local structure change the coupling of the hydroxyl stretch oscillator to other modes and also change the types and density of states of modes that accept the energy upon vibrational relaxation. The waterlike fraction, f_w, decreases monotonically as the water content is decreased. Of particular interest is that bi-exponential population relaxation is observed at the lowest concentrations, and the water-like component has significant amplitude. In the 1:1 sample, there are only two hydroxyls for five ether oxygens. If the hydroxyls were hydrogen bonded uniformly among the ether oxygens, the population decay would be single exponential. The significant amplitude in the water-like vibrational relaxation component is a strong indication that water clusters such that a fraction of the water hydroxyls are bound to water oxygens with the majority bound to ether oxygens. Significant changes in the structure of the TEGDE hydroxyl binding sites are indicated for the lowest two water content samples, 2.7:1 and 1:1, by the substantial increase in the hydroxyl-ether population relaxation time, T_1e (see Table 3).

The most striking feature of the orientational relaxation is that the concentration dependence is quite mild. With the exception of the 1:1 sample, the water-like component, τ_rw, is at most a factor of 1.5 slower than that found in pure water (2.6 ps). This result indicates that for hydroxyls bound to water oxygens, orientational relaxation is not greatly hindered by the presence of TEGDE even at high TEGDE concentrations. The orientational relaxation of hydroxyls associated with the polyether is considerably slower than that of pure water, but the dependence on water content is not great. The orientational relaxation times are all ∼20 ps, with the times being somewhat slower in the intermediate concentration range where the bulk viscosity is the highest. Water is not locked into quasi-static configurations even in very low water content samples. Between the 50:1 sample and the 7:1 sample, the bulk viscosity changes by over a factor of three (see Figure 4), but the water orientational relaxation displays a much smaller variation. The water content has a much more pronounced effect on the bulk viscosity than it does on the water reorientation times. The relationship between the water content and the TEGDE orientational relaxation of the bulk solution is currently under investigation from ∼100 fs to ∼1 ns using optical heterodyne detected optical Kerr effect experiments.