Quantum computing with defects

Abstract

Identifying and designing physical systems for use as qubits, the basic units of quantum information, are critical steps in the development of a quantum computer. Among the possibilities in the solid state, a defect in diamond known as the nitrogen-vacancy (NV^-1) center stands out for its robustness—its quantum state can be initialized, manipulated, and measured with high fidelity at room temperature. Here we describe how to systematically identify other deep center defects with similar quantum-mechanical properties. We present a list of physical criteria that these centers and their hosts should meet and explain how these requirements can be used in conjunction with electronic structure theory to intelligently sort through candidate defect systems. To illustrate these points in detail, we compare electronic structure calculations of the NV^-1 center in diamond with those of several deep centers in 4H silicon carbide (SiC). We then discuss the proposed criteria for similar defects in other tetrahedrally coordinated semiconductors.

A quantum computer is a device that would exploit the rules of quantum mechanics to solve certain computational problems more efficiently than allowed by Boolean logic (1). Over the past two decades, qubits have been implemented in a wide variety of materials, including atoms (2), liquids (3), and solids such as superconductors (4), semiconductors (5), and ion-doped insulators (6). Recently, the diamond nitrogen-vacancy (NV^-1) center has emerged as a leading qubit candidate because it is an individually addressable quantum system that may be initialized, manipulated, and measured with high fidelity at room temperature (7). Interestingly, even though these successes stem largely from the defect’s nature as a deep center (a point defect with highly localized electronic bound states confined to a region on the scale of a single lattice constant), no systematic effort has been made to identify other deep centers that might behave similarly. We outline the physical features that such deep centers and their hosts should exhibit and show how these criteria can be used to identify potential qubit candidates within a large class of defects structurally analogous to the diamond NV^-1. To aid in the illustration of these points, we compare density functional theory (DFT) calculations of the diamond NV^-1 with those of several defects found in 4H-SiC.

Searching for deep centers that behave like the diamond NV^-1 is worthwhile for several reasons. From an engineering perspective, it is currently quite difficult to grow and fabricate devices from diamond. The discovery of a similar defect in a more technologically mature host material might allow for more sophisticated implementations of single- and multiqubit devices. Additionally, because deep centers and semiconductors as a whole exhibit a diverse set of physical characteristics, innovative areas of device functionality may potentially arise once the quantum properties of these defect systems are more fully explored. From a physics perspective, other deep centers with highly controllable quantum states might help to resolve outstanding questions regarding the structure and dynamical properties of the diamond NV^-1 or of deep centers in general.

Defect and Host Criteria for NV-Like Systems

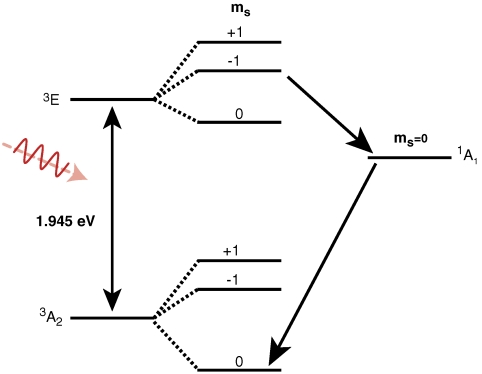
Structurally, the diamond NV^-1 consists of a carbon vacancy and an adjacent substitutional nitrogen impurity. The bound states of this deep center are multiparticle states composed of six electrons: five contributed by the four atoms surrounding the vacancy, and one captured from the bulk. As shown in Fig. 1, the lowest energy bound state is a spin triplet (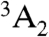) whose spin sublevels differ slightly in energy. The m_s = 0 and -1 sublevels of this ground state can be chosen to function as the qubit state, and coherent rotations between the two sublevels may be induced by applying microwave radiation tuned to the energy splitting between them. A spin-conserving optical transition exists between the 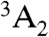state and an excited-state triplet (³E) 1.945 eV higher in energy. In addition, there exists a spin-selective decay path between these two states that includes a nonradiative transition from ³E to an intermediate spin singlet (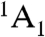). In combination, these transitions allow the center to be optically initialized and measured. That is, they allow the defect to be optically pumped into the m_s = 0 sublevel of 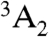, and they cause the fluorescence intensity between ³E and 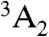to be spin-dependent (8).

Fig. 1.

Multiplet structure of the NV^-1 center in diamond. A 1.945-eV spin-conserving optical transition exists between the ground- (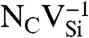) and excited- (³E) state triplets. Transitions from the m_s =  ± 1 sublevels of ³E to an intermediate spin singlet (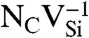) are much stronger than those from the m_s = 0 sublevel. The spin-selective nature of this decay path can be used in conjunction with the 1.945 eV transition to optically polarize and measure the spin state of .

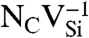Two features of the diamond NV^-1 help to distinguish it from other solid state qubit systems. First, the center’s highly localized bound states are well isolated from sources of decoherence. At room temperature, the ground state can exhibit extremely long spin coherence times of up to 1.8 ms (9), which is close to the regime needed for quantum error correction, given that manipulation rates greater than 200 MHz have been demonstrated (10, 11). Second, the structure of the defect’s excited-state manifold allows the defect to be optically initialized and measured with high fidelity under ambient conditions. Many other solid state systems are initialized via thermal equilibration and therefore require cryogenic operating temperatures (12–14). And, whereas other systems can be initialized optically (15) or can operate at room temperature (16), they currently can be measured with high fidelity only in an ensemble.

To reproduce these two features, there are several criteria that a candidate deep center and its host should meet. Specifically, centers should exhibit the following five characteristics (for simplicity, we restrict discussion of these characteristics to centers for which, like the diamond NV^-1, spin can be treated as a good quantum number):

• (D1)A bound state that is suitable for use as a qubit. This state must be paramagnetic and long-lived, and an energy splitting must exist between at least two of the state’s spin sublevels. If the qubit state is to be manipulated via electron spin resonance, the size of this energy splitting must fall within an appropriate range of the radio frequency spectrum.
• (D2)An optical pumping cycle that polarizes the qubit state. This cycle will most likely consist of an optical transition from the ground state to an excited state, followed by a spin-selective decay path that includes one or more nonradiative transitions between states of differing spin multiplicity.
• (D3)Luminescence to or from the qubit state that varies by qubit sublevel in some differentiable way, whether by intensity, wavelength, or other property. If fluorescence from an excited state is used to probe the qubit, the fluorescent transition should be spin-conserving. In addition, the strength of this fluorescent transition, which depends on the lifetime of the excited state, should be large enough to enable efficient, high fidelity measurement of individual defect qubit states.
• (D4)Optical transitions that do not introduce interference from the electronic states of the host. All optical transitions used to prepare and measure the qubit state must be lower in energy than the energy required to transfer an electron into (out of) the center from (to) the electronic states of the host.
• (D5)Bound states that are separated from each other by energies large enough to avoid thermal excitation between them. If the energy difference between two bound states is too small, thermal excitations may couple states and destroy spin information.

In addition, an ideal crystalline host will have the following qualities, the final three of which should help to reduce decoherence in the defect:

• (H1)A wide band gap, so that it can accommodate a deep center that will satisfy requirement D4 above.
• (H2)Small spin-orbit coupling, in order to avoid unwanted spin flips in the defect bound states.
• (H3)Availability as high-quality, bulk, or thin-film single crystals, in order to avoid imperfections or paramagnetic impurities that could affect the deep center’s spin state.
• (H4)Constituent elements with naturally occurring isotopes of zero nuclear spin, so that spin bath effects may be eliminated from the host via isotopic engineering (9).

It is relatively easy to identify hosts that satisfy criteria H1–H4, and this is discussed in detail in Identifying Candidate Host Materials in SI Text. However, it is not as simple to predict whether a given defect will satisfy criteria D1–D5. Nevertheless, certain aspects of a defect’s electronic structure can be predicted in a straightforward manner by using first-principles calculations. For example, the spin of a defect bound state can be calculated, determining whether the defect is paramagnetic or not, which is a major component of criterion D1. However, it is difficult to accurately compute the energy splittings between the spin sublevels of a bound state. In the case of criterion D2, the defect-induced gap levels obtained via first-principles calculations can be used to predict whether a paramagnetic defect will possess internal optical transitions. In addition, the energies of these optical transitions can be calculated by using constrained DFT, and excitonic effects can be included through the Bethe–Salpeter formalism (17). An explicit characterization of nonradiative decay paths, on the other hand, is much more challenging and is generally beyond the reach of current first-principles methods (18). The application of first-principles calculations to criterion D3 depends on the desired method of qubit measurement. In cases like the diamond NV^-1, where the intensity of luminescence to the qubit state should vary by spin sublevel, first-principles predictions are again limited by the challenging nature of nonradiative transitions. In cases where the wavelength of luminescence is meant to vary by spin sublevel, the small magnitude of the spin sublevel splittings (in the microwave range for qubits manipulated via electron spin resonance) renders it difficult to quantitatively evaluate luminescence energies on the basis of first-principles calculations. Still, in combination with perturbation theory, first-principles calculations can provide information about the ordering of sublevels, and this can help guide experimental identification of observed optical transitions. Additionally, the excited-state lifetime discussed in criterion D3 can be characterized by calculating the magnitudes of the dipole matrix elements associated with the internal optical transitions. Finally, the properties associated with criteria D4 and D5 can be studied explicitly by analyzing the energies of calculated defect-induced gap levels, both relative to each other and relative to the band edges of the host material.

Even though some aspects of D1–D5 are difficult to evaluate by using standard first-principles methods, potential qubit candidates can still be identified by observing that a close relationship exists between the atomic configuration of a defect and its electronic structure (19). In tetrahedrally coordinated semiconductors, vacancies and vacancy-related complexes similar to the NV^-1 center in diamond are likely to possess bound states with comparable physical properties. Within this group of defects, one can then use first-principles calculations to determine which members are compatible with criteria D1–D5. In the next section, we demonstrate in detail how this assessment can be made, by using as an example the results of calculations performed for several defects in diamond and SiC.

Formation Energies, Defect-Level Diagrams, and Configuration-Coordinate Diagrams

DFT calculations have become an indispensable tool for studying the properties of defects. Recent advances using hybrid functionals, which incorporate some degree of the Hartree–Fock exchange interaction, have led to very accurate descriptions of defect states by overcoming the well-known band-gap problem of traditional DFT. We apply this methodology to defect systems analogous to the NV^-1 defect in diamond. Specifically, we discuss defect formation energies and configuration-coordinate diagrams for defect excitations, as well as the arrangement of the defect-induced gap levels, which we discuss in terms of “defect-level diagrams” (DLDs).

One of the most important quantities that can be extracted from first-principles calculations is the formation energy (E^f) of a defect. E^f provides information on the overall stability of a given defect, as well as the relative stabilities between different atomic configurations and charge states. E^f determines the defect concentration through a Boltzmann relation (20):

where N_S is the number of possible defect sites. Strictly speaking, this expression is valid only in equilibrium; however, formation energies are informative even when defects are created in nonequilibrium processes, such as ion implantation. Specifically, the magnitude of E^f still provides an indicator of which defects are most likely to form. Once a defect is formed, the relative stability of different charge states for a given defect is always determined by the dependence of E^f on the Fermi level, whatever the creation process of the defect.

The NV Center in Diamond.

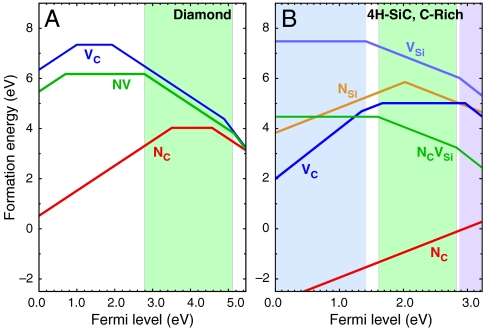
As explained in Methods, E^f depends on the charge state of the defect and on the Fermi level (ε_F), which is referenced to the valence-band maximum (VBM) of the bulk host material. Fig. 2 shows E^f for the NV center in diamond, as well as for the carbon vacancy (V_C), and substitutional nitrogen (N_C). For each defect, only the charge state with the lowest E^f is included at each value of ε_F. For a given ε_F, the charge state of a defect is equal to the slope of that defect’s E^f curve at that point. The kinks in the E^f curves correspond to charge-state-transition levels, i.e., ε_F values where the charge state of the defect changes. Fig. 2 thus shows the range of ε_F for which each charge state of the defect is stable; both the isolated vacancy and the NV center can be stable in the +1, 0, -1, or -2 charge states. Determining which charge states are stable, and under what conditions, is crucial to evaluating whether these vacancy-related defects satisfy criterion D1. This determination is crucial because each charge state will correspond to a different spin configuration, with some having paramagnetic ground states and others not.

Fig. 2.

Formation energy, E^f, as a function of Fermi level, ε_F. E^f was calculated for various defects in (A) diamond and (B) 4H-SiC (in C-rich conditions). The shaded areas show the range of stability of NV^-1 in diamond, and 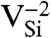(Blue), 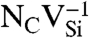(Green), and 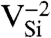(Purple) in SiC.

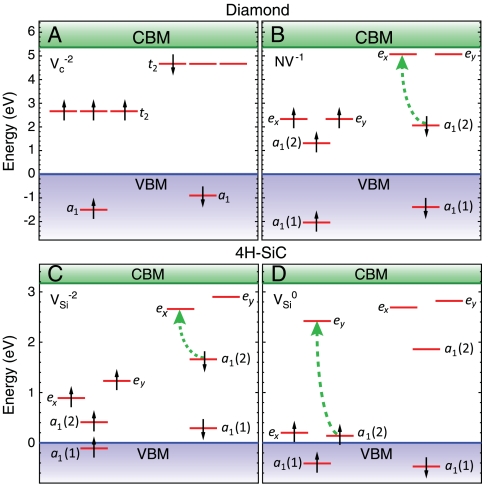
The ground-state spin of each charge state can be determined by considering the defect’s electronic structure. The electronic structure of vacancy-related centers in tetrahedrally coordinated semiconductors can be understood in terms of atomic sp³ orbitals and the corresponding single-particle levels. In an environment with tetrahedral symmetry, the four degenerate sp³ dangling-bond (DB) orbitals neighboring a vacancy are split into a low-energy symmetric a₁ level and three degenerate t₂ levels (as seen in Fig. 3A for the -2 charge state of V_C, which is stable in N-doped diamond). Because of the high symmetry of the isolated vacancy, this level structure does not lead to a ground-state triplet. However, a ground-state triplet can be achieved by placing an impurity atom next to the vacancy, thus shifting the a₁ level [becoming a₁(1)] and splitting the degeneracy of the t₂ levels into a₁(2), e_x, and e_y levels (21); Fig. 3B shows the DLD for NV^-1.

Fig. 3.

Defect-level diagrams for vacancy-related complexes. These diagrams show the single-particle defect states for (A) the 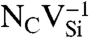and (B) the NV^-1 in diamond, as well as for (C) the 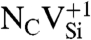and (D) the 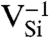in 4H-SiC. The spin-majority (spin-minority) channel is denoted by upward- (downward-) pointing arrows.

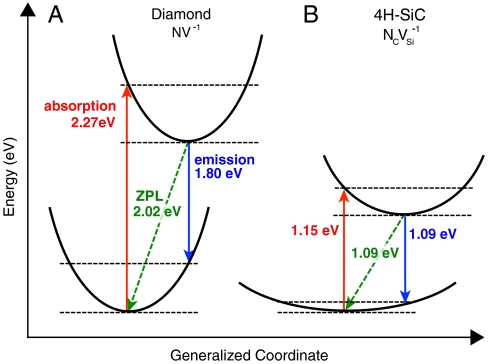
The NV^-1 defect is stable for ε_F between 2.78 and 5.14 eV, consistent with the likely position of ε_F in N-doped diamond [N being a deep donor located ∼1.9 eV below the conduction-band minimum (CBM) (22)]. The associated single-particle eigenvalues are listed in Table 1; their occupation determines the spin state (i.e., a spin-one triplet). The location of the defect-induced gap levels illustrates the defect’s compliance with D4 and D5, because they are well isolated from the bulk bands, with a relatively large spacing between occupied and unoccupied levels. As shown by the green dashed arrow in Fig. 3B, we can remove an electron from the spin-minority channel of the a₁(2) level and place it into one of the e_i spin-minority levels, keeping the ground-state atomic configuration fixed. The corresponding absorption energy of 2.27 eV is shown in the configuration-coordinate diagram of Fig. 4A. If we subsequently allow the atomic positions to relax, maintaining the excited-state triplet electronic configuration, we obtain a zero-phonon line (ZPL) energy of 2.02 eV and a Frank–Condon shift of 0.26 eV, both in good agreement with experiment (23) as well as with recent calculations (24). This discussion illustrates how the computationally accessible properties relevant to criterion D2 can be obtained.

Table 1.

Defect-level energies for various vacancy and NV centers in diamond and SiC (underlined values indicate the level is occupied)

Material	Defect	No. of els.	Spin majority				Spin minority
			a1(1)	a1(2)	ex	ey	a1(1)	a1(2)	ex	ey
Diamond	V-2	6	−1.46	2.66	2.66	2.66	−0.09	4.67	4.67	4.67
Diamond	NV-1	6	−2.04	1.31	2.33	2.33	−1.39	2.06	5.07	5.07
4H SiC		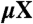6	−0.41	0.06	0.29	0.33	−0.72	0.93	2.35	2.51
4H SiC		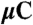6	−0.11	0.41	0.89	1.23	0.29	1.66	2.66	2.90
4H SiC		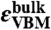5	−0.11	0.43	0.43	0.67	0.53	2.66	2.67	3.14
4H SiC		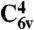4	−0.41	0.14	0.20	2.42	−0.47	1.86	2.69	2.82

Fig. 4.

Configuration-coordinate diagrams for spin-conserving triplet excitation. Excitation cycles for (A) the NV^-1 center in diamond and (B) the 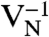center in SiC are shown. Absorption, emission, and ZPL transitions are indicated, along with their energies.

Defect Centers in SiC.

SiC shares many similarities with diamond, and recent experimental evidence indicates that it may also harbor deep centers suitable for quantum computing (25–28). We focus on the 4H polytype because large single crystals are readily available, and because its band gap (3.27 eV) is larger than that of 3C-SiC (2.39 eV) and 6H-SiC (3.02 eV) (29). Fig. 2B shows E^f for the silicon and carbon vacancies (V_Si and V_C), as well as for substitutional nitrogen (N_Si and N_C). E^f is more than 4 eV larger for N_Si than for N_C, so N has an extremely strong energetic preference to sit on a C site. This large energy difference implies that only nitrogen-vacancy centers composed of a N_C and a V_Si will form in SiC. According to Fig. 2B, N_CV_Si is stable in the 0, -1, and -2 charge states. Similar to the diamond NV^-1 defect, six electrons are confined to the 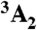defect, which is stable for ε_F between 1.60 and 2.83 eV. The levels for the corresponding DLD are listed in Table 1. Note that the degeneracy of the e_i levels is lifted because of the lower symmetry of the crystal structure.

The calculated configuration-coordinate diagram for 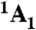is shown in Fig. 4B. Comparing these numbers with the diamond NV^-1 (Fig. 4A), we see that the vertical transitions are about half as large in the 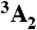center, whereas the relaxation energies are more than 75% smaller. The difference in transition energies can be attributed to the larger lattice constant of SiC compared with diamond: Although the vacancy is surrounded by C atoms in both materials, the larger lattice constant of SiC leads to a smaller overlap among the sp³ DB orbitals and therefore to a smaller splitting between a₁(2) and e_i levels.

It is interesting to also consider isolated vacancies in SiC. 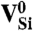in SiC can support a spin-conserving triplet excitation because the broken tetrahedral symmetry of the host splits the t₂ levels (Fig. 3 C and D). Our calculated formation energies in Fig. 2B show that the 0, -1, and -2 charge states are all stable. Similar to the diamond NV^-1 or SiC 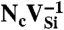defects, six electrons are bound to 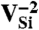, which is stable in n-type material for Fermi levels within 0.3 eV of the CBM. The DLD in Fig. 3C (energies in Table 1) shows that the spin-minority a₁(2) level lies above the spin-majority e_i levels, which raises the possibility that V_Si may also exhibit a ground-state triplet when occupied with four electrons instead of six. This result is indeed borne out by explicit calculations, as shown in Fig. 3D. In principle, a similar situation could occur by removing two electrons from the 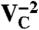defect; however, 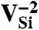is not a stable charge state, as evident from Fig. 2B. However, the close proximity of the spin-majority a₁(2) level to the VBM is cause for concern in light of criterion D4. Finally, we note that 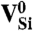forms a ground-state quartet (i.e., spin 3/2; see Table 1), and therefore this defect does not allow for spin-conserving triplet excitations.

Discovering NV Analogs in Other Material Systems

Moving beyond SiC, it is important to establish some general guidelines and procedures for identifying defects that may be analogous to the NV center in diamond. For the purposes of this discussion, we will focus on tetrahedrally coordinated compound semiconductors, considering both cation and anion vacancies.

Cation Vacancies.

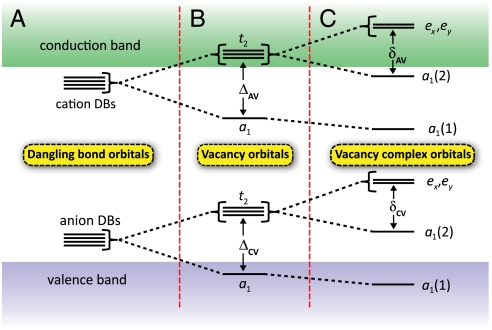
In cation vacancies, the defect levels are determined by interacting anion sp³ DBs. Because anion DBs lie close to the VBM (30) (Fig. 5B), the t₂ vacancy levels will tend to be located in the lower half of the band gap. To satisfy criterion D4, these t₂ levels should be well separated from the VBM. The t₂ levels will be split by (i) Jahn–Teller distortions, (ii) the presence of an impurity, and/or (iii) crystal-field splitting in hosts with lower than cubic symmetry. This splitting should be sufficiently large to satisfy criterion D5, but small enough to satisfy D4, and to avoid pushing the a₁(2) level too close to the VBM. The energy position of the anion DB orbitals and the splitting between the a₁ and t₂ vacancy orbitals (Δ_CV, Fig. 5B) are therefore important quantities for identifying defect systems for quantum computing applications, and in Trends in Defect-Level Splitting in SI Text we address how the choice of host and defect center impacts their value.

Fig. 5.

Development of defect-level structure in tetrahedrally coordinated compound semiconductors. Atomic sp³ DBs (A) interact to form a₁ and t₂ levels in an ideal vacancy (B), with the t₂ levels splitting further in vacancy complexes (C).

Further design flexibility is added by placing an impurity next to the vacancy, thus creating a complex. The energy of the impurity’s sp³ orbital relative to that of the host anion DB orbital affects the splitting between the a₁(2) and e_i orbitals (δ_CV, Fig. 5C). If the impurity DB orbital is significantly lower in energy than the host anion DB, the splitting δ_CV will be large. Too large a δ_CV value (relative to the band gap) is undesirable, because it might push the a₁(2) level close to or below the VBM. An attractive interaction is needed between the vacancy and impurity in order for the complex to form. Therefore, because cation vacancies tend to be negatively charged, we should choose impurities that act as donors, i.e., elements to the right of the host anion in the periodic table. An example of such a defect is the self-activation center in ZnSe, which is a complex formed by a Zn vacancy and a donor impurity. In the positive charge state (which would be stable in p-type material), this defect gives rise to a ground-state triplet with six electrons (see Electron Counting for Defects in SI Text). It remains to be determined whether this defect satisfies all the other proposed criteria.

Anion Vacancies.

Anion vacancies are less likely to lead to triplet configurations, because the cation DBs that give rise to their defect levels tend to be located in the upper part of the band gap (30) (Fig. 5B) and the vacancy orbital splitting (Δ_AV) will tend to push the t₂ orbitals close to or above the CBM. This result is indeed what occurs for an oxygen vacancy in ZnO, for which only the a₁(1) level lies within the band-gap (31). To avoid this, the semiconductor needs to have a large enough band gap, the cation sp³ DB orbitals need to be well below the CBM, and the vacancy orbital splitting (Δ_AV) needs to be small. These criteria are met in AlN, in which the V_N has t₂ levels within the band-gap. The arguments about further splitting of the levels are similar to our discussion of cation vacancies. Regarding the choice of impurity, because anion vacancies tend to act as donors, one might think that acceptor-type impurities might be the best choice, in order to maximize attraction. However, electron counting then reveals that a level occupation similar to that of the diamond NV^-1 cannot be achieved because this requires that the anion vacancy (or complex) be in a negative charge state. But in AlN, 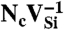is stable if ε_F is in the upper part of the band gap, and a donor impurity will fulfill the requirements of (i) being attracted to the vacancy and (ii) supplying additional electrons to achieve the desired orbital occupation.

Beyond NV Analogs

The world of deep centers is vast, and only one small subset has been discussed here in detail. Future work is needed to determine which other classes of deep centers are compatible with the defect and host criteria that have been outlined. For example, many isolated substitutional or interstitial impurities act as deep centers (19), but no such center satisfying D1–D5 has been identified so far. In the octahedrally coordinated hosts MgO and CaO, optical spin polarization has been reported in vacancy-related complexes with D_4h symmetry (32, 33), but more exploration is required to determine what other features these centers have in common with the NV^-1 center in diamond. Still other classes of deep centers become open to investigation if the stipulation that spin be a good quantum number is removed. In this case, optical selection rules are relaxed, and alternative mechanisms of optical polarization may then be possible (34).

Methods

The following expression gives E^f for the NV center in diamond in charge state q:

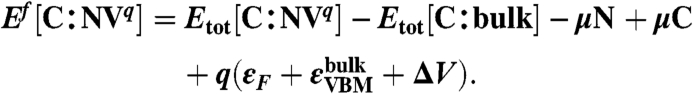The E_tot[C∶X] terms are the total energies of the diamond supercell with the NV^q defect and of the bulk supercell. The 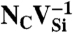terms are the chemical potential references used for N and C. For diamond, 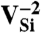is simply the energy per C atom in the crystal. ε_F is the Fermi level, referenced to the VBM in the bulk, 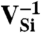; the ΔV term is used to align the bulk VBM to that of the defect supercell (20, 35).

The first-principles calculations were performed by using supercells of 64 atoms for C in the diamond structure and 96 atoms for SiC in the 4H polytype (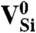 space group), with finite-size corrections for the charged-defect calculations (35). Projector augmented wave pseudopotentials were used as implemented in the Vienna Ab-initio Simulation Package (36, 37). We used a 400-eV plane-wave cutoff and a 2 × 2 × 2 special-k-point mesh to carry out integration over the Brillouin zone. The hybrid functional calculations (including atomic relaxations) were performed within the HSE06 formalism (38, 39). The calculated band gaps are 5.36 eV for diamond and 3.17 eV for 4H-SiC. Defects in 4H-SiC can occur on two possible inequivalent Si or C sites; tests indicate the corresponding energies differ by less than 0.1 eV. The results reported here are for the hexagonal site. For the NV defect in SiC, there are two choices for the position of the substitutional N atom: one associated with the single longer bulk Si-C bond length (along the c axis), and the other associated with the three shorter bulk Si-C bond lengths. For our calculations, we chose the site associated with the shorter Si-C bond. All defect excitation energies were calculated by using constrained DFT, by removing an electron out of an occupied defect level and placing it into an unoccupied defect level. We note that transitions between internal defect levels are likely to be more accurately calculated than defect-to-band transitions (40). For the purposes of assessing our criteria, this trend is advantageous, because information about defect-to-band transitions is used only qualitatively in determining whether such transitions are suppressed.