Abstract
Defective interfering particles (DIPs) are virus-like particles that arise during virus growth, fail to grow in the absence of virus, and replicate at the expense of virus during co-infections. The inhibitory effects of DIPs on virus growth are well established, but little is known about how DIPs influence their own growth. Here vesicular stomatitis virus (VSV) and its DIPs were used to co-infect BHK cells, and the effect of DIP dose on virus and DIP production was measured using a yield-reduction assay. The resulting dose–response data were used to fit and evaluate mathematical models that employed different assumptions. Our analysis supports a multiple-hit process where DIPs inhibit or promote virus and DIP production, depending on dose. Specifically, three regimes of co-infection were apparent: (i) low DIP – where both virus and DIPs are amplified, (ii) medium DIP – where amplification of both virus and DIPs is inhibited, and (iii) high DIP – with limited recovery of virus production and further inhibition of DIP growth. In addition, serial-passage infections enabled us to estimate the frequency of de novo DIP generation during virus amplification. Our combined experiments and models provide a means to understand better how DIPs quantitatively impact the growth of viruses and the spread of their infections.
INTRODUCTION
Defective interfering particles (DIPs) arise spontaneously during virus growth, but are unable to cause productive infections owing to large deletions in their genomes. However, when DIPs and normal virus co-infect the same cell, DI genomes compete with the normal viral genomes for replication and encapsidation resources, amplifying DIPs at the expense of virus particles. DIPs have been studied for more than 60 years (Henle & Henle, 1943; von Magnus, 1954), and they have been found for virtually every class of DNA and RNA virus (Huang & Baltimore, 1970; Lazzarini et al., 1981; Roux et al.,1991). The effects of DIPs on infections of normal virus have also been extensively investigated in animal and plant models (Holland, 1987; Simon et al.,2004), but what role DIPs play in the behaviour of natural infections is unknown. Physical measures and biological assays have been developed to detect and characterize DIPs (Holland, 1987), and PCR-based methods have revealed defective viral genomes in natural infections (Aaskov et al., 2006; Roux et al., 1991). However, DIPs remain challenging to study because they arise spontaneously from natural virus infections, they require co-infection with helper virus to reproduce, but their co-infection also inhibits the production of helper virus (Huang & Baltimore, 1970). Further, viruses can evolve resistance to interference by DIPs, but DIP populations can also adapt to circumvent such resistance (DePolo et al., 1987). In a technological context, the productivity of recombinant proteins from viral expression vectors can be adversely affected by DIPs (Wickham et al., 1991; Kool et al., 1991). Finally, DIPs can activate host immune responses that inhibit virus growth (Sekellick & Marcus, 1982).
To begin to understand how multiple factors may influence the behaviour of virus–DIP populations, mathematical models have been developed. For example, Bangham & Kirkwood (1990) showed that large fluctuations in virus and DIP populations could arise from relatively simple processes of growth, transmission, and death or decay among viruses, DIPs and host cells. This model has served as a foundation for models that have explored virus and DIP co-evolution (Kirkwood & Bangham,1994; Szathmary, 1992, 1993), spatial spreading co-infections (Frank, 2000), and applications of DIPs to control infections (Nelson & Perelson, 1995). Such models can be useful for testing how different mechanisms affect the system's behaviour. The behaviour of such models, however, may depend critically on parameters such as average virus yields from infected cells, yields of DIPs from cells co-infected with virus and DIPs, and rates of virus or DIP production. In the absence of experimentally determined parameters, ‘representative’ values from different virus–cell systems may be combined to explore more qualitative behaviours (Bangham & Kirkwood, 1990; Frank, 2000; Kirkwood & Bangham, 1994; Nelson & Perelson, 1995; Szathmary, 1992, 1993).
A common assumption in models of DIP–virus interaction is that co-infection of a cell with at least one DIP will prevent the cell from making any virus particles, and the co-infected cells will produce only DIPs (Bangham & Kirkwood, 1990; Frank, 2000; Kirkwood & Bangham, 1994; Nelson & Perelson, 1995; Szathmary, 1992, 1993). By assuming such a single-hit mechanism of DIP interference one may estimate the DIP concentration in a sample by employing a yield-reduction assay (Bellett & Cooper, 1959), and this has become an accepted method to quantify DIPs (Holland, 1987). Other assays based on inhibition of cytopathology have supported single-hit mechanisms of interference (McLain et al., 1988). However, physical measures of DIP effects on virus and DIP production have, by contrast, supported a multi-hit model of DIP-mediated infection interference (Khan & Lazzarini, 1977).
To understand better the mechanisms of DIP-mediated interference, we studied the growth of vesicular stomatitis virus (VSV) and its DI particles in BHK cells, which ranks among the best studied virus–DIP systems to date. Moreover, we extended the yield-reduction assay to quantify not only the effects of DIPs on virus growth, but also their effects on DIP growth.
METHODS
Cell and virus culture.
Baby hamster kidney (BHK-21) cells, originally obtained from Isabel Novella (Medical College of Ohio, OH, USA), were cultured at 37 °C and 5 % CO2 in Eagle's minimum essential medium (MEM; CellGro) with 5 % GlutaMAX (Gibco) with 10 % characterized fetal bovine serum (FBS, HyClone), and medium was switched to medium with the FBS reduced to 2 % for all virus infections.
Virus was quantified by plaque assay (Lam et al., 2005). VSV-N1, a molecularly well-defined strain with the wild-type genome organization (Wertz et al., 1998), generously provided by Gail Wertz, University of Virginia, VA, USA, was plaque-to-plaque purified six times to minimize DIPs (Holland & Villarreal, 1975). To make virus stock, 0.2 ml purified virus at 104 p.f.u. ml−1 was added to 8×106 cells in a T-75 flask (BD Falcon), incubated 24 h, filtered with a 0.22 μm filter (Nalgene), and stored at −80 °C. This stock had 109 p.f.u. ml−1, and the absence of DIP activity was confirmed by the yield-reduction assay.
Quantification of interference by yield reduction.
DIP-mediated interference of infection in samples was quantified by adapting the yield-reduction assay of Bellett & Cooper (1959). Prior to all infections the cells were counted, enabling control of the m.o.i. and quantification of virus and DIP yields on a per-cell basis. The cell count was 3.9×104 cells well−1 for the first yield reduction assay and 2.5×104 cells well−1 for the second. Cells were then infected with a range of serial 1 : 10 or 1 : 2 dilutions of each sample, adsorbed 1 h, stock virus was added at a m.o.i. of 20, adsorbed 1 h, each well was rinsed twice with Hank's balanced salt solution (HBSS, HyClone), replaced with MEM containing 2 % FBS, incubated 24 h, and stored at −80 °C until quantification by plaque assay.
Passaging.
Before each infection, cells were counted, the media was switched from 10 % to 2 % FBS, and the inoculum was diluted to the desired m.o.i. Passage infections were performed using an average of 1.3×107 cells per T-75 flask or an average of 1.6×106 cells well−1 in a six-well plate.
Preparation and characterization of high-interference sample.
Stock virus was passaged three times (m.o.i.=1) in three parallel T-75 flasks, pooled, and the resulting 60 ml product was centrifuged 10 min at 113 g and 4 °C in a Beckman GS-15R centrifuge (S4180 rotor). The supernatant was put in Oakridge-type tubes containing a 5 % sucrose cushion in TEM and centrifuged at 4 °C and 33 000 g for 1 h in a Beckman J2-21 centrifuge (JA-21 rotor). The resulting pellet was resuspended in 1 ml of minimal TEM solution. Sucrose steps were prepared by layering 70–20 % sucrose in TEM (10 mM Tris-HCl, 0.1 mM EDTA, 2.5 mM MgCl2), in 10 % sucrose increments, into ultracentrifuge tubes (Beckman). The resuspended pellet was layered on the last sucrose step, and samples were subjected to ultracentrifugation (Beckman, L8-M) at 4 °C and 120 000 g for 1 h (SW-41 rotor). Viruses were visible as faint bands at 1.14 and 1.17 g cm−3, based on their relative positions in the sucrose steps; wild-type VSV has a density of 1.16 (McCombs et al., 1966). The contents of the tube were then manually fractionated into 100 μl aliquots from the top of the tube, and the sample containing the highest DIP concentration was serially diluted and characterized by the plaque-reduction assay.
Model construction.
As detailed in the Results section, difference equations linking inputs and outputs of infection were employed to estimate overall yields of virus and DIPs. Parameter values (p) were estimated by least-squares:
with the summation spanning the available data points. The corresponding confidence intervals were constructed by parametric bootstrapping percentile method using multiple resamples from the fitted model, as detailed elsewhere (Efron & Tibshirani, 1993). For the data from Khan & Lazzarini (1977), where the uncertainty in the data was not available, we employed the relative standard deviations estimated for our results.
RESULTS
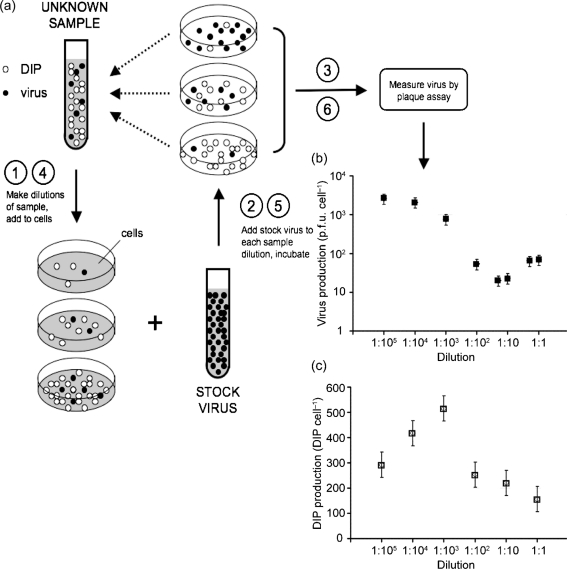
Fig. 1(a) summarizes the two assays that were central to this work: the established yield-reduction assay (steps 1, 2, 3) to measure the effects of DIP level on virus production, and our extended yield-reduction assay (steps 1, 2, 4, 5, 6) to estimate the effects of DIP level on DIP production in cells co-infected with virus and DIPs. By combining our results from the established and extended yield-reduction assays we were able to estimate virus yields (Fig. 1b) and DIP yields (Fig. 1c) for samples containing the same DIP level.
Fig. 1.
(a) Quantifying how DIPs affect production of virus and DIPs by co-infected cells. The yield-reduction assay is used to quantify inhibitors of virus growth, such as DIPs, based on their ability to reduce yields of virus progeny from infected cells (steps 1, 2, 3). Extension of the yield-reduction assay enables one to use measures of viable virus to deduce how DIPs affect their own production from co-infected cells (steps 1, 2, 4, 5, 6). (b) Effect of DIP level on virus production from co-infected cells. Different dilutions of a DIP sample were combined with excess virus to create a range of infection conditions spanning from cells infected primarily with virus (made with a 1 : 105 dilution of DIP sample) to cells co-infected with virus and DIPs (made with a 1 : 1 dilution of DIP sample). Virus production from these cells was quantified by plaque assay. (c) Effects of DIP level on DIP production from co-infected cells. The productivity of DIPs from the cells under the same co-infection conditions as (b) was deduced by measured reductions in virus yield.
DIPs interfere with production of virus
Three regimes of DIP-mediated co-infection were apparent in Fig. 1(b). The highest dilutions of DIPs were too dilute to impact virus production, so virus yields attained their maximum value. As dilutions decreased, the virus yield dropped 100-fold, indicating significant interference. At the lowest dilutions the virus yield exhibited as much as a threefold recovery, reflecting conditions where DIP–DIP interactions inhibited effects of DIP interference (Sekellick & Marcus, 1980).
DIPs interfere with production of DIPs
Further yield-reduction assays were performed on each of the DIP-rich sample dilutions, producing the dependence of DIP production on DIP inoculum levels in Fig. 1(c). For the highest dilutions, DIP yields gradually increased about twofold for decreases of 100-fold in the dilution of the DIP inoculum. This trend then changed abruptly when DIP yields dropped twofold as the inoculum dilution decreased from 1 : 1000 to 1 : 100. Finally, another twofold drop in DIP yields occurred as the DIP inoculum dilution decreased from 1 : 10 to 1 : 1.
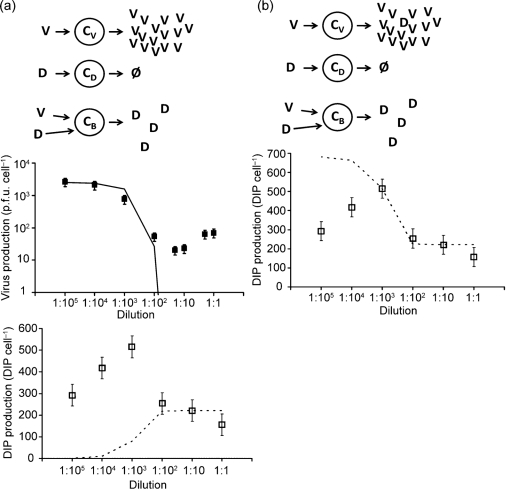
Model 1: co-infected cells amplify DIPs
All models track three species: cells (C), virus particles (V), and defective interfering particles (D). We wrote difference equations to relate initial (i) and end (e) states of each passage. We assumed all cells were initially infected with at least one virus particle owing to the high m.o.i. in our experiments. Model 1, shown in Fig. 2(a), has five species and three parameters:
| (1) |
| (2) |
| (3) |
| (4) |
where Ve is the end concentration of virus particles, bV is the number of virus particles produced by cells initially infected with virus alone (CV), De is the end concentration of DIPs, dB is the number of DIPs produced by cells co-infected by virus and DIPs (CB), Ci is the concentration of all cells, and Di is the concentration of added DIPs. Here, bV was estimated by fitting the model to virus yields at high sample dilution (Fig. 1b). We assumed that the number of DIPs entering a cell follows a Poisson process, so the concentration of DIP-free cells is given by equation 3. It is conceivable that newly generated DIPs could exit producer cells and enter another cell during a single passage, requiring a more dynamic modelling approach than employed here. However, high levels of input DIPs inhibit virus replication processes and delay the release of DI and virus particles (Von Laer et al., 1988). Therefore, newly generated DIPs are unlikely to be produced rapidly enough to impact a second round of infection during a passage. Further, in order to cause interference, DIPs need to be present early in the infection (Huang & Wagner, 1966), so DIPs produced during a first round of infection will be less likely to impact a second round of infection. Equation 4 reflects the assumption that all cells are initially infected with a virus, as
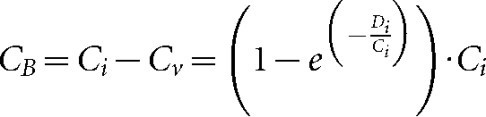 |
When fit to the data, model 1 captures inhibitory effects of added DIP on virus yields (Fig. 2a, middle panel), but fails to describe DIP yields (Fig. 2a, lower panel). Average yields of virus in the absence of DIPs reflect the highest values of virus production (Fig. 2a, middle panel), corresponding to bv (2500 p.f.u. cell−1). The volume of sample needed to reduce the virus yield depends on the original concentration of DIPs in the sample, estimated to be 5.0×109 DIPs ml−1. The only source of DIPs in this model are cells infected with both virus and DIP (CB), so one expects that increasing amounts of added DIPs should produce higher levels of co-infected cells (CB), and more total DIPs.
Fig. 2.
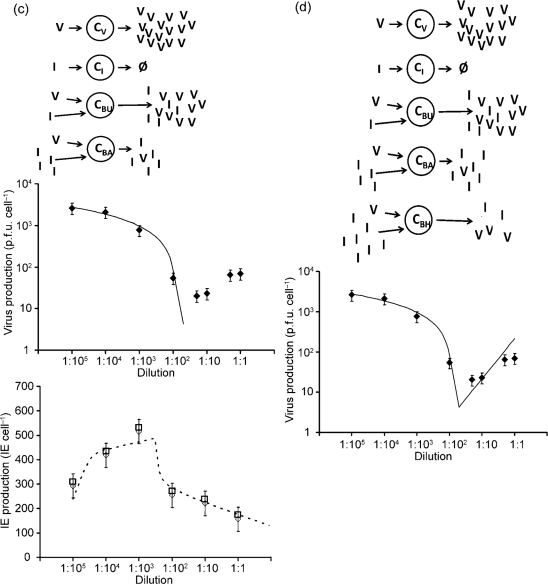
Models of virus and DIP production. (a) Model 1: co-infected cells amplify DIPs. Upper panel: virus-infected cell (CV) produces only virus (V), cell infected by DIP (CD) produces nothing, cell co-infected with DIP and virus (CB) produces only DIPs (D). Middle panel: effect of added DIPs on virus production; data (points) vs model (solid line). Lower panel: effect of added DIPs on DIP production; data (points) vs model (dashed line). Estimated parameters are bV (2500), bB (20) and dB (220). (b) Model 2: virus-infected cells generate DIPs. Upper panel: virus-infected cell (CV) produces virus (V) and generates new DIPs (D), cell infected by DIP (CD) produces nothing, cell co-infected with DIP and virus (CB) produces only DIPs. Lower panel: effect of added DIPs on DIP production; data (points) vs model (dashed line). Parameters are bV (2500), bB (20), dB (222) and g (680). (c) Model 3: higher DIP multiplicities cause more interference. Upper panel: virus-infected cell (CV) produces only virus, cell infected by interfering units (CI) produces nothing, cell co-infected with low IE and virus (CBU) produces both V and IEs with minimal interference, and cell co-infected with high IE and virus (CBA) produces IEs at the expense of virus production. Middle panel: effect of added IEs on virus production; data (points) vs model (solid line). Lower panel: effect of added IEs on IE production; data (points) vs model (dashed line). Parameters are b (2670), d (420), z (180), p (−880), w (290), r (30) and s (−80). (d) Model 4: IEs fail to shut down virus production completely. Upper panel: model 4 extends model 3 to account for co-infected cells with very high levels of IEs and virus (CBH), allowing for production of virus at the expense of IEs. Lower panel: effect of added IEs on virus production; data (points) vs model (solid line). Parameters are b (2670), d (420), z (180), p (−880), w (290), r (30), s (−80) and q (0.47).
The corresponding monotonic rise in DIP production with increasing initial DIP levels was observed in both experiments and the model for small sample volumes, but the simple monotonic rise to a plateau failed to capture the more complex DIP data (Fig. 2a, bottom panel).
Model 2: virus-infected cells generate DIPs
We modified model 1 to allow for de novo generation of DIPs from cells infected only with virus (Fig. 2b):
| (1) |
| (5) |
| (3) |
| (4) |
where g in equation (5) accounts for generation of DIPs by virus-infected cells (CV). Model 2 accounts for the production of DIPs at lower volumes of added DIP, but now overpredicts DIP production at very low sample volumes (Fig. 2b, bottom panel). By this mechanism all cells infected only with virus produce DIPs at a fixed level (680 DIP cell−1) that is higher than the estimated production of DIPs from co-infected cells (222 DIP cell−1). Therefore, the predicted drop in DIP production with added DIPs reflects a transition in the cell population from high-DIP producers (CV) to low-DIP producers (CB). With respect to virus production, model 2 behaves as model 1 (Fig. 2a, middle panel).
Model 3: higher DIP multiplicities cause more interference
We relaxed the assumption in model 1 that a single DIP completely interferes with virus replication, and we allowed virus and DIP productivity of co-infected cells to depend on the level of infecting DIPs. Here, higher levels of input DIPs more readily inhibit production of virus and DIPs (Fig. 2c). To interpret our data using this mechanism, we needed to clarify a subtle but important feature of the yield-reduction assay. Specifically, the assay quantifies a degree of infection interference, not the specific activity of individual interfering particles. We emphasized this point by quantifying yield-reduction in terms of interference equivalents (IE), where one IE delivered to a single infected cell prevents that cell from producing virus particles. IEs were quantified here in the same manner as Bellett & Cooper (1959) for their ‘transmissible interfering components’, except that we now allowed IEs to be defined by multiple particles that collectively interfere with infection. We assumed that each particle contributes its own equivalent share of the interference, a quantity we defined as one interference unit (IU). It follows that multiple IUs may be needed to achieve the effect of one IE. As shown in Fig. 2(c), model 3 now allowed for two kinds of co-infected cells, ones with low IUs that exhibit minimal interference, and ones with sufficiently high IUs to create an IE and thereby shut down virus growth. Model 3 accounts for the production of viruses and IEs as follows:
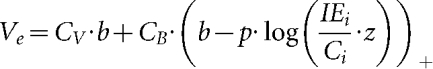 |
(6) |
| (7) |
| (8) |
| (4) |
Model 3 incorporates five additional parameters. Equation 6 is similar to equation 1 because they both account for virus released from CV and CB. Here b is equivalent to bV in models 1 and 2, representing the normal virus yield. This value falls as a function of the number of IEs per cell using the new parameters of z and p. The logarithm function was used to enable accounting for inputs that vary over multiple orders of magnitude. The parameter z multiplies the number of IEs measured in the yield reduction assay and accounts for the multiplicity of IUs needed to define one IE. This parameter in equation 6 captures the relaxation of the single-hit deactivation model – a single IU does not completely deactivate virus production. Rather, the deactivation effect of IUs is cumulative. The yield of virus from co-infected cells is adjusted through p, which accounts for the inhibitory effect of IUs on virus yield.
The other parameters adjust amplification of virus and IEs as IEs increase. The parameter ‘r’ is a multiplier for the IUs per cell, allowing for the amplification of IU with added IUs so long as levels of IUs do not cause significant interference. Added IUs reduce IEs through the parameters w and s, where ()+ indicates that only the positive part of the difference is used; thus s does not change the DIP yield until 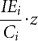 equals w.
equals w.
The estimated parameters for model 3 are presented in Table 1. Small doses of IEs reduce virus production and increase IE production, acting through p and r, respectively. As larger doses are added the IE production also drops off at point w. While model 3 defines a model for multiple-hit interference, it fails to account for the production of virus at high levels of IEs (Fig. 2c, middle panel).
Table 1.
Model parameter values
*95 % confidence intervals as determined by the bootstrapping method.
Model 4: DIPs fail to shut down virus production completely
We accounted for the recovery of virus production at high IEs using q to describe how high levels of added IEs affect virus yields, defining a further subdivision of cells to account for CBH, cells infected with large amounts of IUs (Fig. 2d). The model becomes:
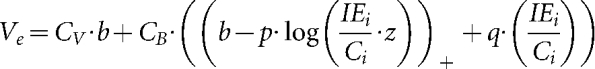 |
(9) |
| (7) |
| (8) |
| (4) |
The parameter q, in equation (9), is positive and it represents the recovery of virus yield at high levels of interference in CBH cells. Model 4 captures essential features of the dependence of added IEs on virus production (Fig. 2d). Model 4 also retains the equations and behaviour of model 3 in its accounting for effects of added IEs on IE production.
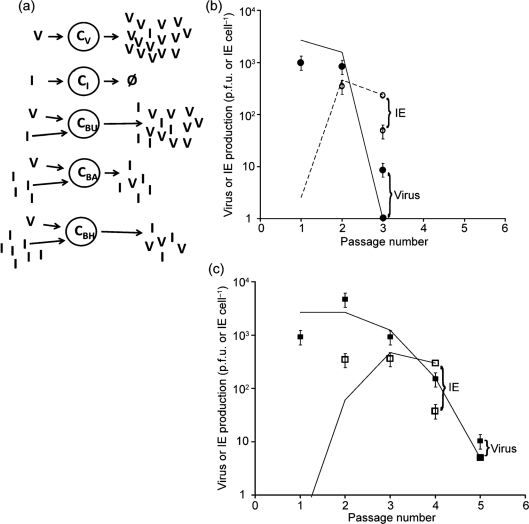
Model 5: IEs are generated and amplified during serial-passage culture
To estimate the rate of IE generation we passaged virus stock at high multiplicities, a process that promotes de novo generation and amplification of IEs to a level that could be quantified using the yield-reduction assay. As shown in Fig. 3(b, c), initial high productivities of infectious virus (p.f.u.) declined more than 100-fold within only three and five passages when m.o.i. was fixed at 100 and 10, respectively. In both cases production of IEs that were below our detection limit in passage one became detectable and quantifiable by passage two. By passages three and four the productivities of IEs from co-infected cells dropped about tenfold for m.o.i. of 100 and 10, respectively. Using model 4 as a foundation, we allowed for de novo generation of IEs from virus-infected only cells (CV). This model is shown in Fig. 3(a).
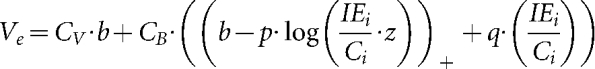 |
(9) |
| (10) |
| (8) |
| (4) |
Here g in equation (10) accounts for generation of IEs. Using the established parameters of model 4, and accounting for the different m.o.i. in the passage experiments, we fitted the passage data to estimate g at 0.001 IE cell−1, corresponding to 0.2 IU cell−1. This single-parameter fit of model 5 to the passage data, shown by the lines in Fig. 3(b, c), falls within an order of magnitude of the data for m.o.i. of both 100 and 10. Table 1 summarizes the full parameter set for model 5.
Fig. 3.
IEs are generated and amplified during serial-passage culture (model 5). (a) Here we allowed for the generation of new IUs from cells infected with virus alone (CV), producing both virus and new IUs. Model 5 (lines) captured the essential features of passage results of both virus and IE at a fixed m.o.i. of (b) 100 p.f.u. cell−1 and (c) 10 p.f.u. cell−1. Data are p.f.u. (filled symbols) and IE (open symbols) and model results are p.f.u. (solid lines) and IE (dashed lines). The parameter for IE generation was g (0.001) and the other parameters remained unchanged from model 4.
The model can account for quantitative physical measures of virus and DIP production
Khan & Lazzarini (1977) studied how DIPs can influence the production of VSV particles and DIPs, but they employed physical rather than biological measures of virus and DIPs. DIPs in the inoculum were counted by electron microscopy (Galasso, 1967), wild-type virus particles and DIPs were [3H]uridine-labelled during growth and their relative levels were measured following fractionation by gradient centrifugation. DIP inocula ranged from 1 to 3 DIPs cell−1 to about 100 DIPs cell−1, causing a greater than tenfold drop in virus production and a detectable though relatively small drop in DIP production, as shown in Fig. 4. The model fit using the equations corresponding to model 3 (equations 4 and 6–8) are shown in Fig. 4 and parameters are provided in Table 2.
Fig. 4.
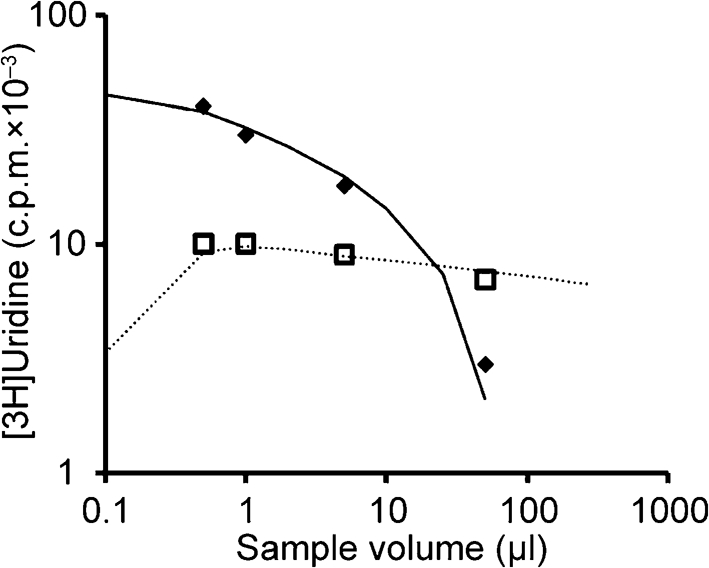
Modelling physical measures by Khan & Lazzarini (1977). Model 3 was used because the dataset is limited to the middle range of DIP m.o.i. (1–100) and data are insufficient for fitting higher DIP levels and DIP generation. Data are p.f.u. (filled diamonds) and IE (open squares) and the model results are shown as p.f.u. (solid lines) and IE (dashed lines). Parameters were b (42), d (11), z (1), p (−17.5), w (2), r (0.1) and s (−2.0).
Table 2.
Model parameter values for data of Khan & Lazzarini (1977)
3H-U, [3H]uridine; na, not applicable.
*95 % confidence intervals as determined by the bootstrapping method.
DISCUSSION
The yield-reduction assay has long served as a useful biological assay to quantify the inhibitory effects of DIPs on the production of viruses (Holland, 1987, 1990), but interpretation of its results have been primarily based on a single-hit mechanism, initially by Bellett & Cooper (1959), which assumes that one DIP in an infected cell is sufficient to inhibit completely production by the cell of progeny virus particles. This assumption, though untested, was initially useful because it enabled inhibitory effects of added DIPs on virus yield to be modelled using a Poisson distribution, ultimately allowing estimation of the DIP concentration in a sample. However, quantitative physical assays of virus and DIPs suggested DIPs caused interference by a multi-hit rather than a single-hit mechanism (Khan & Lazzarini, 1977). While the issue of single- or multi-hit mechanism remained unresolved, the single-hit mechanism was nevertheless adopted in models of DIP and virus growth and their population dynamics (Bangham & Kirkwood, 1990; Kirkwood & Bangham, 1994), and these models further served as a foundation for infection-interference models by others (Frank, 2000; Nelson & Perelson, 1995; Szathmary, 1992, 1993). Our experiments, together with relatively simple input–output models of virus and DI particle production, highlight limitations of interference models that allow only for single-hit mechanisms of interference and provide a foundation for the development of new multi-hit models based on quantitative data. One should note that our models, as presented here, are neither mechanistic nor predictive. Instead, their value is in the framework they provide for extracting quantitative information from experiments.
In contrast to the models of Bangham and Kirkwood, where infected cells produced either virus or DIPs, our VSV experiments provide a basis for classifying productive infections into at least four types, in each case amplifying virus and interference units to different extents. For type A infections, cells were infected with wild-type virus alone. Such infections efficiently amplified wild-type VSV, producing on average 2500 p.f.u. cell−1 in this study, and they produced only about 0.001 IE (infected cell)−1. We estimated that 190 IUs are required to achieve the extent of interference equivalent to one IE. Thus interfering particles, quantified as IUs, may be generated at approximately 0.2 IUs (infected cell)−1. The total productivity level for this type of infection is therefore about 103 particles per cell, reflecting primarily infectious virus particles (p.f.u.).
For type B infections, cells were infected with both wild-type virus and interference units, but IU levels were too low to interfere detectably with virus production. This was the most productive infection with respect to total particles produced. Virus was amplified at 2670 p.f.u. cell−1, and interference equivalents were produced at 420 IE (or 7×104 IUs) cell−1. Our estimates for IUs are in the range observed by Holland & Villarreal (1975) for VSV DIPs, where production rates of 104 DIPs cell−1 were found for low DIP input m.o.i. On a total particle (combined p.f.u. and IUs) per cell basis, this second type of infection was 100 times more productive than the first type, which lacked input IUs. We speculate that the higher particle productivities of cells may arise in part from the ability of interfering particles to prevent or delay cytopathic effects, making the establishment of persistent infections possible (Holland & Villarreal, 1974) and providing a longer period of productive synthesis. In addition, the DIP genomes are typically less than half the length of the wild-type genome (Lazzarini et al., 1981), so more copies may be made, even if material and time resources are fixed. Owing to a lack of obvious signs or symptoms of interference by the plaque assay, type B infections represent the least studied and most poorly understood of the different infection types.
For type C infections, cells were infected under conditions where the balance of added virus and IUs create significant interference in the production of both virus and IUs, representing the DIP-mediated interference of infection that has been most widely studied. Here, particles were amplified to 20 p.f.u. cell−1 and 100–200 IEs cell−1 (or 1.5×104 IUs cell−1). Although type C infections were about fivefold less productive than type B on a total particle basis, they were nevertheless sixfold more productive than type A, which lacked inputs of interfering particles. By comparing type B and type C infections, one sees that while interference affects the production of both viruses and IUs, it more greatly inhibits production of viruses than it does IUs. The IU production rate dropped about fivefold from 7×104 to 1.5×104 IU cell−1, while the virus rate dropped more than 100-fold from 2500 to 20 p.f.u. cell−1, suggesting that, under conditions of interference, the defective viral genomes are replicated preferentially over the wild-type genomes. This preferential replication never fully drives wild-type virus production to zero on a population level, though it may do so for individual cells (Sekellick & Marcus, 1982).
Type D infections occurred at the highest levels of interference where addition of interfering particles enabled production of virus particles to exhibit a small but quantifiable recovery while production of IUs dropped, an effect also observed by Sekellick & Marcus (1982). While our model required an additional parameter to account for the recovery of virus yield in type D infections, no additional parameters were needed to capture the continuing decline in production of IUs with added IUs.
By examining the magnitude of ratios of estimated model parameters, one can compare results from the physical measures of interference by Khan & Lazzarini (1977) with the biological measures of the current work, as shown in Table 3. For example, the ratio (p/b), which describes the relative impact an interfering particle has on the overall virus productivity, was 0.41 and 0.33 for physical and biological measures, respectively, suggesting that the DIPs from their study were more potent in their interference of virus production than the DIPs in the present study. Similarly, the ratio (s·z)/(r·d) reflects the ability of available DIPs to interfere with DIP production, and the values of 1.7 and 1.2, respectively, suggest that the DIPs used by Khan & Lazzarini (1977) were also more potent in their effects on DIP production. As a third measure, the magnitude of (d·z)/b reflects yields of DIP relative to virus, and the values of 0.27 and 30 for physical and biological measures, respectively, suggest that DIPs used by Khan & Lazzarini (1977) were produced at significantly lower levels relative to the interfering particles of the current work. Such model-based comparisons suggest trends that should be tested by performing physical and biological measures on the same virus and DIP samples. Finally, while the parameters have been determined for VSV infections of BHK cells, our approach and the structure of our models should provide a foundation for characterizing the generation, amplification and interfering properties of defective particles associated with other viruses.
Table 3.
Ratios of the absolute values of related parameters
3H-U, [3H]Uridine.
To interpret our experiments, we have sought in each of our models to minimize the number of parameters needed to describe the phenomena. Each of our models assumes that the behaviour of each type of cell, virus or interfering particle may be described by an average behaviour. However, the genetic heterogeneity of VSV, physiological differences among host cells and the stochastic behaviour of virus–DIP–cell infections will probably contribute to broad distributions in growth phenotypes (Zhu et al., 2008). A limitation of our modelling, for example, is the estimated virus productivity of 20 p.f.u. cell−1 for cells that have been co-infected with high levels of interfering particles. This relatively low virus yield is a population average that neglects potentially high virus productivity from a small minority of cells that may be immune to the effects of interfering particles, which have been observed (Sekellick & Marcus, 1980). Future models of virus and DIP growth and dynamics will need to move beyond average measures and embrace the diversity of phenotypes that arise at the level of individual cells, virus and DI particles.
Although our models of infectious and interfering particle production have provided evidence for the existence of at least four infection types, three involving co-infections of virus and DIPs, these input–output models cannot explain mechanistically how viral and defective infections interact. Models of an RNA bacteriophage, phage Qβ, have suggested how defective genomes interfere with intracellular replication of the wild-type genomes by competing for the replication resources of the phage (Kim & Yin, 2004). For VSV, the self-regulated nucleocapsid protein may affect interactions between DIP and viral RNA templates (Blumberg & Kolakofsky, 1983). In this context, extension of recent models of VSV intracellular development (Lim et al., 2006), together with quantitative intracellular measurements, may eventually provide a better quantitative and mechanistic understanding of interference.
Acknowledgments
We thank Laura Juckem (Novagen, WI, USA), Karl Boehme (Vanderbilt University School of Medicine, TN, USA) and Johan den Boon (University of Wisconsin-Madison, WI, USA) for technical advice. The National Science Foundation (EIA-0130874, DMS-0553687), the National Institutes of Health (AI071197), and the Graduate School of the University of Wisconsin-Madison provided support. K. A. S. T. received a fellowship from the NIH Genomic Sciences Training Program at UW-Madison (5T32HG002760). This research was also partially sponsored by the Center for Environmental Genomics and Integrative Biology at the University of Louisville, which receives funding from the National Institute of Environmental Health Sciences (1P30ES014443).
References
- Aaskov, J., Buzacott, K., Thu, H. M., Lowry, K. & Holmes, E. C. (2006). Long-term transmission of defective RNA viruses in humans and Aedes mosquitoes. Science 311, 236–238. [DOI] [PubMed] [Google Scholar]
- Bangham, C. R. & Kirkwood, T. B. (1990). Defective interfering particles: effects in modulating virus growth and persistence. Virology 179, 821–826. [DOI] [PubMed] [Google Scholar]
- Bellett, A. J. & Cooper, P. D. (1959). Some properties of the transmissible interfering component of vesicular stomatitis virus preparations. J Gen Microbiol 21, 498–509. [DOI] [PubMed] [Google Scholar]
- Blumberg, B. M. & Kolakofsky, D. (1983). An analytical review of defective infections of vesicular stomatitis virus. J Gen Virol 64, 1839–1847. [DOI] [PubMed] [Google Scholar]
- DePolo, N. J., Giachetti, C. & Holland, J. J. (1987). Continuing coevolution of virus and defective interfering particles and of viral genome sequences during undiluted passages: virus mutants exhibiting nearly complete resistance to formerly dominant defective interfering particles. J Virol 61, 454–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron, B. & Tibshirani, R. J. (1993). An Introduction to the Bootstrap. New York: Chapman & Hall/CRC Press.
- Frank, S. A. (2000). Within-host spatial dynamics of viruses and defective interfering particles. J Theor Biol 206, 279–290. [DOI] [PubMed] [Google Scholar]
- Galasso, G. J. (1967). Enumeration of VSV particles and a demonstration of their growth kinetics by electron microscopy. Proc Soc Exp Biol Med 124, 43–48. [DOI] [PubMed] [Google Scholar]
- Henle, W. & Henle, G. (1943). Interference of inactive virus with the propagation of virus of influenza. Science 98, 87–89. [DOI] [PubMed] [Google Scholar]
- Holland, J. J. (1987). Defective interfering rhabdoviruses. In The Rhabdoviruses, pp. 297–360. Edited by R. R. Wagner. New York: Plenum Press.
- Holland, J. J. (1990). Defective viral genomes. In Virology, 2nd edition, pp. 151–165. Edited by B. N. Fields, D. M. Knipe, P. M. Howley, R. M. Chanock, T. P. Monath, J. L. Melnick, B. Roizman & S. E. Straus. New York: Raven Press.
- Holland, J. J. & Villarreal, L. P. (1974). Persistent noncytocidal vesicular stomatitis virus infections mediated by defective T particles that suppress virion transcriptase. Proc Natl Acad Sci U S A 71, 2956–2960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland, J. J. & Villarreal, L. P. (1975). Purification of defective interfering T particles of vesicular stomatitis and rabies viruses generated in vivo in brains of newborn mice. Virology 67, 438–449. [DOI] [PubMed] [Google Scholar]
- Huang, A. S. & Baltimore, D. (1970). Defective viral particles and viral disease processes. Nature 226, 325–327. [DOI] [PubMed] [Google Scholar]
- Huang, A. S. & Wagner, R. R. (1966). Defective T particles of vesicular stomatitis virus II. Biologic role in homologous interference. Virology 30, 173–181. [DOI] [PubMed] [Google Scholar]
- Khan, S. R. & Lazzarini, R. A. (1977). The relationship between autointerference and the replication of defective interfering particle. Virology 77, 189–201. [DOI] [PubMed] [Google Scholar]
- Kim, H. & Yin, J. (2004). Quantitative analysis of a parasitic antiviral strategy. Antimicrob Agents Chemother 48, 1017–1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkwood, T. B. & Bangham, C. R. (1994). Cycles, chaos, and evolution in virus cultures: a model of defective interfering particles. Proc Natl Acad Sci U S A 91, 8685–8689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kool, M., Voncken, J. W., Van Lier, F. L. J., Tramper, J. & Vlak, J. M. (1991). Detection and analysis of Autographa californica nuclear polyhedrosis virus mutants with defective interfering properties. Virology 183, 739–746. [DOI] [PubMed] [Google Scholar]
- Lam, V., Duca, K. A. & Yin, J. (2005). Arrested spread of vesicular stomatitis virus infections in vitro depends on interferon-mediated antiviral activity. Biotechnol Bioeng 90, 793–804. [DOI] [PubMed] [Google Scholar]
- Lazzarini, R. A., Keene, J. D. & Schubert, M. (1981). The origins of defective interfering particles of the negative-strand RNA viruses. Cell 26, 145–154. [DOI] [PubMed] [Google Scholar]
- Lim, K. I., Lang, T., Lam, V. & Yin, J. (2006). Model-based design of growth-attenuated viruses. PLoS Comput Biol 2, e116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCombs, R. M., Melnick, M. B. & Brunschwig, J. P. (1966). Biophysical studies of vesicular stomatitis virus. J Bacteriol 91, 803–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLain, L., Armstrong, S. J. & Dimmock, N. J. (1988). One defective interfering particle per cell prevents influenza virus-mediated cytopathology: an efficient assay system. J Gen Virol 69, 1415–1419. [DOI] [PubMed] [Google Scholar]
- Nelson, G. W. & Perelson, A. S. (1995). Modeling defective interfering virus therapy for AIDS: conditions for DIV survival. Math Biosci 125, 127–153. [DOI] [PubMed] [Google Scholar]
- Roux, L., Simon, A. E. & Holland, J. J. (1991). Effects of defective interfering viruses on virus replication and pathogenesis in vitro and in vivo. Adv Virus Res 40, 181–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekellick, M. J. & Marcus, P. I. (1980). Viral interference by defective particles of vesicular stomatitis virus measured in individual cells. Virology 104, 247–252. [DOI] [PubMed] [Google Scholar]
- Sekellick, M. J. & Marcus, P. I. (1982). Interferon induction by viruses. VIII. Vesicular stomatitis virus: [±]DI-011 particles induce interferon in the absence of standard virions. Virology 117, 280–285. [DOI] [PubMed] [Google Scholar]
- Simon, A. E., Roossinck, M. J. & Havelda, Z. (2004). Plant virus satellite and defective interfering RNAs: new paradigms for a new century. Annu Rev Phytopathol 42, 415–437. [DOI] [PubMed] [Google Scholar]
- Szathmary, E. (1992). Natural selection and dynamical coexistence of defective and complementing virus segments. J Theor Biol 157, 383–406. [DOI] [PubMed] [Google Scholar]
- Szathmary, E. (1993). Co-operation and defection: playing the field in virus dynamics. J Theor Biol 165, 341–356. [DOI] [PubMed] [Google Scholar]
- Von Laer, D. M., Mack, D. & Kruppa, J. (1988). Delayed formation of defective interfering particles in vesicular stomatitis virus-infected cells: kinetic studies of viral protein and RNA synthesis during autointerference. J Virol 62, 1323–1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Magnus, P. (1954). Incomplete forms of influenza virus. Adv Virus Res 2, 59–79. [DOI] [PubMed] [Google Scholar]
- Wertz, G. W., Perepelitsa, V. P. & Ball, L. A. (1998). Gene rearrangement attenuates expression and lethality of a nonsegmented negative strand RNA virus. Proc Natl Acad Sci U S A 95, 3501–3506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickham, T. J., Davis, T., Granados, R. R., Hammer, D. A., Shuler, M. L. & Wood, H. A. (1991). Baculovirus defective interfering particles are responsible for variations in recombinant protein production as a function of multiplicity of infection. Biotechnol Lett 13, 483–488. [Google Scholar]
- Zhu, Y., Yongky, A. & Yin, J. (2008). Growth of an RNA virus in single cells reveals a broad fitness distribution. Virology [Epub ahead of print] doi: 10.1016/j.virol.2008.10.031. [DOI] [PMC free article] [PubMed]