Abstract
Using new national data from Adolescent Health and Academic Achievement (AHAA), this article examines high school math patterns for students of different race-ethnicity and gender. Compared with white males, African American and Latino males receive lower returns from taking Algebra I during their freshman year, reaching lower levels of the math course sequence when they begin in the same position. This pattern is not explained by academic performance, and, furthermore, African American males receive less benefit from high math grades. Lower returns are not observed for minority female students, suggesting that more attention to racial-ethnic inequality in math among male students is needed.
Students’ academic achievement in high school has clear consequences for their lives after graduation, including their college attendance and persistence, as well as success in the labor force (Adelman 1999; Csikszentmihalyi and Schneider 2000; Lee and Frank 1990). A key component of high school achievement is the completion of advanced level courses in math, as such courses expose students to cognitively demanding curriculum, offer opportunities to interact with highly skilled teachers and classmates, and provide an important educational credential on students’ high school transcripts (Gamoran 1987; Gamoran et al. 1995; Hallinan 1996; Hallinan and Kubitschek 1999; Lucas 1999). Previous research has clearly demonstrated that math course-taking patterns are characterized by strong racial and ethnic disparities, such that African American and Latino students take fewer advanced level math courses by the end of high school compared with their white peers (Jones et al. 1992; Ladson-Billings 1997; Lucas 1999; National Center for Education Statistics 2001; Oakes 1990). Yet much less is known about the process that leads up to this inequitable outcome. By examining whether all students benefit equally from beginning high school at the key threshold of Algebra I, or whether in fact African American and Latino students remain behind their white peers in the level of math reached by the end of high school even when they start at the same place, this article offers new empirical evidence about the process through which inequality emerges.
Additionally, while previous research has brought attention to the under-representation of African American and Latino students in advanced level math courses, there has been much less attention to the intersection between gender and race-ethnicity (Hanson 1996; Muller et al. 2001; Tate 1997). Recently, the gender gap in advanced level math course taking has closed, such that females are now as likely to take advanced classes such as Precalculus and Calculus as their male peers (Bae et al. 2000; Freeman 2004; Xie and Shauman 2003). While this indicates clear progress for young women generally, understanding how such patterns relate to the educational attainment of African American and Latina girls is complex, as minority females may outperform their male peers at the same time that they remain behind white students of their own gender. Thus, the intersection between gender and race-ethnicity with regard to course taking warrants further attention and is a main focus of this article.
Finally, this article examines the role of academic performance in shaping the progress of students of different genders and racial-ethnic groups through the sequence of high school math courses. Course failure is a major obstacle to students’ attainment of advanced level math courses, regardless of their initial math course, and therefore could help to explain why minority students might not receive the same return from their math courses early in high school. Yet it is also possible that the link between performance and advanced level math course taking is not the same for students of different genders and racial-ethnic groups. Examining how grades shape the process of students’ math course taking from the beginning to the end of high school is an important part of understanding racial-ethnic and gender inequality in math attainment.
To assess disparities in math course-taking patterns across high school and the role of academic performance, the analyses utilize a new nationally representative educational data set, the Adolescent Health and Academic Achievement (AHAA). The AHAA is a recently completed high school transcript study and a component of the National Longitudinal Study of Adolescent Health (Add Health), and it provides the chance to examine inequality in high schools during the 1990s. Specifically, I address two main issues. First, I examine whether African American and Latino students, both male and female, ultimately reach comparable level math courses as their white peers when they begin in the same course position. Second, I examine the role that academic performance plays in the process of students’ math course taking to discern whether students from different genders and racial-ethnic groups might not reach comparable levels of math despite starting in the same position because of receiving lower grades, or whether, in fact, the consequences of grades themselves vary by race-ethnicity and gender.
The Path through Math: Course Sequences
High school course taking in math is typically organized in a hierarchical sequence of courses, where individual courses that are part of a larger unified subject are taught with progressive levels of difficulty throughout each year of high school (Adelman 1999; Schneider et al. 1998; Stevenson et al. 1994). Previous research has documented a hierarchical math sequence categorized at the lower end by general math and beginning Algebra classes and, at the high end, by advanced courses such as Trigonometry and Calculus (Adelman 1999; Schiller and Hunt 2003; Schneider et al. 1998). Skills and concepts build on one another throughout the sequence, meaning that curricula in one class must generally be mastered before students can successfully move to the next course in the sequence.
The hierarchical nature of math course taking and its accompanying structure of prerequisites create a positional advantage for those students who begin high school taking courses that are higher in the sequence (Schneider et al. 1998). In contrast to other subjects such as English, math offers a much less “open” path, so that where students begin the math sequence is strongly connected to how far they can reach by the end of high school (Lucas 1999).1 Specifically, if students do not begin high school taking Algebra I or Geometry, they have little chance of reaching advanced courses such as Trigonometry and Calculus–and it is these courses that most strongly predict college attendance, both overall and at elite postsecondary institutions (Adelman 1999, 2003; Schneider 2003).
Yet while starting at a higher position in the math sequence is a necessary step for reaching advanced courses by the end, it is not sufficient. Throughout the intervening high school years, certain students may be at a higher risk of losing this initial course advantage than others. Research focusing on broadly defined academic tracks has addressed whether the course trajectories of minority groups follow patterns similar to those of other students (see, e.g., Hallinan 1996; Lucas 1999; Lucas and Berends 2002; Oakes 1990).2 In general, this research offers evidence that African American and Latino students may be more likely to “fall out” of an initial position of advantage compared with their white peers.
In regard to the highly sequenced math courses that students take throughout high school, the issue of potentially different returns from initial math course position has clear implications for understanding educational inequality in high school and for designing policies to reduce it. For example, if in fact African American and Latino students receive the same returns from early course taking—such that when they begin high school in the same level of the math sequence, they subsequently reach the same level by the end of high school—then the biggest hurdle to racial-ethnic inequality is the initial course position and the processes that led up to it. However, if these minority students do not receive the same return from beginning in a relatively high course position, then we need to focus on understanding the factors that operate throughout the years of high school that push them out of this initial position of advantage. This detailed focus on students’ movement through math course sequences will enable more definitive conclusions to be drawn and policies designed to promote equitable outcomes among students of different races and ethnicities.
Math and the Intersection of Race-Ethnicity and Gender
While race and ethnicity represent a key axis of stratification within contemporary society, such categories simultaneously intersect with other characteristics of individuals’ identities and histories, such as gender, that have additional implications for inequality. Currently, there is evidence that the gender gap in high school math course taking has disappeared, such that overall girls are as likely as boys to take Calculus, for example (Bae et al. 2000; Freeman 2004; Xie and Shauman 2003). Yet little attention has been paid to whether this new and more gender-equitable pattern extends equally to girls of all racial and ethnic groups (Tate 1997). It is likely, for example, that factors previously noted as influencing girls to leave the math-science pipeline, such as gendered stereotypes and differential socialization, are still operating (Correll 2001; Eccles 1994; Eccles et al. 1999; Forgasz et al. 1999). As members of two groups that have historically been subjected to stereotypes of lower innate ability, minority girls may suffer a double penalty (Barajas and Pierce 2001). In particular, Latinas may be more sensitive to stereotypes or gender norms, and to the extent that stereotypes of math as a predominantly male white field continue to operate (Forgasz et al. 1999), Latinas may be less inclined than other females to pursue advanced courses in math (Catsambis 1994).
However, prior research is somewhat equivocal with regard to gender differences in educational achievement among disadvantaged minority students. In fact, there is some evidence of Latinas and African American females outperforming their male peers (Clewell and Anderson 1991; Mickelson 1989; Roderick 2003). For example, Latinas have lower rates of school dropout compared with Latino males, and both Latinas and African American females are more likely to complete a bachelor’s degree compared with their male peers of the same racial-ethnic group (Bae et al. 2000; Freeman 2004). Finally, in some cases minority females may be more inclined toward math than their white female peers. Among adolescents, black females report more favorable attitudes toward math than white females and higher self-confidence about their math abilities (Catsambis 1994; Mau and Domnick 1995).
The complexity of the intersection between gender and race-ethnicity for students’ academic outcomes has been acknowledged in prior research (Hanson 1996; Mickelson 1989; Muller et al. 2001; Tate 1997). This article pays explicit attention to whether gender shapes the math course-taking patterns of students of different racial-ethnic groups in high school and whether the returns from initial course positions are equivalent among different racial-ethnic and gender groups.
The Role of Student Performance in Shaping Students’ Math Sequences
Given the sequential basis of math course taking, a key reason why any student, regardless of gender or race-ethnicity, might not progress as far as others in the math course sequence is low performance. The grades that students earn in high school reflect several different aspects of the process of educational attainment (Linn and Kessel 1996). First, they represent students’ ability to master the curricular material of a certain class. Yet they also capture the degree to which a student meets teacher expectations, both in terms of actual performance and, more subjectively, in terms of attitude and behavior (Farkas et al. 1990; Moreno and Muller 1999). Additionally, grades reflect students’ effort and engagement, as they make choices concerning how hard to work and study for a certain course ( Johnson et al. 2001; Rosenbaum 2001).
Low grades can be a major impediment to moving forward, and, alternatively, high grades can act as a major facilitator of moving ahead. On the extreme end, if students fail a course, they will likely be required to take it again before moving onward in the sequence. Even when students fail only one semester, this may function to discourage them from continuing. At the opposite end of performance, students who receive high grades clearly meet the prerequisites for progress on to the next course in the sequence, and teachers, counselors, and parents may encourage such students more in the presence of this tangible record of academic achievement. Additionally, while performance throughout high school is important for shaping students’ trajectories, performance in the first year of high school is critical (Weiss 2001). At this crucial juncture, grades serve not only as a structural prerequisite for continuing in the sequence but are also likely to influence students’ expectations for themselves and others’ perceptions of their potential (Roderick and Camburn 1999).
With regard to differences across groups, Latino and African American students have higher rates of course failures (Roderick and Camburn 1999) and generally receive lower grades than their white peers (Ainsworth-Darnell and Downey 1998; Ferguson 2001). In general, high schools girls earn higher grades compared with boys in all subjects, including math (Mickelson 1989; Muller 1998; National Center for Education Statistics 2001). This gender advantage in grades is often viewed in the context of girls’ greater desire to please others, meet expectations, and generally comply with rules (Catsambis 1994; Johnson et al. 2001; Xie and Shauman 2003).
It is logical to expect that, other things being equal, girls’ higher grades will lead to further progress in the sequence of math courses and that African American and Latino students’ generally lower grades will lead to less progress. Yet there are many reasons why the link between performance and course taking might not function similarly for all students. For example, the greater prevalence of academic failures among students in their own racial-ethnic group may lessen the psychological blow of individual failure to African American and Latino students. Alternatively, failure may reinforce negative racial-ethnic stereotypes and therefore function as more of a deterrent to advanced level course taking for these students. With regard to gender, girls of all racial-ethnic groups may be more responsive to the signals that grades provide than boys, but high grades may be more important to minority girls compared with white girls, if they are in need of more encouragement to overcome negative stereotypes of gender and race-ethnicity (Barajas and Pierce 2001). Once again, the intersection of gender and race-ethnicity is relevant to the shaping of students’ math trajectories.
Research Questions and Data
The subsequent analyses address two primary questions. First, when African American and Latino students begin high school at the same level of the math sequence, do they subsequently reach the same level by the end of high school, and does this differ by gender? Second, does academic performance help to explain why students who start at comparable positions in the math sequence do not ultimately reach equivalent positions, or, alternatively, do the consequences of performance differ by race-ethnicity and gender?
This study uses data from two related data sets: Add Health and the new AHAA, the education component to Add Health. The purpose behind the Add Health survey was to explore the health-related behaviors of adolescents in grades 7–12 and the causes of these behaviors, with an emphasis on the influence of social context. Beginning in 1994, Add Health selected a representative sample of 80 high schools and 52 “feeder” middle schools. About 200 adolescents were selected from each school, with approximately equal numbers of males and females in each of the six grades (7–12), resulting in a total sample of 20,745 (Bearman et al. 1997). The complex longitudinal design of Add Health includes the initial student survey in 1994–95, with follow-ups in 1995 and 1996. In 2001–2, Add Health administered a third wave of data collection for 15,197 respondents, or 73 percent of the original wave 1 sample.3 The AHAA data set contributes major new education data to the Add Health data base. Approximately 92.9 percent of wave 3 Add Health respondents signed a valid transcript release form (N = 14,113), and the AHAA collected high school transcripts from 87 percent of them (N = 12,258), or approximately 81 percent of the wave 3 sample. Because of the different years during which the six nationally representative cohorts of students (seventh to twelfth graders in 1994) attended high school, the AHAA study includes high school transcripts ranging from the beginning to the end of the 1990s.
Each course that appeared on a student’s transcript was coded with Classification of Secondary School Courses (CSSC) codes, which have been used in all major transcript studies, including High School and Beyond (HSB), the National Education Longitudinal Study (NELS), and the National Assessment of Educational Progress. Grades and credits earned were also coded to be comparable across the nation.4 A major advantage of using AHAA data for the analyses of racial-ethnic and gender inequality in math course taking is the study’s recent time frame. Given the changes in the past two decades in patterns of gender equity in math course taking, increasing math requirements for graduation, and general policy efforts aimed at promoting equity in attainment, it is important to examine the more recent picture of equality in academic trajectories (see, e.g., Schiller and Muller 2000; Teitelbaum 2003). In contrast to national education data sets such as HSB and NELS that reflect high school attainment in the 1980s and early 1990s, the AHAA study provides a national picture of high school students throughout the decade of the 1990s.
Several filters were applied to the AHAA data to create the analytic sample appropriate for analysis here. First, I utilize data from only four cohorts, the ninth to twelfth grade cohorts, as they are representative of high school students across the nation in 1994–95. I further limit the sample to students in public schools. Third, I exclude students who dropped out of high school, in order to ensure that the lower levels of course taking reached by some students at the end of high school were not due to the fact that they left school and therefore had fewer years of data.5 These filters resulted in an analytic sample of 7,101 students in 69 schools, or approximately 60 percent of the AHAA sample. Analysis of this data reduction indicated that the final analytic sample did not differ significantly from either the complete AHAA sample or the larger wave 3 Add Health sample with regard to demographic and academic characteristics such as race, gender, parent background, and academic performance.
Dependent Variable
Math course sequence level at the end of high school
Using the CSSC codes referred to above, the AHAA study constructed a math sequence variable to identify the course position of students in each year of high school, as well as the highest level of math they reached by the end of high school (Riegle-Crumb et al. 2005). The latter is the dependent variable in this study. The categories are 1, Remedial or Basic Math; 2, General or Applied Math; 3, Pre-Algebra; 4, Algebra I; 5, Geometry; 6, Algebra II; 7, Advanced Math; 8, Precalculus; and 9, Calculus.6 It is important to point out that students do not necessarily have to progress through every level of the math sequence. Many students will begin high school at level 4, Algebra I, without ever taking courses in the lower categories. Most students follow the order of Algebra I, followed by Geometry and then Algebra II (Schiller and Hunt 2003).
Independent Variables
Math sequence position at the beginning of high school
To capture students’ math sequence position for the first year of high school, I recoded the math sequence variable for that year into a dichotomous variable coded one for a student beginning high school and taking Algebra I or a higher course and zero otherwise. I chose this threshold because Algebra I is the most common math course taken by students in the first year of high school. In addition, beginning in Algebra I or a higher course is considered “on time” for reaching Algebra II (or higher) by the end of high school, a key course for admittance into most colleges and universities (Adelman 1999, 2003; Pelavin and Kane 1990; Schiller and Hunt 2003). For the sake of simplicity, I often refer to this variable as “Algebra I,” but it should be noted that approximately 25 percent of students with a “one” on this variable began high school in a higher course. I constructed interaction terms separately by gender between the dichotomous variable for Algebra I in the first year of high school and categories of race-ethnicity: African American, Latino, and Asian.7 Variables for race-ethnicity were taken from the student surveys of Add Health.
Math performance variables
The AHAA study constructed indicators for students’ grade point averages and the proportion of courses failed, both overall and for specific subjects such as math and science, based on the grades recorded on students’ high school transcripts. Because most students took courses on a semester basis, these variables are based on semester-length units. Thus, students’ grade point averages for math in a given year represent the average of the grades they received in each semester, while the failure index measures the proportion of semesters they failed.
Using these variables, I created two dichotomous variables to capture students’ math performance in the first year of high school. One variable measures whether or not a student failed one semester or more of his first-year math course, and the other variable measures whether or not he received a grade of B or higher. The omitted contrast category is havingaCorD average without failing a semester. I also constructed interaction terms (separately by gender) between these measures of math performance and each category of race-ethnicity.
Background individual variables
Additional background variables in the analyses come from Add Health. Parent education level is an ordinal variable ranging from “1” for parents who receive a high school diploma or less to “4” for parents who receive a college diploma or higher. The higher education level of a student’s parents is used. I also include variables measuring family structure (intact two-parent family vs. other) and income (logged). For students who were missing values for income, I employed mean substitution and included a flag for missing. Additionally, I also included flags to control on students’ cohort (ninth, tenth, eleventh, or twelfth graders in 1994). None of the flags for imputed mean or cohort was statistically significant in any of the analyses conducted and therefore are not shown in the tables here.
Method and Results
In addition to descriptive techniques, the analyses were conducted with hierarchical linear modeling (HLM). Because students (level 1 units) are clustered within schools (level 2 units), standard ordinary least squares regression techniques will misestimate standard errors by not taking into account the dependence or correlation among individual student responses within the same school. Hierarchical linear modeling resolves this problem by incorporating a random effect for each level 2 unit (school) into the estimation of robust standard errors for coefficients and therefore adjusts for intraclass correlations (see Bryk and Raudenbush 1992). Given the school-based design of Add Health and the corresponding large samples of students within schools, HLM is the ideal analytic technique for using these data.
The analyses begin with descriptive statistics to examine variation by race-ethnicity and gender for the variables of interest. This includes the dependent variable of the highest math course reached by the end of high school and the key independent variables of initial math position and early academic performance in math. Subsequently, I turn to the results of the hierarchical linear models to examine differences in returns from initial math position by race-ethnicity and gender and to study whether academic performance helps to explain differential returns. Separate models are conducted for male and female students to clearly discern the math course-taking patterns of different racial-ethnic groups for each gender. All analyses utilize the Add Health longitudinal sample weights to ensure representativeness.
Descriptive Results
Table 1 displays the distribution of students’ highest math course by the end of high school, separately for each gender and racial-ethnic group. Table 1 shows that there is no male advantage in the proportion of students who reach the most academically elite levels of math (i.e., Advanced Math, Precalculus, and Calculus). Generally, at the end of high school, this segment of the math sequence can be characterized as gender equitable within each racial-ethnic group. The exception to this trend is that both white and African American female students have significantly higher levels of representation than their male peers in Precalculus.
TABLE 1.
Highest Math Course Taken by End of High School: Proportional Distribution of Students by Racial-Ethnic and Gender Category
|
MALES |
FEMALES |
|||||||
|---|---|---|---|---|---|---|---|---|
| White | AA | Latino | Asian | White | AA | Latino | Asians | |
| Remedial-basic | .01 | .01 | .01 | .00 | .01 | .01 | .01 | .00 |
| General-applied | .03 | .02 | .03 | .01 | .02 | .02 | .02 | .00 |
| Prealgebra | .03 | .06 | .06 | .04 | .02 | .02 | .04 | .03 |
| Algebra I | .11 | .15 | .18 | .08 | .09 | .11 | .14 | .08 |
| Geometry | .14 | .19 | .23 | .09 | .13 | .18 | .21 | .11 |
| Algebra II | .23 | .28 | .24 | .23 | .25 | .29 | .27 | .18 |
| Advanced Math | .07 | .09 | .06 | .05 | .07 | .09 | .06 | .07 |
| Precalculus | .26 | .14 | .14 | .24 | .31 | .22 | .20 | .28 |
| Calculus | .12 | .06 | .06 | .25 | .12 | .06 | .06 | .25 |
| N | 1,868 | 569 | 608 | 363 | 2,000 | 786 | 598 | 309 |
NOTE.—AA = African American students; columns sum to one (i.e., 100%) for each racial-ethnic and gender group.
Racial-ethnic differences remain, however, within both genders. White students of both genders have significantly higher representation than African American and Latino students of the same gender in the elite math categories. Thus, recent data from the new AHAA study confirm previously found trends of stratification in high school course taking by race and ethnicity.
Table 2 displays proportions by gender and race-ethnicity for the distribution of students’ math course taking in their first year of high school. In all categories of race-ethnicity, girls display slightly higher representations in Algebra I (or higher) than their male peers. However, this female advantage is statistically significant only among white students. Within each gender group, white and Asian students have significantly higher levels of representation in Algebra I compared with African American and Latino students of the same gender. These minority students trail behind their white and Asian peers by at least 15 percent in each gender, indicating that there is a considerable degree of inequality at the beginning of high school.
TABLE 2.
Math Course Taking and Grades in the First Year of High School: Proportional Distribution of Students by Racial-Ethnic and Gender Category
|
MATH COURSE TAKING |
MATH GRADES |
||||
|---|---|---|---|---|---|
| Prealgebra or Below |
Algebra I or Higher |
Any Failure |
C or D | A or B | |
| Males: | |||||
| White | .27 | .73 | .11 | .47 | .42 |
| African American | .44 | .56 | .18 | .57 | .25 |
| Latino | .44 | .56 | .18 | .49 | .33 |
| Asian | .31 | .69 | .05 | .41 | .54 |
| Females: | |||||
| White | .20 | .80 | .07 | .40 | .53 |
| African American | .35 | .65 | .14 | .58 | .28 |
| Latino | .36 | .64 | .14 | .51 | .35 |
| Asian | .25 | .75 | .04 | .27 | .69 |
NOTE.—N = 3,408 for males and 3,693 for females. For the proportion distribution of course taking and grades, rows sum to one (i.e., 100%) for each racial-ethnic and gender group.
Table 2 also displays descriptive statistics by gender and racial-ethnic category for the distribution of students’ grades in their first-year math course. Failure rates are significantly higher among African American and Latino students compared with white and Asian peers of the same gender. Approximately 20 percent of all male African American and Latino students fail their freshman year math course, with slightly fewer of their female peers exhibiting a similar disadvantage. This is part of a general pattern of lower failures for all female students compared with male peers of the same race-ethnicity, but this gender difference is statistically significant only among white students. Failure rates are significantly lowest among Asian students of both genders.
A corresponding pattern is observed for high grades. Within each gender, the percentage of African American and Latino students with high grades is significantly lower than the percentage for whites. Additionally, well over 50 percent of Asian students of both genders receive an A or B in their first-year math course, which is significantly greater than any other racial-ethnic group. And while females of every group appear to have higher grades than their corresponding male peers, the difference is significant only among white students.
In sum, these bivariate descriptive analyses indicate racial-ethnic disadvantages among both genders at the beginning and at the end of high school. African American and Latino male and female students begin high school at lower levels of the math sequence and remain at lower levels at the end of high school. In the next section, I examine whether, after holding this initial disparity in math course position constant, there are equal benefits to taking Algebra I or higher the first year of high school for students of different racial-ethnic and gender groups.
Results of Hierarchical Linear Modeling
Examining the returns from Algebra I
Table 3 displays the results of HLM analyses, performed separately by gender, predicting the highest math course taken by the end of high school.8 The results from the first model for each gender (model 1 for males and model 3 for females) reveal that, controlling on the other variables in the models, there are no significant main effects for African American or Latino students of either gender, compared with white students. Asian students of both genders reach significantly higher levels of math. Taking Algebra I or higher in the first year of high school has a strong effect on the level of math attained by students’ senior year. This is consistent with prior research on math course taking and confirms the hierarchical and sequential nature of math in high school. The higher students start in the math sequence, the higher they finish.
TABLE 3.
Predicting Highest Math Course Taken by the End of High School: Regression Coefficients from HLM
|
MALES |
FEMALES |
|||
|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | |
| Student background: | ||||
| African American | −.142 | −.054 | −.134 | −.054 |
| Latino | .044 | .095 | −.102 | .030 |
| Asian | .692*** | .463** | .849*** | .602*** |
| Parent education level | .292*** | .262*** | .220*** | .172*** |
| Family income | .062 | .024 | .044 | .059 |
| Intact family | .365*** | .280*** | .309*** | .154** |
| Initial math course position: | ||||
| Algebra I or higher (ninth grade) | 2.41*** | 2.31*** | 2.11*** | 2.07*** |
| African American × Algebra I | −.767** | −.734*** | −.223 | −.113 |
| Latino × Algebra I | −.925*** | −.731*** | −.297 | −.151 |
| Asian × Algebra I | −.503 | −.645 | −.395 | .025 |
| Academic performance: | ||||
| Failure in ninth-grade math course |
−.643*** | −.763*** | ||
| African American × failure | −.055 | .559** | ||
| Latino × failure | .081 | .330 | ||
| Asian × failure | −.143 | .399 | ||
| High grade in ninth-grade math coursea |
.827*** | .913*** | ||
| African American × high grade | −.363 | −.047 | ||
| Latino × failure × high grade | −.355 | −.103 | ||
| Asian × high grade | .206 | −.110 | ||
| Intercept (U0) | 3.10*** | 3.186*** | 3.91*** | 3.75*** |
NOTE.—N = 3,408 for males and 3,693 for females, with level 2, N= 69, public high schools.
High grade = A or B; contrast category = C or D.
p < .01
p < .001
Yet the results in model 1 for male students also indicate that the returns from Algebra I are not equal for all students. Thus, in reference to the first research question, the effect of taking Algebra I is significantly lower for both African American and Latino male students, compared with white students. This pattern is unique to male students. As seen in model 3 for female students, there are no significant effects of the racial-ethnic interactions with Algebra I, and tests between the coefficients in the male and female models confirm that they are significantly different. Therefore, for female students, the returns from Algebra I do not differ according to race-ethnicity. If a female African American or Latino student takes Algebra I, she receives the same advantage as her white female peers in terms of reaching a higher level of math by the end of high school.
Considering academic performance
Next, I added measures of academic performance in math during the first year of high school, as well as interaction terms between these performance variables and categories of race-ethnicity, to the baseline models for each gender. Beginning with model 2 for male students, the results indicate that even after taking students’ grades into account, the relatively lower returns to Algebra I for African American and Latino males are virtually unchanged. The interaction between racial-ethnic group and Algebra I remains negative and statistically significant for these students.
Among all male students, model 2 also indicates that failure has a strong negative main effect on the level of the math sequence reached by the end of high school, and receiving high grades early in high school has a strong positive main effect. Thus, to the extent that minority male students are more likely to fail, they will reach lower levels of math. Nevertheless, in reference to the second research question, this does not explain the fact that African American and Latino males who begin high school in Algebra I receive lower returns from doing so than their white peers.
Additionally, the interaction effects for male students in model 2 also reveal lower returns for African American male students who receive a high grade of A or B in their initial math course. The positive effect of high grades on the math sequence level is significantly lower for these students compared with their white peers. Therefore, earning high grades does not have the same beneficial consequences for African American males as it does for white males.
Model 4 displays a parallel model introducing measures of academic performance for female students. Comparing this to model 2 for male students, the main effects for failure and high grades are comparable for female students and male students. However, the interaction term measuring the effect of failure of African American female students is positive and statistically significant. Thus, while failure generally decreases the level of math that female students attain by the end of high school, it has less of a negative effect for African American females compared with white females. This suggests a some-what greater resiliency of African American females to academic difficulties and discouragement in math, and it again suggests that the meaning and consequences of grades are not uniform across all student groups.
Finally, I also modeled level 2 effects where the slopes for the interaction between race-ethnicity and Algebra I course taking (at level 1) are the dependent variable, and the independent variables, including size, location, the racial composition of the student body, and the average educational back-ground of the parents of the students in the school (analyses not shown here), are characteristics of schools (level 2). None of these school characteristics had significant effects, indicating that the differential returns from Algebra I for male students of different racial-ethnic groups do not vary according to these aspects of the school context.
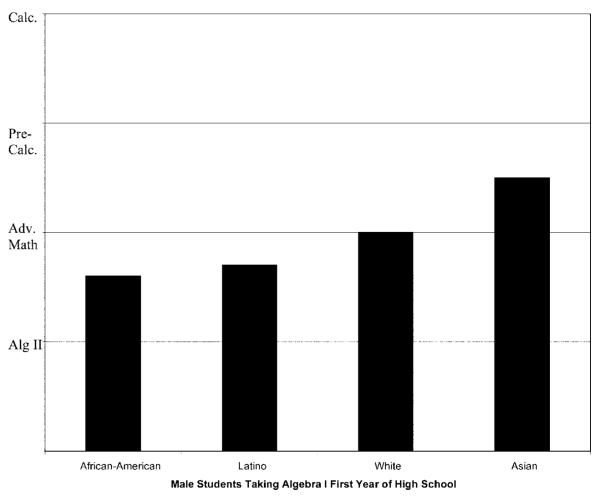
To understand better the relatively reduced advantage of Algebra I for African American and Latino males, figure 1 graphically displays the lower returns from Algebra I for these male students compared with white males. The figure shows the predicted level of the math sequence by the end of high school separately by racial-ethnic group for male students who begin high school in Algebra I. These values are calculated for male students who come from intact families with average levels of parent education and income. Although I also calculate the predicted returns from Algebra I for Asian male students, it should be noted that there are not statistically different returns from Algebra I for these students compared with white male students.
Fig. 1.
Predicted values for level of math sequence by the end of high school for male students by race-ethnicity.
The lower returns to initial math position for African American and Latino males are visibly apparent in figure 1. The difference between African American and white males is 0.4, or almost half of a sequence level, and the difference between Latino and white males is 0.3. For African American male students of otherwise average background, this translates into a predicted math sequence level of 6.6 at the end of high school. Similarly, Latino males have a predicted math sequence of 6.7. Thus, both groups have predicted levels lower than the threshold for Advanced Math. This is in contrast to white males, who have a predicted level of 7 on the math sequence, indicating that when they take Algebra I, they will on average reach Advanced Math by the end of high school.
The differential returns to Algebra I for African American and Latino males compared with white males are therefore not only statistically significant but substantively so. Research by Adelman (1999, 2003) indicates that while taking Algebra II by the end of high school does increase the chances of going to college compared with those who do not take Algebra II, the crucial threshold in predicting matriculation to a four-year college is reaching a course beyond Algebra II. The implications of the differential racial-ethnic returns to initial course position observed here are that white male students who begin high school taking Algebra I will on average successfully reach a critical course position by the end of school, while African American and Latino students will not. Thus, the reduced benefits of initial course position for minority male students signal not only stratification in the high school years but an inequality that has tangible consequences for success after high school.
Discussion and Conclusions
This article examined the high school math course-taking trajectories of high school students of different racial-ethnic groups and genders using nationally representative data from the 1990s. While much has been written focusing on patterns or disparities based on one distinction or the other, there has been little work that specifically focuses on the intersection of gender and race-ethnicity. The analyses in this article clearly reveal that race-ethnicity does not shape math course taking in identical ways for male and female students. Yet in the midst of a continuing focus in academic research on gender inequality in math, and the recent media attention on that topic, the story here is not specifically one of feminine disadvantage. Instead, this article focuses much-needed attention on the particularly disadvantaged position of African American and Latino males in a core high school subject.
While African American and Latino students of both genders generally start high school in lower math courses compared with their white peers, for minority female students, this appears to be the primary hurdle to reaching comparable levels of math with white female students by the end of high school. It is, of course, important not to downplay this initial obstacle. The lower percentages of African American and Latino females who begin high school taking Algebra I is a real and tangible problem with clear negative consequences, given the strong connection between early and ultimate levels of math course taking. The positive side of the story is that when minority female students do begin high school in Algebra I, they receive the same return to this initial course position.
The same cannot be said for African American and Latino males. Like their female peers, they are less likely to begin high school in Algebra I. Yet their disadvantage does not end there but is exacerbated by the lower returns from Algebra I they receive compared with white male peers. All students, including minority males, who start high school taking Algebra I reach higher levels of math compared with their peers in the same racial-ethnic group who begin high school in Prealgebra or a lower course. But as shown in figure 1, this Algebra I advantage is considerably less for minority male students than for their white male peers, as the former will on average fall short of a critical math course-taking threshold for college matriculation. Therefore, the inequalities in math course-taking trajectories shown here signal inequality that exists in high school but also suggest a primary mechanism through which opportunities for postsecondary attendance are stratified by race-ethnicity.
The role of academic performance was also considered here as a potentially strong reason why some students might not progress as far as others, even when they begin high school at the same position. Yet the results indicated that the patterns of inequality in math sequence level at the end of high school cannot be explained away as the result of early performance. Instead, the analyses further revealed that just as the benefits of early course taking do not accrue equally to all students, neither do the benefits of early performance. Specifically, African American males have lower returns from high grades in math at the beginning of high school. From this perspective, African American males are the group that is most severely restricted from getting ahead in high school math.
One interpretation of the results presented here is that African American males are more impervious to the feedback about their performance that grades provide. The reduced effect of failure on the final math sequence level observed for African American females compared with white females could be interpreted in a similar manner. Generally, minority students may be less responsive to institutional feedback, whether positive or negative. Ogbu (1978, 2003) offered the notion of oppositional culture, suggesting that when African American students perceive that they will receive lower returns to their educational investments or will not receive equal treatment, they proactively reject the dominant educational goals of schools. Such explanations could help explain why both African American and Latino students receive lower grades, why these minority male students do not ultimately reach the same level of math when they begin at the same initial position as their white male peers, and even why African American males receive less of a benefit from higher grades. In other words, the traditional math trajectory may be perceived as part of a system in which they are unlikely to succeed and thus rejected.
Yet the evidence for oppositional culture is equivocal, as others have suggested that rather than downplaying educational priorities, in fact minority students display more positive attitudes toward school and education (see, e.g., Ainsworth-Darnell and Downey 1998; Horvat and Lewis 2003; Mickelson 1990). Recent research finds that rather than rejecting prevailing educational norms, minority students may feel uncomfortable and unsupported in an academically intense environment that is dominated by white students (Yonezawa et al. 2002), but they respond favorably to high teacher expectations (Gutierrez 2000). Minority students may also be subject to “stereotype threat,” such that negative academic stereotypes concerning race-ethnicity psychologically influence their math performance (Steele and Aronson 1995). Additionally, the patterns observed here may be partly a consequence of teachers’ perceptions of minority students’ lower academic abilities and motivation (Oakes and Guiton 1995), as well as the content and form of the curriculum within math courses, which has been shown to have little connection and relevance to minority students’ cultures and experiences (Gutstein et al. 1997; Ladson-Billings 1997; Tate 1994).
The analyses here are limited to examining academic indicators and, therefore, did not consider the role of such factors. Yet even within the realm of previous literature, there is arguably little on which to draw to explain why the patterns of differential returns observed here apply only to minority male students and not to their female peers. Clearly, more work is needed to determine the critical factors in the public educational system, as well as the broader society, that function to place African American and Latino males in a position of educational disadvantage.
Biography
CATHERINE RIEGLE-CRUMB is a postdoctoral research associate at the University of Texas at Austin. Her research focuses primarily on gender inequality and educational stratification. She is also currently working on examining the educational intersection between gender and race-ethnicity, as well as the links between education and health behaviors among adolescents.
Footnotes
Additionally, the math sequence actually begins taking shape in middle school, where many students take Prealgebra or Algebra as eighth graders and then continue into high school having met these prerequisites for higher-level courses.
Students within a given track often take different levels of courses for different subjects, such that their track designation does not reflect the potential complexity of course-taking patterns (Lucas 1999; Schneider et al. 1998).
Additional information about Add Health can be found at http://www.cpc.unc.edu/projects/addhealth.
Additional information about the AHAA study is available at http://www.prc.utexas.edu/ahaa.
This is consistent with previous research on racial-ethnic differences in course taking (see, e.g., Hallinan 1996).
The category of Advanced Math includes Statistics and Probability, Algebra III, and Finite Math. In addition to courses by the same name, the category for Precalculus includes Trigonometry and Elementary Analysis.
To create the interaction terms, I first centered each of the two component variables by subtracting the variable mean from each original value. I then multiplied together the centered versions of these two variables. By doing this, the problem of colinearity between the interaction term and the main effects is avoided.
The coefficients in the models are uncentered and, therefore, in their natural metric. Additionally, the coefficients for Asian, students’ cohort, and the flag for imputed income are fixed across models. An analysis of variance of the dependent variable using HLM reveals that for female students, 12 percent of the variance in the highest course reached in the math sequence by the end of high school occurs between schools, and for male students, 16 percent of the variance occurs between schools.
References
- Adelman Clifford. Government Printing Office; Washington, DC: Answers in the Tool Box: Academic Intensity, Attendance Patterns, and Bachelor’s Degree Attainment. 1999 U.S. Department of Education, Office of Educational Research and Improvement.
- Adelman Clifford. Government Printing Office; Washington, DC: Postsecondary Attainment, Attendance, Curriculum, and Performance: Selected Results from the NELS:88/2000 Postsecondary Education Transcript Study (PETS), 2000. 2003 NCES 2003-39, U.S. Department of Education, Institute of Education Sciences.
- Ainsworth-Darnell James, Downey Douglas. Assessing the Oppositional Culture Explanation for Racial/Ethnic Differences in School Performance. American Sociological Review. 1998;63(4):536–53. [Google Scholar]
- Bae Yupin, Choy Susan, Geddes Clarie, Sable Jennifer, Snyder Thomas. Government Printing Office; Washington, DC: Trends in Gender Equity for Girls and Women. 2000 NCES 2000-030, U.S. Department of Education, National Center for Education Statistics.
- Barajas Heidi, Pierce Jennifer. The Significance of Race and Gender in School Success among Latinas and Latinos in College. Gender and Society. 2001;15(6):859–78. [Google Scholar]
- Bearman Peter S., Jones Jo, Udry Richard J. The National Longitudinal Study of Adolescent Health: Research Design. Carolina Population Center, University of North Carolina; Chapel Hill: 1997. [Google Scholar]
- Bryk Anthony, Raudenbush Stephen. Hierarchical Linear Models: Applications and Data Analysis Methods. Sage; Newbury Park, CA: 1992. [Google Scholar]
- Catsambis Sophia. The Path to Math: Gender and Racial-Ethnic Differences in Mathematics Participation from Middle School to High School. Sociology of Education. 1994;67(3):199–215. [Google Scholar]
- Clewell Beatriz, Anderson Bernice. Women of Color in Mathematics, Science, and Engineering: A Review of the Literature. Center for Women Policy Studies; Washington, DC: 1991. [Google Scholar]
- Correll Shelley. Gender and the Career Choice Process: The Role of Biased Self-Assessments. American Journal of Sociology. 2001;106(6):1691–1730. [Google Scholar]
- Csikszentmihalyi Mihaly, Schneider Barbara. Becoming Adult: How Teenagers Prepare for the World of Work. Basic; New York: 2000. [Google Scholar]
- Eccles Jacquelynne. Understanding Women’s Educational and Occupational Choices: Applying the Eccles et al. Model of Achievement-Related Choices. Psychology of Women Quarterly. 1994;18(4):585–609. [Google Scholar]
- Eccles Jacquelynne, Barber Bonnie, Jozefowicz Debra. Linking Gender to Educational, Occupational, and Recreational Choices: Applying the Eccles et al. Model of Achievement-Related Choices. In: Swann W, Langlois J, Gilbert L, editors. Sexism and Stereotypes in Modern Society: The Gender Science of Janet Taylor Spence. American Psychological Association; Washington, DC: 1999. [Google Scholar]
- Farkas George, Grobe Robert, Sheehan Daniel, Shuan Yuan. Cultural Resources and School Success: Gender, Ethnicity, and Poverty Groups within an Urban School District. American Sociological Review. 1990;55(1):127–42. [Google Scholar]
- Ferguson Ronald. A Diagnostic Analysis of Black-White GPA Disparities in Shaker Heights, Ohio. Brookings Papers on Education Policy. 2001:347–414. [Google Scholar]
- Forgasz Helen, Leder Gilah, Gardner Paul. The Fennema-Sherman Mathematics as a Male Domain Scale Reexamined. Journal for Research in Mathematics Education. 1999 May;30:342–48. [Google Scholar]
- Freeman Catherine. Government Printing Office; Washington, DC: Trends in Gender Equity for Girls and Women: 2004. 2004 NCES 2005-016, U.S. Department of Education, National Center for Education Statistics.
- Gamoran Adam. The Stratification of High School Learning Opportunities. Sociology of Education. 1987;60(3):61–77. [Google Scholar]
- Gamoran Adam, Nystrand Martin, Berends Mark, LePore Paul C. An Organizational Analysis of the Effects of Ability Grouping. American Education Research Journal. 1995;32(4):687–715. [Google Scholar]
- Gutierrez Rochelle. Advancing African American, Urban Youth in Mathematics: Unpacking the Success of One Math Department. American Journal of Education. 2000;109(1):63–112. [Google Scholar]
- Gutstein Eric, Lipman Pauline, Hernandez Patricia, de los Reyes Rebecca. Culturally Relevant Mathematics Teaching in a Mexican American Context. Journal for Research in Mathematics Education. 1997 December;28:709–37. [Google Scholar]
- Hallinan Maureen. Track Mobility in Secondary School. Social Forces. 1996;74(3):983–1002. [Google Scholar]
- Hallinan Maureen, Kubitschek Warren. Curriculum Differentiation and High School Achievement. Social Psychology of Education. 1999;3(1–2):41–62. [Google Scholar]
- Hanson Sandra. Lost Talent: Women in the Sciences. Temple University Press; Philadelphia: 1996. [Google Scholar]
- Horvat Erin, Lewis Kristine. Reassessing the ‘Burden of Acting White’: The Importance of Peer Groups in Managing Academic Success. Sociology of Education. 2003;76(4):265–80. [Google Scholar]
- Johnson Monica, Crosnoe Robert, Elder Glen. Students’ Attachment and Academic Engagement: The Role of Race and Ethnicity. Sociology of Education. 2001;74(4):318–40. [Google Scholar]
- Jones Lee, Mullis Ina, Raizen Senta, Weiss Iris, Weston Elizabeth. The 1990 Science Report Card. Educational Testing Service; Washington, DC: 1992. [Google Scholar]
- Ladson-Billings Gloria. It Doesn’t Add Up: African American Students’ Mathematics Achievement. Journal for Research in Mathematics Education. 1997 December;28:697–708. [Google Scholar]
- Lee Valerie, Frank Kenneth. Students’ Characteristics that Facilitate the Transfer from Two-Year to Four-Year Colleges. Sociology of Education. 1990;63(3):178–93. [Google Scholar]
- Linn Marcia, Kessel Cathy. Grades or Scores: Predicting Future College Mathematics Performance. Educational Measurement: Issues and Practice. 1996;15(4):10–14. [Google Scholar]
- Lucas Samuel R. Tracking Inequality: Stratification and Mobility in American High Schools. Teachers College Press; New York: 1999. [Google Scholar]
- Lucas Samuel R., Berends Mark. Sociodemographic Diversity, Correlated Achievement, and De Facto Tracking. Sociology of Education. 2002;75(4):328–48. [Google Scholar]
- Mau Wei-Cheng, Domnick Margaret. Characteristics of Female Students Who Aspire to Science and Engineering or Homemaking Occupations. Career Development Quarterly. 1995;43(4):323–38. [Google Scholar]
- Mickelson Rosyln A. Why Does Jane Read and Write So Well? The Anomaly of Women’s Achievement. Sociology of Education. 1989;62(1):47–63. [Google Scholar]
- Mickelson Roslyn A. The Attitude-Achievement Paradox among Black Adolescents. Sociology of Education. 1990;63:44–61. [Google Scholar]
- Moreno Susan, Muller Chandra. Success and Diversity: The Transition through First-Year Calculus in the University. American Journal of Education. 1999;108(1):30–58. [Google Scholar]
- Muller Chandra. Gender Differences in Parental Involvement and Adolescents’ Math Achievement. Sociology of Education. 1998;71(4):336–56. [Google Scholar]
- Muller Partricia, Stage Frances, Kinzie Jillian. Science Achievement Growth Trajectories: Understanding Factors Related to Gender and Racial-Ethnic Differences in Precollege Science Achievement. American Educational Research Journal. 2001;38(4):981–1012. [Google Scholar]
- National Center for Education Statistics Government Printing Office; Washington, DC: The 1998 High School Transcript Study Tabulations: Comparative Data on Credits Earned and Demographics for 1998, 1994, 1990, 1987, and 1982 High School Graduates. 2001 NCES 2001–498, U.S. Department of Education, Office of Educational Research and Improvement.
- Oakes Jeannie. Multiplying Inequalities: The Effect of Race, Social Class, and Tracking on Opportunities to Learn in Mathematics and Science. RAND Corporation; Santa Monica, CA: 1990. [Google Scholar]
- Oakes Jeannie, Guiton Gretchen. Matchmaking: The Dynamics of High School Tracking Decisions. American Educational Research Journal. 1995;32(1):3–33. [Google Scholar]
- Ogbu John. Minority Education and Caste: The American System in Cross-Cultural Perspective. Academic Press; New York: 1978. [Google Scholar]
- Ogbu John. Black American Students in an Affluent Suburb: A Study of Academic Disengagement. Erlbaum; Mahwah, NJ: 2003. [Google Scholar]
- Pelavin Sol, Kane Michael. Changing the Odds: Factors Increasing Access to College. College Board; New York: 1990. [Google Scholar]
- Riegle-Crumb Catherine, Muller Chandra, Frank Ken, Schiller Kathryn. National Longitudinal Study of Adolescent Health: Wave III Education Data. Carolina Population Center, University of North Carolina; Chapel Hill: 2005. [Google Scholar]
- Roderick Melissa. What’s Happening to the Boys? Early High School Experiences and School Outcomes among African American Male Adolescents in Chicago. Urban Education. 2003;38(5):538–607. [Google Scholar]
- Roderick Melissa, Camburn Eric. Risk and Recovery from Course Failure in the Early Years of High School. American Educational Research Journal. 1999;36(2):303–43. [Google Scholar]
- Rosenbaum James. Beyond College for All: Career Paths for the Forgotten Half. Russell Sage; New York: 2001. [Google Scholar]
- Schiller Kathryn, Hunt Donald. Accumulated Disadvantages: Racial and Social Class Differences in High School Mathematics Course Trajectories. Paper presented at the annual meeting of the American Education Research Association; Chicago. 2003. [Google Scholar]
- Schiller Kathryn, Muller Chandra. External Examinations and Account-ability, Educational Expectations, and High School Graduation. American Journal of Education. 2000;108(2):73–103. [Google Scholar]
- Schneider Barbara. Strategies for Success: High School and Beyond. In: Ravitch D, editor. Brookings Papers on Education Policy. Brookings Institution Press; Washington, DC: 2003. [Google Scholar]
- Schneider Barbara, Swanson Christopher, Riegle-Crumb Catherine. Opportunities for Learning: Course Sequences and Positional Advantages. Social Psychology of Education. 1998;2(1):25–53. [Google Scholar]
- Steele Claude, Aronson Joshua. Stereotype Threat and the Intellectual Performance of African Americans. Journal of Personality and Social Psychology. 1995;69(5):797–811. doi: 10.1037//0022-3514.69.5.797. [DOI] [PubMed] [Google Scholar]
- Stevenson David, Schiller Kathryn, Schneider Barbara. Sequences of Opportunities for Learning. Sociology of Education. 1994;67(3):184–98. [Google Scholar]
- Tate William. Race, Retrenchment, and the Reform of School Mathematics. Phi Delta Kappan. 1994;75(6):477–85. [Google Scholar]
- Tate William. Race-Ethnicity, SES, Gender and Language Proficiency Trends in Mathematics Achievement: An Update. Journal for Research in Mathematics Education. 1997 December;28:652–79. [Google Scholar]
- Teitelbaum Peter. The Influence of High School Graduation Requirement Policy in Mathematics and Science on Student Course-Taking Patterns and Achievement. Educational Evaluation and Policy Analysis. 2003;25(1):31–58. [Google Scholar]
- Weiss Christopher. Difficult Starts: Turbulence in the School Year and Its Impact on Urban Students’ Achievement. American Journal of Education. 2001;109(2):196–227. [Google Scholar]
- Xie Yu, Shauman Kimberlee. Women in Science: Career Processes and Outcomes. Harvard University Press; Cambridge, MA: 2003. [Google Scholar]
- Yonezawa Susan, Wells Amy Stuart, Serna Irene. Choosing Tracks: ‘Freedom of Choice’ in Detracking Schools. American Educational Research Journal. 2002;39(1):37–68. [Google Scholar]