Universal model for water costs of gas exchange by animals and plants

Abstract

For terrestrial animals and plants, a fundamental cost of living is water vapor lost to the atmosphere during exchange of metabolic gases. Here, by bringing together previously developed models for specific taxa, we integrate properties common to all terrestrial gas exchangers into a universal model of water loss. The model predicts that water loss scales to gas exchange with an exponent of 1 and that the amount of water lost per unit of gas exchanged depends on several factors: the surface temperature of the respiratory system near the outside of the organism, the gas consumed (oxygen or carbon dioxide), the steepness of the gradients for gas and vapor, and the transport mode (convective or diffusive). Model predictions were largely confirmed by data on 202 species in five taxa—insects, birds, bird eggs, mammals, and plants—spanning nine orders of magnitude in rate of gas exchange. Discrepancies between model predictions and data seemed to arise from biologically interesting violations of model assumptions, which emphasizes how poorly we understand gas exchange in some taxa. The universal model provides a unified conceptual framework for analyzing exchange-associated water losses across taxa with radically different metabolic and exchange systems.

All terrestrial animals and plants exchange O₂ and CO₂ with the atmosphere and thereby incur costs in the currency of water vapor (1–4). The inevitability of water loss stems from universal characteristics of terrestriality—(i) adequate gas exchange requires large surface areas of high-conductance tissues, usually invaginated; (ii) high-conductance tissues saturate internal exchange spaces with water vapor; and (iii) those surfaces must be ventilated by the atmosphere, at least intermittently. Consequently, water vapor tends to escape into surrounding drier air. Terrestrial organisms—here defined to include air-breathing marine mammals—thus face a gas–water tradeoff in which higher rates of gas exchange give higher rates of water loss. For individual organisms, this tradeoff shapes patterns of ventilation and behavior. For populations and species, the tradeoff influences diverse phenomena, including the evolution of hibernation, dormancy, and diapause (5–8), the evolution of nasal physiology in vertebrate homeotherms (9–11), and the evolution and ecology of plants with different modes of carbon fixation (C3, C4, and CAM) (12). In general, the severity of the tradeoff for any species will depend on the fraction of total water lost through the gas-exchange system, which in turn is related to the temperature and aridity of its habitat (13).

The diversity of gas-exchange systems among taxa has spawned a large set of models for predicting respiratory and stomatal water losses (14–21). Although the models are all quite similar, they have failed to provide unification and generality as a group, because each uses different terminology and is built on taxon-specific details. Broader conceptualization of the problem may give insight into how diverse organisms function across biomes and during environmental change, and it will provide a common framework for evaluating evolutionary adaptations to water stress. Our analysis of tradeoffs in gas-acquisition systems takes a first-principles approach: we do not aim to predict exact water costs of, for example, oxygen acquisition by particular species of mammals; rather, we develop a model that captures features of water–gas tradeoffs for all terrestrial plants and animals.

Model of Gas Uptake and Water Loss

Most major terrestrial taxa exchange gases through tubes. In organisms with diffusive exchange—plant leaves and bird eggs—gases and water vapor move through short tubes (stomata and eggshell pores, respectively). In organisms with convective exchange—mammals and adult birds—gases and water vapor move by bulk flow through nasal and tracheal spaces, which can be approximated as long tubes. In insects that use both convective and diffusive exchange (14), fluxes occur through spiracles, which are short tubes much like those used by plant leaves and bird eggshells. Models for the uptake of gases (oxygen for animals and carbon dioxide for plants) and the loss of water vapor have been developed for all five groups (14–21). Here, we show that the models are all specific statements of an underlying general model and that a common expression for respiratory water lost per unit of gas taken up can be readily developed.

Models of diffusive flux of a gas through a tube generally are based on the Fick equation (22) (Eq. 1)

where 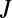is the molar flux, 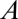is the cross-sectional area of the tube, 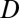is the diffusion coefficient of the gas, 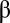is the capacitance coefficient, 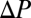is the partial-pressure gradient of the gas being consumed (gradient is defined as positive when external P is higher than internal P), and 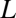is the length of the tube. Most organisms with diffusive exchange do not use a single tube; rather, they use multiple tubes distributed across a surface, which can be modeled by letting 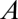be the total cross-sectional area of all tubes. In addition, for comparison with convective models, it is convenient to rewrite Eq. 1 as (Eq. 2)

where 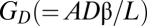is a diffusive conductance.

Eqs. 1 and 2 ignore known complications that arise in some situations, including effects of end diffusion, interference between adjacent tubes on a surface, interactions between water vapor leaving and gases entering through the tubes, and Knudsen diffusion in tubes of very small diameter (less than a few micrometers) (19, 23, 24). However, these complications usually require small corrections and in the model below, make little difference to the predictions. They will, however, be revisited in the discussion of the plant results.

There are also well-known models for convective gas flux. In respiratory physiology, such models often take the form used by Welch and Tracy (18) (Eq. 3)

where 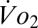is the volume of oxygen consumed per unit of time, 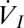and 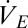are the inspired and expired volumes per unit of time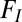, and and 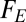are the inspired and expired fractions of oxygen. If we ignore the variation in inspired and expired volumes arising from the variation in the respiratory quotient and the water vapor added in the lungs (18), then 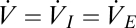. Therefore, Eq. 3 can be rewritten as 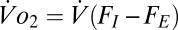. By applying the ideal gas law to both sides and rearranging the equation, we have (Eq. 4)

where 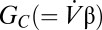is a convective conductance with the same units as the diffusive conductance 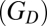and 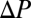is the difference in partial pressure of oxygen between inspired and expired air. To further emphasize the similarity of Eqs. 2 and 4, we note that the 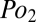of expired air is effectively identical to the mean 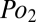in well-mixed parts of the lung. Therefore, the general equation expressing both diffusive and convective movement is (Eq. 5)

In all taxa, water vapor moves in the opposite direction through the same spaces and can be described by an analog of Eq. 5 (Eq. 6)

where the superscript denotes water vapor. Here, conductance 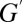can also take two forms: 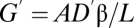for diffusion and 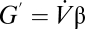for convection. Further refinement is obtained by recognizing that partial pressures of water vapor are saturating at sites of gas exchange (12). Saturation vapor pressures depend on the water potential of the nearby liquid phase, and this, in turn, depends on osmotic, matrix, and pressure potentials of water (14, 25). However, in respiratory systems, the most important factor affecting vapor pressure is temperature (26). Moreover, the relevant temperature is not the core temperature but the temperature of the opening to the atmosphere. For example, mammals and birds often recapture significant portions of excurrent water vapor by condensing it onto nasal turbinates, whose surface temperatures are depressed below body temperature (9, 10). Eq. 6 can, therefore, be rewritten for water flux as (Eq. 7)

where 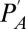is ambient vapor pressure and 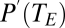is the saturation vapor pressure as a function of the temperature (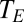) of the external openings to the exchange system.

To obtain water loss (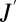) as a function of gas exchange (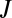), we combine Eqs. 5 and 7, taking advantage of the fact that both fluxes occur in the same physical spaces, giving (Eq. 8)

where 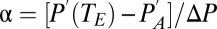, the relative magnitude of the driving gradients for water vapor and gas, and 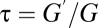, the relative magnitude of the conductances for water vapor and gas. When convection predominates, 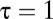, because gas and water vapor flow at the same speed. When diffusion predominates, 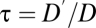, the ratio of diffusion coefficients. In animals, , the ratio of the diffusion coefficients of water vapor and oxygen; in plants, , the ratio of the diffusion coefficients of water vapor and carbon dioxide. These values of 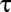show that generally, as pointed out for insects by Kestler (14), water loss can be minimized by switching from diffusive to convective exchange. Because system physical structures are identical with respect to metabolic gases (CO₂ and O₂) and water vapor, the physical dimensions (cross-sectional area, 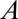, and length, 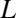) in 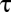cancel and therefore, disappear from the model. This simple vapor–gas relationship has been developed explicitly in the plant literature (20) and in models of respiratory water loss in vertebrates (18) and insects (14), but it has never been expressed in a general form like the one expressed here.

Eq. 8 makes profoundly simple predictions about the relationship between respiratory water loss and metabolism and, likewise, between stomatal water loss and photosynthesis. In particular, the factor 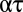represents the ratio of moles of water lost to moles of gas taken up. That ratio should depend only on the temperature at the external opening to the atmosphere (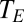), the ambient vapor pressure, the diffusion coefficient and driving gradient of the gas acquired (O₂ or CO₂), and the mode of exchange (convective versus diffusive). The ratio should not depend on details of system physical structure. Moreover, if the factors embedded in 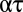do not change systematically with size, then Eq. 8 predicts that water loss scales to gas exchange with an exponent of 1. And indeed, although core body temperature scales weakly with body mass in birds and mammals (positive scaling in some groups and negative scaling in other groups) (27, 28), there is no indication that 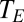varies systematically with body size. In mammals and birds, the fraction of excurrent water vapor recaptured by turbinates is, in general, about 0.6 (9, 10). Further, ambient water-vapor concentrations, although obviously variable in nature, do not vary systematically with body size. Finally, gas-concentration gradients between ambient air and the interior of the organism do not vary systematically. In mammals and birds, for example, the fraction of O₂ extracted from ventilated air is essentially invariant with body size (29–31) across species. Plants acquire CO₂ rather than O₂, but similar considerations apply; although leaf internal CO₂ concentrations vary, they do not vary systematically with plant size (3, 32).

Model Tests

To evaluate Eq. 8, we assembled literature data on gas exchange and water losses for five major groups of terrestrial organisms—mammals, birds, bird eggs, insects, and plants. The data that we used are available in Dataset S1.

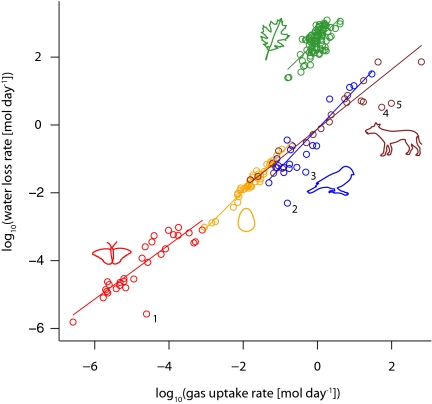
Altogether, there were data on 202 species—87 plants, 30 insects, 42 bird eggs, 22 adult birds, and 21 mammals—spanning approximately nine orders of magnitude in rate of gas uptake. As predicted by the model, there was a strong positive relationship between water loss and gas uptake (Fig. 1). The two nontaxonomic regression analyses, least-squares linear regression (LM) (Table 1) and standardized major-axis regression (SMA) (Table 2), gave qualitatively consistent results. In both, there were statistically significant interactions between log₁₀(gas uptake) and taxonomic group, indicating that water loss scales to metabolic rate differently in different groups. In particular, mammals and insects had slopes <1 and adult birds, bird eggs, and plants had slopes >1 in both analyses. In the LM analysis, the interaction term had a small F value (Table 1), and we, therefore, refit the model without the interaction term [i.e., log₁₀(water loss) ∼ log₁₀(gas uptake) + taxonomic group] as a means of estimating the common slope for all of the data; it was 0.94 [95% confidence interval (CI) = 0.88–1.00]. The SMA analysis automatically estimates a common slope; it was 1.10 (95% CI = 1.05–1.16). It is possible that the leaf-exchange data, because they are not expressed on a per plant basis, dominated these results. To check, we reran the analyses using only animal data; the results were similar to those from the full dataset (SI Text and Table S1). One could also argue that gas exchange and water loss are not related mechanistically (although our model development refutes this idea) but instead, are both driven independently by body size (33, 34). To evaluate this possibility in the animal groups (plant data were not expressed in terms of body size), we performed linear regressions of log₁₀(oxygen consumption) and log₁₀(respiratory water loss rate) separately against log₁₀(body mass) and then, examined the residuals. There was a highly significant relationship between metabolic and water residuals with a slope of 1.07 (95% CI = 0.90–1.27) (Fig. S1), indicating that the relationship in Fig. 1 is not simply driven by independent correlations of the two variables with body size.

Fig. 1.

Scaling of water loss to gas exchange—O₂ for animals and CO₂ for plants (n = 202). Solid lines represent lines from a fitted linear model that allowed interactions between group (plants, mammals, etc.) and log₁₀(gas uptake rate). The labeled points are outliers that were not included in the formal modeling. They are Blatella germanica (German cockroach; 1), Bolborhynchus lineola (lineolated parakeet; 2), Falco mexicanus (prairie falcon; 3), Tursiops truncatus (bottlenose dolphin; 4), and Delphinapterus leucas (beluga whale; 5).

Table 1.

Summary of least-squares linear modeling of the data shown in Fig. 1

Source	df	SS	MS	F	P
Log10(gas uptake)	1	975.6	975.6	15,196	<0.00001
Group	4	239.9	60.0	934	<0.00001
U × G	4	1.38	0.34	5.4	0.0004
Residuals	187	12.0	0.1

Five outliers were not included in this analysis. U, log₁₀(gas uptake); G, group.

Table 2.

Summary of standardized major-axis regression implemented in R statistical software (package smatr, function slope.com)

Group	Fitted slope	95% CI
All groups together	1.10	1.05–1.16
Insects	0.85	0.74–0.98
Bird eggs	1.11	1.05–1.18
Adult birds	1.22	1.03–1.44
Mammals	0.90	0.80–1.02
Plants	1.53	1.31–1.78

The function calculates a likelihood ratio to test if the slopes of the groups are different. Here, the likelihood ratio was 39.0 (P < 0.00001). The function also calculates a common slope and slopes for each group. CI, confidence interval.

Finally, to better control for taxonomic nonindependence in the data, we used linear mixed-effects models with Group (e.g., plants and insects), Order, Family, and Genus incorporated as nested random effects (35); this analysis was chosen in lieu of more powerful methods that use tree topologies, because many of our taxa are only distantly related and well-supported phylogenies are not available for all of them. This analysis indicated that evolutionary associations had very weak effects on the data; aside from Group, which accounts for the major differences in the design of gas-exchange systems, taxonomy accounted for <1% of the total variance (Table S2).

How well does the general model predict these data? From the same studies, we extracted the additional data needed to parameterize Eq. 8—ambient and internal partial pressures of oxygen or carbon dioxide (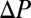), ambient vapor pressure (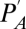), ambient temperature, and temperature of the respiratory opening to the environment (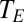). 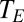for plants, bird eggs, and insects was estimated as the temperature in the experimental chamber or cuvettete; 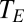for adult birds and mammals was estimated as the temperature of exhaled air (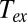). Then, using 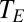, we estimated the saturating vapor pressure (kPa) from a standard equation (20): .

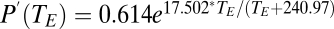Experimentally measured transpiration ratios, 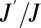, were well-predicted by the parameterized model (Fig. 2), although they were better for some groups than for others. Pooling across taxonomic groups, we found, using linear regression, that log₁₀(observed transpiration ratio) was related to log₁₀(predicted transpiration ratio) with a slope of 1.06 (95% CI = 1.03–1.09); if the model predicted the observations perfectly, the slope would have been 1. In addition, the fitted model accounted for 96% of the variance. It is possible that plants, because they are quite distinct from the animal groups (Fig. 2), drive this relationship. The refitted model, without plants, had a fitted slope of 1.17 (95% CI = 0.94–1.40) and accounted for 49% of the variance; the slope was higher, because transpiration ratios of insects were particularly poorly predicted. To quantify taxon-specific model performance, we calculated, for each species within a group, the distance between observed and predicted transpiration ratios (on log₁₀ scale) and evaluated if they were significantly different from zero using a Student's t test; good model performance would be indicated by an insignificant t value and small CI for the mean estimated distance. This approach (Table 3) indicated that the model performed well in three groups—mammals, adult birds, and bird eggs. In insects and plant leaves, by contrast, there were significant and large positive deviations from zero. Both insects and plant leaves had significantly higher transpiration ratios than predicted. A sensitivity analysis of model parameters is presented in SI Text.

Fig. 2.

Observed transpiration ratio [log₁₀(water loss rate/gas uptake rate)] versus predicted transpiration ratio from Eq. 8 (n = 197; five outliers in Fig. 1 omitted). For each species, Eq. 8 was parameterized using data extracted from the study in which it occurred. The 1:1 line provides a visual means of evaluating how close observed values are to predicted values.

Table 3.

Summary of distances between observed and predicted transpiration ratios for each of the five groups

Group	Difference*	95% CI	df	t value	P
Insects	0.36	0.22–0.50	28	5.3	<0.00001
Bird eggs	0.03	0.00–0.07	41	2.1	0.04
Adult birds	0.00	−0.15–0.15	17	−0.06	0.95
Mammals	0.01	−0.10–0.12	18	0.2	0.86
Plants	0.25	0.21–0.30	86	11.2	<0.00001

*Difference refers to the mean value of log₁₀(observed transpiration ratio) − log₁₀(predicted transpiration ratio).

Discussion

Terrestrial multicellular organisms have evolved an astonishing diversity of gas-acquisition mechanisms that belie a deep simplicity: gases (O₂ or CO₂) are obtained from the atmosphere, gas partial pressures are low at sites of internal exchange, gas arrives from the atmosphere at sites of exchange by diffusion or a combination of convection and diffusion, and sites of uptake are uniformly large in area and highly permeable to water vapor. Collectively, these characteristics suggest that simple models of exchange (e.g., Eq. 8) should capture, for essentially all air-breathing animals and aerial plants, how respiratory and stomatal water losses scale to gas acquisition.

Our data on five major groups of organisms support this idea: the first-principles model (Eq. 8) was reasonably successful at predicting quantitative relationships between gas exchange and water loss across taxonomic groups, with three implications. First, in all groups, water loss scaled to gas uptake with slopes of 1 or close to 1. This result implies a strong but not absolute constraint on the water costs of gas exchange: higher rates of gas exchange lead to higher water costs. Second, water costs per unit of gas exchanged are much higher for plants than animals; the two groups are constrained to nonoverlapping fundamental niches with respect to relative fluxes of water and carbon (36). For animals, much lower unit water costs allow both greater energy throughputs (e.g., to be used for locomotion) and the freedom to move intermittently away from water sources. Third, there is real and substantial variation among animal groups, and this variation stems from differences in mode of transport (diffusion versus convection) and the magnitude of the O₂ gradient from environment to organism.

However, the model performed poorly in two respects. First, in all groups, there was substantial intragroup residual variation (vertical spread in Fig. 2). Residual variation could stem from experimental error or differences in methods among studies, but these sources are likely small. Second, net error could arise from errors in the individual parameter values used to predict transpiration ratios; this is more likely. More likely still is that one or more of the model assumptions were violated. Such violations could be interpreted to mean that the respiratory characteristics captured in our model do not operate as strict constraints among taxonomic groups. In other words, although the simple processes captured in Eq. 8 shape the overall relationship, individual species clearly can evolve alternative mechanisms that give higher or lower unit water costs in some circumstances.

However, the violations are themselves biologically interesting, and they emphasize the value of the model as a tool for establishing null expectations. One class of violations probably explains the extraordinarily low transpiration ratios for the outliers labeled 1–5 on Fig. 1. These include one insect (1), two birds (2 and 3), and two marine mammals (4 and 5). The authors of the marine mammal study (37) and bird studies (38) state that exhaled air was not saturated with water vapor. The mechanisms leading to subsaturation are unknown and therefore bear attention, but, obviously, these are not accounted for by Eq. 8. The transpiration ratio for the insect, the cockroach Blatella germanica, was far lower than expected from the other insects and was 10-fold lower than predicted by the model. Again, the mechanism is unknown but worth examining or at least confirming.

The second major way in which the model performed poorly in predicting the observed transpiration for the entire insect and plant groups probably also reflects violations of model assumptions. For insects, water losses per unit O₂ consumed were up to 8-fold higher than predicted (mean = 2.3-fold). This discrepancy may stem from the unusual pattern of respiratory exchange used by many insects but not other taxa in our study: discontinuous gas-exchange cycles (DGCs; 20 of 30 species used cyclic or discontinuous respiration). During DGCs, external openings of the tracheal system, the spiracles, are sealed shut for extended periods punctuated by brief openings (39). During the closed phase, CO₂, which is far more soluble than oxygen (26), is forced into the body fluids (40, 41). However, maintaining acid–base homeostasis over time scales longer than individual ventilation cycles requires that insects rid themselves of essentially as much CO₂ as they consume O₂. Following Hetz and Bradley (42) and others, we propose that ridding themselves of sufficient CO₂ requires spiracles to open longer or more frequently than necessary simply for taking up adequate O₂. An adequate model of spiracular water loss would, therefore, have to incorporate the dynamics of CO₂ solution and dissolution from the body fluids. Additional tests of this idea, using insect data, are presented in Fig. S2.

Plants also had higher than predicted transpiration ratios by a mean of 1.8-fold and up to 6-fold (Fig. 2), and in general, the model captured C4 transpiration ratios better than it did C3 ratios (Fig. S3). Although plants use stomata much like insects use spiracles, discontinuous opening of stomata does not force as much of the unwanted gas (O₂) into leaf tissues, because it is not nearly as soluble. We suggest instead that the high observed transpiration ratios stem from convective flow from the interior of the leaf through the stomata to the outside (19) and possibly also from differential effects of multicomponent diffusion on transport of water vapor and carbon dioxide (19, 43). For a leaf at steady state, Leuning (19) showed that the slight excess pressure inside leaves (arising from the evaporation of water vapor into intercellular spaces) results in convective flow out through the stomata. Flow changes predicted transpiration ratios. In particular, water losses will be magnified, and carbon dioxide gain (for a given partial-pressure gradient) will be depressed; together, these effects will increase observed transpiration ratios. Similar combined effects of diffusion and convection for insects are discussed by Kestler (14).

More broadly, the patterns in Fig. 2 suggest that transpiration ratios in organisms with valved respiratory openings (insects and plants) deviate significantly from predictions derived from simple gas-exchange models. Despite fundamental differences between plant and insect physiologies, we suggest that problems of gas exchange and water vapor loss are quite similar; additional progress may be possible by applying common theoretical and empirical approaches.

Data and Methods

Data.

Suitable data on gas and vapor exchange were identified from searches in Web of Science and by tracing references in newer studies back into the past. Our coverage of animal taxa is relatively complete—there are surprisingly few data for many of the groups, and many of the available studies did not clearly partition respiratory from cutaneous water losses. By contrast, there were abundant data on plants, both because plant physiologists use commonly available commercial devices (often a Licor LI-6400) for measuring leaf parameters under reasonably comparable conditions and because almost all leaf-vapor efflux can be considered respiratory (it comes out through stomata). When more than one study analyzed a particular species, we either averaged the results or chose the one carried out under the most benign conditions. Often, authors manipulated temperature; if so, we chose values from the range of 25–30 °C, if available. Otherwise, no temperature corrections were made. For animals, data on metabolic rate and respiratory water loss were accepted only if measurements were made on nonactive (i.e., not running or flying) individuals.

From each study, we extracted data on carbon dioxide (plants) or oxygen uptake (animals). For animal studies that measured metabolism as carbon dioxide emission, we converted the measurements to oxygen consumption using stated respiratory exchange ratios (or if these were not explicitly stated, using the respiratory exchange ratio from a related species or similar study). We also extracted data on respiratory water loss. For plants and bird eggs, respiratory water losses were assumed to be equivalent to total water losses, which is reasonable because essentially all water vapor moves out through stomata and eggshell pores, respectively. For birds, mammals, and insects, respiratory water losses have been measured using a variety of methods; however, we used data only from studies in which the measurements were direct or were estimated by quantitatively partitioning respiratory losses from other losses (e.g., cutaneous or cuticular). Finally, all water losses were converted to units of mol day⁻¹ organism⁻¹ with the exception of plants, for which losses were converted to mol day⁻¹ m⁻² leaf area. For comparison with the animal data, the plant data, ideally, would be expressed on a per plant basis. However, very few studies estimated total leaf area; plant physiologists have converged on reporting exchanges on a per area basis. To access a sufficiently large dataset, we therefore used the area-specific data and, for analyzing total fluxes, assumed that each plant had 1 m² of leaf area.

To predict transpiration ratios, we also extracted data on experimental temperature, ambient humidity, and for plants, ambient carbon dioxide levels. Many plant studies reported carbon dioxide levels in internal spaces, and many animal studies reported oxygen levels in the lungs (or equivalently, in expired air). If any of these data were unavailable, we estimated their levels by analyzing the experimental design or from studies on related taxa.

Statistics.

We analyzed the data using both nonphylogenetic and phylogenetic methods. The nonphylogenetic analyses included LM and SMA (44) implemented in the R statistical software v. 2.10.0 (functions lm, slope.com, and line.cis; the latter two are available in the package smatr). We also omitted five clear outliers (numbered data points in Fig. 1) from regression analyses. The factors underlying their anomalously low water losses are discussed in SI Text. To control for phylogeny, we used linear mixed-effects modeling (35) with nested random effects: Group, Order, Family, and Genus (lme function in R). Lack of good phylogenies for some groups precluded implementing more powerful analyses that takes into account tree topologies and branch lengths.