Decoding of MSTd population activity accounts for variations in the precision of heading perception

Abstract

Humans and monkeys use both vestibular and visual motion (optic flow) cues to discriminate their direction of self-motion during navigation. A striking property of heading perception from optic flow is that discrimination is most precise when subjects judge small variations in heading around straight ahead, whereas thresholds rise precipitously when subjects judge heading around an eccentric reference. We show that vestibular heading discrimination thresholds in both humans and macaques also show a consistent, but modest, dependence on reference direction. We used computational methods (Fisher information, maximum likelihood estimation, and population vector decoding) to show that population activity in area MSTd predicts the dependence of heading thresholds on reference eccentricity. This dependence arises because the tuning functions for most neurons have a steep slope for directions near straight forward. Our findings support the notion that population activity in extrastriate cortex limits the precision of both visual and vestibular heading perception.

INTRODUCTION

A fundamental challenge for neuroscience is to characterize how populations of neurons encode and decode sensory information. The problem of encoding, i.e., predicting neural responses to known stimuli, has been a central focus of sensory physiology for many years. The reverse problem of decoding, that is determining what takes place in the world from neuronal spiking patterns, has received substantially less attention. Understanding how patterns of activity across populations of neurons shape sensory perception has been facilitated by recent advances in theoretical and computational neuroscience (Abbott and Dayan, 1999; Averbeck et al., 2006; Ma et al., 2006; Pouget et al., 1998; Sanger, 1996; Seung and Sompolinsky, 1993). These advances have provided experimentalists with analytical tools to examine neural correlates of sensory perception (Arabzadeh et al., 2004; Chacron and Bastian, 2008; Gardner et al., 2004; Jazayeri and Movshon, 2006, 2007; Romo et al., 2006; Shadlen et al., 1996). Although theory has suggested that information estimates from populations of neurons should account for the precision of behavior, few studies have actually demonstrated this.

If neural activity in a particular brain area limits perception, then dependencies of behavioral performance on stimulus parameters should be explainable by decoding population responses. Here we evaluate neural decoding for heading perception, where heading refers to the current direction of translational self-motion. When human subjects judge heading from optic flow, they show high sensitivity (low thresholds) for discriminating small variations in heading around straight ahead, but thresholds rise steeply when subjects discriminate heading around an eccentric reference (Crowell and Banks, 1993). We show that the same property is shared by vestibular heading perception: both humans and monkeys are better at discriminating small changes in heading direction around straight-ahead than around lateral movement directions.

Which properties of neuronal responses could account for the variable precision of heading judgments with eccentricity? The medial superior temporal area (MSTd) is hierarchically the first multisensory area in the dorsal visual stream and contains neurons that represent heading based on visual and vestibular cues (Bremmer et al., 1999; Britten and van Wezel, 1998; Chowdhury et al., 2009; Duffy, 1998; Gu et al., 2006; Page and Duffy, 2003; Takahashi et al., 2007). If MSTd plays a central role in visual and vestibular heading perception, as suggested by previous studies (Britten, 1998; Britten and Van Wezel, 2002; Gu et al., 2008b; Gu et al., 2007), then the neural representation of heading in MSTd should account for the dependence of heading thresholds on eccentricity. One possible explanation is that MSTd contains many neurons that prefer forward motion with sharp tuning (e.g., Duffy and Wurtz, 1995), but other studies have found that most MSTd cells prefer lateral motion directions (Gu et al., 2006; Lappe et al., 1996). Alternatively, broadly-tuned neurons with lateral direction preferences may have their peak discriminability (steepest tuning-curve slopes) for motion directions near straight ahead. To distinguish these possibilities, we measured visual and vestibular heading tuning functions for a large, unbiased sample of MSTd neurons. We then used computational methods (Fisher information, maximum likelihood estimation, and population vector analysis) to measure the accuracy and precision of population activity for many reference headings. We find that predictions of behavioral performance based on Fisher information, as well as two specific decoding methods (maximum likelihood and population vector), largely account for the variable precision of heading perception with eccentricity.

RESULTS

Behavioral observations

To quantify the precision with which subjects discriminate heading, 7 human subjects and 2 macaques were tested in a two-interval task in which each trial consisted of two sequential translations, a ‘reference’ and a ‘comparison’ (Fig. 1A). The subjects' task was to report whether the comparison movement was to the right or left of the reference (see Methods). Subjects performed this task either during inertial motion in darkness (‘vestibular’ condition) or while stationary and viewing optic flow stimuli that simulated the same trajectories (‘visual’ condition). In the visual condition, the stimulus simulated self-translation through a rigid volume of fronto-parallel triangles distributed uniformly in 3D space. We have previously shown, for monkeys, that intact vestibular labyrinths are critical for high precision performance in the vestibular condition (Gu et al., 2007). Thus, performance in the ‘vestibular’ condition likely depends critically on signals of vestibular origin.

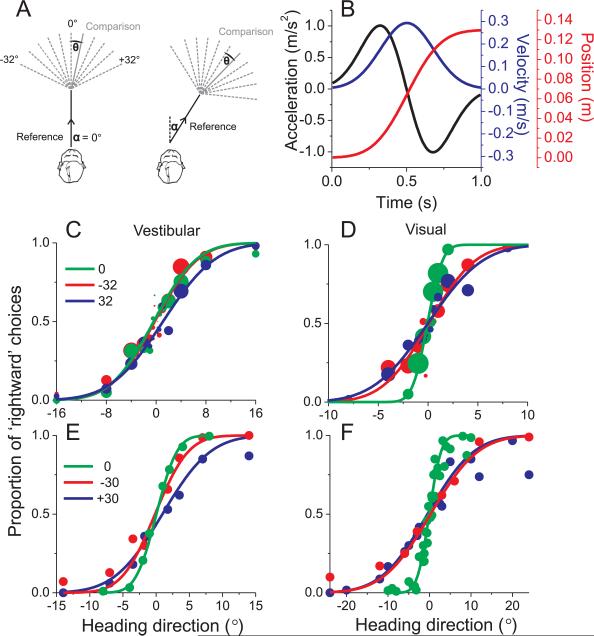
Fig. 1. Heading Discrimination Task and Performance.

(A) Schematic illustration of the experimental protocol. Two different reference directions (α=0° and 32°) are shown, along with various comparison directions. (B) Each interval of the motion stimulus has a Gaussian velocity profile (blue), with a corresponding biphasic acceleration profile (black) and sigmoidal position variation (red). (C), (D) Example psychometric functions (vestibular and visual conditions, respectively) from one human subject for three reference headings, 0° (straight-ahead), −32° and 32° (n = 750 trials each). Solid curves illustrate cumulative Gaussian fits in which each data point is weighted according to the number of trials that contribute to it (represented by symbol size). (E), (F) Example data from a macaque monkey. Here the method of constant stimuli was used, thus all data points have the same number of stimulus repetitions (>70).

Choice data were pooled to construct a single psychometric function for each reference heading (percent ‘rightward’ choices vs. comparison heading), as shown for one human subject in Fig. 1C, D and for one macaque subject in Fig. 1E, F. The greatest sensitivity (steepest slope) was seen for the straight-forward (0°) reference heading (green), whereas the slope of the psychometric functions became shallower as reference eccentricity increased (red, blue). This effect appears to be stronger for visual (Fig. 1D,F) than vestibular (Fig. 1C,E) responses. Behavioral data from each subject and each reference heading were fit with a cumulative Gaussian function and ‘threshold’ was taken as the standard deviation of the Gaussian fit (corresponding to ~84% correct).

Across all human subjects, behavioral thresholds increased as reference heading deviated from straight-forward (0°), as shown in Fig. 2A, B. The dependence on reference heading was highly significant in both the vestibular (F₂₀, ₈₄=3.52, p<<0.001, random effects ANOVA, Fig. 2A) and visual conditions (F_{18, 38}=2.51, p=0.0084, Fig. 2B). Subjects were most sensitive for heading discrimination around straight-forward (0°) and least sensitive for discrimination around side-to-side motions (±90°). As the vestibular reference heading increased beyond 90° (Fig. 2A), thresholds decreased again, reaching smaller values for backward reference headings (±180°). Thresholds for reference headings within ±30° of straight forward were significantly lower than thresholds for references within ±30° of backward (Mann-Whitney U test, p<<0.001), such that humans were almost two-fold more sensitive when discriminating heading around forward than backward motion.

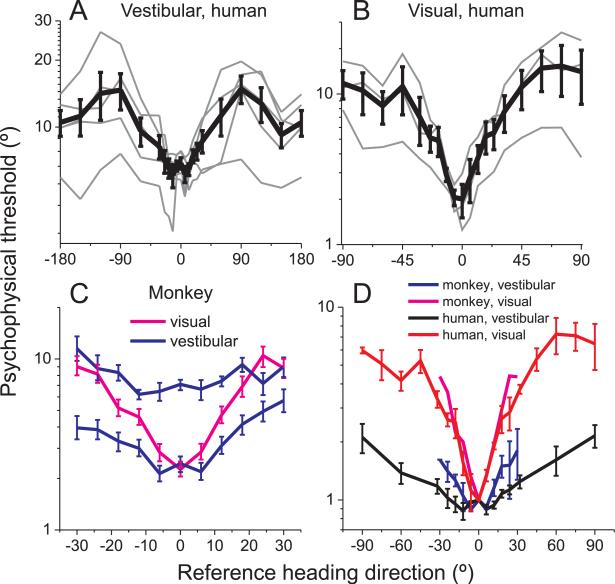
Fig. 2. Dependence of heading discrimination thresholds on reference eccentricity.

(A), (B) Human behavioral thresholds (thin lines: single subjects; thick lines: mean±SE across subjects) as a function of reference heading for the vestibular task (A, N=5 subjects) and the visual task (B, N=3 subjects). (C) Macaque behavioral thresholds, as a function of reference eccentricity, in the vestibular task (blue, 2 animals) and the visual task (pink, 1 animal). Error bars illustrate 95% confidence intervals. (D) Normalized mean thresholds, comparing monkey visual and vestibular thresholds (magenta and blue, respectively) with human visual and vestibular thresholds (red and black, respectively). Data from each subject are normalized to unity at the 0° reference heading before computing the mean and SE across subjects.

The V-shaped dependence of human visual heading thresholds (Fig. 2B) was shallower than reported by Crowell and Banks (1993), a difference that is likely attributable to the much larger field of view (~90×90°) in the present experiments. Moreover, the effect of eccentricity in the vestibular condition was significantly weaker than that seen in the visual condition (ANCOVA, p<<0.001, data from ±90° references were folded around 0°). Thus, when heading is discriminated using optic flow, thresholds increase more sharply with eccentricity than when similar judgments are made from vestibular cues in darkness (Fig. 2A, B).

Similar results were found for monkeys (Fig. 2C). Here, average heading thresholds are plotted as a function of reference eccentricity for two animals tested in the vestibular condition (blue) and one animal tested in the visual condition (magenta). To compare human and macaque data, Fig. 2D plots normalized thresholds (relative to the 0° reference heading) as a function of reference eccentricity in the ±90° range. The increase in threshold with eccentricity is steeper for macaques than humans in the vestibular condition (ANCOVA, p<<0.001) but not in the visual condition (ANCOVA, p=0.09, data folded around 0°). The shallower dependence of vestibular thresholds on eccentricity, relative to visual thresholds, is also evident in Fig. 2D. Specifically, human vestibular thresholds increase ~2 fold (mean±SE: 2.1 ± 0.3) for forward versus lateral headings, whereas the corresponding change in visual thresholds is ~6-fold (6.2±0.97).

Fisher information analysis and neuronal discrimination thresholds

Which properties of neuronal heading tuning constrain discrimination thresholds and how do these features account for the observed dependence of heading thresholds on reference eccentricity? To examine whether MSTd population activity can predict the behavioral effects, we computed Fisher information to quantify the heading sensitivity that could be achieved by an unbiased decoding of our sample of neurons (see Methods). Assuming Poisson statistics and independent noise among neurons (see Discussion), the contribution of each cell to Fisher information is the square of its tuning curve slope (at a particular reference heading) divided by the corresponding mean firing rate (equation [1]). Figure 3 illustrates this computation for an example cell tested with 8 directions of translation in the horizontal plane (45°, steps). The slope of the tuning curve is computed by interpolating the coarsely sampled data using a spline function (resolution: 0.1°; Fig. 3A, black curve), and then taking the spatial derivative of the fitted curve at each possible reference heading.

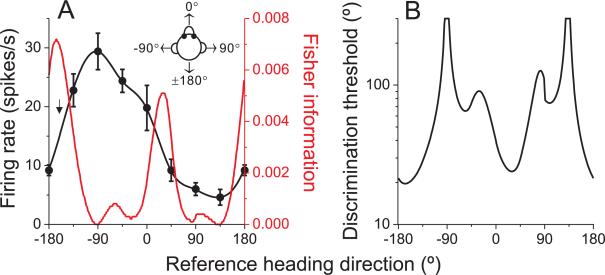
Fig. 3. Calculation of Fisher information and discrimination thresholds for an example neuron.

(A) Example tuning curve (black) and Fisher information (red). Arrow indicates the direction corresponding to peak Fisher information. (B) Neuronal discrimination thresholds as a function of reference heading direction for the same example cell. See also Figure S2.

The contribution of this example neuron to Fisher information is shown by the red curve in Fig. 3A; the corresponding neuronal discrimination thresholds, corresponding to d'=√2 (equation [2]), are shown in Fig. 3B. Note that maximum Fisher information (minimum neuronal threshold) is encountered at approximately the steepest point along the tuning curve (arrow in Fig. 3A), not at the peak. This is because neurons contribute to Fisher information in proportion to the squared derivative of the tuning curve. In this sense, Fisher information formalizes the notion that fine discrimination depends most heavily on neurons whose tuning curves are steepest around the reference direction (Gu et al., 2008b; Jazayeri and Movshon, 2006; Purushothaman and Bradley, 2005; Seung and Sompolinsky, 1993).

This analysis was performed for 882 MSTd neurons with significant visual tuning in the horizontal plane and a subgroup of 511 neurons that were also significantly tuned in the vestibular condition. Figs. 4A and 4C show distributions of the reference heading at which each neuron exhibits its minimum neuronal threshold (i.e., peak discriminability) for the vestibular and visual conditions, respectively. Both distributions have clear peaks around forward (0°) and backward (180°) headings. To further illustrate the relationship between peak discriminability and peak firing rate, Figs. 4B and 4D show the cells' tuning width at half maximum plotted versus heading preference (location of peak firing rate).

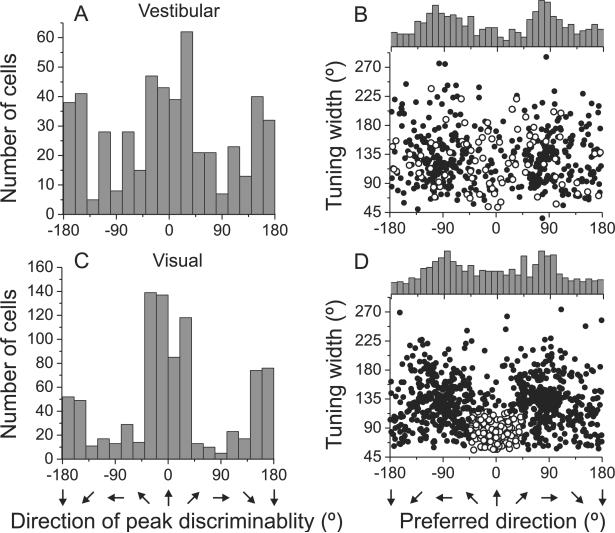
Fig. 4. Summary of MSTd population responses.

(A), (C) Distribution of the direction of maximal discriminability, showing a bimodal distribution with peaks around the forward (0°) and backward (±180°) directions for vestibular (n=511) and visual conditions (n=882), respectively. (B), (D) Scatter plots of each cell's tuning width at half maximum versus preferred direction. The top histogram illustrates the marginal distribution of heading preferences. A subpopulation of neurons with visual direction preferences within 45° of straight ahead and tuning width <115° are highlighted (open symbols). See also Figure S1.

As reported previously (Gu et al., 2006), the distribution of heading preferences (Fig. 4B, D) is bimodal for both the vestibular and visual conditions, with peaks at −90° and 90° azimuth (lateral headings). Comparing Fig. 4A,C with Fig. 4B,D, it is clear that peak discriminability often occurs for reference headings ~90° away from the tuning curve peak, consistent with the broad heading tuning shown by most MSTd cells. Closer inspection of Fig. 4B, D reveals that most cells that prefer lateral headings have tuning widths between 90° and 180°. In the vestibular condition, few cells have heading preferences close to straight ahead (0°). In the visual condition, however, there is a subpopulation of narrowly-tuned neurons that prefer forward headings. Open symbols in Fig. 4D represent an arbitrarily defined subset of cells with visual heading preferences within 45° of straight ahead and tuning widths that are <115°. These neurons have vestibular heading tuning that is broadly distributed in both preferred direction and tuning width (Fig. 4B, open symbols). This group of cells was not obvious in previous publications (Gu et al., 2006; Takahashi et al., 2007) due to the smaller data sets in those studies.

Multimodal MSTd neurons can have congruent or opposite heading preferences in the visual and vestibular conditions (Gu et al., 2006; Page and Duffy, 2003; Takahashi et al., 2007). We used the difference in direction preference between visual and vestibular tuning to place neurons into three groups: ‘congruent’ cells, ‘opposite’ cells, and ‘intermediate’ cells (Figure S1A). For visual-only and opposite cells, visual heading preferences were bimodally distributed and with modes around ±90° (Figure S1B, C: uniformity test, p<<0.001, modality test: p_uni<0.01 and p_bi>0.6, Supplementary methods). In contrast, congruent and intermediate cells had visual heading preferences that were more uniformly distributed in the horizontal plane (uniformity test, p>0.05; Figure S1D, E). Notably, cells with narrow tuning and forward heading preferences (Fig. 4B, D, open symbols) were found among all cell types, but constituted a larger proportion of congruent cells (18.8%) than opposite cells (11.5%).

Fisher information analysis of MSTd population responses

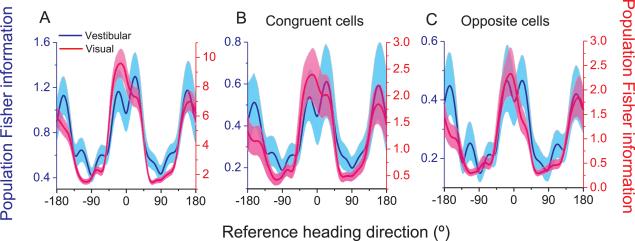
We can now compute population Fisher information by summing the contributions of all MSTd cells with significant heading tuning (Visual: n=882; Vestibular: n=511). There is a clear dependence of Fisher information on reference heading for both visual and vestibular conditions (Fig. 5A), with a maximum for headings near 0° and a minimum for headings near ±90°. This dependence is similar for vestibular and visual conditions (blue and red curves in Fig. 5A), although the magnitudes of Fisher information differ due to the different sample sizes and differences in signal-to-noise ratio between conditions. This computation assumes that all neurons contribute equally to discrimination and have independent noise (see Discussion), such that d' increases with the square root of the number of neurons in the pool.

Fig. 5. Population Fisher information.

(A) Comparison between vestibular (blue, n=511 neurons) and visual (red, n=882 neurons) population Fisher information computed from all neurons with significant tuning in the horizontal plane. (B&C) Fisher information for subsets of congruent neurons only (B, n=223) and opposite neurons only (C, n=193). Solid curves: population Fisher information; Error bands: 95% confidence intervals derived from a bootstrap procedure. See also Figure S3.

Given the congruent/opposite subclasses of MSTd neurons, we wondered whether the dependence of Fisher information on reference heading changes when specific subpopulations are selectively decoded. As shown in Fig. 5B and 5C, results are similar when Fisher information is computed only from congruent cells (Fig. 5B, n=223) or only from opposite cells (Fig. 5C, n=193).

In the analysis of Fig. 5, we assumed that MSTd activity follows Poisson statistics (variance=mean) when computing Fisher information (eq. [1]). To examine how the results might be affected by this assumption, we repeated the analysis using estimates of variance computed by linear interpolation of the variance-mean relationship (Nover et al., 2005; Supplementary methods). Because the relationship between the mean and variance of spike counts is approximately linear for most MSTd neurons (Celebrini and Newsome, 1994; Gu et al., 2008b), a type II linear regression in log-log coordinates was used to estimate response variance for any mean firing rate (Figure S2). The dependence of Fisher information on reference heading is very similar when using the measured variance versus the Poisson assumption (Fig. S3A). Moreover, the results depend little on the time window of analysis (Figure S3B, C). For the rest of the presentation, we continue to use the independent Poisson assumption for simplicity, with spikes counted within a 1s window.

Predicted population thresholds

To compare neural predictions with the psychophysical data of Fig. 2, we transformed population Fisher information into predicted behavioral thresholds using equation [2] with a criterion of d'=√2. Because psychophysical data were obtained under stimulus conditions very similar to those of the physiology experiments, such a comparison is justified with the implicit assumption that heading perception arises from decoding a population of neurons similar to those we recorded in MSTd.

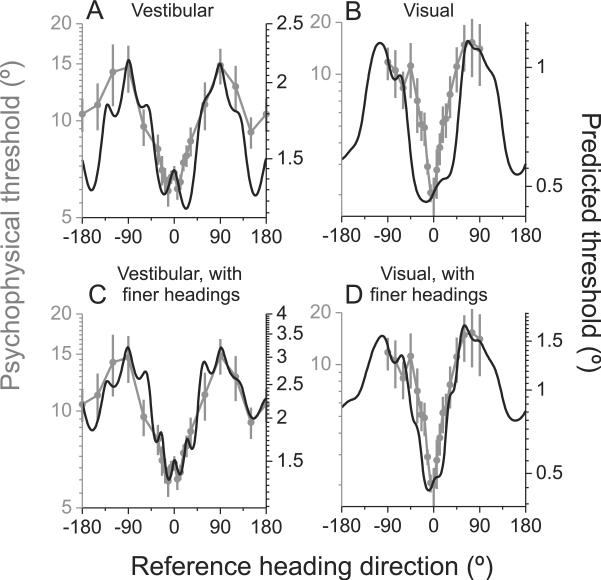
This comparison of predicted and measured thresholds, as a function of reference heading, is shown for the vestibular and visual task conditions in Fig. 6A and 6B, respectively. Note that the ordinate scale for predicted thresholds has been adjusted such that the minimum/maximum values roughly align with those of the measured psychophysical thresholds. In other words, we focus on comparing the shape of the predicted and measured data rather than the absolute threshold values. This is justified because predicted thresholds depend on the number of neurons that contribute to Fisher information, and the number of neurons that contribute to the behavior is unknown.

Fig. 6. Comparison of predicted and measured heading thresholds as a function of reference direction.

(A) Vestibular: n=511 neurons; (B) Visual: n=882 neurons; (C&D) For a subset of neurons (vestibular: n=248; visual: n=472), Fisher information was calculated from tuning curves that included two extra headings around straight ahead (±22.5°). Gray symbols with error bars illustrate human behavioral thresholds (replotted from Fig. 2A, B). Black lines illustrate population predictions from Fisher information. See also Figure S4.

There is overall good agreement between population predictions and behavioral data in both the vestibular (R=0.852, p<<0.001, linear regression, 95% confidence interval from bootstrap = [0.776 0.887], Fig 6A) and the visual conditions (R=0.878, p<<0.001, 95% confidence interval = [0.854 0.897], Fig 6B). This agreement between the shape of predicted and measured threshold functions also holds for the subpopulations of congruent and opposite neurons (Figure S4 C–F). However, there are also some quantitative discrepancies between predicted and measured thresholds. For the vestibular condition, predicted thresholds are lower than measured thresholds for backward reference headings (±180°; Fig. 6A). MSTd activity predicts roughly equal discrimination thresholds for forward and backward reference headings, whereas humans are substantially more sensitive when discriminating heading around a forward reference (Fig. 2). For the visual condition, measured visual thresholds increase more steeply than predicted thresholds as reference heading deviates from straight ahead (Fig. 6B). This same discrepancy holds when comparing MSTd predictions to visual thresholds measured in the monkey (Fig. 2D).

We reasoned that the overly broad central trough in the predicted visual thresholds (Fig. 6B) might result from the subpopulation of neurons that have heading preferences close to straight ahead (open symbols in Fig. 4D), since these neurons show poor discrimination performance for references close to 0° (Figure S4A). Indeed, removing these forward-preferring neurons somewhat narrows the trough in predicted visual thresholds and marginally improves the correspondence between predicted and measured thresholds (R=0.918, p<<0.001, linear regression, 95% confidence interval from bootstrap = [0.898 0.932], Figure S4B). However, predicted thresholds are still somewhat broader than behavior even after removal of these neurons, suggesting that they do not account completely for this discrepancy.

Our procedure for computing Fisher information involves estimating the slope of tuning curves through extensive interpolation of coarsely-sampled data. Thus, a potential concern is that we may have systematically under-estimated neuronal discriminability. To address this issue, we examined data from a subpopulation of neurons (N = 472) that were tested with two additional heading directions around straight forward (±22.5° relative to 0° heading). If underestimating the slope of the tuning curve due to coarse sampling were a major factor, results from these cells should more closely match behavior. In the visual condition, predicted thresholds computed from this sub-population indeed rose more steeply with heading eccentricity and more closely matched the behavioral data (Fig. 6D). Quantitatively, the correlation between predicted and measured thresholds was significantly greater for this subpopulation of neurons (R=0.942, p<<0.001, linear regression, 95% confidence interval = [0.924 0.953], Fig. 6D) than for the entire population shown in Fig. 6B. In the vestibular condition, the agreement between predicted and measured thresholds was also improved for the subset of neurons tested with additional heading values (Fig. 6C), but the significance of this improvement was marginal (R=0.911, p<<0.001, 95% confidence interval = [0.855 0.937]). Thus, finer sampling of heading tuning curves does improve the agreement between predicted and measured thresholds.

Some neurons were also tested while the animal performed a heading discrimination task around a straight-ahead reference direction (Gu et al., 2008b). This allowed us to compare neuronal thresholds estimated via Fisher information (including the ±22.5° headings) with those measured by applying ROC analysis to firing rate distributions measured over a range of finely-spaced headings. Figure S4G, H shows that there is reasonably good agreement between neuronal thresholds estimated from Fisher information and those computed by ROC analysis (vestibular condition: R=0.49, p<<0.001; visual condition: R=0.65, p<<0.001, Spearman rank correlation). However, average thresholds predicted from Fisher information were slightly greater than those measured using ROC analysis (vestibular condition: geometric mean of 46.6° vs. 34.4°, p=0.011, Wilcoxon matched pairs test; visual condition: geometric mean of 19.4° vs. 17.7°, p>0.6). This modest difference suggests that interpolation of coarsely-sampled tuning curves underestimates neuronal sensitivity even when the additional headings at ±22.5° are included. Indeed, Figure S4I, J shows that the slope of the interpolated tuning curve around straight ahead frequently underestimates the true slope of the tuning curve as measured in the discrimination task.

Together, these analyses indicate that the broader shape of predicted visual thresholds around straight forward (Fig. 6B) can be largely attributed to underestimation of tuning slopes due to coarse sampling. Addition of headings at ±22.5° reduces this discrepancy considerably (Fig. 6D), and the remaining difference may be attributable to residual underestimation of tuning slopes (Figure S4I, J). Taking these factors into account, there appears to be quite good agreement between predicted and measured thresholds, in terms of their dependence on heading eccentricity.

Maximum likelihood decoding of MSTd population responses

The results described above show that the behavioral dependence on reference heading can be largely explained by the precision of an MSTd-like population code. Recall, however, that Fisher information provides an upper bound on sensitivity but does not specify a type of decoding. There are multiple ways that MSTd responses could be decoded, and it is beyond the scope of this paper to consider these broadly. An optimal decoding strategy computes the likelihood function, i.e., the likelihood that different heading stimuli gave rise to the observed population response.

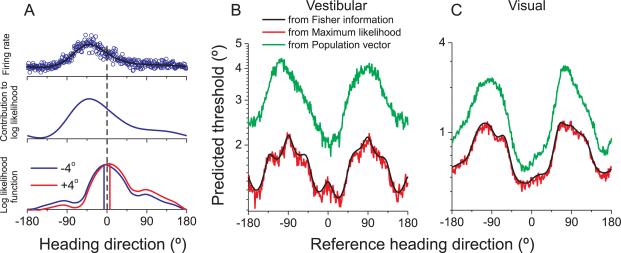
Fig. 7A illustrates how the likelihood function is computed. A spline function is again used to interpolate the coarsely sampled heading tuning curve (black curve in Fig. 7A, top row). We then simulate the response of the cell for each possible heading direction (at the 0.1° resolution of the spline fit) by drawing random values from a Poisson distribution having a mean specified by the interpolated tuning curve. Open blue symbols in Fig. 7A (top row) show a single draw of the neuron's response to each heading.

Fig. 7. Comparison between predicted thresholds computed from Fisher information and population decoding.

(A) Computation of the log likelihood function used for maximum likelihood decoding. (B), (C) Comparison of predicted thresholds from Fisher information (black), maximum likelihood decoding (red), and population vector decoding (green). See also Figure S5.

For neural populations that follow Poisson statistics, each cell's contribution to the logarithm of the likelihood function is given by the product of the spike count with the logarithm of its tuning curve (Dayan and Abbott, 2001; Jazayeri and Movshon, 2006; Sanger, 1996). For example, for a stimulus direction of −4°, the contribution of the example cell to the log likelihood function is shown in Fig. 7A (middle row). Assuming independent neuronal responses, the log likelihood function for a particular stimulus is computed by summing the contributions from all neurons (Fig. 7A, bottom). For a single trial in which the −4° heading stimulus was presented, the blue curve in Fig. 7A (bottom) shows the log likelihood function computed from our population of MSTd neurons, and the maximum likelihood estimate of heading is shown by the blue vertical line.

By computing likelihood functions for single trials, we can simulate performance of the heading discrimination task. For each simulated trial, we compute the likelihood function of heading for both the reference and comparison stimuli. For example, with a reference heading of straight-forward (0°), a ‘left’ choice would be registered based on the blue curve in Fig. 7A (bottom) if the ML estimate for this comparison stimulus is to the left of the ML estimate for the reference stimulus. For another example trial with a comparison heading at +4° (red curve in Fig. 7A, bottom), a ‘rightward’ choice would be registered if the ML estimate is to the right of that for the 0° reference. This process is repeated for several repetitions of each combination of reference and comparison headings. The simulated ‘choices’ of the ML decoder are then compiled into predicted psychometric functions that are analogous to the behavioral data collected from humans and monkeys, and a predicted psychophysical threshold is obtained for each possible reference heading. The resulting predictions show a very similar dependence on reference heading as the predictions computed from Fisher information (Fig. 7B, C, red vs. black curves). As expected (see Discussion), the upper limit of discriminability described by Fisher information can be attained by the maximum likelihood decoding scheme.

For comparison, we also simulated heading discrimination using the population vector algorithm (Georgopoulos et al., 1986), a widely used decoder in which each neuron votes for its preferred direction according to the strength of its response. In each simulated trial, the population vector provided an estimate of the reference and comparison headings, and the decision rule described above was used to construct simulated psychometric functions. Green curves in Fig. 7B, C show predicted thresholds for the population vector decoder. Although population vector thresholds are much larger than those obtained via ML decoding (i.e., the population vector is clearly non-optimal), the qualitative dependence of predicted thresholds on heading eccentricity is very similar for the two decoding schemes (see also Figure S4K). This indicates that optimal decoding is not essential to account for the behavioral results. Results were also quite similar when heading was decoded from populations of congruent or opposite neurons (Figure S5).

Biases in population decoding of heading direction

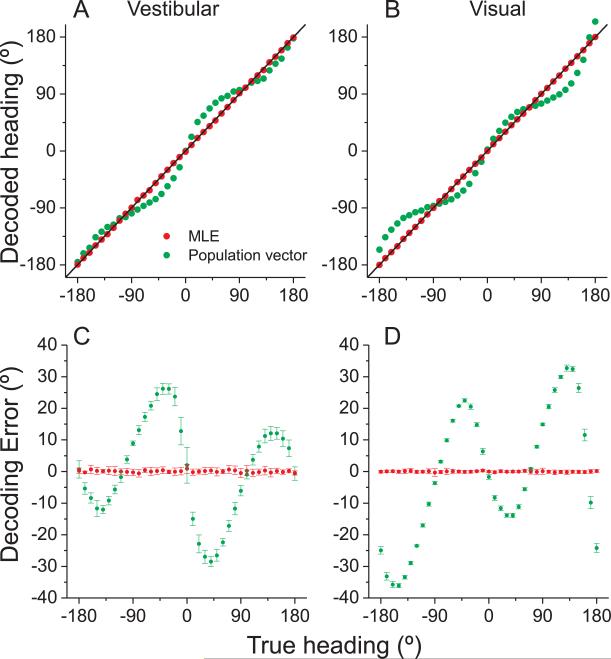
The ML decoding approach illustrated in Fig. 7 assumes that heading can be estimated accurately (without systematic bias) from population activity. To evaluate this assumption, we examine the error in heading estimates obtained using ML decoding. Red data points in Fig. 8A, B show the ML estimate of heading, computed from a single sample of firing rate for each neuron in our sample, plotted against true stimulus heading, in increments of 10°. ML estimates closely match the stimulus heading for both the vestibular (Fig. 8A) and visual (Fig. 8B) stimulus conditions, indicating that the ML decoder produces unbiased estimates.

Fig. 8. Accuracy of heading estimation for maximum likelihood (ML) and population vector decoding schemes.

(A), (B) The decoded heading direction from vestibular (A) and visual (B) population activity is plotted as a function of the true heading. Data points represent single-trial estimates for 10° increments of true heading. (C), (D) The error between predicted and actual headings is plotted versus true heading. Data shown are mean ±SD (10 repetitions). Red: ML decoding; green: population vector predictions. See also Figure S6.

For comparison, performance of the population vector decoder is illustrated by green symbols in Fig. 8A, B, and substantial errors in the estimates are evident. These errors are shown more clearly in Fig. 8C, D, which plots the errors in heading estimates relative to the true heading (mean ±SD across 10 simulated trials for each heading). For the ML decoder, errors are close to zero for all headings. For population vector decoding, heading errors are fairly small for lateral (±90°) directions, but can be substantial otherwise. For example, a true 40° leftward heading (−40°) is estimated to be about 70° leftward (−70°). The large biases in the output of the population vector decoder stem from the fact that heading preferences of MSTd neurons are not distributed uniformly on the sphere, as shown in Fig. 4B,D (see also Figure S6, which plots decoding errors separately for congruent and opposite cells). As reported previously (Sanger, 1996), population vector estimates are biased toward directions (±90°) that are overrepresented by the population.

Although the overabundance of neurons preferring lateral motion predicts improved heading discrimination around straight forward, it can strongly influence the accuracy of some decoders. Optimal (ML) decoding produces unbiased estimates of heading, whereas the more conventional population vector produces large biases. It is unlikely that humans or monkeys exhibit behavioral biases in heading estimation as large as those predicted by the population vector decoder, but at present there is no data to verify or contradict this assertion. Because humans and monkeys performed a relative judgment in our 2-interval heading task, our data do not address the accuracy of heading estimation.

DISCUSSION

We tested whether decoding of population activity from macaque area MSTd could account for the eccentricity dependence of vestibular and visual heading discrimination. With a few assumptions, we were able to predict how vestibular and visual heading thresholds vary with the eccentricity of the reference heading. Although theory has long suggested that information estimates from neuronal populations should account for the precision of behavior, the present work represents one of few demonstrations of this. Importantly, we have compared the theoretical limits of neural precision, quantified using Fisher information, with the results of specific decoding algorithms including maximum likelihood estimation and population vector analysis.

As expected from previous work (Gu et al., 2008b; Gu et al., 2007; Pouget et al., 1998; Purushothaman and Bradley, 2005; Seung and Sompolinsky, 1993), maximal discriminability for single neurons occurs for reference headings near the steepest slope of the tuning curves, with the exact point of peak discriminability also depending on spike count statistics. Because most MSTd neurons have broad, cosine-like tuning curves, the over-representation of lateral heading preferences in MSTd (Fig. 4) causes many neurons to have the steep slope of their tuning curves near straight ahead. Our findings complement studies in which choice probabilities (Gu et al., 2008b; Gu et al., 2007), electrical microstimulation (Britten and van Wezel, 1998; Gu et al., 2008a) and chemical inactivation (Gu et al., 2009) have provided support for the hypothesis that MSTd plays a central role in heading perception based on visual and vestibular cues.

Behavioral Dependence on Heading Eccentricity

Psychophysical studies have established that humans and monkeys can discriminate differences in heading direction as small as 1–2° based on optic flow (Britten and van Wezel, 1998; Warren et al., 1988), and this precision is largely maintained in the presence of eye and head rotations (Crowell et al., 1998; Royden et al., 1992; Warren and Hannon, 1990). A striking property of heading perception from optic flow is that discrimination is most precise around straight-forward and falls off steeply when observers discriminate headings around an eccentric reference (Crowell and Banks, 1993). This suggests neural mechanisms that are specialized to discriminate heading around straight forward, but the nature of this specialization has remained unclear. Our primary goal was to test whether MSTd population activity could account for this aspect of behavior.

Comparison of MSTd responses to previous human psychophysics would be severely hampered by potential species differences, and by the fact that the stimulus conditions used by Crowell and Banks (1993) differed markedly from those of our physiological studies. Thus, we performed psychophysical experiments to test whether humans and monkeys show a similar behavioral dependence on heading eccentricity, and to allow a more direct comparison of neural and behavioral data obtained under comparable stimulus conditions. As expected from Crowell and Banks (1993), both humans and macaques showed a V-shaped dependence on heading eccentricity, with maximal discriminability around straight-forward. However, the rise in visual thresholds with heading eccentricity is substantially shallower in our data (Fig. 2D) than in the data of Crowell and Banks. This difference is likely due to the smaller visual display (10° diameter) used by Crowell and Banks, which placed the focus of expansion (FOE) of the optic flow field outside the display for larger heading eccentricities. In contrast, our visual displays subtended ~90×90° for both behavioral and physiological experiments.

Interestingly, we show that vestibular heading discrimination is characterized by a similar dependence on reference eccentricity. Human vestibular heading thresholds increase more than two-fold as the reference heading moves from forward to lateral. This effect, while robust, was substantially smaller for the vestibular task than the visual task (Fig. 2D).

Possible Neural Substrates for Eccentricity Dependence of Heading Thresholds

Area MSTd is thought to contribute to heading perception from both optic flow and vestibular cues (Britten and van Wezel, 1998; Gu et al., 2008a, b; Gu et al., 2007, 2009), suggesting that it might limit heading discrimination. One possible mechanism for the eccentricity dependence of heading thresholds could be an over-representation of forward heading preferences and an overabundance of neurons that prefer radial optic flow. Indeed, Duffy and Wurtz (1995) reported that the majority of MSTd neurons prefer radial optic flow with a focus of expansion within 45° of straight ahead.

Our data (Fig. 4) instead show an over-representation of neurons that prefer lateral headings (laminar flow), consistent with the results of Lappe et al. (1996). These differences in findings may be due to sampling procedures. Duffy and Wurtz only varied FOE location for neurons that gave a robust response to radial motion. Thus, they may not have tested neurons that preferred lateral motion. In contrast, we tested every neuron that exhibited spontaneous activity or responded to a large field of flickering dots; thus, we believe that our sample is unbiased with respect to heading preference. Our analyses suggest that it is the over-representation of lateral heading preferences in MSTd that accounts for improved heading discrimination around straight ahead.

Overall, MSTd neurons have a similar distribution of heading preferences for visual and vestibular stimuli (Fig. 4 B,D), with the exception of a small group of neurons (~20%) that are narrowly tuned to forward headings in the visual condition (Fig. 4D, open symbols). The functional role of these neurons is unclear, and their contribution to Fisher information is not consistent with behavior (Figure S4A). Indeed, excluding these neurons from population decoding improves the match with behavior (Figure S4B). As we defined this group of neurons somewhat arbitrarily, a different selective decoding could yield a more accurate prediction of behavioral performance. However, given that a non-selective decoding of all MSTd neurons gives good predictions of behavior after accounting for underestimation of tuning slopes arising from coarsely sampled data (Fig. 6 C, D), we have no strong reason to believe that a selective decoding of MSTd responses is necessary to account for the eccentricity dependence of heading perception.

Decoding algorithms and relationship to Fisher information

Fisher information provides an upper bound for the sensitivity of an unbiased estimator, but does not specify a particular estimator (Seung and Sompolinsky, 1993). As expected for independent Poisson neurons (Dayan and Abbott, 2001), the upper limit of discriminability described by Fisher information was essentially attained by the maximum likelihood decoder (Fig. 7), and ML estimates of heading were unbiased (Fig. 8, red).

Another commonly used decoding scheme is the ‘population vector’ algorithm (Georgopoulos et al., 1986; Lee et al., 1988), in which each neuron votes for its preferred direction according to the strength of its response. This algorithm has been used previously to decode heading from MSTd population activity during pursuit eye movements (Page and Duffy, 2003). However, when direction preferences are not uniformly distributed, population vector estimates are biased toward the overrepresented directions (Sanger, 1996). Given the strongly non-uniform distribution of heading preferences in MSTd (Fig. 4, see also Gu et al., 2006), a population vector decoding indeed yields strongly biased estimates of heading (Fig. 8, green). Despite this bias, the population vector qualitatively predicts the eccentricity dependence of heading thresholds (Fig. 7, green curves).

Assumptions and Limitations

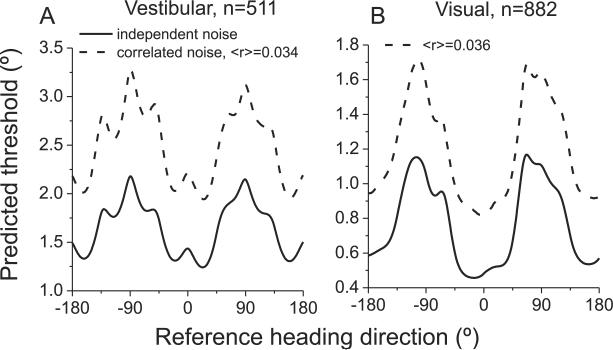
The approach taken here involves relatively few biases and assumptions. We sampled responses of all well-isolated MSTd neurons, we assumed that all neurons contribute to discrimination performance, and we estimated the precision of the population code using Fisher information and ML decoding. However, like all predictions of behavior based on neuronal activity, this approach has limitations. First and foremost, equation [1] assumes that all neurons have independent noise, such that d' increases with the square root of the number of neurons in the pool. If correlated noise among neurons does not vary strongly with heading preference, noise correlations would mainly be expected to change the magnitude of neural sensitivity, not how it varies with reference direction. To address this issue, we incorporated pairwise correlations into a modified computation of Fisher information (Abbott and Dayan, 1999). Preliminary data from pairs of neurons in MSTd show that mean noise correlations are fairly small (~0.05), especially in animals trained to perform heading discrimination (Angelaki et al., 2009). It appears that noise correlations in MSTd of trained animals are smaller than those seen in area MT (Bair et al., 2001; Cohen and Newsome, 2009; Huang and Lisberger, 2009; Zohary et al., 1994). Noise correlations in MSTd do not appear to depend on the average heading preference of a pair of neurons, but they do tend to be stronger among pairs with similar heading tuning (Angelaki et al., 2009). As shown in Fig. 9, incorporating this pattern of noise correlations into our analysis (Supplementary methods) did not alter the dependence of predicted thresholds on heading eccentricity, but did reduce the overall sensitivity of the population code, as expected. Quantitatively, the correlation between predicted and measured thresholds, as a function of heading eccentricity, is similar to that observed when assuming independent noise (Figure S4K).

Fig. 9. Influence of correlated noise on thresholds predicted from Fisher information.

Noise correlations deteriorate heading information encoded by the MSTd population, but this effect is roughly homogeneous across all reference headings for both the vestibular (A) and visual (B) conditions. The overall shape of the threshold dependence on reference heading is similar when assuming independent noise (solid lines) and when incorporating the structure of noise correlations measured in MSTd during heading discrimination (dashed lines, Angelaki et al., 2009).

A second simplification is that we have assumed Poisson spiking statistics in most analyses. However, our results were altered little by incorporating the measured variance-mean relationship of each neuron (Figure S3). Moreover, predictions of neuronal thresholds based on the Poisson assumption were generally in reasonable agreement with those measured directly using ROC analysis in a subset of neurons (Figure S4G, H).

Third, we have ignored the contributions that other areas may make to heading discrimination. For example, neurons in area VIP are known to be tuned for heading based on optic flow and vestibular signals (Bremmer et al., 2002; Schlack et al., 2002), and may contribute to heading discrimination. There may also be subcortical contributions to the behavioral effects, as a predominance of lateral versus forward/backward heading preferences is also characteristic of otolith afferents (Fernandez and Goldberg, 1976), as well as vestibular and deep cerebellar nuclei neurons (Bush et al., 1993; Dickman and Angelaki, 2002; Schor et al., 1984; Shaikh et al., 2005). As tuning properties become available from large numbers of neurons in these and other areas, the ability of these populations to predict heading perception should be explored.

Finally, we have assumed that the decoding of MSTd population activity is unbiased and includes contributions from all neurons. Of course, it is possible that a selective readout of MSTd responses could either enhance or diminish the dependence of heading thresholds on reference eccentricity. Despite these uncertainties, the main characteristics of the behavioral data are consistent with non-selective decoding of MSTd population activity.

MATERIALS AND METHODS

Human Subjects and Behavioral Tasks

Seven subjects (6 male, 1 female), four of whom were naïve to the hypotheses tested, participated in this study. Five subjects participated in the vestibular heading discrimination task, 3 subjects performed the visual task and one subject performed both. Subjects were seated in a padded racing seat, and held in place with a 5-point harness. A thermoplastic mask, which was molded to each subject a day before experiments began, held the head firmly against a cushioned head rest, thus immobilizing the head relative to the platform. The seat was affixed to a 6 degree of freedom motion platform (MOOG 6DOF2000E; Moog, East Aurora, NY) which allowed for translation along any direction in three dimensional space.

The trajectory of inertial motion was controlled at 60 Hz over an Ethernet interface. A 3-chip DLP projector (Barco Galaxy 6) was mounted on top of the motion platform behind the subject, to front-project images onto a 149 × 127 cm tangent screen via a mirror mounted above the subject's head. The display was viewed from a distance of 70 cm (thus subtending 94 × 84° of visual angle), had a resolution of 1280 × 1024 pixels, and was updated at 60 Hz. Visual stimuli were generated by an OpenGL accelerator board (nVidia Quadro FX1400), and were plotted with sub-pixel accuracy using hardware anti-aliasing. The subject was enclosed in a black aluminum superstructure, such that only the display screen was visible in a darkened room. Behavioral tasks and data acquisition were controlled by Matlab.

Vestibular Heading Task

Five blindfolded subjects performed a two-interval, two-alternative forced-choice heading discrimination task based on vestibular cues (‘vestibular’ condition). Each trial was initiated by a button press (accompanied by a tone), and consisted of two 1 second motion intervals separated by a 200 ms delay. One interval was labeled the ‘Reference’ whereas the other was labeled ‘Comparison’ (Fig. 1A). The reference heading is the base direction against which the comparison heading is judged. For example, if the reference is 0° (straight ahead), then a comparison of +20° corresponds to translation along a trajectory 20° to the right of straight ahead. For a reference heading of 12°, a comparison of +20° corresponds to a trajectory 32° to the right of straight ahead. Subjects pressed one of two buttons to indicate whether they perceived the second stimulus to be rightward or leftward relative to the first. If the decision was not recorded within 1 s, the trial was discarded. A second tone indicated the end of the trial.

The temporal order of reference and comparison stimuli was randomized across trials. If the reference heading (0°) was presented first, followed by the comparison (+20°), the correct response would be ‘right’; conversely, if the comparison was presented first followed by the reference, the correct choice would be ‘left’. However, for plotting psychometric functions (e.g., Fig. 1 C–F), both cases were considered a ‘rightward’ judgment of the comparison relative to the reference (Fetsch et al., 2009).

Platform motion in each trial followed a Gaussian velocity profile, with 13 cm displacement, peak acceleration of ±0.1 G (m/s^2), and peak velocity of 30 cm/s (Fig. 1B). The reference headings varied in azimuth as follows: 0° (straight-forward), ±6°, ±12°, ±18°, ±24°, ±32°, ±60°, ±90°, ±120°, ±150°, and ±180°, while reference elevation was fixed at 0° (horizontal plane). Five blocks of 150 trials each were collected for each subject and each reference heading over the course of 8 weeks (one reference heading per block). In each block, the comparison typically started ±32° away from the reference, and the difference was reduced (by multiples of two) toward psychophysical threshold using a staircase procedure (33% probability of a more difficult stimulus following a correct choice, 66% probability of a less difficult stimulus following an error). Choice data for each reference heading were pooled into a single psychometric function and were fit with a cumulative Gaussian function (Wichmann and Hill, 2001), weighting each data point according to the number of trials performed. Threshold was taken as the standard deviation of the fit, which corresponds to ~84% correct performance.

Visual Heading Task

In the visual version of the heading task, the motion platform remained stationary, and heading was simulated using optic flow. Visual stimuli depicted self-translation through a 3D cloud of stars distributed uniformly within a virtual space 130 cm wide, 150 cm tall, and 75 cm deep. Star density was 0.01/cm³, with each star being a 0.5cm × 0.5cm triangle. From frame to frame, 70% of the triangles moved appropriately to simulate self-translation and 30% moved randomly (70% motion coherence).

Accurate rendering of the optic flow, motion parallax, disparity, and size cues that accompanied translation of the subject was achieved by moving the OpenGL camera through the virtual environment along the exact trajectory followed by the subject's head. Visual stimuli were presented dichoptically, with the display screen located in the center of the star field at stimulus onset. To avoid extremely large (near) stars from appearing in the display, a near clipping plane was placed 5cm in front of the eyes. Reference headings were 0°, ±6°, ±12°, ±18°, ±24°, ±32°, ±45°, ±60°, ±75°, and ±90°, each tested in 5 blocks of trials (150 trials per block). Subjects were instructed to fixate a head-fixed, central target, although fixation was neither reinforced nor monitored.

Animal Behavioral Experiments

Behavioral data were collected in two rhesus monkeys (Macaca mulatta) trained to perform the vestibular heading task, one of which was also tested with the visual heading task (at 100% coherence). The Animal Studies Committee at Washington University approved all animal procedures which are in accordance with NIH guidelines for animal care and use.

The monkey was seated in a custom-built primate chair, fixed into place on top of an identical motion platform as used in the human experiments (MOOG 6DOF2000E). Visual stimuli were rear-projected (Christie Digital Mirage 2000) onto a 60 × 60 cm tangent screen that was viewed from a distance of 30 cm (thus subtending ~90 × 90° of visual angle). The screen was mounted on the front side of a field coil used to measure eye movements. The sides and top of the field coil were enclosed with black matte material to eliminate any other visual motion cues. Data acquisition was controlled by Tempo software (Reflective Computing, Olympia, WA).

In each block of trials, one interval contained the reference heading, and the other interval contained a comparison heading that varied in small steps around the reference (Fig. 1A). The temporal order of reference and comparison headings was varied randomly, and each motion trajectory followed a 1s Gaussian velocity profile (total displacement: 13 cm, peak acceleration: ±0.1 G = ±0.98 m/s², peak velocity: 30 cm/s). The monkey reported whether the heading of the second interval was rightward or leftward relative to that of the first interval, by making a saccade to one of two choice targets that appeared at the end of each trial (5° left and right of the fixation point). The saccade had to be made within 1s after target appearance, and the saccade endpoint had to remain within 3° of the target for at least 150 ms to count as a choice. Correct responses were rewarded with a drop of juice. Trials were aborted if the monkey's eye position deviated from a 2 × 2° electronic window around the fixation point.

There were only a few differences between the monkey and human behavioral experiments: (1) For monkeys, we used the method of constant stimuli in which each relative heading was presented a fixed number of times (typically 20) in a block of trials. For one animal, the heading range was [±16, ±8, ±4, ±2°] for small reference headings, whereas for reference headings of ±24° and ±30°, the heading range was [±20, ±10, ±5, ±2.5°] and [±24, ±12, ±6, ±3°], respectively. For the second animal, the smallest heading range was [±8, ±4, ±2, ±1°] and the largest range was [±14, ±7, ±3.5, ±1.75°]. This variation in range was needed to properly constrain measurement of heading thresholds for each eccentricity. (2) Rather than experiencing vestibular stimuli in darkness, monkeys maintained visual fixation on a central, head-fixed target during movement. This fixation requirement, which matched the experimental conditions of single unit recordings, does not affect the ability of the animal to use vestibular cues to perform this task (Gu et al., 2007). (3) A smaller range of reference headings was tested in monkeys: reference azimuth was varied between 0 and ±30°, while elevation was fixed at 0° (horizontal plane).

Data from 5–10 blocks of trials per reference heading were collected, with each block having a minimum of 20 repetitions of 8 headings each (160 trials). In 3/4 of all blocks, two symmetric reference azimuths were interleaved (e.g., +/− 6, +/− 12) to ensure that the monkey performed a relative-heading task, instead of simply adjusting his bias over time to distribute choices equally.

Neural Recording Experiments

We analyzed neural responses recorded from 4 different macaques. Some aspects of these data have been presented elsewhere (Fetsch et al., 2007; Gu et al., 2008b; Gu et al., 2006) and full experimental details can be found there. Area MSTd was localized using a combination of magnetic resonance imaging scans, stereotaxic coordinates (~15mm lateral and ~3–6mm posterior to the interaural axis), and physiological response properties, as described previously (Gu et al., 2007; Gu et al., 2006). Raw neural signals were amplified, band-pass filtered (400–5000 Hz), and sampled at 25 kHz. A dual voltage-time window discriminator (BAK Electronics) was used to isolate action potentials, and spike times were recorded to disk with 1 ms resolution. Importantly, we recorded from any well-isolated single unit that was spontaneously active or responded to a large pattern of flickering or moving random dots. Thus, our sample of neurons was unbiased with respect to heading preference.

Once a single MSTd neuron was isolated, we measured its heading tuning curve by presenting 8 motion directions in the horizontal plane (0°, ±45°, ±90°, ±135° and 180° relative to straight-ahead). For a subset of neurons (472/882), two additional directions of motion (±22.5°) were included in the heading tuning measurement, helping to constrain interpolation of the tuning curve over the critical range of forward headings. For visual stimuli, motion coherence was set at 100%, and the display contained a variety of naturalistic cues to motion in depth, including binocular disparity, size, and motion parallax. For vestibular stimuli, the display screen was blank except for a head-fixed fixation target. Under both stimulus conditions, animals were required to fixate a central target for 200 ms before stimulus onset, and to maintain fixation throughout the trial. The motion trajectory was similar to the behavioral experiments: Gaussian velocity profile, 13 cm total displacement, ±0.1 G peak acceleration, 30 m/s peak velocity and 2s duration (Fetsch et al., 2007; Gu et al., 2007; Gu et al., 2006). During the middle ~1s of the stimulus duration, the acceleration is larger than human thresholds (~0.005 G) for detecting linear translational motion (Benson et al., 1986; Kingma, 2005). Each stimulus was typically repeated 5 times, with a minimum of 3 repetitions required for inclusion in the analysis.

Data Analysis

All analyses were performed using MATLAB (Mathworks, Natick, MA). To quantify behavioral performance, we plotted the proportion of trials in which the subject reported the comparison heading as ‘rightward’ against the true relative heading between comparison and reference (e.g., Fig. 1C, D). A single psychometric function was obtained for each reference heading and each subject, by combining data across blocks of trials. The psychometric function was fit with a cumulative Gaussian function, and the psychophysical threshold was taken as the standard deviation of this function (as in Gu et al., 2007). We then plotted psychophysical thresholds as a function of reference heading to quantify the eccentricity dependence of heading discrimination (Fig. 2).

For single unit analyses, heading tuning curves were constructed from mean firing rates during the middle 1 s interval of each stimulus. Only MSTd neurons with significant heading tuning (p<0.05, one-way ANOVA) in the visual and/or vestibular conditions were included. Although this criterion excluded very few visual responses, only ~50% of MSTd neurons were included in the vestibular population analysis. Additional population analysis of heading tuning properties are described in Supplementary Methods.

Fisher information analysis

To investigate whether MSTd population activity can account for the dependence of psychophysical thresholds on reference heading, we estimated the precision of heading discrimination by computing Fisher information. Theoretically, Fisher information (I_F) provides an upper limit on the precision with which any unbiased estimator can discriminate small variations in a variable (x) around a reference value (x_ref) (Pouget et al., 1998; Seung and Sompolinsky, 1993). For a population of neurons with Poisson-like statistics, population Fisher information can be computed as:

$$I_F\left(x_{ref}\right)=\sum _{i=1}^N\frac{R_i\prime {\left(x_{ref}\right)}^2}{{\sigma }_i{\left(x_{ref}\right)}^2}$$ [1]

In this equation, N denotes the number of neurons in the population, $R{\prime }_i\left(X_{ref}\right)$ denotes the derivative of the tuning curve for the i_th neuron at x_ref, and ${\sigma }_i^2\left(X_{ref}\right)$ is the variance of the response of the i_th neuron at x_ref. Thus, neurons contribute to Fisher information in proportion to the squared slope of the tuning curve at x_ref, and in inverse proportion to the response variance at x_ref. Neurons with steeply sloped tuning curves and small variance will contribute most to Fisher information. In contrast, neurons having the peak of their tuning curve at x_ref will contribute little. Note that equation [1] assumes independent noise among neurons (addressed further below).

The discriminability (d') of two closely spaced stimuli (x_ref and x_ref + Δx) has an upper bound given by:

$$d\prime \left(x_{ref}\right)=\Delta x\sqrt{I_F\left(x_{ref}\right)}$$ [2]

Thus, we can compute how heading discrimination thresholds should depend on x_ref, assuming that performance is limited by the activity of the recorded neurons. A criterion value of $d’=\sqrt{2}$ was used such that predicted thresholds were comparable to the 84% correct thresholds derived from fits to behavioral data. To compute tuning curve slope, R'_i(x_ref), we used a spline function (0.1° resolution) to interpolate among the coarsely sampled data points (45° spacing). The resolution of the spline interpolation had little effect on the results as long as it was ~1° or smaller. We also computed I_F using linear interpolation of the tuning curves or by fitting the tuning curves with a wrapped Gaussian function, and these variations gave similar results.

Tuning curve slope was then obtained as the spatial derivative of the spline fit. Assuming Poisson statistics, the variance of the neuron's response is equal to the mean firing rate at x_ref, i.e., ${\sigma }_i^2\left(X_{ref}\right)={\mu }_i\left(X_{ref}\right)$. Thus, for each heading direction, the spline fit provides the quantities needed to compute Fisher information. To avoid near-zero variances, we placed a floor on firing rates at 0.5 spikes/s. Consequently, for 18/511 (3.5%) neurons tested in the vestibular condition and 169/882 (19.2%) neurons tested in the visual condition, tuning curves were clipped at 0.5 spikes/s and smoothed by convolving with a Gaussian kernel (SD = 10°). This smoothing operation removed artifactual peaks in I_F that resulted from clipping the tuning curve.

Confidence intervals on population Fisher information were obtained using a bootstrap procedure in which random samples of neurons were generated by resampling with replacement from the population of recorded neurons. This resampling was repeated 1000 times and the 95% confidence interval on I_F was computed for each reference heading (error bands in Fig. 5).

Equation [1] assumes that neurons have independent noise and Poisson spiking statistics. We also computed Fisher information by incorporating correlated noise among neurons and the measured variance-mean relationship of each neuron, as described in Supplementary Methods.

Maximum Likelihood estimation

As an alternative to Fisher information, we decoded MSTd responses using maximum likelihood (ML) estimation (Dayan and Abbott, 2001; Jazayeri and Movshon, 2006; Sanger, 1996). We simulated heading discrimination performance by computing the likelihood function of possible headings from a sample of MSTd responses. In each simulated trial, the ideal observer then judged whether the comparison heading was leftward or rightward relative to the reference according to the relative peak locations of the two likelihood functions. If the peak of the likelihood function for the comparison stimulus was to the right of the peak for the reference, the ideal observer would report ‘right’, and vice-versa. To compute the likelihood function in each simulated trial, the tuning curve of each neuron was again interpolated using a spline fit, and a random spike count for that simulated trial was drawn from a Poisson distribution. The spike count of each neuron was multiplied by the logarithm of its tuning curve, and the result represented this neuron's contribution to the likelihood function. Assuming independent noise across neurons, the full log likelihood function was obtained for each reference/comparison stimulus by summing the contributions of all neurons. Because heading preferences in MSTd are not uniformly distributed (Gu et al., 2006), our computations of log likelihood also included a second term that compensates for the fact that the tuning curves of all neurons do not sum to a constant (Jazayeri and Movshon, 2006).

Ten simulated trials were performed for each combination of comparison and reference headings to construct a simulated psychometric function, similar to those shown in Fig. 1 C–F. Threshold was then computed from each simulated psychometric function using methods identical to those applied to behavioral data. To reduce noise, we constructed the simulated psychometric function for each stimulus 30 times and averaged the resulting threshold measures.

In a separate analysis, we examined how well absolute heading could be estimated from population activity in MSTd using the ML decoding approach. In this case (Fig. 8), we computed the ML estimate of heading for all possible headings in the horizontal plane, sampled every 10°.

Population vector decoding

We also estimated heading from MSTd activity using a simple ‘population vector’ decoder (Georgopoulos et al., 1986). In this estimator, each neuron votes for its preferred heading in proportion to the strength of its response. For a single iteration of the population vector estimate, the firing rate of each neuron was drawn from a Poisson distribution having a mean rate determined by the interpolated tuning curve. The activity of each neuron was considered to be a vector having a length given by its spike count and a direction given by its heading preference. The vector sum of responses across the population of neurons was then taken as the heading estimate in each trial, and heading thresholds were computed as described for the ML estimator.

To quantify the agreement between heading thresholds predicted from MSTd activity and measured psychophysical thresholds, we computed the correlation coefficient (R) between the two curves (as a function of reference heading). 95% confidence intervals for each R value were computed via bootstrapping.