Regularized reconstruction in quantitative SPECT using CT side information from hybrid imaging

Abstract

A penalized-likelihood (PL) SPECT reconstruction method using a modified regularizer that accounts for anatomical boundary side information was implemented to achieve accurate estimates of both the total target activity and the activity distribution within targets. In both simulations and experimental I-131 phantom studies, reconstructions from (1) penalized likelihood employing CT-side information-based regularization (PL-CT), (2) penalized likelihood with edge preserving regularization (no CT) and (3) penalized likelihood with conventional spatially invariant quadratic regularization (no CT) were compared with (4) ordered subset expectation maximization (OSEM), which is the iterative algorithm conventionally used in clinics for quantitative SPECT. Evaluations included phantom studies with perfect and imperfect side information and studies with uniform and non-uniform activity distributions in the target. For targets with uniform activity, the PL-CT images and profiles were closest to the ‘truth’, avoided the edge offshoots evident with OSEM and minimized the blurring across boundaries evident with regularization without CT information. Apart from visual comparison, reconstruction accuracy was evaluated using the bias and standard deviation (STD) of the total target activity estimate and the root mean square error (RMSE) of the activity distribution within the target. PL-CT reconstruction reduced both bias and RMSE compared with regularization without side information. When compared with unregularized OSEM, PL-CT reduced RMSE and STD while bias was comparable. For targets with non-uniform activity, these improvements with PL-CT were observed only when the change in activity was matched by a change in the anatomical image and the corresponding inner boundary was also used to control the regularization. In summary, the present work demonstrates the potential of using CT side information to obtain improved estimates of the activity distribution in targets without sacrificing the accuracy of total target activity estimation. The method is best suited for data acquired on hybrid systems where SPECT-CT misregistration is minimized. To demonstrate clinical application, the PL reconstruction with CT-based regularization was applied to data from a patient who underwent SPECT/CT imaging for tumor dosimetry following I-131 radioimmunotherapy.

1. Introduction

There is much interest in accurate quantitative single photon emission computed tomography (SPECT) imaging for dosimetry in internal emitter therapies such as I-131 radioimmunotherapy (RIT) and radioiodine therapy. It has been hypothesized that the efficacy of such therapies is determined not primarily by the mean radiation absorbed dose to the tumor, but rather by other measures that represent the 3D distribution of absorbed dose. Hence, in recent dose–response studies, in addition to the mean dose, there has been much interest in evaluating other summary measures including the dose–volume histogram and the equivalent uniform dose, which reflects the biologic effect of a non-uniform distribution of absorbed dose (Prideaux et al 2007, Amro et al 2010). For such evaluations it is important to achieve accurate estimates of both the total target activity and the activity distribution within the target.

Hybrid SPECT/CT systems where patient anatomy and radionuclide distribution can be imaged in a single session have the potential to significantly improve SPECT activity quantification and 3D patient-specific dosimetry. The CT data can be used to obtain the density map for patient-specific dose estimation, to define the tumor volume of interest and also to correct for factors that degrade SPECT quantification such as attenuation, scatter and partial volume effects due to the finite resolution of the imaging system. In commercial SPECT reconstruction software available with hybrid systems, the CT information is used only for attenuation correction. In addition to attenuation correction there have been a few recent research studies evaluating quantitative SPECT/CT imaging with CT-based corrections for scatter and partial volume effects. However, the focus of these studies was on determining total target activity and not on target activity distribution (Shcherbinin et al 2008, Willowson et al 2008).

Currently, the conventional iterative reconstruction algorithm for SPECT is unregularized 3D ordered-subset expectation maximization (OSEM), often followed by post-reconstruction filtering to reduce image noise. Indiscriminate smoothing including across region boundaries degrades recovery of activity. However, images produced by iterative reconstruction without filtering have been observed to have edge artifacts that worsen as the iterations proceed (Snyder et al 1987, Tsui et al 1994, Koral et al 2007a). These artifacts are caused by the unstable ‘deconvolution’ of the collimator–detector response when one tries to compensate for that response to improve activity recovery. At large iteration numbers there can be a tendency for over-compensation of collimator–detector response. Tsui et al demonstrate this in their simulation study of objects with sharp edges. When detector response was included in the simulation, no edge artifacts were observed in the reconstructed images due to blurring of the edges, but with detector response compensation the artifacts reappear. In previous I-131 studies, our group has achieved reasonably good target activity quantification accuracy using 3D OSEM with detector response compensation and no filtering (Dewaraja et al 2005, Koral et al 2007b), but the problems with edge artifacts and the resulting distortion of the activity distribution were not addressed. To achieve accurate estimates of the activity distribution within the target, free of edge artifacts, we evaluated a penalized-likelihood approach to SPECT reconstruction using a modified regularizer that accounts for anatomical (CT) boundary information in the present work.

Previously, in positron emission tomography (PET), reconstruction accuracy has been improved by using anatomical side information during the emission tomography reconstruction (Fessler et al 1992, Comtat et al 2002, Nuyts et al 2005). In SPECT, most past studies have focused on using anatomical boundary information in a post-reconstruction step (Du et al 2005, Boening et al 2006, Dewaraja et al 2006). However, it has been shown that incorporating the boundary information during the reconstruction is superior to a post-processing approach (Nuyts et al 2005). In addition, the intra-reconstruction approach does not require an assumption of uniform uptake within the target, inherent to the post-processing approach. There has also been some interest in joint estimation in SPECT combining anatomical and functional information (Gindi et al 1993, Bowsher et al 1996). Although joint estimation can potentially compensate for large alignment error, it is computationally intensive and currently not suitable for clinical processing of 3D data. In the present work, for hybrid systems where SPECT-CT misregistration is minimized, we investigate the simpler method where anatomical boundary information is used during the penalized-likelihood reconstruction. The side information controls the regularization by allowing smoothing in uniform regions, but preventing the smoothing across region boundaries to avoid activity spillover between distinct regions. To incorporate side information, a quadratic regularizer is modified following the previous implementations in PET reconstruction (Fessler et al 1992, Comtat et al 2002). For the first time, the method is applied to SPECT data in the present study. In the present SPECT implementation we also account for the fact that region masks that control the regularization are non-binary in practice, because they are typically defined on CT space and must be re-sampled to SPECT space. In phantom studies the proposed reconstruction method is compared with penalized likelihood methods that regularize without CT information and also with unregularized OSEM. Our goal was to achieve improved estimates of the activity distribution within the target, without sacrificing the total target activity quantification accuracy that can be achieved with unregularized 3D OSEM.

2. Methods

2.1. Measurement model and iterative algorithm

We used the standard Poisson statistical model for emission tomography, where each raw measured SPECT projection value has a mean that is related linearly to the unknown voxelized activity distribution via one row of a system matrix A. For the forward and backprojector we used the rotate-sum method (Zeng and Gullberg 1992) using bilinear interpolation for rotating the current estimate of the activity distribution and the attenuation map.

The negative log-likelihood for the Poisson model for emission tomography is

$$L(f)=\sum _i{h}_i({[Af]}_i),h_i(l)=(l+s_i)-y_{i}log(l+s_i),{[Af]}_i=\sum _j{a}_{ij}{f}_j,$$ (1)

where f = (f₁, …, f_N) denotes the unknown activity image, y_i denotes the projection data, s_i denotes the additive scatter contribution and a_ij denotes the system matrix elements. The function h_i(l) denotes the negative log-likelihood for the ith measurement. For penalized-likelihood image reconstruction we minimize a cost function that is the sum of the negative log-likelihood for Poisson data and a regularization term, i.e., we minimize L(f) + R(f). We consider regularizers of the general form

$$R(f)=\sum _k{w}_k\varphi ({[Cf]}_k),$$ (2)

where the matrix C is typically a matrix that evaluates the finite differences between neighboring voxel values and the convex potential function ϕ has bounded curvature ϕ′(t)/t ≤ 1, where ϕ′ denotes the derivative of ϕ.

For the regularized case, we used an ordered-subsets iterative algorithm based on a paraboloidal surrogates method described in Fessler and Erdogan (1998). The use of ordered subsets with the paraboloidal surrogate curvatures was described in Erdogan and Fessler (1999) for transmission tomography and the extension to emission tomography is straightforward. The one-subset version of the algorithm has the following diagonally preconditioned gradient descent form:

$$f_j^{n+1}={\left[f_j^n-\frac{1}{d_j}\left(\sum _i{a}_{ij}{h}_i^{\prime }({[A{f}^n]}_i)+\sum _k{c}_{kj}{w}_k{\varphi }^{\prime }({[Cf]}_k)\right)\right]}_{+},$$ (3)

where [x]₊ = max(x, 0) enforces the non-negativity constraint. The denominator δ_j is precomputed prior to iteration as given by Fessler and Erdogan (1998)

$$d_j=\sum a_{ij}{\eta }_i\sum _m{a}_{im}+\sum _k\mid c_{kj}\mid w_k\sum _m\mid c_{km}\mid ,$$ (4)

where c_km denotes the elements of C and where the ‘precomputed’ log-likelihood curvatures are

$${\eta }_i(l)=\{\begin{array}{ll}1/y_i,\hfill & y_i>0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$ (5)

See Jacobson and Fessler (2007) for a general discussion of the convergence properties of this type of algorithm. To accelerate convergence of the algorithm, we used the 6-subset version in this investigation, where we replace the summations over i above with a summation over the measurements in a subset of the projection views, scaled by the number of subsets. This algorithm requires one forward projection and one backprojection per iteration, unlike the method in Fessler and Erdogan (1998) that needs two backprojections per iteration. Software for this method is available (Fessler 2004).

2.2. Regularizing penalty function

For simplicity we describe the regularizers in 1D; the extension to 3D is straightforward but notationally cumbersome. In 1D the conventional quadratic regularizer (Fessler 1994) for an object with N voxels with values f_j is

$$R(f)=\beta \sum _{j=2}^N{(f_j-f_{j-1})}^2,$$ (6)

where the regularization or the smoothness parameter β controls the strength of the regularization. This regularizer will control noise but also blur the activity across image boundaries between different regions.

To reduce this blur, we also investigated edge-preserving regularization using the convex, nonquadratic, Huber function ψ (Huber 1981)

$$R(f)=\beta \sum _{j=2}^N\psi (f_j-f_{j-1}).$$ (7)

The Huber function can be written as ψ(t) = min(t²/2, δ|t| − δ²/2), where δ is a parameter that controls the contrast level at which edges begin to be conserved. If δ is too large, then the Huber function is approximately quadratic and edges are not preserved. If δ is too small, then even small variations due to noise can be ‘preserved’ and the reconstructed image can be too noisy or exhibit blocky textures. For the simulations we selected δ to be 10% of the difference between the target voxel values and the background voxel values. This choice helps ensure that the boundaries can be preserved while still smoothing noise in uniform regions. For measured data, we used the initial OSEM reconstruction to determine target and background concentrations and then set δ to be 10% of the difference. These values may be suboptimal but they were chosen by this simple and practical procedure without further manual refinement.

Neither of the preceding regularizers uses any anatomical side information. To incorporate side information, we follow previous work in PET reconstruction (Fessler et al 1992, Comtat et al 2002) and modify the quadratic regularizer as follows:

$$R(f)=\beta \sum _{j=2}^N{w}_j{(f_j-f_{j-1})}^2,$$ (8)

where the regularization weights w_j control the strength of regularization between neighboring voxel values f_j and f_j−1. Ideally we would like w_j = 1 within uniform regions and w_j = 0 when voxels j and j − 1 correspond to regions with different activity levels, to avoid blur or spillover between those distinct regions.

In the present implementation we accounted for the non-binary nature of the region masks that determine regularization weights. In practice there are not distinct boundaries between different regions because of the finite voxel size, particularly in SPECT. Suppose that the CT image is segmented into K different regions, and let l_jk denote the ‘labels’ that indicate whether voxel j belongs to region k. Ideally these region masks would be binary, with each voxel belonging to one and only one region. In our application however, tumors are outlined on CT space (typically 512 × 512) and must be re-sampled to SPECT space (typically 128 × 128). Due to the finite size of the SPECT voxels relative to the CT voxels, our region masks take values in the interval [0, 1], with ${\sum }_{k=1}^K{l}_{jk}=1$. In the interior of a region the values of l_jk are 0 or 1, but there are intermediate values around the boundaries of each region. The presence of these intermediate values leads to an open question of how to choose the corresponding regularization weights w_j. In the present implementation we used the following approach. First we formed a ‘label’ image $l_j={\sum }_{k=1}^K{kl}_{jk}$. Most voxels in this label image take discrete values in the set {1, 2, …, K} but there are intermediate values near region boundaries. Then we defined the regularization weights using thresholded differences of the label image:

$$w_j=\{\begin{array}{ll}1,\hfill & \mid l_j-l_{j-1}\mid \le \epsilon \hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$ (9)

We chose the threshold ε = 0.1; using this small value ‘disables’ the regularization at all region edges to avoid blur or spill-over. If the region masks were binary then the label image would be discrete and for any value of ε ∈ (0,1) this approach would provide ideal binary regularization weights in the absence of mismatch between CT and SPECT.

We also investigated the ‘blurred label’ method (Comtat et al 2002) for defining the regularization weights to account for the uncertainty associated with mismatched anatomical information. Labels were smoothed with a Gaussian kernel of FWHM 4.0 and 5.0 mm. As discussed in section 3, the ‘blurred labels’ did not work as well as the above approach for the non-binary region masks of the present application. Optimizing regularization weights w_j for non-binary masks remains an open problem for future work.

We chose the regularization parameter β to obtain a desired resolution of the reconstructed image as previously proposed (Fessler and Rogers 1996). When β is too small the reconstructed image will be very noisy, while if β is too large the image will be very smooth, hence resulting in a loss of useful information. We took the practical approach of choosing β by looking at the point spread function (away from region boundaries) to get a target FWHM of ~1 cm (2 pixels). This corresponded to a β value of 2⁻⁵ in the x- and y-directions and 2⁻⁹ in the z-direction (we needed to adjust the regularization strength separately in x, y and in z to make the reconstructed resolution approximately isotropic). All regularized reconstructions presented in section 3 were evaluated at this same choice of β (initially, phantom profiles were investigated at other values of β and it was evident that at smaller values there was insufficient regularization to get rid of the edge artifacts and the solution approached that of OSEM).

2.3. Phantom and patient studies

Both simulated and experimental I-131 phantom studies were performed to evaluate the reconstructions. The camera modeled/used was a Siemens Symbia TruePoint SPECT/CT with a high-energy parallel-hole collimator, a 5/8″ NaI crystal and the following acquisition parameters for the experimental measurements: 180° and 30 stops per head; body contouring; 20% photopeak at 364 keV; two adjacent 6% scatter correction windows and a 128 × 128 matrix with a pixel size of 4.8 mm. The collimator parameters were as follows: septa, 2 mm; hole diameter, 4 mm; and hole length, 59.7 mm. The CT component of acquisition used full circle rotation, 130 kV, 35 mAs and 5 mm slices. The CT data were reconstructed with a 512 × 512 × 196 matrix and 0.98 mm × 0.98 mm × 2 mm voxel size using commercial ESOFT (Siemens) software. The SPECT data were reconstructed using the OSEM and PL algorithms developed at the University of Michigan.

The SPECT camera evaluated here uses a contouring orbit, so the depth-dependent detector/collimator response was adjusted for each projection view based on the corresponding distance of the collimator to the isocenter. Our implementation uses a backprojector that is exactly matched to the transpose (adjoint) of the forward projector. The detector/collimator response model was based on a combination of a 2D Gaussian function for the central core and exponential tails to model penetration, important for I-131. The parameters of this approximate analytical model were determined by least-squares fitting to point spread function measurements at several distances from the collimator. No modeling of the fine-grained collimator hole pattern was used. To account for collimator scatter, the measured point source data were first corrected using a triple energy window (TEW) scatter estimate, prior to the least-squares fitting. For object scatter, a TEW-based scatter estimate was included in the statistical model as a known additive term as appropriate for Poisson statistics. We have previously implemented 3D OSEM with this system model for I-131 SPECT (Koral et al 2007b).

2.3.1. Simulations

Targets with uniform activity

The simulated phantom geometry consisted of six (95 mL, 61 mL, 17 mL, 11 mL, 8 mL and 4 mL) hot spheres in a warm elliptical tank with dimensions 23 cm × 32 cm × 21 cm (figure 1). Activity within the spheres was uniformly distributed; however, when synthesizing the phantom we accounted for partial filling at the edges of the sphere by setting the activity at the boundary voxels to an intermediate value depending on the fraction of the voxel occupied. All spheres had the same contrast; the sphere to background activity concentration ratio was 6:1, which is a realistic distribution for tumor imaging following I-131 RIT (Dewaraja et al 2005). The SPECT projection data for this digital phantom were generated using an analytical projector, which included non-uniform attenuation and the measured depth-dependent detector response of the SPECT camera. Projections were scaled to 50 million total counts before the addition of Poisson distributed noise to obtain ten noisy realizations. This represents a typical noise level for patient imaging in I-131 RIT.

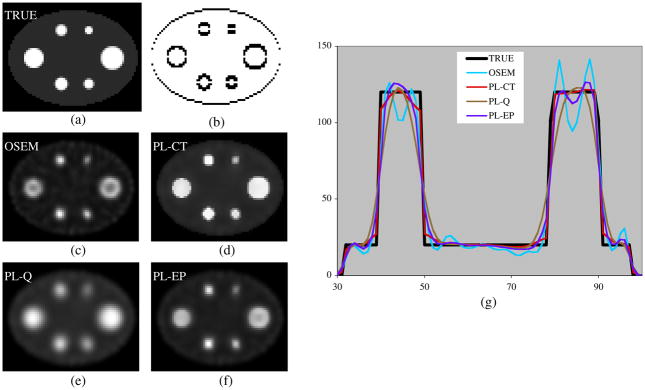
Figure 1.

Images and profiles for a single noisy realization of the simulation with uniform activity spheres. (a) True activity, (b) regularization weights in the vertical direction, (c) OSEM, (d) PL-CT, (e) PL-Q, (f) PL-EP and (g) profiles across the center of the image.

The true boundaries of the simulated object were used when defining the label image. The label image was non-binary with intermediate values near region boundaries as will be the case with clinical data. Simulation studies were performed for two conditions (1) with accurate alignment of the SPECT data and the target boundaries, representing perfect side information and (2) with the SPECT data translated by 5 mm with respect to the target boundaries, mimicking imperfect side information due to SPECT-CT misregistration.

Targets with non-uniform activity

In patient imaging the activity distribution within tumors can be non-uniform. Hence, the target activities of the three largest spheres of the previous simulation were changed to add some degree of non-uniformity within the target. These spheres had an inner core and an outer shell, with an activity concentration ratio of 6:4:1 for core to shell to background (figure 2). All other aspects of the phantom geometry, including target volumes, were kept the same. Multiple noisy realizations were generated as before.

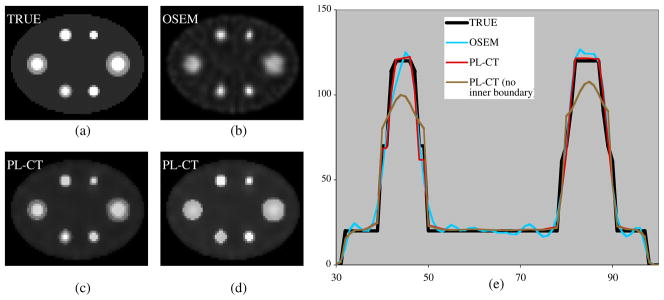
Figure 2.

Images and profiles for a single noisy realization of simulation with non-uniform activity spheres. (a) True activity, (b) OSEM, (c) PL-CT with inner and outer boundaries, (d) PL-CT with only outer boundary and (e) profiles across the center of the image.

The label image for the non-uniform targets was defined in two ways: (1) using boundaries of both the inner core and the outer shell and (2) using only the outer boundary of the target. The first represents the case where the non-uniformity in the target uptake visible on SPECT is matched by a corresponding anatomical change visible on CT. The second case represents the situation where there is a mismatch between the inhomogeneity seen on SPECT and that visible on CT.

2.3.2. Experimental measurements

Targets with uniform activity

The phantom geometry for the experimental measurement consisting of six hot spheres in an elliptical tank was similar to that of the simulation. Here the I-131 activities were chosen not only to obtain a realistic tumor to background contrast but also to consider radiation safety regulations and the limits of the dose calibrator, which is certified to ±5% down to 30 μCi. The background activity in the elliptical tank was 4.8 mCi and the sphere activities were 210 μCi, 133 μCi, 39 μCi, 32 μCi, 31 μCi and 32 μCi going from the largest to the smallest sphere. Thus the sphere to background activity concentration ratio ranged from 5:1 for the larger spheres to 18:1 for the smallest sphere. Multiple (eight) 30 min sequential acquisitions were performed under identical conditions. To form the label image the sphere outlines were defined slice-by-slice on CT and were re-sampled to SPECT space. This mimics the situation in patient studies where tumor outlines are defined on CT.

Targets with non-uniform activity

Two spherical shells (Data Spectrum, Inc.) with an inner core and an outer shell fillable with different activity concentrations were positioned on either side of a uniform sphere in the elliptical tank (figure 3). The uniform sphere was 95 mL and was filled with 207 mCi while the background activity in the elliptical tank was 5.2 mCi (center sphere to background activity concentration ratio of 4:1). In the larger spherical shell the inner core was 31 mL and was left ‘cold’ (representing a tumor with a necrotic center) while the outer shell was 84 mL and was filled with 135 μCi (outer shell to background activity concentration ratio of 3:1). In the smaller spherical shell the inner core was 5.5 mL and was filled with 43 μCi while the outer shell was 21 mL and was filled with 50 μCi (core to shell to background activity concentration ratio of 13:4:1). As with the previous experiment, eight 30 min acquisitions were performed. Target boundaries (including inner core) were drawn in CT space and were re-sampled to SPECT space to define the label image (1) using both inner core and outer shell boundaries and (2) using only the outer boundaries of the targets.

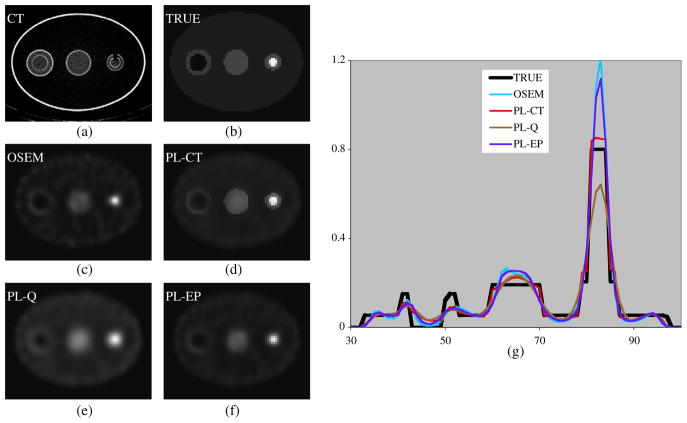
Figure 3.

Images and profiles for measurement with non-uniform activity spheres. (a) CT image, (b) true activity, (c) OSEM, (d) PL-CT, (e) PL-Q, (f) PL-EP and (g) profiles across the center of the image.

2.3.3. Patient study

To demonstrate clinical application, the penalized-likelihood reconstruction with CT-side information-based regularization was applied to SPECT/CT imaging data from a patient imaged at our clinic 2 days after a 2.8 GBq (76 mCi) administration of I-131 Tositumomab therapy for non-Hodgkin’s lymphoma (NHL). In NHL, typically the tumors are well defined on CT and are relatively large (Dewaraja et al 2009). Previously as part of an ongoing research study, SPECT data had been reconstructed with 3D OSEM and tumors in the inguinal region had been defined on 512 × 512 CT to determine tumor absorbed dose. For the present work, these tumor outlines were interpolated to SPECT space to determine the weights for the PL-CT regularization.

2.4. Evaluation

For both simulated and measured phantom data, we compared reconstructions from (1) unregularized OSEM with no post-filtering; (2) penalized likelihood employing CT-side information-based regularization (PL-CT); (3) penalized likelihood with edge preserving regularization (PL-EP) (no CT) and (4) penalized likelihood with conventional spatially invariant quadratic regularization (PL-Q) (no CT). The OSEM reconstruction was used as the initial estimate for the regularized reconstructions. To determine the number of iterations, we considered convergence, noise, the edge artifacts and the computation time. Initial phantom studies showed that convergence is not achieved for the smallest spheres even after 70 iterations. However as the numbers of OSEM iterations increase, the noise and the severity of the edge artifacts (evident in figure 1(c)) also increase. Based on these observations we chose to use 40 OSEM iterations (6 subsets) for the initial estimate followed by 30 iterations (6 subsets) with the regularized algorithm. The computation time for the OSEM reconstruction and that for the PL-CT reconstruction were similar; 185 s for ten OSEM iterations compared with 200 s for ten PL-CT iterations on a 3 GHz dual processor Mac Pro.

In addition to visual comparison of images and profiles, quantitative evaluation of the different SPECT reconstructions was carried out for each target based on the mean estimated bias, STD and RMSE in counts (simulation) or activity (experiments). In the case of experimental measurement, the conversion from SPECT counts to activity was carried out using the camera calibration factor (counts per second per MBq) determined from experimental measurement with a known amount of activity distributed in an elliptical phantom. The bias as defined below is a measure of how close the estimated total target activity is to the true total target activity, while the RMSE as defined below is a measure of how close the activity distribution within the target is to the true target activity distribution. The VOI for the target was the true object in the case of simulation and the CT-defined object in the case of experimental measurement. In addition, evaluations were also performed for VOIs with a radius 5 mm larger than the object radius.

For object i, if $\overline{C_i}$ is the mean VOI counts (or activity) from the N realizations/acquisitions, then the mean estimated bias is given by

$${\text{Bias}}_i=\frac{C_i^T-\overline{C_i}}{C_i^T},$$ (10)

where $C_i^T$ is the true VOI counts (or activity) for the object i.

The standard deviation for object i is given by

$${\text{STD}}_i=\sqrt{\frac{1}{N-1}\sum _{j=1}^N{(\overline{C_i}-C_{ij})}^2},$$ (11)

where C_ij is the VOI counts (or activity) for realization j for the object i.

The RMSE of object i with voxels n_i is given by

$${\text{RMSE}}_i=\sqrt{\frac{1}{N}\frac{1}{n_i}\sum _{j=1}^N\sum _{k=1}^{n_i}{(x_{j,k}-t_k)}^2},$$ (12)

where x_j,k is the estimated count (or activity) value of voxel k for realization j and t_k is the true value.

3. Results

3.1. Simulation studies

Targets with uniform activity

Figure 1 compares different reconstructions of a single noisy realization of the phantom with uniform activity targets. Reconstructions were compared at the same number of iterations (70 OSEM or 40 OSEM followed by 30 with the regularized algorithm). Visually, the PL-CT reconstruction (using the regularization weights shown in figure 1(b)) is closer to the true image than the other reconstructions. As evident from the images and profiles, unregularized OSEM with no post-filtering is noisy and produces significant edge overshoots, which result in a ‘cavity’ at the center of the larger spheres. This artifact is not evident in the PL-CT reconstruction. The images and profiles corresponding to regularization without side information are less noisy, but there is considerable blurring across boundaries, which is minimized with PL-CT.

We verified the source of the edge artifacts by carrying out the OSEM reconstruction without collimator–detector response compensation. In this case, in agreement with previous observations (Tsui et al 1994), the artifacts were not evident in the images and profiles even after 70 iterations, but recovery of sphere counts was significantly worse than 3D OSEM with collimator–detector response compensation. Since our goal was to improve estimation of activity distribution within the target without sacrificing total target quantification accuracy, OSEM without collimator–detector response compensation was not an option and was not evaluated further.

The bias, STD and RMSE in SPECT counts with the different reconstructions are compared in table 1 for the case where there is no SPECT-CT mis-alignment and in table 2 for the case where the SPECT and CT data are mis-aligned by 5 mm. The mis-alignment affects the results for all of the reconstructions because the CT-based target outline was used not only to determine the regularization weights for PL-CT, but also to determine the VOI for the bias, STD and RMSE calculations. For all the targets, the PL-CT reconstruction is superior to OSEM in terms of RMSE and STD and is superior to the regularization without side information in terms of RMSE and bias. The bias with PL-CT is almost the same as with unregularized OSEM for the larger spheres, but is slightly worse for the two smallest spheres. The spatially invariant regularization results in the lowest STD, which is to be expected.

Table 1.

%Bias, %STD and %RMSE in VOI counts for the simulation of uniform activity spheres with perfect SPECT-CT registration (figure 1).

Sphere (mL)	OSEM			PL-CT			PL-Q			PL-EP
	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE
95	5	0.2	17	5	0.2	13	19	0.1	23	9	0.2	17
61	6	0.4	18	6	0.3	14	23	0.2	26	11	0.3	19
17	12	1.4	25	12	1.2	19	37	0.9	34	20	1.4	27
11	11	1.3	23	12	1.1	18	39	0.6	36	20	1.2	26
8	14	1.9	23	16	1.8	21	45	1.4	39	26	2.0	26
4	24	3.4	26	28	2.8	27	54	1.7	47	39	3.3	36

Table 2.

%Bias, %STD and %RMSE in VOI counts for the simulation of uniform activity spheres with SPECT-CT misregistration of 5 mm.

Sphere (mL)	OSEM			PL-CT			PL-Q			PL-EP
	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE
95	8	0.3	24	8	0.3	19	21	0.2	26	12	0.3	23
61	10	0.2	26	9	0.2	21	24	0.1	28	14	0.2	26
17	17	0.9	33	17	0.8	26	39	0.6	37	24	0.8	34
11	18	0.9	34	18	0.8	27	42	0.5	39	26	0.9	35
8	21	1.3	34	23	1.2	29	47	0.8	41	31	1.2	35
4	32	2.2	38	35	2.1	36	56	1.4	49	44	2.4	42

The PL-CT results with the ‘blurred labels’ approach (Comtat et al 2002) are not presented in tables 1 and 2, but the bias and RMSE with blurred labels were inferior to the present implementation with no blurring for both the perfectly aligned data set and for the data set with misregistration. For example, for the misregistered data set, the bias values ranged from 15% to 48% and RMSE values ranged from 21% to 42% when labels smoothed with a kernel of 4 mm FWHM were used. These values were slightly worse for labels smoothed with a kernel of 5 mm FWHM. The STD was either unchanged or slightly superior with blurred labels compared with no blurring. For the rest of the evaluations presented below, labels with no blurring were used.

Targets with non-uniform activity

Figure 2 compares images and profiles of a single noisy realization of the phantom with non-uniform activity targets. The OSEM reconstruction is compared with the two PL-CT reconstructions (with and without using the inner boundaries when determining regularization weights). Although the OSEM reconstruction is still noisy, the significant edge artifacts evident in the case of uniform activity targets are greatly reduced here (the ‘cavity’ evident in the OSEM reconstruction of figure 1 is not evident in figure 2). The PL-CT reconstruction using both inner and outer boundaries (figure 2(c)) is closer to the true activity distribution than both OSEM and the PL-CT reconstruction using only the outer boundary. When the inner boundary is not used to control the regularization, there will be blurring across this boundary leading to loss of useful information as evident in figure 2(d) and the corresponding profile. The PL-Q and PL-EP reconstructions are not shown in figure 2, but as before these reconstructions resulted in too much blurring across boundaries.

The results shown in table 3 follow the same trends as seen for the uniform activity targets (PL-CT consistently gives lower RMSE values and comparable or lower bias). There was no significant difference in the bias and STD for PL-CT with and without using the inner boundaries because these measures use the total counts within the VOIs defined by the outer boundaries. However, when the inner boundary is not used to control the regularization, the RMSE, which is a measure of the inaccuracy of the count distribution, increases due to the blurring across the inner boundary. In this case, the RMSE for PL-CT (given in parentheses) is no longer superior to OSEM or the regularization without side information.

Table 3.

%Bias, %STD and %RMSE in VOI counts for the simulation of non-uniform activity spheres (figure 2). The values in parentheses for PL-CT correspond to the case where only the outer boundary was used for the regularization.

Sphere (mL)	OSEM			PL-CT			PL-Q			PL-EP
	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE
95	4	0.3	15	3	0.3	12 (17)	14	0.2	17	8	0.3	15
61	5	0.4	15	4	0.4	12 (18)	17	0.3	20	10	0.4	15
17	7	0.9	15	8	0.7	14 (18)	31	0.4	31	17	0.8	19

The results given in tables 1–3 were calculated for a VOI corresponding to the physical size of the object. When a VOI larger than the true size was used the results followed the same trends as shown in these tables. However, with a larger VOI the bias values for the smaller spheres were significantly improved in all the reconstructions.

3.2. Experimental studies

Targets with uniform activity

Table 4 compares bias, STD and RMSE in the SPECT measured activity. These results follow the same trends demonstrated for the simulation with uniform activity targets. The PL-CT results are superior to OSEM in terms of RMSE and STD while the bias is comparable. The PL-CT results are superior to regularization without side information in terms of RMSE and bias, while the spatially invariant regularization gives the lowest STD.

Table 4.

%Bias, %STD and %RMSE in SPECT measured activity for the experimental phantom with uniform activity spheres.

Sphere (mL)	OSEM			PL-CT			PL-Q			PL-EP
	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE
95	−2	1.0	30	−1	0.8	20	5	0.7	23	2	0.8	26
61	8	1.5	24	8	1.5	17	15	1.4	21	12	1.4	21
17	17	2.5	28	20	2.4	22	30	2.1	26	25	2.4	25
11	14	5.4	35	17	4.9	24	31	4.2	26	23	5.1	29
8	17	2.5	31	23	2.3	22	40	1.9	29	29	2.4	26
4	31	3.7	25	37	3.4	23	56	2.8	36	41	3.6	26

Targets with non-uniform activity

Images and profiles from the experimental phantom study, which included non-uniform activity spheres, are compared in figure 3. Figure 3(a) is the CT image used to define the region boundaries, which were then re-sampled to SPECT space to determine the weights for the PL-CT regularization. The images and profiles show that in general the activity distribution from PL-CT (using both inner and outer boundaries) is closer to the true distribution than OSEM and the regularizations without CT information.

Table 5 compares bias, STD and RMSE for the uniform center sphere and the two nonuniform spherical shells. PL-CT (using both the inner and outer boundaries) is superior to regularization without side information in terms of RMSE and bias and is superior to OSEM in terms of RMSE and STD while the bias is comparable. As in the simulation, when the inner core boundary information is not used in the PL-CT reconstruction, the bias and STD are not significantly affected, but the RMSE (given in parentheses) increases due to blurring across this boundary.

Table 5.

%Bias, %STD and %RMSE in SPECT measured activity for the experimental phantom with two non-uniform activity spheres (figure 3). The value in parentheses for PL-CT corresponds to the case where only the outer boundary was used for the regularization.

Sphere	OSEM			PL-CT			PL-Q			PL-EP
	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE	Bias	STD	RMSE
Uniform	2	0.8	42	1	0.8	26	12	0.7	31	5	0.7	40
Small non-uniform	−2	0.8	39	−3	0.7	18(49)	13	0.7	42	0	0.7	35
Large non-uniform	14	1.4	42	15	1.4	41(49)	22	1.3	53	18	1.4	47

3.3. Patient study

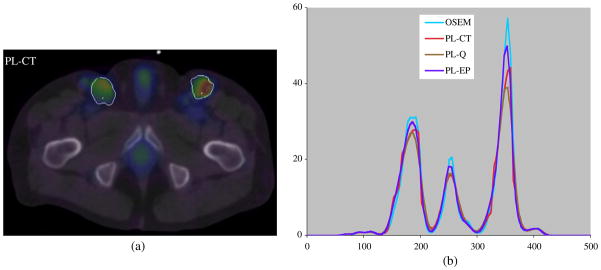
As in the phantom studies the patient data were reconstructed with 40 OSEM iterations (6 subsets) for the initial estimate followed by 30 iterations (6 subsets) with the regularized algorithm. A slice of the PL-CT reconstruction superimposed on CT is shown in figure 4(a). The profile compares the PL-CT reconstruction with OSEM, PL-Q and PL-EP. The true distribution is not known in this case, but the differences in the profiles for the different reconstructions can be observed. Note that CT boundaries were used to control the regularization for the tumors only and normal organs such as the bladder, which also show significant uptake, were not outlined.

Figure 4.

(a) Patient PL-CT SPECT reconstruction superimposed on CT with tumor outlines and (b) profiles across the tumor for the different reconstructions.

4. Discussion

A penalized likelihood reconstruction method employing CT side information-based regularization was implemented and compared with regularization without side information and with unregularized OSEM. We chose to compare the PL reconstructions to 3D OSEM with no post-filtering because currently we use this algorithm to quantify tumor activity for I-131 radioimmunotherapy dosimetry studies (Dewaraja et al 2009).

In both simulation and experimental phantom studies with uniform activity targets, the PL-CT reconstruction was clearly superior to OSEM and regularization without CT information in terms of visual evaluation. The large distortions near the target edges with OSEM become more severe as iterations proceed and have been reported previously in EM reconstructions of objects with sharp edges (Snyder et al 1987, Tsui et al 1994, Koral et al 2007a, Shcherbinin and Celler 2008). PL-CT images and profiles did not display the significant edge overshoots or the blurring across region boundaries evident in the methods where CT information was not used in the regularizer. Comparison of RMSE values also confirms that the PL-CT reconstruction resulted in the most accurate determination of target activity distribution. The improvement in estimation of activity distribution with PL-CT comes without sacrificing the accuracy of total target activity estimation as evident from the bias results. This is because the anatomical information controls the regularization, allowing smoothing within the target but avoiding smoothing across boundaries. For quantification of total target activity, PL-CT was superior to regularization without side information and in general was comparable to unregularized OSEM. In both simulation and experimental measurement, the bias in activity estimate with PL-CT and OSEM was better than 10% for sphere sizes down to 61 mL, better than 20% for sphere sizes down to 17 mL but was up to 37% for the smallest 4 mL sphere. These relatively high bias values result from incomplete count recovery due to partial volume effects, although in the experimental studies some of the error may be associated with the dose calibrator measurement and/or the definition of target boundaries on CT. Incomplete count recovery is particularly significant when imaging higher energy emitters such as I-131 due to the poor spatial resolution.

In phantom studies with non-uniform activity targets, superior results with PL-CT were achieved only when the regularizer used anatomical boundary information that matched the activity non-uniformity. In phantom studies using a spherical shell with an inner core and an outer shell filled with different activity concentrations, PL-CT images, profiles and RMSE values were superior to OSEM and regularization without side information only when both inner and outer boundaries were used to determine the regularization weights. When the inner boundary was not used, the blur across this boundary resulted in the loss of useful information. In practice, the inner boundaries will not always be available since the non-uniformity may not be present in the anatomical image, or may not be visible on CT scans that are typically acquired with low-dose modes in hybrid systems.

The improvements with PL-CT were achieved even with misregistered side information. The 5 mm translation simulated here is well within the capabilities of integrated SPECT-CT imaging (by inspection of overlaid SPECT and CT point source images, the SPECT-CT alignment was estimated to be accurate to within 2 mm). In patient imaging larger mis-alignment due to breathing or movement between the sequential scans is possible. Blurring the weights of the penalty function with a kernel whose width corresponds to the uncertainty of the side information as proposed previously (Comtat et al 2002) was investigated here to account for SPECT-CT misregistration. However, no improvement in bias or RMSE was demonstrated compared with the approach of the present study of defining binary weights using thresholded differences of the label image, which was non-binary due to the finite size of the SPECT voxels relative to CT voxels. Further investigation is needed on optimizing regularization weights for non-binary masks. Past studies in PET reconstruction using smoothed weights or smoothed labels to account for misregistered side information also did not demonstrate clear improvement (Fessler et al 1992) or only showed moderate improvement (Comtat et al 2002) over using the side information without smoothing. In the study of Fessler et al the blurred weights approach was shown to be superior to the approach of using ideal weights in a 1D simulation, but was inferior for the 2D case.

Of the two regularization methods that did not use CT side information, the edge preserving regularization consistently gave lower RMSE and bias. However, the spatially invariant regularization gave the lowest noise of all the methods compared. Note that noise is not a major concern in high-count rate imaging following the therapy administration in internal emitter therapies, but is a consideration in tracer studies for treatment planning, which typically use <10% of the activity administered for the therapy.

The clinical example with SPECT/CT data demonstrated the feasibility of using PL-CT in patient studies. The method is particularly well suited for applications such as tumor dosimetry in non-Hodgkin’s lymphoma, since in this case the tumors are typically well defined on CT. The computation time for PL-CT is comparable to OSEM and the CT-side information is readily available if target VOIs are already defined for tumor dosimetry. In our patient study, the only additional step involved re-sampling of the tumor outlines from CT space to SPECT space.

5. Conclusion

A penalized-likelihood SPECT reconstruction using a modified regularizer that accounts for CT-side information was implemented and compared to regularization without side information and to unregularized OSEM. Phantom evaluations demonstrated the potential of PL-CT to provide improved estimates of the activity distribution within targets, without sacrificing total target activity quantification accuracy, when there is a good match between the SPECT and the CT information.