A DERATING METHOD FOR THERAPEUTIC APPLICATIONS OF HIGH INTENSITY FOCUSED ULTRASOUND

Abstract

Current methods of determining high intensity focused ultrasound (HIFU) fields in tissue rely on extrapolation of measurements in water assuming linear wave propagation both in water and in tissue. Neglecting nonlinear propagation effects in the derating process can result in significant errors. In this work, a new method based on scaling the source amplitude is introduced to estimate focal parameters of nonlinear HIFU fields in tissue. Focal values of acoustic field parameters in absorptive tissue are obtained from a numerical solution to a KZK-type equation and are compared to those simulated for propagation in water. Focal waveforms, peak pressures, and intensities are calculated over a wide range of source outputs and linear focusing gains. Our modeling indicates, that for the high gain sources which are typically used in therapeutic medical applications, the focal field parameters derated with our method agree well with numerical simulation in tissue. The feasibility of the derating method is demonstrated experimentally in excised bovine liver tissue.

I. INTRODUCTION

In both diagnostic and therapeutic applications of medical ultrasound, it is necessary to know the values of acoustic field parameters in situ, i.e. in the tissue region exposed to ultrasound. These values are estimated using ultrasound measurements performed in water in a process called derating [1]. The measurements in water are usually performed at low output levels and are then linearly scaled to higher source outputs that are used for medical procedures. To obtain values of in situ acoustic parameters, the measurement in water is multiplied by an exponential term to account for losses that occur in tissue over the propagation path [1, 2]. For example, the ultrasound intensity in tissue, I_t, at the depth L is derated (estimated) as

$$I_t=I_{w}exp(-2\alpha L),$$ (1)

where I_w is the wave intensity in water at the same location linearly scaled from the low output measurements, and α is the attenuation coefficient in tissue at the source frequency. Then, the magnitudes of the pressure amplitude p_t and heating rate H_t in tissue are obtained from the intensity estimate using the relations:

$$p_t=\sqrt{2I_t{\rho }_0{c}_0},H_t=2\alpha I_t,$$ (2)

where the subscript t denotes tissue. Here the density, ρ₀, and the sound speed, c₀, are assumed to be the same in water and in tissue. The attenuation of tissue is usually chosen to have a value of 0.3 ÷ 0.7 dB cm⁻¹ MHz⁻¹. Various indices are formulated based on the acoustic field magnitudes in tissue given by Eqs. (1,2). The main indices used in safety standards of diagnostic ultrasound are the mechanical index (MI) and the thermal index (TI) [1]. The MI is proportional to the peak negative pressure and is related to the likelihood of adverse bioeffects resulting from acoustic cavitation. The TI is related to the likelihood of inducing significant heating in tissue. In therapeutic ultrasound, much higher intensities are applied and different indices to characterize the efficacy of the procedure have to be used.

The primary problem encountered when estimating acoustic fields in tissue using the derating approach described by Eqs. (1,2) is in choosing the proper value for the attenuation coefficient. Attenuation values vary significantly by tissue type and are not precisely known under clinical conditions [1]. Another problem arises when high amplitude ultrasound waves are applied. In Eqs. (1,2), the propagation of ultrasound both in water and in tissue is assumed to be linear. However, even in diagnostic applications, high amplitude pulses are used in Doppler or harmonic imaging modes and propagation is highly nonlinear. In therapeutic applications of high intensity focused ultrasound, the in situ pressure levels can be two orders of magnitude higher than in diagnostic applications, so nonlinear propagation effects are critical [2–4].

If nonlinear propagation effects are significant, there are several sources of error included in the linear derating method based on Eqs. (1, 2). First, low amplitude measurements of acoustic fields in water cannot be linearly extrapolated to high amplitudes where nonlinear effects are important [3, 4]. This step can be improved by performing measurements in water over the entire range of operational outputs, which is now a regular procedure in calibrating both diagnostic and therapeutic systems. However, even nonlinear measurements in water cannot be directly extrapolated to tissue by simply accounting for linear attenuation in Eq. (1), which contributes to additional errors. Nonlinear distortion of the waveform accumulates differently in tissue and in water due to higher attenuation and thus less wave amplitude over the propagation path in tissue [5, 6]. The attenuation of nonlinearly distorted waves in tissue is also higher than predicted by Eq. (1) because of the generation of higher harmonics that are absorbed more readily than the fundamental frequency. Lastly, the main acoustic quantities in nonlinear fields, such as intensity, peak pressures, and heating rates, are not related by the simple formulae, Eq. (2). In focused ultrasound beams, the combined effects of nonlinearity and diffraction result in asymmetric waveforms, with higher peak positive and lower peak negative pressures than predicted with linear assumptions. The wave intensity consists of contributions from all the harmonics and is not a quadratic function of the pressure amplitude at the fundamental frequency. The heating rate is no longer proportional to intensity because of the contribution of additional absorption of higher frequency components. More acoustic quantities in addition to intensity, and, ideally, the nonlinearly distorted waveform should therefore be derated [7]. The use of the derating approach, Eq. (1), based on the extrapolation from either low or high amplitude measurements in water may result in both underestimation and overestimation of acoustic quantities in tissue at the focus of a medical device [8, 9].

Several methods have been proposed for including acoustic nonlinearity in the derating process [5, 10]. In contrast to the standard derating factor for a harmonic wave, Eq. (1), Schafer proposed a broadband attenuation factor, based on multiplication of the spectrum of a measured waveform in water by the attenuation α(f) and phase velocity dispersion Δc(f) of typical tissue values at each frequency: $exp\left(\left(-\alpha (f)+2\pi if\mathrm{\Delta }c(f)/c_0^2\right)L\right)$ [10]. This broadband attenuation multiplication is more accurate than a single frequency derating but it is still a local correction that does not account for the interplay of nonlinearity and attenuation over the propagation path.

Other methods have also been proposed to better understand basic phenomena of ultrasound focusing in water and absorptive tissue and to introduce local nonlinear corrections to high amplitude water measurements. Christopher [6] used numerical modeling to demonstrate the difference between nonlinear propagation in water and in tissue and corresponding errors in derating for typical diagnostic sources and tissue types. A different approach to compensate outputs was considered by Szabo [5], who observed that if the source output for measurements in water was lowered to match the peak negative pressure in the waveforms measured behind tissue-mimicking phantoms, then the peak positive pressure and time average intensity of the measured waveforms were in good agreement as well. The correspondence obtained using this method was better than using the broadband attenuation factor. Unfortunately, it was indicated that the compensation of outputs was nonlinear itself and the correct choice of source pressure for matching would not be generally available. At the present time, there is no accurate analytic approach to predict high amplitude focal fields in tissue based on measurements in water.

The major difficulty encountered when derating nonlinear fields in diagnostic ultrasound is that diagnostic transducers have low focusing gains of 3–8 and the pressure level in the focal region is not much higher than pressures over the whole propagation path. Nonlinear effects therefore interplay with absorption all the way to the focus. In HIFU, nonlinear effects are much stronger than in diagnostic ultrasound, but the geometry of high gain therapeutic sources can be used to simplify the problem.

In this work, a new derating method is proposed to calculate focal values of nonlinear HIFU fields in biological tissue using the results obtained in water. The method relies on scaling the source pressure amplitudes [5], rather than the focal pressures or intensities as is done in the linear derating method, Eqs. (1, 2). To validate the proposed approach, nonlinear HIFU fields are simulated in water and in tissue over a wide range of source pressures and linear focusing gains. Focal waveforms and spectra, peak positive and negative pressures, intensities, and heating rates are calculated in water, then the derating procedure is applied, and the values of acoustic quantities obtained at the focus are compared with the results of direct modeling in tissue. The method is further tested experimentally by comparing focal waveforms measured behind excised bovine liver samples with those derated from measurements in water.

II. DERATING METHOD

The method relies on the fact that transducers used for HIFU therapy typically have focusing gains of 20–50; therefore, the pressure amplitude in the main focal lobe is significantly higher than on the way to the focus and the length of the focal region is much shorter than the focal length [2, 11]. Under these conditions, it is hypothesized that nonlinear effects in the high amplitude focal region will dominate prefocal nonlinear propagation; furthermore, the degree of nonlinear waveform distortion at the focus will be determined mainly by the pressure levels in the focal region.

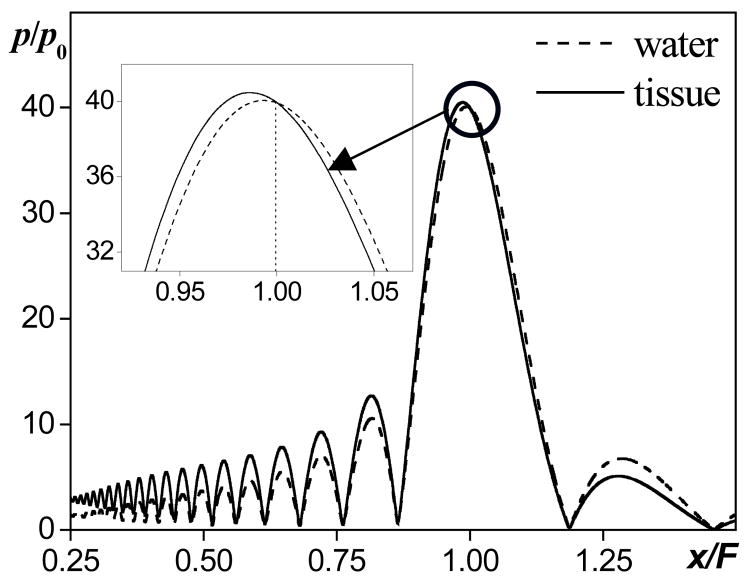
Following these assumptions, consider linear focusing of an ultrasound beam in water and in tissue for source pressures that yield the same amplitude p_F at the geometric focus of the transducer in both media. All of the acoustic properties of tissue except for the absorption are assumed to be the same as in water. The distributions of the pressure amplitude along the beam axis are shown in Fig. 1 for a single element piston source with a linear gain G = p_F/p₀ = 40. Solutions are obtained numerically using the linearized KZK equation [7]. The propagation distance x along the axis is normalized to the focal length F and the acoustic pressure amplitude p is normalized to the source pressure p₀ in water. The solid curve corresponds to propagation in tissue and the dashed curve to propagation in water. If the absorption parameter in tissue at the source frequency is α, then the pressure amplitude at the source in the case of propagation in tissue should be exp(α F) times higher than in the case of propagation in water (in Fig. 1, parameter αF = 1 and exp(αF) = 2.7) so that the focal pressures are the same in both cases. The hypothesis to be tested is that the focal waveforms in a nonlinear beam will also be similar both in shape and peak values if the source pressures are scaled using the same method:

$$p_0(\text{tissue})=p_0(\text{water})exp(\alpha F).$$ (3)

FIG. 1.

Illustration of the derating method based on scaling source pressure. Axial distributions of the pressure amplitude in linear focused beam in tissue (solid line) and in water (dashed line). Pressure is normalized by the source pressure in water, the focusing gain of the source G = 40, absorption in tissue αF = 1, source pressure in tissue is exp(1)=2.7 times higher than in water so that to compensate absorption in the prefocal path and provide the same focal pressure as in water.

If nonlinear focal waveforms obtained in water and in tissue using the proposed method are similar, then the focal waveforms, peak pressures, and intensity of nonlinear ultrasound fields in biological tissue can be determined from measurements or modeling in water using the value of the linear absorption coefficient α only.

III. NUMERICAL MODEL

The acoustic field of a focused piston source was simulated in water and in tissue using a KZK-type evolution equation that can be written in dimensionless form as [7,11,12]:

$$\frac{\partial }{\partial \theta }\left[\frac{\partial P}{\partial z}-NP\frac{\partial P}{\partial \theta }-A_w\frac{{\partial }^{2}P}{\partial {\theta }^2}-A_{t}L(P)\right]=\frac{1}{4G}{\mathrm{\Delta }}_{\perp }P,$$ (4)

with the boundary condition, specified at the source:

$$P(z=0,R,\theta )=\{\begin{array}{ll}sin(\theta +{GR}^2),\hfill & R<1\hfill \\ 0,\hfill & R>1\hfill \end{array}.$$ (5)

Here P= p/p₀ is the acoustic pressure normalized to the pressure amplitude at the source p₀, θ= ω₀(t − x/c₀) is the dimensionless retarded time, ω₀ = 2πf₀, f₀ is the source frequency, c₀ is the sound speed at the frequency f₀; z= x/F is the propagation distance normalized to the focal length F, R= r/a₀ is the coordinate across the beam axis normalized to the source radius a₀, L(P) is the linear operator that accounts for frequency dependent absorption and sound dispersion in tissue; Δ_⊥ is the transverse Laplacian, ${\mathrm{\Delta }}_{\perp }=\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial }{\partial R}\right)$ for axially symmetric beams. The dimensionless parameters in Eq. (4) are N= F/x_sh (nonlinearity), G= x_d/F (diffraction), A_w= α_wF (absorption in water), and A_t = αF (tissue absorption), where $x_{sh}=c_0^3{\rho }_0/\epsilon p_0{\omega }_0$ is the shock formation distance in the case of plane wave propagation, ρ₀ is the is the ambient density of the medium, $x_d={\omega }_0{a}_0^2/2c_0$ is the diffraction length, α_w is the absorption coefficient in water at the frequency f₀. The thermoviscous absorption in water, α_w(f₀) = 2.53·10⁻⁴ cm⁻¹ at 1 MHz, is very low, therefore the nonlinear acoustic field of a focused piston source in water is determined by only two parameters in Eq. (4): nonlinearity N and diffraction G [7]. The small absorption parameter A_w = 5.2·10⁻³ ≪ 1 in modeling corresponded to the parameters of the transducer used in the experimental part of the paper.

In tissue, the frequency-dependent absorption α_t(f) was introduced in the numerical model as a combination of the linear power low and weak thermoviscous quadratic power law, as in water:

$${\alpha }_t(f)=\alpha ·(f/f_0)+{\alpha }_w·{(f/f_0)}^2.$$ (6)

The dispersion of sound velocity was calculated from the linear absorption law using local dispersion relations of the Kramers–Kronig type [12,13]:

$$\frac{\mathrm{\Delta }c}{c_0}=\frac{2c_0}{\pi }\frac{\alpha }{{\omega }_0}ln\left(\frac{\omega }{{\omega }_0}\right),$$ (7)

where Δc= c(ω)−c₀, c(ω) is the sound speed at the frequency ω. In therapeutic applications, the source frequency usually is chosen so that the propagation depth in tissue is about one-half of the absorption length, i.e. 1/2α. This criterion corresponds to the maximum heat deposition rate at the focus [2]. In clinical practice, the typical propagation path of a HIFU beam from the transducer to the focus is first through water and then through biological tissue. If the water-tissue interface is located halfway between the transducer and the focus, i.e., at the distance F/2, the absorption parameter A_t will be equal to 1. This is the most clinically relevant case, so in this work, A_t = 1 is chosen for modeling in tissue.

A numerical frequency-domain algorithm to solve Eqs. (4,5) has been described in detail in previous publications [7, 12, 14]. Briefly, the solution for acoustic pressure is represented as a Fourier series expansion:

$$P(z,\theta ,R)=\sum _{n=-\infty }^{N_{max}}{C}_n(z,R)e^{-in\theta },$$ (8)

where C_n is the complex amplitude of the nth harmonic in the spectrum of the wave. A set of coupled nonlinear equations for the harmonic amplitudes is obtained and solved using the method of fractional steps with an operator splitting procedure to account for nonlinearity, diffraction, and frequency-dependent absorption. The equation for the absorption operator in tissue in the frequency domain has the following form:

$$\frac{\partial C_n}{\partial z}=iK(n)C_n,$$ (9)

where K(n)= k(nω)F= K′+iK″ is the complex wave number in moving coordinate system; K′ and K″ are the dimensionless real and imaginary parts of K(n):

$$\begin{array}{c}{K}^{″}(n)=\alpha ({nf}_0)F=A_{t}n+A_w{n}^2,\\ K^{\prime }(n)=n{\omega }_0(1/c_0-1/c({nf}_0))F=A_t\frac{2n}{\pi }ln(n).\end{array}$$ (10)

The frequency dependence of the absorption K″ is simulated by Eq. (6), and the dispersion of sound velocity K′ is calculated according to the known dependence, Eq. (7).

To increase the rise time of the shock fronts and thus provide stability in the numerical scheme when shocks develop, an additional artificial viscosity that increased with distance along the beam axis and that was proportional to the frequency squared was included: K″(n)_art = T· A_wn² exp[−((z−F)/l)²]. As the nonlinear parameter N was increased, the value of the coefficient T was changed from T = 0 before shocks form to T = 0.5G when high amplitude shocks were present. Parameter l determines the length of the focal region and was chosen from l = 0.5 for G = 5 to l = 0.1 for G = 60.

The following parameters of the numerical scheme were used: the maximum number of harmonics was N_max = 512; the integration distance along the beam axis was 0≤z≤ 1.5 ; the grid boundaries in the transverse coordinate were 0≤R≤3. The number of grid points along the coordinate R and the spatial steps were adjusted depending on the linear focusing gain G of the system. The step in the longitudinal hz coordinate was proportional to the square of the transverse step hr. The number of grid points along R varied from 1500 to 6000. For smaller values of the focusing gain, G = 5–10, the steps were hz = 1·10⁻⁴ and hr= 2·10⁻³. As the parameter G increased, the grid step along R was decreased inversely with G, following the narrower focal width of the beam. Simulations were performed over a wide range of the values of parameters N = 0 ÷ 5 and G = 5 ÷ 60. The results here are presented mainly for G = 40, which is a typical value for transducers used in HIFU applications.

The amplitudes of harmonics, C_n, were obtained in simulations. The pressure waveforms then were reconstructed using Eq. 8 and the peak positive and peak negative pressures were obtained. The intensity of the wave $\stackrel{\sim }{I}(z,R)={\displaystyle \sum _{n=1}^{N_{max}}}{\stackrel{\sim }{I}}_n(z,R)$, and the heating rate $\stackrel{\sim }{H}(z,R)=2{\displaystyle \sum _{n=1}^{N_{max}}}(K^{″}(n)+K^{″}{(n)}_{\mathit{art}}){\stackrel{\sim }{I}}_n(z,R)$ normalized to the corresponding initial values at the source, z = 0, were calculated from the intensities of the harmonics Ĩ_n(z, R)= 4|C_n|², included in the modeling.

IV. EXPERIMENT

To validate experimentally the proposed derating method, acoustic pressure waveforms were measured at the focus of an ultrasound source in water and of that close to but behind a liver sample. The derating method was applied to the free field measurements and the resulting focal waveforms were compared to the tissue measurements and to the results of numerical simulations

The ultrasound source had parameters typical of those used in HIFU therapy (f₀ = 2.158 MHz, a₀ = 21 mm, F = 44 mm, linear focusing gain G = 48) and was characterized in previous work [11]. The transducer was driven in a “burst” mode with a 30-cycle excitation by a function generator (Agilent 33250A, Agilent, Palo Alto, CA) and a linear RF amplifier (ENI A-300, ENI, Rochester, NY). A fiber optic probe hydrophone (FOPH 2000, RP Acoustics, Germany) of 100 MHz bandwidth was used to measure focal waveforms after propagation through an excised liver sample that was obtained from a local abattoir on the same day as experiments. The hydrophone signals were recorded using a digital oscilloscope (Lecroy LT344, Chestnut Ridge, NY). The liver samples were prepared by cutting the liver into 8 cm wide by 8 cm tall by 2.7 cm thick pieces to fit a custom-designed tissue sample holder and an effort was made to avoid the presence of large vessels in the samples. Subsequently, the samples were degassed in a desiccant chamber for an hour and brought to room temperature (20°C) before being placed in a tank filled with degassed water for experiments. The liver capsule was maintained on one side of each sample and was oriented towards the HIFU source. Waveforms were measured at the spatial maximum of the peak positive pressure and there was less than 1 mm between the hydrophone tip in water and the liver sample.

V. RESULTS

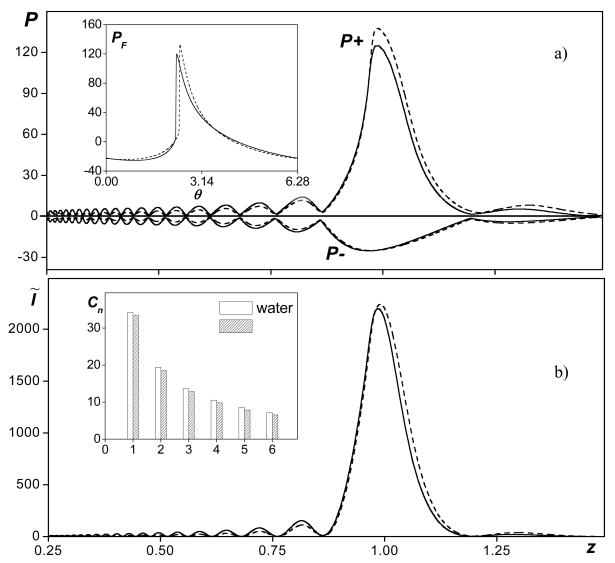
Figure 2 shows axial distributions of the dimensionless peak positive and negative pressures (Fig. 2a) and intensity (Fig. 2b) calculated in tissue (solid curves) and in water (dashed curves). The pressures and intensity in the figure are normalized to the corresponding source values used for modeling in water. Shown as insets to each figure are pressure waveforms (a) and corresponding amplitudes of the first six harmonics (b) calculated in water and in tissue at the focus, z = 1. Calculations in water were performed with the boundary condition specified by Eq. (5) with a linear focusing gain G = 40 and a nonlinear parameter N = 0.25. At this output level (for G = 40) shock fronts form close to the focus and the nonlinear enhancement of focusing gain is the highest for the peak positive pressure [7]. Calculations in absorptive tissue (A_t = 1) were performed for the same values of linear focusing gain G but the source amplitude and therefore the nonlinear parameter N was exp(1) = 2.7 times higher (obtained by setting the absorption parameter, A_t = 1). The pressures and intensity in the figure are normalized to the corresponding source values used for modeling in water, therefore, at the source in tissue, the dimensionless pressure amplitude is 2.7 and the dimensionless intensity is 7.4. If propagation were linear, the increase in source pressure for propagation in tissue would exactly compensate for the energy losses on the way to the focus, and the focal pressures and intensity in water and in tissue would be exactly the same, as shown in Fig. 1. In Fig. 2, nonlinear propagation case is considered and even shocks are present. However, the focal pressures and intensities still agree very well. The focal values in tissue are slightly lower than those in water because of higher absorption of harmonics in tissue generated on the way to the focus. However, this difference is almost negligible for the intensity and peak negative pressure, and it is less than 10% for the peak positive pressure. The focal waveforms (Fig. 2a) and the spectra (Fig. 2b) are also in good agreement. Although the peak positive pressure is 10% higher in the waveform calculated in water (dashed line) than in tissue (solid line), the shock amplitudes in both waveforms are the same. The shock front, as a whole, is slightly shifted down in the waveform in tissue, which is typical for shock formation in dispersive media [15].

FIG. 2.

Axial distributions of dimensionless peak positive and negative pressures (a) and intensity (b) in nonlinear focused beams in tissue (solid curves) and in water (dashed curves). The pressures and intensity are normalized to the source values in water. Linear focusing gain G = 40, nonlinearity N = 0.25, absorption in tissue A_t = 1. Shown in small frames are focal waveforms (a) and their spectra for the first six harmonics (b).

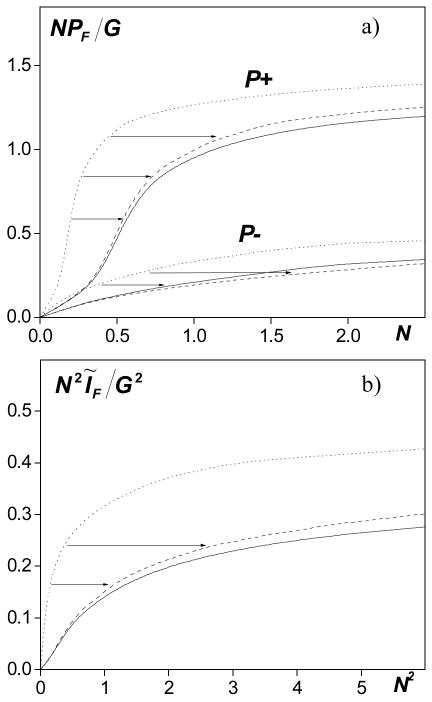
The results shown in Fig. 2 demonstrate one example for which the proposed derating method works well for the high gain source and for initial pressure amplitude (nonlinear parameter N), when shocks are present at the focus. To further validate the feasibility of the method, simulations were performed for the same focusing gain over the range of 0<N<2.5 and the results are summarized in Fig. 3. Peak pressures (a) and intensity (b) at the focus z = 1 are plotted versus their initial values at the source. Dimensionless quantities are used in the figure: NP_F/G= p_F·N/p₀G (a) is proportional to the focal peak pressures p_F and N²Ĩ_F/G²= I_F·N²/I₀G² (b) is proportional to the focal intensity I_F (ordinate axes). The abscissa axes correspond to the initial pressure N ~ p₀ and intensity N² ~ I₀ at the source. The dotted line corresponds to the results of direct modeling in water and the solid line to the results of direct modeling in tissue with the boundary condition shown in Eq. (5). If propagation is linear, the focal values are proportional to the source values and the curves in Fig. 3 then would be straight lines in water. In normalized variables used in the figure the focal values of intensity, peak positive and negative pressures in water would be equal to the source intensity and pressure amplitude, respectively. In tissue, the focal pressures are exp(1) and synonymously, the intensity is exp(2) lower. When nonlinear effects are taken into account, the curves are much more complicated and the results in tissue cannot be obtained by simply multiplying the results in water by some factor. However, if the results in water are transformed by scaling the source output by a factor of exp(1) for pressures or exp(2) for intensity as shown by the arrows in the figure, these new derated curves (dashed lines) are very close to the results of direct modeling in tissue (solid lines). For example, as in Fig. 2, the results obtained in water with a nonlinear parameter N = 0.25 correspond to the results in tissue for N = 0.25·exp(1) = 0.68. The difference between the derated results and direct simulations in tissue is less than 10 %. The proposed derating approach thus can be applied with good accuracy to estimate in situ values of peak pressures and intensity for a high gain source operating at high outputs.

FIG. 3.

Peak pressures (NP_F/G ~ p_F, a) and intensity (N²Ĩ_F/G² ~ I_F, b) of the wave as a function of initial pressure (N~p₀) and intensity (N²~I₀) in three cases: the solid line and dotted line correspond to the results of direct modeling of the wave propagation in tissue and in water with the boundary condition (4); the dashed line corresponds to the derated values from water to tissue. Linear focusing gain G = 40.

The results shown in Fig. 3 also illustrate the concept of acoustic saturation in nonlinear focused ultrasound beams: at high outputs, the parameters of the field at the focus no longer depend on the source pressure amplitude because of effective energy absorption at the shocks [7]. These phenomena are of fundamental physical interest and the results in Fig. 3 can be used to answer the question about the limiting values of acoustic quantities in focused beams in nonabsorptive (water) and absorptive (tissue) media. Although absorption is tissue and water are very different and greater output levels are required in tissue to overcome the greater absorption, the focal saturation values reached in tissue are only slightly smaller than the saturation levels in water (less than 10%).

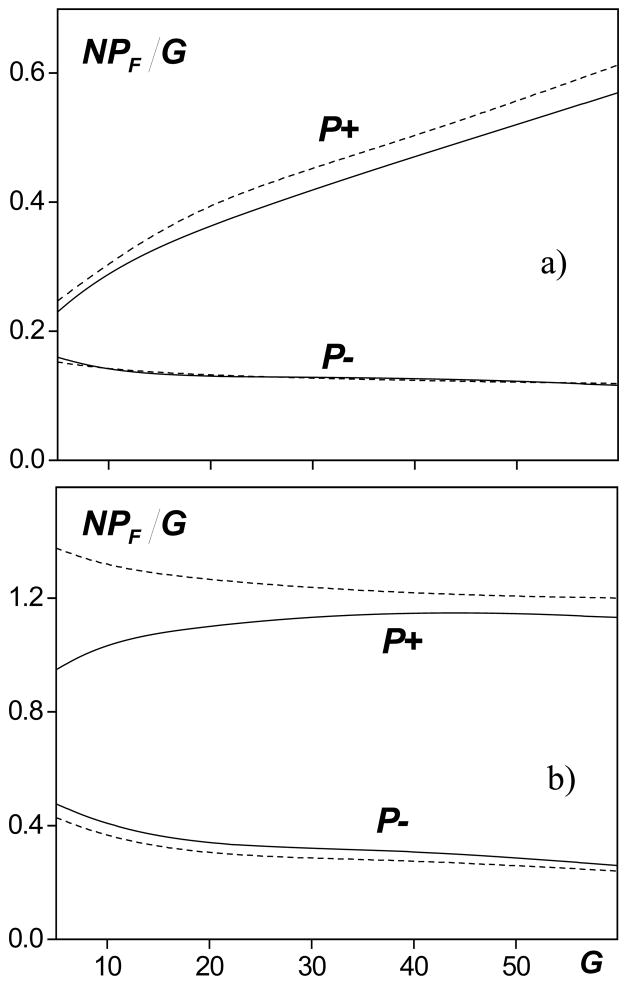
As discussed above, the proposed derating method is based on the assumption that in highly focused beams of therapeutic devices, the pressure amplitude in the focal region is significantly higher than on the way to the focus and, therefore, nonlinear effects close to the focus dominate prefocal nonlinear propagation. This hypothesis was tested by modeling focal pressures for transducers with different linear focusing gains, from G = 5 to G = 60, and the results are shown in Fig. 4. The graphs depict the focal values of peak pressures for two source outputs that correspond to quasilinear focusing (Fig. 4a, N = 0.5 in tissue and N = 0.18 in water) and when shocks are present in the focal waveform (Fig. 4b, N = 2 in tissue and N = 0.7 in water). The same dimensionless variables, as in Fig. 3a, are used for plotting peak pressures: NP_F/G= p_F·N/p₀G ~ p_F. The solid curves correspond to propagation in tissue, and the dashed curves are the results derated from modeling in water. If propagation were linear, the focal pressure amplitude in water p_F would be equal to the gain parameter G; the dimensionless focal pressures in Fig. 4 would be equal to the nonlinear parameter N used in simulations in water; and the curves in both graphs would be horizontal lines at the ordinate level of 0.2 (a) and 0.7 (b). In both quasilinear and shocked beams, the focal values of peak negative pressure, P−, in tissue are nearly identical to those derated from water for all linear focusing gains G (Fig. 4a, b). For the peak positive pressure, P+, the derated values are noticeably higher than those obtained in direct modeling. In the case of quasilinear focusing, the difference is slightly larger for higher gain sources, but the difference is less than 7 % over the entire range of linear focusing gains. When the output is very high, the difference increases for low gains (G<20) as prefocal nonlinear propagation effects become stronger. For G = 5 the difference between the curves is significant and is more than 35 %. At higher linear focusing gains, the simulated and derated values of the peak positive pressure are closer (5 % for G = 60). These results show that the proposed derating method works well and can be used to obtain accurate estimates of peak positive pressure (<10% error) for strongly focused transducers with linear focusing gains of G = 30 ÷ 60. In addition, it provides a good estimate of the peak negative pressure irrespective of focusing gain.

FIG. 4.

Quantities of focal peak pressures versus linear focusing gain G for nonlinearity parameters N = 0.5 (a) and N = 2 (b) in the case of wave propagation in tissue (solid line) and derated from water (dashed line).

In Fig. 5, experimental data are presented to test the proposed derating method. Figure 5a shows a diagram of the experimental arrangement used to measure focal waveforms in water and behind the tissue sample (bovine liver) of L = 27 mm width [11, 16]. Figure 5b shows the waveforms measured in water at an output level of p₀ = 0.18 MPa (dashed curve) and behind the sample at a higher source pressure p₀ = 0.3 MPa (solid curve). These conditions correspond to the focusing gain G = 48, nonlinear parameter N = 0.11, and quasilinear focusing [7, 11]. The focal waveforms are distorted, with peak positive pressure of 14 MPa and peak negative of 6 MPa, but are not yet shocked. The waveform measured behind the liver sample yields a very similar waveform shape and peak pressure as the free-field water measurement. To attain the agreement in the measured focal waveforms, the source pressure amplitude was scaled according to the derating method, Eq. (3): p₀(liver) = p₀(water)exp(αL), where α is the unknown lumped attenuation over the tissue path of thickness L. The waveform measured in water for an initial pressure of p₀ = 0.18 MPa agrees well with the measurements for p₀ = 0.3 MPa in tissue, which yields overall losses of 4.3 dB in the pressure amplitude. The attenuation coefficient α is then equal to 1.6 dB/cm at the source frequency of 2.158 MHz or 0.7 dB/(cm MHz) if the attenuation is assumed to have a linear dependence with frequency. This result is within the range of attenuation values in liver of 0.35–0.7 dB reported in other studies [1, 4].

FIG. 5.

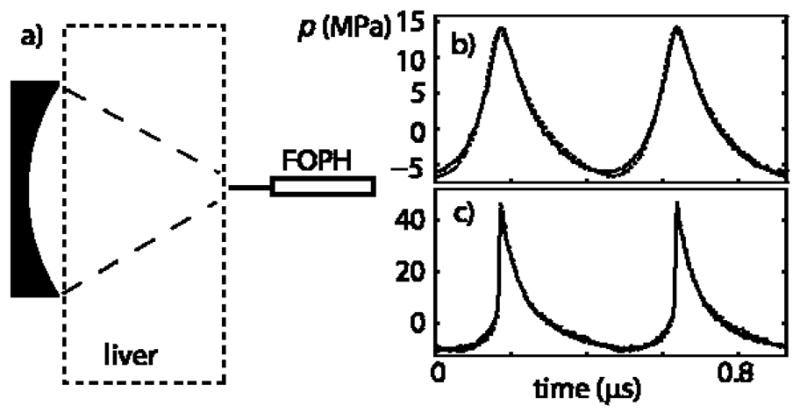
(a) Diagram of the experimental arrangement for measurement of focal waveforms in ex vivo bovine liver. (b) Focal waveform measured in water at p₀ = 0.18 MPa (dashed line) compared with the focal waveform measured after propagation through a 27-mm thick sample at p₀ = 0.3 MPa (solid line). By matching experimental focal waveforms obtained in water and behind the liver sample, the attenuation of liver was determined as 1.6 dB/cm at 2.158 MHz. (c) Focal waveform measured in water at p₀ = 0.36 MPa (dashed line) compared with the focal waveform measured behind the liver sample at p₀ = 0.57 MPa (solid line). The initial pressure in tissue was chosen using the absorption coefficient α and the proposed soure pressure scaling approach, Eq. (3).

The results shown in Fig. 5c were obtained when the HIFU source was operating at an output level of p₀ = 0.36 MPa and a shocked waveform with peak positive pressure of 45 MPa and peak negative pressure of 9 MPa was measured at the focus in water (dashed line). This output level corresponds to the nonlinear parameter N = 0.23 when the focusing gain for peak positive pressure is the highest [16]. An output level of p₀ = 0.57 MPa was chosen for propagation in liver using the attenuation coefficient α obtained in the first measurement. The waveform measured behind the tissue (solid line) still agrees very well with the waveform measured in water. Comparison of nonlinear waveforms measured in water and in tissue with appropriate scaling of the source amplitude thus provides a method to obtain the absorption coefficient in tissue. Furthermore, if the absorption is known, the nonlinear derating approach provides a good estimate of the focal waveform in tissue even for high amplitude shocked focal waveforms.

The experimental data (Fig. 5) can be related to the results of numerical modeling shown in Fig. 2. The curves in Fig. 2 are plotted for nearly the same parameters as shown in Fig. 5c: the nonlinear parameter N = 0.25 in water, linear focusing gain G = 40, and absorption A_t = 1, that yields nearly 4.3 dB linear attenuation losses in tissue over the path to the focus. The dimensionless peak positive pressures in the modeled waveforms are P+ = 133 in water and P+ = 120 in tissue; the dimensionless peak negative pressures are approximately P− = 25 in both media (Fig. 2a). In dimensional values (p₀ = 0.36 MPa in water), the pressures are p₊(F) = p₀·P+ = 47 MPa for water and p₊(F) = p₀·P+ = 43 MPa for tissue, p−(F) = p₀·P−=9 MPa, which is in excellent agreement with the peak parameters of the measured waveforms (p₊ = 45 MPa and p₋ = 9 MPa) shown in Fig. 5c. The numerical algorithm together with the proposed derating method therefore can be used to determine focal fields in tissue with high accuracy even in the presence of shocks, and the results of modeling can be used as an alternative to physical measurements.

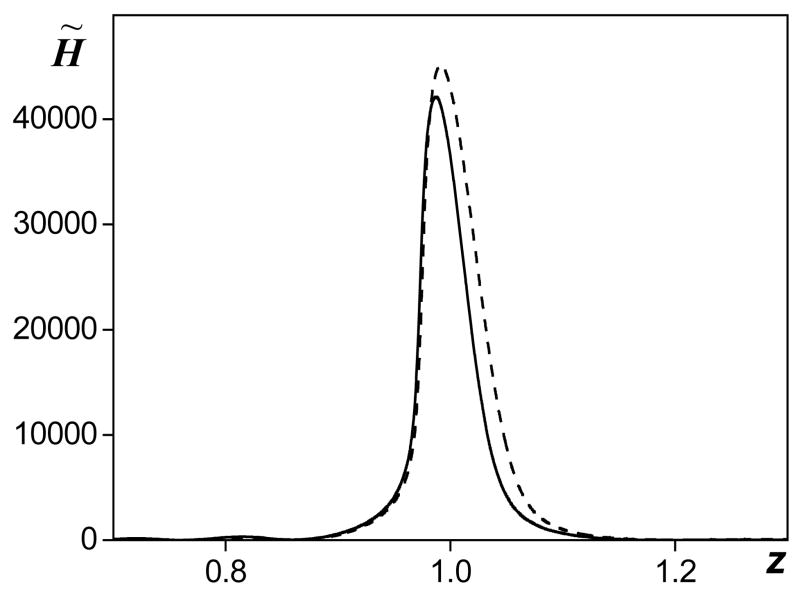
In addition to calculations of in situ focal waveforms, peak pressures and intensity using the proposed derating method, heating rates were also predicted. In nonlinear fields, the heating rate is calculated by summing the contribution of each harmonic component, since the absorption coefficient is different at each frequency. In water, absorption depends on the square of frequency whereas in tissue the relationship is linear. The heating rates [in water, in tissue?] therefore are much more sensitive to the spectral distribution of the energy. Although focal waveforms can be predicted using the proposed derating technique, it is not obvious that heating rates can be predicted as well. To test whether heating rates can be predicted, they were calculated using the waveform derated from simulations in water and compared to the direct calculations from modeling in tissue. The intensity of each harmonic component was determined from the spectrum of the waveform in water, multiplied by the twofold absorption coefficient in tissue at this frequency, and summed. In dimensionless notation, Eq. 10, the derated heat deposition in tissue is ${\stackrel{\sim }{H}}_t^{\mathit{der}}=2{\displaystyle \sum _{n=1}^{N_{max}}}({K_t}^{″}(n)){\stackrel{\sim }{I}}_n^w$, where ${\stackrel{\sim }{I}}_n^w$ is the intensity of the nth harmonic in water and K_t″(n) is the absorption coefficient in tissue. In Fig. 6, axial distributions of the heating rate modeled in tissue ${\stackrel{\sim }{H}}_t=2{\displaystyle \sum _{n=1}^{N_{max}}}({K_t}^{″}(n)){\stackrel{\sim }{I}}_n^t$ (solid curve) and derated from water ${\stackrel{\sim }{H}}_t^{\mathit{der}}$ (dashed curve) are shown. Calculations were performed for the same parameters as in Fig. 2 (G = 40, A_t = 1 in tissue, N = 0.25 in water and exp(1) times higher in tissue). Within the main focal lobe, the curves practically coincide before the focus and the derated values are only slightly higher than those obtained in direct simulations postfocally. The difference between the derated and simulated heating rate in the geometrical focus is less than 15% and only 7% in the values of the peak heating rate. These results indicate that focal waveforms measured or modeled in water can also be used to obtain (derate) heating rates in tissue. However, more detailed studies are necessary to better understand the applicability of the derating method for various focusing conditions and waveform distortions

FIG. 6.

Axial distributions of heat deposition rate calculated as a combination of heating by each harmonic component in the spectrum of the derated waveform ${\stackrel{\sim }{H}}_t^{\mathit{der}}$ (dashed line) and simulated in tissue H̃_t (solid line). The parameters used in simulations were: linear focusing gain G = 40, nonlinearity N = 0.25, and absorption in tissue A_t = 1.

VI. CONCLUSIONS

This paper presents a novel derating method to determine focal peak pressures, intensities, and heating rates in nonlinear HIFU fields in tissue. The proposed method relies on comparing the focal waveforms calculated or measured in water and in tissue not for the same source pressures, as is usually done in existing derating techniques, but for the same focal pressures equalized by scaling the source outputs. The scaling factor that accounts for losses over the prefocal path in tissue is approximated by the linear attenuation in tissue at the source frequency. The accuracy of the method was tested numerically and experimentally. Good agreement was demonstrated between focal waveforms obtained in direct simulations in tissue and those calculated in water for lower outputs that were scaled with a proper factor. It is shown that the derating method works well for both slightly distorted and shocked focal waveforms. The accuracy [Is accuracy the correct term here/} of the method to predict focal intensity and peak positive pressure increased from 35% for weakly focused diagnostic transducers having a linear gain of 5–10 to 5% for strongly focused therapeutic transducers with linear gain of 40–60. Peak negative pressure was derated with an accuracy of 5% for both low and high gain sources. A table of focal waveforms measured or simulated for a particular source in water thus can be used to obtain nonlinear focal waveforms in tissue with a known linear absorption coefficient [7, 11].

The experimental data are in good agreement with the results of modeling and demonstrate the feasibility of the proposed derating method as well. Thus, measurement or modeling of HIFU fields in water over the range of source outputs used for treatments, in combination with the attenuation of the tissue path, yield accurate prediction of nonlinear waveforms and therefore peak pressures, intensities, and even heating rates in tissue.

In the paper, the ultimate levels of acoustic field parameters in focused beams in media with different absorptions were also considered. It was shown that the limiting quantities of the acoustic field at the focus are very similar in water and in tissue, with only slightly smaller values in tissue than in water (the difference is less than 10%).