Image-based models of cardiac structure in health and disease

Abstract

Computational approaches to investigating the electromechanics of healthy and diseased hearts are becoming essential for the comprehensive understanding of cardiac function. In this article, we first present a brief review of existing image-based computational models of cardiac structure. We then provide a detailed explanation of a processing pipeline which we have recently developed for constructing realistic computational models of the heart from high resolution structural and diffusion tensor (DT) magnetic resonance (MR) images acquired ex vivo. The presentation of the pipeline incorporates a review of the methodologies that can be used to reconstruct models of cardiac structure. In this pipeline, the structural image is segmented to reconstruct the ventricles, normal myocardium, and infarct. A finite element mesh is generated from the segmented structural image, and fiber orientations are assigned to the elements based on DTMR data. The methods were applied to construct seven different models of healthy and diseased hearts. These models contain millions of elements, with spatial resolutions in the order of hundreds of microns, providing unprecedented detail in the representation of cardiac structure for simulation studies.

The heart is a complex three-dimensional (3D) structure whose cyclic mechanical activity is essential for the sustenance of body function. Indeed, cardiac disease is the leading cause of morbidity and mortality in the developed world.¹ A comprehensive understanding of cardiac structure and function in health and disease is the central goal of basic and clinical heart research. To achieve this goal, experimental investigations study animal and human myocardium in health and disease, from the molecular to whole body levels. A key challenge remains the integration of insight, obtained at various levels of structural and functional integrations, such as from ion channel function and calcium cycling to cardiac activation maps and regional strain distributions. In addition, a host of relevant processes is not open to direct experimental manipulation or observation, and precise methods for 3D assessment of regional stress or transmembrane potential distribution are not yet available. Furthermore, the invasive nature of many observation techniques prevents their application to human subjects, highlighting the need for intelligent and quantitative tools to interrelate findings from different species. Computational modeling can address these issues and has thus become essential for an integrated understanding of the functioning of the heart. Advanced computational approaches to cardiac electromechanical function complement the experimental approach by aiding data integration, extraction of information, interpretation, hypothesis formation, and new targeted investigations.^2,3

Cardiac tissue and whole-heart electromechanical computations are based on principles of continuum mechanics and reaction–diffusion systems. Numerical solutions to the governing equations are computed using the framework of finite element methods. The finite element methods require a representation (or model) of the geometry and the fiber structure of the myocardial preparation. Most of the established ‘whole-heart’ models are in fact biventricular models,^4,5 built largely using data from animal anatomies, such as rabbit⁶ or dog.^7,8 These models are based on structural information obtained by a combination of mechanical and histological measurements.

Recent advances in magnetic resonance (MR) technologies have facilitated the imaging of geometry and tissue architecture of the heart at significantly improved spatial resolution. Thus, modern anatomical MR imaging provides continuous 3D representations of cardiac histoanatomy of small experimental animal, such as rabbit, with an isotropic resolution in the order of 10⁻⁵ m.⁹ Advanced diffusion tensor (DT) MR scanning of the diffusivity of water in the tissue yields whole-heart information with a resolution in the order of 10⁻⁴ m.¹⁰ The primary eigenvector of the DTs has been shown to be aligned with the prevailing cardiomyocyte orientation, commonly referred to as ‘fiber orientation’.^11,12 The secondary and tertiary eigenvectors are believed to be oriented normally to the main cell axes, in the myocardial laminar plane and perpendicular to it, respectively.^11,12

The goal of the present paper is twofold. Firstly, we present a brief review, which primarily focuses on image-based methods of previous efforts for construction of computational models of cardiac structure. Secondly, we describe a processing pipeline which we have recently developed to construct anatomically detailed models of cardiac structure from high-resolution 3D structural MR and DTMR images ex vivo. The presentation of the pipeline incorporates a review of the methodologies that can be used to reconstruct models of cardiac structure from ex vivo images. The pipeline has been used to generate models of normal mouse, rabbit, canine, and human hearts; of infarcted rabbit and canine hearts; and of a failing canine heart. These models represent cardiac geometry and fiber structure with unprecedented detail.

The normal rabbit, infarcted rabbit, and infarcted canine models, along with summaries of our processing pipeline, have been published previously.^13,14 The present paper contains a reproducible explanation of the pipeline, four new models, and a review of image-based models of cardiac structure. In the following, the second section reviews the previous efforts to reconstruct the structure of the heart, the third section describes the processing pipeline, the fourth section describes the data acquired by a number of collaborating teams for our research, the fifth section illustrates the models generated, and the sixth section concludes the article.

REVIEW OF MODELS OF CARDIAC STRUCTURE

Among the existing models of ventricular structure, the canine ventricular model constructed at Auckland University⁸ and the rabbit ventricular model developed at the University of California, San Diego⁶ have been widely used.^15–23 The data for the canine model were obtained using a specially designed mechanical rig, whereas for the rabbit model, digital imaging of histological sections was used. The models were generated by fitting the nodal parameters of piecewise polynomials in a prolate coordinate system using least squares. Smooth estimates of the geometry and the fiber structure of the ventricles were obtained using Hermite interpolation. Similar methods have been used by Helm et al. to reconstruct canine ventricular geometry from DTMR data for the purpose of statistical analysis of computed fiber orientations.^10,24,25 Although these models are compact and thus enable efficient solution of numerical problems, they provide only a coarse representation of the overall cardiac structure, and are lacking in fine detail such as endocardial trabeculations and papillary muscles, which play an important role in cardiac electrophysiology and mechanics. The feasibility of building whole-heart models with such fine details has been demonstrated recently by some studies.^3,26 Plotkowiak et al.²⁶ reconstructed models from high resolution structural MR images of rabbit hearts. Although these models contain detailed geometric features, fiber orientations were not incorporated, and the ventricles were not separated from the rest of the tissue. Plank et al.³ reconstructed high resolution models of normal rabbit and rat hearts from structural MR and DTMR images, and demonstrated how the structural MR data can be co-registered with histological data.

In addition to the models of animal hearts, human ventricular models have been constructed, and used to study propagation and the dynamics of fibrillation^27,28 The geometrical data for the model by Panfilov’s group^27,28 were obtained from histological slices of a human heart, which was excised from a normal subject, and digitized at a resolution of 500 μm.²⁹ The fiber orientation data were not acquired from the human subject. To account for the anisotropic structure of the heart, the authors mapped the fiber architecture of a canine heart onto their model. In a similar fashion, Potse et al. used a model of the whole human heart to compare monodomain and bidomain solutions to action potential propagation.³⁰ The geometry of this model was constructed from computed tomography (CT) data, scanned at a resolution of 1 mm. The computational mesh for the model was a 3D finite difference grid with a uniform resolution of 200 μm, and as a result, the size of the model was large, consisting of about 45 million nodes. Fiber orientations for the model were calculated based on mathematical functions, which attempted to mimic structural data.

While the above simulation studies have focused on ventricular function, attempts to model the atria have been also made. Harrild and Henriquez generated a model of the human atria from commercially available surface meshes (Viewpoint Digital), and used the model for studies of normal conduction along atrial structures.³¹ The model was 3D, and incorporated the major muscle bundles of the atria. However, as only surface information was used to build the model geometry, uniform thicknesses were assigned to the left and the right atria (3 and 2 mm, respectively). Muscle bundles were represented as anisotropic structures with faster conduction along their axes. The rest of the atrial tissue was assumed to be isotropic.

Structural MR data were used for the first time in atrial modeling by Jacquemet et al., who constructed a monolayer model of the atria to study electrogram morphologies during atrial fibrillation (AF).³² Wall thickness of the atria was not taken into consideration in this model, and fiber orientations were manually mapped onto the surface. The most structurally detailed atrial model to date was recently presented by Reumann et al., who studied ablation strategies for preventing AF using a model generated from the cryosection images of the Visible Female dataset.³³ Although the model contains more anatomical detail than other existing models, the fiber orientations in the model were not measured but synthesized, using rule-based methods.³⁴ The same atrial model has been used in other studies^35–37 with some improvements in assigning fiber orientations.³⁵

To construct structural models of cardiac tissue at resolutions that approach or go below cardiomyocyte dimensions, optical imaging modalities including extended confocal microscopy and optical coherence tomography (OCT) have been used.^38–41 Tice et al. used OCT to reconstruct the histoanatomical features of rabbit endocardial regions, which were 4 mm³ in size,³⁸ at a resolution of 10 microns. Hooks et al. used extended confocal microscopy to reconstruct the 3D architecture of myocytes in a transmural segment of rat left ventricular myocardium⁴¹; the imaged volume was 0.8 × 0.8 × 3.7 mm in size, and had a resolution of about 1.5 μm. Smith et al. employed confocal microscopy in combination with optical clearing to obtain a high resolution reconstruction of the geometry of a large portion of a mouse heart, and to measure the fiber orientations in guinea pig ventricular strips, which were about 4 mm thick.³⁹ Despite the very high resolution of these techniques, their application in the reconstruction of whole hearts, especially the hearts of large animals, for electromechanical modeling, is limited. Optical measurements suffer from absorption and scattering of light, limiting the penetration depth and therefore the thickness of tissue that can be scanned at one time. Additionally, superficial structures such as the trabeculations cast shadows making the extraction of fiber orientation in subendocardial layers difficult. As high resolution optical scanners typically have small fields of view, only small tiles of the tissue are scanned at a time, and need to be ‘stitched’ together, which is a nontrivial task. Nonetheless, successful reconstructions of transmural cardiac tissue segments have been obtained, for example, using an iteration of confocal imaging of embedded intact tissue and subsequent removal of the imaged tissue segment, yielding high resolution descriptions for subsections of the ventricular wall.⁴² These descriptions have given rise to the current view that the structural organization of ventricular myocardium is such that the aligned cardiomyocytes are packed in layers, 4–5 cells thick, which may be relevant for the interpretation of secondary and tertiary eigenvectors once DTMR resolution and noise levels allow their clear quantification.

Finally, efforts have been made to reconstruct models of cardiac structure from serial histological sections.^9,43,44 This method, in combination with DTMR technology and immunochemistry, has been used to reconstruct a model of the rabbit sinoatrial node.⁴⁵ These models incorporate not only general 3D anatomy and fiber orientations, but also allow cell type identification, which is not currently possible with noninvasive imaging techniques. Because of the labor-intensive nature of the histological reconstruction, the methodology has thus far been used only to reconstruct specific small fragments of the heart, such as the sinoatrial and atrioventricular (AV) nodes, or to obtain regional information to validate MR and DTMR based data interpretation.^12,46 Furthermore, the individual digitized histological slices need to be assembled (or registered) to reconstruct a 3D image, and this procedure is prone to errors because of misalignment and tissue distortion that occur during slicing. Model development based on digitized serial histological sections from whole rabbit and rat hearts are underway,⁴⁷ and have highlighted the challenges associated with the systematic co-registration of histological and MR-based data modalities.

THE PROCESSING PIPELINE FOR IMAGE-BASED CONSTRUCTION OF HEART MODELS

To generate image-based models of the heart, it is necessary to classify (or segment) the voxels in the structural MR image into different groups, such as normal tissue, diseased tissue (or infarct), and background. Segmentation of high resolution cardiac images, similar to the segmentation of detailed images of other biological tissues, is a very challenging task. In particular, the geometry and topology of the myocardium is highly complex, measurement noise is present, object boundaries in the images are blurred, and there is overlap of image intensities between different voxel groups. After extensive experimentation with various existing segmentation techniques such as edge detection, deformable models, region growing, level set methods, and k-means clustering, whose descriptions are given in Ref. 48, we developed a processing pipeline for model generation as outlined in Figure 1. The steps of the pipeline are explained in detail below. Note that the explanation below primarily focuses on methods for the segmentation and processing of ex vivo images. However, there have been efforts to generate cardiac atlases and models from in vivo images,^49,50 and such efforts use methods similar to the ones described below.

FIGURE 1.

The pipeline for model generation.

Suspension medium removal

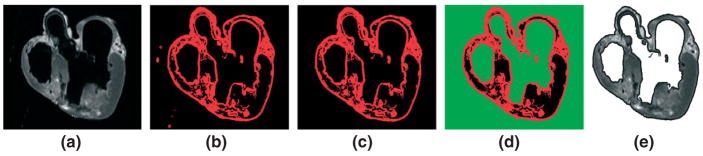
In the first step of our segmentation pipeline, the structural MR image is processed to label and ‘remove’ the voxels corresponding to the cavity content, and the medium in which the heart was suspended during the image acquisition.^9,24 A combination of edge detection, region growing, and manual editing is used in this step. The edge detection⁵¹ is performed in each slice of the image using the ImageJ software system (http://rsbweb.nih.gov/ij/), by first computing the intensity variance of the 2D local neighborhood of each voxel in the slice, and then by selecting voxels with a variance above a certain threshold. Appropriate values for the threshold and the radius of the local neighborhood are determined manually by trial and error experiments on a few slices of the image. Figure 2(a) shows a representative slice taken from one of the images that we acquired, and Figure 2(b) shows the detected edges. A radius value of 2 pixels and a threshold value of 26 were used to detect the edges in Figure 2(b). The collection of image slices after the edge detection forms the edge image, a 3D map of the 2D edges.

FIGURE 2.

The suspension and cavity medium are removed using edge detection and region growing: (a) original slice; (b) detected edges in red; (c) myocardial boundary; (d) suspension and cavity medium in green; (e) original slice after removal of the medium.

From the edge image, the myocardial boundary of the whole heart is extracted using a 3D region growing algorithm.⁵² This is an iterative algorithm in which a list of voxels that belong to the region of interest is maintained. In each iteration, a new voxel is added to the list if it is located adjacent to a voxel in the list, and its intensity equals the intensity of the voxels in the list. Here, two voxels are considered adjacent if they share a face. The algorithm terminates if there are no new voxels that can be added to the list. All voxels that belong to the myocardial boundary are identified by executing the algorithm with an initial list that contains a voxel which is manually selected from the myocardial boundary. Figure 2(c) shows the myocardial boundary corresponding to the slice shown in Figure 2(a).

Next, the 2D variant of the above-described region growing algorithm is applied to each slice of the myocardial boundary image to identify the voxels that correspond to the suspension and cavity medium. All voxels in a slice that correspond to the suspension medium outside the heart are identified by executing the 2D region growing algorithm with an initial list that contains a voxel manually selected from the region outside the heart. The voxels in a slice that correspond to the medium inside the cardiac chambers are similarly identified. The green regions in Figure 2(d) illustrate the results for the representative slice. In certain slices, some of the voxels identified by the 2D region growing algorithm may belong to the myocardial tissue. This error occurs because of gaps in the detected myocardial boundary. Such gaps are manually corrected and the region growing algorithm is restarted. Finally, the suspension medium is removed from the original structural MR image by assigning the background intensity to all voxels that correspond to the medium. Figure 2(e) shows the representative slice after this procedure.

As mentioned previously, the detection of edges that is used in the suspension medium removal involves two parameters: the radius of the local neighborhood and the threshold for the variance. Figure 3 illustrates how these parameters affect the accuracy of edge detection for the slice shown in Figure 2(a), for which a radius value of 2 pixels and a threshold value of 26 detect the edges successfully. Figure 3(a) shows the edges detected using a radius value of 2 pixels, and a threshold value of 50. As indicated by the cyan arrow in the panel, there is a large gap in the edge that corresponds to the endocardial boundary. Figure 3(b) shows the edges detected using a radius value of 10, and a threshold value of 26. The edges in this panel are swollen, and the fine features of the myocardial boundary are not preserved. Thus, a threshold value that is too high results in edges with large gaps, and a radius value that is too high results in swollen coarse edges. Similarly, our experiments have shown that a threshold value that is too low results in swollen coarse edges, and a radius value that is too low results in edges with large gaps. For the data presented in this article, appropriate radius values ranged from 1 to 3 pixels, and threshold values ranged from 20 to 40.

FIGURE 3.

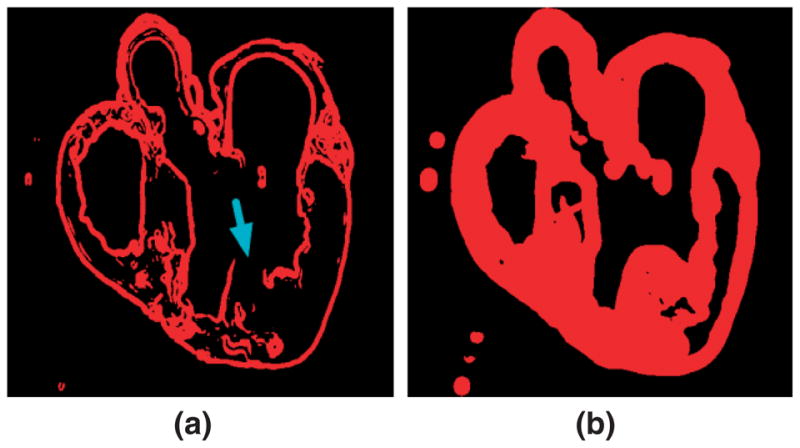
The effect of variance threshold and local neighborhood radius on edge detection: (a) edges detected using a radius value of 2 pixels and a threshold value of 50; (b) edges detected using a radius value of 10 pixels and a threshold value of 26.

The collection of 2D image slices after the removal of the suspension medium gives rise to the 3D image of the myocardium. It must be noted that the procedure retains a thin layer of the suspension medium around the myocardial boundaries because the detected edges are several voxels wide. This thin layer of suspension medium is removed using level set segmentation in the next stage of the pipeline.

Level set segmentation

In the next step, a level set method is applied to the image of the myocardium using the Seg3D software system (http://software.sci.utah.edu/SCIRunDocs/index.php/CIBC:Seg3D), to separate the larger coronary arteries and interlaminar clefts. The level set method also separates the gaps between the endocardial wall and trabeculations, and refines the myocardial boundary. Level set methods have the inherent capability to implicitly track complex topologies. This characteristic makes them highly suitable for the delineation of the complex coronary artery network and interlaminar clefts. In the level set methods, the segmentation is achieved through the evolution of a surface Γ, which is implicitly represented as the zero level set of a time-dependent 3D function Φ(x, y, z, t), i.e. Γ(t) = {x, y, z|Φ(x, y, z, t) = 0}, where x, y, z are the cartesian coordinates, and t is the time. In the implementation of the level set method, the equation for the evolution of Φ is given by:

$$\{\begin{array}{c}{\mathrm{\Phi }}_{\text{t}}=\alpha P(x,y,z)\mid \nabla \mathrm{\Phi }\mid +\beta \kappa (x,y,z)\mid \nabla \mathrm{\Phi }\mid \\ \mathrm{\Phi }(x,y,z,t=0)=\text{given}\end{array}$$ (1)

where P(x, y, z) is the propagation term, κ(x, y, z) is the mean curvature term, Φ_t is the partial derivative of Φ with respect to time, and α, β are constants whose values are determined empirically. The propagation term is defined as:

$$P(x,y,z)=\{\begin{array}{ll}I(x,y,z)-L\hfill & \text{if}I(x,y,z)<(U-L)/2+L\hfill \\ U-I(x,y,z)\hfill & \text{otherwise}\hfill \end{array}$$ (2)

where the 3D function I(x, y, z) represents the intensity values of the 3D image to be segmented, and U and L are the user-defined upper and lower intensity limits, respectively. The user defines these intensity limits by selecting a region in the input image; U and L are the highest and lowest intensities in the selected region, respectively. The propagation term forces the evolving surface to expand in the image regions where the intensity values lie between L and U; in other regions, the propagation term forces the surface to contact. The mean curvature is defined as the divergence of the gradient of Φ. Thus,

$$\kappa (x,y,z)=\nabla •\left(\frac{\nabla \mathrm{\Phi }}{\mid \nabla \mathrm{\Phi }\mid }\right)$$ (3)

The mean curvature term smoothes the evolving surface. The criteria used for selecting the value of α were evolution speed and accuracy. The evolution speed increases with α. However, large values of α result in incorrect segmentation because of the occurrence of large expansions in a single iteration. For the data used in this article, α was assigned a value of 3, which provided a good trade-off. Similarly, the parameter β was assigned a value of 1, which provided sufficient smoothness while segmenting fine structures accurately. The solution to Eq. (1) is calculated efficiently using the so-called narrow band method. For more detailed information on the level set segmentation, the reader is referred to Refs ⁵³ and ⁵⁴.

Figure 4(a) shows the user initialization of a level set segmentation, overlaid on the processed slice shown in Figure 2(e). Figure 4(b) and (c) presents the evolution of the surface near the gap between a trabeculation and the endocardial wall. Once the surface is fully evolved, the result is visually inspected and manually corrected for any errors such as incomplete rendering of vessel walls located close to the epicardial surface. Figure 4(d) illustrates the final level set segmentation for the same slice. The amount of manual work required for correcting the automatic level set segmentation was in the order of hours for the images used in this article.

FIGURE 4.

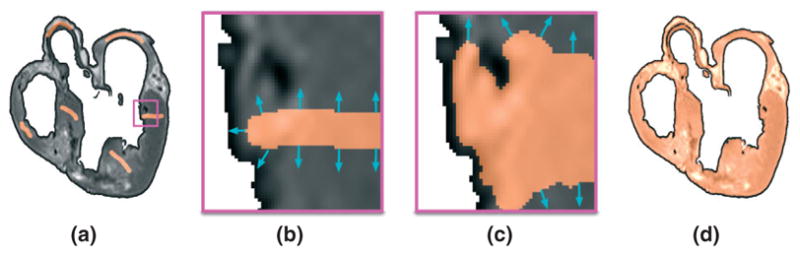
A detailed segmentation of the ventricular myocardium is obtained using a level set method: (a) user initialization of the level set segmentation; (b), (c) enlarged views of the evolution of the surface near the gap between endocardium and trabeculation in the region enclosed by the magenta box in (a); (d) final segmentation.

It must be noted that it is necessary to remove the suspension medium before the level set segmentation, because the surface may otherwise evolve (or leak) into the medium in image regions where the boundary between myocardium and medium is blurred. Figure 5 illustrates this leaking using a slice of the structural image of the normal rabbit dataset described in Table 1. Figure 5(a) shows the user initialization of the level set segmentation. Figure 5(b) shows the evolution of the surface into the suspension medium in the region enclosed by the black box in Figure 5(a). It is possible to prevent some of this leaking by increasing β, the scaling parameter for mean curvature. However, the sizes of some of the regions with blurred edges in our images are so large that the surface can smoothly evolve into the medium. Besides, increasing the value of β can prevent the surface from correctly segmenting fine structures such as interlaminar clefts and trabeculations.

FIGURE 5.

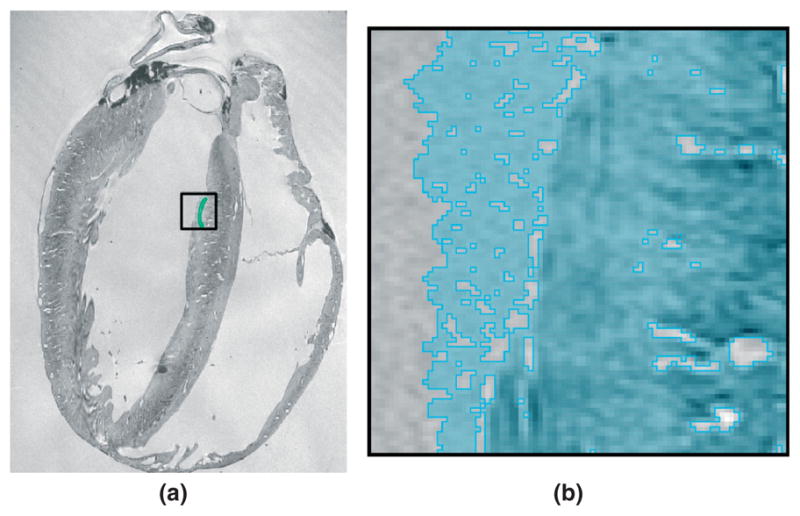
The leaking effect in level set segmentation in the image regions where the boundary between the myocardium and the suspension medium is blurred: (a) user initialization of the level set segmentation; (b) evolution of the surface into the suspension medium in the region enclosed by the black box in (a).

TABLE 1.

The Datasets

	Image Resolution (μm3)		Image Size (voxels)
Data Description	Structural MR	DTMR	Structural MR	DTMR
Normal mouse	64 × 64 × 60	128 × 128 × 500	128 × 128 × 137	64 × 64 × 17
Normal rabbit9	26.5 × 26.5 × 24.5	NA	1024 × 1024 × 1357	NA
Rabbit with cardiac infarction	61 × 61 × 60	122 × 122 × 500	512 × 512 × 507	256 × 256 × 66
Normal canine24	200 × 200 × 200 (interpolated from 300 × 300 × 800)	200 × 200 × 200 (interpolated from 300 × 300 × 800)	400 × 400 × 520	400 × 400 × 520
Canine with cardiac infarction61,62	200 × 200 × 200 (interpolated from 300 × 300 × 800)	200 × 200 × 200 (interpolated from 300 × 300 × 800)	500 × 500 × 480	500 × 500 × 480
Canine with heart failure10	200 × 200 × 200 (interpolated from 300 × 300 × 800)	200 × 200 × 200 (interpolated from 300 × 300 × 800)	500 × 500 × 612	500 × 500 × 612
Normal human63	200 × 200 × 200 (interpolated from 400 × 400 × 1000)	200 × 200 × 200 (interpolated from 400 × 400 × 1000)	550 × 550 × 670	550 × 550 × 670

Segmentation of ventricles

In the third step of our model generation pipeline, segmentation of the ventricular myocardium is performed in order to account for the presence of an insulating layer of connective tissue between the atria and the ventricles (annulus fibrosus), as well as to assign different electrophysiological properties (atrial versus ventricular) to the tissue on either side of this boundary. The AV border has a complex geometry, whose delineation requires expert knowledge in cardiac anatomy. Accordingly, we used semi-automatic method as described below.

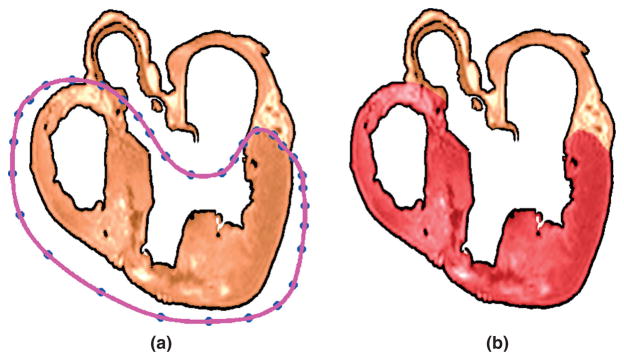
In each slice, the ventricular portion of the tissue is labeled by fitting a closed spline curve through landmark points placed around the ventricles and along the AV border. All voxels that belong to tissue inside the curve are marked as ventricular. Figure 6(a) illustrates the landmarks and the spline for the processed slice shown in Figure 4(d). Figure 6(b) presents the results after the segmentation, where the ventricular myocardium is overlaid in dark red. The identification of landmark points is performed manually for a number of slices that are evenly distributed in the image. The manual placement of the landmarks is guided by the elevated voxel intensity of the dense tissue along the AV border, the location of AV valves, and expert knowledge of overall wholeheart anatomy. The landmarks for the remaining slices are obtained by linearly interpolating the manually identified points. Note that the AV valves are not considered as part of the ventricular tissue, and the valves are not modeled separately in the present work.

FIGURE 6.

The ventricular myocardium is segmented by fitting splines through semi-automatically identified landmarks: (a) landmarks and spline for the processed slice shown in Figure 4(d); (b) segmented ventricular tissue highlighted in dark red.

Mathematically, let s₁, s₂, s₃, …, s_n denote the sequence of slices in the image, and let s_i1, s_i2, s_i3, …, s_im denote the slices for which the land-marks are identified manually, where i₁ < i₂ < i₃ < … < i_m. The number of landmarks is the same in every slice. Let p denote the number of landmarks, and let l₁, l₂, l₃, …, l_p denote the landmarks. Note that a landmark in one slice is denoted by the same index as the corresponding landmark in any other slice. If ( $x_j^{i_a},y_j^{i_a}$) and ( $x_j^{i_{a+1}},y_j^{i_{a+1}}$) are the coordinate pairs of landmark l_j on slices s_ia and s_ia+1 respectively, then the coordinates of l_j on slices s_k, i_a < k < i_a+1 are given by:

$$\{\begin{array}{l}{x}_j^k=x_j^{i_a}+\frac{(k-i_a)}{(i_{a+1}-i_a)}(x_j^{i_{a+1}}-x_j^{i_a})\hfill \\ y_j^k=y_j^{i_a}+\frac{(k-i_a)}{(i_{a+1}-i_a)}(y_j^{i_{a+1}}-y_j^{i_a})\hfill \end{array}$$ (4)

Manually identifying the landmarks on every tenth slice was sufficient for the datasets presented in this article.

Infarct segmentation

If the heart is infarcted, the infarct tissue is labeled following the delineation of ventricles. Previous experimental studies have confirmed that myocardial necrosis, the influx of inflammatory cells with a more spherical morphology, and the deposition of collagen result in less anisotropic water diffusion within the infarct region as compared to healthy myocardium.⁵⁵ Thus, any infarct tissue present is labeled using a combination of level set segmentation of the fractional anisotropy (FA) image, intensity thresholding of the anatomical image, and manual editing. In this procedure, the DTMR image is interpolated to the resolution of the structural MR image (if the resolution of the latter is higher, which is usually the case). The interpolation of the DTMR image is performed by first linearly interpolating the diffusion-weighted images to the desired resolution, and then recalculating the local DTs using existing methods.⁵⁶ From the interpolated DTMR image, the FA image is generated by computing the FA of the DT at each voxel.⁵⁷ The FA of a DT is defined as:

$$\begin{array}{l}\text{FA}=\frac{\sqrt{3}}{\sqrt{2}}\frac{\sqrt{{({\lambda }_1-\lambda )}^2+{({\lambda }_2-\lambda )}^2+{({\lambda }_3-\lambda )}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}\\ \lambda =\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{3}\end{array}$$ (5)

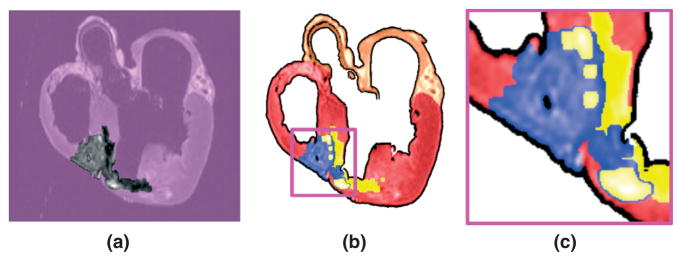
where λ₁, λ₂, and λ₃ are the eigenvalues of the tensor. The FA is a measure of the directional diffusivity of water, and its value ranges from 0 to 1. A value of 0 indicates perfectly isotropic diffusion, and that of 1 indicates perfectly anisotropic diffusion. The infarct region is characterized by lower anisotropy, and therefore lower FA values, compared to the healthy myocardium,⁵⁵ because of the myocardial disorganization in the infarct. Based on this difference in FA values, the infarct region is separated from the normal myocardium by applying a level set segmentation to the 3D FA image. Figure 7(a) illustrates the user initialization of the level set segmentation for the FA image slice that corresponds to the slice shown in Figure 2(a). Figure 7(b) presents the segmentation after the level set is fully evolved.

FIGURE 7.

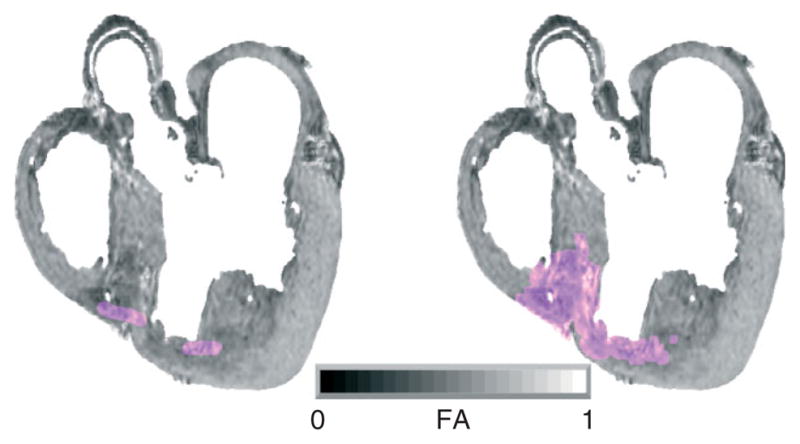
The infarct region is separated from the normal myocardium by applying a level set segmentation to the 3D fractional anisotropy (FA) image: (a) user initialization of infarct segmentation for the original FA slice; (b) segmented infarct.

Next, the infarct region is subdivided into two areas by thresholding the structural MR image based on the intensity values. Figure 8(a) shows the infarct region of the slice shown in Figure 2(a). It is evident that the infarct region incorporates heterogenous image intensities. This is because of the presence of two distinct regions within the infarct: a core scar, which is assumed to contain inexcitable scar tissue, and a border zone, which is assumed to contain excitable but pathologically remodeled tissue. The two regions are separated by thresholding the structural MR image based on the intensity values of the voxels; regions of high (>75%) and low (<25%) gray-level intensities were segmented as core scar, whereas tissue of medium intensity was segmented as border zone.^58,59 Finally, the result is visually inspected and corrections are manually applied in regions where the normal tissue was classified as infarct. For the datasets used in this article, the amount of manual intervention was small. Figure 8(b) shows the two areas superimposed on the pre-processed slice shown in Figure 6(b); yellow identifies the core, and blue shows the border zone. Figure 8(c) shows the enlarged view of a small region in Figure 8(b). The accuracy of infarct area identification is limited by the image resolution because of the volume averaging effect of the signal at the edge of the infarct tissue. Although histological measurements can achieve higher resolutions than MR, the former is more susceptible to measurement errors that arise from tissue deformation and alignment of individual slices to construct a 3D image. Once any infarct areas present are identified, segmentation of the structural MR image is complete. The final result of the segmentation is a 3D image consisting of at most four regions, namely infarct core (if any), infarct border zone (if any), normal ventricular myocardium, and the rest of the heart tissue.

FIGURE 8.

The infarct region is subdivided into two areas, core and border zone, by thresholding the structural magnetic resonance (MR) image based on the intensity values: (a) the infarct region of the slice shown in Figure 2(a); (b) the core (yellow) and border zone (blue) superimposed on the pre-processed slice shown in Figure 6(b); (c) enlarged view of the small region enclosed by the magenta box in (b).

Mesh generation

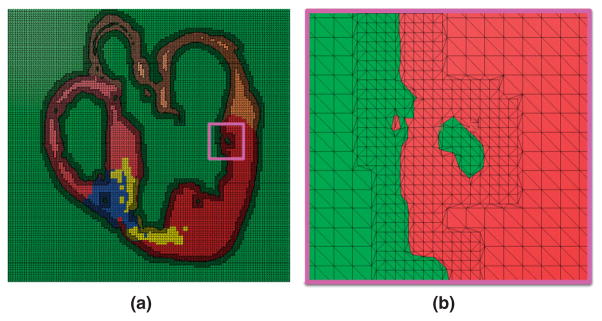
Next, a finite element mesh is generated from the segmented structural MR image using Tarantula, a commercial software (http://www.meshing.at/Spiderhome/Tarantula.html). For details regarding the mesh generation methodology as well as the examination of mesh quality metrics such as aspect ratio, skewness, maximum angle, and minimum angle, the reader is referred to a recent article.⁶⁰ The article also contains performance metrics of benchmark electrophysiological simulations and a comparison with other mesh generation techniques. The unique advantage of the software is that it can generate unstructured meshes directly from segmented images. In addition, the software is very robust, produces boundary-fitted, locally refined, smooth conformal meshes. The software uses an octree based meshing method for computational efficiency. To ensure conformal transitions between elements, an algorithm based on the dual mesh, i.e. the mesh constructed by connecting the element centers, is applied. The surface of the mesh as well as its interior is smoothed by minimizing a Laplace based local energy functional, which takes into account the shape of the surface. The meshing software allows the user to generate the region near the interface between tissue and nontissue at a higher resolution. This local adaptation of the resolution significantly reduces the number of elements in the mesh without compromising the geometric detail. The software automatically assigns region identifiers to the elements based on the segmentation, thereby differentiating the elements that belong to the infarct regions, the ventricles, or the rest of the tissue. Figure 9(a) shows a mesh generated for the processed slice shown in Figure 8(b). Figure 9(b) presents a small region of the mesh in detail. As the figure illustrates, the interior tissue volume is meshed at low resolution, whereas the interface between tissue and nontissue is refined by a factor of about two.

FIGURE 9.

Mesh generation: (a) mesh corresponding to the slice shown in Figure 8(b); (b) enlarged view of the small region enclosed by the magenta box in (a).

Fiber mapping

In the final step of the model generation pipeline, fiber orientations are mapped onto the anatomical mesh by interpolating the primary diffusion vectors on the centroids of the elements. First, a reference vector field is constructed by computing the primary eigenvector of each tensor in the previously interpolated DTMR image. This vector field is in the same coordinate system as the finite element mesh. The fiber orientation assigned to an element in the mesh is the direction of that vector in the reference field nearest to the centroid of the element. It must be noted that the two-step interpolation process correctly handles cases where two diffusion vectors that form an obtuse angle are close together, because the reference field is constructed based on the interpolation of original diffusion-weighted images, and the nearest neighbor interpolation does not involve spatial averaging of multiple vectors. Also the nearest neighbor interpolation performed here does not produce any artifacts because the spatial resolution of the reference vector field is greater than or equal to that of the mesh in all our data. Figure 10(a) shows the 2D projection, on the xz plane, of derived fiber orientations that are mapped to the mesh shown in Figure 9(a). The arrows are colored according to the y component of the diffusion vectors. Because of the transmural rotation of the fibers,^10,24,25 the arrows are lighter near the epi- and endocardial surfaces, and darker near the midwall. Figure 10(b) shows the enlarged view of a small region in the septum. As the slice shown in Figure 2(a) intersects the septum nearly at a right angle, the rotation of the fibers is evident in Figure 10(b): the arrows are longer near the surfaces, where the fibers are oriented in the base-apex direction, and shorter near midwall, where the fibers aligned with the circumferential direction.^10,24,25 Figure 10(c) shows an enlarged view of a small region in the left ventricular myocardium. The arrows are densely distributed near the surfaces, demonstrating the higher resolution of the mesh in those regions. Currently, our models do not incorporate any information on the laminar organization of the myocardial fibers, and accordingly, the models presented in this article do not incorporate orthotropy, but only rotational anisotropy. There is evidence which shows that the tertiary eigenvectors of the DTs align with the normals to the fiber sheets,^11,12,24,25 although the correspondence between the tertiary eigenvectors and sheet normals has not been proved beyond question.

FIGURE 10.

Assignment of fiber orientations: (a) 2D projection, on the xz plane, of orientations assigned to the mesh shown in Figure 9(a); (b) enlarged view of the small region enclosed by the green box in (a); (c) enlarged view of the small region enclosed by the yellow box in (a).

DATASETS AND DATA ACQUISITION

MR datasets were acquired ex vivo from seven different hearts as shown in Table 1. Both the structural MR and DTMR images were acquired for all cases except the normal rabbit, for which only the high-resolution structural data were available. All hearts were fixed in diastole. The normal rabbit, three canine, and normal human datasets have been used in previous studies,^{9,10,24,61–64} where data acquisition techniques have been described. The infarcts in the rabbit and canine hearts were 4 weeks old and induced, respectively, by occlusion of the posterolateral division of the left coronary artery⁶⁴ and the left anterior descending coronary artery.^61,62 The heart failure dataset was obtained from the canine after radiofrequency ablation of the left bundle branch, followed by 3 weeks of pacing-induced tachycardia.¹⁰ The canine datasets were originally scanned at a native resolution of about 300 × 300 × 800 μm³, and used for statistical analysis of cardiac anatomy.^10,24,25 These datasets were subsequently interpolated by the original authors to the resolution given in Table 1. The human dataset was similarly interpolated from an original native resolution of about 400 × 400 × 1000 μm³ (see Ref 63); see Table 1 for final resolution.

To acquire the normal mouse and infarcted rabbit hearts, the hearts were isolated after anesthesia, washed by coronary perfusion, and fixed using previously reported methods for imaging similar hearts.^55,65 Structural MR imaging experiments were performed on an 11.74 T Varian UNITY-INOVA spectrometer (Varian Associates, Palo Alto, CA, USA), equipped with an 8 cm inner diameter gradient insert (maximum gradient strength = 120 G/cm). To increase contrast and minimize susceptibility artifacts, the hearts were embedded into 2% (w/w) agarose gel, which has been widely used to construct ‘tissue equivalent’ MRI phantoms.⁶⁶ Briefly, the agarose gel was diluted in boiled distilled water. After the temperature of the agarose solution dropped to about 50 degrees, the heart was immersed in the solution and the ventricles were injection-filled with the agarose solution using a syringe. Care was also taken to remove any visible air-bubbles attached to the heart surface. The heart was left in the solution until it finally turned into gel form at room temperature. The rabbit and mouse hearts were imaged with a 4 and 1 cm birdcage radiofrequency coils, respectively. Scout images were acquired using a standard spin echo sequence to determine multiple sets of interleaved imaging slices covering the entire heart. A standard gradient-echo sequence was used to acquire structural MR images. Acquisition parameters were (for rabbit/mouse hearts, respectively) repetition time, 1.0/1.2 s; echo time, 13/8 ms; field of view, 3.1 × 3.1/0.82 × 0.82 cm²; data matrix, 512 × 512/128 × 128; resolution, 61 × 61 × 60/64 × 64 × 60 μm³; number of averages, 8/32; sets of interleaved images, 10/3; total image acquisition time, 11.3/4 h. A spin-echo sequence incorporating a pair of diffusion sensitizing gradients was used for the DTMR imaging. Acquisition parameters included repetition time, 1.3/1.3 s; echo time, 42/31 ms; diffusion-weighting time, 20/15 ms; diffusion gradient on time, 5/5 ms; b-value, 840/792 s/mm²; field of view, 3.1 × 3.1/0.82 × 0.82 cm²; data matrix, 256 × 256/64 × 64; resolution, 121 × 121 × 200/64 × 64 × 500 μm³; number of averages, 4/32; sets of interleaved images, 2/1; total image acquisition time, 9.6/9.6 h. For each DTMR imaging experiment, a nondiffusion-weighted image and six diffusion-weighted images were acquired with diffusion weighting gradients applied in six directions.⁵⁵ To minimize the background magnetic field gradient effects on the diffusion measurement, a pair of diffusion-weighted images was acquired in each direction with positive and negative diffusion gradients, respectively.⁶⁷

EXAMPLES OF WHOLE-HEART MODELS

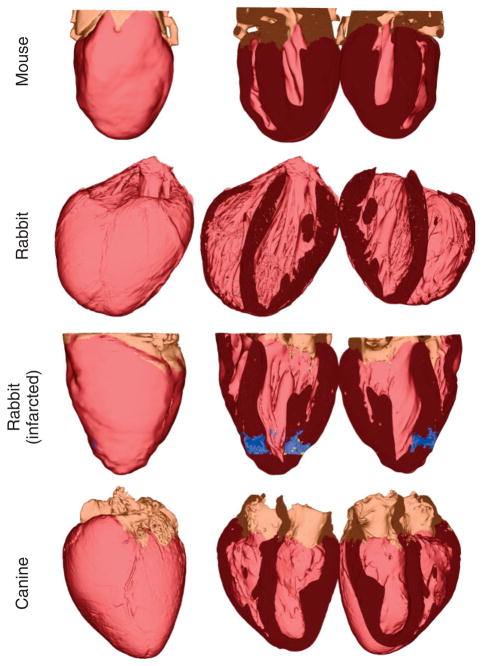
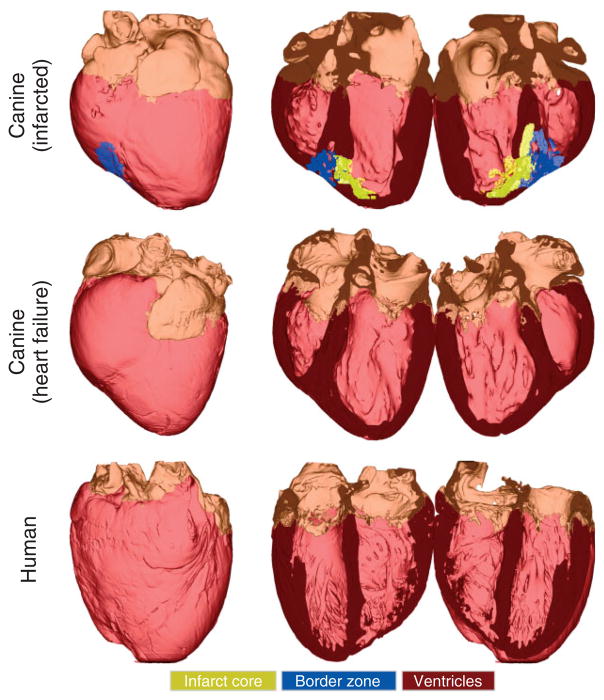
Models were generated from high-resolution 3D images of the seven animal hearts (see Table 1). Figures 11 and 12 show the generated whole-heart models. In each row, the first column shows the anterior view of the entire organ model, and the second and third columns show the model split open along the horizontal long axis view plane.⁶⁸ Ventricles, infarct cores, and border zones are shown in dark red, yellow, and blue, respectively. In the normal rabbit heart dataset, the atria had collapsed in the process of data acquisition, which necessitated the removal of all tissue that does not belong to the ventricular myocardium. The developed methods have reconstructed the overall geometries of the hearts. Figures 11 and 12 qualitatively show that the gross anatomy of the whole heart varies from one species to another. A quantitative analysis of such differences can be performed using techniques of computational anatomy.^49,69–72 Table 2 provides the sizes and the average resolutions of the models. Note that the resolution of a model can be altered by appropriately defining the input parameters for mesh generation. However, given the resolution of the image data, our models cannot resolve structures which are smaller than 10⁻⁴ m, such as the smaller blood vessels and laminar clefts. Such unresolved structures are represented using an averaged description in the computational framework.

FIGURE 11.

The generated models for normal mouse, normal rabbit, infarcted rabbit, and normal canine hearts. In each row, the first column shows the anterior view of the entire model, and the second and third columns show the model split in half along a horizontal long axis view plane.

FIGURE 12.

The generated models for infarcted canine, canine with heart failure, and normal human hearts. In each row, the first column shows the anterior view of the entire model, and the second and third columns show the model split in half along a horizontal long axis view plane.

TABLE 2.

The Sizes and the Resolutions of the Meshes

Model Description	Number of Vertices	Number of Elements	Average Edge Length (μm)
Normal mouse	614,193	829,503	210
Normal rabbit	22,820,440	31,005,031	51
Infarcted rabbit	702,729	963,853	236
Normal canine	7,314,367	9,929,860	218
Infarcted canine	11,309,592	15,304,323	221
Canine with heart failure	15,907,936	21,564,917	221
Normal human	21,902,184	29,673,683	220

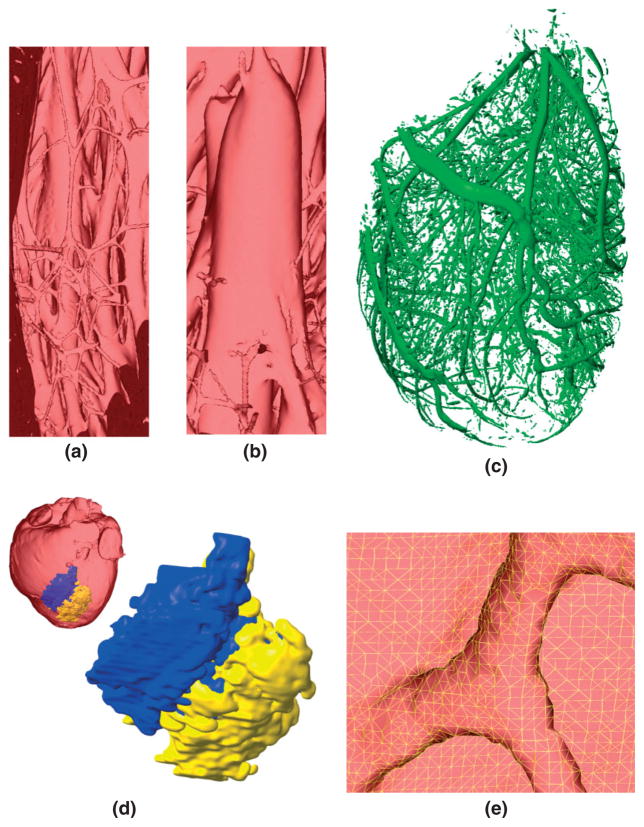
Figure 13(a) shows an enlarged view of the muscular trabeculations in the apical region of the left ventricular chamber in the normal rabbit model. Figure 13(b) presents a papillary muscle that is attached to the mitral valve in the normal rabbit model. Figure 13(c) shows the extracted coronary vessels and interlaminar clefts in the normal rabbit model. As mentioned previously, the vessels, clefts, and the gaps between the endocardium and trabeculations are separated from the rest of the myocardium during the level set segmentation of the myocardium. In the level set segmented image, these three structures are represented by the same image intensity. Accordingly, the models generated using our methods do not distinguish between the three structures. For the purpose of generating Figure 13(c), an image of only the vessels and clefts was constructed by manually eliminating the gaps between the endocardium and trabeculations from the level set segmented image. In the simulations, the vessels, clefts, suspension medium, and gaps between trabeculations and endocardium are assigned the same material properties, which are different from the properties of the myocardial tissue. The reconstruction of the papillary muscles and of the complex network of trabeculations, arteries, and interlaminar clefts illustrates the high resolution of the structural detail that can be obtained using the methods developed here. Incorporation of these geometric heterogeneities in cardiac models is important as these structures could affect the spatiotemporal dynamics of propagating fronts, particularly those involved in reentrant circuits. For example, trabeculations provide alternate pathways for propagating wavefronts that promote arrhythmogenic activity in the atria and ventricles.^73,74 Similarly, papillary muscles have been shown to stabilize reentrant activity that drives fibrillation.^75,76 An important structural detail which our models currently do not incorporate is the Purkinje fiber network. There have been efforts to automatically reconstruct the free-running Purkinje network from MR images using nonlinear filtering,⁷⁷ and such reconstructions of the network can be added to our models. Reconstruction of the endocardial Purkinje system, i.e. the part of the Purkinje system that overlays the endocardium, still remains a problem as these cells cannot be discriminated with MR imaging. One solution is to use staining techniques, and this requires the cutting open of the ventricles for staining and imaging, and reconstruction of the 3D object from the 2D images. However, note that the level of detail which models should incorporate depends on the problem that will be simulated and hypothesis that will be tested. Our methods are applicable regardless of the resolution of the images, and capable of constructing models with coarse as well as fine resolutions. Note that the level of detail which is necessary to resolve microscopic structures such as interlaminar clefts can, at present, be achieved only in hearts that are small enough to fit in the bore of a high field strength (~11.7 T) MR scanner.

FIGURE 13.

Demonstration of the structural detail that can be obtained using our processing pipeline: (a) the endocardial trabeculations in the apical region of the left ventricle in the normal rabbit model; (b) a papillary muscle that is attached to the mitral valve of the normal rabbit model; (c) blood vessels and interlaminar clefts in the normal rabbit model; (d) 3D view of the infarct in the canine model; (e) enlarged view of the mesh near the insertion point of a trabeculation in the apical region of the normal rabbit model.

In addition to geometric heterogeneities, the methods that we have presented also accurately represent the structural modeling within the heart as a result of disease. Figure 13(d) shows the enlarged view of the infarct region in the canine model. The inset in Figure 13(d) shows the location of the infarct in the whole-heart model. Note that the infarct core and border zone are interdigitated as shown in Figure 8(c), with regions of border zone traversing the core in a tortuous way. This interdigitation is not visible in Figure 13(d), because the surface view of the extensive epicardial region of the core obscures channels of border zone within the core. Identifying the role of infarct geometry and composition in reentry formation and maintenance is of clinical importance as such knowledge could aid in eradicating the arrhythmogenic substrate.⁷⁸ Figure 13(e) shows the enlarged view of the mesh near the insertion point of an endocardial trabeculation in the apical region of the normal rabbit model. The figure illustrates that the meshing algorithm retains fine structures, simultaneously producing well-shaped finite elements.

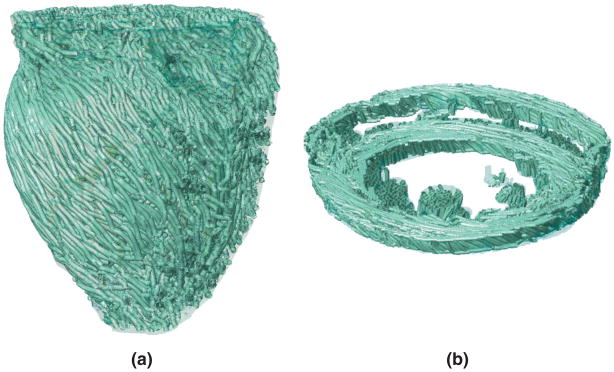
Visualization of the 3D arrangement of fiber orientations in the heart is a challenging problem. A common solution is to use the so-called streamlining method.⁶³ In this method, fiber orientation is displayed as a track, which is traced by moving a particle according to the velocity field defined by the primary diffusion vectors. To obtain a smooth visualization, it is important to remove measurement noise by filtering the velocity field. To do so, we used a locally regularizing filter called the Perona–Malik nonlinear anisotropic filter.⁷⁹ Figure 14 displays the primary eigenvector tracks for the infarcted rabbit model, both in the ventricles and in the atria. The fibers are oriented in the base-apex direction near the epi-and endocardial surfaces, and in the circumferential direction near the midwall. On the epicardial surface, the fibers form a counterclockwise helix, whereas on the endocardial surface, they form a clockwise helix. The fibers are aligned in the axial direction in the papillary muscles. A visual comparison of the tracks with existing anatomical data^25,80 verifies the qualitative correlation of the fiber orientations in these models. The fiber orientations delineated using DTMR data reflect the mean orientation of the group of myocytes located in individual image voxels. Thus, it is not possible to delineate the orientation of a single myocyte with DTMR, and the accuracy of the measured fiber orientations in both ventricles and atria is proportional to the resolution of the DTMR image. However, the DTMR measurement is sufficiently accurate because myofiber orientations vary smoothly across the transmural wall. During simulations, the electrical propagation and mechanical contraction of the models are directly linked to the fiber orientations that are measured using DTMR imaging.⁸¹

FIGURE 14.

Visualization of fiber tracks, indicative of regionally prevailing cell orientation, in the infarcted rabbit model: (a) epicardial view of tracks in the entire model; (b) tracks in a slab of tissue between two short axes planes.

As the results demonstrate, the presented methods successfully generate species-specific models of cardiac geometry and fiber architecture. The methods described here are applicable to any anatomical MR or DTMR dataset of the heart, and can be used to reconstruct both atrial and ventricular geometry and structure. The reconstructed models offer hitherto unavailable structural detail, heralding enhanced opportunities for modeling cardiac function. The models presented in this article overcome a number of limitations and drawbacks of previous attempts to construct the detailed cardiac histoanatomy. The models retain fine details of the cardiac geometry, such as endocardial trabeculations, and incorporate fiber data measured at resolutions in the order of 10⁻⁴ m. In particular, these models are the first that contain measured fiber orientations in the atria. The AV boundaries in these models were identified, and the ventricular portions were separated from the rest of the tissue. The models were meshed using an advanced algorithm, which generates smooth finite element representations of cardiac geometries, while keeping the number of elements low enough such that simulations are computationally tractable. For example, it takes about 5.6 s to simulate 1 ms of activity of the infarcted canine model using the monodomain formulation and 16 nodes of our Linux cluster, where each node is equipped with four Dual-Core AMD Opteron processors and 8 GB of memory. These models are among the first in a new generation of highly detailed cardiac reconstructions; those that contain DTMR-based realistic fiber orientation information have ventured into unchartered territory. Indeed, the model of the infarcted canine heart has already been used in electrical simulation studies, which revealed a possible explanation for the observation that the border zone of an infarct frequently acts as the site of arrhythmia initiation and maintenance.^62,82 The normal and infarcted rabbit models have been used for the study of arrhythmia and defibrillation.^13,14 The pipeline that we have created to construct the models is generic, and therefore can be applied to image stacks from a variety of imaging modalities.

A limitation of the proposed pipeline is the amount of time required for model generation. Currently, this time is in the order of days, a significant portion of which is spent for the manual intervention that is required during segmentation. Reducing the amount of manual labor will be a direction for future development. Also, while MR data is sufficient to build models that can be used to study the effects of structures such as endocardial trabeculations¹³ and myocardial infarct⁸² in cardiac function, other studies such as investigation of fibrosis require data from alternative sources, in particular, histology. Plank et al. have recently demonstrated how MR data can be combined with histological data for the purpose of generating whole-heart models.³ Building on this earlier work, a direction for our future research will focus on accurate co-registration of histological and MR data.

CONCLUDING REMARKS

This article presents a review of the previous efforts to construct computational models of the heart, and describes a processing pipeline which we have developed for constructing species-specific models of cardiac structure from high resolution 3D structural MR and DTMR images ex vivo. The processing pipeline was applied to construct models of normal mouse, rabbit, canine, and human hearts; of infarcted rabbit and canine hearts; and of a failing canine heart. The generated models provide novel tools with unprecedented structural detail for simulation of cardiac electromechanical behavior, and overcome a number of limitations and drawbacks of previous attempts to construct the detailed cardiac histoanatomy.