Abstract
The level of genetic variation in a population is the result of a dynamic tension between evolutionary forces. Mutations create variation, certain frequency-dependent interactions may preserve diversity, and natural selection purges variation. New sequencing technologies offer unprecedented opportunities to discover and characterize the diversity present in evolving microbial populations on a whole-genome scale. By sequencing mixed-population samples, we have identified single-nucleotide polymorphisms present at various points in the history of an Escherichia coli population that has evolved for almost 20 years from a founding clone. With 50-fold genome coverage we were able to catch beneficial mutations as they swept to fixation, discover contending beneficial alleles that were eliminated by clonal interference, and detect other minor variants possibly adapted to a new ecological niche. Additionally, there was a dramatic increase in genetic diversity late in the experiment after a mutator phenotype evolved. Still finer resolution details of the structure of genetic variation and how it changes over time in microbial evolution experiments will enable new applications and quantitative tests of population genetic theory.
Several next-generation platforms capable of sequencing more than a billion DNA bases in a single run have recently become commercially available (Mardis 2008), and more are under development (Gupta 2008). The compact genomes of microorganisms put them at the forefront of efforts to open new windows on the study of genetic diversity and evolution using the massive throughput of these technologies. Metagenomic surveys that profile the species abundance and metabolic composition of microbial communities by sampling environmental DNA (Vieites et al. 2009) can also be used to infer some population genetic parameters in nature (Johnson and Slatkin 2006). Population genomic approaches have begun to fill in our knowledge of sequence diversity among isolates of a single species and between closely related species. For example, one study characterized the patterns of genome-wide mutational variation in yeasts and reconstructed details of their life history since domestication from next-generation sequencing data (Liti et al. 2009). Ultra-deep sequencing of genes from viruses such as HIV has even begun to reveal patterns of within-host diversity during infections, including subpopulations with drug-resistance mutations (Wang et al. 2007; Eriksson et al. 2008).
We are interested in how these new technologies can be used to better understand evolutionary processes and advance population genetic theory in the context of experiments with microorganisms (Elena and Lenski 2003; Kassen and Rainey 2004; Buckling et al. 2009). Evolution experiments have the advantage over studies of natural and clinical populations that they take place under laboratory conditions where environmental conditions and sampling regimens are rigorously controlled. To date, whole-genome re-sequencing has mainly been used to find the beneficial mutations in "winning" clones isolated at the end of bacterial evolution experiments. For example, next-generation sequencing platforms were used to identify a single mutation responsible for the re-acquisition of social swarming in a population of Myxococcus xanthus that previously lost that capacity (Fiegna et al. 2006) and several mutations that improve the growth of E. coli in a glycerol-based medium after 44 days of continuous culture (Herring et al. 2006). Next-generation platforms have not yet been used to examine the genetic variation present in these populations and how that diversity changes over time.
The frozen "fossil record" of a long-term experiment with E. coli spanning almost 20 years and 40,000 generations of evolution provides a unique opportunity for exploring these issues (Lenski and Travisano 1994). In this experiment, 12 populations of E. coli were founded from the same ancestral strain and maintained by the daily transfer of 1% of each culture into fresh glucose minimal media. After years of intensive study, a great deal is known about the fitness trajectories, phenotypic changes, and beneficial mutations that occur in this environment (Lenski 2004; Philippe et al. 2007). We have recently re-sequenced E. coli clones isolated at different time points from one of these populations to examine the coupling between the rates of genomic evolution and adaptation to the environment (Barrick et al. 2009). We found that fitness increased dramatically during the first 20,000 generations of the experiment, but that new mutations accumulated at a near-constant rate during this time. This result was surprising because a clock-like accumulation of mutations is usually taken as a signature of neutral evolution, yet several lines of evidence indicate that most of these mutations are beneficial.
These clone genomes offer only a fragmentary picture of the history of this E. coli population. Knowledge of the details of the ebb and flow of genetic diversity could potentially reveal how the population’s adaptive trajectory was influenced by selective sweeps driving mutations to fixation, beneficial mutations that transiently accumulated but were ultimately unsuccessful, changes in mutation rates, and ecological interactions between divergent lineages. Here, we show that it is possible to identify mutational variants in mixed bacterial population samples and follow these processes on a genome-wide scale with current DNA sequencing technologies.
MATERIALS AND METHODS
DNA samples
During the long-term E. coli evolution experiment, mixed-population samples (M) and clones (C) isolated from these populations were periodically frozen at −80°C in 15% (w/v) glycerol. We revived clones from traces of frozen cultures by growing them overnight (16–24 h) as 10-ml cultures in 50-ml Erlenmeyer flasks at 37°C with shaking at 120 rpm in LB media, and mixed populations from 100 µl of frozen sample under the same conditions except in Davis minimal medium supplemented with 2 mg/L glucose. Genomic DNA was harvested and purified from several milliliters of each culture using a Qiagen Genomic-tip 100/G kit. Any deviations in the frequencies of mutations in DNA samples from the source populations due to these revival and re-culturing steps appear to be minor.
Genome re-sequencing
We sequenced DNA fragment libraries derived from these samples on Genome Analyzer systems (Illumina, San Diego, CA) in two separate runs. Clones were sequenced as paired-end libraries on a Genome Analyzer 1G machine by Macrogen (Seoul, South Korea), and mixed-population samples were sequenced in an unpaired library format using a Genome Analyzer 2G system by the Research Technology Support Facility at Michigan State University (East Lansing, MI). Both devices generate 36-base reads, and the overall number of bases obtained for each sample was roughly equivalent. Per-base quality scores were calibrated on the basis of alignments to the genome sequence of the ancestral E. coli B strain REL606 using the standard Illumina re-sequencing pipeline.
Read alignment
We aligned reads from each dataset to the ancestral genome using MUMmer v3.20 (Kurtz et al. 2004). Only reads where the entire 36-base length mapped with no base insertions or deletions and at most one base mismatch with respect to the reference genome were analyzed, because reads with indels or multiple discrepancies are more likely to be mapped incorrectly and may exhibit different error signatures. We also restricted our attention to "unique-only" reference genome positions, where all of the bases that mapped to a given position came from reads matching only a single site in the reference genome. It is not as straightforward to predict and interpret polymorphisms in repeat regions and sites on their periphery, where a mixture of reads uniquely and degenerately map to a position.
Base error model
For each dataset, we created a null model that gives the probability of observing each of the four possible bases in a read, given the quality score assigned to that base and the identity of the base that was sequenced in the reference genome. We estimated the values in this series of 4×4 matrixes directly from the observed counts of base discrepancies. This simple empirical strategy, which neglects the presence of real mutations, is justified because the vast majority of base mismatches are due to sequencing errors. The maximum number of point mutations found in the clone samples was 627 at generation 40,000 (Barrick et al. 2009). Assuming average coverage of these sites, this means only 2.4% of the mismatches in this dataset are due to consensus mutations. If the same number of base mismatches were due to mutations in the 40,000-generation mixed-population sample and they all had the highest quality score typically found in this dataset, they would still raise the inferred error rate by only 2-fold. As the sensitivity analysis shows (see below), a change in the error rate of this magnitude barely alters our ability to discover SNPs. Thus, this simple error rate estimate should suffice. For a given quality score and reference base, there is typically at most 2- or 3- fold variation among the inferred rates of each of the three possible base errors.
SNP prediction
To predict SNPs, we began by identifying the two most common bases aligned to each reference position. We then used a likelihood ratio test to decide between the null hypothesis that the underlying population had only the most common base at this position and the alternative hypothesis that the population contained a mixture of alleles at this site. The probability of the observed data given the null hypothesis was calculated from the identities of the aligned bases, their quality scores, and the error model. The maximum likelihood of the alternative hypothesis was determined by scanning prospective mixtures of the two bases at 0.1% intervals. Twice the negative logarithm of the ratio between the two likelihoods was then compared to a χ2 distribution with one degree of freedom to calculate a p-value for rejection of the null hypothesis of no polymorphism. Finally, we multiplied each p-value by the number of sites with unique-only coverage in the genome to obtain an E-value that reflects the number of SNP predictions expected to have this level of significance by chance.
For individually significant SNPs, we estimated the maximum likelihood frequency of the mutated allele in the underlying population. For this calculation, we only considered observations of the two most frequent bases. We performed 105 simulations of each alignment column at underlying base compositions in 0.1% intervals and recorded the underlying allele frequency that generated the actual mixture of bases at each site with the maximum likelihood, taking into account the chances of sequencing errors between these two bases.
When applied to the clone genomes, this procedure discovered all known point mutations outside of repeat regions as sites where a majority of the observed bases correspond to the new allele and there is no prediction of a polymorphism. Some spurious SNP predictions arose because the underlying genomic structure had changed due to large deletions or IS insertions, but whole reads reflecting this changed sequence still aligned to the reference genome with one or fewer mismatches. We therefore manually eliminated, from all samples, SNP predictions adjacent to examples of these changes identified previously in clone genomes.
Bias filtering
We further rejected SNP predictions when bases supporting the mutant allele had consistently low quality scores or reads supporting the mutant allele showed a strand bias. To test for quality score bias, we performed a Kolmogorov-Smirnov test for the one-sided hypothesis that the quality scores supporting the mutant allele were lower than those supporting the ancestral base at that position. To test for strand bias, we performed Fisher's exact test on the two-tailed hypothesis that the distributions of mutant and reference base observations in reads on each genomic strand were different. Finally, we combined the p-values from these two independent tests using Fisher's method, and we rejected those predicted SNPs for which there was <5% chance of observing these differences in signature between the mutated and ancestral alleles by chance alone.
Sensitivity analysis
We performed the SNP prediction procedure without bias filtering on two sets of simulated data in order to estimate the chances of discovering SNPs at various frequencies. In the first set, we fixed the proportion of the mutant allele over a range of values, then resampled alignment columns according to the coverage and quality score distributions observed in the 2,000-generation mixed-population data. Observations were also subject to a simplified error model where the overall chances of error for each quality score were the same as in the sample, but the probabilities of all base errors were made equal. In the second set of simulations that explores limits on rare SNP detection, all resampled alignments were uniformly assigned the same coverage and all bases had the same error rate.
RESULTS
Expectations of diversity in an evolving bacterial population
The E. coli populations in the long-term evolution experiment were each founded from a genetically homogeneous clone. No plasmids, viruses, or other mechanisms for horizontal gene exchange are present in the populations, and they evolve in a strictly clonal (asexual) manner. How quickly do we expect measurable diversity to accumulate in one of these populations, and what evolutionary forces will impact the patterns of variation within a population over time?
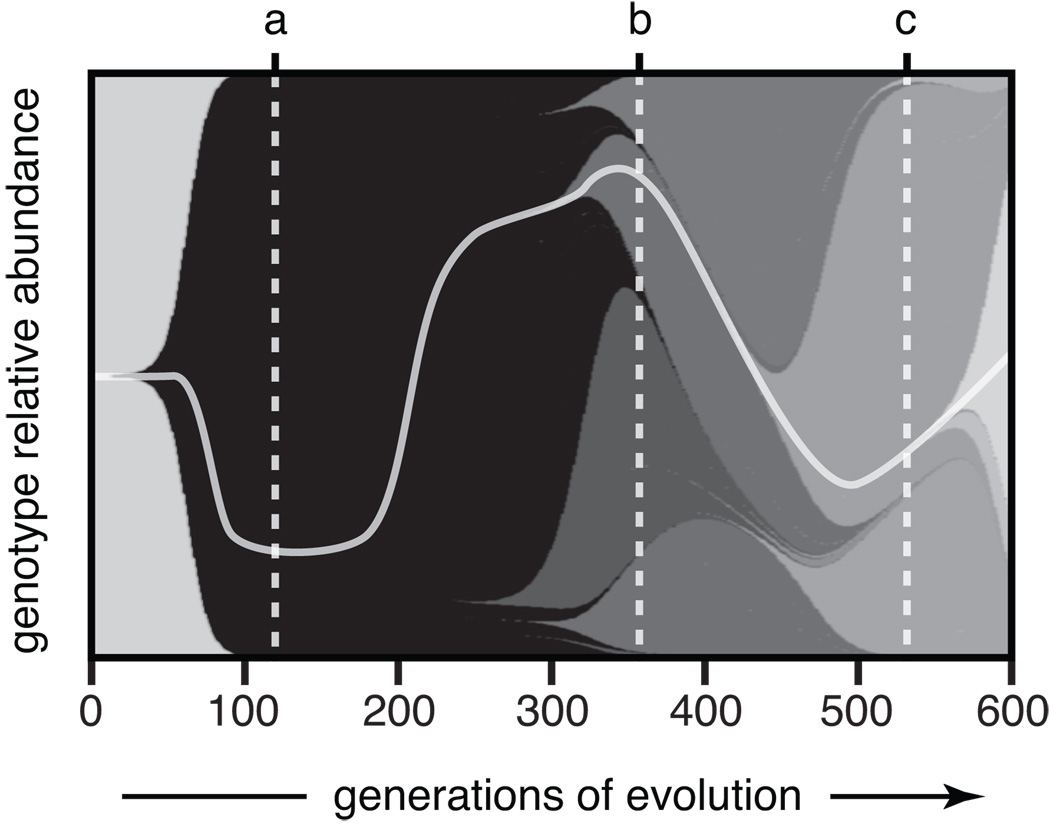
Figure 1 shows a numerical simulation of the spread of beneficial mutations in a population with parameters similar to the E. coli long-term evolution experiment (Woods 2005). Many beneficial mutations will be lost to drift when they are rare (Lenski et al. 1991), with only those that achieve substantial frequency visible in the evolving frequency distribution. Among those that survive drift, some will eventually fix, but others will be eliminated by clonal interference (Gerrish and Lenski 1998). In some cases, the winning lineage may be decided not by the effects of single beneficial mutations, but rather by the combined effects of multiple mutations that accumulate before any one lineage is fixed (Fogle et al. 2008). Note that diversity does not increase monotonically, but rather it waxes and wanes as new beneficial mutations take hold and their fates are resolved by selection.
Figure 1. Expected dynamics in an evolving bacterial population.
Lineages with new beneficial mutations are depicted as shaded wedges that originate in a previous genetic background and rise in frequency as they outcompete their ancestor and other lineages (Muller 1932). The same shading indicates lineages have equivalent fitnesses, and the path to the final dominant genotype containing five mutations is highlighted by the light gray curve. This figure was produced using a simulation with population size and mutation parameters meant to model the first 600 generations of the E. coli long-term evolution experiment (Woods 2005). Notice how the level of genetic diversity changes over time. Early on, a new beneficial mutation sweeps to fixation and the population has little diversity (a). Later, four lineages with different mutations coexist at appreciable frequencies for a time (b) before the descendants of one lineage become a majority (c).
As beneficial mutations spread, they will perturb the frequencies of neutral and deleterious mutations owing to linkage disequilibrium in an asexual population. These perturbations are the classic signature of periodic selection (Atwood et al. 1951). However, we do not expect to detect many neutral or deleterious mutations in the evolution experiment. Under a pure drift process, the number of generations required for a neutral mutation to drift to fixation is on the order of the population size (Kimura 1983), which is many millions even after accounting for the bottlenecks during serial transfers (Lenski et al. 1991). Selective sweeps, however, reduce the effective size so that a rare neutral mutation may hitchhike to fixation much faster than it can spread by pure drift, although the vast majority of neutral mutations will be purged by these sweeps. In this case, the expected number of neutral mutations that fix equals the product of the genomic mutation rate, the proportion of neutral sites, and the number of generations (Kimura 1983). For E. coli, the genomic mutation rate is on the order of 10−4–10−3 per generation (Lenski et al. 2003), and perhaps 50% of sites are neutral, so we expect it to take on the order of 2,000–20,000 generations for even one neutral mutation to fix in the population. It is unlikely, therefore, that many neutral mutations would reach high frequency in the first few thousand generations of evolution. Deleterious mutations will fare even worse. Mutations causing extreme fitness defects will be rapidly be lost from the population. A pool of many slightly deleterious mutations may accumulate and persist at mutation-selection balance, but these mutations are less likely to fix or reach high frequency than neutral ones.
If the genomic mutation rate were much higher, however, then neutral and weakly deleterious alleles could spread more easily and more would potentially reach high frequency. Several populations in the long-term experiment evolved mutator phenotypes, leading to mutation rates roughly two orders of magnitude higher than the ancestral rate (Sniegowski et al. 1997). In fact, a mutT mutator phenotype evolved in the population studied here, making its first appearance by generation 26,500 and becoming numerically dominant by generation 29,000 (Barrick et al. 2009).
Other polymorphisms may evolve and be maintained by negative-frequency-dependent interactions, in which some genotype has a selective advantage when rare but is disadvantaged at high frequency. Acetate and short chain fatty acids are byproducts of glucose fermentation by E. coli. These compounds are normally excreted during growth on glucose, then reabsorbed and used after the glucose is depleted. Mutants that are better competitors for acetate have been observed to evolve and persist via frequency-dependent selection in some chemostat experiments with E. coli (Rosenzweig et al. 1994). The low concentration of glucose and serial-transfer regime used in the long-term experiment lead to low cell densities and correspondingly low levels of excreted metabolites, so that cross-feeding genotypes should be rarer and harder to detect. Indeed, a sustained cross-feeding interaction is only known to have evolved in one of the long-term populations (Rozen and Lenski 2000; Rozen et al. 2005; Rozen et al. 2009), and not the one that is the focus of our study, although there appear to be weaker frequency-dependent interactions in some other populations (Elena and Lenski 1997).
Mixed-population sequence datasets
We examined the genetic diversity over time in one experimental line from the long-term E. coli evolution experiment (designated Ara-1) by sequencing whole-population samples from 2,000 (M2K), 5,000 (M5K), 10,000 (M10K), 15,000 (M15K), 20,000 (M20K), 30,000 (M30K), and 40,000 (M40K) generation time points. Clones that were the subject of a previous study (Barrick et al. 2009) serve as controls for the mixed-population analysis. These clones were isolated from the same population at 2,000 (C2K), 5,000 (C5K), 10,000 (C10K), 15,000 (C15K), 20,0000 (C20K), and 40,000 (C40K) generations. We also include the founder of the Ara+1 experimental population that differs by two point mutations from the ancestor of the Ara-1 line (C0K).
Clones and mixed-population samples were sequenced, one per lane, in two separate runs of the Genome Analyzer system. Alignment of the resulting 36-base reads to the ancestral sequence yielded 40- to 60-fold average coverage outside of repeat regions for each genome (Table 1). Positions with zero coverage are not counted in these estimates, as they almost always proved to represent true deletions relative to the ancestral sequence in clone genomes (Barrick et al. 2009). The ancestral clone (C0K) has at least 10-fold read coverage at 99.9% of the positions in the reference genome. The decrease in the number of sites with coverage at later generations in both the clone and mixed-population samples is consistent with sizable deletions becoming fixed in the population.
Table 1. Dataset statistics and SNP prediction summary.
Bacterial clone (C) and mixed-population samples (M) from different generations of the Ara-1 population of the long-term E. coli evolution experiment were sequenced on Genome Analyzer systems. Each dataset had the specified number of positions with coverage only from reads with unique best matches to the ancestral genome; mean (μ) and index of dispersion (σ2/μ) for the distribution of read coverage depth at these unique-only positions; and number of base mismatch errors in reads with a unique best alignment to the ancestral genome. The numbers of SNPs predicted by our procedure using a E–value cutoff of one and after further filtering out predictions with biased base quality score and strand distributions are also reported for each sample. Ratios of non-synonymous to synonymous substitutions are shown in parentheses.
| Sample | Unique-only positions |
Coverage | Base errors |
SNP predictions (dN/dS) | ||||
|---|---|---|---|---|---|---|---|---|
| μ | σ2/μ | E-value ≤ 1 | Bias filtered | |||||
| clone samples | ||||||||
| C0K | 4,475,960 | 40.2 | 3.1 | 1,282,378 | 22 | (17/3) | 8 | (6/2) |
| C2K | 4,469,732 | 45.1 | 3.2 | 1,332,415 | 29 | (18/5) | 5 | (3/0) |
| C5K | 4,468,358 | 53.5 | 3.6 | 1,497,884 | 38 | (25/9) | 7 | (4/3) |
| C10K | 4,441,204 | 51.8 | 3.3 | 1,366,094 | 47 | (37/4) | 5 | (5/0) |
| C15K | 4,442,023 | 52.3 | 3.4 | 1,248,779 | 51 | (38/11) | 2 | (1/1) |
| C20K | 4,441,245 | 48.0 | 3.2 | 1,252,909 | 42 | (30/9) | 7 | (5/1) |
| C40K | 4,411,765 | 53.8 | 3.4 | 1,394,982 | 53 | (33/13) | 8 | (4/2) |
| mixed-population samples | ||||||||
| M2K | 4,476,202 | 54.2 | 4.1 | 702,687 | 59 | (51/3) | 7 | (7/0) |
| M5K | 4,476,629 | 56.7 | 3.6 | 716,580 | 70 | (46/10) | 5 | (4/1) |
| M10K | 4,465,577 | 57.4 | 4.3 | 688,297 | 117 | (71/25) | 20 | (10/1) |
| M15K | 4,469,198 | 58.7 | 4.2 | 667,182 | 115 | (72/24) | 19 | (12/0) |
| M20K | 4,443,151 | 40.6 | 4.4 | 776,788 | 34 | (22/3) | 6 | (4/1) |
| M30K | 4,444,156 | 52.1 | 4.5 | 720,115 | 415 | (314/50) | 364 | (270/46) |
| M40K | 4,449,187 | 58.3 | 5.5 | 611,554 | 1150 | (817/167) | 1062 | (754/148) |
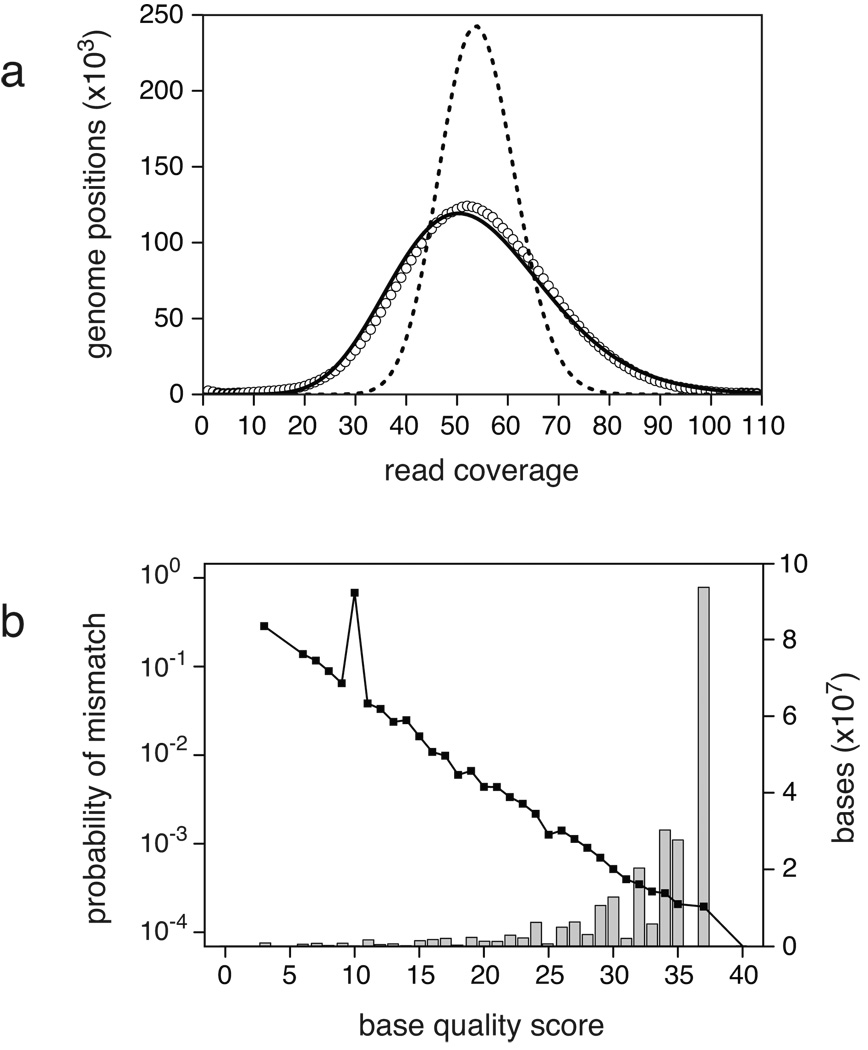
If the sampling of reads from different locations in the genome were perfectly random, the number of sites with a given coverage depth would fit a Poisson distribution with equal mean and variance. We find that the index of dispersion (the variance divided by the mean) for the coverage distribution is much greater than unity in these genomes, ranging from 3.1 to 5.5 (Table 1), with the mixed samples showing slightly more dispersion. A maximum likelihood fit to a negative binomial distribution, which is commonly used to model over-dispersed count data, reproduces most of the observed coverage structure (Fig. 2a). Higher coverage within GC-rich regions has been reported for Genome Analyzer sequence data, possibly due to more efficient processing of these fragments during library preparation on account of their greater duplex stability (Dohm et al. 2008). This bias may contribute to the over-dispersion we observe and could systematically affect the recovery of polymorphisms in specific chromosomal regions.
Figure 2. Example coverage distribution and base error rates.
The 2K mixed-population sample is displayed as representative of the sequence datasets. (a) The distribution of the number of ancestral genomic positions with a given read coverage depth (open circles) is over-dispersed relative to a Poisson model (dashed line) but is fit reasonably well by a negative binomial model (solid line). Repeat regions were excluded from this analysis. (b) The probability of a base error at a given quality score estimated from the number of observed mismatches in reads aligned to the reference genome usually decreases as a higher quality score is assigned to a base. Bases assigned a quality score of 10 had an anomalously high error rate in this dataset. The accompanying histogram shows that most bases in the dataset had high quality scores. Bases assigned a quality score of 40 do not appear on the log scale because they had zero errors.
There are hundreds of thousands to millions of base mismatches in the reads with unique best alignments to the ancestral genome in each dataset (Table 1). When constructing a model for the base error rate, we verified that bases assigned high quality scores by the re-sequencing analysis software usually have fewer mismatches to the ancestral sequence (Fig. 2b). A majority of the bases in each run were assigned high quality scores. However, there were fewer overall errors, and bases with higher quality scores had fewer errors, in the mixed-population dataset. For example, 50% of the base calls have quality scores corresponding to error rates of roughly 0.02% or lower per base, and 75% have error rates below 0.04%, in the 2K mixed-population sample. By comparison, 68% of bases in the 2K clone data have quality scores with error rates below 0.04%, but only about 1% have error rates below 0.02%.
Distinguishing SNPs from sequencing errors
Our aim is to determine what diversity in a set of a whole-population genome sequences is due to biological variation, as opposed to confounding mechanical errors and biases introduced during DNA preparation and sequencing. We restrict our analysis here to single nucleotide polymorphisms (SNPs), representing new mutations that have risen to a measurable frequency, but not fixed, in a bacterial population at the time of sampling. While there is information about deletions, insertions, and rearrangements in genome re-sequencing data, it is more difficult to interpret in terms of population frequencies, and so we have not yet attempted to analyze these other polymorphisms. Roughly 2/3 of the changes found in a more detailed analysis of the 20K clone from this population were point mutations (Barrick et al. 2009).
After aligning the reads in each dataset to the reference genome, we employed a likelihood ratio test to determine whether there was evidence of a SNP at each site. This test compares the likelihood of observing the collection of bases at a site under the null hypothesis of no genetic variation (i.e., all mismatches due to sequencing errors) to the maximum likelihood possible under the alternative hypothesis that there is a mixture of two alleles in the population. A much greater probability of the data given the alternative hypothesis indicates that the population from which DNA fragments were sampled consisted of subpopulations with different bases at this position. We report an E-value for each SNP prediction that is an estimate of its genome-wide significance, i.e., the likelihood ratio test p-value at a given site corrected for multiple testing. An E-value thus also represents the approximate number of false-positive predictions expected in a genome at a given significance level by chance.
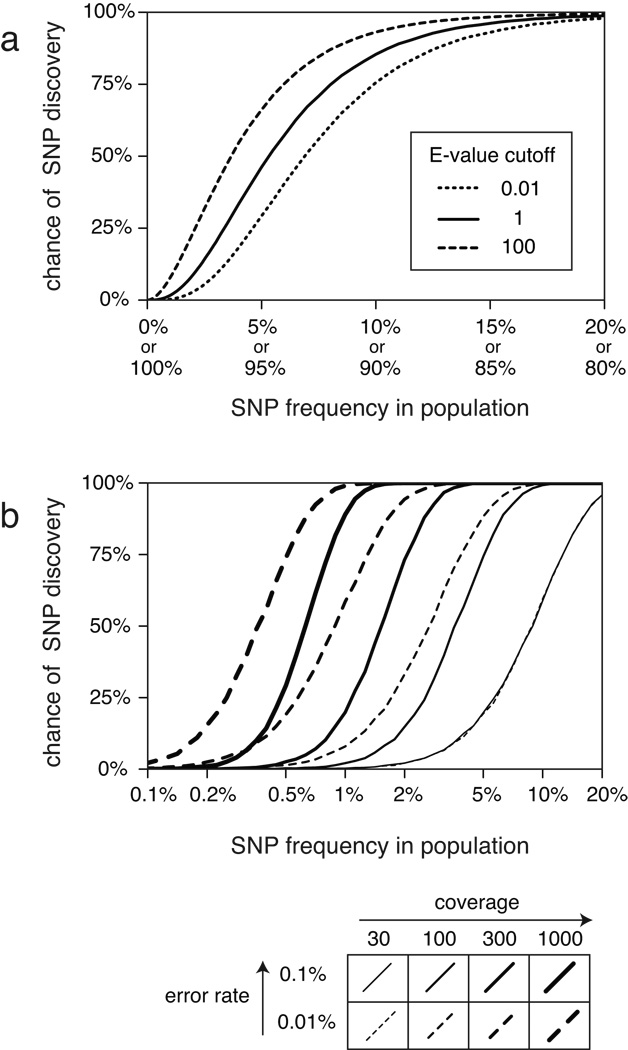
Owing to the stochastic nature of both sequencing errors and sampling DNA fragments from different individuals, a true polymorphism that has a 50% frequency in the population is far more likely to achieve a significant E-value than one at 5%. We used simulated data with the same coverage and quality score distributions as the 2K mixed-population sample to estimate the chances of discovering polymorphisms at various frequencies in the population by our procedure (Fig 3a). At an E-value threshold of 1, we expect to recover nearly all of the polymorphisms with frequencies of 20–80%, roughly 50% of the polymorphisms present in 5% of the individuals, and only 1.6% of the polymorphisms at a frequency of 1%. Lowering the E-value cutoff to 0.01 reduces the sensitivity by factors of 1.6 and 5.4 for finding polymorphisms at frequencies of 5% and 1%, respectively.
Figure 3. Sensitivity of SNP prediction procedure.
(a) Estimates of the probability that our statistical procedure would detect SNPs present at various frequencies in a mixed-population sample at different E-value cutoffs. For these calculations, the coverage and quality score distributions were those of the mixed-population 2K sample. (b) Estimates of sensitivity improvements possible by increasing sequencing coverage and by reducing the rate of base errors. For these calculations all sites had uniform coverage and the same error rate for all bases.
In light of ever-improving technologies, we also investigated how better coverage and error rates would affect the discovery of SNPs at very low frequencies in a population (Fig 3b). We performed further simulations to address this issue, with a simplified model that assumes uniform coverage and the same rate for all base errors (i.e., no differences in base quality). At an E-value cutoff of 1, the threshold frequency for a 50% chance of SNP discovery drops from 8.9% to 0.63% as coverage increases from 30- to 1000-fold. Reducing the error rate by an order of magnitude to 0.01%, does not affect the recovery of SNPs at 30-fold coverage and only slightly improves the frequency for 50% detection probability to 0.36% at 1000-fold coverage. This sensitivity analysis therefore predicts that increasing coverage would be more effective for improving rare SNP detection than reducing the base error rate by a similar factor.
SNP predictions
We chose to examine SNP predictions below a relatively permissive E-value cutoff of 1 in hopes of identifying real polymorphisms that were at low frequencies in the mixed-population samples. We first discovered that there were many more SNP predictions at this significance level than the average of 1 expected in each of the clone datasets, with the values ranging from 22 to 53 per clone (Table 1). Many of these predictions appear highly significant: 61 have E-values ≤ 0.01. During the outgrowth of a single cell it is highly unlikely that even a single polymorphism will reach a frequency of >1%, as a mutation would have had to occur within the first seven generations (i.e., 27 = 128 cell divisions). Furthermore, if mutations that arose while culturing these samples after picking a clone were responsible for these SNP predictions, we would expect many more in the 40K clone because it is a mutator with a ~100-fold elevated mutation rate, yet we see about the same number in this clone as in any other.
Instead, the unexpectedly high rate of false-positive predictions in the clones appears to result from sequencing or alignment errors that are outside the scope of our statistical model. Certain genomic sites appear to be especially prone to these errors, as many of the exact same SNPs are predicted in multiple samples and in sequence datasets from both the clone and mixed-population runs. Fortunately, many of these spurious predictions can be recognized by two kinds of biases. Base calls supporting the putative mutated base often have consistently lower qualities than those supporting the reference base for these polymorphisms, and reads supporting these SNPs are often derived largely or even exclusively from one strand of the genomic sequence. We developed a bias filtering step to reject putative SNPs with these error signatures. It reduces the number of predictions in clones to at most 8 per genome (Table 1) and removes all but five clone predictions with E-values ≤ 0.01. This filter does not, however, eliminate any SNP predictions in the mixed-population samples thought to be real (see below).
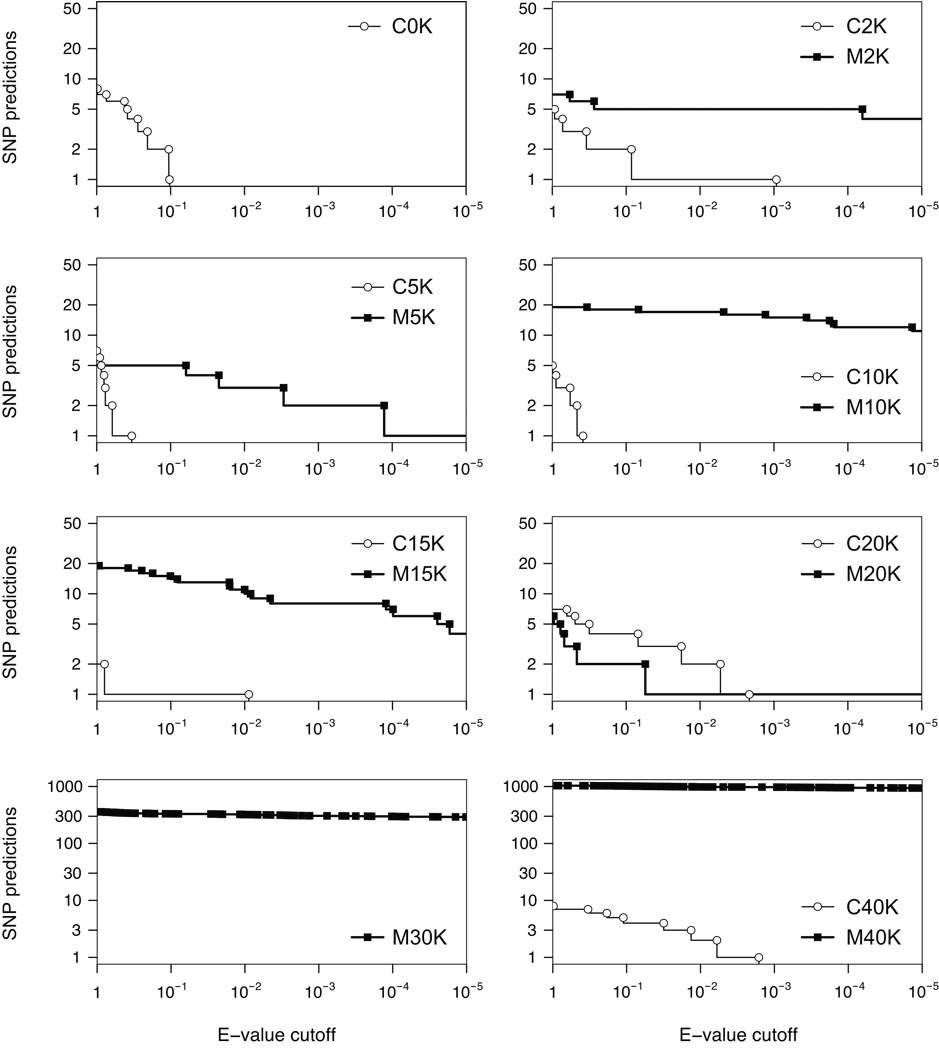
There are many more highly significant predictions in the mixed-population samples than in the clones after bias filtering (Fig. 4). Every population dataset has at least one predicted SNP with an E-value < 10−5, whereas the best prediction in any clone has an E-value almost two orders of magnitude higher. Even at 20K, where the mixed sample has fewer predicted SNPs than the paired clone, one of the mixed-population SNPs is very highly significant. Our detailed knowledge of the long-term experiment allows us to further evaluate these SNP predictions. We believe that 49 of the 57 predicted SNPs in the 2K to 20K population samples (Table 2) are probably both accurate and biologically important for the reasons presented below.
Figure 4. SNP predictions.
The cumulative distributions of predictions below a given E-value threshold that also passed the bias filtering step are plotted for each dataset. Each panel contains a generation-paired mixed-population sample (squares and solid lines) and clone (circles and dashed lines), except there is only a clone at 0K and only a mixed population at 30K.
Table 2. SNPs of particular biological interest.
For selected SNPs in the mixed-population samples, the negative base–10 logarithm of the E-value, maximum-likelihood prediction of the frequency of the derived allele in the population, and gene (e.g., araJ) or intergenic region (e.g., rspA/ynfA) containing the SNP are shown. Samples where the same mutation was fixed (within statistical resolution) in a mixed-population sample (M) or present in a sequenced clone (C) at a given generation are marked in the notes column, with a plus sign further indicating that the mutation was also found in all later samples, and asterisks marking a few SNPs that appeared (erroneously, owing to statistical uncertainty) to have been fixed in earlier population samples. Other mutations are likely to be beneficial because they are in the same gene or promoter region as mutations that later swept to fixation in this population (new allele), probably affect cellular processes known to be targets of selection in this experiment (cell wall, respiration, ribosome, regulation), or possibly improve growth on metabolic byproducts (acetate, SCFA). A complete list of all predicted SNPs that includes further details is available on the author's website (https://myxo.css.msu.edu/papers/)
| −log10 E | Freq | Gene | Notes |
|---|---|---|---|
| 2K mixed-population sample | |||
| 16.7 | 10.0% | mrdB | cell wall |
| 12.2 | 12.8% | mreB | cell wall |
| 12.2 | 14.8% | yegI | M5K+ C5K+ |
| 6.4 | 6.9% | pykF | new allele |
| 4.2 | 10.1% | hslU | M5K+ C5K+ |
| 0.6 | 4.4% | iclR | new allele |
| 5K mixed-population sample | |||
| 5.1 | 94.4% | infB | M10K+ C5K+ |
| 3.9 | 92.9% | malT | M10K+ C5K+ |
| 2.5 | 6.8% | atoC | SCFA |
| 1.7 | 94.9% | spoT | *M2K+ C2K+ |
| 10K mixed-population sample | |||
| 80.8 | 45.6% | yghJ | M20K+ C10K+ |
| 77.0 | 33.1% | hsdM | C10K |
| 72.8 | 61.6% | rpsM | M20K+ C10K+ |
| 69.9 | 43.2% | araJ | M20K+ C10K+ |
| 65.2 | 53.8% | yhdG/fis | M20K+ C10K+ |
| 64.4 | 34.1% | acs/nrfA | acetate |
| 60.1 | 57.3% | rpsA | ribosome |
| 49.0 | 39.0% | yedW/yedX | M20K+ C10K+ |
| 44.3 | 33.1% | maeB/talA | C10K |
| 23.4 | 16.2% | nuoM | respiration |
| 20.7 | 13.6% | nuoG | respiration |
| 20.3 | 23.0% | elaD | synonymous |
| 4.9 | 9.8% | ompF/asnS | new allele |
| 3.8 | 8.1% | nadR | M15K+ C15K+ |
| 3.8 | 10.3% | ompF/asnS | new allele |
| 3.4 | 9.8% | iclR/metH | new allele |
| 2.9 | 8.7% | leuO/ilvI | regulation |
| 2.3 | 5.5% | atoS | SCFA |
| 15K mixed-population sample | |||
| 31.3 | 82.8% | iclR | M20K+ C15K+ |
| 10.5 | 90.6% | rpsM | M20K+ C10K+ |
| 6.8 | 91.2% | pcnB | M20K+ C15K+ |
| 5.2 | 90.3% | arcB | M20K+ C15K+ |
| 4.8 | 94.7% | infB | *M10K+ C5K+ |
| 4.6 | 91.9% | dhaM | M20K+ C15K+ |
| 4.0 | 94.5% | araJ | M20K+ C10K+ |
| 3.9 | 91.3% | narI/ychS | M20K+ C15K+ |
| 2.3 | 4.1% | yaaH | acetate |
| 2.1 | 95.8% | yghJ | M20K+ C10K+ |
| 2.0 | 7.7% | ydiV/nlpC | regulation |
| 1.8 | 91.2% | ompF/asnS | M20K+ C15K+ |
| 1.8 | 7.6% | ycbX/ycbY | ribosome |
| 1.1 | 93.9% | yhdG/fis | M20K+ C10K+ |
| 1.0 | 95.9% | yedW/yedX | M20K+ C10K+ |
| 0.8 | 5.9% | gyrB | regulation |
| 0.6 | 95.2% | yegI | *M5K+ C5K+ |
| 0.4 | 4.6% | rspA/ynfA | regulation |
| 0.0 | 95.6% | ebgR | M20K+ C15K+ |
| 20K mixed-population sample | |||
| 40.0 | 35.3% | hypF | C20K+ |
| 1.3 | 5.6% | mgrB/yobH | regulation |
(1) Elevated dN/dS ratio
We expect most alleles that reach a high enough frequency in the population to be detected as SNPs during the first 20,000 generations will be beneficial mutations. Synonymous substitutions are likely to be neutral, and so an elevated ratio of non-synonymous to synonymous mutations, dN/dS, provides evidence of positive selection. In the ancestral genome there is a 20.4% chance that a random base substitution in a protein-coding region is synonymous. There are 37 non-synonymous and 3 synonymous mutations in the predicted SNPs from the pooled set of 2K to 20K mixed-population samples, which is a significantly higher dN/dS ratio than expected by chance (one-tailed binomial test, p = 0.03). In contrast, taking all putative SNPs in the 7 clone datasets together, there is no evidence that their dN/dS ratio is elevated (p = 0.79).
(2) Mutator phenotype
We expect an increase the amount of genetic variation in this population after a mutator phenotype evolved. Indeed, there is a dramatic increase in the number of predicted SNPs, from an average of 11.4 in the 2K to 20K population samples to 364 and 1062, in the 30K and 40K samples, respectively. The mutT defect that evolved specifically elevates the rate of A·T→C·G transversions, and so we also expect the SNPs in the 30K and 40K samples to exhibit almost exclusively this sequence signature. In the 2K to 20K mixed-population samples 26.3% of the predicted SNPs are A→C or T→G changes. As expected, there is an extremely significant shift in this fraction to 98.1% (one-tailed Fisher's exact test, p = 1.0 × 10−37) and 91.5% (p = 1.3 × 10−29) in the 30K and 40K population samples, respectively.
(3) Selective sweeps reaching fixation
If our procedure finds true polymorphisms, then we would expect some predicted SNPs to be mutations that were rising in frequency during a selective sweep that would ultimately reach fixation. In fact, nearly half (26/57) of the predicted SNPs in the 2K to 20K population samples are mutations that were later found at 100% frequency in the population. By contrast, none of the suspect SNP predictions from clonal samples correspond to mutations that were fixed in the population or observed in other clones.
(4) Unsuccessful mutations in genes where other alleles fixed
If our procedure for SNP discovery is accurate, then we expect to find evidence for selective sweeps that failed due to clonal interference. Consistent with that expectation, 5 predicted SNPs in the 2K to 15K population samples are in genes where a different mutation fixed by 20,000 generations (Table 2). These transient polymorphisms probably represent alternative beneficial alleles at genes under strong selection in the long-term experiment. Given that E. coli has ~4,000 genes and that 26 predicted SNPs from this period did not reach fixation, there is only a small chance (one-tailed Binomial test, p = 8 × 10−7) of picking 5 or more SNPs at random in the 27 genes with mutations that later fixed. Of the putative SNPs in clones, only 1 in 42 impinges on this same set of 27 genes, which is not unlikely by chance (p = 0.25).
Among these unsuccessful mutations, the 10K mixed sample included two different SNPs at adjacent bases upstream of the ompF gene. The ompF allele that eventually fixed is also in the promoter region and appears as a SNP at 15K. Surprisingly, it has a highly deleterious effect when moved alone into the ancestral chromosome (D. Schneider and R.E.L, unpublished data). The finding of two similar contending mutations provides compelling evidence that these ompF mutations are actually beneficial in a genetic background that had become common by 10,000 generations. There are also transient SNPs affecting the pykF and iclR genes, each of which eventually fixed a different allele.
(5) Other unsuccessful beneficial mutations
We would also expect some unsuccessful lineages to have beneficial mutations in other genes. Two predicted SNPs in the 10K population (hsdM and maeB/talA) are clearly real because they were also present in the 10K clone genome, although this clone was off the main line of descent. Though we have no direct evidence that other transient SNPs are biologically significant, it seems plausible that at least 15 of them are beneficial in this environment. Eleven transient SNPs in the 2K to 20K mixed-population samples occur in genes involved in processes thought to be key targets of selection (Table 2) including cell wall synthesis, respiration, ribosomal function, and gene regulation (Philippe et al. 2007; Philippe et al. 2009). For example, mrdA and mrdB are two genes in the same operon involved in cell wall synthesis; a transient SNP in mrdB occurs in the 2K population sample, while a mutation in mrdA has fixed in every population sample from 5K onward.
(6) Cross-feeding adaptations
The 4 remaining transient SNPs in the 2K to 20K mixed-population samples, which occur in genes related to acetate and short chain fatty acids (SCFA) metabolism (Table 2), may be cross-feeding adaptations. Three of these mutations were rare and all of them were ultimately lost from this population. One is in the promoter region of the acs gene, which encodes an enzyme for acetate utilization. A second is a non-synonymous change in yaaH, which is predicted to have a role in acetate transport. The third and fourth cause amino-acid substitutions in atoS and atoC, which together regulate an operon involved in SCFA degradation. Two early transient SNPs in the iclR gene, which encodes a repressor for glyoxylate bypass enzymes that are induced when E. coli grows on acetate or SCFAs, may also promote cross-feeding interactions, even though a different mutation in iclR was eventually adopted by the dominant lineage and fixed in the population by 20,000 generations.
It is possible that cross-feeding genotypes off the main line of descent may have persisted in this population at low levels below our detection limit for SNPs, with occasional increases in frequency, perhaps in association with other beneficial mutations. The presence of such cross-feeding genotypes could explain the weaker frequency-dependent interactions observed in populations other than the one with the stable polymorphism (Elena and Lenski 1997). None of the potential cross-feeding alleles detected as SNPs remain at detectable frequencies in successive samples, so we suspect that they were evolutionary dead ends in this population. However, new cross-feeding genotypes could periodically re-evolve from the main lineage to exploit that niche and, in turn, later go extinct (Rozen et al. 2005).
Changes in genetic diversity over time
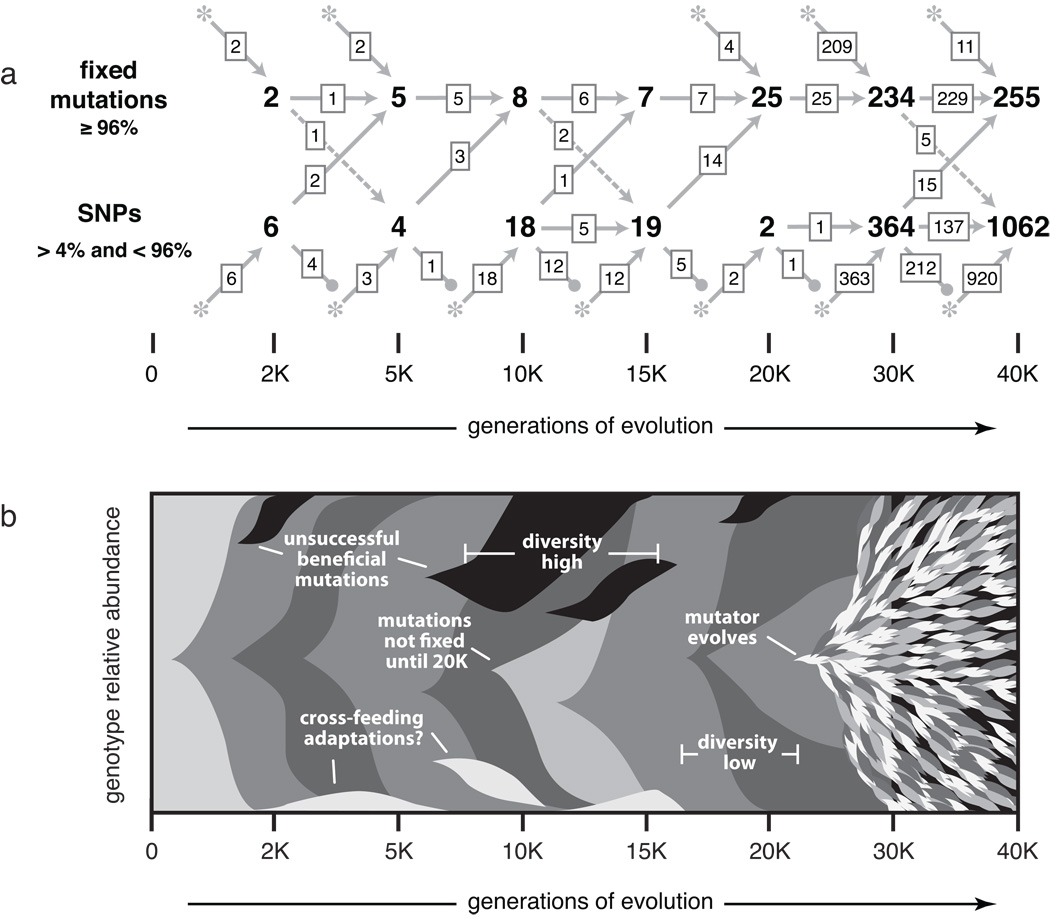
Figure 5 summarizes the genetic diversity observed in mixed-population samples over time and the tempo with which mutations were fixed in the population. The top panel shows the origin and eventual fate of all the point mutations discovered in the 2K to 40K population samples, while the bottom panel provides a visual summary of the main patterns in these data.
Figure 5. Mutational diversity in an evolving E. coli population.
(a) Origin and eventual fate of point mutations in the 2K to 40K mixed-population samples. New mutations that first appear as SNPs or fixed alleles are shown as asterisks along the bottom or top, respectively, with arrows leading to the corresponding pools of SNPs and fixed mutations. Transient SNPs that were lost from the population are shown by descending lines ending in closed circles. Note that we only detect SNPs when they are between roughly 4% and 96% frequency in the population, and that we only recover approximately 50% of the SNPs at 5% frequency. Only the 49 SNP predictions in Table 2 were included for the 2K to 20K samples. (b) Stylized summary of the mixed-population SNP analysis. Shaded wedges represent subpopulations containing new mutations relative to the previous genetic background. Mutations are grouped to highlight their eventual fates, but we do not always have linkage information to resolve which SNPs occurred together. Labeled features are explained in the text.
There was a great deal of allelic diversity in the 10K and 15K samples that was lost by 20K, with the majority of SNPs at 15K becoming fixed in the 20K sample. This pattern seems to indicate a deep branching between two main competing lineages, one of which prevailed and the other of which went extinct. Additional support for this scenario comes from the clone sequences. In particular, the 10K clone carried six mutations that were off the line of descent, including two SNPs that reached intermediate frequencies of ~33% in the 10K sample (hsdM and maeB/talA). Meanwhile, five other mutations on the line of descent were present in 40–60% of the 10K population sample. This diversity was slow to disappear, as these five mutations that would eventually fix were still only at ~90% frequency in the 15K sample. After that lineage finally prevailed, however, there was very little diversity in the 20K population sample.
The mutational dynamics in this population changed dramatically after the mutator phenotype evolved. SNP diversity and the rate at which point mutations fixed both increased dramatically by 30,000 generations. Adaptation had already slowed substantially by this point in the long-term evolution experiment (Lenski and Travisano 1994; Cooper and Lenski 2000). The rate of fitness improvement might have reaccelerated slightly with the emergence of the mutator – that remains to be determined – but previous experiments indicate that any such acceleration is likely to be rather small given the fairly large population size and correspondingly short waiting-time for new beneficial mutations (Sniegowski et al. 1997; de Visser et al. 1999). Although we have population samples at only two time points after the mutator phenotype evolved, the data indicate a dramatic and on-going increase in the standing genetic diversity, and it will be interesting to see whether it continues to increase.
CONCLUSIONS
When analyzing diversity in a mixed-population sequence datasets one must distinguish real polymorphisms from sequencing errors. We have demonstrated that it is possible to identify many SNPs in an evolving E. coli population from micro-read data on a genome-wide scale with 50-fold average coverage of the ancestral genome. In this focal population from a long-term experiment, we were able to discover mutations that were casualties of clonal interference, follow lineages with multiple beneficial mutations as they swept to fixation, watch presumably neutral diversity dramatically increase after a mutator phenotype evolved, and detect minority lineages that may represent transient adaptations to cross-feeding niches.
One limitation of the current study is that we only identified SNP diversity. It should be straightforward to extend our current approach to predict polymorphisms involving short indels that can be recognized as gaps in read alignments to the reference genome. However, it will be more challenging to predict the population-wide frequencies of large deletions and duplications, IS insertions, and chromosomal rearrangements, even when they can be readily identified in single-genome samples. Fluctuations in read coverage across the genome will tend to obscure the boundaries of polymorphic deletions and make it difficult to ascertain what level of coverage represents a given population frequency. Similarly, even when it is possible to find reads or read pairs spanning new sequence junctions, such as those that result from an IS insertion, differences in the probabilities of identifying reads supporting the new and ancestral junctions will confound calculating the prevalence of a mutation.
Nevertheless, as sequencing technologies advance it will become possible to reliably detect more types of mutations and much rarer genetic variants within a population. We anticipate that analyzing fine-scale time series of whole-population samples will reveal new intricacies of evolutionary dynamics. Where it was previously necessary to use a linked genetic marker to follow evolutionary trajectories (Rozen et al. 2002; Hegreness et al. 2006), native mutations will become their own markers, limited only by our ability to detect them when rare. It should be possible to infer the relative fitness of different lineages and to predict linkage relationships from correlations in allelic frequencies over time. Detailed analyses of evolutionary potential that reconstruct the fitness effects of accessible beneficial mutations will also become possible. One can then begin to examine how standing diversity, evolutionary trajectories, and the distribution of selection coefficients change after a shift in the environment or when a population invades a new ecological niche (Blount et al. 2008).
The fundamental evolutionary phenomena that can be studied with these techniques also occur in other systems, including in vitro directed evolution experiments with populations of DNA and RNA molecules (Joyce 2007). A microbial population-genetic perspective on diversity also has applications and relevance for medicine. Emerging pathogens and hazardous biological agents such as anthrax spores can be traced by the fingerprint of rare variants unique to a sample (Read et al. 2002; Lenski and Keim 2005). Chronic populations of pathogenic bacteria, such as those infecting cystic fibrosis patients, evolve in a similar manner to the populations studied here (Oliver et al. 2000). Less obviously, there are also commonalities with the progression of cancer, wherein a cell lineage begins uncontrolled clonal proliferation and accumulates mutations that enable cells to better compete for limited resources in the body. Indeed, next-generation sequencing is already being used to profile cancer diversity in single genes (Campbell et al. 2008), and whole-genome studies are on the horizon. Laboratory experiments with microbes are a particularly useful starting point for understanding the evolutionary underpinnings and implications of within-population diversity.
Supplementary Material
ACKNOWLEDGMENTS
We thank many individuals for maintaining and studying the long-term evolution experiment over the years; Titus Brown, Michael Desai, Jonathon Dushoff, Philip Johnson, Jihyun Kim, Joshua Plotkin, Monty Slatkin, Chris Strelioff, and Jim Tiedje for helpful discussions; Dom Schneider for sharing unpublished data; and Neerja Hajela for purifying genomic DNA. Portions of this research were funded by an NIH Pathway to Independence Award (GM-087550) to J.E.B. and grants from the NSF (DEB-0515729) and DARPA (HR0011-05-1-0057) to R.E.L.
REFERENCES
- Atwood KC, Schneider LK, Ryan FJ. Selective mechanisms in bacteria. Cold Spring Harb. Symp. Quant. Biol. 1951;16:345–355. doi: 10.1101/sqb.1951.016.01.026. [DOI] [PubMed] [Google Scholar]
- Barrick JE, Yu D-S, Yoon SH, Jeong H, Oh TK, Schneider D, Lenski RE, Kim JF. Genome dynamics in a long-term experiment with Escherichia coli. submitted. 2009 doi: 10.1038/nature08480. [DOI] [PubMed] [Google Scholar]
- Blount ZD, Borland CZ, Lenski RE. Historical contingency and the evolution of a key innovation in an experimental population of Escherichia coli. Proc. Natl. Acad. Sci. U.S.A. 2008 doi: 10.1073/pnas.0803151105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckling A, Maclean CR, Brockhurst MA, Colegrave N. The Beagle in a bottle. Nature. 2009;457:824–829. doi: 10.1038/nature07892. [DOI] [PubMed] [Google Scholar]
- Campbell PJ, Pleasance ED, Stephens PJ, Dicks E, Rance R, Goodhead I, Follows GA, Green AR, Futreal PA, Stratton MR. Subclonal phylogenetic structures in cancer revealed by ultra-deep sequencing. Proc. Natl. Acad. Sci. U.S.A. 2008;105:13081–13086. doi: 10.1073/pnas.0801523105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper VS, Lenski RE. The population genetics of ecological specialization in evolving Escherichia coli populations. Nature. 2000;407:736–739. doi: 10.1038/35037572. [DOI] [PubMed] [Google Scholar]
- de Visser JA, Zeyl CW, Gerrish PJ, Blanchard JL, Lenski RE. Diminishing returns from mutation supply rate in asexual populations. Science. 1999;283:404–406. doi: 10.1126/science.283.5400.404. [DOI] [PubMed] [Google Scholar]
- Dohm JC, Lottaz C, Borodina T, Himmelbauer H. Substantial biases in ultra-short read data sets from high-throughput DNA sequencing. Nucleic Acids Res. 2008;36:e105. doi: 10.1093/nar/gkn425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elena SF, Lenski RE. Long-term experimental evolution in Escherichia coli. VII. Mechanisms maintaining genetic variability within populations. Evolution. 1997;51:1058–1067. doi: 10.1111/j.1558-5646.1997.tb03953.x. [DOI] [PubMed] [Google Scholar]
- Elena SF, Lenski RE. Evolution experiments with microorganisms: The dynamics and genetic bases of adaptation. Nat. Rev. Genet. 2003;4:457–469. doi: 10.1038/nrg1088. [DOI] [PubMed] [Google Scholar]
- Eriksson N, Pachter L, Mitsuya Y, Rhee SY, Wang C, Gharizadeh B, Ronaghi M, Shafer RW, Beerenwinkel N. Viral population estimation using pyrosequencing. PLoS Comput. Biol. 2008;4:e1000074. doi: 10.1371/journal.pcbi.1000074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiegna F, Yu YT, Kadam SV, Velicer GJ. Evolution of an obligate social cheater to a superior cooperator. Nature. 2006;441:310–314. doi: 10.1038/nature04677. [DOI] [PubMed] [Google Scholar]
- Fogle CA, Nagle JL, Desai MM. Clonal interference, multiple mutations and adaptation in large asexual populations. Genetics. 2008;180:2163–2173. doi: 10.1534/genetics.108.090019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerrish PJ, Lenski RE. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102–103:127–144. [PubMed] [Google Scholar]
- Gupta PK. Single-molecule DNA sequencing technologies for future genomics research. Trends Biotechnol. 2008;26:602–611. doi: 10.1016/j.tibtech.2008.07.003. [DOI] [PubMed] [Google Scholar]
- Hegreness M, Shoresh N, Hartl D, Kishony R. An equivalence principle for the incorporation of favorable mutations in asexual populations. Science. 2006;311:1615–1617. doi: 10.1126/science.1122469. [DOI] [PubMed] [Google Scholar]
- Herring CD, Raghunathan A, Honisch C, Patel T, Applebee MK, Joyce AR, Albert TJ, Blattner FR, van den Boom D, Cantor CR, Palsson BO. Comparative genome sequencing of Escherichia coli allows observation of bacterial evolution on a laboratory timescale. Nat. Genet. 2006;38:1406–1412. doi: 10.1038/ng1906. [DOI] [PubMed] [Google Scholar]
- Johnson PL, Slatkin M. Inference of population genetic parameters in metagenomics: a clean look at messy data. Genome Res. 2006;16:1320–1327. doi: 10.1101/gr.5431206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joyce GF. Forty years of in vitro evolution. Angew. Chem. Int. Edit. Engl. 2007;46:6420–6436. doi: 10.1002/anie.200701369. [DOI] [PubMed] [Google Scholar]
- Kassen R, Rainey PB. The ecology and genetics of microbial diversity. Annu. Rev. Microbiol. 2004;58:207–231. doi: 10.1146/annurev.micro.58.030603.123654. [DOI] [PubMed] [Google Scholar]
- Kimura M. The Neutral Theory of Molecular Evolution. Cambridge: Cambridge Univ. Press; 1983. [Google Scholar]
- Kurtz S, Phillippy A, Delcher AL, Smoot M, Shumway M, Antonescu C, Salzberg SL. Versatile and open software for comparing large genomes. Genome Biol. 2004;5:R12. doi: 10.1186/gb-2004-5-2-r12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenski RE. Phenotypic and genomic evolution during a 20,000-generation experiment with the bacterium Escherichia coli. Plant Breed. Rev. 2004;24:225–265. [Google Scholar]
- Lenski RE, Keim P. Population genetics of bacteria in a forensic context. In: Breeze RG, Budowle B, Schutzer SE, editors. Microbial Forensics. San Diego, California: Elsevier Academic Press; 2005. pp. 355–369. [Google Scholar]
- Lenski RE, Rose MR, Simpson SC, Tadler SC. Long-term experimental evolution in Escherichia coli. I. Adaptation and divergence during 2,000 generations. Am. Nat. 1991;138:1315–1341. [Google Scholar]
- Lenski RE, Travisano M. Dynamics of adaptation and diversification: a 10,000-generation experiment with bacterial populations. Proc. Natl. Acad. Sci. U.S.A. 1994;91:6808–6814. doi: 10.1073/pnas.91.15.6808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenski RE, Winkworth CL, Riley MA. Rates of DNA sequence evolution in experimental populations of Escherichia coli during 20,000 generations. J. Mol. Evol. 2003;56:498–508. doi: 10.1007/s00239-002-2423-0. [DOI] [PubMed] [Google Scholar]
- Liti G, Carter DM, Moses AM, Warringer J, Parts L, James SA, Davey RP, Roberts IN, Burt A, Koufopanou V, Tsai IJ, Bergman CM, Bensasson D, O'Kelly MJ, van Oudenaarden A, Barton DB, Bailes E, Nguyen AN, Jones M, Quail MA, Goodhead I, Sims S, Smith F, Blomberg A, Durbin R, Louis EJ. Population genomics of domestic and wild yeasts. Nature. 2009;458:337–341. doi: 10.1038/nature07743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardis ER. Next-generation DNA sequencing methods. Annu. Rev. Genomics. Hum. Genet. 2008;9:387–402. doi: 10.1146/annurev.genom.9.081307.164359. [DOI] [PubMed] [Google Scholar]
- Muller HJ. Some genetic aspects of sex. Am. Nat. 1932;66:118–138. [Google Scholar]
- Oliver A, Canton R, Campo P, Baquero F, Blazquez J. High frequency of hypermutable Pseudomonas aeruginosa in cystic fibrosis lung infection. Science. 2000;288:1251–1254. doi: 10.1126/science.288.5469.1251. [DOI] [PubMed] [Google Scholar]
- Philippe N, Crozat E, Lenski RE, Schneider D. Evolution of global regulatory networks during a long-term experiment with Escherichia coli. Bioessays. 2007;29:846–860. doi: 10.1002/bies.20629. [DOI] [PubMed] [Google Scholar]
- Philippe N, Pelosi L, Lenski RE, Schneider D. Evolution of penicillin-binding protein 2 concentration and cell shape during a long-term experiment with Escherichia coli. J. Bacteriol. 2009;191:909–921. doi: 10.1128/JB.01419-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Read TD, Salzberg SL, Pop M, Shumway M, Umayam L, Jiang L, Holtzapple E, Busch JD, Smith KL, Schupp JM, Solomon D, Keim P, Fraser CM. Comparative genome sequencing for discovery of novel polymorphisms in Bacillus anthracis. Science. 2002;296:2028–2033. doi: 10.1126/science.1071837. [DOI] [PubMed] [Google Scholar]
- Rosenzweig RF, Sharp RR, Treves DS, Adams J. Microbial evolution in a simple unstructured environment: genetic differentiation in Escherichia coli. Genetics. 1994;137:903–917. doi: 10.1093/genetics/137.4.903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rozen DE, de Visser JA, Gerrish PJ. Fitness effects of fixed beneficial mutations in microbial populations. Curr. Biol. 2002;12:1040–1045. doi: 10.1016/s0960-9822(02)00896-5. [DOI] [PubMed] [Google Scholar]
- Rozen DE, Lenski RE. Long-term experimental evolution in Escherichia coli. VIII. Dynamics of a balanced polymorphism. Am. Nat. 2000;155:24–35. doi: 10.1086/303299. [DOI] [PubMed] [Google Scholar]
- Rozen DE, Philippe N, de Visser JA, Lenski RE, Schneider D. Death and cannibalism in a seasonal environment facilitate bacterial coexistence. Ecol. Lett. 2009;12:34–44. doi: 10.1111/j.1461-0248.2008.01257.x. [DOI] [PubMed] [Google Scholar]
- Rozen DE, Schneider D, Lenski RE. Long-term experimental evolution in Escherichia coli. XIII. Phylogenetic history of a balanced polymorphism. J. Mol. Evol. 2005;61:171–180. doi: 10.1007/s00239-004-0322-2. [DOI] [PubMed] [Google Scholar]
- Sniegowski PD, Gerrish PJ, Lenski RE. Evolution of high mutation rates in experimental populations of E. coli. Nature. 1997;387:703–705. doi: 10.1038/42701. [DOI] [PubMed] [Google Scholar]
- Vieites JM, Guazzaroni ME, Beloqui A, Golyshin PN, Ferrer M. Metagenomics approaches in systems microbiology. FEMS Microbiol. Rev. 2009;33:236–255. doi: 10.1111/j.1574-6976.2008.00152.x. [DOI] [PubMed] [Google Scholar]
- Wang C, Mitsuya Y, Gharizadeh B, Ronaghi M, Shafer RW. Characterization of mutation spectra with ultra-deep pyrosequencing: application to HIV-1 drug resistance. Genome Res. 2007;17:1195–1201. doi: 10.1101/gr.6468307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods RJ. Ph.D. thesis. East Lansing: Michigan State University; 2005. Population Genetics of Bacterial Adaptation: Experiments with Escherichia coli and a Simulation Model. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.