Comparison of Entropic Contributions to Binding in a “Hydrophilic” versus “Hydrophobic” Ligand−Protein Interaction

Abstract

In the present study we characterize the thermodynamics of binding of histamine to recombinant histamine-binding protein (rRaHBP2), a member of the lipocalin family isolated from the brown-ear tick Rhipicephalus appendiculatus. The binding pocket of this protein contains a number of charged residues, consistent with histamine binding, and is thus a typical example of a “hydrophilic” binder. In contrast, a second member of the lipocalin family, the recombinant major urinary protein (rMUP), binds small hydrophobic ligands, with a similar overall entropy of binding in comparison with rRaHBP2. Having extensively studied ligand binding thermodynamics for rMUP previously, the data we obtained in the present study for HBP enables a comparison of the driving forces for binding between these classically distinct binding processes in terms of entropic contributions from ligand, protein, and solvent. In the case of rRaHBP2, we find favorable entropic contributions to binding from desolvation of the ligand; however, the overall entropy of binding is unfavorable due to a dominant unfavorable contribution arising from the loss of ligand degrees of freedom, together with the sequestration of solvent water molecules into the binding pocket in the complex. This contrasts with binding in rMUP where desolvation of the protein binding pocket makes a minor contribution to the overall entropy of binding given that the pocket is substantially desolvated prior to binding.

Introduction

All biological processes depend critically on highly specific recognition between molecules with carefully tuned affinities. However, despite the universal nature of these interactions, our understanding of their molecular basis is limited. As a result, structure-based design of small molecules that modulate these interactions is seriously compromised, resulting in failure to capitalize on the wealth of data that are being generated from various structural genomics projects worldwide. The ability to design such molecules rapidly and efficiently at will (for example, as drug candidates or biochemical tools) using structural data as a starting point is arguably one of the most important unmet challenges in contemporary science.

Limited ability to predict affinity from structure is largely due to the complexity of the problem, whereby competing thermodynamic processes all contribute to binding affinity. The standard free energy of binding ΔG°_b, which determines interaction strength (eq 1), not only is governed by structural terms but also involves dynamics (eq 2):

where K_a is the association constant, ΔH°_b is the standard enthalpy of binding, ΔS°_b is the standard entropy of binding, R is the gas constant, and T is the absolute temperature. The key to a full understanding of the binding process is a decomposition of the binding into enthalpic (structural) and entropic (dynamic) contributions from the protein, the cognate ligand and solvent water. In this manner we successfully rationalized the thermodynamics of binding of small-molecule ligands to a model “hydrophobic” binder, recombinant mouse major urinary protein (rMUP).¹⁻⁴

In the present study we deconvolute the binding thermodynamics of a second member of the lipocalin family, recombinant histamine binding protein (rRaHBP2), which, as its name suggests, is a “hydrophilic” binder with high affinity for histamine and related amines. We reasoned that the study of binding thermodynamics in a second protein with a fold similar to that of rMUP would enable us to compare and contrast the entropic contributions to binding from protein, ligand, and solvent, in two systems with classically distinct binding signatures.

Materials and Methods

Overexpression and Purification of rRaHBP2 and ¹³C,¹⁵N (>97%)-Enriched rRaHBP2

Plasmid pET23a(+) HBP2(D24R) was transformed into E. coli BL21 (DE3) cells using the heat shock method. A 1 μL aliquot of ligation product was transferred to ∼25 μL of BL21 (DE3) cells and incubated on ice for 20 min. The cells were then heat shocked at 42 °C for 90 s. Next, 75 μL of SOC medium (preheated to 42 °C) was added to the cells, and the culture was incubated with agitation at 37 °C for 60−90 min. Aliquots were streaked on to LB plates containing100 μg/mL carbenicillin and were grown at 37 °C overnight.

Single colonies of fresh transformants were picked and used to inoculate 5 mL of liquid LB medium and incubated at 37 °C overnight. One milliliter was taken from the overnight cultures and used to inoculate 2 × 1 L of single ¹⁵N-labeled or double ¹³C-,¹⁵N-labeled Silantes rich growth medium (Silantes, Germany), which were incubated at 37 °C until the culture density reached OD₆₀₀ ∼0.4. At this point the temperature was lowered to 20 °C. After 30 min, expression was induced with 1 mM IPTG, and the culture was incubated overnight. The cells were harvested by centrifugation at 5000g for 10 min at 4 °C.

The cells were suspended in 5 mL/g 50 mM HEPES at a pH of 6.8 containing 0.16 mg/mL lysozyme and agitated for 20 min followed by addition of 1 mL/g of deoxycholic acid in 20 mM sodium phosphate (4 mg/mL) both at pH 7.0. After 30 min of incubation at 37 °C, 1 μL/g DNaseI (9 μg/μL) was added, and the cells incubated at 37 °C for 20 min with agitation. The lysate was centrifuged at 9384g for 30 min at 4 °C. The supernatant was filtered with a 0.22 μm filter prior to loading on an anion exchange column (Q-Sepharose resin, Sigma-Aldrich). The protein was bound to the column and eluted using a gradient of 0 to 1 M NaCl over 200 mL. Fractions containing the protein were pooled and dialyzed against 50 mM HEPES pH 7.2. The protein was concentrated to approximately 3 mg/mL (0.15 mM) using Vivaspin 20 centrifugal concentrators with a 5 kDa cutoff (Sartorius, U.K.). The protein was then further purified by gel filtration with Sephacryl S-100 resin (Sigma-Aldrich). All chromatography steps were carried out on an Äkta FPLC system (GE Healthcare, Sweden).

NMR Measurements

NMR Resonance Assignments

A 0.4 mL portion of 0.5 mM uniformly enriched ¹³C-,¹⁵N-rRa-HBP2(D24R) in 50 mM potassium phosphate pH 7.4 was placed in a Shigemi tube with sodium azide, and DSS was added to final concentrations of 1 and 0.2 mM, respectively. All experiments were carried out at 298 K. For the complex with histamine, 1.1 molar equiv of ligand was added to the protein sample (0.55 mM). Three-dimensional assignment experiments were carried out on Varian Unity spectrometers equipped with triple resonance probes at proton frequencies of 500 MHz (CBCA(CO)NH) and 750 MHz (HNCA and HNCACB). Experiments carried out at 750 MHz on the apo protein and the histamine-bound complex were acquired using a cryo-probe; all other experiments were acquired using a room temperature probe. CBCA(CO)NH spectra were acquired with 32 scans, 2048 points, and sweep widths of 8510, 7200, and 1620 Hz in the ¹H, ¹³C, and ¹⁵N dimensions, respectively. HNCA spectra were acquired with 16 scans, 1024 points, and sweep widths of 10474, 4320, and 2400 Hz in the ¹H, ¹³C, and ¹⁵N dimensions, respectively. HNCACB spectra were acquired with 40 scans, 2048 points, and sweep widths of 15000, 13000, and 2400 Hz in the ¹H, ¹³C, and ¹⁵N dimensions, respectively.

Data were processed using NMRPipe.(5) The Rance-Kay macro was employed to generate pure absorptive line shapes from sensitivity enhanced spectra. In all cases the data were processed using a cosine-bell function with zero-filling followed by Fourier transformation. Linear prediction was used in the ¹⁵N dimension. Baseline correction was carried out first in the ¹H dimension then the ¹³C followed by the ¹⁵N dimensions and was achieved using the POLY function in NMRPipe. Backbone assignments were made using the CCPN Analysis software package.(6)

NMR Relaxation Measurements

¹⁵N relaxation-time measurements were carried out essentially according to Farrow et al.(7) Amide relaxation times for MUP were obtained at 500 and 600 MHz with T₁ relaxation delays of 10.9, 54.3, 108.6, 217.3, 434.6, 651.8, 923.4, 1195.0, and 1521.0 ms and T₂ relaxation delays of 16.6, 33.2, 49.7, 66.3, 82.9, 99.5, 132.6 ms. Delays of 217.3 and 923.4 ms for T₁ experiments and 33.2 and 99.5 ms for T₂ experiments were repeated to estimate the uncertainty in peak intensity. ¹⁵N steady-state NOE spectra were acquired at a proton frequency of 600 MHz with 80 scans; 2048 and 256 points were acquired with sweep widths of 8510.64 and 2500.00 Hz in the ¹H and ¹⁵N dimensions, respectively. All relaxation experiments were recorded in an interleaved manner so as to reduce the effects of any changes in state of the sample.

Analysis of NMR Relaxation Data

Peak intensities from ¹⁵N relaxation measurements were calculated from the center of the peaks (to minimize peak overlap) using NMRView software in combination with software written in-house.(8) Relaxation rates were calculated by fitting the peak intensities as a function of the relaxation delays to a two-parameter exponential decay using nonlinear Levenberg−Marquardt least-squares fitting. Errors were determined using 1000 bootstrap error simulations seeded from the difference between duplicate experiments. The fitting was carried out using a script written in-house.

Steady-state NOE values were calculated from the ratios of the peak intensities with and without proton saturation. Peak intensities were determined as described above. Uncertainty in the steady-state values was determined from the standard deviation in background noise levels using NMRView.

An initial value for τ_c was calculated using the Stokes−Einstein equation. The hydrodynamic radius of the molecule was estimated by submitting the crystal structure of the protein to Hydronmr.(9) Viscosity values of H₂O:D₂O (90:10%) were taken from data provided with Hydronmr. All residues showing spectral overlap or steady-state NOE values <0.65 were omitted before the data were subjected to model free analysis. Model free analysis of ¹⁵N was performed using the relax software package (v1.0.3) assuming an isotropic diffusion tensor.^10,11 Values of 1.02 Å and −170 ppm were used for the N−H bond length and CSA tensor, respectively. Twenty rounds of Newton minimization were performed for optimization of the model-free parameters. Each round consisted of fitting of the relaxation data to each of the model-free models 1−5 with τ_c held fixed, followed by AIC model selection and then refinement of τ_c based on the model free results. Changes in conformational entropy were determined from the results of the model free analysis using the relationship described by Yang and Kay.(12)

X-ray Crystallography

Crystallization and Data Collection

Optimal conditions for crystallization of 2.6 M ammonium sulfate, 100 mM Bicine buffer pH 8.2, 18 °C were based on initial screening. Drops containing 2 μL of rRaHBP2(D24R) (10 mg/mL, containing 2 mM histamine) and 2 μL of reservoir solution were equilibrated against reservoir solution by vapor diffusion using the hanging drop method. Crystals grew over a period of 3−7 days. Using similar conditions, it was possible to obtain crystals of the apo form of rRaHBP2(D24R), although they grew as multiple crystals and were unsuitable for X-ray analysis. In order to obtain a more single form of crystal, isopropanol (5−10%) was added to the crystallization conditions. After soaking for 10 s in a cryoprotecting solution consisting of reservoir solution with the addition of 20% (v/v) glycerol, crystals were flash-frozen in liquid nitrogen. Data from crystals of rRaHBP2(D24R) complexed with histamine were recorded at 100 K with an ADSC Q315 CCD detector with synchrotron radiation (Beamline I02, wavelength 0.95 nm, Diamond Light Source, U.K.). Data from crystals of the apoprotein were recorded at 100 K with an R-Axis IV++ image plate detector mounted on a Rigaku RU-H3R rotating anode. Both data sets were integrated and reduced using MOSFLM(13) and SCALA(14) respectively. Statistics are shown in Table 1.

Table 1. Data Collection and Refinement Statistics^a.

	rRaHBP2(D24R)	rRaHBP2(D24R)-histamine
wavelength (Å)	1.54	0.95
resolution range (Å)	12−2.25 (2.37−2.25)	55−1.55 (1.63−1.55)
unique reflections	18800 (2735)	65264 (9456)
completeness (%)	99.3 (100.0)	97.2 (96.9)
multiplicity	4.0 (4.0)	2.9 (3)
Rsymi	0.09 (0.30)	0.059 (0.54)
space group	P21	P212121
no. of molecules per asymmetric unit	2	2
unit cell dimensions (nm)	a = 57.96; b = 56.61; c = 63.80; α = γ = 90; β = 107.07	a = 75.22; b = 78.73; c = 77.65; α = β = γ = 90°
Rwork (Rfree) (%)	22.8 (27.6)	17.2 (21.4)
bond length (Å)	0.012	0.011
angles (deg)	1.279	1.305
molprobity clash score	11.9	5.07
Ramachandran favored (%)	97.0	99.1

^aValues in parentheses are for highest resolution shell. R_sym = ∑_hkl∑_i(I_i(hkl) − I_mean(hkl))/∑_hkl∑_i(I_i(hkl)).

Structure Determination and Refinement

The structure of wild-type rRaHBP2 complexed with histamine (PDB accession number 1QFT) with all water molecules and bound ligand removed was used as the starting model and rigid-body refined into the unit cell of the rRaHBP2(D24R) complex with histamine. Structure refinement was carried out using REFMAC (CCP4(15)), and subsequent model building and water placement was carried out in COOT.(16) The protein structure was validated using PROCHECK(17) and MOLPROBITY.(18) Because of different crystal morphology, the structure of the apoprotein was solved by Molecular Replacement using the program AmoRe(19) using 1QFT as trial model. Refinement and model building was carried out as before. Final statistics for the structure are outlined in Table 1. Crystal coordinates and structure factors have been deposited in the RCSB protein data bank with accession numbers 3G7X (rRaHBP2(D24R)-histamine complex) and 3GAQ (rRaHBP2(D24R)).

ITC Experiments

Protein samples were dialyzed against 50 mM Tris at pH 7.4 overnight, and the dialysate was used to prepare ligand solutions. Protein concentration was confirmed by UV absorption (HBP2 ε₂₈₀ = 38 640 M⁻¹ cm⁻¹ calculated using the ExPASy Proteomics Server). Protein concentrations of between 30 and 50 μM were used with ligand concentrations of 500 to 700 μM. Titrations consisted of either 30 or 40 injections. The first injection was a volume of 2 μL, which was discarded during fitting to allow for equilibration of ligand/receptor at the needle tip. The remaining injections were all 5 μL in volume. Fitting was performed using the one-site model present in the Origin 5.0 software (Microcal Inc., USA) for the interaction of histamine with rRaHBP2(D24R) or using the two-site model, present in the same software, to fit the data recorded for the interaction of histamine with wild-type rRaHBP2. Heats of dilution were estimated using the data collected after binding was saturated.

Molecular Dynamics Simulations

The simulations involving rRaHBP2(D24R) were carried out using AMBER 8,(20) with the PARM99SB force field, which was developed by Cornell et al.(21) and modified by Hornak et al.(22) Simulations on free histamine were carried out using the GAFF forcefield.(23) Initial coordinates were based on the crystal structure reported herein. The structures were preprocessed with XleaP, where the hydrogen atoms were added to the system. The histamine ligand [(C₃H₃N₂(CH₂)₂NH₃⁺] was optimized using the ab initio RHF/6-31G* basis set in Gaussian98,(24) and RESP charges(25) were subsequently generated and fitted.

Simulations of rRaHBP2(D24R) (uncomplexed and in complex with histamine) and free histamine were then subjected to 5000 cycles of energy minimization and afterward immersed in a periodic cubic box of TIP3P water. Approximately 6500 waters were added to each system. After initial energy minimization (2500 cycles), MD simulations were carried under NPT conditions at a pressure of 1 atm and a temperature of 298 K. The particle mesh Ewald technique(26) and SHAKE constraints were used. The cutoff for nonbonded interactions was 12 Å, and the time step was 2 fs. Translational and rotational center-of-mass motions were removed every 5 ps. During the initial phase of an equilibration period (20 ps), the protein backbone atoms and heavy atoms of histamine were harmonically restrained (25 kcal/mol A²). As systems were approaching the target temperature, the restraints were gradually removed. Then both systems were further equilibrated for 5 ns. The production period took 45 ns for each system. The coordinates were saved every 1 ps.

MD trajectories were postprocessed and analyzed using the ptraj module of AMBER 8. The water molecules were removed, and the backbone atoms of mutant HBP were superimposed on the corresponding crystal structure. In order to check the stability and equilibration, rms deviation on heavy atoms and atomic fluctuations of these atoms were calculated along the trajectory. Generalized order parameters(27) were calculated from the trajectory of individual backbone amide bond vectors as(28)

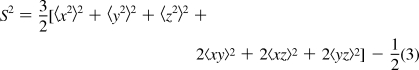where x, y, and z are components of a unit vector along the amide bond and angular brackets denote the time average over the trajectory. Further details behind this approach have been described.^29,30 Convergence of the dynamics of interest was tested using the approach described by Best et al.(31) A cumulative time function S² (τ) is defined using eq 3, with the time averages taken from t = 0 to t = τ. This function was evaluated for 100 equally spaced time-points across the trajectory. The trajectory was deemed to have converged if the difference between the maximum and minimum values of this function over the final 50 time-points was less than 0.05. The statistical error in the derived entropies was estimated by blocking the data into four equal parts and computing the entropies for each part, followed by estimation of the standard error. Mean square displacement and correlation function analysis of solvent water molecules were computed by use of the diffusion and time correlation analysis functionality, respectively, in the ptraj module of AMBER.

Vibrational entropies for the ligand in the free and bound states were computed using the covariance matrix approach of Schlitter.(32) The statistical error in the derived entropies was estimated as above by blocking into eight equal parts followed by estimation of the standard error.

Solvation Thermodynamics Calculations

Ligand free solvation energies were calculated using the COnductor-like Screening MOdel (COSMO).(33) Prior to running calculations, the ligands were optimized using ab initio quantum mechanical calculations (restricted Hartree−Fock), with a 6-31G* basis set. The optimized structures were subjected to COSMO calculations at three different temperature settings (270, 300, and 330 K) in order to extract the enthalpic and entropic contributions to the free energy of solvation. The approximation used herein is based on the assumption that the heat capacity is constant over a certain range of temperatures near the target temperature, T. In the case of solute molecules solvated in water, this approximation (called the finite-difference approach) usually holds near room temperature for temperature ranges (denoted as ΔT) as wide as 50 K. Using the finite-difference approximation, the entropy can be approximated at the target temperature as(34)

where ΔS(T) denotes entropy at target temperature, ΔG(T) is the free energy of solvation energy, and ΔT is the temperature difference. For the calculations presented here ΔT was 30 K.

Results and Discussion

Crystal Structure of rRaHBP2(D24R)-Histamine Complex

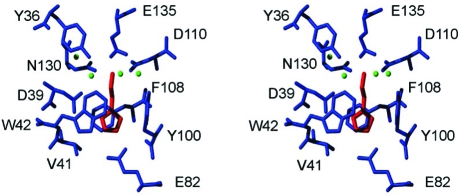
The crystal structure of the complex of rRaHBP2 with histamine revealed two binding sites for the ligand, with one site (H) possessing a higher intrinsic affinity than the other (L).(35) Thus, in order to simplify the thermodynamic analysis of ligand binding, a D24R mutant of the protein was engineered, whereby the bulk and charge of R24 abolishes binding of ligand to the L site. Binding stoichiometry of 1:1 was verified from isothermal titration calorimetry (ITC) experiments (see below). In order to enable a structure-based interpretation of the thermodynamic measurements that follow, the crystal structures of rRaHBP2(D24R) and the rRaHBP2(D24R)-histamine complex were solved. The two structures superimpose well, and the backbone and positioning of many side chains remain consistent. Data collection and processing statistics are shown in Table 1, and a stereo image detailing the binding site with bound histamine is shown in figure 1.

Figure 1.

Stereo view of the binding site of rRaHBP2(D24R) with bound histamine. This site corresponds to the H site of the wild-type protein. Binding-site residues are colored blue, the ligand is colored red, and ordered water molecules are shown as green spheres. Figure prepared using MOLMOL(36)

The ligand is bound in a conformation essentially identical to that in the wild-type protein.(35) There exists an extensive network of hydrogen bonds and ionic interactions involving the nitrogen atoms of the ligand and Y36, D39, E82, D110, and E135. In addition there is a number of ordered water molecules in the binding pocket, which appear to be stabilized in part by hydrogen bond interactions with N130, and the imidazole ring of the histamine is embraced by W42 and F108 as observed by Paesen et al.(35)

ITC Measurements

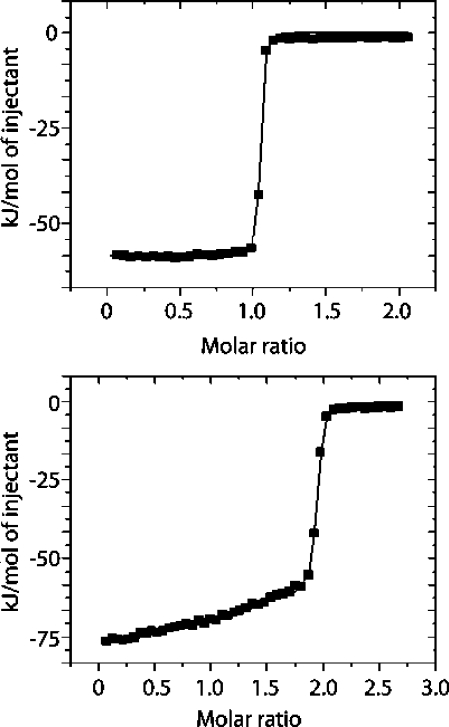
To facilitate an overall assessment of the global thermodynamics of binding of histamine to rRaHBP2 (D24R), isothermal titration calorimetry experiments were performed at 278, 288 and 298 K. Typical isotherms are shown in Figure 2, and the resulting thermodynamic parameters are shown in Table 2. Least-squares fitting of the standard enthalpy at all three temperature gives rise to the change in heat capacity for binding at constant pressure ΔC_p = −780 ± 127 J/mol/K.

Figure 2.

Typical ITC isotherms for the binding of histamine to (above) rRaHBP2(D24R) and (below) wild-type rRaHBP2 at 298 K.

Table 2. Thermodynamic Parameters for the Binding of Histamine to rRaHBP2(D24R) and Wild-Type rRaHBP2 in PBS at pH 7.4.

	temp (K)	ΔH° (kJ/mol)	TΔS° (kJ/mol)	ΔG° (kJ/mol)	Kd (nM)
rRaHBP-2(D24R)
	278	−42.7a ± 0.9b	6.5 ± 1	−49.2 ± 0.6	2.4 ± 0.6
	288	−48.3 ± 3.1	0.4 ± 4.5	−48.8 ± 1.1	2.9 ± 1.3
	298	−58.3 ± 1.2	−9.3 ± 2.5	−49.1 ± 1.4	2.5 ± 1.4
rRaHBP-2 (wt)
H site	298	−70.9 ± 7.1	−24.4 ± 7.3	−46.5 ± 1.3	7.0 ± 3.6
L site	298	−53.2 ± 3.3	−12.0 ± 3.6	−41.2 ± 1.5	59.6 ± 34.8

^aValues are expressed as the mean of three measurements.

^bStandard errors were determined from duplicate experiments by error propagation.

It can be seen that histamine binds with an affinity in the nanomolar range and with 1:1 stoichiometry, in a process that is largely enthalpy driven. By contrast, histamine binds to the wild-type protein with 2:1 stoichiometry (Figure 2). The binding affinity of histamine in the H site of the wild-type protein is similar to that for binding to the D24R mutant, but the binding enthalpies and entropies are somewhat different, which is a manifestation of the enthalpy−entropy compensation phenomenon that is universally observed in biomolecular interactions in solution. Errors in the observed entropies (reported in Table 2) are substantially larger than would typically be anticipated for ITC measurements, which is a reflection of tight affinities that approach the limit of the method. In principle more accurate data could be obtained by use of displacement ITC methods, but this would require a reference ligand with a suitable binding affinity. However, the affinity of histamine for the H site of wild-type rRaHBP-2 derived from ITC (7.0 ± 3.6 nM, Table 2) is in good agreement with that derived from ³H-histamine radioactive binding assays (∼2 nM).(35) The difference in affinity amounts to ca. 3 kJ/mol, and given that ΔH°_b will be faithfully reported by ITC even for very tight binders, this lends confidence that the TΔS°_b values reported in Table 2 are not erroneous.

A further issue concerning the above data concerns the possibility of proton release or binding during the interaction, whereby the observed enthalpy change ΔH°_b may contain contributions from the heat of ionization of the buffer (ΔH°_ion). Such effects must be accounted for to obtain the correct value for ΔH°_b. To assess this effect, titrations between histamine and rRa-HBP2(D24R) were performed in Tris as well as PBS buffer. Tris has a ΔH°_ion of 47.45 kJ/mol at pH 7.4, whereas the relevant ΔH°_ion for phosphate is 3.6 kJ/mol.(37) Any contribution from proton exchange should be easily detectable on the basis of the differences in ΔH°_b for the interaction of histamine with HBP2(D24R) due to the large differences in ionization enthalpy for these buffers. In PBS at 298 K the ΔH°_b for the HBP2(D24R)-histamine interaction is −58.3 ± 1.2 kJ/mol, whereas in Tris it is −61.1 ± 0.2 kJ/mol, suggesting that there are no significant protonation effects for histamine binding to HBP2(D24R).

Entropic Contribution from the Protein Backbone

In order to gain deeper insight into the entropic contribution to binding of histamine to rRaHBP2(D24R), we utilized ¹⁵N NMR relaxation measurements to probe per-residue conformational entropies for backbone amides for the free protein and for the complex. Backbone ¹⁵N longitudinal and transverse relaxation rates (R₁ = 1/T₁ and R₂ = 1/T₂, respectively) were determined for the free protein and the complex with histamine using uniformly ¹⁵N,¹³C (>97%) enriched rRaHBP2(D24R). Amide ¹⁵N and ¹H^N resonance assignments in the free protein (apo) and the complex were determined by use of conventional three-dimensional triple-resonance experiments.^38,39 In total, ¹⁵N R₁, R₂, and NOE data were obtained for 116 amide positions, subject to the requirement for nonoverlapping resonances in both the complex and the apoprotein. Assignments and relaxation data are reported in Supporting Information.

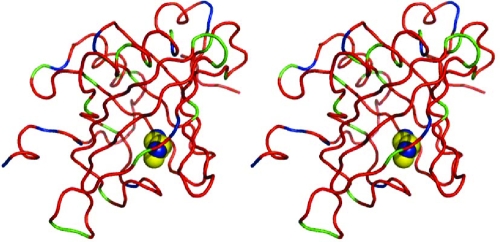
In common with earlier observations and in particular our own measurements on the binding of small pyrazine-derived ligands to a related lipocalin,(1) both positive and negative changes in local backbone entropy (TΔS^P_amide) are observed. These are not restricted to the binding pocket but are dispersed over the protein (figure 3). TΔS^P_amide summed over backbone amides is +12.4 ± 9.8 kJ/mol., i.e., an overall change in backbone entropy that is not statistically different from zero.

Figure 3.

Stereo images of the rRaHBP2(D24R)−histamine complex, showing positive (green) and negative (blue) contributions or no contribution (within the standard error, red) to the overall binding entropy from amide bond vectors on binding histamine (blue and yellow spheres).

Entropic Contribution from Protein Side Chains

Robust methods have been developed for the estimation of protein methyl-containing side-chain entropies by measurement and cross-validation of ²H NMR relaxation parameters for protein side chains.^40,41 However, the dearth of methyl-containing residues in rRaHBP2(D24R), especially in the binding pocket (one valine), renders this approach untenable. In principle, NMR methods could be developed to probe ¹³C relaxation for a more complete set of binding pocket side chains, but as described by Muhandiram et al,(40) the interpretation of such data is fraught with difficulty, particularly in the study of complexes where the relaxation of ¹³C may be influenced substantially by ‘external’ ligand protons.

Thus, in order to examine the contribution of changes in protein side-chain dynamics to overall binding thermodynamics, we resorted to all-atom molecular dynamics simulations of uncomplexed rRaHBP2(D24R) and the analogous complex with histamine with explicit inclusion of solvent water. Side chain entropies for the terminal heavy atom bond of each residue (TΔS^P_side chain) were computed from the simulation (see Materials and Methods), together with TΔS^P_{side chain} for only binding-site residues (D110, F108, Y100, E82, W42, D39, E135, V41, Y36, N130). Moreover, as a test of the robustness of these simulations, TΔS^P_amide values were also computed from the simulation, resulting in the data presented in Table 3. The latter compare favorably with the value (12.4 ± 9.8 kJ/mol) derived above from NMR measurements and taken together suggest an overall increase in entropy on ligand binding. While this result is at first sight counterintuitive, it is not without precedent in the literature.^1,42−45

Table 3. Computed Backbone (N−H) and Side-Chain (Terminal C−C) Entropies for rRaHBP-2(D24R) Derived from a 45 ns All-Atom MD Simulation at 300 K with Explicit Inclusion of Solvent Water.

	ΤΔΔS (complex-apo) kJ/mol
backbone (N−H)	+16.4 ± 1.0
side chain (C−C)	+17.4 ± 1.8
side chain (C−C)a	+12.7 ± 0.16

^aContribution from binding-pocket residue side chains only (namely, D110, F108, Y100, E82, W42, D39, E135, V41, Y36, N130).

Entropic Contributions to Binding from Other Sources

Since the principal thermodynamic parameters are state functions, the binding of a ligand-protein association can conveniently be interpreted using a thermodynamic cycle (Born−Haber cycle) approach,^46,47 leading to the following expression for the overall entropy of binding:

where ΔS°_b is the overall entropy of binding (as determined from ITC experiments for example), ΔS°_i is the “intrinsic” entropic contribution in the absence of solvent, and ΔS°_solvPL, ΔS°_solvP, and ΔS°_solvL are the standard entropies of solvation of the complex, free protein, and free ligand, respectively.

Turning first to ΔS°_i, this comprises changes in protein degrees of freedom on binding that are estimated from the NMR relaxation measurements and MD simulations above, together with changes in ligand degrees of freedom. The latter involve not only changes in internal degrees of freedom but also the loss of translational and rotational entropy. Assuming that internal degrees of freedom of the ligand are essentially “frozen” on binding, the corresponding unfavorable contribution from the three relevant internal degrees of freedom of histamine amounts to ca. −12 kJ/mol.(48) Moreover, the entropic contribution from loss of translational and rotational degrees of freedom of a ligand depends on the logarithm of the molecular mass, and on the basis of earlier work this represents an unfavorable contribution that can be estimated as ca. −25 kJ/mol.(49) In addition to these contributions, there is also a contribution from the loss in vibrational degrees of freedom of the ligand on binding.(50) This was estimated from the covariance matrix approach of Schlitter (see Materials and Methods),(32) leading to an unfavorable contribution of ca. −22 ± 2.4 kJ/mol.

In earlier work on the binding of small hydrophobic ligands to the major urinary protein (MUP), we were able to measure experimentally the solvation entropy of the ligand ΔS°_solvL by use of water/vapor partitioning experiments.(4) In the present case, the nonvolatility of the histamine ligand renders this approach untenable, and hence we resorted to Conductor-Like Screening Model (COSMO) calculations(33) to estimate the solvation thermodynamics of histamine (see Materials and Methods). Clearly it is very difficult to assess the accuracy of such calculations, but the experimental solvation thermodynamics of two related “fragments” of histamine have been reported, and these are given in Table 4 together with the analogous COSMO-derived parameters. It can be seen that the solvation free energies are reproduced very well, and the solvation entropies and enthalpies reasonably well (for n-propylamine) compared with experiment, which lends some confidence in the computed values for histamine.

Table 4. Solvation Thermodynamics for Histamine and Reference Molecules at 300 K Calculated Using COSMO(33).

ligand	ΔH° (kJ/mol)	TΔS° (kJ/mol)	ΔG° (kJ/mol)
histamine	−137.2	−67.1	−70.1
2-methyl imidazole	−96.3	−53.3	−43.0
(experimental)a			−42.9
n-propylamine	−65.5	−49.0	−16.5
(experimental)a	−55.8	−37.4	−18.4

^aValues taken from ref (51).

Decomposition of the Overall Entropy of Binding

Taking together with the above entropic data for the binding of histamine to rRaHBP-2(D24R), it is possible to estimate the entropic contributions to binding from ligand, protein, and solvent, as shown in Table 5. Here, the desolvation contribution from the protein/complex TΔS°_solvPL − ΔS°_solvP is effectively impossible to measure experimentally or to compute, but this can be determined arithmetically since it is the only unknown. For comparison, also shown in Table 5 are the entropic contributions derived previously(4) for the binding of the small hydrophobic ligand 2-methoxy-3-isopropylpyrazine (IPMP) to MUP.

Table 5. Thermodynamic Decomposition of the Entropic Contribution to Binding of Histamine to rRaHBP2(D24R) at 300 K.

Description	MUP-IPMPa	rRaHBP2(D24R)−histamine
TΔS°i
protein DOF	−0.8 ± 3.8	+29.8 ± 9.9
ligand DOF	ca. −37	ca. −59
−TΔS°solvL
ligand desolvation	+26.7 ± 8.4	+67.1
TΔS°solvPL − TΔS°solvP
desolvation of protein/complex	+0.4 ± 9.2	−47 ± 10.2
TΔS°b
observed entropy	−10.7 ± 0.5	−9.3 ± 2.5

^aData taken from ref (4).

Driving Forces for Ligand Binding in rRaHBP2(D24R) Compared with rMUP

A comparison of the entropic contributions to binding in MUP versus rRaHBP2(D24R) offers interesting insight into the binding process. Remarkably, the overall entropy of binding TΔS°_b is the same within error for both proteins, yet the contributions from protein, ligand, and solvent are very different. In MUP, a favorable contribution to binding entropy derives from ligand desolvation, which cannot however overcome the unfavorable contribution from “freezing” ligand degrees of freedom on binding. The favorable entropic contribution from desolvation of the protein binding pocket that one would predict in a “classical” hydrophobic interaction is absent in MUP, since the occluded binding pocket is substantially desolvated prior to binding.(2) This phenomenon has subsequently been observed in other proteins.^52,53

In the case of rRaHBP2(D24R), the dominant favorable entropic contribution to binding again derives from ligand desolvation, with a significant contribution from protein degrees of freedom. However, the overall entropic contribution to binding is still unfavorable, leading to the suggestion that the entropic contribution from desolvation of the protein binding pocket is strongly unfavorable.

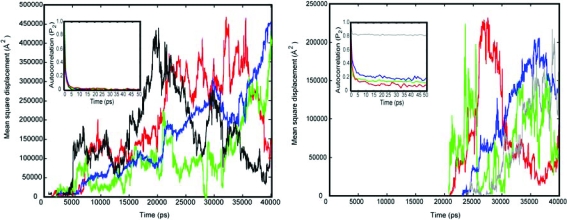
Further insight into the possible source of this contribution can be had by examining the solvation of the binding pocket of rRaHBP2(D24R) and its reorganization on binding histamine during the course of the above MD simulations. An average of five to six water molecules is observed in the binding pocket of the protein over the time-course of the simulation of rRaHBP2(D24R) in the absence of ligand. Analysis of the diffusion and rotational correlation functions of these solvent molecules suggests that their dynamics are very similar to those of bulk water (Figure 4).

Figure 4.

(Left) Typical mean square displacements of solvent water molecules in the binding pocket of uncomplexed rRaHBP2(D24R) (red, green, and blue traces) in comparison with bulk water (black trace). (Right) Typical mean square displacements of solvent water molecules in the binding pocket of rRaHBP2(D24R) in complex with histamine (red, green, blue, and gray traces). In both panels the inset shows rotational autocorrelation functions for these waters using the same color scheme.

Thus, the return of these water molecules to bulk solution on ligand binding would be expected to offer no significant contribution to the binding entropy. In contrast, four solvent water molecules are sequestered in the binding pocket in the complex, whose diffusion (measured by mean square displacement) is indicative of a degree of order substantially higher than bulk; unlike solvent water molecules in the binding pocket of the uncomplexed protein, these water molecules have residence times extending to 20 ns or more during the simulation (Figure 4). Given that the translation entropy represents the dominant contribution to the overall entropy of water,(54) these data indicate that the presence of ligand results in the sequestration of water molecules into the binding pocket with significantly lower entropy than bulk water. This is also borne out by the rotational correlation times of the water molecules in the complex, which do not decay to zero on a time-scale of 50 ps or more, with one water molecule (gray trace in Figure 4) that appears to be very ordered indeed. These results are consistent with stabilization of waters in the bound state by a hydrogen-bonding network subtended by the combined presence of the polar side chains of Glu 135, Asp 110, and Tyr 100 together with the charged amide group of the ligand.

It is difficult to estimate the entropic contribution from these water molecules, but it is possible to set limits. Recent theoretical considerations suggest that the total entropy of liquid water at 298 K is ca. 21 kJ/mol, of which ca. 70% is attributable to the translational entropy, giving a maximum contribution of ca. 15 kJ/mol for “translationally ordered” waters.(54) On the other hand, on the basis of the experimental entropies of salt hydrates, Dunitz estimated that the entropy cost of transferring a water molecule from bulk solvent to protein is in the region from zero to ca. −10 kJ/mol, with the higher values corresponding to water molecules that are most firmly bound to metal centers or polar groups. Thus, the unfavorable entropic contribution from sequestration of four ordered water molecules in the rRaHBP2(D24R)-histamine complex can be estimated as ca. −30 to −40 kJ/mol, which is not inconsistent with the data in Table 5 considering sources of error. These observations are also qualitatively consistent with the observed sign of ΔC_p on binding (see above). Using the qualitative relationship derived by Spolar et al.,(55) the hydration heat capacity of histamine can be estimated as ca. +400 J/mol/K, i.e., a contribution of −400 J/mol/K to ΔC_p on binding. In addition, the sequestration of water molecules into the binding pocket amounts to a net solvation of polar groups, which is known to make a negative contribution to ΔC_p.(56) Our studies suggest that this contribution is on the order of −300 J/mol/K, but this value must be interpreted with caution since there are potentially a number of other contributions to ΔC_p that the present studies are unable to capture.(57)

In reaching the conclusion that the sequestration of solvent water molecules in the complex contributes to the unfavorable entropic binding signature, we were struck with parallels with carbohydrate−protein interactions. These systems typically exhibit extreme enthalpy−entropy compensation, with very large unfavorable entropies of binding.(58) Over a decade ago, in seeking to rationalize this phenomenon, and on the basis of the extremely limited data that were available at the time, Lemieux proposed(59) “At nonpolar surfaces...an organized layer of molecules is formed that, on being released to bulk, provides an increase in entropy. In contrast, the liberation of water molecules from polyamphiphilic surfaces causes important decreases in both ΔH and TΔS....” Given that this hypothesis has yet to find experimental support to the best of our knowledge, the present data suggest that an alternative explanation might entail the sequestration of solvent water molecules on complexation.

Supporting Information Available

Complete refs (20) and (24), backbone resonance assignments, R1, R2 and ssNOE values, ¹⁵N amide model-free parameters and TΔS_conf values for backbone amide groups for rRaHBP2(D24R) and rRaHBP2(D24R) in complex with histamine. This material is available free of charge via the Internet at http://pubs.acs.org.