Evaluation of structural equation mixture models Parameter estimates and correct class assignment

Abstract

Structural Equation Mixture Models(SEMMs) are latent class models that permit the estimation of a structural equation model within each class. Fitting SEMMs is illustrated using data from one wave of the Notre Dame Longitudinal Study of Aging. Based on the model used in the illustration, SEMM parameter estimation and correct class assignment are investigated in a large scale simulation study. Design factors of the simulation study are (im)balanced class proportions, (im)balanced factor variances, sample size, and class separation. We compare the fit of models with correct and misspecified within-class structural relations. In addition, we investigate the potential to fit SEMMs with binary indicators. The structure of within-class distributions can be recovered under a wide variety of conditions, indicating the general potential and flexibility of SEMMs to test complex within-class models. Correct class assignment is limited.

Introduction

Finite mixture models have a long history of being used to test hypotheses about unobserved population heterogeneity (e.g., Pearson, 1894, 1895; Hosmer, 1973; Titterington, Smith, & Makov, 1985; McLachlan & Peel, 2000). Structural Equation Mixture Models (SEMMs) are a special case of finite mixture models which have been proposed to compare latent classes while specifying Structural Equation Models (SEMs) within each class (Jedidi, Jagpal, & DeSarbo, 1997b). SEMMs are a generalization of Factor Mixture Models (FMMs; e.g., Yung, 1997; Dolan & van der Maas, 1998; Muthén & Shedden, 1999; Lubke & Neale, 2006) to include regressions between latent factors within each class (Arminger, Stein, & Wittenberg, 1999; Henson, Reise, & Kim, 2007). FMMs have received more research attention and application than SEMMs, primarily in the special case of the Growth Mixture Model (GMM) and its variants (e.g. Muthén & Muthén, 2000; Nagin & Land, 1993). Applied use of the SEMM has been seen in marketing research on market segmentation (Jedidi, Jagpal, & DeSarbo, 1997a) and in sociological research on individual lifestyles (Arminger & Stein, 1997). Potential applications within psychology are abundant, and include in principle any investigation of structural relations between several factors that might differ across unobserved groups.

Initial work on the performance of SEMM's found that within class parameter estimates can typically be recovered when the correct number of classes is specified and the correct structural relations between factors within classes are specified (Henson et al., 2007). This is true in cases where classes differed with respect to latent variable correlations, with respect to the factor mean separation, or a combination of the two. As expected, within class parameter estimates were less accurate for the smaller of two classes when relative class sizes were imbalanced (e.g., 90% in the larger class and 10% in the smaller class with total sample sizes of 500, 1500, and 2500). However, it was also shown that currently used fit statistics could not always correctly identify the true number of classes when comparing models with increasing numbers of classes, especially for smaller sample sizes (Henson et al., 2007).

The current study extends the prior research in various ways. Substantive research in psychology, psychiatry, health, and aging often posits classes of very small sizes relative to the majority. We examine a greater imbalance in relative class sizes than has previously been explored. In addition, the empirically relevant condition where latent variable variances are imbalanced across classes is considered. For example, depending on the item means or thresholds, respondents in the majority class may have very little variance in their responses while the minority class may have a much larger variability, or vice versa. The aspects of imbalanced class size and imbalanced factor variances are investigated for varying sample sizes, and class separations. While prior research has focused on finding the correct number of classes, the current study focuses on finding the correct regression relationships between latent variables. The number of latent factors within class is extended to three, and different structural relations are investigated across classes. In addition, this study investigates the correct assignment of subjects to their true class. The response format is continuous, as empirical studies with several factors commonly rely on subscale scores. Additional results with binary data are provided.

To demonstrate several practical aspects of fitting SEMM models to data, and to obtain reasonable parameter values to inform data generation for the simulation study, the current study starts with an illustration using a subset of the data from the Notre Dame Longitudinal Study of Aging (Wallace, Bisconti, & Bergeman, 2001). The data are subscales measuring the three factors stress, hardiness, and life satisfaction. The interrelations of these three factors might vary substantially in the elderly, and it might be overly simplistic to assume a homogeneous population. Instead, various subpopulations may exist that differ with respect to the structural relations between the three factors. One way to investigate heterogeneity is to use observed grouping variables such as gender. However, it is often the case that a single observed grouping variable can not fully account for all heterogeneity. Attempting to use multiple grouping variables can quickly lead to a large number of cells in a factorial table of grouping variables, complicating the interpretation of results. An alternative is to attempt to account for heterogeneity using a small number of latent classes. In the current study a SEMM model is used to explore latent class membership and differences in regression relationships between stress, hardiness, and life satisfaction across classes.

The current study combines the illustration of fitting SEMMs to empirical data and a large scale simulation study. The focus of the simulation study is threefold. The first aim is to evaluate the conditions under which differences in the covariance structure of within class factors can be detected when fitting SEMM's. Specifically, we focus on two aspects, namely (i) whether fitting models with unconstrained factor covariance matrices can detect evidence for differences in factor regressions between classes, and (ii) whether models with correctly and incorrectly specified within-class factor regressions can be distinguished. The second goal of this study is the investigation of parameter estimate accuracy for the within-class structural relations. Thirdly, correct assignment of cases to the classes is assessed.

The paper is structured as follows. A description of the SEMM as an extension of the FMM is followed by the application of the model to data from one wave¹ of the Notre Dame Longitudinal Study of Aging. The application serves to highlight aspects of the performance of SEMMs that are investigated in detail in the simulation study. The simulation study addresses the three aims described above, and is supplemented with additional results concerning larger effect sizes of within-class structural relations and models with binary responses.

The Structural Equation Mixture Model

A basic assumption of finite mixture models is that the distribution of the observed data is a mixture distribution. Mixture distributions are a weighted sum of two or more component distributions, and the weights correspond to the relative size of a component. The latent classes of a mixture model correspond directly to the component distributions. Mixture models for k classes assume a mixture distribution with k components, and specify submodels for each of the component distribution, for example which parameters are specific for a given component or latent class, and which parameters are class-invariant. The latent classes can be interpreted in two ways. In a direct interpretation the latent classes are basically equated to naturally occurring qualitatively or quantitatively unique groups of subjects. This interpretation has made mixture modeling an appealing tool for substantive researchers, and has motivated post hoc tests that are based on assigning subjects to the latent classes. Alternatively, an indirect interpretation simply states that the latent classes are used to approximate non-normal distributions, and that there is no necessary one-to-one relation between latent classes and distinct groups of subjects (Titterington et al., 1985; Lubke & Neale, 2006, 2008).

Regardless of how classes are interpreted, the joint distribution of the observed data is the weighted sum of the component distributions. Details of general finite mixture models can be found in Everitt and Hand (1981), Titterington et al. (1985), or McLachlan and Peel (2000). SEMMs assume multivariate normal component distributions, and impose a SEM on the within class mean vector and covariance matrix. The SEMM is given by

$$f(\mathbf{y})=\sum _{k=1}^K{\pi }_k{\mathit{\varphi }}_k(\mathbf{y};{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)$$ (1)

where y is a vector of p observed continuous variables, K is the number of classes, π_k are the class proportions where ${\sum }_{k=1}^K{\pi }_k=1$, ϕ_k are multivariate normal probability density functions (PDF) with class specific mean vectors μ_k and class specific covariance matrices Σ_k. The mean vectors and covariance matrices can be further structured by imposing a factor model, leading to the factor mixture model (FMM)

$${\mathbf{\mu }}_k={\mathbf{\nu }}_k+{\mathbf{\Lambda }}_k{\mathbf{\alpha }}_k$$ (2)

$${\mathbf{\Sigma }}_k={\mathbf{\Lambda }}_k{\mathbf{\Psi }}_k{\mathbf{\Lambda }}_k^{\prime }+{\mathbf{\Theta }}_k,$$ (3)

where ν_k is a p × 1 vector of equation intercepts in class k, p is the number of observed variables, Λ_k is a p × m_k matrix of factor loadings in class k, m_k is the number of factors in class k, α_k is an m_k × 1 vector of factor means in class k, Ψ_k is the m_k × m_k covariance matrix for the factors in class k, and Θ_k is a p × p covariance matrix of the measurement errors with error variances on the diagonal. Extending the FMM to the SEMM, the model implied class specific mean vectors and covariance matrices are given as

$${\mathbf{\mu }}_k={\mathbf{\nu }}_k+{\mathbf{\Lambda }}_k{(\mathbf{I}-{\mathbf{B}}_k)}^{\prime }{\mathbf{\alpha }}_k$$ (4)

$${\mathbf{\Sigma }}_k={\mathbf{\Lambda }}_k{(\mathbf{I}-{\mathbf{B}}_k)}^{\prime }{\mathbf{\Psi }}_k[{(\mathbf{I}-{\mathbf{B}}_k)}^{\prime }]\prime {\mathbf{\Lambda }}_k^{\prime }+{\mathbf{\Theta }}_k$$ (5)

where I is a m_k × m_k identity matrix, and B_k is an m_k × m_k matrix of regression coefficients between factors.

The model implied mean vector and covariance matrices given in Equations 2 and 3 permit specification of within class factor means, factor variances and covariances, factor loadings, intercepts, and error variances (subject to identifiability constraints). FMM's have been described in a growing body of literature including Yung (1997), Vermunt and Magidson (2003), and Lubke and Muthén (2005). The model implied mean vector and covariance matrices given Equations 4 and 5 extend the FMM, allowing the specification of structural relations between factors. SEMM's have been described by Jedidi et al. (1997b), Dolan and van der Maas (1998), Arminger et al. (1999), Bauer and Curran (2004), and Henson et al. (2007).

Ordered categorical and binary data can be modeled by assuming that a continuous latent response variable, typically denoted y*, underlies the observed categorical data, and by imposing a threshold structure on the distribution of the latent response variable (Agresti, 2002). Using this approach, Equation 1 is rewritten for ordered category and binary data as

$$f(\mathbf{y}\ast )=\sum _{k=1}^K{\pi }_k{\mathit{\varphi }}_k({\mathbf{y}}^{\ast };{\mathbf{\mu }}_k^{\ast },{\mathbf{\Sigma }}_k^{\ast }).$$ (6)

Additional constraints are needed to identify this model, and commonly involve assuming standard normal distributions for the latent response variables and setting the regression intercepts ν in equations 2 and 4 to zero. More specific information concerning the model for categorical data can be found in Millsap and Tein (2004) and Muthén and Asparouhov (2002).

Fitting SEMMs to empirical data: An illustration using data from the Notre Dame Longitudinal Study of Aging

In this section the relationship of stress, hardiness, and life satisfaction in an elderly sample of 313 participants is used to illustrate a SEMM. The section focuses on some of the general decisions that play a role when conducting a SEMM analysis.

The data come from the third wave of the Notre Dame Longitudinal Study of Aging. Participants were recruited via systematic phone number sampling as described in Wallace et al. (2001). A stress factor was measured by the items of the Perceived Stress Scale (PSS; Cohen, Kamarck, & Mermelstein, 1983), and asks about feelings during the last month using items such as ‘How often have you felt that things were going your way’. The items of the commitment subscale of a hardiness measure (Bartone, Ursano, Wright, & Ingraham, 1989) were used as a second factor. An example of a commitment item is ‘By working hard you can always achieve your goals’. A life satisfaction factor was measured by items from the Life Satisfaction scale (Wood, Wylie, & Sheafor, 1969). The scale includes items such as ‘I feel my age, but it does not bother me’. All indicators are 4-point ordered category data, and are modeled as such. The stress factor, commitment factor, and life satisfaction factors are use to illustrate the application of SEMM analyses.

Preliminary steps and considerations

Prior to fitting a hypothesized SEMM, researchers should consider the complexity of the model in view of the available sample size. The data subset used in the current illustration consists of 313 participants with complete data. The three scales measuring stress, commitment, and life satisfaction have a total of 41 items, each with 4 response categories. To reduce the number of model parameters for the current illustration, we select 4 items each from the life satisfaction and perceived stress scales, and 2 items from the commitment scale. In an empirical study, item selection should be guided by theoretical considerations as well as considerations concerning the number of parameters and the measurement properties of the items ².

After establishing the structure of the measurement model, factor mixture models are fitted with an increasing number of classes. This is done while imposing minimal constraints on the within class parameters because imposing incorrect restrictions may result in the over-extraction of classes (Lubke & Neale, 2006, 2008). Note that it is usually unrealistic to assume a priori that the variances of the factors are class invariant. When different structural relations between factors are hypothesized, it is especially appropriate to fit models with class specific factor variances. Finding an adequate number of classes and investigating measurement invariance across classes is carried out simultaneously since a measurement invariant model with, say, 3 classes can provide a better fit than a non-invariant model with 2 classes. Issues related to model comparisons and model selection have been described elsewhere (Lubke & Neale, 2006, 2008). To focus on SEMM specific issues, we start the illustration at the point where a 2 class 3 factor FMM with invariant loadings and class-specific thresholds has been determined as the best fitting FMM for the aging data.

In addition to establishing the measurement models and the number of classes, another important issue to consider are random starting values. It is known that multiple sets of random starting values need to be used when fitting mixture models to avoid acceptances of local maxima. In practice, replicating the best log-likelihood value for multiple starting values enhances the confidence in the results. It should be noted though that replicating the best likelihood value is neither necessary or sufficient to guarantee that the global maximum has been found. In practice, software defaults for the number of starting values are not necessarily sufficient. The number of random starting values needed can vary widely depending on model complexity and data quality. In addition, the stability of the solution for the best likelihood can be checked by comparing it to the solutions for random starting values that produced similarly high likelihoods. ³

Empirical data results

The illustration with data from wave 3 of the Notre Dame Longitudinal Study of Aging consists of initially fitting two different SEMM's, which represent two different hypotheses regarding the ways perceived stress is influenced by life satisfaction and commitment. The pattern of class specific factor variances and covariances of a fitted FMM should be consistent with the structural relations among factors that are specified in a SEMM. For both of the initial SEMM's, in the first class we specify commitment and satisfaction to be correlated predictors of stress. The second class differs for the two models. In SEMM 1, commitment predicts satisfaction which in turn predicts stress. In SEMM 2, satisfaction predicts commitment which predicts stress. In sum, the structural model in the first class is rather lenient in both models, whereas in the second class, different causal chains are specified.

It should be noted that models with different structural relations between factors are usually not nested. Model comparisons are carried out based on using the BIC information criteria as recommended for mixture models by Nylund, Asparouhov, and Muthén (2007). Bootstrapping the likelihood ratio test is infeasible in the current analysis due to computation times for categorical indicators, but might be practical when using continuous data. Based on the BIC, SEMM 2 provides the better fit (BIC is 5766.61 versus 5768.99 for SEMM 1). Both models result in similar class proportions, which are approximately .75 and .25 for the first and second classes, respectively. The larger class is more likely than the smaller class to use lower response categories on most items, which corresponds to higher stress, lower satisfaction, and lower commitment. The regression parameters describing the relations between the three factor have signs expected by theory, satisfaction and commitment are positively related, and higher levels of those factors predict lower stress levels.

In the better fitting SEMM 2, the regression of stress on commitment in the larger class (i.e., where commitment and life satisfaction are correlated predictors of stress) is not statistically significant. This may be due to low power related to the relatively small sample size, but might also indicate a more adequate that a model in which this regression parameter is fixed to zero. This can be translated into a model where in one class satisfaction predicts commitment which in turn predicts stress, whereas in the other class commitment predicts satisfaction which in turn predicts stress. The model, SEMM 3, turns out as the best fitting model with a BIC equalling 5760.89. The likelihood values, number of estimated parameters, and BIC's are presented in Table 1. If based on the BIC we decide that SEMM 3 provides the most adequate description of the structural relations between factors, we would then conclude that the smaller class of participants with lower stress levels, higher life satisfaction, and higher commitment can be characterized by a pattern where the effect of satisfaction on stress is fully mediated by commitment, whereas in the large class with higher stress levels, satisfaction has a direct effect on stress, and is predicted by commitment. The reader is cautioned to remember the limitation of structural equation models to provide causal information for data collected at one time point (e.g., Bollen, 1989). The same caution applies to SEMMs.

Table 1. Model fit of the three SEMM's fitted to data of Notre Dame Longitudinal Study of Aging Data.

models	likelihood	number of parameters	BIC
SEMM 1	-2657.519	79	5768.99
SEMM 2	-2656.329	79	5766.61
SEMM 3	-2656.311	78	5760.89

Note. Table entries are the likelihood value, the number of estimated parameters, and the BIC.

The results of the aging data SEMM analysis highlight several issues that deserve consideration when conducting a SEMM analysis. Table 1 illustrates that the differences between the three fitted models are small. This raises the question what the chance is to choose a correct model when comparing complex mixture models. In other words, how confident can one be to draw substantive conclusions based on the best fitting model, especially if competing models have very different interpretations? The issue of model selection is addressed in the simulation study by examining models with true and misspecified regression relationships between factors. A second question concerns the precision of the parameter estimates. In the smaller class in SEMM 3, the regression coefficient of stress on commitment is −.489 with a standard error of .135, and the coefficient of commitment on satisfaction is .438(.156). In the larger class, we have stress on satisfaction equalling −.71(.085), and satisfaction on commitment .359(.140). Although the effects are statistically significant, the standard errors are relatively large. Precision of parameter estimates is also addressed in the simulation, and includes not only regression coefficients, but also the variances of the factors. We investigate simulated data with different factor variances between classes since this is empirically relevant. For example, in psychiatric data the variability might be considerably smaller in the affected class (or vice versa, depending on the measurement instrument).

A third issue pertains to the combination of sample size and effect size needed to detect statistically significant class specific regression coefficients between the factors. In the Notre Dame Longitudinal Study of Aging the sample size is 313 which is not uncommon in longitudinal studies focusing on human development over time. The simulation study is designed to address the question whether complex mixture models require larger sample sizes and/or effect sizes than in the empirical example to produce reliable results.

The final question concerns correct class assignment. Correct assignment is obviously impossible to assess when analyzing empirical data since true class membership is not known.⁴ However, researchers might be interested in an indication of which proportion of correct assignment to expect when fitting these rather complex models. Correct classification becomes important especially if in a given empirical setting a specific class would benefit from receiving class specific treatment. In addition to examining the proportion of correct assignment under a variety of conditions, we compare correct assignment when fitting SEMMs to correct assignment when fitting FMM's. If the SEMM is an adequate model for a given data set, then it may improve correct assignment when compared to the corresponding FMM.

Simulation Study

In the first part of the simulation study, the performance of two-class SEMMs with continuous outcomes is explored under a number of different conditions outlined in detail below. The second part of the simulation consists of two additional analyses. The first additional analysis replicates the first simulation study in its entirety with larger regression coefficients between factors in the first class. This results in larger differences between first and second class factor correlation coefficients, or, in other words, a larger effect size between class factor correlation matrices. The second additional analysis explores SEMM performance with binary observed item scores. Due to the computation time needed to estimate the binary models, this part is carried out only for a small subset of the simulation design.

Simulation Study Design

Research questions in the behavioral and health related sciences often concern conditions with low prevalence rates. This is incorporated into the current study by comparing SEMM performance for data that have severely imbalanced relative class sizes to data that have balanced relative class sizes. The second primary condition in the study design is the relative magnitude of factor variability in each class, where conditions with both balanced and imbalanced class variability are compared. Prior research has shown that class-specific factor variances may lead to the over-extraction of classes when fitting FMM models with class-invariant factor variances and increasing numbers of classes (Lubke & Neale, 2006), but this has not been explored in a SEMM context. These two primary conditions, with two levels each, are crossed in a 2 × 2 factorial design. Within each of the 4 cells there is a 3 × 4 factorial design with 3 sample sizes and 4 levels of class separation as measured by the multivariate Mahalanobis distance.⁵

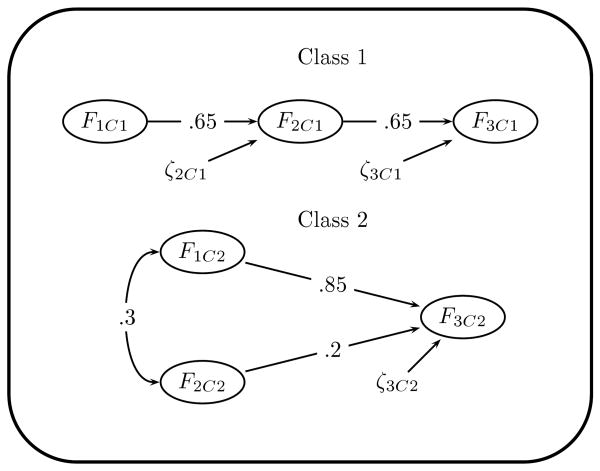
The simulation study conditions are summarized in Table 2, and a diagram of the SEMM model under which the data are generated is given in Figure 1. The structure shown in Table 2, with references to blocks A, B, C, and D will be used throughout the remainder of the paper.

Table 2. Study design matrix.

var(FqC1)	π1 = 0.50		π1 = 0.05
1	A		B
5	C		D
Where the blocks A, B, C, and D are structured as
	Mahalanobis Distance
	0.5	1.0	1.5	2.0
N = 100
N = 300
N = 1000

Note. π₁ is the proportion of cases in the first class, N is the number of cases, and Var(F_qC1) is the factor variance for all factors in the first class. In the second class, π₂ = 1 − π₁, and Var(F_qC2) = 1 for all conditions. For each cell in the lower table, 150 data sets were generated.

Figure 1.

Path diagram for the data generating model (SEMM123) in class 1 and class 2. Regression parameters are given on their corresponding paths. The four indicators per factor are excluded for clarity.

The variances of the factors in the second class are constant and equal 1 for all conditions. The variance of all factors in the first class are either 1 or 5. See the rows of Table 2, that is, blocks A and B versus blocks C and D. The relative class size of class 1 (i.e., the class proportion π_k in Equation 1) is π₁ = 0.50 or π₁ = 0.05. See the columns of Table 2, that is, blocks A and C versus blocks B and D. The class proportions of the second class π₂ are equal to 1 − π₁. Mahalanobis distances are controlled by manipulating the value of the mean of the first factor in class 1 E(F_1C1) while the means of all other factors in both classes are held constant at 0. The population values for the measurement model parameter values are given in the Appendix. The values of the regression parameters between factors are shown in Figure 1.

The second part of the current simulation study consists of two additional simulations focusing on a larger effect size between class specific factor regression parameters, and binary data. In the larger effect size conditions, the first part of the simulation study is replicated in its entirety with larger values for the regression parameters in the first class (both .806 instead of .65; see Figure 1). In the first part of the simulation study, model implied factor correlations are small to medium according to Cohen. For the larger effect size replication, the model implied factor correlations are medium to large according to Cohen. Sample size calculations associated with these effect sizes are described in the additional analyses section below.

Due to the long times needed to fit models with categorical data, only a small number of binary conditions are examined. Results from dichotomized versions of the first 30 data sets found in block A of the N = 300 larger effect size conditions with Mahalanobis distances of 1.0 and 1.5 are reported.

Data Generation

For each condition in the first part of the study, 150 data sets are generated according to the SEMM presented in Figure 1 for each cell of Table 2, resulting in 7200 data sets. Four observed variables are generated as indicators for each of the three multivariate normal factors. Error variances are multivariate normally distributed with zero means and variances equalling 0.5.⁶ The errors for each indicator are uncorrelated with each other and are uncorrelated with the factors. The factor loadings, intercepts, and error variances are class invariant, and there are no cross loadings. The class specific parameters include the regression and/or correlation parameters between factors as shown in Figure 1. Factor means are set to 0 for all factors in both classes except for the mean of the first factor in class 1 (F_1C1). The value of the mean of F1 is varied to obtain the four Mahalanobis distance conditions given in Table 2.

Class membership is generated as a random variable for each individual with the expected class proportions being either π₁ = π₂ = .5 or π₁ = .05 for class 1 and π₂ = .95 for class 2 as shown in Table 2. In N = 100 conditions with π₁ = .05, the expected number of cases for the first class is 5 cases, though it is possible to observe zero cases due to sampling fluctuations. This mimics the potential to not observe any cases of a small class in an empirical analysis when the total sample size is small. In addition to including conditions where the class proportions are imbalanced between classes, conditions of class specific factor variances are included. The factor variances are set to either to 1 or 5 for all factors the first class, while the variance of all factors in the second class are always 1.⁷

Model Fitting

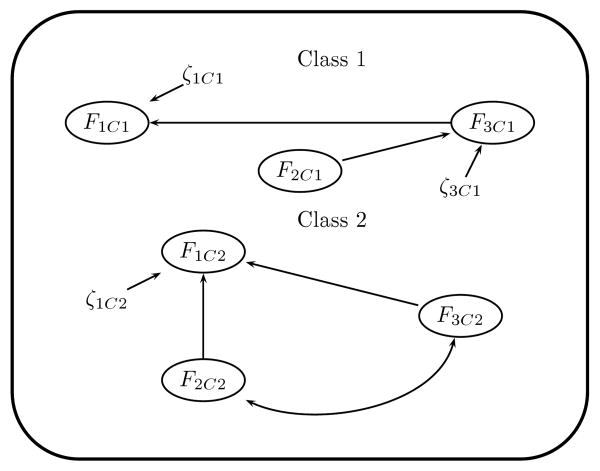
Three models are fit to each data set, resulting in 21,600 analyses. The first model is the model from which the data was generated (SEMM123, see Figure 1), which is referred to as a ‘true’ model. In an empirical data analysis, the ‘true’ model is of course not known, and, as discussed above in the description of the SEMM, any model that fits real data well is only an approximation. The next fitted model is the FMM which does not impose a specific structure on the covariance matrix of the factors. Note that the FMM model is also a true model in the sense that no parameters are misspecified. The true SEMM is nested within the FMM. The third model reflects incorrectly specified structural relations between factors (SEMM231, see Figure 2). Specifically, the order of the causal chain is misspecified, and factor one is misplaced as the terminal rather than an originating factor in both classes, as is shown in Figure 2.

Figure 2.

Path diagram for the data generating model (SEMM231) between factors in class 1 and class 2. Factor indicators are excluded for clarity.

As mentioned in the previous section, only the first factor of the first class had a non-zero mean and factor mean differences between classes have a major impact on class separation as defined by the Mahalanobis distance. One goal of the current study is to explore the performance of SEMMs when class separation is driven by a single variable in a chain of regression relationships. Pilot results found no appreciable differences in model fit, parameter estimation, or correct assignment of cases to classes when comparing data generated with factor mean differences in originating factors versus in terminal factors, which is consistent with what Henson et al. (2007) found. Therefore, the current study is confined to data generated with the separation in the originating factor of the SEMM and exploring the misspecification of reversing the causal chain and specifying the originating factor as the terminal factor of the chain.

For all three models, the loading for the first indicator for each factor is fixed to be one and the loadings, error variances, and intercepts are constrained to be class invariant (Meredith, 1993). The factor variances are free to be estimated in both classes, and the factor means in an arbitrarily chosen reference class are fixed to be zero for reasons of model identification. Class 2 is the reference class throughout this simulation study. Even though the means of the second and third factors in the first class are zero, the model implied means will be non-zero since regression relationships are specified between factors. Because the factor means are fixed to zero in the second class, the estimated factor means in class one are to be interpreted as factor mean differences between classes. Each fitted model had 10 initial iterations computed for 800 sets of random starting values. Of the 800 sets of random starting values, the 10 with the largest log-likelihood values are iterated to convergence and best solution of these 10 is used as the final result.

Model comparisons are based on the Bayesian information criterion (BIC) and the sample size adjusted Bayesian information criterion (saBIC).⁸ Nylund et al. (2007) have shown that these information criteria perform well under a variety of conditions. An alternative would consist of bootstrapping the Likelihood Ratio Test. However, this is not feasible in large scale simulations due to the trade-off between time constraints and the computational demands of bootstrapping procedures.

Parameter estimates are summarized across the 150 data sets within each condition. Computation time restricted this study to 150 replications per condition, which is not sufficient to examine whether standard errors are correct.⁹ At the end of the model fitting process, cases are assigned to their most likely class using the highest posterior class probability (i.e., modal assignment). The membership in the k^th class is computed using Bayes' theorem

$$f_k({\pi }_k|y)=\frac{f_k(y|{\pi }_k)f_k({\pi }_k)}{f_k(y)}$$ (7)

where f_k(y|π_k) is the conditional distribution of Equation 1 for the k^th class, f_k(π_k) is equal to π_k,¹⁰ and f_k(y) is as given in Equation 1. To obtain the probability of membership in the k^th class, an individual's observed scores and the parameters estimates for the k^th class are substituted into Equation 7. This is done for each case for each of the k classes, noting that the k probabilities for each case sum to 1 (within rounding error). The individual is then assigned to the class with the highest probability. Using the known true class and the assigned class memberships, the number of correctly and incorrectly assigned subjects is computed separately for true class 1 and true class 2 subjects. In addition, we compute the Hubert and Arabie Adjusted Rand Index (ARI_HA, a chance corrected proportion correct assignment; Hubert & Arabie, 1985). These measures are summarized (means and standard deviations) across the data sets within each condition. The models are fit to the data using the software program Mplus version 4.2 (Muthén & Muthén, 2006) on 20 dual-processor PC workstations managed by the Condor High-Throughput Computing System (Thain, Tannenbaum, & Livny, 2005). Model fitting for the continuous manifest variables took roughly 15 minutes for each data set.

Results

Convergence rates are considered first, and all subsequent results should be interpreted in the context of the convergence rates. Next, model fit and model comparisons using the fit indices BIC and saBIC are presented. In conjunction with the fit indices, we discuss the feasibility of an approach where the estimated factor covariance matrix of the fitted FMM model is used to determine whether its pattern is consistent with hypothesized relationships between the factors. This is followed by a more general discussion about model performance in terms of accuracy of parameter estimation. The final section presents results on the accuracy of assigning of cases to classes.

In each of these sections, the sample size by Mahalanobis distance sub-structure shown in Table 2 is used for presenting results. The text of the following sections will include references to blocks A, B, C, and D within each results table as shown in Table 2.

Convergence Rates

When fitting complex mixture models to data, researchers may be challenged by non-converging models. Non-convergence can be the consequence of specifying an incorrect model, model non-identification, empirical under-identification, or data characteristics such as multivariate outliers.¹¹ In the current study, an incorrect SEMM model (SEMM231) is specified to explore the consequence of specifying an incorrect model, as discussed below. All three fitted models used in the current study are identified. Empirical non-identification can result from having too few observations in a class to estimate the numbers of parameters specified by the model. Within blocks B and D of the design matrix where the total sample size is 100 and π₁ = .05, the expected number of cases in class 1 is 5 with a lower bound of zero cases. Consequently, a substantial number of data sets have fewer cases in class 1 than parameters to be estimated. Often these data sets would still converge, but the covariance matrix of the factors, Ψ_k (see Equations 3 and 5), would not be positive definite. Data sets with a non-positive definite Ψ_k are excluded from further summaries and are treated as non-converged.

The (expected) general trend for convergence rates is that conditions with larger sample sizes and larger Mahalanobis distances have higher convergence rates. The convergence rates for the true model SEMM123 are given in Table 3, and the convergence rates for the FMM and SEMM231 models are similar. Notice that in block D, the N = 100 conditions had higher convergence rates than N = 300 conditions. This result is a consequence of the class proportions of the smaller class being overestimated, resulting in fewer cases of empirical under-identification.

Table 3. Convergence rates for the true model SEMM123.

var(FqC1)	π1 = 0.50				π1 = 0.05
1	0.33	0.55	0.85	0.85	0.26	0.21	0.21	0.25
	0.63	0.95	0.95	1	0.08	0.07	0.1	0.24
	1	1	1	1	0.09	0.13	0.39	0.66
5	0.8	0.97	0.99	0.99	0.35	0.37	0.38	0.39
	1	1	1	1	0.65	0.72	0.74	0.81
	1	1	1	1	1	1	1	1

Note. The table is structured as described in Table 2. Table entries are the proportion of data sets within each condition that converged. In addition to numeric convergence criteria, data sets that did not have a positive definite factor covariance matrix are excluded as non-converged.

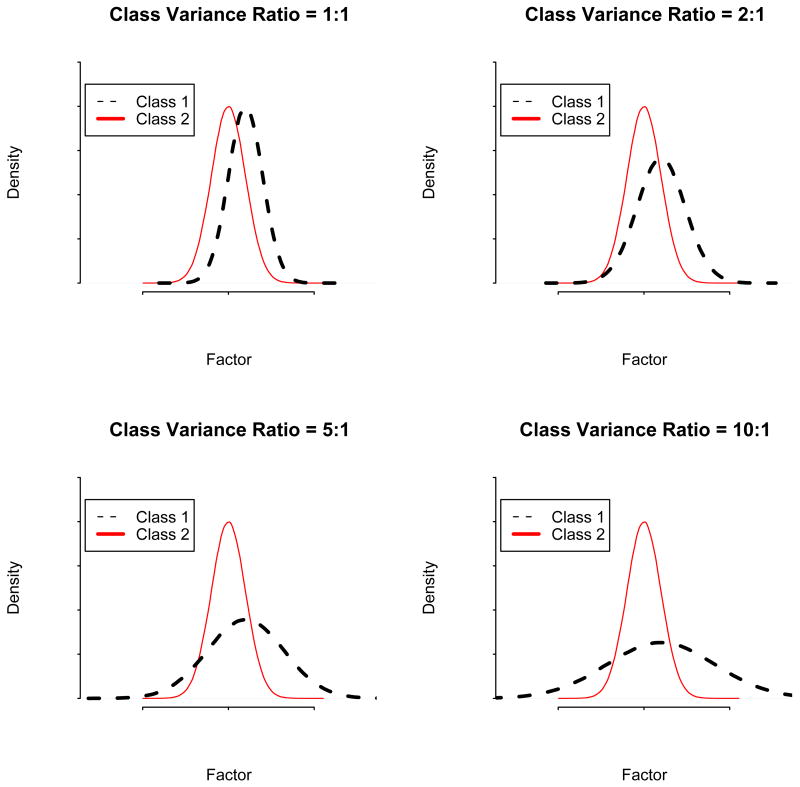
Conditions with imbalanced factor variances (blocks C and D) have higher convergence rates than conditions with balanced factor variances (blocks A and B). As will be seen throughout the results, the imbalanced factor variance conditions generally outperform the balanced factor variance conditions. The reason for this tendency is illustrated in Figure 3 for the balanced class proportion conditions. For a given mean separation between two distributions (in this case, 1.0), increasing the ratio of the variances in class 1 to class 2 at first increases the overlap between distributions. However, as the variance of class 1 continues to increase, the overlap between distributions decreases both above and below the mean of the constant distribution in class 2. While the example in Figure 3 is univariate, the current study can be conceptualized in terms of the three factors within each class, and this provides three dimensions on which distributions can have overlap (or the lack thereof). Data with a greater degree of overlap will under-perform relative to data with a lesser degree of overlap. A similar effect occurs for imbalanced class proportion conditions.

Figure 3.

Class overlap for variance ratios of 1:1, 2:1, 5:1, and 10:1 with the larger variance in the first class. Class proportions are equal. The 1:1 and 5:1 ratios are conditions in the current study, and the 2:1 and 10:1 ratios are included to provide reference.

All results present hereafter should be interpreted in the context of the convergence rates presented in Table 3. For example, results for conditions in all of block B and the N = 100 conditions of block D are based on small proportions of converged data sets, hence there is less confidence in the summary results than in conditions with higher convergence rates. Results in Table 3 also provide an indication that applied data sets under the conditions of block B and the N = 100 conditions of block D will a smaller chance of converging in practice.

Choosing the Correct Model: The Unstructured FMM Model and Fit Indices

Much of the prior FMM and SEMM research has focussed on choosing the correct number of classes and/or factors (Celeux & Soromenho, 1996; Lo, Mendell, & Rubin, 2001; Jeffries, 2003; Lubke & Neale, 2006; Nylund et al., 2007; Lubke & Muthen, 2007; Henson et al., 2007). The current study assumes that the numbers of classes and measurement models within class have been established, and focuses entirely on the (mis)specification of the relationships between factors. Both an exploratory inspection of the factor variances in the FMM model and measures of model fit are considered as approaches to choosing the correct model.

An approach to examining regression relationships between factors is to fit a factor mixture model with an unstructured factor covariance matrix as shown in the illustration with the aging data. The FMM is a ‘true’ model in the sense that no parameters are misspecified. The pattern of factor variances and covariances in the FMM model should be consistent with the hypothesized structural relations between the factors. However, this approach is unlikely to be successful if class specific factor covariance matrices are not estimated correctly.

In the current study, the factor variances are estimated most accurately in conditions with higher convergence rates (blocks A, B, and D) with a pattern of smaller bias for larger sample sizes and class separations. More detail is provided in the following section on the accuracy of parameter estimates. Here, we conclude that using the estimated factor covariance matrices of FMM's to inform the specification of structural relations in a SEMM is a viable approach under more ideal conditions, specifically when sample sizes are larger, class separations are larger, and class proportions are balanced.

Prior research has explored the performance of fit indices to select the correct SEMM in a series of model comparisons (Henson et al., 2007). In the current study, the BIC and the saBIC fit indices generally identified the SEMM123 model as the true model, as is seen in the upper and lower panel of Table 4. As expected, the BIC and saBIC performed relatively worse in conditions with lower sample sizes and smaller Mahalanobis distances. Except in conditions where the BIC or saBIC preferred the true model in 90% or more of the converged data sets, the incorrect SEMM231 model is the second most frequently preferred model. This is related to the exploratory approach to determining possible SEM models within class discussed above. When factor variances are biased, the preferred model is likely to be an incorrect model. Also notice that in block B and the N = 100 condition of block D of both panels of Table 4, the proportions of data sets in which the true model is preferred is exaggerated in comparison to the general pattern described above. Recall that these conditions had the lowest convergence rates, and therefore results may be dominated by a few ideal data sets.

Table 4. Proportion of data sets where the BIC and saBIC favored the true model.

var(FqC1)	π1 = 0.50				π1 = 0.05
BIC
1	0.72	0.57	0.7	0.67	0.81	0.76	0.81	0.79
	0.67	0.81	0.85	0.93	0.86	0.85	0.81	0.75
	0.92	0.97	0.99	1	0.89	0.76	0.73	0.59
5	0.68	0.75	0.87	0.86	0.73	0.68	0.69	0.68
	0.95	0.97	0.97	0.97	0.58	0.57	0.57	0.59
	0.98	0.97	0.98	0.98	0.85	0.87	0.89	0.86
saBIC
1	0.69	0.51	0.6	0.53	0.8	0.76	0.81	0.78
	0.61	0.75	0.79	0.87	0.85	0.85	0.81	0.75
	0.85	0.92	0.95	0.99	0.89	0.76	0.72	0.57
5	0.54	0.57	0.7	0.69	0.71	0.65	0.67	0.67
	0.83	0.87	0.9	0.91	0.54	0.54	0.55	0.55
	0.96	0.95	0.95	0.95	0.81	0.81	0.83	0.82

Note. Each panel is structured as described in Table 2. Table entries are the proportion of converged data sets in which the Bayesian information criteria (BIC; upper panel) and the sample-size adjusted Bayesian information criteria (saBIC; lower panel) selected the true model SEMM123 as the best model in comparison to the incorrect SEMM231 model and unstructured FMM model.

Parameter Estimates

This section reports the accuracy of the estimates of the latent variable parameters and their structural relations.¹² The focus is on general trends, with some specific results reported in tables. In all cases, parameter estimates are more accurate for the more ideal conditions. Lower sample sizes are more problematic than then smaller Mahalanobis distances used in this study.

In what follows, ‘ideal conditions’ refers to all N = 1000 conditions, N = 300 conditions with Mahalanobis distances ≥ 1.5, and N = 100 with a Mahalanobis distance of 2.0. The presentation of results in this section is restricted to the true models (FMM and SEMM123). In both of the true models, the estimation of the measurement parameters (factor loadings, intercepts, and error variances) is accurate for all conditions, and measurement parameters are not commented on further.

In the FMM model, factor variance estimates are more accurate in the second class than in the first class for all blocks. In block A factor variance estimates were reasonable for most conditions in the second class, and for ideal conditions in the first class. In block B factor variance estimates were reasonable for most conditions in the second class, with biases ranging from .1 to .7 in the first class. Recall that class one has the smaller class size in block B. In block C factor variance estimates were reasonable in the first class for sample sizes ≥ 300 and for ideal conditions in the second class. In block D in the first class, which had large model implied factor variances, factor variances were almost always underestimated. In block D in the second class, which had small model implied factor variances in relation to the first class, factor variances were overestimated except in N = 1000 conditions with Mahalanobis distances ≥ 1.5. This pattern of under/over estimation is relatively balanced across classes, just as total variance in a data set is distributed across classes. In conditions with biased factor variances, sample size was almost always more influential on the magnitude of the bias than was class separation.

Accuracy of factor variance estimates for the SEMM123 model were roughly the same as for the FMM model. For conditions where the factor variances in both classes are accurately estimated, the results of the FMM model can be used to check consistency with potential SEMM models as described in the results of the empirical data illustration.

Table 5 shows the estimates of the regression of F_3C1 on F_2C1 in the first class averaged over the 150 data sets when fitting the correct model. The empirical standard errors shown between brackets in the table indicate that there is considerable variability of estimated regression coefficients across data sets, especially in the small class when class proportions are unequal. Point estimates are on target when class proportions are equal. They are also accurate when the overlap between component distributions is low as in the unequal variance conditions, that is, in all conditions of blocks A and C for Mahalanobis distances ≥ 1.5 in block B and for N = 1000 conditions of block D. In the second class, estimates of the regression parameters are reasonable in most conditions of all four blocks of the design matrix. The covariance between the first and second factors in the second class are reasonable for all conditions except for N = 100 conditions of blocks C and D.

Table 5. Regression parameters for the path from F_2C1 to F_3C1 for the true model SEMM123.

var(FqC1)	π1= 0.50				π1= 0.05
1	0.56 (0.48)	0.65 (0.35)	0.64 (0.28)	0.63 (0.24)	0.94 (2.30)	0.59 (0.81)	0.48 (0.56)	0.7 (0.61)
	0.66 (0.29)	0.64 (0.17)	0.65 (0.12)	0.64 (0.11)	0.58 (0.80)	0.96 (0.66)	0.7 (0.75)	0.65 (0.51)
	0.66 (0.10)	0.66 (0.07)	0.66 (0.06)	0.66 (0.06)	0.36 (0.74)	0.45 (0.49)	0.58 (0.63)	0.66 (0.53)
5	0.66 (0.36)	0.68 (0.23)	0.67 (0.19)	0.67 (0.18)	0.49 (0.78)	0.46 (0.98)	0.66 (0.83)	0.83 (0.99)
	0.65 (0.10)	0.66 (0.08)	0.66 (0.08)	0.66 (0.09)	0.57 (0.74)	0.72 (0.52)	0.75 (0.59)	0.73 (0.64)
	0.65 (0.04)	0.65 (0.04)	0.65 (0.04)	0.65 (0.04)	0.65 (0.18)	0.65 (0.19)	0.66 (0.20)	0.66 (0.20)

Note. The table is structured as described in Table 2. Table entries are estimated regression parameters averaged across 150 data sets. Each row with averaged parameter estimates is followed by the corresponding empirical standard errors between brackets. The coefficients concern the regression of F_3C1 on F_2C1 for the true model SEMM123. The data generating value for all cells of the table is .65.

Correct Assignment

For some research questions, correctly recovering class specific variances and covariances of the latent variables, or their structural relations, may be sufficient to answer the relevant research questions. Prior sections show that for many conditions considered in the current study, the correct model is likely to be selected. In addition, for the more ideal conditions, factor variances and the regression parameters between factors can be estimated accurately. In some applications, however, the focus of a mixture analysis might be to assign individuals to their most likely class.

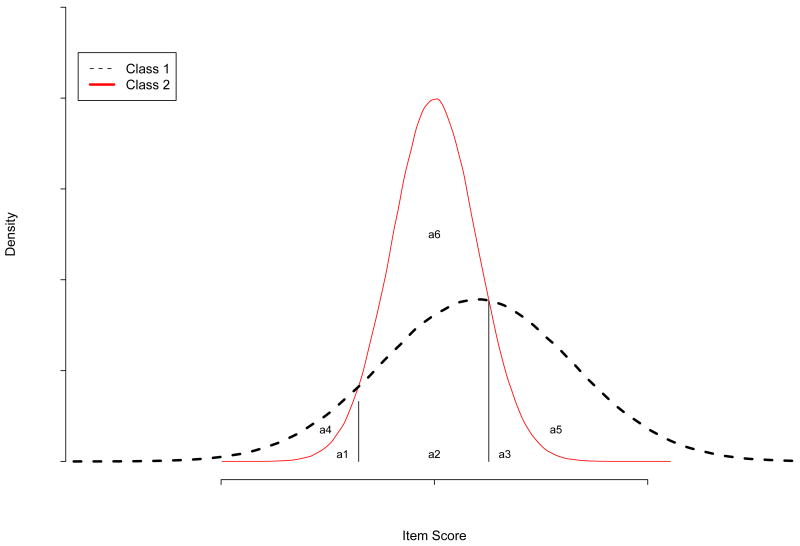
Modal assignment is defined in terms of assignment to the class with the highest posterior probability, which is illustrated in Figure 4. The figure shows a hypothetical item distribution for two classes, where class 1 is represented with a black curve and has larger variance than class 2 which has a red curve. Suppose fitting a mixture model exactly reproduces the true model, and therefore the item distributions. Subjects with an item score between −∞ and the leftmost vertical line would fall into area a4 if they truly belong to class 2, and into area a1 if they truly belong to class 2. Class 2 members would get assigned to their true class, whereas class 1 members would get incorrectly assigned. All subjects between the two vertical lines would be assigned to class 1 since class 1 has a higher probability in that range. True class 2 subjects would fall into area a2, and would be incorrectly assigned to class 1. True class 1 subject would be correctly assigned.

Figure 4.

Two univariate normal distributions where μ₁ = 1, μ₂ = 0, ${\sigma }_1^2=5$, ${\sigma }_2^2=1$, and π₁ = π₂ = 0.5.

During estimation of a mixture model, each subject contributes to the likelihood of all component distributions weighted by the class probabilities of belonging to each of those components. However, the above hypothetical example illustrates that even if the structure of a model is adequately recovered, there can be substantial proportions of the sample that get incorrectly assigned. In fact, the proportion is directly related to the area of overlap between component distributions. A coefficient based on the area of overlap called ‘overlapping coefficient’ was initially proposed by Weitzman (1970). The overlapping coefficient for two normally distributed variables with unequal means and equal variances was presented as a generalization of the t-test by Mishra, Shah, and Lefante (1986) and is also reported in Dudewicz and Mishra (1988, page 351). Multivariate extensions allowing for unequal variances result in highly complicated expressions, which we are currently investigating. In the present study, we computed the overlapping coefficient for the distribution of the first factor which is the factor used to manipulate class separation and factor variance differences. Holding everything else constant, the unequal variance conditions have less overlap than the equal variance conditions. Increasing the Mahalanobis distance decreases overlap within each block of the design matrix. The pattern of correct class assignment in the current study is consistent with the pattern of overlap differences of the distribution of the first factor.

Tables 6 and 7 present cross tabulations of true and assigned class for each of the 4 blocks of the study design. The tables show the average number of subjects (averaged over the 150 data sets in each condition) together with the corresponding standard deviation. The latter indicates the variation of correct assignment across individual data sets.

Table 6. Assigned class by true class cross-tabulations for blocks A and C.

N	MD=0.5		MD=1.0		MD=1.5		MD=2.0
Equal factor variances (F1C1 = 1)
100	29.51 (13.14)	20.08 (11.78)	30.7 (9.23)	13.53 (8.18)	37.43 (8.31)	13.40 (9.99)	42.14 (6.64)	11.20 (8.80)
	21.10 (12.08)	29.31 (13.21)	19.88 (8.65)	35.89 (8.89)	13.13 (7.05)	36.05 (10.54)	8.45 (4.50)	38.21 (9.62)
300	77.36 (41.90)	50.24 (41.37)	98.72 (27.20)	47.62 (34.20)	114.85 (19.20)	38.73 (25.90)	125.59 (11.91)	26.08 (17.92)
	73.00 (40.92)	99.40 (42.53)	51.34 (26.04)	102.32 (35.22)	35.15 (16.48)	111.27 (27.67)	24.35 (8.89)	123.97 (19.74)
1000	271.91 (129.96)	162.90 (121.94)	340.25 (66.38)	144.73 (77.68)	385.11 (36.65)	108.28 (45.29)	416.45 (24.41)	71.30 (22.63)
	226.79 (126.77)	338.39 (125.94)	158.45 (61.58)	356.57 (82.52)	113.60 (29.93)	393.01 (50.32)	82.25 (15.02)	429.99 (29.64)
Unequal factor variances (F1C1 = 5)
100	28.63 (10.25)	5.11 (6.96)	32.48 (7.65)	3.69 (3.55)	37.99 (5.98)	3.30 (3.04)	42.04 (5.38)	2.72 (2.61)
	21.07 (10.65)	45.2 (8.68)	17.17 (7.70)	46.66 (6.03)	11.66 (4.46)	47.05 (5.66)	7.63 (3.29)	47.61 (5.49)
300	109.97 (14.99)	17.01 (8.67)	115.97 (13.39)	14.51 (7.99)	123.71 (11.26)	10.91 (5.58)	131.37 (9.88)	7.57 (4.23)
	40.79 (11.42)	132.23 (13.57)	34.79 (9.39)	134.73 (13.00)	27.05 (7.83)	138.33 (10.93)	19.39 (5.69)	141.67 (10.12)
1000	373.20 (25.22)	52.21 (14.68)	389.62 (23.68)	43.27 (11.53)	412.85 (21.63)	33.00 (8.50)	437.63 (19.19)	23.31 (6.13)
	127.52 (19.23)	447.07 (23.36)	111.10 (16.00)	456.01 (21.98)	87.87 (13.02)	466.28 (20.05)	63.09 (9.45)	475.97 (18.49)

Note. The table corresponds to the imbalanced class proportion conditions in blocks A and C and has a 2 × 2 structure for each combination of sample size and Mahalanobis distance (MD). The upper left cell is the average number of cases in class 1 correctly assigned to class 1. The lower right cell contains the average number of cases in class 2 correctly assigned to class 2. The lower left cell contains the average number of cases in class 1 incorrectly assigned to class 2. The upper right cell contains the average number of cases in class 2 incorrectly assigned to class 1. Standard deviations are in parentheses. For example, for F_1C1 = 1, N=100, and MD=0.05, there are an average of 29.51 subjects correctly assigned to class 1 whereas there are 20.08 subjects assigned to class 1 that truly belong to class 2.

Table 7. Assigned class by true class cross-tabulations for blocks B and D.

N	MD=0.5		MD=1.0		MD=1.5		MD=2.0
Equal factor variances (F1C1 = 1)
100	2.10 (1.62)	29.87 (11.44)	1.72 (1.35)	29.25 (12.33)	2.91 (1.59)	28.94 (12.52)	3.68 (1.63)	20.60 (13.40)
	3.39 (1.84)	64.64 (11.31)	4.00 (1.93)	65.03 (11.77)	2.47 (1.41)	65.69 (11.96)	1.81 (1.45)	73.92 (12.21)
300	2.83 (1.85)	38.67 (24.63)	3.30 (1.95)	16.50 (6.47)	6 (3.40)	19.33 (17.07)	8.81 (3.14)	11.53 (10.66)
	11.67 (4.66)	246.83 (22.36)	11.70 (3.53)	268.50 (8.40)	10.20 (3.36)	264.47 (16.9)	7.03 (3.12)	272.64 (9.69)
1000	4.21 (2.46)	23.36 (16.14)	7.37 (3.47)	19.32 (13.72)	13.40 (5.43)	16.16 (12.00)	19.77 (6.38)	12.71 (8.94)
	44.00 (6.26)	928.43 (15.93)	42.21 (8.25)	931.11 (14.69)	38.19 (6.67)	932.26 (14.03)	30.70 (6.50)	936.83 (11.36)
Unequal factor variances (F1C1 = 5)
100	3.40 (1.65)	8.91 (10.06)	3.20 (1.41)	9.88 (12.77)	3.18 (1.57)	10.79 (13.36)	3.46 (1.57)	10.12 (13.77)
	2.49 (1.86)	85.21 (9.60)	2.55 (1.77)	84.38 (12.44)	2.72 (1.84)	83.32 (12.86)	2.36 (1.64)	84.07 (13.21)
300	7.72 (2.94)	5.39 (16.66)	8.06 (2.76)	2.83 (4.78)	8.41 (2.88)	2.78 (8.27)	8.99 (3.10)	2.46 (9.01)
	8.01 (3.07)	278.88 (16.62)	7.78 (3.12)	281.33 (6.13)	7.24 (2.74)	281.58 (8.64)	6.46 (2.67)	282.09 (9.35)
1000	22.34 (5.98)	4.39 (3.56)	23.54 (5.80)	4.15 (3.33)	25.62 (5.55)	3.92 (3.07)	28.23 (5.89)	3.51 (2.68)
	27.19 (5.37)	946.09 (7.95)	25.99 (5.41)	946.33 (7.83)	23.91 (4.99)	946.55 (7.66)	21.29 (4.74)	946.97 (7.45)

Note. The table corresponds to the imbalanced class proportion conditions in blocks B and D and has a 2 × 2 structure for each combination of sample size and Mahalanobis distance (MD). The upper left cell is the average number of cases in class 1 correctly assigned to class 1. The lower right cell contains the average number of cases in class 2 correctly assigned to class 2. The lower left cell contains the average number of cases in class 1 incorrectly assigned to class 2. The upper right cell contains the average number of cases in class 2 incorrectly assigned to class 1. Standard deviations are in parentheses. For example, for F_1C1 = 1, N=100, and MD=0.05, there are an average of 2.10 subjects correctly assigned to the minority class 1 whereas there are 29.87 subjects assigned to class 1 that truly belong to the majority class 2. Hence, the minority class contains about 6 times more incorrectly assigned subjects than correctly assigned subjects in that particular condition.

Table 6 shows the results for equal class proportions (blocks A and C). Since in this case the overlap is symmetric for the two classes, we can see that the numbers of correctly and incorrectly assigned subjects is generally similar across classes. Larger sample sizes correspond to a more precise estimation of the model, which is reflected in generally higher odds of correct assignment. Correct assignment improves with increasing class separation, and is better for the unequal variance conditions.

Most importantly, the average numbers of incorrectly assigned subjects are high. Table 8 shows proportions correct assignment for balanced class sizes corresponding to Table 6. In the equal variances condition (i.e., larger overlap), the proportion exceeds 80% correct assignment only if MD > 1.5 for all sample sizes. In the unequal variance condition, this is achieved with MD = .5 given sample size ≥ 300, or MD > 1.0 for all sample sizes.

Table 8. Proportion correct assignment for equal class proportions.

var(FqC1)	π1 = 0.50
1	0.59	0.67	0.74	0.80
	0.59	0.67	0.75	0.83
	0.61	0.70	0.78	0.85
5	0.74	0.79	0.85	0.90
	0.81	0.84	0.87	0.91
	0.82	0.85	0.88	0.91

Note. Table entries are proportion correct assignment averaged across data sets that converged when fitting the true model SEMM123. SEMM231 and FMM models had proportion correct tables with identical patterns and roughly the same proportion correct values for each cell.

Table 7 shows the results for unequal class sizes, which are generally worse, especially for the minority class. It is important to note that proportions correct assignment assessed for the whole sample (i.e., pooled over minority and majority class) would provide distorted results since the larger class has a much larger a priori chance of correct assignment. In addition, consider that, on a conceptual level, the unequal class size scenario reflects data where the minority of the population belongs for instance to a risk group. Usually, the focus of these studies is on the minority class. Hence, the interest might be less in correct assignment of subjects to the majority class than in the quality of class assignment to the minority class. In other words, correct assignment to the minority class and incorrect assignment to the minority class. Table 9 shows the odds of incorrectly assigned subjects to correctly assigned subjects in the minority class. The odds are substantially larger than 1 in most conditions. This indicates that if the focus is on using class assignment in subsequent analyses (e.g., post hoc class comparisons, use of class assignment as predicted variable in a regression) then the overlap between classes should be rather small.

Table 9. Assignment to the minority class: Odds of incorrectly assigned subjects to correctly assigned subjects.

N	MD=0.5	MD=1.0	MD=1.5	MD=2.0
Equal factor variances (var(FqC1) = 1)
100	17.79	19.47	14.41	8.88
300	15.45	6.76	4.75	1.54
1000	6.68	2.96	1.21	0.63
Unequal factor variances (var(FqC1) = 5)
100	3.82	3.91	4.78	4.57
300	0.83	0.35	0.43	0.38
1000	0.19	0.17	0.15	0.12

Note. Table entries are average odds of class 2 subjects who are incorrectly assigned to class 1 and class 1 subjects who are correctly assigned to class 1 for imbalanced class proportion conditions in blocks B (upper panel) and D(lower panel). Ideally, the values would be close to zero.

As mentioned above, proportions correct assignment when pooled over classes with different sizes are biased due to differences in a priori probabilities of correct assignment. An alternative index that corrects for chance is the Hubert and Arabie Adjusted Rand Index (ARI_HA, Hubert & Arabie, 1985). In a large simulation study, Steinley (2004) devoloped a useful heuristic for interpreting ARI_HA values where “(a) values greater than 0.90 can be viewed as excellent recovery, (b) values greater than 0.80 can be considered good recovery, (c) values greater than 0.65 can be considered moderate recovery, and (d) values less than 0.65 reflect poor recovery.” ARI_HA values in the current study were computed using the ARI function in the R (R Development Core Team, 2008) package MCLUST version 3 (Banfield & Raftery, 1993; Fraley & Raftery, 1999, 2002, 2003, 2006). See Steinley (2004) for the formula and description of the ARI_HA. ARI_HA values are presented in Table 10.

Table 10. ARI_HA based on fitting the true model SEMM123.

var(FqC1)	π1 = 0.50				π1 = 0.05
1	0.03	0.11	0.23	0.38	0.01	0.01	0.06	0.19
	0.04	0.12	0.27	0.45	0.04	0.12	0.23	0.44
	0.05	0.16	0.31	0.48	0.07	0.15	0.28	0.43
5	0.26	0.35	0.49	0.63	0.39	0.38	0.38	0.44
	0.38	0.45	0.56	0.67	0.53	0.57	0.6	0.65
	0.41	0.48	0.58	0.68	0.55	0.57	0.61	0.66

Note. The table is structured as described in Table 2. Table entries are the Hubert and Arabie Adjusted Rand Index ARI_HA averaged across conditions that converged for the true model SEMM123. SEMM231 and FMM models had ARI_HA tables with identical patterns and roughly the same ARI_HA values for each cell.

The pattern of results in Table 10 is consistent with the average numbers of correct and incorrect assignment in the cross-tabulation tables. As for proportions correct assignment, there are no important differences in correct assignment for the correctly and incorrectly specified SEMM's, hence only the ARI_HA for the correctly specified SEMM are presented. Importantly, the magnitudes of the ARI_HA's in this study using Steinley's criteria mirror correct and incorrect assignment in the cross tabulation tables and indicate weak performance at best. For the conditions in this study (e.g. mean differences between classes, etc.), the correct assignment was moderate only for the largest Mahalanobis distance conditions with N ≥ 300 in blocks C and D. The general pattern of correct assignment mirrored results concerning parameter estimation. The ARI_HA in imbalanced factor variance conditions (blocks C and D) outperformed the ARI_HA balanced factor variance conditions (blocks A and B), which is due to the larger overlap of component distributions in the balanced variance condition. The general pattern of better performance in larger sample sizes and larger Mahalanobis distances also occurred for the ARI_HA.

Additional Analyses

As indicated in the methods section, the first part of the simulation study is replicated with a larger effect size between the class 1 and class 2 factor correlation matrices, and partially replicated with binary versions of the manifest variables. The first part is accomplished by increasing the magnitude of both of the regression coefficients in class 1 from .65 to .806 (see Figure 1). The second part is carried out using dichotomized versions of the data in the N = 300, Mahalanobis distances of 1.0 and 1.5 conditions of block A. We begin with the results of the larger effect size followed by results with for the binary data conditions.

Large Effect Size Replication

The main part of the study uses factor correlations that are mainly small to medium according to Cohen. These are increased from to medium to large in the larger effect size conditions. The model implied factor correlations for each class and the difference between them are presented in Table 11. In what follows, we refer to the effect sizes in the main and additional parts of the study as the small effect size conditions and large effect size conditions, respectively.

Table 11. Model implied factor correlations and class differences in factor correlations for small and large effect size simulations.

Factor	Class 1	Class 2	Difference
	Main study
cor(F2, F3)	0.75	0.34	0.42
cor(F1, F3)	0.32	0.68	-0.36
cor(F1, F2)	0.54	0.30	0.24
Large effect size replication
cor(F2, F3)	0.91	0.34	0.58
cor(F1, F3)	0.41	0.68	-0.26
cor(F1, F2)	0.63	0.30	0.33

Note. Table entries are the model implied correlations based on the data generating model parameters. The differences between the main simulation study and large effect size replication are .09 for cor(F₁, F₂), .10 for cor(F₁, F₃), and .16 for cor(F₂, F₃).

Sample size calculations indicated that N = 100 was sufficient to find differences in correlations between class one and class two for the large effect size conditions in blocks A and C. Samples of N = 300 where sufficient to find differences in correlations for the small effect size conditions in blocks A and C. For blocks B and D, sample sizes greater than N = 1000 were needed to find differences in correlations for both the small and large effect size conditions. The difference of the correlation difference between the large and small effect size conditions gives a metric of effect size. These are .09 for cor(F₁, F₂), .10 for cor(F₁, F₃), and .16 for cor(F₂, F₃). Given the sample size calculations, very large sample sizes would be needed to reliably detect moderately sized differences in factor correlations.

When fitting the true SEMM model to generated data with the larger effect size, there is no noticeable improvements in convergence rates or accuracy of parameter estimates. Importantly, correct assignment is not better in this condition where classes have more pronounced differences in the structural relations between factors. This is likely due to the fact that the difference in effect sizes between the main part of the study and large effect size replication had little impact on the overlap of the component distributions.

Results for Selected Conditions with Binary Data

As described above, the true model SEMM123 was fit to dichotomized versions of the data found in the N = 300, Mahalanobis distances of 1.0 and 1.5 conditions of block A using the larger effect size conditions. Due to the long times required to fit models to binary data, the SEMM123 model is fit to 30 data sets for each of these two conditions. The number of random starts is set to 2000 which is sufficient to replicate the likelihood for this particular model. The model is fitted to the data using Mplus 5, and takes approximately 25 hours to fit for each data set.

The convergence rates are lower than for continuous counterparts. In addition to excluding results from data sets in which the latent variable matrix was not positive definite, two data sets for each Mahalanobis distance have results with unacceptable parameter estimates for variances for the third (terminal) factor in class 1. These are also excluded as unconverged. The convergence rate for the MD=1.0 binary data is .57 (compare to .95 for continuous data), and the convergence rate for the MD=1.5 data is .67 (compare to .95 for continuous data; see Table 3).

Since the converge rates are low and a limited number of data sets are used, the average parameter estimates are neither trustworthy or informative. Though computing power has improved drastically in recent years, the long times needed to fit models to categorical data make a larger simulations unpractical at the moment. The low convergence rates are indicative of the difficulties when using categorical data rather than continuous data in complex mixture models such as the SEMM used here.

Conclusions

The current study highlights both the promising flexibility of the SEMM and its limitations. Following an illustration with one wave of data from the Notre Dame Longitudinal Study of Aging, several aspects of SEMM analyses are further investigated in a simulation study. These include the comparison of SEMMs with correctly and incorrectly specified structural relations between factors, accuracy of parameter estimates of structural relations and factor variances, and correct class assignment.

The illustration with the empirical data shows that SEMM analyses permit the detection of classes that differ with respect to their within class covariance structure. However, differences in model fit between alternative models with conceptually diverging interpretations are small. Potential explanations include small sample size, class separation, and/or effect size. The ordered categorical response format of the manifest variables in the illustration may attenuate effects, and certainly limits the exploration of a larger set of alternative models due to computation times.

The first two aims of the simulation study are to provide insight regarding the conditions under which structural equation mixture modeling performs adequately, both with respect to choosing the correct model, and with respect to estimates of the structural relations between factors. In empirical settings, class specific factor variances and unbalanced class sizes may influence performance in important ways. These effects are combined with differences in sample size, class separation, effect size, and response format. The data are generated using model parameters that are largely based on the estimates found in the empirical analysis.

Based on the BIC, the SEMM with the correctly specified structural model is chosen in most settings. Regarding convergence and parameter estimates, the SEMM consistently performs well when the sample size is ≥ 300 and when class separation is ≥ 1.5, and often performs well when sample size is N = 100 but class separation is 2.0, or when class separation is .5 but sample size is 1000. These ranges are relevant for equal class sizes. If class size is unbalanced, the sample size of the minority class is obviously critical. In general, sample size has a substantial effect on model performance, especially in cases where class separation is low. This result can be regarded as encouraging since it might be more feasible to control sample size than to increase class separation by designing conceptually useful items that have large mean differences across classes but no floor or ceiling effects.

The study also provides evidence of potential trade-offs between mean differences between classes and imbalanced factor variances. As illustrated with the settings in this study, class differences in factor variance do not necessarily increase the overlap between the class specific factor distributions, but can actually decrease this overlap. Smaller overlap obviously increases model performance. In case factor variance differences induce smaller overlap they can counterbalance smaller mean differences between classes.

The replication of the simulation study with larger effect sizes shows that it is possible to detect class differences based primarily on differences in factor covariance matrices. Hence, even if classes have only small mean differences, it may still be possible to detect differences between classes regarding their structural relations.

Limitations of SEMM's are evident when fitting models with binary rather than continuous outcomes. Binary data drastically increase the computation times needed to estimate the specified models. With 12 manifest variables and three factors, computation times reached up to 25 hours. Depending on the number of random starting values needed to replicate the best likelihood with different stating values, computation time is likely to increase even more when manifest variables have more than two response categories. Due to this limitation, investigating the effect of response format on detecting class differences in structural relations is not feasible in the current simulation. Convergence rates are substantially lower for binary than for continuous outcomes. Taken together, it might be advisable to limit structural equation mixture modeling with several factors to subscale level data that have approximately normal distributions. More research regarding response format is clearly needed.

The third aim of the simulation is to assess correct class assignment. Although the study shows that the structure of the data within class can be adequately recovered in a wide variety of empirically relevant settings, the quality of class assignment is generally poor for most of the settings in this study. Compared to previous studies with less complex factor structures (e.g., single factor within class, see Lubke & Muthen, 2007), the current results indicate a worse performance of more complex models. It is noteworthy that correct assignment is not better for the SEMM than for the corresponding FMM, hence correctly specifying the structural relations between factors does not improve class assignment. Especially in conditions with a considerable difference in class size, the correct assignment in the minority class is worrisome. In substantive research, the focus is often on the minority class representing a risk group. Computing the odds of incorrectly assigned subjects versus correctly assigned subjects shows that in some settings it is 17 times more likely to have incorrectly assigned subjects in the minority class than correctly assigned subjects. One might argue that differences between classes might be mainly quantitative, and that the incorrectly assigned subjects would have scores on the underlying factor that are more similar to subjects in the minority class. However, in the case of factors within class this will depend on the reliability of the observed items. Incorrect assignment is at least partially due to the sign and size of an individual's error term. The argument can not be applied to latent class models because variability within class is error variance. It should be noted though that the current simulation focuses on correct assignment when class specific distributions have considerable overlap. The results under these conditions warrant caution to use class assignments in post hoc analyses. It is therefore advisable to obtain an indication of the separation between classes and/or the overlap of component distributions before carrying out such analyses. We are currently investigating the extent to which error rates in class assignment affect post-hoc analyses.

In sum, the study provides evidence that hypotheses concerning the structural relations between a small number of factors can be investigated in the mixture context if the number of classes is small. Models with incorrectly specified structural relations can be rejected given sufficient sample and effect size. The use of SEMM's to assign individuals to a given class is much more limited. The settings of the simulation presented here (i.e., number of classes and factors, measurement models) are based on the results of fitting a SEMM to an empirical data set, and only factor means and variances, sample size, and class proportions are varied. Generalizability of simulation results obviously depends on the chosen settings, and results may be different for larger models and/or substantially different settings (e.g., more than 2 classes). In light of the fact that increasingly complex mixture are being proposed in the literature, applications of a given model type to empirical data should be accompanied by an evaluation of model performance with simulated data under relevant conditions.

Appendix

Data generating parameter values

Factor loadings, error variances, and intercepts are class invariant:

• Factor 1 loadings [1 .8 .8 .8 0 0 0 0 0 0 0 0]^t

• Factor 2 loadings [0 0 0 0 1 .8 .8 .8 0 0 0 0]^t

• Factor 3 loadings [0 0 0 0 0 0 0 0 1 .8 .8 .8]^t

• Error variances MVN(0, .5 * I₁₂)

• Intercepts are all 0

• Factor variances class 1: 1, 1, 1 or 5, 5, 5

• Factor variances class 2: 1, 1, 1 for all conditions

The factor covariance matrices within class are structured according to the structural models and parameter values given in Figure 1.

Information criteria

All information criteria used in the present study are penalized log-likelihood functions with the general form −2L + f(N)p where L is the loglikelihood of the estimated model with p free parameters and f(N) is a function that may depend on the total sample size N (Sclove, 1987). The BIC and the sample size adjusted BIC integrate N in different ways, and the penalty terms are log(N)p for the BIC Schwarz, 1978 while the sample size adjusted BIC uses (N* = (N + 2)/24) instead of N.