Biophysical basis for the geometry of conical stromatolites

Abstract

Stromatolites may be Earth’s oldest macroscopic fossils; however, it remains controversial what, if any, biological processes are recorded in their morphology. Although the biological interpretation of many stromatolite morphologies is confounded by the influence of sedimentation, conical stromatolites form in the absence of sedimentation and are, therefore, considered to be the most robust records of biophysical processes. A qualitative similarity between conical stromatolites and some modern microbial mats suggests a photosynthetic origin for ancient stromatolites. To better understand and interpret ancient fossils, we seek a quantitative relationship between the geometry of conical stromatolites and the biophysical processes that control their growth. We note that all modern conical stromatolites and many that formed in the last 2.8 billion years display a characteristic centimeter-scale spacing between neighboring structures. To understand this prominent—but hitherto uninterpreted—organization, we consider the role of diffusion in mediating competition between stromatolites. Having confirmed this model through laboratory experiments and field observation, we find that organization of a field of stromatolites is set by a diffusive time scale over which individual structures compete for nutrients, thus linking form to physiology. The centimeter-scale spacing between modern and ancient stromatolites corresponds to a rhythmically fluctuating metabolism with a period of approximately 20 hr. The correspondence between the observed spacing and the day length provides quantitative support for the photosynthetic origin of conical stromatolites throughout geologic time.

Stromatolites—attached, laminated, lithified sedimentary rocks accreting from a point or limited surface (1)—are commonly thought to record microbial interactions with sediments as old as 3.4 billion years (Ga) (2–4). In general, stromatolites are complex products of physical, chemical, and biological processes. Consequently, their shapes and textures may tell us little about specific microbial metabolisms. Past biological activity is, however, thought to be a prerequisite for the formation of a number of conical stromatolites that grew in quiet conditions, in the apparent absence of sediment, and in the presence of fast lithification (5–7).

Assuming that small conical stromatolites were built by microbial communities throughout geologic history, one is led to ask what biological processes are implied by the presence of these structures. Notably, all modern conical stromatolites form in the presence of filamentous cyanobacteria growing under precipitating conditions without sedimentation (8–10). Because these and similar photosynthetic communities form cones even in the absence of lithification (8, 11–13), this morphology must arise from biological processes. The qualitative similarity between the shape of modener and ancient stromatolites has led to the hypothesis that ancient cones were also built by photosynthetic communities (8). However, the relationship between photosynthesis and the growth of conical stromatolites remains to be elucidated in both ancient and modern stromatolites.

Here we show that the diffusion of metabolites associated with photosynthesis plays a central role in setting the spatial organization of modern conical stromatolites. We begin by identifying a geometric feature common to many modern and ancient stromatolites: Neighboring structures are separated from one another by approximately 1 cm. We hypothesize that the regular spacing results from competition between neighboring structures for nutrients. To test this hypothesis, we identify the maximum distance over which stromatolite-forming microbes can take up nutrients during the time they are photosynthetically active. We next confirm experimentally that the spacing between tufts of modern cone-forming bacteria varies systematically with day length in accordance with the model. Finally, we identify the spatial organization of stromatolites that maximizes the available space for the mat to grow while limiting competition for nutrients. These observations lead us to conclude that the common geometry of many conical stromatolites is rooted in the common biophysical processes of competition for nutrients and photosynthesis.

Results

Field Observations of Regularly Spaced Conical Stromatolites.

We begin with an observation about the morphology of conical stromatolites that grew in still water as long ago as the Archean. A survey of these proposed fossils reveals that many grew with a regular spacing between neighboring stromatolites. Fig. 1 shows examples of this regular spacing in both ancient and modern conical stromatolites. Moreover, as shown in Table 1, the spacing between the apex of neighboring conical structure is often approximately 1 cm.

Fig. 1.

Small conical stromatolites often grow into fields with a regular spacing between neighboring structures. Such fields can be found in laboratory cultures (A), hot springs in YNP (B), 2.8 billion years old Archean stromatolites [reproduced from Grey (14)] (C), and 1.7 billion years old Proterozoic stromatolites from the Aphebian Mistassini Group (19) (D). Each scale bar is 1 cm. Image in (B) courtesy of the Geological Survey of Western Australia, Department of Mines and Petroleum. © State of Western Australia 2009.

Table 1.

Regularly spaced, small conical stromatolites in the rock record

Sample	Spacing (cm)	Age (Gya)	Reference
Gindalbie	1–2	2.8–2.7	(14)
Belingwe	1–2	2.7	(5)
Hurwitz	0.5–1	2.1	(15)
Rocknest	1	1.89	(16)
Pethei	3	1.88	(17)
Pethei	0.3	1.88	(18)
Mistassini	0.5–1	1.7	(19)
Satka	1	1.6	(20)
Tokaanu, New Zealand	1	0	(10)
YNP, United States	1	0	(21)
Baja California, Mexico	1	0	(11)

To understand the biophysical origin of this feature, we study the processes that shape modern, regularly spaced conical stromatolites growing in the effluent of alkaline hot springs in Yellowstone National Park (YNP) (8). Each of Yellowstone’s conical stromatolites is precipitated within a microbial mat largely composed of cyanobacteria. The mat stretches over each cone as well as the flat region separating cones. These structures are found in nearly still pools that are largely separated from the main flow by barriers consisting of mats and silica precipitate (Fig. 2A). In regions where the flow is relatively fast, the mat is instead flat (Fig. 2B) or occasionally forms regularly spaced long ridges parallel to the flow.

Fig. 2.

(A) Regularly spaced conical structures grow in in still side pools of hot springs in Yellowstone National Park. (B) In fast moving sections of the stream, the mat is often flat. The purple knife in is 8.1 cm long.

Nutrient Gradients Form Around Growing Mats.

Because modern cones tend to grow in stagnant pools where gradients in nutrient concentration can form (8), we hypothesize that regular spacing may arise from competition between neighboring cones for diffusing nutrients. Here we consider the role of diffusion in the formation of nutrient gradients around modern cone-forming bacteria. If concentration gradients can extend far from the mat, then competition provides a mechanism by which neighboring cones can interact.

During photosynthesis, mats take up nutrients from the surrounding fluid, which are then replenished by diffusive transport. In this process, bacteria deplete nutrients within a distance ℓ, which in turn provides the mat with a nutrient flux

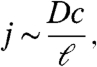[1]

where c is the ambient nutrient concentration and D is its diffusion coefficient. When the mat’s growth is limited by the rate at which diffusion provides nutrients, the mat is said to be diffusion limited. The abundance of isotopically heavy carbon in coniform mats from YNP suggests that cone-forming bacteria are often limited by the diffusion of dissolved inorganic carbon (22). This hypothesis is also consistent with estimates of j from the field (Appendix).

Two observations from laboratory samples suggest that the initial stages of the growth of modern conical stromatolites, the appearance of approximately 100 μm diameter rounded clumps (8), is associated with the formation of large diffusive gradients. Firstly, cyanobacteria grown in still media aggregate into clumps after roughly a week, whereas those growing in gently moving media form flat biofilms (Fig. S1). As concentration gradients can only form in still media, a likely explanation of this observation is that bacteria aggregate in response to large diffusive gradients, although shear may also influence their growth. This explanation is also consistent with the second observation: soon after a mat begins photosynthesizing, cyanobacterial filaments orient themselves normal to the surface of the mat (Fig. S2). Similar behavior has been observed in certain elongated sulfur-oxidizing bacteria that extend themselves through diffusive gradient gradients to reach higher nutrient concentrations (23). If the early stages of a cone’s growth are indeed governed by bacterial responses to concentration gradients, the final organization of stromatolites may also record the influence of large diffusive gradients on the growing mat.

Modern Stromatolites Are Spaced to Limit Competition: Theory.

When the diffusive length-scale becomes large, neighboring cones compete directly for resources. We proceed to estimate the maximum extent of these gradients for a photosynthetic mat growing in still liquid.

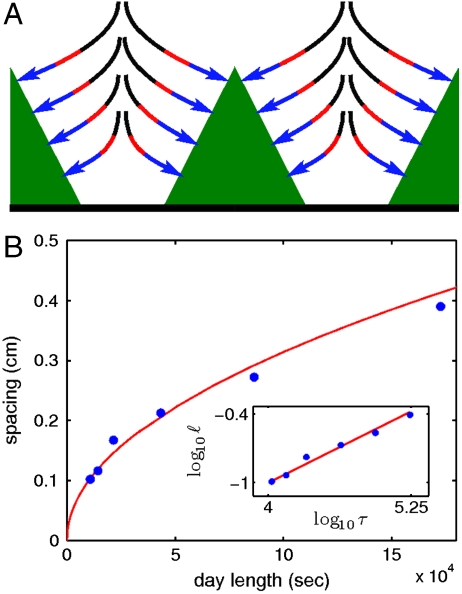
When the mat is active, photosynthesis depletes nutrients within a characteristic distance from the active biomass (Fig. 3A). At night, these flows reverse. The diffusive length-scale is therefore set by the distance nutrients and metabolites can diffuse while the mat is photosynthetically active. Thus, the diffusion length is

[2]

where τ is the average length of day light. The dimensionless factor α is of order one; its exact value is determined by the details of the system (e.g., nutrient requirements, growth rate, mineral precipitation). Cones that are closer than ℓ compete directly for resources. Cones spaced much further than ℓ take resources from a common pool, but do not directly interact.

Fig. 3.

Periodically spaced stromatolites record periodic forcing. (A) Initially the mat (green) only takes in nutrients from its immediate surroundings (blue arrows). As time progresses, nutrients become locally depleted and the mat takes up nutrients from a larger volume (red lines). Because the radial extent of the harvest grows with the square root of time, the maximal extent of these gradients ℓ is set by the span of time that the mat is active (black). To avoid direct competition for nutrients, vertical structures must be spaced as to prevent overlapping harvests; i.e., of order ℓ. Thus, the spacing between cones records the span of time they are active. Centimeter spacing corresponds to a rhythmically fluctuating metabolism with a period of approximately 20 hr. (B) Cultures grown in the lab display the predicted square-root dependence of spacing on day length.

A field of stromatolites minimizes direct competition for nutrients when the spacing between neighbors is the diffusive length-scale. Consequently, Eq. 2 relates the geometry of a cone-forming microbial mat to the metabolic activity of its microbial constituents. Given that many important metabolites are small molecules, the diffusion coefficient of the limiting nutrient—and thus the spacing between neighbors—is nearly independent of exactly which nutrient limits growth (24). Empirically, the diffusion coefficient for a number of important carbon sources (e.g., CO₂, ), photosynthetic electron donors (e.g., H₂, H₂S), and nutrients (e.g., , ) are all approximately 10^-5 cm² sec^-1 (25). Thus, assuming a 12 hr day, Eq. 2 predicts the observed cm-scale spacing between small conical stromatolites. Furthermore, because we assume that the net accumulation of biomass is ultimately limited by the diffusion of nutrients from outside, this result is independent of the cycling of nutrients within the mat. More generally, it predicts a square-root dependence of ℓ on Dτ with a proportionality constant of order one.

Modern Stromatolites Are Spaced to Limit Competition: Experiment.

To test this prediction, we grew mats under a range of day-night cycles that varied from 3 hr/3 hr to 48 hr/48 hr. Fig. 3 shows that the distance between neighboring clumps as a function of day length (seconds of continuous light) conforms well to the square-root dependence predicted by Eq. 2. Assuming D = 10^-5 cm² sec^-1, a least-squares fit yields α = 0.30 ± 0.02; note, however, that this value may differ in different environments while remaining approximately unity. The square-root dependence of the spacing between growing vertical structures on the duration of the day-night cycle confirms that competition mediated by diffusion is central in organizing the mat. Because this scaling depends exclusively on diffusive transport, it can be used as an indicator of diurnal cycling in both modern and fossil mats. The empirical confirmation that the spacing between modern stromatolites is set by diffusive competition is our main result.

Centimeter-Scale Spacing as a Record of Photosynthesis.

Nutrient limitation is known to influence the formation of sub-mm scale three-dimensional heterotrophic biofilms (23, 26, 27). Our results suggest that nutrient limitation also controls the morphology of photosynthetic biofilms that are almost two orders of magnitude taller and wider, and consequently more likely to be preserved. The initial aggregation of filamentous microbes into nascent cones is consistent with a response to diffusion limitation. Furthermore, in still media, we observe that the spacing between neighboring structures is proportional to the distance metabolites diffuse when the mat is active. The cm-scale spacing observed in all modern conical stromatolites and many small Archean stromatolites as old as 2.8 Ga (14) and possibly as old as 3.1 Ga (6), is consistent with a mat that is active during the day and inactive at night. This expression of biological and physical processes in the geometric arrangement of sedimentary structures allows us to recognize spatial organization consistent with photosynthesis in stromatolites throughout geologic time, especially those from the Archean (5, 14, 15, 28) and the Proterozoic (15, 17, 20, 29).

Spatial Organization.

Given that the competition for nutrients sets the spacing between modern conical stromatolites, we proceed to conjecture how competition may effect their spatial organizations under different flow regimes. We assume that a mat will tend to grow into any available spaces, thus we expect spatial organizations that maximize the density of stromatolites while limiting competition for nutrients. We focus on how the organization varies between stagnant and turbulent ponds.

In still water, each structure competes with neighbors on all sides. A field of stromatolites then reaches a maximum density while preventing direct competition by growing into a hexagonally symmetric pattern (30). Indeed, we often observe that nascent clumps form into a roughly hexagonal arrangement (Fig. 4A). Because these aggregates grow on smooth surfaces such as glass beakers, the regular spacing must be intrinsic to the growth of these biofilms, rather than inherited from the topography of the underlying surface. A similar hexagonally symmetric arrangement can also be observed growing on the surface of a mat that had been deformed by a gas bubble (Fig. 4B). Although regularly spaced aggregates grow over the entire mat, they only grow into large cones on the top of the mat, suggesting that other factors such as the proximity to a light or a nutrient source may be important in the growth of cones.

Fig. 4.

When cone-forming bacteria grow in still water, they grow into a roughly hexagonal arrangement. Laboratory cultures grow into such an organization on both the smooth surface of a glass beaker (A) or on the surface of a growing mat (B); both scale bars are 1 mm. When stromatolites grow in moving water, competition is mediated by advection as well as diffusion. (C) In a unidirectional flow, long ridges grow with a centimeter-scale spacing between ridges. The blue arrow indicates the direction of flow. On either side of the channel the mat is too thick to permit flow. The scale bar is 30 cm. (D) The regular spacing and roughly hexagonal arrangement of 1.4 Gya conical stromatolites from the Bakal formation (31, 32) may be due to competition for nutrients mediated by eddy diffusivity. The hammer is 27.9 cm long.

Thus far, we have only considered the role of molecular diffusion in mediating the competition between cone-forming microbial mats. Because this mechanism can lead to the formation of only small gradients, this model can only explain the organization of centimeter-scale stromatolites. Here we consider a possible generalization of Eq. 2, which may be applicable to decimeter to meter-scale structures. We note that, as there are no known large modern conical stromatolites, the applicability of this generalization to stromatolites can be neither confirmed nor rejected.

In general, moving water destroys diffusive gradients and therefore limits competition between structures. If we assume that cone-forming bacteria might remain limited by the rate at which nutrients arrive to the mat in the presence of a net flow (as might happen when the limiting resource is very scarce), the effects of competition can be identified in two cases: isotropic turbulence and unidirectional flow.

When the ambient flow is turbulent, nutrients are advected by eddies. Given a large Reynolds number Re, one can then define an effective diffusion coefficient D_eff ∼ Re D (33). If stromatolites compete for nutrients in a turbulent field, Eq. 2 predicts an arrangement of structures spaced by . Because the flow is isotropic, the effective diffusion of nutrients is also isotropic, thus producing a hexagonal arrangement. In weak turbulence (Re ≈ 5,000 corresponding, for example, to a velocity of 1 cm sec^-1 and a length-scale of 50 cm), diurnal forcing produces structures spaced by tens of centimeters. The 20 cm spacing and roughly hexagonal symmetry of some conical stromatolites (Fig. 4D) may be interpreted as the result of microbial growth in a weakly turbulent environment.

In a unidirectional flow, the effect of diffusion is negligible in the direction of flow but is essential for the transport of nutrients orthogonal to the flow. In YNP, long ridges often grow with an approximately 1 cm spacing in flows with a typical surface velocity (as measured by timing a passive tracer on the surface of the flow) of 10 cm sec^-1 (Fig. 4C). These scales correspond to a Reynolds number of around 1,000. Nutrients are therefore only advected by the downstream flow, while molecular and eddy diffusion transport nutrients across the stream. Consequently, there is little variation in the shape of structures along the flow, leading to the growth of long ridges. The organization of some ancient lanceolate stromatolites may be explained by this process, notably regularly spaced ridges observed in some Proterozoic samples (20).

Conclusions

Our primary finding, that the organization of modern conical stromatolites results from competition between neighboring structures for nutrients, is the result of four observations. First, the bacterial aggregates in the field and in the laboratory display a regular spacing between neighboring structures. Next, cone-forming bacteria in both the field and laboratory are able to take up nutrients, notably inorganic carbon, faster than diffusion can replenish them, leading to the growth of gradients in nutrient concentration. The lateral extent of these gradients, which is set by the day length, gives a typical length-scale over which competition between neighboring structures is possible. Finally, we found that the spacing between bacterial aggregates in laboratory cultures remains proportional to this length-scale even as the we varied the length of day. We therefore conclude that the diffusive length scale sets the spacing between aggregates.

Given this understanding of the biophysical basis for the geometry of modern conical stromatolites, we asked if our results inform our understanding of ancient stromatolites as well. We identify two observations that are likely to be generally applicable to biogenic stromatolites formed throughout geologic time. First, small stromatolites compete with one another for nutrients. Because many microbial mats are limited by the same physical processes (e.g., diffusion), the competition for nutrients outside all such mats can be understood in terms of these processes regardless of their internal complexity and diversity. The ubiquity of diffusion limitation in modern microbial mats strongly suggests that these processes also shaped ancient microbial mats. Consequently, these interactions should be included along with the previously identified processes of mat growth and mineral precipitation (34) when considering the growth of stromatolites. Furthermore, we have found that when stromatolites grow in still water, this competition occurs over a length scale set only by the diffusion of the limiting nutrient and the time that the mat is metabolically active. Because diffusion coefficients of nearly all small-molecule nutrients are similar (25), periodically spaced conical stromatolites record periodic metabolic forcing. Fields of stromatolites with approximately 1 cm spacing record a rhythmically fluctuating metabolism with a period of approximately 20 hr, suggesting solar forcing. This interpretation of the geometry of many ancient stromatolites (Table 1) provides a record of photosynthesis in stromatolites as old as 2.8 billion years. Although the biological origin of some precipitated stromatolites can be questioned (35), our results demonstrate that many small conical Archean stromatolites can be recognized as mileposts (4) marking the evolution of Earth’s earliest photosynthetic communities.

Materials and Methods

Culturing Techniques.

The cone-forming cyanobacteria used in these experiments was collected from Sentinel Meadows in YNP under permit YELL-2008-SCI-5758. Cone-forming cyanobacteria were grown in modified CastenholzD medium (36) in which the concentrations of and were lowered to 2.3 mM and 0.8 mM, respectively. With the exception of the day-length experiment, cultures were grown under a 12 hr light, 12 hr dark cycle using a fluorescent cold light source.

Day-Length Experiment.

To gauge the effect of day length on the spacing between structures, we grew mats under 3, 4, 6, 12, 24, and 48 hr of light; each sample was illuminated for 48 out of every 96 hr. In each case, the mat was inoculated onto silica sand in a 10 cm diameter crystallizing dish. The dish was placed below a cold fluorescent light source to produce a light intensity of 10⁴ lux. To ensure that each culture was only exposed to light at the appropriate times, each culture was placed in a conical sheath made from black poster board. The light source was placed at the apex of the cone 26 cm above the sample. After two weeks, regularly spaced structures could be seen over large sections of the mat (Fig. S3).

We used two different methods to measure the spacing between structures. First, we measured the spacing between clumps by identifying unambiguous bacterial aggregates in the photographs (Fig. S3). We then measured the spacing between each structure and the nearest clump (Fig. S4). To remove bias, two individuals independently measured the spacing. Assuming a value of D of about 10^-5 cm² sec^-1, the two individuals found α = 0.30 ± 0.02 and α = 0.30 ± 0.04. To further confirm that the spacing between clumps was measured accurately, we also measured the spacing from the number density of clumps (Fig. S5). The number density n of clumps was found by identifying an area where clumps grew and then counting the number of clumps in the area. In general, the mean spacing between clumps scales with the square root of the area per clump. For closely packed disks with a packing fraction η,

[3]

For a hexagonal lattice, 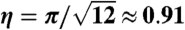. For random close packing, η = π/(4 sin(105°)) ≈ 0.81 (37). Taking the geometric factor consistent with hexagonal packing, this measurement gave the estimate α = 0.24 ± 0.08. Although all three estimates of the spacing gave consistent results, the data were substantially tighter when clumps were chosen by hand (Fig. S6). The increased scatter found in the estimation of ℓ from the number density may be due to variations in η between samples.

Appendix

The scaling argument for diffusion limitation. Here we show that cone-forming bacteria in YNP take up nutrients at a rate sufficiently fast to become limited by the diffusion of nutrients to the mat and thus allow to formation of large nutrient gradients.

A microbial mat becomes diffusion-limited when its growth is limited by the rate nutrients arrive. Diffusion provides the mat with a maximum nutrient flux of Dc/ℓ, where D is the diffusion coefficient and c is the concentration of the nutrient at a distance ℓ from the mat. We proceed to estimate the nutrient flux to the mat by independently estimating c and ℓ for microbial mats in YNP, while assuming a diffusion coefficient of D = 10^-5 cm^-2 sec^-1. We then compare this flux to the measured flux. If the maximum estimated diffusive flux is less than or approximately similar to the measured flux, the mat can take up nutrients at least as fast as diffusion can provide them, and thus become diffusion-limited.

Clearly, the concentration of the limiting nutrient depends on which nutrient limits growth. However, if a small-molecule nutrient becomes substantially more abundant than inorganic carbon, the photosynthetic mat will become carbon limited. Thus, the concentration of inorganic carbon (principally ) gives an upper bound on c. The concentration of 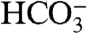in YNP is of order 10^-3 M (22).

An estimate of ℓ changes with the flow conditions. In perfectly still water, this length is the maximum extent that the diffusion gradient can grow while the mat is active. From the main text, ℓ is of order 1 cm. In moving water, however, the relevant length scale is the distance from the mat at which viscosity balances inertia. Within this distance, the flow is parallel to the mat and diffusion is the only mechanism available to transport nutrients to the mat. This length scale is of order L(Re )^-1/2, where L is the length scale of the main flow and Re is the Reynolds number (33). Taking L as the 1 cm and a Reynolds number of < 100 (i.e., a characteristic flow velocity < 1 cm sec^-1), this scaling predicts that diffusion transports nutrients to the mat within at least 0.1 cm around the mat.

Combining these estimates, the maximum diffusive flux of inorganic carbon to the mat is between 0.01 μM cm sec^-1 (Re = 0) and 0.1 μM cm sec^-1 (Re = 100). This flux is an upper limit that decreases as the limiting nutrient becomes more scarce.

To determine if mats are diffusion-limited, we compare the estimated diffusive flux to the measured rate that nutrients are taken up. Because the photosynthetic rate of a mat is set by the rate at which the mat takes up the limiting nutrient, oxygen leaving the mat gives a lower bound on the rate the limiting nutrient is used. Thus, the flux of oxygen out of a structure gives a lower bound on the flux of the limiting nutrient into the structure. We measured the oxygen flux in slow-moving water by measuring the concentration of oxygen at the surface of the mat and 500 μm above the mat using a microelectrode as has been previously described (12). The flux of oxygen measured above three cones was 0.32 ± .06 μM cm sec^-1. Because this flux is approximately the estimated upper bound of the diffusive flux (i.e., between 0.01 μM cm sec^-1 and 0.1 μM cm sec^-1), we conclude that the mats are able to consume nutrients at least as quickly as diffusion can provide them and thus become diffusion limited.