Abstract
We developed a multiscale approach for the computationally efficient modeling of morphogen gradients in the syncytial Drosophila embryo, a single cell with multiple dividing nuclei. By using a homogenization technique, we derived a coarse-grained model with parameters that are explicitly related to the geometry of the syncytium and kinetics of nucleocytoplasmic shuttling. One of our main results is an accurate analytical approximation for the effective diffusivity of a morphogen molecule as a function of the nuclear density. We used this expression to explore the dynamics of the Bicoid morphogen gradient, a signal that patterns the anterior-posterior axis of the embryo. A similar approach can be used to analyze the dynamics of all three maternal morphogen gradients in Drosophila.
A morphogen gradient is defined as a concentration field of a molecule that acts as a dose-dependent regulator of cell differentiation. Morphogen gradients can be formed by proteins that diffuse from a localized source of production. Cells located different distances from the source are exposed to different levels of the morphogen, express different genes, and assume different cell fates (1–3). Some of the earliest experimental tests of this model were provided by studies of pattern formation in Drosophila, at a stage when the embryo is a syncytium, a cell with multiple dividing nuclei (4).
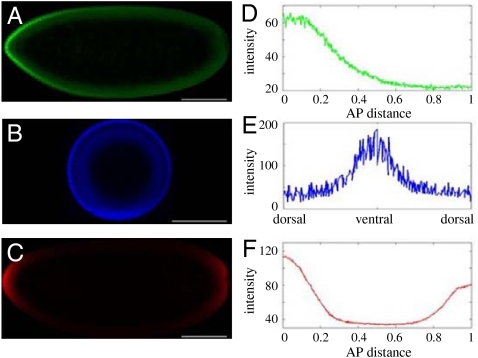
Nuclear divisions in the syncytial embryo are accompanied by the formation of morphogen gradients that control gene expression along the anteroposterior (AP) and dorsoventral (DV) axes (5). The AP axis is patterned by the concentration gradient of the transcription factor Bicoid (Bcd), the DV patterning depends on the nuclear localization gradient of the transcription factor Dorsal (Dl), and the embryonic termini are patterned by the phosphorylation gradient of the MAPK. Thus, the AP morphogen is distributed in a gradient of protein concentration, the DV morphogen is distributed in a gradient of subcellular localization, and the terminal morphogen is distributed in a gradient of protein phosphorylation (Fig. 1).
Fig. 1.
Maternal morphogen gradients in the early embryo. See ref. 7 for the method used to quantify the profiles. Embryos imaged for (A) Bicoid, (B) Dorsal, and (C) phosphorylated MAPK. (Scale bar: 100 μm.) (D) Gradient of Bicoid along the scaled AP axis. (E) DV gradient of nuclear dorsal. (F) Phosphorylation gradient of MAPK with peaks at the termini of the embryo.
The mechanisms leading to the formation of these three gradients are all different: Bcd is translated from an anteriorly localized maternal transcript. Dl, sequestered in the cytoplasm in an inhibitory complex, is released from this complex and enters the nuclei only on the ventral side of the embryo. The terminal patterning gradient depends on the localized phosphorylation of a uniformly distributed protein (MAPK). Bcd and Dl control gene expression by binding to the regulatory regions of their transcriptional targets. MAPK, on the other hand, controls gene expression indirectly, through enzymatic modification of uniformly distributed transcriptional repressors. Despite these important mechanistic differences in the formation and interpretation of the AP, DV, and terminal gradients, they share a number of similarities. In each case, a morphogen molecule (Bcd, Dl, or phosphorylated MAPK) is produced from a localized source, diffuses between the syncytial nuclei, and shuttles between the nuclear and cytoplasmic compartments.
Experiments with fixed embryos quantified the distributions of the AP, DV, and terminal gradients (6–8). Live imaging studies characterized the lateral mobilities of Bcd and Dl in the syncytium and the rates of their nucleocytoplasmic shuttling (6, 9). In order to test the models proposed for the formation of maternal morphogen gradients, it is necessary to determine whether the observed shapes of morphogen gradients are consistent with the observed diffusivities and nuclear exchange rates, as well as with the assumed patterns of morphogen production. Answering this question requires a modeling framework that can connect the rates of constituent processes, such as diffusion and nuclear import/export, to the dynamics of concentration fields. Development of such a framework is the main goal of this work.
We model the syncytium as a periodic arrangement of compartments, each of which contains a single nucleus and an associated region of the cytoplasm. We then use a homogenization technique to derive a spatially averaged diffusion model, with the diffusion coefficient related to the sizes and densities of nuclei and rates of nucleocytoplasmic shuttling (10, 11). To illustrate our approach, we use the homogenized model to explore the dynamics and stability of the Bcd gradient. A similar approach can be used to study the dynamics of all three maternal morphogens.
Model
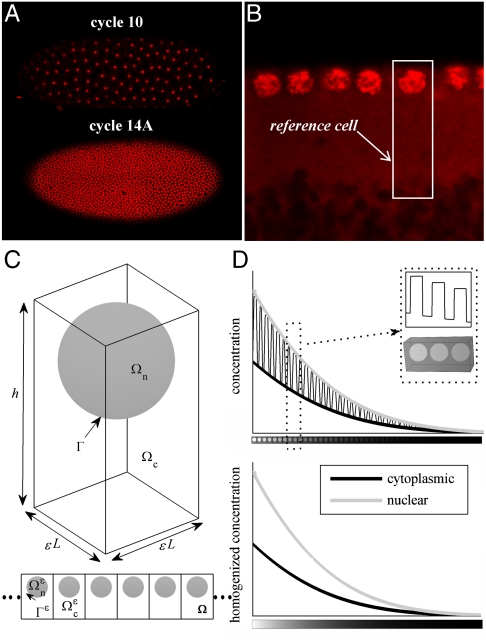
We focus on the embryo during the last five nuclear division cycles, when nuclei are arranged in the cortical region between the yolk and the plasma membrane (Fig. 2). Depending on the nuclear cycle, there can be anywhere from 500 to over 6,000 nuclei in the cortical region. The system is characterized by a clear separation of length scales: The size of a single nucleus is several microns, whereas the dimension of the embryo is on the order of hundreds of microns. Morphogen molecules, such as Bcd, Dl, and phosphorylated MAPK, diffuse between the nuclei and undergo nucleocytoplasmic shuttling (6, 9). We are interested in determining the influence of these processes on the dynamics of morphogen gradients.
Fig. 2.
Geometric model of the syncytial blastoderm. Nuclei were marked by using SYTOX Green (Invitrogen; 1∶10,000 dilution). Top cross-section images were taken by using Zeiss LSM510 confocal microscope with a Zeiss 20× (NA 0.45) A-plan objective. (A) Top view of nuclei in cycle 10 and 14A embryos. (B) Layer of nuclei in the cortical region at the beginning of cycle 14A. (C) Reference cell composed of a nucleus Ωn and surrounding cytoplasm Ωc, where the boundary separating the two compartments is denoted Γ. The reference cell is periodically repeated to make up the cortical region of the embryo Ω. The method of homogenization requires a small scale parameter, defined as ϵ = l/L, where l is the size of the reference cell and L is the length of the embryo. (D) Illustrative example showing that the method of homogenization effectively smooths substructure variations caused by the presence of the nuclei. A cross-section of the solution at a given time (Top) is compared to the solution of the homogenized equation (Bottom).
To analyze this problem, we model the cortical region of the syncytium as a periodic repetition of a reference cell, which contains a single nucleus and an associated cytoplasmic region (Fig. 2C). We denote the height of the reference cell h, its length (and width) l, nuclear radius r, and nuclear distance from the outer membrane a. The fraction of the reference cell occupied by the cytoplasm is denoted ϕ, and conversely 1 - ϕ is the fraction of space occupied by the nucleus, precisely defined as
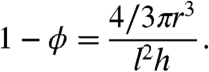 |
[1] |
Cytoplasmic and nuclear concentrations, as well as diffusivities, are defined in their respective regions. Specifically, the cytoplasmic (nuclear) variables are positive if the position lies in the cytoplasm (nucleus), and zero elsewhere. Thus, we begin with a reaction-diffusion problem with spatially periodic coefficients (Fig. 2D).
In this framework, a mathematical model for morphogen dynamics incorporates diffusion in both compartments of the reference cell coupled with an interfacial boundary condition on the surface of the nucleus. To model nuclear import and export, we characterize the surface of the nucleus by a partially absorbing boundary condition. For instance, the rate of import per unit area is given by the product of the surface reaction rate constant, denoted by k+, and the cytoplasmic concentration. The integral of this product over the surface of the nucleus gives the total rate of nuclear import. Nuclear export is modeled in a similar way (here, the surface reaction rate constant is denoted k-).
For continuity, the resulting set of equations in the reference cell must be solved for every syncytial nucleus and be linked to the problems for neighboring nuclei. Finding a solution to such a complex problem is not a trivial task, considering the complex boundary conditions and the sheer number of nuclei in the late syncytium. Thus, we seek a more manageable model that describes gradient formation in the entire embryo.
Results
Homogenization.
We start by considering diffusion and nucleocytoplasmic shuttling of a stable protein. Our model syncytium belongs to the class of spatially periodic heterogeneous materials that can be successfully studied by using a technique called homogenization. The formal approach of homogenization theory, namely, the method of asymptotic expansions, has been widely used to study a variety of processes in physics, engineering, and biology (10–12).
The main goal of homogenization is to average out substructure variations in materials that are spatially heterogeneous (Fig. 2D). Homogenization theory relies on the assumption that the medium can be composed of the spatial repetition of a much smaller reference cell (Fig. 2C) (11). First, a microscopic description of the phenomena is established in the reference cell. The asymptotic expansion technique is then employed to derive a simplified macroscopic problem for the entire domain, with coefficients depending on the microscopic properties. Details of the multiscale expansion method are described in SI Text; see also refs. 10, 11, 13, and 14.
Before carrying out a formal homogenization procedure, we make an additional approximation. Live imaging experiments with fluorescently tagged Bcd and Dl proteins suggest that the system operates in a regime of rapid nuclear kinetics; the time required for the two concentrations to reach local equilibrium through surface reactions is much faster than the establishment of the gradient (6, 9). Within the framework of our model, the nuclear and cytoplasmic concentrations are related as follows:
| [2] |
In this equation, Cc is defined as the volume average over the cytoplasmic region of the reference cell; similarly, Cn is the volume-averaged nuclear concentration, and κ ≡ k+/k- is the equilibrium constant that characterizes the nucleocytoplasmic shuttling. With this assumption, the homogenization approach leads to the following equation for the dynamics of the cytoplasmic concentration:
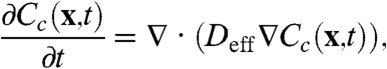 |
[3] |
where 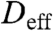 is the effective diffusivity. Variations in the vertical direction are negligible because the cortical thickness is much smaller than the size of the embryo, and hence x defines the lateral dimensions of the embryo.
is the effective diffusivity. Variations in the vertical direction are negligible because the cortical thickness is much smaller than the size of the embryo, and hence x defines the lateral dimensions of the embryo.
The main result of homogenization is the derived effective reaction rates and diffusivities that are directly related to the parameters of the spatially heterogeneous problem (15). For the problem above, these parameters are related to the geometry of the reference cell, diffusivity in the cytoplasm, and rates of nucleocytoplasmic shuttling. As described in SI Text, a multiscale expansion approach leads to the following expression for the effective diffusivity:
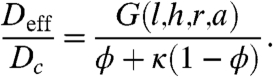 |
[4] |
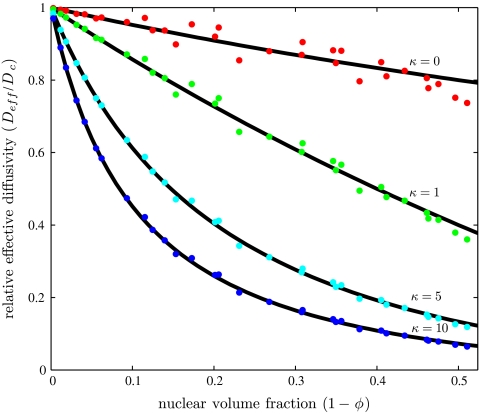
The numerator of this expression, G, depends only on the parameters that define the geometry. This function can be found numerically by using a finite element solution of the auxiliary boundary value problem that emerges from the homogenization approach (see SI Text for details). Once computed, G is used to evaluate the effective diffusivity for arbitrary values of κ and the geometric parameters (Fig. 3).
Fig. 3.
The relative effective diffusivity plotted as a function of nuclear volume fraction (up to the maximum π/6 ≈ 0.52), for multiple values of the equilibrium constant. Each dot represents the effective diffusivity found computationally for the indicated equilibrium constant and a particular set of geometric parameters chosen from the following ranges: r∈[1,6], h∈[10,30], a∈[0.1,5], and l∈[6,24]. The solid lines are the analytical expression Eq. 6; see text for details.
Analytical Approximation of the Effective Diffusivity.
In addition to computing the effective diffusivity numerically, we also found an approximate analytical expression. When κ = 0, our problem reduces to finding the effective diffusivity in a system with periodically arranged reflective obstacles. This problem has a long history, starting from the seminal work by Maxwell (16). Although there are no analytical expressions for our particular geometry, existing analytical expressions for the effective diffusivity are relatively insensitive to the precise arrangement of obstacles (17–20). One approximation is given by the following equation (20):
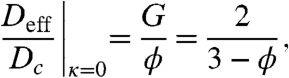 |
[5] |
which leads to G = 2ϕ/(3 - ϕ). After substituting G into Eq. 4, we obtain the following analytical approximation for the effective diffusivity:
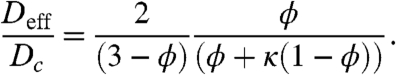 |
[6] |
Within the framework of this approximation, the effect of nuclei has been reduced to the product of two factors. The first, 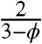 , depends only on ϕ and reflects the scattering effect of molecular trajectories by nuclei. This factor would be present even for molecules that are not imported into the nucleus. The second factor,
, depends only on ϕ and reflects the scattering effect of molecular trajectories by nuclei. This factor would be present even for molecules that are not imported into the nucleus. The second factor, 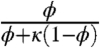 , depends both on the ratio of nuclear and cytoplasmic volumes and on the equilibrium shuttling constant. One can easily show that it can be interpreted as the fraction of time that the diffusing particle spends in the cytoplasm. This factor commonly arises in the analysis of diffusion problems with reversible binding (21).
, depends both on the ratio of nuclear and cytoplasmic volumes and on the equilibrium shuttling constant. One can easily show that it can be interpreted as the fraction of time that the diffusing particle spends in the cytoplasm. This factor commonly arises in the analysis of diffusion problems with reversible binding (21).
Thus, our computer-assisted homogenization approach led to an analytical approximation that has a very clear physical interpretation. Furthermore, we found that this approximation is very close (within 6%) to our numerical results for the entire physical range of nuclear volume fractions (Fig. 3). In the absence of nuclei, ϕ = 1 and Eq. 6 predicts that the effective diffusivity is equal to the cytoplasmic diffusivity. When κ = 0, we recover the well-known Maxwell expression, scaled by the cytoplasmic volume fraction.
We note that the ad hoc algebraic expression derived in our earlier model of the Bcd gradient is 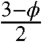 times larger than the effective diffusivity derived here in a more systematic way (21). We ultimately find that for maximal density of spherical nuclei in the syncytial blastoderm (1 - ϕ ≈ 0.3), the presence of impenetrable nuclei causes only a 10% decrease in diffusivity relative to the free cytoplasmic case with no nuclei. Diffusivity is further decreased once nucleocytoplasmic shuttling is introduced into the system. For a nucleocytoplasmic shuttling constant of 5 (6), the effective diffusivity is 30% of the free cytoplasmic diffusivity.
times larger than the effective diffusivity derived here in a more systematic way (21). We ultimately find that for maximal density of spherical nuclei in the syncytial blastoderm (1 - ϕ ≈ 0.3), the presence of impenetrable nuclei causes only a 10% decrease in diffusivity relative to the free cytoplasmic case with no nuclei. Diffusivity is further decreased once nucleocytoplasmic shuttling is introduced into the system. For a nucleocytoplasmic shuttling constant of 5 (6), the effective diffusivity is 30% of the free cytoplasmic diffusivity.
Modeling the Bcd Gradient.
On the basis of the fact that Eq. 6 is accurate over a wide range of model parameters, we propose to use it for the analysis of the dynamics of maternal morphogen gradients. To illustrate this approach, we use the homogenized model to explore the dynamics of the Bcd gradient. One can show that a homogenized version of the model that accounts for the production, diffusion, cytoplasmic degradation, and nucleocytoplasmic shuttling of Bcd molecules is the following reaction-diffusion problem:
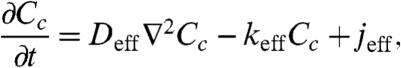 |
[7] |
where it is assumed that the anterior and posterior ends of the embryo are impermeable to Bcd molecules. Thus, the only modification of the derived homogenized equation (Eq. 3) is the appearance of effective parameters: the effective rate for Bcd degradation in the cytoplasm, keff, and the effective term for the source of the protein, jeff.
The effective rate of degradation is equal to the product of the cytoplasmic degradation rate, kc, and the fraction of time that the diffusing Bcd molecule spends outside the nuclei: 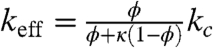 . Similarly, the source function is scaled to reflect the fact that Bcd molecules are produced only in the cytoplasm:
. Similarly, the source function is scaled to reflect the fact that Bcd molecules are produced only in the cytoplasm: 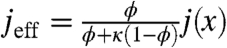 . Here, we assume an exponentially distributed source,
. Here, we assume an exponentially distributed source, 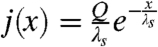 , where Q is the rate of production and λs is the characteristic length of the source.
, where Q is the rate of production and λs is the characteristic length of the source.
To model the effect of nuclear doubling, we partition the developmental time into distinct intervals that correspond to different nuclear cycles (4). We solve the homogenized equation (Eq. 7) with the appropriate diffusivity over each time interval. Free diffusion is assumed during the first nine cycles, a time when nuclear density is very low, and also during mitosis, a period when the nuclear envelope breaks down and Bicoid molecules are released from the nuclei to the surrounding cytoplasm. During interphase, the effective diffusivity is determined by Eq. 6. The timings for the interphase and mitosis of each nuclear cycle vary and are taken from ref. 4. Thus, the dynamics of the Bcd gradient is modeled by a diffusion problem with piecewise constant, time-dependent diffusivity (SI Text), where we have assumed that nuclei have constant radius and that their maximum size is reached instantaneously following mitosis.
A model for the dynamics of Bcd contains three free parameters: free diffusivity Dc, the cytoplasmic degradation rate kc, and the characteristic length of the source λs. The cytoplasmic diffusion constant has been reported to be anywhere from 0.3 (6) to 20 μm2/s (22). The time scale of Bcd degradation (23) has been estimated to range from ∼5–10 minutes (24) to infinite (21). Last, it has been commonly assumed that a constant source of Bcd is localized to the anterior pole of the embryo (6, 21, 22, 25), corresponding to λs = 0. However, a recent paper proposed that the Bcd source (bcd mRNA) is itself distributed in a gradient (26). In this case, 0 < λs ≤ λp, where λp is the characteristic length of the protein gradient.
By using the homogenized model, we can easily scan the three-dimensional space of model parameters. On the basis of the geometry of the syncytium and the experimentally determined value of the shuttling constant (κ = 5) (6), we look for values of the three unknown parameters (Dc, kc, and λs) that are consistent with the observed gradient dynamics. In particular, it is known that the concentration profile of Bcd has an exponential shape with a decay length between 50 and 100 μm, or about 10–20% of the embryo length (22). It has also been observed that, following mitosis, the nuclear gradient rapidly reestablishes to a quasi-steady state within 10% of its premitotic levels (6). See SI Text for solution examples and details of the procedure used to check criteria.
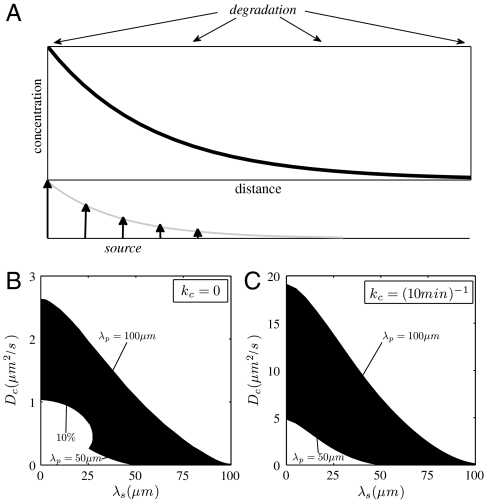
For a tightly localized source (λs ≪ λp), we find that large cytoplasmic diffusion constants are needed to produce gradients with the correct characteristic length. This is true for two extreme cases of Bcd degradation, kc = 0 and kc = (10 min )-1 (Fig. 4). The diffusion coefficient must be particularly high when the protein is degraded, about 10 times larger than for an infinite half-life, in order to avoid gradients that are too sharp. Nevertheless, we find that a small cytoplasmic diffusion coefficient is feasible when protein production is delocalized. For example, in the absence of degradation, a diffusion constant of 0.3 μm2/s [a value that has been obtained in live imaging experiments with GFP-tagged Bcd (6)] is possible if the distributed source has a decay length between 5% and 15% of the length of the embryo (Fig. 4A). When the protein is degraded, the source must extend further to 10–20% of the embryo length (Fig. 4B). Essentially, this means that for a Bcd lifetime ∼10 minutes, the source must have the same shape as the protein gradient itself.
Fig. 4.
(A) Schematic of morphogen gradient formation by synthesis, diffusion, and spatially uniform degradation. The source of morphogen production is distributed exponentially in the tissue. (B–C) Designating the times of nuclear division (4), the geometry of the syncytium, r = 3.25 μm and h = 18 μm, the nucleocytoplasmic shuttling constant, κ = 5, and the cytoplasmic degradation rate, (B) kc = 0 and (C) kc = (10 min )-1, leaves the diffusivity, Dc, the characteristic length of the extended source, λs, as the only free parameters in the model. Their values are constrained by the experimental measurements of the shape and accuracy of the Bicoid gradients, as indicated by the shaded region. λp = 50 μm and λp = 100 μm indicate the lower and upper bounds for the decay length of the protein gradient. Gradients above the shaded region are too shallow, whereas gradients below are either too sharp or the nuclear-stability condition is not satisfied (the accuracy of the nuclear gradient is worse than 10%). See SI Text on how to test the criteria.
We have also analyzed a model when Bcd is degraded inside the nuclei (22). A model that includes nuclear degradation is governed by Eq. 7, where Deff and jeff remain the same, but an additional term is added to keff: 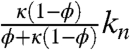 . This effective rate is a product of the nuclear degradation rate, kn, and the fraction of time that the diffusing molecule spends inside the nuclei. We find that the criteria to match experimental gradients cannot be satisfied for a Bcd nuclear lifetime of less than 30 min.
. This effective rate is a product of the nuclear degradation rate, kn, and the fraction of time that the diffusing molecule spends inside the nuclei. We find that the criteria to match experimental gradients cannot be satisfied for a Bcd nuclear lifetime of less than 30 min.
Discussion
Studies of pattern formation in the early Drosophila embryo are now at a stage that requires quantitative models (27, 28). To model the earliest steps of embryonic patterning, it is essential to develop computationally efficient descriptions of diffusion and nucleocytoplasmic shuttling of maternal morphogens. Here we have demonstrated how this goal can be achieved by using a homogenization theory. The main outcome of the homogenization procedure is a clear relation of the effective transport parameters and reaction rates of the spatially averaged problem to the original microscopic problem.
Whereas, in general, this relation must be obtained numerically, we were able to find a simple analytical expression that is accurate over a wide range of model parameters. We illustrated how the homogenized equations can be used as an efficient tool for exploring the parameters of the original problem, such as the nuclear density, rates of nucleocytoplasmic shuttling, and the spatial pattern of Bcd synthesis. A similar approach can be used to model the dynamics of all three maternal morphogen gradients, as well as their interactions (29).
A key prerequisite of the homogenization approach is a wide separation of geometric length scales, which is clearly satisfied for the syncytial blastoderm. Indeed, the characteristic size of the nucleus is much smaller than the characteristic length scales of the patterning gradients and size of the embryo.
The proposed homogenization approach can be readily extended to models that account for more realistic descriptions of nuclear import/export and chemical modifications of the morphogen molecules (10, 11, 30, 31), as well as additional physical effects, such as convective flows during the early nuclear division cycles (32). Moreover, the approach is not limited to linear problems and can be implemented in models with nonlinear reactions (10), such as the model of the Dorsal morphogen gradient (8). We stress that most of the work to formulate such problems has already been accomplished with the derivation of the effective diffusivity.
Finally, our multiscale framework provides an efficient method for exploring the effects of different types of model uncertainty (33). In the context of the Bcd gradient, one can straightforwardly investigate the effects of variability of the strength and dynamics of the source of Bcd production and degradation. Data presented in Fig. 4 correspond to the two extreme regimes of Bcd degradation kinetics: the infinitely stable protein and protein degraded on the time scale of minutes. In our ongoing work, we are examining a model with more complex kinetics, where both the source term and the degradation rate constant depend on time (e.g., the production of Bcd can start later than time zero and its active degradation can be delayed until the late syncytial cell cycles). Our preliminary results with this model strongly favor the regime with a significantly delocalized Bcd source.
Supplementary Material
Acknowledgments.
The authors thank Yoosik Kim and Jitendra Kanodia for providing the images in Figs. 1 and 2. We also thank Alexander Berezhkovskii, Oliver Grimm, and Eric Wieschaus for numerous helpful discussions and Mathieu Coppey and Alistair Boettiger for comments on the manuscript. This work was supported by Grants P50 GM071508 and R01 RM078079 from the National Institutes of Health (to S.Y.S.) and by National Institutes of Health Contract HHSN266200500021C, ADB no. N01-AI-50021 (to S.Y.S. and C.S.).
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1001139107/-/DCSupplemental.
References
- 1.Wolpert L. Positional information and the spatial pattern of cellular differentiation. J Theor Biol. 1969;25:1–47. doi: 10.1016/s0022-5193(69)80016-0. [DOI] [PubMed] [Google Scholar]
- 2.Crick F. Diffusion in embryogenesis. Nature. 1970;225:420–422. doi: 10.1038/225420a0. [DOI] [PubMed] [Google Scholar]
- 3.Martinez Arias A, Stewart A. Molecular Principles of Animal Development. Oxford: Oxford Univ Press; 2002. [Google Scholar]
- 4.Foe VE, Alberts BM. Studies of nuclear and cytoplasmic behaviour during the five mitotic cycles that precede gastrulation in Drosophila embryogenesis. J Cell Sci. 1983;61:31–70. doi: 10.1242/jcs.61.1.31. [DOI] [PubMed] [Google Scholar]
- 5.St Johnston D, Nüsslein-Volhard C. The origin of pattern and polarity in the Drosophila embryo. Cell. 1992;68:201–219. doi: 10.1016/0092-8674(92)90466-p. [DOI] [PubMed] [Google Scholar]
- 6.Gregor T, Wieschaus EF, McGregor AP, Bialek W, Tank DW. Stability and nuclear dynamics of the Bicoid morphogen gradient. Cell. 2007;130:141–152. doi: 10.1016/j.cell.2007.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Coppey M, Boettiger AN, Berezhkovskii AM, Shvartsman SY. Nuclear trapping shapes the terminal gradient in the Drosophila embryo. Curr Biol. 2008;18:915–919. doi: 10.1016/j.cub.2008.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kanodia JS, et al. Dynamics of the Dorsal morphogen gradient. Proc Natl Acad Sci USA. 2009;106:21707–21712. doi: 10.1073/pnas.0912395106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.DeLotto R, DeLotto Y, Steward R, Lippincott-Schwartz J. Nucleocytoplasmic shuttling mediates the dynamic maintenance of nuclear Dorsal levels during Drosophila embryogenesis. Development. 2007;134:4233–4241. doi: 10.1242/dev.010934. [DOI] [PubMed] [Google Scholar]
- 10.Bensoussan A, Lions JL, Papanicolaou G. Asymptotic Analysis of Periodic Structures. Amsterdam: North–Holland; 1978. [Google Scholar]
- 11.Hornung U. Homogenization and Porous Media. New York: Springer; 1997. [Google Scholar]
- 12.Othmer HG. A continuum model for coupled cells. J Math Biol. 1983;17:351–369. doi: 10.1007/BF00276521. [DOI] [PubMed] [Google Scholar]
- 13.Auriault J-L, Lewandowska J. Modelling of pollutant migration in porous media with interfacial transfer: Local equilibriumnon-equilibrium. Mech Cohes-Frict Mat. 1997;2:205–221. [Google Scholar]
- 14.Peter MA, Böhm M. Different choices of scaling in homogenization of diffusion and interfacial exchange in a porous medium. Math Method Appl Sci. 2008;31:1257–1282. [Google Scholar]
- 15.Kalnin JR, Kotomin EA, Maier J. Calculations of the effective diffusion coefficient for inhomogeneous media. J Phys Chem Solids. 2002;63:449–456. [Google Scholar]
- 16.Maxwell JC. Treatise on Electricity and Magnetism. Oxford: Clarendon Press; 1873. [Google Scholar]
- 17.El-Kareh AW, Braunstein SL, Secomb TW. Effect of cell arrangement and interstitial volume fraction on the diffusivity of monoclonal antibodies in tissue. Biophys J. 1993;64:1638–1646. doi: 10.1016/S0006-3495(93)81532-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McPhedran RC, McKenzie DR. The conductivity of lattices of spheres. I. The simple cubic lattice. Proc R Soc Lond A. 1978;359:45–63. [Google Scholar]
- 19.McKenzie DR, McPhedran RC, Derrick GH. The conductivity of lattices of spheres. II. The body centred and face centred cubic lattices. Proc R Soc Lond A. 1978;362:211–232. [Google Scholar]
- 20.Tao L, Nicholson C. Maximum geometrical hindrance to diffusion in brain extracellular space surrounding uniformly spaced convex cells. J Theor Biol. 2004;229:59–68. doi: 10.1016/j.jtbi.2004.03.003. [DOI] [PubMed] [Google Scholar]
- 21.Coppey M, Berezhkovskii AM, Kim Y, Boettiger AN, Shvartsman SY. Modeling the bicoid gradient: Diffusion and reversible nuclear trapping of a stable protein. Dev Biol. 2007;312:623–630. doi: 10.1016/j.ydbio.2007.09.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gregor T, Bialek W, de Ruyter van Steveninck RR, Tank DW, Wieschaus EF. Diffusion and scaling during early embryonic pattern formation. Proc Natl Acad Sci USA. 2005;102:18403–18407. doi: 10.1073/pnas.0509483102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Niessing D, Dostatni N, Jäckle H, Rivera-Pomar R. Sequence interval within the PEST motif of Bicoid is important for translational repression of caudal mRNA in the anterior region of the Drosophila embryo. EMBO J. 1999;18:1966–1973. doi: 10.1093/emboj/18.7.1966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Surkova S, et al. Characterization of the Drosophila segment determination morphome. Dev Biol. 2008;313:844–862. doi: 10.1016/j.ydbio.2007.10.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bergmann S, et al. Pre-steady-state decoding of the bicoid morphogen gradient. PLoS Biol. 2007;5:232–242. doi: 10.1371/journal.pbio.0050046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Spirov A, et al. Formation of the bicoid morphogen gradient: An mRNA gradient dictates the protein gradient. Development. 2009;136:605–614. doi: 10.1242/dev.031195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jaeger J. Modelling the Drosophila embryo. Mol Bio Syst. 2009;5:1549–1568. doi: 10.1039/b904722k. [DOI] [PubMed] [Google Scholar]
- 28.Gursky VV, Jaeger J, Kozlov KN, Reinitz J, Samsonov AM. Pattern formation and nuclear divisions are uncoupled in Drosophila segmentation: Comparison of spatially discrete and continuous models. Physica D. 2004;197:386–302. [Google Scholar]
- 29.Kim Y, et al. MAPK substrate competition integrates patterning signals in the Drosophila embryo. Curr Biol. 2010;20:1–6. doi: 10.1016/j.cub.2010.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Goel P, Sneyd J, Friedman A. Homogenization of the cell cytoplasm: the calcium bidomain equations. Multiscale Model Simul. 2006;5:1045–1062. [Google Scholar]
- 31.Kopito RB, Elbaum M. Reversibility in nucleocytoplasmic transport. Proc Natl Acad Sci USA. 2007;104:12743–12748. doi: 10.1073/pnas.0702690104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hecht I, Rappel W-J, Levine H. Determining the scale of the Bicoid morphogen gradient. Proc Natl Acad Sci USA. 2009;106:1710–1715. doi: 10.1073/pnas.0807655106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Saunders TE, Howard M. Morphogen profiles can be optimized to buffer against noise. Phys Rev E. 2009;80:041902. doi: 10.1103/PhysRevE.80.041902. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.