Spinal interneuron circuits reduce approximately 10-Hz movement discontinuities by phase cancellation

Abstract

Tremor imposes an important limit to the accuracy of fine movements in healthy individuals and can be a disabling feature of neurological disease. Voluntary slow finger movements are not smooth but are characterized by large discontinuities (i.e., steps) in the tremor frequency range (approximately 10 Hz). Previous studies have shown that these discontinuities are coherent with activity in the primary motor cortex (M1), but that other brain areas are probably also involved. We investigated the contribution of three important subcortical areas in two macaque monkeys trained to perform slow finger movements. Local field potential and single-unit activity were recorded from the deep cerebellar nuclei (DCN), medial pontomedullary reticular formation, and the intermediate zone of the spinal cord (SC). Coherence between LFP and acceleration was significant at 6 to 13 Hz for all areas, confirming the highly distributed nature of the central network responsible for this activity. The coherence phase at 6 to 13 Hz for DCN and pontomedullary reticular formation was similar to our previous results in M1. By contrast, for SC the phase differed from M1 by approximately π rad. Examination of single-unit discharge confirmed that this was a genuine difference in neural spiking and could not be explained by different properties of the local field potential. Convergence of antiphase oscillations from the SC with cortical and subcortical descending inputs will lead to cancellation of approximately 10 Hz oscillations at the motoneuronal level. This could appreciably limit drive to muscle at this frequency, thereby reducing tremor and improving movement precision.

Tremor is a key limitation to human fine motor performance. However, in tremor research, the puzzle is not so much why our hands shake, but why they often do not. Numerous mechanisms can contribute to unstable contraction: motoneurons are recruited at a fixed frequency, limb segments have mechanical resonance, the monosynaptic stretch reflex arc can produce feedback oscillations, and there are a plethora of central neural oscillators. These factors often converge to produce mechanical oscillations at approximately 10 Hz, the dominant frequency of physiological tremor. Yet despite these multiple sources of instability, in most people, most of the time, tremor is small enough not to impact daily life. We have hypothesized that a specific neural system might have evolved to reduce tremor (1), with clear survival advantages.

Slow finger movements in man are characterized by steps or discontinuities that occur at approximately 10 Hz (2). These discontinuities provide a good model for studying tremor, as even though they occur within the same frequency range, they are an order of magnitude bigger (2), facilitating quantitative analysis. Work on both physiological tremor and slow finger movement discontinuities has shown that there is an approximately 10 Hz modulation of motoneuron firing rates (3), which is shared across all cells within a motoneuron pool. This modulation is produced by synchronous input to motoneurons, but the source of this input is at present unknown.

The primary motor cortex (M1) is a likely candidate for some of the 10 Hz drive on to the motoneurons; it has oscillations of approximately 10 Hz and 20 Hz (4–6) and direct monosynaptic connections to the motoneurons (7). In a previous article, we reported activity in M1 local field potentials (LFPs) and single units to be coherent with finger acceleration at approximately 10 Hz during slow finger movements in monkeys (8). However, M1 is unlikely to be the only source of motoneuron inputs at approximately 10 Hz. From previous work, we identified three other neural systems that could contribute. The first is the pontomedullary reticular formation (PMRF), which gives rise to the reticulospinal tract. In primates, the PMRF is involved in control of shoulder and forearm muscles (9); more recent work suggests that it can also influence distally projecting motoneurons innervating hand muscles (10). Two findings are consistent with a role for the PMRF in generating discontinuities during slow finger movements. First, the discontinuities are synchronized between the left and right fingers when they are tracking in-phase targets (11). This could be mediated by the bilaterally organized reticulospinal projections; it is known that PMRF neurons involved in reaching often have bilateral actions (9). Second, discontinuities are present during smooth pursuit eye movements, and are coherent between the eye and finger when they track a common target (12). It is well known that the PMRF is an important center for eye movement control (13).

Magnetoencephalographic recordings in humans (14) suggest that the cerebellum may be a second area responsible for movement discontinuities. Oscillations at 5 to 10 Hz have been seen in the vibrissa representation of rat cerebellum (15), and in the deep cerebellar nuclei (DCN) of monkeys (16). Neurons from the inferior olive have a spontaneous 3 to 10 Hz rhythmicity (17) and can influence cerebellar rhythms by climbing fiber projections (18). Just as for the PMRF, the cerebellum accesses a bilaterally organized output network (19) and can influence eye movements (20). Cerebellar outputs pass through the DCN, and any rhythmic outflow should be detectable as oscillations in DCN activity. However, a previous report failed to find such oscillations during wrist flexion/extension movements or natural reaches (21).

A final possible source of central oscillations at approximately 10 Hz is the spinal cord (SC). Spinal circuits can spontaneously generate rhythms around this frequency (22) which survive afferent section and are not therefore simply caused by feedback loop resonance. SC oscillations are synchronous with similar oscillations in dorsal root potentials, indicative of temporally modulated presynaptic inhibition (23), are under descending control (22), and synchronize with somatosensory cortical activity (24).

In this study, we made direct recordings of neural activity from these three subcortical centers (PMRF, DCN, SC), in monkeys trained to perform slow finger movements that generated approximately 10 Hz movement discontinuities. The activity of each region was synchronized with the peripheral tremor, confirming that this is a highly distributed network. However, SC interneurons fired approximately in antiphase with the other motor centers for frequencies near 10 Hz. We suggest that this allows spinal circuits to reduce the amplitude of approximately 10 Hz discontinuities by phase cancellation. Such selective removal of power at tremor frequencies by a spinal “filter” could have important consequences for our ability to execute fine movements.

Results

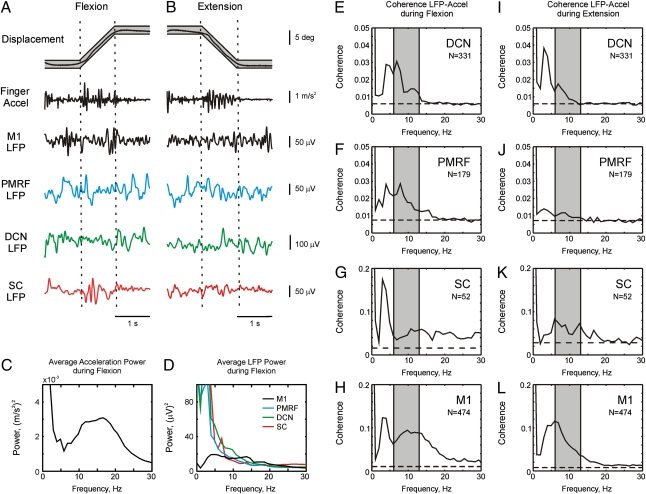
Results are based on data from two monkeys and 227 experimental sessions (62 from M1, 65 from the DCN, 39 from the PMRF, and 61 from the SC). During these sessions we recorded 1,032 LFPs from different sites (474 in M1, 331 in DCN, 179 in PMRF, and 52 in SC), with monkey R contributing 54% to 63% of the LFPs in each area. We were also able to discriminate a total of 525 single units (231 from M1, 157 from DCN, 120 from PMRF, 21 from intermediate zone of SC). Recordings were made while the animals performed a finger flexion/extension tracking task; an accelerometer attached to the finger provided a measure of peripheral oscillations. Fig. 1 A and B show raw data of the finger displacement, finger acceleration, and LFPs recorded from M1, PMRF, DCN, and SC during a single flexion (Fig. 1A) and extension (Fig. 1B) trial. Both flexion and extension movements produced movement discontinuities. The two trial types were analyzed separately because Vallbo and Wessberg (2) identified subtle differences in the discontinuities during flexion and extension in their original publication, and also because the different movements showed differences in the coherence between M1 and finger acceleration in our previous work (8).

Fig. 1.

(A and B) Raw data showing discontinuities during slow finger movements in monkeys. Examples of raw data during a single trial of the behavioral task. Actual finger displacement (black) is shown against the allowed target window (gray). Finger acceleration is shown, as is LFP from M1, PMRF, DCN, and SC, respectively. (C) Acceleration power during flexion ramp phase of the task. (D) LFP power during flexion ramp from the four different brain areas. (E–L) Coherence between LFP and finger acceleration, averaged over all LFPs and all sessions for different areas of the brain and SC. Coherence was calculated during flexion (E–H) or extension (I–L) tracking movements. Dashed line shows the significance level (P < 0.05). Shaded area shows the 6- to 13-Hz tremor band used for subsequent analysis.

Fig. 1C shows the average finger acceleration power spectrum. There was a broad acceleration peak from 6 to 25 Hz, reflecting a mixture of mechanical, reflex, and neurogenic contributions to tremor (25). However, here we are interested in centrally generated tremor; we previously showed in these animals that coherence between finger acceleration and electromyography (EMG) is significant over a limited band of 6 to 13 Hz (figure 1 D and H of ref. 8). We therefore focused our analysis on this band.

Fig. 1D shows the averaged LFP power spectra for M1, DCN, PMRF, and SC. In all cases there was power over a wide range of frequencies, presumably reflecting the broadband motor commands required to achieve success in this demanding motor tracking task. Fig. 1 E–L shows the coherence between LFP and acceleration, averaged over all available recordings from each area. There was significant coherence in the 6- to 13-Hz band for all areas examined during the two task conditions. Many of the spectra also contained peaks near 4 Hz. Previous research suggests that oscillations around this frequency are an independent process reflecting visual feedback from the moving target (2, 12), although to our knowledge this is the first time that coherence between these peripheral oscillations and central activity has been demonstrated in the PMRF, DCN, and SC. The 4-Hz peak was less apparent in M1 than the other areas; however, this was not a consistent finding (Fig. S1B uses M1 recordings made approximately 6 months later than Fig. 1D). The variation in this peak probably reflects changes in the animal's reliance on visual feedback during the long duration of this experiment.

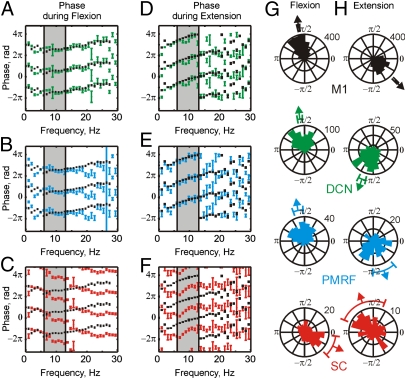
All the neural centers we studied are thus part of the distributed network responsible for discontinuities in finger acceleration. However, each region influences motoneurons via different pathways, which may have different conduction delays or other dynamics. This can be measured by the phase spectrum of the coherence. Fig. 2 A–F shows the circular mean of the coherence phase over all available recordings. On each plot the phase for a subcortical or spinal dataset is overlaid with that from M1 (black) for comparison.

Fig. 2.

Circular mean coherence phase calculated from individual LFP-acceleration phase spectra, averaged over both monkeys during flexion (A–C) and extension (D–F) movements. Average phase (mean ± SEM) was calculated for DCN (green, n = 331), PMRF (blue, n = 179), and SC (red, n = 52) and compared with average M1 phase (black, n = 474). Shaded area shows the 6 to 13 Hz range. (G and H) rose plots of the circular mean phase of each LFP from 6 to 13 Hz during flexion (G) and extension (H). Arrows and bars show mean and 95% confidence limits for all of the recordings within that area. The bin width in rose plots is π/24.

The M1 phase showed a clear linear relationship with frequency over the 6- to 13-Hz band for both task types (Fig. 2). Such a linear phase–frequency relationship indicates a constant time lag between the two signals (26); the positive slope indicates that acceleration leads the M1 activity. The slopes of the linear relationships can be used to estimate time delays; for M1, these were 18 ± 14 ms (significantly different from zero, P = 0.020) during flexion and 38 ± 6 ms during extension (P < 0.001). We previously showed that coherence methods may estimate longer delays than those expected from purely neuronal conduction (27).

For the DCN, the coherence phase over the 6- to 13-Hz band showed no significant linear relationship with frequency (P > 0.2; Fig. 2 A–D). The phase in the 6- to 13-Hz band was generally similar to M1, although some small phase differences were evident at less than 10 Hz, especially for extension. In the PMRF (Fig. 2 B–E), phase was linearly related to frequency, with slopes implying delays of 46 ± 20 ms (P = 0.0017) during flexion (i.e., LFP leads acceleration) and 57 ± 36 ms (P = 0.0099) during extension (i.e., acceleration leads LFP). Again, the phase between 6 and 13 Hz closely matched that measured for M1.

The coherence phase from the SC was substantially different from that seen for the other areas (Fig. 2 C–F), and was significantly different from that measured for M1 over a large proportion of the 6- to 13-Hz band. Phase was linearly related to frequency to a significant extent; the estimated delays were 55 ± 40 ms (P = 0.0172, LFP leads acceleration) and 66 ± 40 ms (P = 0.0081, acceleration leads LFP) for flexion and extension, respectively. These delays were slightly longer but with a similar direction to those found for the PMRF.

Fig. 2 A–F presents circular mean phase data combined across recording sites; this allows relationships to frequency to be examined, but any heterogeneity across recordings sites is lost in the averaging process. Fig. 2 G and H presents a complementary display, in which the distribution of the coherence phase averaged over the 6- to 13-Hz range is presented in circular histograms. Each count in these histograms represents a single recording site. The mean and its 95% confidence limits are shown as arrows and bars outside each histogram. In M1 (Fig. 2 G and H, black) the mean phase for flexion (1.77 ± 0.03 rad) and extension (−0.78 ± 0.04 rad) differed by approximately π rad. A similar difference between the phases during different movement types was seen in all the areas examined. The average difference in mean phase between flexion and extension was 2.59 ± 0.04 for M1, 3.58 ± 0.12 for DCN, 3.61 ± 1.95 for PMFR, and 4.10 ± 0.57 for SC (mean ± SEM of pairwise differences significant at P < 0.05, angular test equivalent to paired t test). Possible reasons for the difference between flexion and extension have been discussed in detail in our previous publication (8).

Comparing across areas, the mean phases during flexion (Fig. 2G) for M1 (1.77 ± 0.03 rad), DCN (1.73 ± 0.08 rad) and PMRF (1.80 ± 0.16 rad) were not significantly different [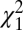 test, P > 0.05; see Fisher (28), pp. 115–117]. By contrast, the mean phase for the SC was −0.66 ± 0.34 rad, approximately 1.2π rad greater than for M1 and significantly different ( 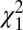test, P < 0.05). The same pattern could be observed in the rose plots during extension (Fig. 2H). The mean phase of M1 (−0.78 ± 0.04 rad) showed small but significant differences from the mean phase of the DCN (−1.93 ± 0.12 rad) and PMRF (−1.22 ± 0.36 rad). In contrast, the SC mean phase was 1.94 ± 0.66 rad, and differed significantly from M1 by 1.1π rad ( 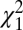test, P < 0.05). It is notable that the differences between SC phase and that of the other motor centers were consistent, even though the relationships with acceleration changed between flexion and extension movements.

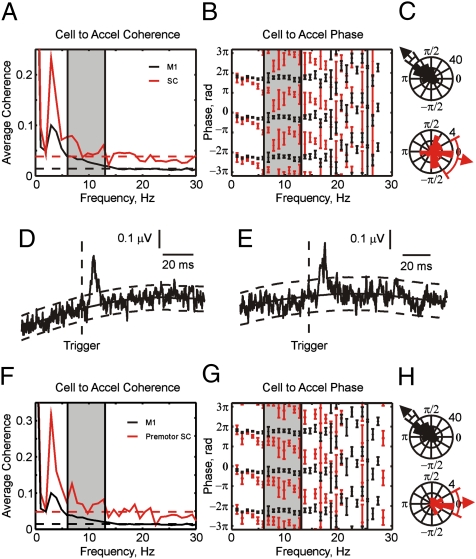
The results in Fig. 2 show that LFP oscillations in the SC are approximately phase-inverted in their relationship to peripheral discontinuities in acceleration compared with the other areas. However, in some circumstances in the cerebral cortex phase reversal of LFP oscillations occurs with increasing cortical depth (5); this is believed to occur if the source of the cortical LFP oscillations is in the superficial layers. The SC exhibits a laminar organization (29), although the orientation of dendritic trees is not as well ordered as in the cortex. If the generator of the spinal oscillations were in the dorsal horn, it is possible that our recordings from the intermediate zone would show the observed phase reversal simply as a trivial consequence of the electrode location. To test for this, we calculated the coherence between single unit firing in the SC and acceleration, and compared this with similar measurements for M1 (Fig. 3A). The coherence between acceleration and single neurons was small, accordingly results are shown only for flexion movements in which coherence was greater.

Fig. 3.

(A) Average coherence between cell spiking and acceleration, for cells from M1 and SC. Dashed lines show significance limits (P < 0.05) for each plot. (B) Circular mean coherence phase between cell spiking and acceleration. (C) Rose plots of the phase for each cell averaged over the 6- to 13-Hz range. (D and E) Spike-triggered average of rectified EMG from the flexor digitorum profundus (D) and first dorsal interosseus (E) muscles, triggered by discharge of SC cells. (F–H) Same as A–C, but red traces relate to the subset of premotor SC cells, which showed postspike facilitation in spike-triggered averages of EMG.

Fig. 3B shows mean phase spectra of the cell-acceleration coherence for M1 (black, n = 231 cells) and SC (red, n = 21 cells). Coherence phase was significantly different for the two areas over the 6- to 13-Hz band (P < 0.05, paired t test). The circular histograms of Fig. 3C present the distribution of the averaged phase across the different cells recorded. The circular mean phase for M1 was 2.35 ± 0.18 rad, compared with −0.24 ± 0.75 rad for SC. These were significantly different (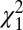 test, P < 0.05), with the mean values differing by 1.2π. The phase difference observed in Fig. 2 is thus a genuine reflection of oscillatory neural activity at the recording sites, and not a result of the detection of distant oscillators with a phase reversal in the LFP.

It is important to know if the recorded SC cells made connections to motoneurons, and whether these were excitatory or inhibitory inputs. For example, if the SC interneurons we recorded were inhibitory cells, their phase-inverted firing relative to excitatory inputs from M1 would produce in-phase summation of activity at the motoneuron. To assess this, we computed spike-triggered averages of EMG (30). Six cells of the SC intermediate zone produced postsynaptic facilitations (PSFs). Fig. 3 D and E show examples of PSF in the flexor digitorum profundus and first dorsal interosseous muscles, respectively. The mean onset latencies of the PSFs for all these cells was 4.50 ± 0.67 ms and the mean peak width at half maximum for these cells was 5.20 ± 0.38 ms. The short onset latencies and narrow peaks indicate that these cells are likely to be premotor cells with mono- or oligosynaptic excitatory connections to motoneurons (31–33). The coherence and circular mean phase for these premotor cells are shown in Fig. 3 F and G (red lines), with results from M1 overlaid (black lines). The premotor cells showed significant coherence between 6 and 13 Hz (Fig. 3F). The average phase was significantly different between M1 and premotor cells (P < 0.05, paired t test; Fig. 3G). This difference can also be seen in the circular histograms (Fig. 3H). The mean phase for M1 was 2.35 ± 0.18 rad, compared with 0.043 ± 0.47 rad for SC. These mean values were significantly different by 0.7π [P < 0.05, using bootstrap method; see Fisher (28), pp. 213–214]. The results show that identified excitatory premotor cells behaved similarly to the entire population of SC interneurons, and had a phase relationship with the discontinuities that was phase-inverted compared with M1.

Discussion

Multiple Motor Centers Contribute to Discontinuities.

All of the motor areas investigated in this study exhibited activity coherent with finger acceleration in the 6 to 13 Hz range, which we have previously shown to be the main centrally generated tremor range in these animals (8). The cerebellum has previously been suggested to play a role in the network that generates the movement discontinuities (14) because its activity is coherent with that recorded from the motor cortex during a slow finger movement task. However, to our knowledge, this is the first direct demonstration that cerebellar activity at approximately 10 Hz is coherent with a peripheral measure such as acceleration. The DCN can influence motor output via multiple pathways, including via the motor cortex (16, 34) and reticular formation (35). The realization that the reticulospinal tract is likely to provide some of the descending oscillatory command during slow finger movements marks an important contribution to understanding the highly distributed nature of this system. Interestingly, there is a case report of bilaterally synchronous pathological tremor (36). The authors suggested this was abnormally enhanced physiological tremor mediated by the reticulospinal tract because of its lack of coherence with sensorimotor EEG and evidence for reticular formation hyperexcitability (i.e., enhanced startle response).

Spinal Contribution to Production and Reduction of Discontinuities.

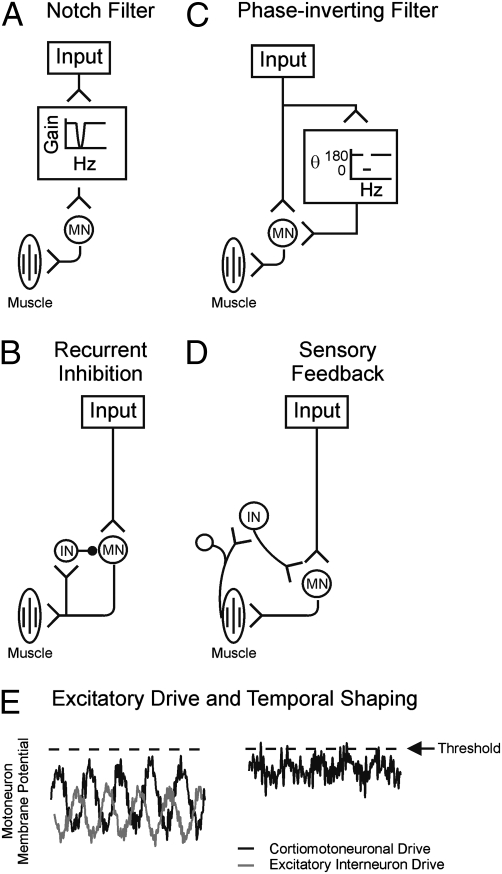
Our previous work (1) suggested that a neural circuit of unknown identity might act to filter or cancel approximately 10 Hz inputs to motoneurons, thereby accounting for a lack of 10-Hz corticomuscular coherence during steady contractions (1). Possible architectures for such a system are shown in Fig. 4.

Fig. 4.

Schematic diagrams of possible neural circuits to reduce oscillations in motoneuron firing: (A) frequency selective attenuation (notch filter); (B) recurrent inhibition; (C), frequency selective phase inversion; (D) sensory feedback from periphery. MN, motoneuron; IN, interneuron. E is an example of temporal shaping with excitatory input to membrane potential of motoneuron. Dashed line is the threshold.

One obvious possibility would be to interpose a filter between the input and the motoneurons, which would selectively remove the band around 10 Hz (a “notch filter,” Fig. 4A). Although attractive, this option is unlikely to exist in the nervous system. Many inputs from the motor cortex to motoneurons pass via the monosynaptic corticomotoneuronal system (7). This synapse appears to have relatively straightforward temporal properties, and there is no evidence that it is capable of selectively removing frequencies around 10 Hz (37, 38). A similar situation exists for inputs from muscle spindle stretch receptors, which form the monosynaptic stretch reflex arc and also unlikely to exhibit any frequency selective attenuation.

We recently demonstrated using a computer model that recurrent inhibition from spinal Renshaw cells could remove the approximate 10 Hz components of motoneuron discharge (circuit of Fig. 4B), although our quantitative results suggested that this forms only one component of the overall system (39). Based on the present data (Fig. 3 A, B, F, and G), we suggest that excitatory SC interneurons in the intermediate zone also participate in reducing oscillations in motoneuron output, by phase-inverting inputs to motoneurons (circuit of Fig. 4C). Convergence of antiphase activity from spinal interneurons with descending oscillations from both M1 and the PMRF will produce cancellation, reducing the amplitude of oscillations propagated to the periphery. This will have functional utility, rendering movement smoother and hence more accurate. There are likely to be advantages in locating cancellation at a spinal level. Multiple sources of unwanted rhythmicity converge at the level of the spinal motoneuron, Sherrington's “final common path” for motor output. Sensing these rhythmic inputs may be best carried out physically close to the motoneuron, minimizing additional phase shifts due to axonal conduction delays. In addition, many modern strategies for robotic control emphasize “active damping” of oscillations, in which sensor feedback is a key component. SC interneurons are supplied with a rich range of inputs from receptors in the periphery (40) (circuit in Fig. 4D) and it is possible that this may allow them to implement even more complex schemes of oscillation reduction, effectively combining the different concepts outlined in Fig. 4 into a unified system.

Interestingly, the phase difference between SC and M1 activity of approximately π was not limited to the tremor band, but also occurred at higher and lower frequencies (Fig. 2C and F); this would tend to remove oscillations from motor outflow at these frequencies too. In some circumstances, frequencies of approximately 15 to 20 Hz did not show a phase difference (Fig. 2C); this may allow these frequencies to pass uncanceled to motoneurons. Corticomuscular coherence is commonly observed within this range, and may have a role in sensorimotor processing (41).

Moment-by-moment changes in the efficacy of the proposed system should alter the amplitude of tremor. We checked for this possibility in our data by analyzing separately trials with especially high or low tremor. The results (detailed in SI Materials and Methods) suggested that fluctuations in tremor amplitude result from a limited capacity of the spinal circuitry to adjust the amplitude of its oscillatory output to changing cortical drive (Figs. S1 and S2), and provide further evidence for the functional importance of this system.

An important modern challenge in neuroscience is to define the contribution of spinal interneuron circuits to movement control. In primates, most corticospinal terminals target interneurons rather than motoneurons (42). Yet paradoxically, stimulation of the corticospinal tract produces monosynaptic excitation of motoneurons, with almost no disynaptic excitatory effects from segmental circuits (43–45). It is clear that we cannot view spinal circuits as mere relays of descending commands, but as active systems that modulate, gate, and filter inputs in complex ways. Direct input from descending pathways is unlikely to be sufficient, on its own, to recruit motoneurons to fire (27), and there is an increasing realization that summation with inputs from spinal interneurons must occur if motoneurons are to be activated (46). In this article, we suggest that, as well as amplifying descending commands so that they are sufficient to reach motoneuron firing threshold, another action of spinal circuits is to phase-invert inputs at approximately 10 Hz, specifically cancelling these frequencies in motoneuron drive (Fig. 4E).

Finding ways to change the activity of spinal interneurons artificially might provide a novel approach to treating pathological tremor. It is known that spinal circuits are powerfully modulated by descending monoaminergic systems (47). We speculate that such modulation may also alter the efficacy of the spinal cancellation circuits, and that this could partly underlie the changes seen in tremor amplitude with different levels of behavioral arousal and anxiety (48).

Materials and Methods

The behavioral task and surgical procedures used in this article have been described fully in a previous publication (8), and only a brief description is given here.

Behavioral Task.

Two female macaque monkeys (Macaca mulatta) were trained to perform a slow (12 °/s) finger flexion or extension task while tracking a target visually displayed on a computer screen. This task produced slow finger discontinuities during the 1-s-long ramp tracking movements. During all movements, a motor generated torque that acted to oppose flexion. Flexion movements were thus active movements against this torque, whereas extension movements were a controlled release of the finger, which moved under the action of the motor.

Surgical Procedures.

Animals were prepared for EMG recording by implantation with up to 10 epimysial patch electrodes, sutured to hand and forearm muscles. Wires from these electrodes led subcutaneously to a connector mounted on the animal's back. M1 recordings were made through a recording chamber placed over the central sulcus contralateral to the trained hand, whereas for DCN and PMRF recordings, a chamber was placed over the occipital cortex ipsilateral to the trained hand. After completing recordings in these areas, a spinal chamber was implanted over the cervical SC, involving fusion of vertebrae from C4 to T2 (49).

Recordings.

Recordings in the PMRF and DCN were made using up to six simultaneous tetrode penetrations independently controlled via an Eckhorn microdrive (Thomas Recording). Cells in the DCN were characterized by examination of unit receptive fields and the motor responses to intracortical microstimulation (13–18 biphasic pulses, 300 Hz, 0.2 ms per pulse). The cells in the DCN were, on average, 8.8 mm below tentorium. The PMRF recordings were located with reference to the position of the abducens nucleus and the inferior colliculus, which are easily identified during penetrations by the eye movements elicited by stimulation and the neural responses to sound respectively. All recording sites were plotted on a map and aligned to stereotaxic coordinates, and this was used to guide penetrations that had not, by chance, included the abducens nucleus or the inferior colliculus. Cells in the PMRF were recorded only if they showed motor responses in the arm or hand to ICMS, or if the cells had a receptive field located on the forelimb.

Spinal recordings targeted segments C7 to T1, ipsilateral to the moving finger, and used a five-channel Eckhorn microdrive loaded with tetrodes. During a penetration, the depth of the first cellular activity was noted, and all depths were expressed relative to this. Cells were assumed to be in the intermediate zone if they were at least 1 mm below the first cells, and intraspinal microstimulation produced responses in the hand or forearm with a threshold between 10 and 50 μA. Recordings more than 4 mm below the first cells were excluded. These sites often had very low intraspinal microstimulus thresholds (<10 μA) and were likely to be from motoneurons in lamina IX.

Analysis.

Coherence and average coherence were calculated as in our previous work (27). The circular mean of the phase was calculated according to Fisher (28). Averaged phase plots were calculated by finding the circular mean phase at each frequency from the available coherence spectra, and linear regression analysis was used to estimate the time delays. Circular histograms (rose plots) show the distribution of the circular mean phase in the 6- to 13-Hz range and were calculated from all available coherence spectra. CIs (95%) on circular mean phases were calculated using equations given in Fisher (28), and used for error bars on graphs.