Protein interface conservation across structure space

Abstract

With the advent of Systems Biology, the prediction of whether two proteins form a complex has become a problem of increased importance. A variety of experimental techniques have been applied to the problem, but three-dimensional structural information has not been widely exploited. Here we explore the range of applicability of such information by analyzing the extent to which the location of binding sites on protein surfaces is conserved among structural neighbors. We find, as expected, that interface conservation is most significant among proteins that have a clear evolutionary relationship, but that there is a significant level of conservation even among remote structural neighbors. This finding is consistent with recent evidence that information available from structural neighbors, independent of classification, should be exploited in the search for functional insights. The value of such structural information is highlighted through the development of a new protein interface prediction method, PredUs, that identifies what residues on protein surfaces are likely to participate in complexes with other proteins. The performance of PredUs, as measured through comparisons with other methods, suggests that relationships across protein structure space can be successfully exploited in the prediction of protein-protein interactions.

The knowledge of whether two proteins form a complex is a problem of central importance in the description of cellular networks and in a large number of other biological applications. Much effort has been devoted recently to high-throughput experimental determination and literature curation of protein-protein interactions (see refs. 1 and 2 for a review), and the results have been deposited into numerous databases (3, 4). In addition, a variety of computational approaches have been developed to predict protein interaction partners (2, 5–7). Three-dimensional structural information has not been widely used in large-scale studies, in part because the number of complexes for which such information is available is far smaller than the number of interactions that can be inferred by other techniques.

A number of groups have shown that the use of homologous relationships can expand the range of structural information by providing plausible models for a protein complex that can then be evaluated with other methods (8–10). However, the extent to which a known 3D structure of a complex can be used reliably as a template for a model of two related proteins is unclear, especially if the relevant sequence and/or structural relationship is remote. Model reliability should, in general, increase if the proteins involved are closely related, but the use of close homologs necessarily limits the number of possible interactions that can be detected. We have recently shown (11) that the use of remote structural relationships can detect functional relationships between proteins that are obscured by classification schemes. One of the aims of the current paper is to evaluate whether structural relationships that can go beyond classification can be exploited in the structure-based prediction of protein-protein interactions. Our longer-range goal is to expand the range of applicability of structural information to the point that it can be used on a scale comparable to that of other, non-structure-based methods.

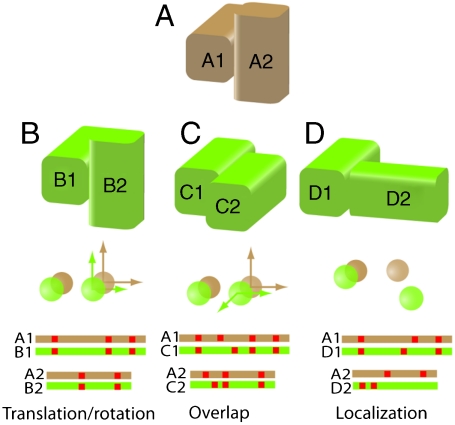
Most current methods that build models of complexes by homology rely in part on criteria for model reliability that have been established by comparative studies of different complexes (12–19). A nagging reality of such studies is that there is no unambiguous way of determining whether two complexes are similar. Fig. 1 illustrates some of the underlying the issues. In the figure, a representative protein complex, A, is compared to three others (see the caption for general details on how this comparison is carried out). Although each of the complexes B, C, and D has some relationship with complex A, this will not necessarily be identified by every measure of similarity. For example, measures that rely on translations/rotations of individual subunits (13, 18, 20) would characterize A and B as similar complexes, but not A and C since a 90 ° rotation would be required to superpose C2 on A2. Criteria that depend on the relative location of the centers of mass (14) would characterize A and C as similar, but not A and D.

Fig. 1.

Types of geometric conservation and their measures. Protein complex A is compared here to three other complexes B, C, and D. Typically one subunit is superposed on a structurally similar subunit in the complex to which it is being compared (i.e., A1 would be superposed on B1) and the transformation that relates the first subunits is applied to the second so that all proteins are in the same coordinate system. Measures of conservation generally involve calculating: the transformation (translation/rotation) required to optimally superimpose the second subunits on each other (brown/green arrows); distances and angles between the centers of mass of the second subunit (brown/green spheres); and the alignment (independent of residue identity) of interfacial residues in a primary sequence alignment of the two subunits (red squares). Although there is some similarity between A and each of the other three complexes, recognizing it will depend on which measure is used (see text).

Other similarity measures rely on the equivalence of interfacial residues once the proteins in two complexes have been rotated into a common coordinate frame. Using a residue equivalency measure, A and B are clearly similar, whereas A and C might also be considered similar because some of the residues on both sides of the interface are aligned. There is also a relationship between complexes A and D because some interfacial residues in one of the monomers are well-aligned. This feature is a property of only one subunit of the complex and would be recognized only by a criterion such as the “localization index” introduced by Sali and coworkers (15). Throughout the text we refer to this phenomenon as “interface conservation” and take it to mean that two proteins interact with their partners at geometrically similar locations (independent of the identity of the residues involved).

In order to correlate structural relationships between complexes with standard measures of sequence and structural similarity, complexes have been classified based on the properties of the individual subunits. Using a measure of geometric conservation that depends on translations/rotations, Aloy et al. (13) found that below 30% pairwise sequence identity, little geometric conservation is expected. Other studies using different measures of interface similarity and protein classification have been reported (16, 18–20), but general rules have been difficult to establish. Nevertheless, reported results suggest that little interface conservation is to be expected in the absence of an obvious evolutionary relationship between the proteins that form the two complexes. However, the type of relationship that exists between complexes A and D in Fig. 1 (conservation of the interface locations in just one of the subunits) has not been extensively studied. In this case, the underlying question is whether two proteins that share a geometric relationship, e.g., A1 and D1, use a common region of their surface to form an interface independent of the identity or orientation of the second member of the complex. Significant localization of interfaces has been found at the family (15) and superfamily (14) levels; however, there has not, to our knowledge, been a systematic study of the extent to which protein structural similarity can be used as a basis for predicting the interfacial residues.

A number of studies have suggested that this may be possible. Nussinov and coworkers (21, 22) identified similarities in the relative positions of small sets of secondary structure elements within the interfaces of structurally dissimilar interacting proteins suggesting a relationship between patterns of secondary structure and interface formation. Russell et al. (23) showed that groups of proteins classified as belonging to different superfamilies or folds interact with their ligands in structurally equivalent locations. Remote similarities such as these have been exploited in a wide range of applications including the prediction of protein-ligand interactions (24), protein-protein interactions (10), and function annotation (11, 25).

In this paper, we report a comprehensive analysis of the degree to which the location of protein-protein interaction sites is conserved in sets of proteins that share varying degrees of similarity. We start by identifying structural neighbors of the query protein independent of classification and then, using the statistical approach developed by Russell et al. (23), quantify interface conservation both among close homologs and among remote structural neighbors. Our results show that while, in general, the conservation of interface locations is greatest among close neighbors, significant information is also provided by remote structural neighbors that have no obvious evolutionary relationship to the query. Based on these findings, we develop PredUs (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:PredUs), a method for predicting a protein binding region on the surface of a query protein based entirely on information derived from structural neighbors. PredUs compares favorably with methods that, given a three-dimensional structure, predict interfacial regions based on specific features (e.g., sequence conservation and amino acid properties) of clusters of surface residues. Our findings have important implications, both regarding the nature of protein sequence/structure/function space and for the possibility of using structural information as a basis for predicting protein-protein interactions on a genome-wide scale.

Results

Interface Conservation.

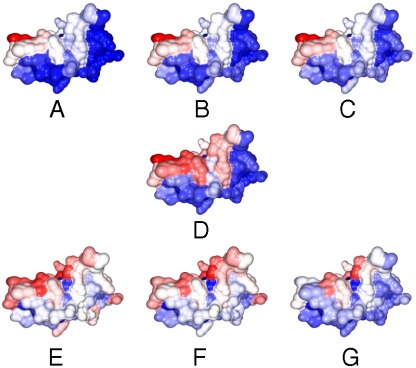
We used the procedure described in Materials and Methods to quantify interface conservation. Briefly, structural neighbors are identified for a given query protein, and the locations of interfacial residues of the neighbors that are part of a complex are “mapped” to residues in the query protein to generate a “contact map” associated with each structural neighbor. Interface conservation can be visualized by summing individual contact maps and generating a contact frequency heat map. Fig. 2 shows the surface of the T-cell receptor protein CD8 [Protein Data Bank (PDB) ID code 1akj, chain D] with each residue colored according to the frequency with which interactions are mapped to it when structural neighbors are taken from the same SCOP (Structural Classification of Proteins) family, superfamily, and fold.

Fig. 2.

The surface of T-cell receptor protein CD8 (PDB ID code 1akj, chain D) colored according to the frequency with which interactions made by its structural neighbors are mapped to individual residues on its surface (red/white/blue = high/intermediate/low frequency). Each surface is colored based on a different set of structural neighbors: (A) SCOP family b.1.1.1; (B) superfamily b.1.1; (C) fold b.1; (D) PSD < 0.6 (found by Ska); (E) PSD < 0.6 in different families; (F) PSD < 0.6 in different superfamilies; (G) PSD < 0.6 in different folds. The red high contacting frequency regions show conserved protein interface.

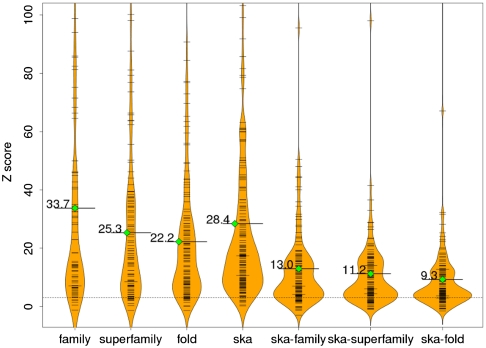
Using the approach of Russell et al. (23), a Z score that reflects overlap in the set of contact maps (i.e., whether or not there is a set of residues in the query that preferentially has interactions mapped to it) is then calculated. Fig. 3 shows the distribution of Z scores for the proteins in our test set [188 protein chains curated from a docking benchmark dataset (26); see Materials and Methods]. To ensure reasonable statistics, at least 6 structural neighbors are needed to calculate Z scores (83 structures had at least 6 structural neighbors in the same family, 106 in the same superfamily, and 130 in the same fold). As can be seen from the figure, most of the proteins in the test set have Z scores larger than 3, which is our cutoff for statistical significance (78 out of 83, 95 out of 106, and 118 out of 130, for the same family, superfamily, and fold, respectively).

Fig. 3.

Distributions of Z scores reflecting interface conservation. Each column in the graph shows a Z-score distribution when interface conservation for proteins in our docking benchmark set is calculated based on a different set of structural neighbors. The black bars and the width of each plot reflects the density of Z scores near the corresponding value on the y axis. Solid lines with green diamonds show the mean value of each distribution. The dashed line corresponds to a Z score of 3, which we take as the cutoff of statistical significance. The individual plots have been scaled so that their areas are proportional to the number of proteins for which a valid Z score could be calculated.

As expected, less conservation is observed when more remote structural neighbors are considered, with average Z scores decreasing as neighbors are taken from the same family, superfamily, or fold (average Z scores 34, 25, and 22, respectively). However, there are many individual cases where the opposite is true and the Z scores are still significant, suggesting that while there is certainly increased variability in the location of interfaces in the more remote neighbors, significant interface conservation remains. Details about each query protein in our test set including individual Z scores, the number of structural neighbors, and the highest residue contacting frequencies are given in Table S1 at http://honiglab.c2b2.columbia.edu/PredUs/html/pnas_si.html.

We also identified structural neighbors using the structure alignment program Ska (27, 28) independent of classification into family, superfamily, or fold groups. The average Z score for the 176 query proteins that had more than 5 structural neighbors is 28, and 166 have a Z score larger than 3 (see Fig. 3 and Table S1). The set of structural neighbors identified by Ska was generally significantly larger than the number of proteins classified as belonging to a given grouping in SCOP and contained significant structural diversity. For example, Ska found 978 structure neighbors contained in at least one complex for the structure 1akj.D. These proteins came from 87 different SCOP families, 71 superfamilies, and 57 folds. Despite the structural diversity, the difference in average Z scores for structural neighbors identified independent of classification and for those classified as belonging to the same family, superfamily, or fold was small. Since Z scores reflect overlap in the contact maps calculated for each structural neighbor, these results suggest that there are a significant number of structures classified differently whose protein-protein interactions sites overlap those of even the close sequence neighbors of the query.

It is possible, of course, that the results obtained independent of classification are due to the presence of family and superfamily members in the set of structural neighbors we identify for each query protein. In order to determine the contribution of neighbors outside of a particular grouping, we carried out a further analysis in which proteins belonging to a particular SCOP classification were excluded (structures with no SCOP annotation were also excluded). Although the Z scores were not as high as for families, superfamilies, and folds, they were still statistically significant (i.e., Z score > 3) with mean values of 13/11/9 (over 138/135/129 query proteins) when family, superfamily, and fold were, respectively, excluded (see Fig. 3 and Table S1 for details).

As described above, this can be visualized using a heat map. For example, for the T-cell receptor CD8 (1akj.D), we identified 254 structural neighbors in 86 families different from that of 1akj.D, 143 structures in 70 different superfamilies, and 90 structures in 56 different folds. Although all these structures come from different families, superfamilies, and folds, there is still a well-defined set of residues that preferentially has interactions mapped to it and overlaps with that obtained by considering only more closely related structures (Fig. 2).

Interface Prediction.

Based on the above results, we developed a method, PredUs, to predict interfacial residues based entirely on structural neighbors (only the top 50 Ska hits are used; see Materials and Methods). Our approach was tested on the docking benchmark described in Materials and Methods and also on the set of structures used in the Critical Assessment of Prediction of Interactions (CAPRI) exercise (29). Results were compared to the top three programs [cons-PPISP (30), PINUP (31), and ProMate (32)] reported in a recent comparative study of interface prediction methods (33), which also performed best in a small-scale evaluation we carried out. We also compared a random prediction in which surface residues are classified as interfacial with a probability of 0.25, which is roughly the portion of interface residues in our test set and is consistent with other studies (30).

Results are summarized in Table 1 (see SI Table S2 and S3 at http://honiglab.c2b2.columbia.edu/PredUs/html/pnas_si.html). PredUs results are clearly of comparable quality for both datasets and offer the best combination of precision and recall among all methods tested. This conclusion is based on inspection of Table 1, but it is also consistent with the Matthew’s Correlation Coefficient (see SI Table S4 at http://honiglab.c2b2.columbia.edu/PredUs/html/pnas_si.html). The precision of PredUs is similar to that of other methods, but its recall is significantly higher. In order to evaluate the results obtained based on classification, we used PredUs to make predictions but restricted structural neighbors to members of the same family, superfamily, and fold. Results are summarized in Table 2. As expected, the highest precision is obtained when only members of the same family are used, and precision decreases as more distant neighbors (superfamily, fold, and the top 50 Ska hits) are included. The trend of the recall value is in the opposite direction. The significant increase in recall when Ska50 is used reflects the additional information available by going beyond SCOP fold. On average, within the Ska50 set there are only 8.6/10.5/11.9 neighbors from the same family/superfamily/fold, whereas there are 18.1/16.1/14.7 from different ones (unannotated proteins are excluded).

Table 1.

Precision and recall averages of different interface prediction methods on the docking benchmark dataset and CAPRI bound/unbound targets

Dataset	Prediction methods	Cases	Np	Nc	Precision average	Recall average
DKBM	PredUs	185	7,862	3,429	43.6%	45.7%
	Promate	90	689	322	46.7%	4.3%
	cons-PPISP	188	4,936	2,310	46.8%	30.8%
	PINUP	188	4,227	1,798	42.5%	24.0%
	Random	188	6,827	1,638	24.0%	21.9%
CAPRI bound	PredUs	56	2,221	921	41.5%	42.2%
	cons-PPISP	56	1,497	630	42.1%	28.9%
	PINUP	56	1,204	424	35.2%	19.4%
	Random	56	2,155	492	22.8%	22.6%
CAPRI unbound	PredUs	55	2,393	952	39.8%	44.6%
	cons-PPISP	56	1,542	618	40.1%	29.0%
	PINUP	56	1,320	466	35.3%	21.8%
	Random	56	2,167	544	25.1%	25.5%

Here DKBM stands for the dataset of docking benchmark, and N_p and N_c stand for the numbers of total and correctly predicted interfacial residues, respectively.

Table 2.

Precision and recall averages of PredUs when using structure neighbors from the same and different SCOP groupings on the docking benchmark dataset

Prediction methods	Cases	Np	Nc	Precision average	Recall average
Family	141	4,990	2,536	50.8%	33.8%
Superfamily	147	5,907	2,710	45.9%	36.2%
Fold	153	6,948	2,904	41.8%	38.7%
Ska50-family	162	8,338	2,541	30.5%	33.9%
Ska50-superfamily	161	8,331	2,370	28.4%	31.6%
Ska50-fold	159	8,603	2,497	29.0%	33.3%

Here N_p and N_c stand for the numbers of total and correctly predicted interfacial residues, respectively.

In order to gain insight as to the contributions of increasingly remote structural neighbors to the results, we used PredUs to make predictions where neighbors identified by SCOP were progressively removed from the dataset (unannotated proteins also removed). Predictions made in this way are indentified in Table 2 as Ska50-family, superfamily and fold, respectively. As is evident from Table 2, not considering close family members significantly decreases prediction accuracy, but the results are very similar when members of the same fold and superfamily are also removed. Even when considering only members of a different fold, the results are better than random. It is clear from Tables 1 and 2 that the combined use of close and distant neighbors offers the best combination of precision and recall. Most importantly, only by combining in-fold and cross-fold information is it possible to increase recall to above 40%.

Overall, PredUs performed very well for 125 out of 188 docking benchmark proteins. In particular, whenever a successful prediction was achieved using PredUs (both precision and recall better than random), the average precision and recall significantly outperformed other methods (see Table 3). There were also some cases where interface information could be extracted from the structural neighbors but where PredUs still made predictions with low precision and recall (26 of the docking benchmark chains). However, the performance in these cases was not due to poor interface conservation in the set of structural neighbors (because the Z scores were still significant for those cases), but seems to be due to the fact that the particular interface to be predicted for these cases was rarely seen in the set of structural neighbors. This issue is addressed below.

Table 3.

Precision and recall averages of PredUs good predictions, bad predictions, and the others on the docking benchmark dataset

	Prediction methods	Precision average	Recall average
Good predictions (125 cases)	Pred-us	60.2%	57.2%
	cons-PPISP	54.6%	36.5%
	PINUP	51.9%	29.0%
	ProMate	47.4%	12.1%
Bad predictions (26 cases)	Pred-us	7.3%	8.5%
	cons-PPISP	27.7%	24.6%
	PINUP	29.7%	24.5%
	ProMate	15.2%	5.1%
Others (37 cases)	Pred-us	24.4%	39.7%
	cons-PPISP	36.1%	30.5%
	PINUP	34.4%	24.2%
	ProMate	35.4%	13.5%

Discussion

The central result of this study is that there are localized regions on protein surfaces that are conserved among structural neighbors that participate in protein-protein interactions. These regions are properties of a set of neighbors even though the individual proteins will, in general, form complexes with different proteins using different interface geometries. Thus it is not the geometry of the complex that is conserved but rather the location of surface residues that participate in complexes. The neighbors may belong to the same family or superfamily, and thus bear a clear evolutionary relationship, or belong to the same fold or to different folds, in which case an evolutionary relationship may be present, but its existence is hard to prove. Our findings are consistent with previous work that identified cross-fold functional relationships that are properties of protein fragments and not of the entire structure (11, 22, 23, 34).

Our results do not imply that a set of structural neighbors will always interact with their partners at a single structurally equivalent patch. Because all interfaces from all structural neighbors are mapped to the query protein in the construction of the contact frequency map, this set of positions may be localized and contiguous or may consist of multiple disjoint patches. Thus, even if there are multiple, distinct protein-protein interactions observed in a set of structurally similar proteins, a high Z score will be obtained as long as there are enough proteins in the set under consideration that interact with their partners at some set of structurally equivalent locations.

The results in Tables 1 and 2 highlight the advantages of basing an interface prediction method entirely on information about complexes formed by structural neighbors of a protein. While it is expected that PredUs yields good precision if it is based only on neighbors in the same family or superfamily, that precision is so high when all neighbors are considered seems quite remarkable and reflects the conservation we describe above. Moreover, using remote structural neighbors produces a significant improvement in recall at the cost of only a moderate decrease in precision. This suggests that current structural databases are surprisingly complete, in the sense that it is generally possible to find representatives of the possible binding modes of a given protein within the 36,888 complexes in the PQS (Protein Quaternary Structures) database (35). This conclusion depends, however, on the use of the large set of structural neighbors generated using our loose definitions of similarity as well as on the definition of interface conservation that we use.

Structural information also appears to be a principal source of the improvement in recall of PredUs relative to methods that rely primarily on differences in characteristics [e.g., hydrophobicity, sequence conservation, interface propensity, accessibility, and side-chain entropy (30–32)] between interfacial and noninterfacial residues. Because it may be generally expected that not all of the residues in a given interface will be distinct in terms of such characteristics, this may have a deleterious effect on recall. In our approach, all the interfacial residues from structural neighbors are mapped to the query protein regardless of their characteristics and this difficulty is thus avoided. Because the two approaches are quite distinct and use largely complementary information, it may be of value to combine them in some way in future work.

There are potential drawbacks to the heavy reliance on structural neighbors implicit in our method, but they do not appear to be significant based on an analysis of our test sets. For example, only a small percentage of the proteins did not have enough structural neighbors to enable a prediction (three in the docking benchmark and one in the CAPRI set). Some proteins may have multiple binding sites, and our method depends on identifying those locations that are most frequently associated with protein-protein interactions. An important question, then, is whether or not other approaches will perform better when predicting interfaces that are distinct from the most frequently observed ones. To determine this, we calculated the average precision and recall for the 26 cases where PredUs made bad predictions (both precision and recall are less than random). They were quite low (< 10%; see Table 3) suggesting that the interfaces to be predicted in these cases are indeed distinct from those most frequently observed. Although the other methods used in this study performed better for these cases, only cons-PPISP made predictions that on average were even slightly better than random, suggesting that these interfaces are not only geometrically distinct, but also distinct in terms of the residue characteristics typically used to describe protein-protein interaction sites. Hence, there seems to be little cost to using the most frequently observed interface, at least compared to other approaches. Moreover, for the 125 cases where a successful prediction was made, using structure resulted in a significant increase in performance (Table 3).

Our results have implications for how structural information may be used to analyze and characterize protein-protein interactions, especially on a large scale. Although there may be increased variability in the geometric binding properties of pairs of proteins with increasingly remote relationships, structural similarity can be effectively used to identify the sites of protein-protein interaction. As long as structural information is available for a given pair of proteins, the accuracy of our predictions suggests that the set of “template complexes” available in the current structural databases can be used to generate coarse-grained models of protein-protein interactions. Most importantly, we see that using remote structural neighbors produces a significant improvement in recall, which suggests that remote structural relationships have the potential to yield a much larger number of hypotheses for protein-protein interactions than has been previously possible (8–10). Together these findings suggest that the use of remote structural similarity can potentially significantly increase the number of functional relationships that can be detected, modeled, and evaluated.

Materials and Methods

Protein Dataset and Interface Definition.

We used a set of proteins originally created to evaluate protein docking methods by Hwang et al. (26). This dataset was designed to have significant diversity in both overall protein shape and binding mode and has been used by other groups to evaluate protein interface prediction methods (31, 33). The benchmark contains 124 pairs of interacting structures and 309 protein chains. We created a nonredundant set at 40% sequence identity using the program cd-hit (36) and also removed chains shorter than 50 amino acids. This left 188 individual protein chains as our test dataset, coming from 137 SCOP families, 124 superfamilies, and 105 folds. The interface in each case is determined based on its interactions with all other members of its associated complex in PQS. A residue was defined to be on the surface if its solvent accessible surface area (calculated using the isolated chain) was ≥10 Å², and it was defined to be in the interface if the distance between any of its heavy atoms and any heavy atoms from a partner chain was ≤ 5 Å (33). In total, the 188 chains contained 39,780 residues and 7,496 in an interface. We also tested our interface prediction method on targets T01 ∼ T27 from the CAPRI (29). These 56 bound/unbound chains contain 12,124/12,181 residues with 2,180/2,134 in the interface.

Structural Neighbors.

Structural neighbors were defined in two ways. Structural neighbors belonging to the same family, superfamily, or fold were taken from the SCOP 1.73 database (37). We also used the program Ska (27, 28) to identify neighbors independent of classification. Neighbors were defined based on a protein structural distance (28) from the query of less than 0.6. In the procedures described below, only structural neighbors that are involved in any PQS complex (36,888 as of August 2009) are used and if a structural neighbor has multiple binding partners, all are considered. The complete PQS database was used to identify structural neighbors, but to avoid overcounting of highly similar complexes, we applied the following procedure: PQS chains were clustered using cd-hit at a 40% sequence identity cutoff. Given structural neighbors N₁ and N₂ of a protein and their interacting partners P₁ and P₂, if N₁ belongs to the same cluster as N₂, and P₁ belongs to the same cluster as P₂, only one structural neighbor/partner would be considered.

Z Score to Evaluate Interface Conservation.

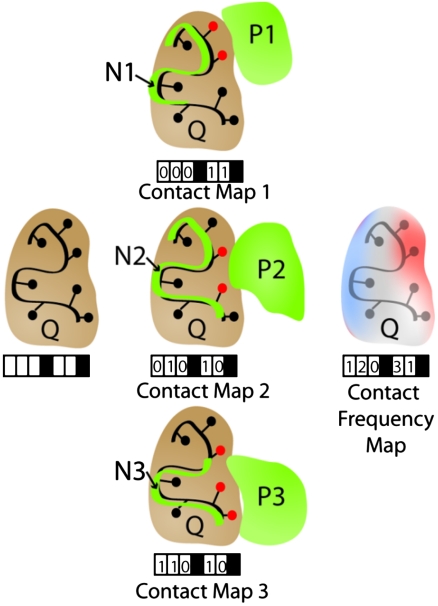
To evaluate the degree of interface conservation, we used a variant of the statistical test introduced by Russell et al. (23) in an analysis of interactions between proteins and small molecules. For each query protein, Q, and each structural neighbor, N, the interactions N makes with its partner, P, are mapped to the surface residues of Q to create the contact map for this particular structural neighbor. This procedure is repeated for all structure neighbors of Q, and the contact maps are then summed to form the contact frequency map (see Fig. 4 for details).

Fig. 4.

Calculating the contact map and contact frequency map. In the above example, a given query protein (Q, brown) with seven residues has five residues on the surface. Structural neighbors (Ni, green lines) involved in protein complexes are superimposed on Q, and the same transformation is applied to their interacting partners (Pi, green surfaces). Whenever a heavy atom from a residue of Pi is 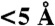of an atom of a surface residue of Q after applying the transformation, that residue is marked (red circles), generating a contact map for each structural neighbor (black boxes represent nonsurface residues that are not included). The “contact frequency map” is generated by summing the individual contact maps.

We then ask whether or not there is a statistically significant set of residues on the surface of the query protein that preferentially has interaction sites mapped to it. Following Russell et al. (23), the statistical significance is determined by counting the number of times any pair of contact maps overlap at a residue. This can be calculated as

where |S| is the number of structural neighbors and O_i is the number of surface residues in the query that interact with i structural neighbors. It was shown in ref. 23 that this number is statistically equivalent to

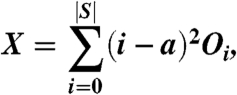where a is the average of frequencies of the contact frequency map. The number X represents bias in the distribution of the O_is. To measure the statistical significance of X for a given query protein, we calculate an approximate pivotal independent of the number of structural neighbors and the number of contacted residues:

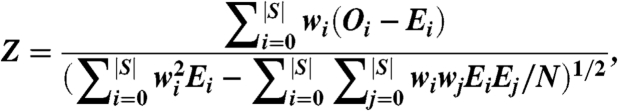where w_i = (i - a)², and E_i is the expected value of O_i under the assumption that the contact maps are randomly distributed over the surface of the query protein (calculated as described below). This score then essentially indicates the chance of observing the value X and can be used to evaluate degrees of interface conservation (please refer to ref. 23 for details). The larger the Z score, the more significant the conservation will be.

We estimated the values of E_i for each query protein by simulation. For each contact map generated for a structural neighbor of the query, we constructed a corresponding random surface patch that has the same number of contacting atoms using the subroutine MAKE_REGION of the program MODELLER (38). This is repeated 100 times, and E_i is taken to be the average of the O_is generated in each run. Ideally, the simulation should be done that each contact map and its random maps have the same number of residues. We compared the Z scores from simulation of the same number of atoms and the same number of residues and found little difference. Because the generation of random maps with the same number of contacting residues will take much more time, we generate random maps of the same number of contacting atoms in our simulation.

Using Conservation to Predict Interfaces.

We exploited the observed conservation to develop an interface prediction method. Given a query structure, we first identified its structure neighbors using Ska and kept only the 50 most similar neighbors that were also contained in complexes (for benchmarking purposes, complexes that contain the query protein were excluded). We calculated the contact frequency map as described above and turned the contact frequencies into residue-based interfacial scores using a logistic function:

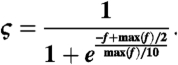Here f is the contacting frequency of a residue, and max(f) is its maximum value for the whole structure. We chose an interfacial score cutoff of 0.05 because this results in 20%–25% of residues being predicted as interfacial (roughly the portion of interface residues in our datasets). Prediction accuracy is assessed in terms of recall = N_c/N_i and precision = N_c/N_p, where N_c = the number of correctly predicted interface residues, N_i = the number of real interface residues, and N_p = the total number of predicted interfacial residues. When comparing our approach to other methods, we used the Web services Promate (http://bioinfo.weizmann.ac.il/promate/many.html) and obtained the cons-PPISP and PINUP from the developers and ran them locally.