Quantum rotor induced hyperpolarization

Abstract

Despite its broad applicability NMR has always been limited by its inherently low sensitivity. Hyperpolarization methods have the potential to overcome this limitation and, in the case of ex situ dynamic nuclear polarization (DNP), large enhancement factors have been achieved. Although many other polarization methods have been described in the past, including chemically and parahydrogen-induced polarization and optical pumping, DNP has recently been the most popular. Here we present an additional polarization mechanism arising from quantum rotor effects in methyl groups, which generates polarizations at temperatures < 1.5 K and interferes with DNP at such temperatures. The polarization generated by this mechanism is efficiently transferred via carbon bound protons. Although quantum rotor polarizations have been studied for a small range of molecules in great detail, we observe such effects for a much broader range of substances with very different polarization rates at temperatures < 1.5 K. Moreover, we report transfer of quantum rotor polarization across a chain of protons. The observed effect not only influences the polarization in low-temperature DNP experiments but also opens a new independent avenue to generate enhanced sensitivity for NMR.

Many developments in NMR technology, including cryogenically cooled probes, digital receivers and high field strengths, have targeted increased sensitivity. Hyperpolarization methods owe their success to the immense signal enhancements they can achieve. Dynamic nuclear polarization (DNP) was the first hyperpolarization technique to be explored (1, 2, 3) although several alternatives have been described. These include parahydrogen-induced polarization (4, 5, 6), chemically induced dynamic nuclear polarization (CIDNP) (7), and optical pumping (8, 9). Current implementations of DNP use low temperatures, typically 90 K for solid-state applications (10) or 1.1–1.5 K for ex situ DNP (11).

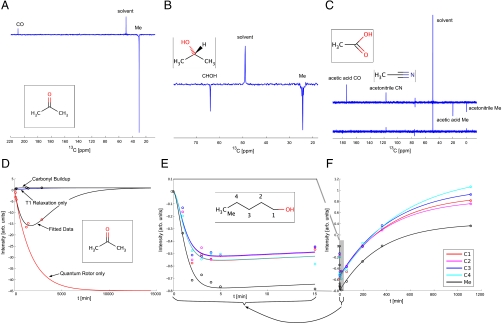
We recently observed “negative” resonances for methyl groups in ex situ DNP experiments, which we have attributed to rotational tunneling systems of hindered quantum rotors (12). This polarization can interfere constructively or destructively with DNP. In some samples, significant negative signals can be observed for methyl groups without the addition of a radical or microwave irradiation. Such samples usually involve methyl groups representing quantum rotors with a sufficiently high tunneling frequency. Fig. 1A shows a spectrum obtained for pure acetone with negative methyl signals after 20 h cooling as an example.

Fig. 1.

Time evolution of quantum rotor polarization. (A) ¹H decoupled ¹³C spectrum of acetone following a 20 h cooling period at 1.4 K to build up QR polarization for the methyl group (Me) followed by dissolution and transfer to a 11.75 T magnet. The carbonyl (CO) signal is much weaker when the maximum of QR polarization has been reached and has an opposite sign. (B) ¹H decoupled ¹³C spectrum of isopropanol showing transfer of polarization via the proton network after 60 min at 1.4 K, specifically from the methyl protons (Me) to the H₂ proton. Subsequent cross-relaxation generates observable ¹³C magnetization. (C) (Bottom) ¹³C spectrum of acetonitrile after 60 min at 1.4 K. (Top) Same spectrum for a mixture of acetonitrle and acetic acid. (D) Experimental and fitted QR polarization buildup curve for pure acetone. (Red Circles) Experimental signal intensities for the methyl group. (Black Circles) Signal intensities for CO. (Black Lines) Fitted data according to Eq. 6 for the methyl carbon and to a saturation recovery curve for CO. (Red Line) Simulated QR buildup curve using values obtained from the experimental data. (Blue Curve) Simulated Boltzmann buildup for the methyl ¹³C neglecting the quantum rotor contribution. (E, F) Different time frames for experimental and fitted curves for the QR buildup of pentanol. E focuses on the first 15 min, whereas F shows the time course over 20 h. Black, experimental data and simulated curve for CH₃; C1, C2, C3, and C4 in red, magenta, blue, and cyan, respectively.

Quantum rotor (QR) tunneling has in the past been studied in great detail from different aspects (reviewed in ref. 13) although applications have been limited to a small number of molecules. The most pronounced effect is the Haupt effect (14), which yields large dipolar polarizations following a temperature jump but has been limited to very few molecules, primarily to γ-picoline (4-methyl-pyridine) with a tunnel splitting of 125 GHz and lithium acetate with a tunnel splitting of 60 GHz (14, 15). Here we describe QR effects observed after cooling samples to temperatures of 1.2–1.5 K, which can be observed for a much broader range of molecules with smaller tunnel splittings. We also show that this polarization is transferred between CH_x protons. Signals arising from QR effects have an opposite sign to the Boltzmann polarization and develop on different timescales, simply following the cooling of samples from ambient temperatures to ≈1.5 K in a magnet.

Haupt (14) used a theoretical approach to explain the formation of dipolar order following the cooling or heating of γ-picoline, where he attributed the effect to transitions between A and E states, the irreducible representations of the C3(v) rotational group. Here A represents invariance under C3 rotation, whereas the degenerate E_a/b levels represent ± 120° rotations, respectively. Because the order of the lowest energy tunneling energy level alternates between A and E through excited rotational states, A and E levels are approximately equally populated at room temperature. At a sufficiently low temperature, the state with lowest energy, |3/2,A〉 (see Fig. S1), is increasingly populated. The A and E states for C3 symmetry can be seen as an analog to triplet and singlet states for systems with C2 symmetry and only two spins involved.

The coupling between these rotational states and the spin states of the methyl protons cause a dipolar order on protons which can be observed after generating observable Zeeman order. This dipolar polarization arises from the partial orientation of the nuclear magnetic moments relative to the dipolar fields of neighboring protons. The Hamiltonian causing this polarization has been described as (16)

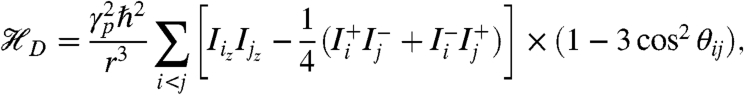[1]

where r is the interproton distance, γ_p the proton gyromagnetic ratio, and θ_ij the angle between the orientation of the external magnetic field and the internuclear vector.

Haupt (14) described his observations with a Hamiltonian

[2]

which considers methyl rotation, Zeeman, and dipolar terms, respectively. The individual contributions to this Hamiltonian were previously derived by Haupt (15) and are reviewed in ref. 13. The sign of the Haupt effect depends on the direction of the temperature change. Haupt saw an interaction of the methyl rotation with phonons in the crystal as the driving force of relaxation (15). The Haupt effect was previously described employing an empirical equation

[3]

where p_d is the dipolar polarization, and a and b are the polarization and depolarization times, respectively. The size of the Haupt enhancement factor C is determined by the initial and final temperature.

Results and Discussion

Fig. 1D illustrates the time dependence of the methyl QR effect for a sample containing pure acetone which was cooled to 1.3 K for 20 h in a Hypersense™ (Oxford Instruments) polarizer. No radical was added and no microwave irradiation applied. A ¹³C-NMR-spectrum was acquired in a high field NMR spectrometer (11.75 T, Fig. 1A) after dissolution with hot methanol and rapid transfer (see Fig. 2). In comparison to the signals arising from unpolarized methanol from the dissolution solvent, the acetone methyl signal has a negative sign and is relatively intense, considering that the dissolved sample contains only ≈5% of acetone in methanol. In contrast, the acetone carbonyl signal has a low intensity and the same sign as the solvent signal. Such negative methyl resonances are observed for many substances that possess hindered methyl rotors with a sufficiently high tunneling frequency (e.g., acetone, ethanol, isopropanol, DMSO, and acetic acid). The small positive enhancement of the carbonyl resonance arises from the Boltzmann polarization at low temperature.

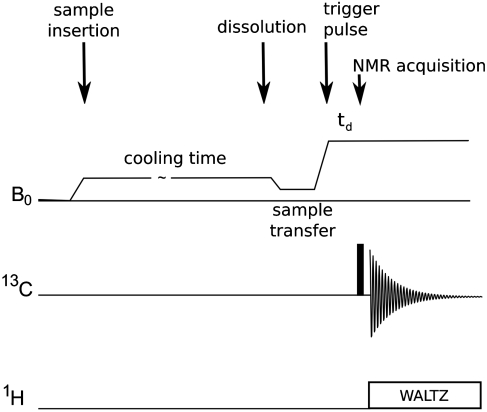
Fig. 2.

Time sequence of the overall QR experiment.

Quantum rotor polarization builds up over a period of time until it reaches a maximum absolute value and decays again as depicted in Fig. 1D. When left at the low temperature for a long duration, e.g., 50 h, enhancements start to decay in absolute value. For most substances, positive Boltzmann polarization builds up after a sufficiently long time. Acetone has a QR tunnel splitting of 96 MHz (17). There seems to be a trend for quantum rotors with larger tunnel splittings to have longer buildup periods and to show more intense QR polarization, although this is not consistent for all substances.

The experiment described here differs from the Haupt experiment (14) in various aspects. Samples are cooled to a much lower temperature, and high resolution ¹³C resonances are observed after dissolution, rather than ¹H spectra. This enables the resolution of individual lines at the expense of a loss of information about the original spin state on protons.

For the rotational tunneling system, cooling leads to an increased population for the A state. For systems where the energy difference between E and A rotational tunneling levels, ΔE_E,A, is larger than the energy difference between the Zeeman states ΔE_α,β, E → A transitions can drive α → β transitions, at least for a short period of time as the new equilibrium gets established. This is expected to cause larger polarizations for substances with larger rotational tunneling energies, ΔE_E,A. The buildup of magnetization with opposite sign compared to the Boltzmann magnetization requires that the equilibration process leads to an increased population of β spin states. This would be consistent with |1/2,E_a〉↔| - 1/2,A〉 and |1/2,E_a〉↔| - 3/2,A〉 transitions (see energy level diagram, Fig. S1). The lower the temperature, the higher the buildup of polarization of the lowest energy state |3/2,A〉. Whether other possible transitions occur is unclear although the net effect of increased Zeeman β population renders them rather unlikely. The need of a spin flip associated with a change of the overall symmetry (from E to A) can also be associated with the Pauli Principle, thus causing polarization of proton spins.

It should be noted that the relatively large signal intensities observed for small tunneling frequencies must be driven by relaxation between excited and the ground torsion states, which increase the population of the E ground state. Haupt (14) attributed such relaxation processes to interactions with external phonon modes.

The question whether the buildup of polarization involves an intermediate dipolar polarization (Eq. 1) cannot be answered from our experiments because the observed nucleus is inevitably ¹³C under our experimental arrangement (¹H longitudinal relaxation is too fast to observe a signal after dissolution and sample transfer).

An additional term describing the dipole–dipole interaction between the protons and the directly attached carbon nuclei needs to be considered as part of the Hamiltonian:

[4]

As for the Haupt effect, the buildup of negative methyl rotor polarization can be modeled assuming an empirical exponential buildup and decay. To account for dipolar cross-relaxation from protons to ¹³C, a heteronuclear cross-relaxation rate σ must be considered. R_1C represents the longitudinal carbon relaxation rate.

The time evolution of the carbon polarization can be described using the following differential equation:

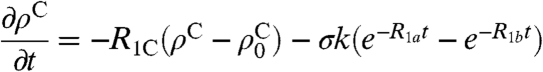[5]

ρ^C represents the carbon polarization at time t, 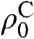is a steady-state polarization influenced by the tunnel splitting and by the temperature after cooling. R_1a describes the polarization buildup, R_1b the proton relaxation or depolarization rate, and k depends on the initial and final temperature.

Integration of the differential equation leads to

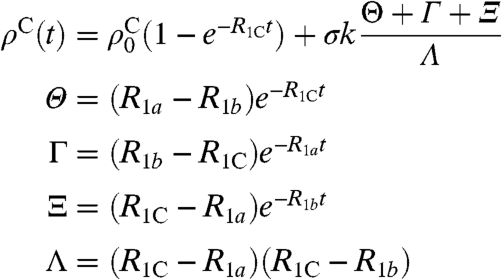[6]

This equation fits the experimental data for acetone very well (Fig. 1D) and allows for the definition of an enhancement factor relative to carbonyl (or other quaternary carbon) Boltzmann polarization. Once all the constants have been determined by fitting the original data, several predictions are possible and a maximum enhancement can be defined as follows. Using the carbonyl carbon in acetone its polarization buildup determines 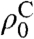in the absence of quantum rotor effects. This assumption follows the consistent observation that nonprotonated carbons do not show any effects leading to negative signals. From the calculated rate constants, the individual components contributing to the overall QR polarization can be simulated, i.e., the buildup of Boltzmann polarization (Fig. 1D, shown in black) and the polarization transferred from the proton system, neglecting longitudinal relaxation of the carbon nucleus (Fig. 1D, shown in red). The enhancement then is defined as the maximum absolute value of the QR polarization in units of the maximum Boltzmann polarization (Fig. S2 and SI Text provide a more detailed description).

This definition of the maximum enhancement has the advantage that it describes the QR enhancement of the sample at the low field in low temperature. No field or temperature corrections have to be applied. For acetone, we obtain an enhancement factor of ≈20, the QR buildup rate is 1.5 × 10^-4 Hz (buildup time of 1.77 h), the carbon relaxation rate is 2.24 × 10^-6 Hz (T_1C = 124 h). Table 1 summarizes fitted rates for different systems. It should be noted that the buildup rate increases considerably for acetone when mixed with other substances such as DMSO.

Table 1.

Fitted parameters

Compound	Nucleus	R1C, 10-5 Hz	R1A, 10-5 Hz	R1B, 10-5 Hz	σk, 10-5 Hz		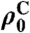Maximum enhancement
Acetone	Me	0.224 ± 0.137	15.67 ± 14.85	4.83 ± 1.34	−127.50 ± 71.41	1.00 ± 0.037	18.6
	CO	10.00 ± 1.31				1.00 ± 0.037
6-chloro-2-hexanon	CO	12.83 ± 0.49				1.00 ± 0.0109
	C1	20.47 ± 2.53	376.76 ± 47.26	185.92 ± 11.37	−86.56 ± 10.89	0.1116 ± 0.0084	2.11 (0.24)
	C2	21.34 ± 2.17	376.76 ± 47.26	185.92 ± 11.37	−102.89 ± 12.49	0.1434 ± 0.0085	1.95 (0.28)
	C3	22.52 ± 2.30	376.76 ± 47.26	185.92 ± 11.37	−109.42 ± 13.18	0.1492 ± 0.0085	1.99 (0.29)
	Me	27.08 ± 4.68	376.76 ± 47.26	185.92 ± 11.37	−170.89 ± 21.01	−0.2334 ± 0.0082	−1.99 (0.47)
	C4	23.39 ± 2.65	376.76 ± 47.26	185.92 ± 11.37	−98.25 ± 12.47	0.1292 ± 0.0084	2.07 (0.27)
Pentanol	C1	4.016 ± 0.243	2603 ± 82	2375 ± 72	−15515 ± 15500	0.9230 ± 0.0377	0.62
	C2	4.310 ± 0.281	2603 ± 82	2375 ± 72	−14675 ± 14485	0.8308 ± 0.0372	0.65
	C3	3.669 ± 0.234	2603 ± 82	2375 ± 72	−14582 ± 14715	1.0607 ± 0.0439	0.51
	C4	3.073 ± 0.203	2603 ± 82	2375 ± 72	−15432 ± 15161	1.3073 ± 0.0574	0.43
	Me	4.708 ± 0.335	2603 ± 82	2375 ± 72	−21487 ± 21098	0.4227 ± 0.0343	1.87
Acetic acid	CO	3.5243 ± 0.83				1.00 ± 0.0531
	Me	0.5316 ± 0.194	14.626 ± 16.57	5.511 ± 1.55	−121.65 ± 84.7	1.00 ± 0.0531	13.76
Acetic acid/water	CO	3.157 ± 0.65				1.00 ± 0.0712
	Me	0.0860 ± 0.033	262 ± 316	88 ± 15	−72.6 ± 17.6	1.00 ± 0.0712	0.55

To assess intramolecular transfer of such polarizations, we initially compared spectra for acetone and isopropanol. Acetone has no protons other than those of the methyl groups and a carbonyl group. Isopropanol has an equivalent structure with the carbonyl replaced by a CHOH group. The two systems therefore allow a comparison of polarization transfer from CH₃ to CO vs. CH₃ to CH. As depicted in Fig. 1 A and B, both substances show negative signals for their methyl groups. For isopropanol, we also observe a negative enhancement for the C(2) carbon with an intensity comparable to that of the methyl carbon, indicative of an intramolecular transfer of magnetization to C(2)H.

To study the mechanism behind this transfer in more detail, we referred to alkanes with only one terminal methyl group, such as pentanol and 6-chloro-2-hexanone. Such systems allow to identify the mechanism of transfer from the hindered methyl rotor to other nuclei in the molecule with known distance between methyl and various CH₂ groups. We hypothesized two possible mechanisms, one where individual dipolar interactions between the methyl QR protons and CH₂ carbons are responsible for the polarization transfer. The other option is an initial buildup of proton polarization for the methyl group which transfers to the CH₂ protons via spin diffusion. Although the exact tunnel splittings are not known for these two compounds, similar substances had tunnel splittings in the range of 60–500 kHz (2-butanone, 495 kHz; 2-hexanone, 152 kHz) (18). Pentanol is likely to have very low tunnel splittings considering that it lacks the carbonyl group close to the methyl group.

The data obtained for pentanol shown in 1 E and F clearly support the second hypothesis. For all systems studied, we observe transfer only via protons, although observed via the bound ¹³C nucleus. Moreover, the buildup curves for pentanol show a different behavior for the methyl group compared to all the CH₂s which behave similarly among each other. Most interestingly, the polarization for this system reaches a maximum after only ≈5 min, although the signal intensity at the maximum is much smaller than that observed for the carbonyl. This polarization persists during the initial period of 15–20 min as the ¹³C longitudinal relaxation time is comparably long (T_1C ≈ 14 h). The rates obtained from the simulation according to Eq. 6 are summarized in Table 1.

A similar, yet again intriguingly different, behavior is observed for 6-chloro-2-hexanone (see Fig. S3). The data obtained for 6-chloro-2-hexanone confirm the view of transfer via protons, with CH₂ groups showing a different behavior to the methyl group. As for any other molecules we have studied, the CO remains unaffected by the QR polarization. The time frame of QR polarization buildup is considerably longer than for pentanol; a maximum absolute value is reached after 20 min. Intriguingly, even after 75 h, the methyl polarization has not reached a Boltzmann equilibrium; signals remain negative, suggesting that the long-term recovery of this signal is driven by another, slower mechanism than the initial decay of QR polarization.

We therefore propose that the following relaxation processes drive the observed effects. At very low temperature (1.4 K), the dynamics of the methyl group is dominated by rotational tunneling associated with a motional spectrum with sharp lines at the tunneling frequencies (± ω_t). For high barrier heights, i.e., strong hindrance of the methyl rotor, virtually no longitudinal relaxation occurs. This is the likely cause for the lack of longitudinal relaxation in the 6-chloro-2-hexanone system. Considering that the CH₂s in both pentanol and 6-chloro-2-hexanone relax twice as fast as their methyl groups, we have to assume that residual vibrations in the carbon chain are responsible for relaxation. For the initial processes after cooling, the energy stored in the system via the temperature jump is dissipated through additional relaxation mechanisms (i.e., the same that lead to the buildup of the nuclear carbon polarization), so that at least part of the carbon polarization will be relaxed. For smaller molecules such as acetone and for end groups (CH₃ in pentanol and 6-chloro-2-hexanone) additional intermolecular relaxation must be considered, as proposed by Haupt (14).

Although the underlying relaxation mechanisms at 1.5 K are not well understood, the experiments presented here demonstrate transfer of QR polarization via the proton network with subsequent transfer to ¹³C nuclei. Transfer to other protons must be guided by fast spin diffusion in the solid state which is continuously driven by the ongoing buildup of QR polarization. In our simulations, the spin diffusion becomes part of the σk term. We also observe buildup and decay of QR polarization on very different time frames.

In contrast, results regarding intermolecular transfer in the solid state are less conclusive. Transfer between molecules depends on the contact between molecules which are determined by the packing of the glass state or crystal. Although pure acetonitrile does not show a QR effect, as expected for a linear molecule, this can be induced by the addition of other substances, e.g., small amounts of acetic acid. It is therefore difficult to judge whether this initiation of QR polarization is caused by transfer from acetic acid or by breaking the symmetry of acetonitrile in the crystalline solid state. This effect has previously been reported by Häberlen and coworkers for hydroquinone/acetonitrile clathrates (19).

Although the ¹³C polarizations observed in our experiments are small compared to those obtained by ex situ DNP, the extent of ¹³C enhancement suggests a significant proton polarization. The most limiting factor is probably the low efficiency of proton-carbon cross-relaxation in the absence of efficient relaxation mechanisms. If this transfer rate can be improved, it is highly likely that enhancements observed on ¹³C will become much larger. For γ-picoline, Tomaselli et al. (20, 21) have shown that efficient transfer of methyl-rotor-induced polarization to ¹³C nuclei is feasible by various cross-polarization schemes. The described effect is also likely to be field dependent; this applies to the formation of QR-induced ¹H polarization as well as to the cross-relaxation transfer to ¹³C, and may yield a much larger polarization once the magnetic field strength in the polarizer has been optimized, an experiment that is not feasible with our current equipment. Nevertheless, the ability to polarize molecules without any addition of a radical and in the absence of a chemical reaction adds another dimension to NMR hyperpolarization techniques.

Materials and Methods

For all experiments, 200 μL of the natural abundance sample was placed in the Hypersense polarizer (Oxford Instruments) equipped with a 3.35 T superconducting magnet. NMR spectra were acquired following dissolution and sample transfer using a 500 MHz (11.74 T) NMR Bruker spectrometer.

The cooling and transfer process was performed as follows:

1. In the polarizer, the sample was initially cooled to 4 K by immersion in liquid He.

2. The sample was further cooled to 1.4 K by immediately starting vacuum pumping of the He bath. A temperature of 2 K was reached after 1 min, 1.75 K after 3 min, and 1.5 K after 5–6 min.

3. The sample was left at the low temperature for a specified time period. Cooling times reported in the manuscript were always times after reaching a temperature of 1.5 K.

4. Subsequently, the sample was dissolved and transferred to the 11.74 T NMR spectrometer by methanol dissolution, using methanol preheated to 459 K at 9 bar. The dissolution and transfer process required a total of 2.6 s, and the final temperature of the sample was 303 K. During the transfer, the sample passed through lower field strengths, although never through zero field (see field map, Fig. S4). After transfer, the sample was allowed to stabilize in the NMR tube for 3.6 s to allow turbulences to settle prior acquisition of the NMR spectrum.

5. The NMR spectrum was acquired in a ¹³C observe probe by using a single 90° pulse with proton decoupling during signal acquisition. The temperature at which the final spectrum was recorded is mainly determined by the temperature of the dissolution solvent. This is highly reproducible when the volume of the sample and dissolution solvent are kept constant.

This overall process is summarized in a time diagram in Fig. 2. All solvents and substances were obtained from Sigma-Aldrich.