Visualizing the formation of the Kondo lattice and the hidden order in URu₂Si₂

Abstract

Heavy electronic states originating from the f atomic orbitals underlie a rich variety of quantum phases of matter. We use atomic scale imaging and spectroscopy with the scanning tunneling microscope to examine the novel electronic states that emerge from the uranium f states in URu₂Si₂. We find that, as the temperature is lowered, partial screening of the f electrons’ spins gives rise to a spatially modulated Kondo–Fano resonance that is maximal between the surface U atoms. At T = 17.5 K, URu₂Si₂ is known to undergo a second-order phase transition from the Kondo lattice state into a phase with a hidden order parameter. From tunneling spectroscopy, we identify a spatially modulated, bias-asymmetric energy gap with a mean-field temperature dependence that develops in the hidden order state. Spectroscopic imaging further reveals a spatial correlation between the hidden order gap and the Kondo resonance, suggesting that the two phenomena involve the same electronic states.

A remarkable variety of collective electronic phenomena have been discovered in compounds with partially filled f orbitals, where electronic excitations act as heavy fermions (1, 2). Like other correlated electronic systems, such as the high temperature superconducting cuprates, several of the heavy fermion compounds display an interplay between magnetism and superconductivity and have a propensity toward superconducting pairing with unconventional symmetry (1–5). However, unlike cuprates, or the newly discovered ferropnictides, the heavy fermion systems do not suffer from inherent dopant-induced disorder and offer a clean material system for the study of correlated electrons. The local f electrons interact both with the itinerant spd electrons as well as with each other, resulting in a rich variety of electronic phases. In many of these materials, screening of the local moments by the Kondo effect begins at relatively high temperatures resulting in a heavy fermion state at low temperatures. Exchange interactions between the local moments become more important at lower temperatures and can result in the formation of magnetic phases as well as superconductivity at even lower temperatures. Among the heavy fermion compounds perhaps the most enigmatic is the URu₂Si₂ system, which undergoes a second-order phase transition with a rather large change in entropy (6–8) at 17.5 K from a paramagnetic phase with Kondo screening to a phase with an unknown order parameter (9). This material possesses low-energy commensurate and incommensurate spin excitations, which are gapped below the hidden order (HO) transition temperature (10–13). These features are believed to be signatures of a more complex order parameter, the identification of which has so far not been possible despite numerous investigations (12–18). Moreover, analogous to other correlated systems, this unusual conducting phase is transformed into an unconventional superconducting state at 1.5 K (6, 8, 19), the understanding of which hinges on formulating the correct model of the HO state.

We report scanning tunneling microscopy (STM) measurements on URu₂Si₂ single crystals that allow atomic scale examination of this system in the paramagnetic Kondo phase and its phase transition into the HO state. We isolate electronic signatures of the Kondo lattice state and their transformation at the HO transition. Although there have long been reports on modification of the electronic structure of URu₂Si₂ at the onset of the HO transition, such as those in specific heat (6, 8) as well as optical (20, 21), point contact (21, 22), and angle resolved photoemission spectroscopy measurements (17, 23, 24), our experiments provide an unprecedented determination of these changes with high energy and spatial resolutions. We find a particle-hole asymmetric energy gap that turns on with a mean-field temperature dependence near the bulk HO transition. More importantly, spectroscopic mapping as a function of temperature further reveals that the HO gap is spatially correlated on the atomic scale with the electronic signatures of the Kondo lattice state.

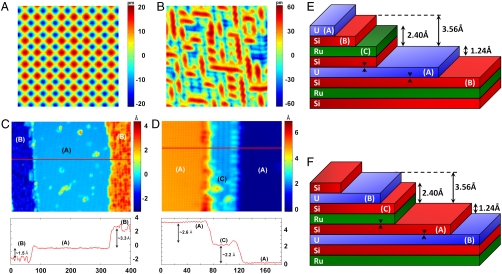
We carried out our experiments in a specially designed STM by using high quality single crystal URu₂Si₂ samples that were cleaved in situ in ultrahigh vacuum prior to measurements. The STM topographies show that cleaved surfaces can be terminated with primarily two types of surfaces, one of which is atomically ordered with a lattice spacing corresponding to either the U or the Si layer (Fig. 1A; termed surface A), whereas the other is reconstructed (Fig. 1B; termed surface B) (see more information in SI Text). The occurrence of surfaces A and B with roughly equal probabilities (55% and 45%, respectively) implies that these surfaces are the two sides of the same cleave, suggesting that the cleaving process involves breaking of a single type of chemical bond. Moreover, the relative height between surfaces A and B shown in Fig. 1C reveals that surface A lies ∼1.5 Å above and ∼3.3 Å below surface B. This asymmetry allows us to uniquely identify surfaces A and B as the U and Si layers, respectively (see Fig. 1E). Any other possibility (i.e., Fig. 1F) will require the breaking of two bonds, the result of which would be the observation of four surfaces with 25% probabilities. Occasionally (< 5% of the time), small patches of a different surface (termed surface C) have also been observed (Fig. 1D). The presence of multiple surfaces for cleaved URu₂Si₂ samples indicates that obtaining local surface structure information is critical to identifying which spectroscopic properties are most related to the bulk properties. This requirement puts other surface sensitive spectroscopic techniques, such as angle resolved photoemission or point contact spectroscopy, at a disadvantage.

Fig. 1.

STM topography. (A and B) Constant current topographic image (-200 mV, 60 pA, 33 Å) showing an atomically ordered surface (termed surface A) and (100 mV, 200 pA, 90 Å) showing an atomic layer with surface reconstruction (termed surface B), respectively. (C) The relative heights between surfaces A and B. (D) Constant current topographic image (-50 mV, 100 pA) over a 185 × 140 Å² area showing a (2 × 1) reconstructed surface (surface C) lying ∼2.2 Å above surface A. A horizontal line cut through the data in C and D is shown on the bottom panels. (E) Schematic diagram illustrating the different atomic layers of URu₂Si₂. U is identified as the atomically ordered surface (surface A) that lies 1.24 Å above and 3.56 Å below surface B. In this case, obtaining surfaces A and B requires breaking of a single bond only (U-Si; see arrows). (F) Schematic diagram illustrating a different possibility for the cleaved surfaces, which requires the breaking of two bonds (Ru-Si and U-Si; see arrows). This scenario cannot explain why surfaces A and B occur with roughly equal probabilities. The step heights in A and B are obtained (or calculated) from ref. 6.

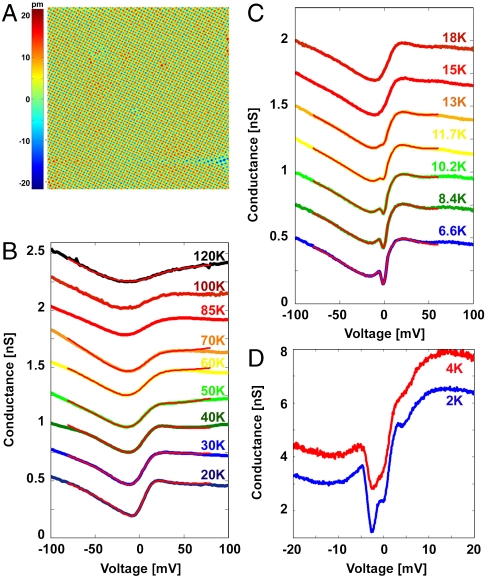
The temperature evolution of the spatially averaged STM spectra on the atomically ordered terraces (U terminated, surface A), shown in Fig. 2B, reveals the development of electronic correlations in URu₂Si₂ below 120 K, which evolve into dramatic spectroscopic signatures of the HO phase as the temperature is reduced (Fig. 2 C and D). At high temperatures (above 120 K), the spectrum presents a broad feature that has weak energy dependence, although it shows a slightly asymmetric density of states (DOS) for electron or hole tunneling. As the temperature is lowered, we find that the background is modified with an asymmetric resonance near the Fermi level, which sharpens as the temperature is reduced. On further cooling below the HO transition, we find the opening of a low-energy gap that widens with decreasing temperature and reveals an unusual asymmetry relative to the Fermi energy and an even sharper structure within the gap (Fig. 2D). The unusual shape of the low-energy spectral properties and their dramatic evolution with temperature provide important clues to the underlying correlations responsible for the thermodynamic phases of URu₂Si₂.

Fig. 2.

STM topography and spectroscopy on URu₂Si₂. (A) Constant current topographic image (-200 mV, 60 pA) over a 200-Å area showing the atomically ordered surface where the spectroscopic measurements are performed. (B and C) Averaged electronic DOS above (B) and below (C) the HO temperature. The red lines in B and C are the results of least squares fit described in the text and SI Text. Spectra are offset by 0.25 nS for clarity. (D) Averaged electronic DOS at low temperatures showing additional features within the gap. Spectra are offset by 1 nS for clarity.

Focusing on the spectroscopic features above the HO transition, we note that the asymmetric line shape near the Fermi level developing below 120 K is reminiscent of a Fano spectral line shape (25–28) measured for single Kondo impurities on the surface of noble metals (29–31). Recent calculations of the local electronic DOS on URu₂Si₂ reveal a Kondo resonance with a Fano line shape on the U layer in qualitative agreement with our data (18). Previous thermodynamic and transport studies have also identified the temperature range above the HO transition as being dominated by Kondo screening of the f electron moments (6, 8, 19). For STM experiments, the Fano line shape naturally occurs because of the presence of two interfering tunneling paths from the STM tip, one directly into the itinerant electrons, and the other indirectly through the Kondo resonance. The Fano line shape,

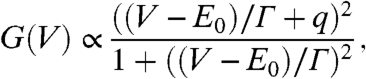[1]

is characterized by the resonance energy E₀, its width 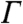, and the ratio of probabilities between the two tunneling paths q. The addition of this line shape to the high temperature background DOS accurately fits the spectroscopic data over a wide range of temperatures (red line in Fig. 2B; see also SI Text). The extracted values of q = 1.3 ± 0.3 and E₀ = 5 ± 2 meV show no significant temperature dependence within the uncertainty of our fits above the HO transition, whereas 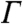clearly broadens with increasing temperature as shown in Fig. 3A. Results for the single channel spin one-half Kondo impurity model in a Fermi liquid regime have been used to describe the temperature dependence of 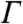(31),

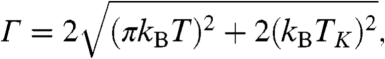[2]

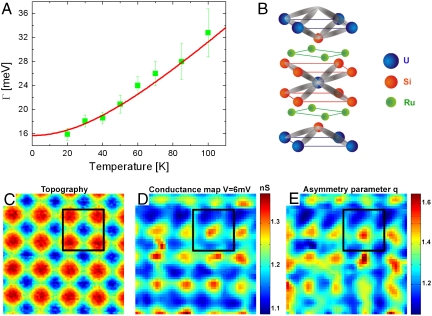
and to extract the value of the Kondo temperature, T_K = 129 ± 10 K (Fig. 3A). The success of this model at describing the spectra above the HO transition is somewhat surprising given that the spins associated with the f levels reside on a periodic U sublattice (32) and that the material displays non-Fermi liquid transport properties at low temperatures (33).

Fig. 3.

Kondo lattice. (A) Temperature dependence of the Kondo resonance width Γ extracted from the fits in Fig. 2B. The red line represents the temperature dependence for a single Kondo impurity described in the text, which results in a Kondo temperature T_K = 129 ± 10 K. (B) Crystal structure of URu₂Si₂ indicating the different atomic layers and a schematic of the orbitals that bond the Si atoms to the U atoms. (C) A high-resolution constant current topography of 4 × 4 atoms taken at 18 K. (D) Conductance map at 6 mV (Kondo resonance energy) corresponding to the topography in C showing atomic scale modulations. (E) The dimensionless q(r) map on the same area as in C obtained by fitting the spectra at each location to a Fano line shape. The larger values of q (indicating higher tunneling probability to the Kondo resonance) lie in between the atomic sites as depicted by the black square.

To obtain information about the influence of the periodic arrangement of Kondo “impurities” in our lattice, we now turn to the spatial dependence of the STM spectra. Obtaining topographies and STM differential conductance maps (dI/dV) with sub-Angstrom resolution, we find that the DOS modulates with the same periodicity as the atomic lattice (Fig. 3 C and D). Such a variation can be expected because the amplitudes for the two interfering paths that cause the Kondo–Fano resonance depend sensitively on the path that the electrons have to travel from the tip to the sample. Fitting individual spectra at each location with the Fano line shape, we find that the extracted ratio q, which describes the relative strength for tunneling into the Kondo resonance and the spd bands, shows measurable variation on the atomic scale (Fig. 3E). Naively, we would expect q to be maximal when the tip is over the U atoms. However, the orientation and shape of the atomic orbitals also plays a role in the tunneling into the Kondo resonance (34). In fact, the spatial dependence of q shows enhanced tunneling into the resonance when the tip is over the locations between the surface U atoms. A schematic of the orientation of the U’s f orbitals at a cleaved surface, shown in Fig. 3B, provides a possible way to understand such spatial dependence.

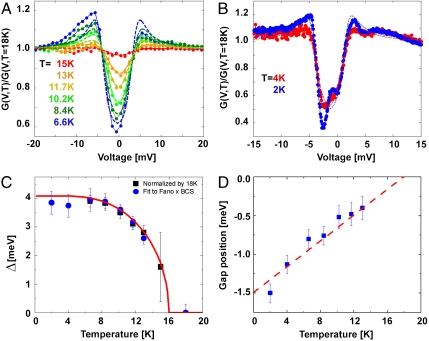
As illustrated by the spectra in Fig. 2, the development of the HO has a dramatic influence on the Kondo–Fano resonance and contains key information on the electronic correlations responsible for this transition. In order to isolate the spectroscopic changes at the onset of the HO, we divide the spectra obtained at temperatures below T_HO = 17.5 K with the spectrum measured at 18 K just above the bulk HO transition, as shown in Fig. 4 A and B (see SI Text). The normalized spectra reveal the onset of a low-energy gap centered at an energy below the Fermi level. Whereas the presence of a gap associated with the HO has been indicated by previous thermodynamic (6, 8) and spectroscopic measurements (20–22, 35), our high-resolution data and their spatial dependence allows identification of several of its fundamental features.

Fig. 4.

Temperature dependence of the HO gap. (A and B) The experimental data below T_HO divided by the 18-K data. The data are fit to the form 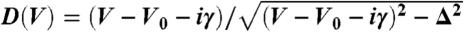, which resembles an asymmetric BCS-like DOS with an offset from E_F. V₀, γ, and 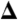are the gap position (offset from the Fermi energy), the inverse quasi-particle lifetime, and the gap magnitude, respectively. A quasi-particle lifetime broadening of γ ∼ 1.5 mV was extracted from the fits. (C) Temperature dependence of the gap extracted from the fits in A (Black Squares) and from a direct fit to the raw data of Fig. 2C (Blue Circles). Both results are comparable within the error bars. The transition temperature T_HO = 16.0 ± 0.4 K is slightly lower than the bulk transition temperature presumably as a consequence of the measurement being performed on the surface. (D) Temperature dependence of the gap position V_o extracted from the fits. The line is a guide to the eye.

A phenomenological way to characterize the HO gap, 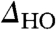, is to fit the spectra to a thermally convoluted DOS with a Bardeen–Cooper–Schrieffer (BCS) function form, from which we can extract the magnitude and temperature dependence of 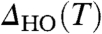. Following this procedure (Fig. 4 A and B), we extract 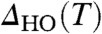, which evolves more rapidly than simple thermal broadening (see SI Text). However, as we approach the transition temperature, 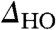becomes comparable to thermal broadening, making the precise determination of the onset temperature difficult. Regardless, we find the temperature dependence of 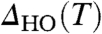to follow a mean-field behavior with an onset temperature of T_HO ∼ 16 K (Fig. 4C). Broken symmetry at the surface is likely to influence the HO state and may account for the slightly reduced observed onset temperature relative to that of bulk measurements. An important aspect of the 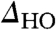is the fact that it develops asymmetrically relative to the Fermi energy and it shifts continuously to lower energies upon lowering of the temperature (Fig. 2 C and D). We quantify the changes to 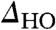and its offset by fitting the data to a BCS function form with an offset energy relative to E_F (Fig. 2 Cand D and Fig. 4D; see the caption of Fig. 4).

The low temperature extrapolation, 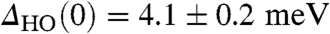, yields 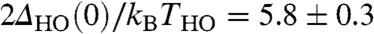, which together with the value of the specific heat coefficient γ_c = C/T for T > T_HO (8) within the BCS formalism results in a specific heat jump at the transition of ΔC = 6.0 ± 1.3 J K^-1 mol^-1, consistent with previous measurements (7, 8, 12). The partial gapping of the Fermi surface observed in our spectra also corroborates the recently observed gapping of the incommensurate spin excitations by inelastic neutron scattering experiments (12). Finally, the spectrum develops additional, sharper features within 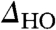at the lowest temperatures (Fig. 4B). Such lower energy features may be related to the gapping of the commensurate spin excitations at the antiferromagnetic wave vector below T_HO also seen in inelastic neutron scattering at an energy transfer of about 2 meV (11–13).

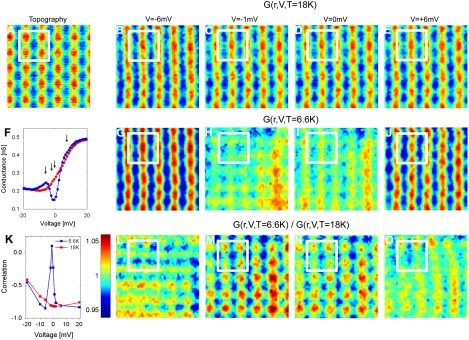
The spatial variation of the STM spectra provides additional information about the nature of redistribution of the electronic states that gives rise to 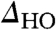. In Fig. 5, we show energy-resolved spectroscopic maps measured above and below T_HO, all of which show modulation on the atomic scale. The measurements above T_HO show no changes in their atomic contrast within the energy range where the 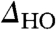is developed. In fact, the modulations in these maps (Fig. 5 B–E) are because of the surface atomic structure but occur with a contrast that is opposite to that of the STM topographies of the same region (Fig. 5A). However, observation of reverse contrast in STM conductance maps is expected as a consequence of the constant current condition. Similar measurements below T_HO are also influenced by the constant current condition, as shown in Fig. 5 G–J; nonetheless, these maps show clear indication of the suppression of contrast associated with 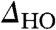at low energies (within the gap; see Fig. 5F) and the consequent enhancement at high energies (just outside the gap).

Fig. 5.

Atomic origin of the HO. (A) A constant current topography at T = 18 K corresponding to 5 × 5 atoms. Spatial conductance maps on the area in A at different bias voltages V obtained at 18 (B–E) and 6.6 K (G–J). The junction is stabilized at -100 mV and 100 pA. All conductance maps are normalized to their mean value to emphasize the atomic contrast. The maps display an atomically periodic modulation. (F) Average dI/dV spectra at 18 and 6.6 K. The arrows indicate the energies where the conductance maps are performed. (L–O) Division of the G(r,V,T = 6.6 K) maps with the G(r,V,T = 18 K) maps showing a contrast reversal of the conductance when moving from outside the gap (L; V = -6 mV) to within the gap (M and N). The loss of the spectral weight in the gap and the transfer to higher energies occurs principally between the surface U atoms as is shown by the white square boxes. (K) Correlation of the conductance maps with the atomic locations above and below the HO temperature showing a dramatic change of correlation (change of contrast) within the gapped region between the surface U atoms. Homogeneous gapping should result in no change of correlation.

To isolate the spatial structure associated with 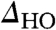and to overcome any artifacts associated with the measurement settings, we divide the local conductance measured below T_HO by that above for the same atomic region, as shown in Fig. 5 L–O. Such maps for 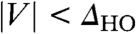illustrate that the suppression of the spectral weight principally occurs in between the surface U atoms. These maps are essentially the spatial variation of the conductance ratios, shown in Fig. 4A. Therefore, consistent with the BCS-like redistribution of spectral weight, we find that conductance map ratios at energies just above 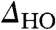illustrate an enhancement between the surface U atoms. Quantifying these spatial variations further, we also plot the correlation between the conductance map ratios and the atomic locations above and below T_HO (Fig. 5K) to show that 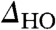is strongest in between the surface U atoms—i.e., at the same sites where tunneling to the Kondo resonance is enhanced (Fig. 3E). Our observation that the modulation in the tunneling amplitude into the Kondo resonance correlates with the spatial structure of the HO gap shows that the two phenomena involve the same electronic states.

Our finding of an asymmetric mean-field-like energy gap would naively suggest the formation of a periodic redistribution of charge and/or spin at the onset of the HO because of Fermi surface nesting. However, consistent with previous scattering experiments (8, 11–13), we find no evidence for any conventional density wave in our experiments. Recently, it has been suggested that the opening of a gap may be a consequence of hexadecapole ordering emerging from the crystal field splitting of U’s 5f² states (18). Whereas the experimentally observed gap can be the consequence of the hexadecapole ordering, no signatures of the higher temperature crystal field splitting was observed in our data. Other proposals indicate that the development of the gap is the effect of a hybridization gap (36, 37). Though a conventional hybridization gap should not manifest itself as a second-order phase transition with a mean-field-like order parameter, an exotic form of hybridization accompanied by orbital ordering can be a possible candidate for the HO phase. Regardless, our spatial mapping, which reveals the enhancement of the Kondo–Fano signature between the surface U atoms and the relatively stronger HO gap at these same locations, provides a key to identifying the electronic states responsible for these phenomena and therefore the understanding of the nature of the HO phase.