Entropy driven self-assembly of nonamphiphilic colloidal membranes

Abstract

We demonstrate that homogeneous monodisperse rods in the presence of attractive interactions assemble into equilibrium 2D fluid-like membranes composed of a one-rod length thick monolayer of aligned rods. Unique features of our system allow us to simultaneously investigate properties of these membranes at both continuum and molecular lengthscales. Analysis of thermal fluctuations at continuum lengthscales yields the membranes’ lateral compressibility and bending rigidity and demonstrates that the properties of colloidal membranes are comparable to those of traditional lipid bilayers. Fluctuations at molecular lengthscales, in which single rods protrude from the membrane surface, are directly measured by comparing the positions of individual fluorescently labeled rods within a membrane to that of the membrane’s continuum conformation. As two membranes approach each other in suspension, protrusion fluctuations are suppressed leading to effective repulsive interactions. Motivated by these observations, we propose an entropic mechanism that explains the stability of colloidal membranes and offers a general design principle for the self-assembly of 2D nanostructured materials from rod-like molecules.

In hard-body fluids, interactions between individual particles are described by a steep repulsive potential that imposes an infinite energetic penalty for any overlapping particles. It follows that any accessible state of a hard particle fluid has no internal energy and that minimizing the free energy of such a system is equivalent to maximizing its entropy. Hard particles have served as essential model systems for our understanding of the liquid and solid state, demonstrating the existence of nematic and smectic phases in hard rods (1, 2) and a 3D crystalline phase in hard spheres (3). These results exemplify the counterintuitive yet well established notion that entropy alone can drive the self-assembly of ordered structures. In this paper, we extend these ideas of entropic self-assembly to a equilibrium structure, a colloidal membrane. We demonstrate that in the presence of attractive (depletion) interactions mediated by nonadsorbing polymer, monodisperse rod-like colloids (filamentous viruses) spontaneously assemble into 2D membranes. In contrast to the previous examples of entropic self-assembly, in which the constituent molecules assemble into 3D structures, the self-assembly of homogeneous rods into colloidal membranes is self-limited to two dimensions, similar to what is observed for the assembly of amphiphilic lipids into ubiquitous biological membranes (4). However, unlike amphiphilic molecules that have a heterogeneous molecular structure, all the molecules involved in assembly of colloidal membranes are homogeneous, suggesting that geometry as well as chemical heterogeneity can be used to design pathways for self-assembly of various molecular species (5).

In what follows, we utilize two unique features of our model experimental virus/polymer system to characterize the properties of colloidal membranes in great detail. The first feature of the rod/polymer system is the ability to precisely tune the strength and the range of the attractive potential that drives the condensation of rods into membranes (6). The second feature is the colloidal lengthscale of the viral building blocks that permits simultaneous observations of membranes at both the continuum and molecular levels. Differential interference contrast (DIC) microscopy reveals that colloidal membranes are soft structures with significant continuum lengthscale fluctuations, while fluorescence microscopy uncovers the dynamics of individual rods within various assemblages. Furthermore, DIC and fluorescence images can be acquired simultaneously and overlaid with nanometer precision, allowing us to correlate the behavior of membranes across different lengthscales. These unique features of our model system enable us to (i) characterize continuum lengthscale fluctuations of colloidal monolayer membranes and demonstrate that they are described by the well-known Helfrich Hamiltonian, (ii) measure the dynamics of individual rods within a membrane and correlate continuum fluctuations with those of individual rods, (iii) determine the stability of membranes as a function of the attractive intermolecular potential, and (iv) formulate a simple model of membrane stability based on protrusion fluctuations and test its predictions against experimental data. When taken together, these results suggest a widely applicable design principle for the assembly of 2D membranes from homogeneous rods with hard-core repulsive interactions and outline an experimental system to study the behavior of model membranes with great detail.

Experimental Results

As model rod particles, we use the filamentous virus fd, which has a contour length of 880 nm, diameter of 7 nm, and persistence length of 2.8 μm (7). Viruses are mixed with a nonadsorbing polymer (Dextran), which induces attractive interactions between rods via the depletion mechanism (6) (see SI Text). As two viruses approach each other in the polymer suspension, an additional free volume becomes available to polymer coils, thus increasing the overall entropy of the mixture. This results in an effective attractive (depletion) potential between rods, whose strength and range can be tuned by changing the polymer concentration and size, respectively. Under high-salt conditions, hard-core repulsive interactions dominate the behavior of fd/polymer mixtures, and consequently all phase transitions in this system are entropically driven (8). Similar mixtures have been used to explore the influence of attractive interactions on the isotropic-nematic phase transition and kinetics of various liquid crystalline phase transitions (9–11). In these studies, the qualitative observation of 2D membrane-like structures was reported. However, the properties of these structures were not studied, and there was no indication of whether these were transient or equilibrium structures. More importantly, previous studies contained a low-volume fraction of longer rods, which greatly alters the phase diagram by destabilizing colloidal membranes. Here, using suspensions enriched in monodisperse rods (see SI Text), we discuss in quantitative detail the physical properties of colloidal membranes and present evidence that these are true equilibrium structures.

The hierarchical self-assembly of membrane structures in a simple rod/polymer mixture can be understood to originate from the anisotropic potential. Unlike spherical molecules, the depletion potential between anisotropic particles such as rods or disks is highly dependent on both their mutual orientation and their center-of-mass separation along the axial and radial directions. A pair of rods will minimize their interaction energy via lateral association, whereas disk-like molecules prefer face-on interactions. In a mixture of isotropic rods and depleting polymers, the assembly of membranes proceeds in two distinct steps. In a first step, highly anisotropic interactions between rods lead to the formation of mesoscopic disk-like structures consisting of a single monolayer of aligned rods (Fig. 1A). Within minutes of sample preparation, essentially all isolated isotropic rods are incorporated into these intermediate structures. At this point, it is possible to approximate the behavior of the virus/polymer mixture with that of a suspension of mesoscopic self-assembled disks interacting with each other via depletion interactions that drive their self-assembly into higher-order structures. The assembly pathway of this subsequent slow step is highly dependent on the depletant concentration. At high polymer concentration, due to the orientational dependence of the depletion interaction, disks stack on top of one another to form smectic filaments (Fig. 1B). Based on purely energetic interactions, one would always expect to observe such a stacking transition as has been described by a theoretical model (12). However, with decreasing polymer concentration, we observe an unexpected transition to a regime where disks no longer stack on top of one another, but instead continue to coalesce laterally to form monolayer membranes, which can be hundreds of microns in diameter (Fig. 1C and Movie S1). Colloidal membranes remain stable over a period of months to years. Once membranes become sufficiently large, their diffusion slows down and thus also their coalescence. We believe that eventually the sample will consist of a single large membrane coexisting with polymer solution. However, this final state is rarely if ever observed in our samples. The diagram in Fig. 1D indicates regions of phase space in which the self-assembly of membranes and smectic filaments is observed. While the phase diagram was mapped over a wide range of parameters, we characterized in detail membranes assembled at initial fd concentrations of 17 mg/mL and Dextran concentrations anywhere between 45 mg/mL and 53 mg/ml. None of the measured membrane properties changed within this narrow polymer concentration range.

Fig. 1.

(A) DIC micrographs and schematics of disk-like structures composed of one-rod length thick monolayer of aligned fd rods. (B) At high dextran concentration, mesoscopic disks stack up on top of each other and form filaments with smectic structure. (C) At intermediate dextran concentration (within the lightly shaded region of phase pace), disks coalesce laterally and form large macroscopic monolayer membranes. DIC micrographs of a membrane viewed from (i) the side or edge-on and (ii) face-on. (D) Regions of phase space where bound membranes (darker shading) and unbound membranes (lighter shading) are observed. Highly monodisperse viruses are essential for reproducibility of this phase diagram. All scale bars are 2 μm.

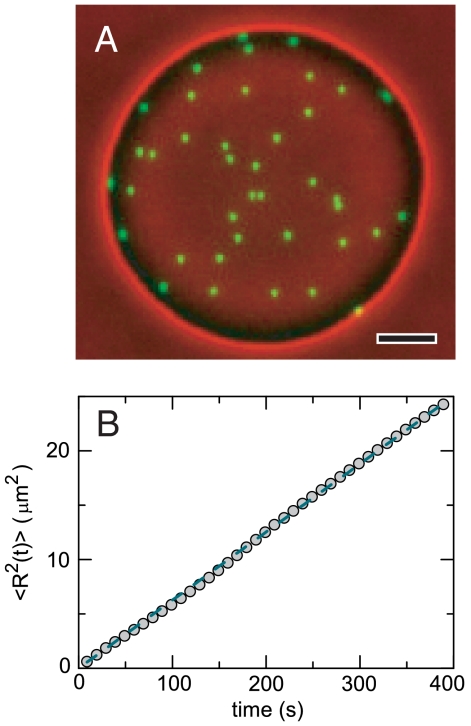
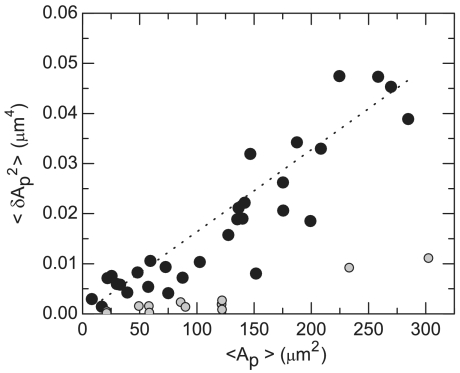
We first study the behavior of mature membranes observed in a face-on configuration. A composite phase contrast/fluorescence face-on image of a membrane is shown in Fig. 2A. Here, fluorescently labeled rods are viewed along their axial direction and appear as green isotropic spots. Such images provide a wealth of information about colloidal membranes. First, we observe that the exchange of individual rods between the surrounding polymer phase and colloidal membranes does not occur on experimental time scales, indicating a complete phase separation between a background polymer-rich phase and rod-rich membranes. Second, rapid lateral diffusion of individual viruses within a membrane is directly visualized (Movie S2). Using particle tracking, we measure the mean square displacements (MSD) of individual rods. MSD curves increase linearly with time (Fig. 2B), indicating an internal fluid-like structure. The measured diffusion coefficient (0.9 × 10^-2 μm²/s) is 2 orders of magnitude slower than diffusion in conventional bilayers (13) and 2 orders of magnitude larger when compared to the diffusion of an isolated rod in aqueous suspension, which is estimated from the expression 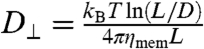, where η_mem is membrane viscosity. Assuming that long-time diffusion is related to membrane viscosity, this would indicate that η_mem ≈ 0.1 Pa s. Third, by counting the number of fluorescently labeled rods, measuring the total membrane area, and knowing the exact ratio of labeled to unlabeled rods, the virus concentration within various membranes is directly measured. Averaging measurements over 30 different membranes yields a density of 96 ± 8 mg/mL or approximately 3,200 particles/μm². Within measurement error, the density of membranes does not change as the polymer concentration varies between 45 mg/mL and 53 mg/mL. Finally, we also observe that the membrane area, A, extracted from a sequence of phase images (Movie S3) fluctuates around a mean value, 〈A〉. By measuring how area fluctuations scale with membrane size (Fig. 3), we estimate that the membrane compressibility is κ_A = 4,500 ± 2,500 k_BT/μm². In comparison, the compressibility of lipid bilayers is on the order of 10⁷ k_BT/μm² (14).

Fig. 2.

(A) A composite phase contrast/fluorescence face-on image of a membrane where approximately 1 out of 30,000 rods are fluorescently labeled. Florescence (green channel) and phase contrast images (red channel) were taken simultaneously and subsequently overlayed (Movie S2). (B) Mean square displacements of individual fluorescently labeled rods increase linearly over long time scales, demonstrating that the internal structure of the membranes is fluid-like. The diffusion coefficient is 0.9 × 10^-2 μm²/s. Scale bar is 5 μm.

Fig. 3.

The membrane area, A, extracted from a sequence of images is observed to fluctuate around a mean value, 〈A〉, and the fluctuations around the average membrane area scale linearly with the overall membrane size (Movie S3). The membrane compressibility κ_A is extracted using the following relation: 〈(A - 〈A〉)²〉 = k_BT〈A〉/κ_A, where A and 〈A〉 are, respectively, the instantaneous and average projected membrane area. The data for dried membranes where all fluctuations are due to imaging noise are shown (○). This measurement allows us to estimate the contributions of noise to our data. The membrane’s compressibility is determined to be 4,500 ± 2,500k_BT/μm².

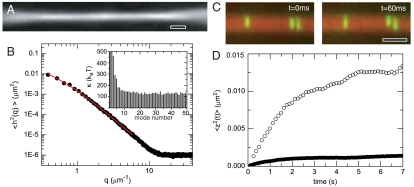
Next, we examine colloidal membranes viewed in edge-on configurations (Fig. 4A), which exhibit significant thermally excited undulations (Movie S4). These undulations are analyzed in order to extract the membranes’ bending rigidity. Instantaneous membrane conformations of the entire 2D surface are described by a height function h(x,y). We note that edge-on images reveal only a 1D cut, h(x) = h(x,y = const), of the 2D surface. To analyze these fluctuations, a sequence of uncorrelated images is taken at the approximate midplane to minimize edge effects. Subsequently, the data are decomposed into a Fourier series, 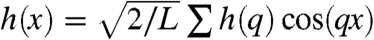, where q = nπ/L and L is the length of the analyzed membrane segment. The variance of the Fourier coefficients, 〈δh²(q)〉, is plotted as a function of wavelength q in Fig. 4B. This fluctuation spectrum is analyzed by the same curvature free energy used to describe lipid bilayers (15). The prediction for the fluctuation spectrum of a 1D-membrane cut is given by

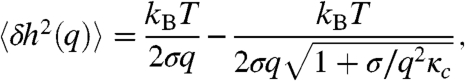[1]

where κ_c is the bending modulus and σ is the effective lateral tension (16). Good agreement between theoretical prediction and experiment demonstrates that curvature elasticity governs the long-wavelength fluctuations of the monolayer membranes (Fig. 4B) and yields the value of the bending moduli κ_c. Averaging over 50 membranes, we obtain the bending modulus κ_c = 150 ± 20 k_BT. In comparison, the moduli of conventional lipid bilayers are only a few k_BT (4). Furthermore, the measurement of κ_c in combination with the previously described measurement of κ_A allows us to test a relation that predicts that the bending modulus κ_c of a thin elastic sheet (membrane) is related to its area compressibility κ_A as follows: 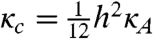, where h is the effective sheet thickness (17). Using values of κ_A = 4,500 k_BT/μm² and κ_c = 150 k_BT, we obtain the effective membrane thickness of 632 nm, which is in reasonable agreement with the expected membrane thickness of one rod length (880 nm). It is expected that protrusion fluctuations (discussed below) will reduce the effective thickness of the membranes. In principle, from the fits of Eq. 1, we should be able to extract the value of the effective lateral tension in addition to the bending modulus. However, lateral tension measurements obtained in this way varied by more then an order of magnitude (10 k_BT/μm² to 500 k_BT/μm²). A likely reason for this is that membranes in edge-on configurations are frequently attached to the glass surface or other membranes via defects. These attachments greatly influence measurements of the effective lateral tension by primarily affecting the large wavelength fluctuations of membranes. It is also of interest to compare the properties of colloidal membranes to single layers in a bulk smectic phase. For example, the dynamics of rods in these two structures is very different (18), and the concentration of the rods in the colloidal membranes is significantly smaller than the concentration of rods in a smectic layer formed at comparable ionic strength (19). In addition, light scattering experiments on the bulk smectic phase also indicate a very large bending rigidity in agreement with our real space analysis of isolated membranes (19).

Fig. 4.

(A) Polarization micrograph of a membrane viewed from the side or edge-on. (B) Fluctuation spectrum is obtained by performing a Fourier analysis of a sequence of uncorrelated membrane conformations (Movie S4). The spectrum saturates in the high q limit due to imaging noise. The red line is the best fit to Eq. 1, which yields a bending modulus of 135k_BT. (Inset) Bending moduli measured from individual Fourier modes. (C) Composite polarization/flourescence images show individual rods protruding into the surrounding polymer suspension (Movie S5). The height of the protrusion fluctuation is defined as the difference between the position of an individual fluorescently labeled virus and the continuum lengthscale conformation of the same membrane obtained from a simultaneously acquired DIC or polarization image. (D) Mean square displacements of the individual rods undergoing protrusion fluctuations are shown for particles in both isolated membranes (○) and stacked membranes (•). Clearly, particle protrusions in membrane stacks are suppressed. All scale bars are 2 μm.

Finally, we study the fluctuations of individual rods within a membrane observed in an edge-on configuration. Using multimode microscopy, we simultaneously obtain a continuum conformation of a membrane and positions of individual fluorescently labeled rods within the membrane (Fig. 4C and Movie S5). We quantify the amount by which a single rod protrudes into the surrounding depletant solution by measuring the displacement of individual rods with respect to the midplane of the membrane’s surface, which is determined from simultaneously acquired polarization images. MSDs measured along the protrusion direction increase at short time scales and reach a plateau at long time scales, indicating confinement of rods within a membrane. We find that protrusion fluctuations are significant in isolated membranes, and the transition from isolated disks to stacks of disks is accompanied by a significant suppression of these fluctuations (Fig. 4D).

Theoretical Model

Motivated by our characterization of protrusion fluctuations and drawing on an analogy with lipid bilayers, we propose an entropic mechanism that explains the stability of colloidal membranes and indicates that these are true equilibrium structures. In lipid bilayers, individual molecules protrude from the membrane and roughen its surface on molecular as well as continuum lengthscales (20, 21). As two bilayers approach each other, protrusion fluctuations become sterically hindered resulting in strong repulsive interactions of entropic origin (20). In analogy with lipid bilayers, we expect repulsive interactions between two colloidal membranes at short separation. As shown above, protrusion interactions in colloidal membranes can be directly visualized and quantified (Fig. 4C). In order for protrusions to take place in this system, a rod has to displace the surrounding depleting agent. Therefore, the average magnitude of the protrusion is determined by the depletant concentration, with higher depletant concentrations suppressing protrusion fluctuations and resulting in smoother membrane surfaces. While in a bilayer system protrusion interactions dominate at separations of about 1 Å, the range of these interactions in colloidal membranes will be on the scale of tens of nanometers. This is comparable to the range of the attractive depletion potential, whose upper bound is set by the size of the depleting polymer.

Based on the above arguments we develop a highly simplified model that captures the essential physics required to describe the unbinding of two mesoscopic membranes (disks). The model involves competition between attractive depletion forces that favor stacks of membranes and repulsive protrusion forces that favor unbound membranes. The attractive depletion potential between two parallel plates (membranes) is given by the following expression:

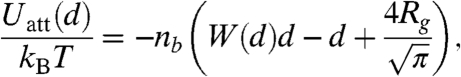[2]

where W(d) is defined as

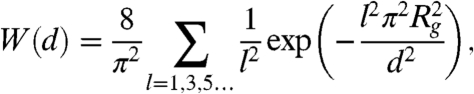[3]

where n_b is the depletant bulk number density, d is the distance between the membranes, and R_g is the depletant radius of gyration (6). The repulsive potential between two surfaces is modeled according to Israelachvili and Wennerstrom (20). The probability of an individual rod protruding some distance z is proportional to e^-α_pz/k_BT, where α_pz = ΠV_ex. Here, Π is the osmotic pressure of the surrounding polymer suspension, and V_ex is the excluded volume inaccessible to the polymer that occurs due to a protrusion. This excluded volume is taken as π(R_ps + D/2)²z, where 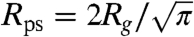, and D is the diameter of the rod. A simple expression for the protrusion repulsion can be written as

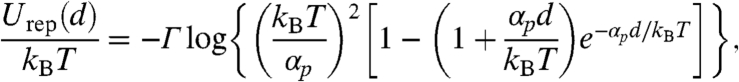[4]

where Γ is the number of protruding molecules per unit area (an areal density), and d is the separation between two membranes. On the one hand, the upper bound on the range of the attractive depletion potential, U_att, is set by the polymer radius of gyration, R_g as described by the Asakura-Oosawa depletion potential (6). If the polymer concentration is in the semidilute regime, the range of interactions is going to be smaller. On the other hand, the range of the repulsive protrusion potential, U_rep, is highly sensitive to the polymer concentration. Lower polymer concentration leads to larger protrusions that result in longer-ranged repulsive forces.

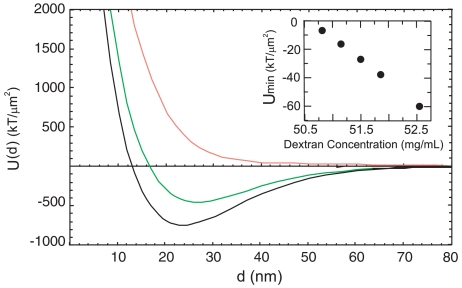
The effective interaction potential between two membranes is shown in Fig. 5. At high polymer concentration, protrusion fluctuations are suppressed and there is a strong attractive interaction as evidenced by a local minima in free energy. In this regime, we predict the formation of smectic filaments (Fig. 1B). At lower polymer concentration, longer-ranged repulsive protrusion interactions dominate the depletion attraction, and the minima in free energy disappears. This is the regime where colloidal membranes are stable. Our observation of dramatically enhanced protrusion fluctuations accompanying the unbinding of membranes supports the proposed entropic mechanism for the stability of nonamphiphilic membranes. Experimentally, the transition to isolated membranes occurs at ∼55 mg/mL, which is close to the theoretical prediction of 50.5 mg/mL, considering that there are no adjustable parameters in our theoretical model. While we believe that the proposed theoretical model captures the essential physics, its quantitative predictions should be treated with some caution. A number of effects are not accounted for by our model, including the renormalization of protrusion fluctuations by collective modes (22), additional repulsive interactions arising due to continuum modes described by the Helfrich mechanism (15), and failure of the penetrable sphere model to accurately describe various aspects of the depletion interaction such as the transition of the depleting polymer to semidilute regime, branching of Dextran polymer, and other effects described elsewhere (23). In all likelihood, these effects will shift the exact location of the transition of membrane to smectic filaments and might cancel each other out, thus seemingly making the agreement between theory and experiment better.

Fig. 5.

The effective interaction potential, U(d) = U_att(d) + U_rep(d), between two membranes is plotted for polymer concentrations of 44, 54, and 58 mg/mL, shown respectively in red, green, and black. (Inset) The value of the interaction free energy at its minimum (in units of k_BT/μm²). At 50.5 mg/mL, the minima shifts to positive values and the membrane stacks become metastable with respect to isolated colloidal membranes. At 49.5 mg/mL stacks become unstable.

Discussion

In this paper, we demonstrate the existence of 2D fluid-like surfaces or membranes in a simple mixture of hard rods and nonadsorbing polymers with properties that are comparable to those of lipid bilayers. The formation of these structures critically depends on the depletant concentration. At high depletant concentrations, attractive rods initially aggregate laterally to form one-rod length thick smectic disks (Fig. 1A). Once these self-assembled mesoscopic disks reach a critical diameter, attractive interactions begin to favor face-on stacking interactions over lateral association (Fig. 1B). Unexpectedly, for weaker attractive interactions we find a very different assembly pathway. In this regime, stacking of disks is suppressed, and instead mesoscopic disks continue to aggregate laterally and form macroscopic 2D colloidal membranes. The transition between these two regimes is controlled by the surface roughness of the membranes, which is dependent on the magnitude of protrusion fluctuations. These fluctuations are in turn determined by the depletant concentration. Disks with smooth surfaces at high depletant concentration experience strong attractive interactions leading to a stacking transition. In contrast, disks at lower depletant concentration are roughened by protrusion fluctuations and thus experience repulsive face-on interactions because no free volume is gained as two rough surfaces approach each other. Similar phenomena have been demonstrated for disk-like colloids that have been synthesized with different degrees of surface roughness (24). The difference between these two cases is that colloidal membranes are roughened by entropic fluctuations so that bringing together two mesoscopic disk assemblages not only reduces the excluded volume overlap, but also costs entropy associated with protrusion degrees of freedom of the intermediate disk-like structures.

These results carry important implications for several lines of inquiry in the fields of physics, chemistry, and material science. First, a number of previous studies have shown that polydisperse filaments in the presence of attractive interactions assemble into filament bundles (25). Our experiments demonstrate that polydispersity of rods used in these studies hides a more complex behavior found in a system of monodisperse rods. This indicates a need to extend theoretical models of rod bundling to account for the possible formation of 2D membranes. Second, hierarchical self-assembly has already been studied for colloidal disk-like particles in the presence of attractive interactions (26). It has been shown that in a first step attractive disks aggregate face-on, forming mesoscopic 1D rod-like structures. Subsequently, in the second step these self-assembled columns associate laterally to form bulk 3D columnar structures. The difference between a hierarchical assembly of rods and disks is that in the former case, the entropy associated with protrusion fluctuations suppresses the second association step and leads to equilibrium formation of 2D membranes. In contrast, no mechanism has been found that would stabilize mesoscopic 1D stacks of disks. Third, there have been a few previous reports indicating assembly of membrane-like structures in rod-like suspensions. The first report of depletion-driven membrane-like structures was published in ref. 27. However, this work did not study the properties of colloidal membranes, nor did it address the questions whether colloidal membranes are equilibrium or transient structures. Recently these ideas were also shown to be applicable to a suspension of nanorods (28). Another report has demonstrated that β-FeOOH rods condense into structures reminiscent of colloidal membranes (29); however, in this case the condensation is driven by van der Waals forces. Our present work offers an explanation for the stability of these structures. Furthermore, colloidal membranes might also be relevant to structures of nanorods that are obtained via nonequilibrium convective assembly (drying) methods and are similar to colloidal membranes (30, 31). It is plausible that the mechanism outlined in this paper contributes to the stability of these nanorod structures. However, great caution is required when interpreting nonequilibrium samples with equilibrium theoretical models. Finally, in addition to the experimental work described above, recent computer simulations have examined the phase separation kinetics of a rod/polymer mixture at isotropic-crystalline coexistence (32). Interestingly, the authors find metastable monolayer structures, but no evidence of thermodynamically stable membranes. A possible reason is that simulations investigated behavior of the rods with L/D ≈ 5, whereas our experiments use rods with L/D ≈ 100. The stability of colloidal membranes should be very sensitive to the length of the rods. If the rod length is increased by a factor of 2, the strength of the attractive (depletion) interaction per unit length necessary for condensation of rods is decreased by the same amount. However, this decrease of depletant concentration also results in an enhancement of protrusion fluctuations (membrane roughness). Thus, increasing rod length increases the region of phase space where colloidal membranes are stable, and we expect that there is a lower rod aspect ratio beyond which no stable membranes are observed.

Conclusions

The self-assembly of membranes is a ubiquitous process in nature whose importance spans disparate scientific fields and many technological applications. The paramount example of lipid bilayer assembly has inspired the synthesis of numerous amphiphilic building blocks for studies of membrane self-assembly including various block-copolymers, heterogeneous nanorods, and hybrid protein-polymer complexes (33–35). In all of these systems, covalent cross-linking between chemically heterogeneous parts of the molecules, such as a hydrophobic chain and hydrophilic head, introduce a molecular frustration that acts to suppress macroscopic phase separation and instead drives the formation of microphase separated structures such as membranes. In contrast to the extensive work on amphiphilic self-assembly, the possibility of membrane formation from nonamphiphilic components remains relatively unexplored (29, 36, 37).

In the present paper, we have demonstrated the existence of nonamphiphilic membranes in a model rod/polymer mixture and have shown that their physical behavior is comparable to that of conventional amphiphilic membranes. The importance of these results lies in their potential to establish a fundamentally different route toward solution based on self-assembly of 2D materials: One that does not rely on the well-established paradigm of amphiphilic self-assembly. Because the only requirements for this self-assembly to take place are uniform rod-like particles and attractive interactions, this method is universal and applicable to a wide range of rod-like systems. We believe this will have an especially large impact on the field of nanotechnology, where nanorods have emerged as an important building blocks of nanostructured materials (38, 39). An example of practical importance is the assembly of an aligned array of semiconducting nanorods, a nanorod membrane, which holds great promise for inexpensive collection of solar energy (40). Colloidal membranes present a promising pathway for the assembly of such devices. Without much effort, we are able to obtain monodomain monolayer membranes that are aligned over centimeter distances (41). Simultaneously, our work also extends research on the phase behavior of hard particle fluids in unexpected directions. Systems with hard-core interactions have played an essential role for our understanding of liquid and solid matter (42). We present a widely applicable mechanism based on protrusion fluctuations, which guides the assembly of hard rods into entropically stabilized membranes. These structures reinforce the general notion that through a careful choice of particle shapes, sizes, and concentrations it is possible to “engineer entropy” (5) in order to build structures of ever-increasing complexity.