Abstract
This article offers reflections on the development of the Rubin Causal Model (RCM) that were stimulated by the impressive discussions of the RCM and Don Campbell's superb contributions to the practical problems of drawing causal inferences written by Will Shadish and by Steve West and Felix Thoemmes. It is not a rejoinder in any real sense, but more of a sequence of clarifications of parts of the RCM combined with some possibly interesting personal historical comments, which I do not think can be found elsewhere. Of particular interest in the technical content, I think, are the extended discussions of SUTVA, the explication of the variety of definitions of causal estimands, and the discussion of the assignment mechanism.
Keywords: Assignment mechanism, Campbell's causal contributions, Potential outcomes, Rubin Causal Model, SUTVA
I thank the editor, Scott Maxwell, for the opportunity to discuss these very thoughtful, well-written and scholarly articles (Shadish – S, and West and Thoemmes – WT) comparing Don Campbell's perspective on causal inference and my framework, sometimes referred to as the Rubin Causal Model (RCM – Holland 1986) for a sequence of papers written in the 1970's (Rubin, 1974, 1975, 1976, 1977, 1978, 1979, 1980). I agree with essentially all of the points made by S and WT. But, to go point by point would make for very dull and laborious writing and reading – I tried! I have written, edited, and discarded many versions of this discussion before settling on the current version, which also benefits from careful readings and helpful comments from S, WT, the editor, and an anonymous reviewer.
This version includes some more personal comments and some previously unwritten history that I hope will interest readers. As suggested by my title, this document consists of reflections and clarifications stimulated by the S and WT comments, rather than a direct discussion of their contributions. I begin with some general brief comments on the compatibility of Campbell's and my perspectives on causal inference. Second, I offer some historical comments regarding my introduction to Campbell himself and my earlier introduction to his work via my PhD advisor at Harvard University, the renowned statistician, William (Bill) G. Cochran. Third, I give a cursory summary of the early evolution of the RCM's use of potential outcomes, and I give a further explication of SUTVA (the Stable Unit-Treatment Value Assumption) and describe how it drives the distinction between causal and descriptive statements; more discussion of SUTVA is desired, as S and WT suggest, and I provide that here. Fourth, I offer a description of the variety of definitions of causal effects allowed in the RCM, a point sometimes missed. Fifth, I offer some historical comments involving Cochran and Jerzy Neyman, and the non-use of potential outcomes to define causal effects outside of randomized experiments until Rubin (1974). Sixth, I summarize the definition of the assignment mechanism and indicate how it leads naturally to extensions of classical randomization-based methods of inference, including to propensity score methods (Rosenbaum and Rubin, 1983a). I then very briefly discuss model-based (Bayesian) posterior predictive causal inference as proposed in Rubin (1975, 1978). I conclude with some comments on how the discussions by S and WT have generated an even greater respect for Campbell's contributions to causal inference.
Complementary Perspectives
S and WT are far more capable than I am at summarizing Campbell's contributions, but I agree that Campbell's focus was on “threats to validity” and practical advice for avoiding or compensating for them through creative study designs. I believe that many of these threats can be summarized by the simple statement they lead to “nonignorable treatment assignment” (Rubin, 1978) or ignorable but still “confounded treatment assignment” mechanisms (Rubin, 1990a), both of which are formal mathematical concepts within the RCM, whose definitions are provided later in this commentary. S and WT are certainly correct that my focus was on finding the precise mathematical assumptions under which various designs and analyses led to valid estimation of causal effects, especially in the face of real world complications such as unplanned missing data or noncompliance with assigned treatment. By “valid estimation” I mean assertions having the statistical properties claimed for them, not necessarily unbiased point estimation in Neyman's technical sense (described here subsequently).
Of course, having precise mathematical concepts without accompanying advice about their real world propriety or advice for ways to make the mathematical assumptions more plausible is not all that helpful in practice, and this is exactly why Campbell's and my perspectives are, in broad generality, complementary not competitive. I tried to give advice in my technical academic papers in the 1970's, but it was impossible at that stage in my career to have as much wisdom as the much more experienced Campbell (I hope, and think, that I've done much better in this regard in my real-world consulting work and more recently in my publications). The advantage of the mathematical formalism is that it is context-free, and so generalizes across all fields. But focusing only on the formalism has the undeniable limitation that it is essentially impossible to give sage and general context-free advice.
And S and WT are clearly correct in stating that Campbell provided far more advice on topics such as construct validity than I did – I was virtually silent on that topic in my earlier statistical publications, except to some extent through my discussions of SUTVA, as I briefly address later here, and in my more recent work on noncompliance (e.g., Angrist, Imbens and Rubin, 1996; Mealli and Rubin, 2002a) and, more generally, on problems related to principal stratification (Frangakis and Rubin, 2002). For example, my work on “Censoring Due To Death” is relevant to this issue, and discussed abstractly in Rubin (2006a) and in the job-training context in Zhang, Rubin, and Mealli (2008) in Zhang, Rubin, and Mealli (2009)). Even more relevant to education and psychology are Mealli and Rubin (2002b) and Jin and Rubin (2009). Some might even consider that my early willingness and eagerness to confront causal inference in observational studies, and to consider the associated sensitivity of inference to assumptions, as in Rubin (1973a, b) or Rosenbaum and Rubin (1983b), revealed a deep concern with aspects of construct validity, and a desire to provide guidance and advice for how to think about these assumptions.
My Introduction to Don Campbell
His Work
My memory of my first introduction to Don Campbell's work on causality was through Bill Cochran in the late 1960's. Bill not only referred to Campbell and Stanley (1966) in his class on observational studies, but he also seemed to know Campbell fairly well personally. He clearly greatly admired Campbell's common sense and his tremendous practical contributions. He did, however, alert me that when Campbell tried to do more “mathy” sorts of things, he could, at times, be off-target in Bill's view. Campbell (1988, e.g., page 20), in an autobiographical chapter, commented on his own mathematical limitations.
The Man Himself
I personally met Campbell only a few times, all after I was employed at The Educational Testing Services (ETS) in Princeton, New Jersey. We first met sometime around 1971 or 1972 when I was involved in an observational study of some educational intervention on which Campbell was an advisor; Cook (2008) and Campbell (1988) offer much more complete historical pictures of Campbell's work at this time than I can. Since my Ph.D. thesis was on matched sampling in observational studies under Cochran, I thought that I understood the general context fairly well, and so I was asked by ETS to visit Campbell at Northwestern University in Evanston, Illinois, which is, incidentally, where I grew up. I remember sitting in his office with, I believe, one or two current students or perhaps junior faculty. The topic of matching arose, and my memory is that Campbell referred to it as “sin itself” because of “regression to the mean issues” when matching on fallible test scores rather than “true” scores. I was flabbergasted! But I recently realized that I misunderstood the context for Campbell's comment, which is accurately expressed in Campbell and Erlebacher (1970).
Subsequently, I had repeated disagreements with a variety of people about the following point: If treatment assignments are based on a fallible test score, I argued, then matching on the fallible scores is the correct thing to do, not matching on the hypothetical true scores, even if we had them available for matching. At that time, not everyone seemed convinced, so I finally wrote what I thought was a quite obvious paper (Rubin, 1977) showing this formally. This article generalized previous more specific results of David Cox, Art Goldberger, and others cited in that article, which treated the regression discontinuity design (Thistlethwaite and Campbell, 1960) as a special case of “assignment to treatment group on the basis of a covariate”. Of course, the situation with an unobserved covariate used for treatment assignment is far more complex, and that situation, coupled with the naïve view that matching can fix all problems with non-randomized studies, appears to have been the context for Campbell's comment on matching.
Campbell and I met a couple more times at various advisory committees we both attended; all were cordial. My lasting impression of Don Campbell was that of a very smart and sharp intellectual, but also a true gentleman, with an intense interest in addressing real problems with wisdom – very much like Cochran himself, but with less technical/mathematical knowledge but more exposure to the intricate problems that arise when doing research on possible interventions with human subjects, especially in psychology and education, but also in medicine.
The Early Evolution of the RCM
My introduction to formal causal inference was Cochran's course at Harvard on Classical Experimental Design, Statistics 140, which I took in the Spring of 1969. This was an extremely fortunate occurrence for me in that I learned the importance of clear thinking about causal inference in the context of the design of randomized experiments, rather than in the generally confused context of regression models, or path analyses, or various pictures, which even then appeared to be the standard approaches to the analysis of nonrandomized/observational data for causal effects. In classical experimental design, there was a clear separation between the object of inference - which I now like to call “The Science”, and what we do to learn about the Science - randomly assign treatments to units.
Perhaps due to my physics background1, it seemed to me to make no sense to discuss statistical methods and estimators without first having a clear concept of what we are attempting to estimate, which, I agree with S, was a limitation of Campbell's framework. Nevertheless, Campbell is not alone when implicitly, rather than explicitly, defining what he was trying to estimate. A non-trivial amount of statistical discussion (confused and confusing to me) eschews the explicit definition of estimands; see, for example, Holland and Rubin (1983) on the previous literature concerning Lord's paradox; Rubin (1994) and the issue of “definitional bias” (Efron, 1994); and Rubin (2004, 2005) on direct and indirect causal effects. My attitude is that it is critical to define quantities carefully before trying to estimate them. A specific example of this attitude is the discussion by Mealli and Rubin (2003) of what we considered to be a confused description of “direct and indirect” causal effects attacked by regression models based on implausible underlying assumptions.
The Science
In the context of causal inference, the Science is a matrix where the rows represent N units, which are physical objects at a particular point in time (e.g., students today), and the columns represent covariates and potential outcomes. The units could be the same physical object at different points in time or different physical objects at the same point in time, or a mixture of both.
Consider the simple case with one covariate, X (e.g., pretest score), which cannot be affected by which of two treatments (e.g., a new educational program and a standard educational program) each unit receives, and one outcome Y (e.g., post-test score), which can be affected by which treatment each unit receives. Each row of the Science, indexed by i = 1,…,N, is written as (Xi, Yi(1), Yi(0)), where Xi is the covariate value for unit i, Yi(1) is the value of Y for unit i if unit i receives treatment 1 (the new treatment, indicated by Wi = 1), and Yi(0) is the value of Y for unit i if unit i receives treatment 0 (the standard or control treatment indicated by Wi = 0). In this simple case, the Science is the N × 3 matrix
| (1) |
where X, Y(1), and Y(0) are all N-component column vectors. The generalization to multicomponent X and Y, and to more than two treatments, is conceptually obvious.
SUTVA
This representation of the Science is adequate under the “Stable Unit Treatment Value Assumption” (SUTVA, Rubin, 1980): For a specific unit, say i, and the treatment that unit i receives, Wi, SUTVA asserts that the value of Yi(Wi) is stable (i.e., determined). SUTVA rules out hidden versions of treatments (i.e., there are no unrepresented treatments) as well as interference between units (i.e., unit i's value of Yi(Wi) cannot be affected by the treatments the other units receive). Both aspects of SUTVA deserve some more commentary.
In the interest of clarity, I'll use an example that I've used since 1974. Consider a study of the effectiveness of aspirin versus placebo on the intensity of headache pain in two hours. With only one unit, say ME, if there is only one aspirin tablet and only one placebo tablet available, then there are no hidden versions of treatments. If there are two aspirin tablets available for me, and one is strong and the other weak, and the science represents only two treatments, aspirin and placebo, then there is a hidden treatment: Y(aspirin) is not stable because it will depend on which aspirin tablet is chosen. If I specified that I randomly chose one of the two aspirin tablets, then the value is stable, although it then has a probability distribution. But if I do not specify how I select the aspirin tablet, SUTVA is generally violated unless the Science is represented by three treatments. The “generally” is there in the previous sentence because if Y simply were an indicator for some reduction in headache pain, then arguably both the weak and strong aspirin tablets would result in some reduction, thereby allowing SUTVA to be satisfied.
The no interference aspect of SUTVA is more obvious in that it simply states that, in this example of a study of aspirin tablets, my potential outcomes cannot be affected by which tablets the other units receive. Moreover, SUTVA only need hold for the values of W = (W1, …, WN)T being contemplated in the real or hypothetical study. For example, perhaps only 5% of the units will be assigned to the new treatment, a special on-site job-training program, and the rest will be assigned to a control program consisting only of at-home reading materials; this might be done to avoid the interference between units that could occur from flooding local markets with better trained individuals. Then, in this example, SUTVA need hold only for vectors W such that .2
The definition of SUTVA forces the distinction between causal statements and descriptive statements, as I argued in Rubin (1986), which expanded on the same argument in Rubin (1975, p. 234). For example, is the statement “She did well on that literature test because she is a girl” causal or merely descriptive? If W = 0 means that this unit remains a girl and W = 1 means that this unit is “converted” to a boy, the factual Y(0) is well defined and observed, but the counterfactual Y(1) appears to be hopelessly ill-defined and, therefore, unstable. Does the hypothetical “converted to a boy” mean an at birth sex-change operation, or does it mean massive hormone injections at puberty, or does it mean cross-dressing from two years of age, etc.? Only if all such contemplated hypothetical interventions can be argued to have the same hypothetical Y(1), will the “no hidden versions of treatments” requirement of SUTVA be appropriate for this unit. If not, either each possible intervention for effecting a female to male conversion must be explicated and represented by a different W with a corresponding different Y(W) to avoid hidden versions of treatments, and a consequential violation of SUTVA, or the specific hypothetical intervention to convert her to a boy must be described with enough detail to convince us that Y(1) would be stable. Notice that SUTVA could hold for some outcome variables but not for others, as mentioned earlier in the context of the aspirin example.
An example of a legitimate causal statement involving an immutable characteristic, such as gender or race, occurs when the unit is a resume of a job applicant sent to a prospective employer, and the treatments are the names attached to the resume, either an obviously Anglo-Saxon name (W = 0), or an obviously African-American name (W = 1), where Y is an indicator of an invitation to apply for the job after receipt of the resume (Bertrand and Mullainathan, 2004).
Definitions of Unit-level Causal Effects and Population-level Causal Effects
The causal effect of treatment 1 versus treatment 0 for the ith unit is a comparison of the corresponding potential outcomes for that unit: Yi(1) versus Yi(0) (e.g., their difference or their ratio). The “fundamental problem facing inference for causal effects” (Rubin, 1978) is that only one of the potential outcomes can ever be observed for each unit, the one corresponding to the actual assignment, and so unit-level causal effects must be inferred and can never be exactly known. After the assignment of treatments, only one of a unit's potential outcomes can be observed – the rest are missing.
However, this missingness in the potential outcomes does not mean that unit-level causal effects cannot be validly estimated unless assumed constant, as sometimes is asserted. Unit-level causal effects can be predicted, although in general not perfectly, with the help of covariates, as developed in Rubin (1978) from the Bayesian perspective, and very briefly discussed here toward the end, and can, in randomized experiments, be unbiasedly estimated from Neyman's (1923) perspective, briefly discussed shortly, if we include the random sampling of the unit (for which an unbiased estimate is desired), from all those units with the same value of X, as part of the expectation operator for calculating bias. Of course, estimation of unit-level causal effects from either the Bayesian or Neymanian perspective will generally be imprecise relative to the estimation of population or subpopulation causal effects because predictions of summaries are usually more precise than individual predictions.
Population or subpopulation causal effects are comparisons of the potential outcomes under treatment 1 versus treatment 0 on a common set of units. To illustrate a population-level causal effect, the average causal effect of W = 1 versus of W = 0 is the average value of Yi(1) minus the average value of Yi(0) across all N units. To illustrate a subpopulation-level causal effect, the median unit-level causal effect of W = 1 versus W = 0 on Y for units who are female, as indicated by Xi, is the median value of Yi(1) - Yi(0) across all females. Both of these “typical” causal effects are summaries of unit-level causal effects.
Some causal effects, however, are not summaries of unit-level causal effects, although they still must be defined by comparisons of the ordered sets of Yi(1) values and Yi(0) values on a common set of units. For example, the causal effect of W = 1 versus W = 0 for the median Y for units with Yi(1) > Yi(0) is the median value of Yi(1) for the set of units with Yi(1) > Yi(0) minus the median Yi(0) for the set of units with Yi(1) > Yi(0). This example involves the idea of principal stratification (Frangakis and Rubin, 2002) because it uses the potential outcomes themselves to define a stratum of units where the causal effect is desired; principal stratification is a substantial generalization of the idea underlying instrumental variables, as discussed, for example, in Angrist, Imbens, and Rubin (1996).
Although average causal effects are common estimands in much of social science, in some fields, it is also common that the causal estimands are not summaries of individual unit-level causal effects, for instance, in epidemiology. For example, the units are people in a specific region of a country, where Wi = 1 indicates that unit i is vaccinated for influenza and Wi = 0 indicates that unit i is not vaccinated. The binary outcome Yi indicates whether or not unit i got influenza within one month after the choice to vaccinate or not. The “risk ratio” in the entire population of not vaccinating everyone to vaccinating everyone is the disease rate under Wi = 0 divided by disease rate under Wi = 1:
| (2) |
In this example, SUTVA must be carefully considered; if every unit gets vaccinated except unit 1, its chance for getting flu may be lower than if no unit got vaccinated.
Some causal estimands even involve the treatment assignment indicator. For example, in some settings, especially common when creating matched samples (e.g., Rubin, 2006b), we may want to estimate the effect of treatment versus control on those units who received treatment. Two prominent examples come to mind. The first involves the effect on earnings of serving in the military when drafted following a lottery, and the attendant issue of whether society should compensate those who served for possible lost wages (Angrist, 1990). The second example involves the effect on health care costs of smoking cigarettes for those who chose to smoke because of misconduct of the tobacco industry (Rubin, 2000).
The reason for providing these different examples of definitions of causal effects is to emphasize that there is no reason to focus solely on the average causal effect, although this quantity is especially easy to estimate unbiasedly using standard statistical tools in randomized experiments under simple assumptions. This generality of possible causal estimands was always present in the RCM Framework, as stated in Rubin (1974, p. 690). Also, there is no need to assume anything about the constancy of unit-level causal effects, although, once again, this assumption simplifies estimation.
Neyman (1923), Cochran (1965), and Neyman a Half-Century Later
The potential outcome notation, originally due to Neyman in 1923 (see Neyman, 1990, the introduction to that article by Speed, 1990, and the discussion by Rubin, 1990b), in the context of randomized experiments and randomization-based inference, was extremely important and clarifying, and it dominated formal statistical discussions in the context of randomized experiments (for example, see the classic text by Kempthorne 1952, and the earlier and later references cited in Rubin, 1990b).
Although I learned about that notation in Cochran's Statistics 140 (not knowing about the then recondite source, Neyman, 1923), that notation was entirely limited to inference about average causal effects in randomized experiments; for example, Cochran's course on observational studies never mentioned it, and instead used the “observed outcomes” notation described just below. I know of no reference that used the potential outcomes notation in discussions of causal inference outside this restricted context until I did so in Rubin (1974). Even in 1970, I found the lack of use of this marvelous notation in non-randomized studies most surprising.
Everyone, including my statistical heroes, such as Cochran, could simultaneously use the potential outcomes notation when discussing randomized experiments and the inadequate “observed outcomes” notation when discussing causal inference in non-randomized studies. The observed outcome notation replaces Yi(1) and Yi(0) with the observed value,
| (3) |
where Yobs = (Yobs,1, …, Yobs,N)T; for completeness, let Ymis = (Ymis,1, …, Ymis,N)T, where Ymis,i = WiYi(0) + (1 − Wi)Yi(1). This notation entangles the Science (Yi(1), Yi(0)) and what we do to learn about the Science (the Wi). Using this notation, it even becomes impossible to state formally the major benefit of randomization, as we see later. For a specific example, Cochran's (1965) paper on observational studies, read at the Royal Statistical Society, used this observed-outcome notation, as did (I believe) all the papers that he cited (e.g., written by famous authors, such as Doll, Dorn, Hill, etc.), with Wi used as an indicator (in regressions) for treatment received.
I vaguely remember asking Cochran about this use of the observed outcome notation when we were writing Cochran and Rubin (1973) in 1971, and his reply was to the effect that everyone “did” observational studies that way, and he never thought of trying to use the potential outcomes notation in a non-randomized study. In fact, the last section of Cochran (1965) is entitled “The Step from Association to Causation”, and it is very “Campbellesque” – full of sage advice, but all words. Associations were all that could really be formally estimated in a nonrandomized study, so the advice was to examine associations among observed variables, and make informed, wise assessments concerning which of the observed associations might reflect a causal mechanism.
Furthermore, when I was visiting the Department of Statistics at Berkeley in the mid-1970's, where Neyman was Professor Emeritus, I asked him why no one ever used the potential outcomes notation from randomized experiments to define causal effects more generally, noting that my article, Rubin (1974), was (by my reading) the first to do so. I did not know then that Neyman invented the notation, and I did not find that out until 1989, when I was asked to write a discussion (Rubin, 1990b) of the previously unpublished, at least in English, Neyman (1923). Nevertheless, in Rubin (1990a – written in 1987, I believe) I attributed the use of his mode of inference in randomized experiments using that notation to Neyman (1934), which concerned the analogous unbiased estimation and repeated sampling inference in sample surveys3. Somewhat remarkably in hindsight, at this meeting in the mid 1970's, Neyman never mentioned that he invented the notation, and his reply to my question about why it was not used outside experiments was to the effect that defining causal effects in non-randomized settings was too speculative, and in such settings, statisticians should stick with statements concerning descriptions and associations. Neyman is even quoted in his biography by Reid (1982; page 45) as saying “…without randomization an experiment has little value irrespective of the subsequent treatment.” Cochran was a bit more lenient toward the use of observational studies to try to infer causality, as he admitted it to me, saying something like, “That's why the consumers of statistics, such as doctors, ask us to analyze their observational data”.
The Assignment Mechanism
In contrast to Neyman's “conservative” attitude towards causal inference outside randomized experiments, an attitude that was totally dominant in the field of statistics at the time, as was Berkeley's version of mathematical statistics, I saw randomization as just one way to create missing and observed data in the potential outcomes. There are many other “processes for creating missing data”, as I called them in Rubin (1976), that could be used, which were called “assignment mechanisms” in Rubin (1978) in the context of causal inference.
Definition of the Assignment Mechanism
The assignment mechanism gives the probability of each vector of assignments, W, given the Science:
| (4) |
Before Rubin (1975), there were written descriptions of assignment mechanisms, such as (obviously) randomized ones, and nonrandomized ones (e.g., Roy, 1951), but to the best of my knowledge, there was no formal mathematical statement or notation showing the possible dependence of treatment assignments on the potential outcomes.
I regard the formal statement of the assignment mechanism as an important contribution, and not at all obvious except from a formal “missing data perspective”. It states that probability of something that we “do now”, that is, select the treatment assignment vector, W, can depend, not only on things that we observe now, X, and Yobs in a sequential experiment, but moreover on other things that will never even be realized, Ymis. Yet as a formal probability statement, it is mathematically coherent, and I believe is the key to clear conceptual understanding of the benefit of randomization.
The crucial bridge to understanding the assignment mechanism's possible dependence on values of the potential outcomes is to think of unobserved – to the analyst of the data – covariates U that are associated with the future potential outcomes and are used by the assigner of treatments, hypothetical or real, in addition to X. Thus, the assigner of treatments uses X and U to make decisions in some possibly stochastic way, but given X and U, the assigner does not use Y(1) or Y(0), so that
| (5) |
But when this expression is averaged over the values of U for fixed values of X, Y(1), Y(0) to calculate the assignment mechanism, the result yields dependence on Y(1), Y(0). For example, suppose Wi = 0 indicates a standard educational treatment and Wi = 1 indicates a new educational treatment, and U is the teacher's assessment of the students' future performances under the standard treatment, and U is used in addition to X (=observed test scores) to assign students to the new versus standard treatment. Then, depending on the accuracy of the teacher's assessments, U is very predictive of Y(0), and the assignment mechanism then depends on X and Y(0).
The assignment mechanism is unconfounded (with the potential outcomes, Rubin, 1990a) if:
| (6) |
that is, if treatment assignments are (stochastically) determined by observed covariates. An unconfounded assignment mechanism is probabilistic if all the unit-level probabilities, the propensity scores (Rosenbaum and Rubin, 1983),
| (7) |
are between 0 and 1,
| (8) |
so that all units have a chance of receiving each of the treatments.
An unconfounded probabilistic assignment mechanism is called strongly ignorable in Rosenbaum and Rubin (1983), a stronger version of an ignorable assignment mechanism (Rubin, 1978), defined by
| (9) |
which is especially important for Bayesian inference, because everything on the right side of the equal sign is observed (ignoring issues such as sampling units from a population and unintended missing data). Ignorable but confounded assignment mechanisms arise in sequential experiments, for example, when the apparently more successful treatment, based on results from earlier units, is assigned with higher probability to future units.
Classical randomized experiments are special cases of strongly ignorable assignment mechanisms (similar to regular designs in Imbens and Rubin, 2010), that often have symmetries and multiple treatments, such as a 2 × 2 factorial with the same number of units in each of the four treatment conditions. To return to an earlier point, we cannot even formally state the unconfoundedness benefit of randomized experiments using the observed outcome notation. If we try to do so using Yobs = (Yobs,1,…, Yobs,N)T, and write
| (10) |
we are asserting that the new versus control treatment does not affect Y, that is, Yi(1) = Yi(0) for all i. To repeat: Using the observed outcome notation entangles the Science (Yi(1), Yi(0), Xi) and the assignments (Wi) – bad! Yet the reduction to the observed outcome notation is exactly what regression approaches, path analyses, directed acyclic graphs (DAGs), etc. essentially compel us to do. For an example of the confusion that regression approaches create, see Holland and Rubin (1983) on Lord's paradox or the discussion by Mealli and Rubin (2003) on the effects of wealth on health and vice-versa. For an example of the bad practical advice that the DAG approaches can stimulate, see Rubin's (2009) response to letters in Statistics in Medicine.
Distinguish Between the Science and the Assignment Mechanism
Using the potential outcomes notation in the RCM maintains the critical distinction between what we are trying to estimate, the Science, and what we do to learn about it, the assignment mechanism, whether the latter is actually randomized, or hypothetically randomized, or self-selection, etc. It is no surprise that magnificent statisticians who eschewed the potential outcomes notation in observational studies, or even in randomized experiments, got wrong answers in relatively complicated situations – even the great R. A. Fisher was not immune when discussing direct and indirect effects in randomized experiments (Rubin, 2005)!
Because this distinction (between the Science and the assignment mechanism) is maintained in the RCM, extensions of classical methods of inference in classical randomized experiments, due to Fisher (1925) and Neyman (1923), are natural within the RCM framework. These methods, and the extensions beyond classical randomized experiments, are now briefly discussed. The text by Imbens and Rubin (2010) has several chapters on such extensions.
Causal Inference Based Solely on the Assignment Mechanism
Both Fisher and Neyman proposed methods of causal inference based solely on the randomization distribution of statistics induced by a classical randomized assignment mechanism. And both of these could be extended to strongly ignorable, or even to some nonignorable, assignment mechanisms in what I regard as fairly natural ways.
Fisher's Exact p-values for Sharp Null Hypotheses
Fisher's method was essentially a stochastic proof by contradiction. First, assume what you want to prove is wrong, here that means assuming that the new and control treatments are identical
| (11) |
Under this assumption, there are no missing values in the Science for the units in this experiment; thus, the value of every statistic, such as the difference in the mean Yi(1) for those assigned Wi = 1, , and the mean Yi(0) for those assigned Wi = 0, , is known, not only for the observed W but for all possible W. The Fisher proposal is to locate in the distribution of possible under the randomized assignment mechanism, and see how extreme the observed value is relative to the possible values. The proportion as extreme or more extreme gives the significance level (or p-value) associated with H0, as assessed for the observed data by the statistic , and the definition of extremeness.
Extensions of Fisher's Method
Notice, however, that Fisher's method can be applied with any sharp null hypothesis (e.g., Yi(1) = exp(Yi(0)), as pointed out in Rubin, 1974, p. 694) and even with nonignorable assignment mechanisms if they are fully specified in their dependence on the potential outcomes, because all potential outcomes are known, and thus so are all possible values of all statistics for all assignment vectors W, as are all probabilities of each assignment. Instead of simply counting the proportion of possible statistics that are as extreme or more extreme than the observed statistic, however, now we must take a weighted proportion, where the weights reflect the probability of each vector of treatment assignments. Bayesian extensions of this method were proposed in Rubin (1984) and further extended by others (e.g., Gelman, Meng, and Stern, 1996), and are called posterior predictive p-values.
Neyman's Randomization-Based Estimates and Confidence Intervals
Neyman (1923) showed that, in a completely randomized experiment, is unbiased (averaging over all randomizations) for the average causal effect, and he showed that the usual estimate of the standard error of is conservative unless additivity holds, that is, unless Yi(1) - Yi(0) = constant for all i. These results led Neyman to propose a large-sample interval estimate for the average causal effect, which he later (Neyman, 1934) called a “confidence interval”, which he defined to have at least its nominal coverage, to reflect, I believe, the generally conservative asymptotic estimation of the standard error in experiments.
Neyman's approach, despite its asymptotic nature, became the standard one in much of statistics and applied fields, leading to such things as tables of expected mean squares in ANOVAs (e.g., see Green and Tukey, 1960). Neyman's approach, which essentially involved repeated sampling evaluations of the operating characteristics of statistics, has advantages over Fisher's in that it can deal with random sampling of units from a population and with alternative hypotheses that were not sharp null hypothesis, which Fisher's approach required. This latter difference led to a sharp attack by Fisher (1935) on Neyman at a Royal Statistical Society meeting (Neyman, 1935) even though Neyman's presentation was complimentary about Fisher's contributions. Fisher's approach has the obvious advantage over Neyman's in not requiring large samples for the exactness of its probabilistic statements.
Extensions of Neyman's Approach
Neyman's approach “works”, in the sense that the bias of various statistics and the coverage of various interval estimates can be evaluated, even for nonignorable assignment mechanisms, but rarely can one derive exactly unbiased estimates (e.g., the standard instrumental variables estimate generally has infinite bias for all finite samples) or asymptotically useful interval estimates (e.g., randomly choosing the interval (-∞, ∞) 95% of the time, and any point the other 5% of the time, is an exact 95% confidence interval for all sample sizes and all data sets, but it is not very useful!) Nevertheless, the essential idea behind Neyman's approach, repeated sampling evaluations, today remains the basis for much statistical work; for example, it still dominates sample survey practice. In fact, much of the theory behind propensity score methods, which are really generalizations of Neyman's approach, rests on the fact that an unconfounded probabilistic assignment mechanism very generally can be written as proportional to the product of the propensity scores for all W that have positive probability.
A Final Comment on Fisher's and Neyman's Methods
Notice that a key feature of both Fisher's and Neyman's approaches is that the Science is treated as fixed but unknown, yet is the object of inference, and the vector of treatment assignments, W, is the only random variable (except for a sampling indicator, which can be incorporated in Neyman's approach). Also, realize that the concepts created by these methods, p-values, significance levels, unbiased estimation, confidence coverage, all defined originally by averaging over the randomization distribution, remain fundamental today. These fundamental ideas with the Science fixed cannot be clearly represented by graphs or paths, which are wedded to the observed outcome notation, and these other approaches do not create a clear distinction between the Science and the assignment mechanism; for example, see Rubin (2004), the discussion by Lauritzen (2004), and the rejoinder, and the previously mentioned exchange of letters in Statistics in Medicine (Rubin, 2009). To borrow Don Campbell's expression, I believe that the greatest threat to the validity of causal inference is ignoring the distinction between the Science and what we do to learn about the Science, the assignment mechanism – a fundamental lesson learned from classical experimental design, but often forgotten. My reading of Campbell's work on causal inference indicates that he was keenly aware of this distinction.
Formal Limitations of the RCM Without Its Bayesian Component
In a formal sense, however, Fisher's and Neyman's approaches rarely addressed the real reasons we conduct studies – to learn about which interventions should be applied to future units, for example, which educational programs are most likely to succeed next year. Fisher's p-values for sharp null hypothesis only formally work for the units actually exposed to one treatment or the other, and leave generalizations informal. And Neyman's approach only works for populations from which the units in the study have been sampled in some probabilistic way, and we never are fortunate enough to have a random sample of units from the future. Thus, given any real study, even a perfect randomized experiment, in order to inform future decisions, we must rely on subjective judgments, as I argued in Rubin (1974), and making such subjective judgments rest on a more formal basis is important, I believe.
Thus, to me, the third leg of the RCM, which derives the Bayesian posterior predictive distribution of the missing potential outcomes, although optional, is critical. That is, the first leg is using potential outcomes to define causal effects no matter how we try to learn about them: First define the Science. The second leg is to describe the process by which some potential outcomes will be revealed: Second, posit an assignment mechanism. The third leg is placing a probability distribution on the Science to allow formal probability statements about the causal effects, not only in the past, but also in the future: Third, incorporate scientific understanding in a model for the Science. That is, the Bayesian approach directs us to condition on all observed quantities and predict, in a stochastic way, the missing potential outcomes of all units, past and future, and thereby make informed decisions, based on explicitly stated assumptions, about which interventions look most promising for future application.
Final Comments
In conclusion, reading S and WT helped me to appreciate, much more than before, the vast contributions made by Don Campbell and his associates to many practical aspects of causal inference, and how these contributions complement my work and that of my associates. Don Campbell's contributions focused on real life problems from a deep but common-sense perspective that led to clear guidance for causal inference. I hope that my reflections and clarifications written here concerning the RCM, and the few historical comments that I have noted here about the evolution of the RCM, combined with the S and WT target articles and the other discussions of them, create an interesting and informative package for the readers of Psychological Methods.
Acknowledgments
The work was partially supported by National Science Foundation Grant SES 0550887 and National Institutes of Health Grant R01 DA023879-01.
Footnotes
I entered Princeton University in 1961 in a program designed by the physicist John Wheeler, a Nobel Laureate commonly credited with inventing the term “black hole”, to get a few of us PhDs in physics five years after entering as freshman – to the best of my knowledge, no one succeeded.
More generally, each of the N units can be exposed to one of K treatments as indicated by Wi, i = 1, …, N, where each Wi can take values in the set W. Thus the vector W = (W1, …, WN)T takes values in a set W*, which is a subset of the product set WK. In our current example, W = (0, 1), 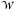 K = {0, 1} × {0, 1} × ⋯ × {0, 1}, and
K = {0, 1} × {0, 1} × ⋯ × {0, 1}, and 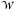 * = {W∣Wi = 0 or 1, and ΣWi = 0.05 · N}. In the general case, the ith unit has potential outcomes Yi(W), W ∈ W* because in general the ith unit's potential outcomes could depend on all the units' treatment assignments. The no interference assumption is that Yi(W1) = Yi(W2) for all W1, W2 ∈ W* such that the ith component of W1, Wi1, is the same as the ith component of W2, Wi2, and therefore Yi(W) can be unambiguously written as Yi(Wi).
* = {W∣Wi = 0 or 1, and ΣWi = 0.05 · N}. In the general case, the ith unit has potential outcomes Yi(W), W ∈ W* because in general the ith unit's potential outcomes could depend on all the units' treatment assignments. The no interference assumption is that Yi(W1) = Yi(W2) for all W1, W2 ∈ W* such that the ith component of W1, Wi1, is the same as the ith component of W2, Wi2, and therefore Yi(W) can be unambiguously written as Yi(Wi).
It is extremely interesting to note that the American psychologist and philosopher, Charles Sanders Peirce appears to have anticipated, in the late 19th Century, Neyman's concept of unbiased estimation when using simple random samples and appears to have even thought of randomization as a physical process to be implemented in practice (Peirce, 1931). I owe Keith O'Rourke and Steven Stigler the credit for this scholarship.
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/met
References
- Angrist JD. Lifetime earnings and the Vietnam era draft lottery: Evidence from Social Security Administrative Records. American Economic Review. 1990;80:313–335. [Google Scholar]
- Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. Journal of the American Statistical Association. 1996;91:444–472. [Google Scholar]
- Bertrand M, Mullainathan S. Are Emily and Greg more employable than Lakisha and Jamal? A field experiment on labor market discrimination. The American Economic Review. 2004;94:991–1013. [Google Scholar]
- Campbell DT. In: Methodology of epistemology for social science: selected papers. Overman ES, editor. Chicago: University of Chicago Press; 1988. [Google Scholar]
- Campbell DT, Erlebacher A. How regression artifacts in quasi-experiments can mistakenly make compensatory education look harmful. In: Helmuth J, editor. The Disadvantaged Child. New York: Brunner-Mazel; 1970. [Google Scholar]
- Campbell DT, Stanley JC. Experimental and quasi experimental designs for research. Chicago: Rand McNally; 1966. [Google Scholar]
- Cochran WG. The planning of observational studies in human populations (with discussion) (A).The Journal of the Royal Statistical Society. 1965;128:234–255. [Google Scholar]
- Cochran WG, Rubin DB. Controlling bias in observational studies: a review. Sankhya - A. 1973;35:417–446. [Google Scholar]
- Cook TD. Waiting for life to arrive: a history of the regression-discontinuity design in psychology, statistics and economics. Journal of Econometrics. 2008;142:636–654. [Google Scholar]
- Efron B. Missing data, imputation, and the bootstrap. Journal of the American Statistical Association. 1994;89:463–478. with discussion and rejoinder. [Google Scholar]
- Fisher RA. Statistical methods for research workers. 1st. Edinburgh: Oliver and Boyd; 1925. [Google Scholar]
- Fisher RA. Discussion of Neyman, J. (1935). Statistical problems in agricultural experimentation. Supplement of the Journal of the Royal Statistical Society. 1935;2:107–180. [Google Scholar]
- Frangakis C, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58:21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Meng XL, Stern H. Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica. 1996;6:733–808. with discussion and reply. [Google Scholar]
- Green BF, Jr, Tukey JW. Complex analyses of variance: General problems. Psychometrika. 1960;25:127–152. [Google Scholar]
- Holland PW. Statistics and causal inference. Journal of the American Statistical Association. 1986;81:945–970. [Google Scholar]
- Holland PW, Rubin DB. On Lord's paradox. In: Wainer H, Messick S, editors. Principles of Modern Psychological Measurement: A Festschrift for Frederick Lord. Philadelphia: Erlbaum; 1983. [Google Scholar]
- Imbens G, Rubin DB. Causal inference in statistics, and in the social and biomedical sciences. New York: Cambridge University Press; 2010. [Google Scholar]
- Jin H, Rubin DB. Public schools versus private schools: causal inference with extended partial compliance. The Journal of Educational and Behavioral Statistics. 2009;34:24–45. [Google Scholar]
- Kempthorne O. The design and analysis of experiments. New York: Wiley; 1952. [Google Scholar]
- Lauritzen S. Discussion of “Direct and indirect causal effects via potential outcomes” by D. B. Rubin. The Scandinavian Journal of Statistics. 2004;31:189–192. [Google Scholar]
- Mealli F, Rubin DB. Assumptions when analyzing randomized experiments with noncompliance and missing outcomes. Health Services Outcome Research Methodology. 2002a;3:225–232. [Google Scholar]
- Mealli F, Rubin DB. Discussion of “Estimation of intervention effects with noncompliance: alternative model specification,” by Booil Jo. Journal of Educational and Behavioral Statistics. 2002b;27:411–415. [Google Scholar]
- Mealli F, Rubin DB. Assumptions Allowing the Estimation of Direct Causal Effects: Discussion of ‘Healthy, Wealthy, and Wise? Tests for Direct Causal Paths Between Health and Socioeconomic Status' by Adams et al.’. Journal of Econometrics. 2003;112:79–87. [Google Scholar]
- Neyman J. On the application of probability theory to agricultural experiments: essay on principles, section 9. Translated in Statistical Science. 1923;5:465–480. 1990. [Google Scholar]
- Neyman J. On the two different aspects of the representative method: the method of stratified sampling and the method of purposive selection. (A).Journal of the Royal Statistical Society. 1934;97:558–606. [Google Scholar]
- Neyman J. Statistical problems in agricultural experimentation. (B).Supplement to the Journal of the Royal Statistical Society. 1935;2:107–180. (with discussion). (With cooperation of K. Kwaskiewicz and St. Kolodziejczyk.) [Google Scholar]
- Neyman JS, Dabrowska DM, Speed TP. On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Statistical Science. 1990;5:465–472. [Google Scholar]
- Peirce CS. In: Collected papers of Charles Sanders Peirce. Hartshorne C, Weiss P, editors. Vol. 1. Cambridge: Harvard University Press; 1931. pp. 19–49. [Google Scholar]
- Reid C. Neyman from life. New York: Springer; 1982. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983a;70:41–55. [Google Scholar]
- Rosenbaum PR, Rubin DB. Assessing sensitivity to an unobserved binary covariate in an observational study with binary outcome. (B).The Journal of the Royal Statistical Society. 1983b;45:212–218. [Google Scholar]
- Roy AD. Some thoughts on the distribution of earnings. Oxford Economic Papers. 1951;3:135–146. [Google Scholar]
- Rubin DB. Matching to remove bias in observational studies. Biometrics. 1973a;29:159–183. Printer's correction note 30, 728. [Google Scholar]
- Rubin DB. The use of matched sampling and regression adjustment to remove bias in observational studies. Biometrics. 1973b;29:184–203. [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and non-randomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Rubin DB. Bayesian inference for causality: the importance of randomization. The Proceedings of the Social Statistics Section of the American Statistical Association. 1975:233–239. [Google Scholar]
- Rubin DB. Inference and missing data. Biometrika. 1976;63:581–592. [Google Scholar]
- Rubin DB. Assignment to treatment group on the basis of a covariate. Journal of Educational Statistics. 1977;2:1–26. Printer's correction note 3, p. 384. [Google Scholar]
- Rubin DB. Bayesian inference for causal effects: the role of randomization. The Annals of Statistics. 1978;6:34–58. [Google Scholar]
- Rubin DB. Discussion of “Conditional independence in statistical theory”, by A. P. Dawid. (B).The Journal of the Royal Statistical Society. 1979;41:27–28. [Google Scholar]
- Rubin DB. Discussion of “Randomization analysis of experimental data in the Fisher randomization test”, by Basu. Journal of the American Statistical Association. 1980;75:591–593. [Google Scholar]
- Rubin DB. Bayesianly justifiable and relevant frequency calculations for the applied statistician. Annals of Statistics. 1984;12:1151–1172. [Google Scholar]
- Rubin DB. Which ifs have causal answers? Discussion of Holland's “Statistics and causal inference”. Journal of the American Statistical Association. 1986;81:961–962. [Google Scholar]
- Rubin DB. Formal modes of statistical inference for causal effects. Journal of Statistical Planning and Inference. 1990a;25:279–292. [Google Scholar]
- Rubin DB. Comment: Neyman (1923) and causal inference in experiments and observational studies. Statistical Science. 1990b;5:472–480. [Google Scholar]
- Rubin DB. Comments on “Missing data, imputation, and the bootstrap” by B. Efron. Journal of the American Statistical Association. 1994;89:475–478. [Google Scholar]
- Rubin DB. Statistical Issues in the Estimation of the Causal Effects of Smoking Due to the Conduct of the Tobacco Industry. In: Gastwirth J, editor. Chapter 16 in Statistical Science in the Courtroom. New York: Springer-Verlag; 2000. pp. 321–351. [Google Scholar]
- Rubin DB. Direct and indirect causal effects via potential outcomes. The Scandinavian Journal of Statistics. 2004;31:161–170. with discussion and reply. [Google Scholar]
- Rubin DB. Causal inference using potential outcomes: design, modeling, decisions. 2004 Fisher Lecture. The Journal of the American Statistical Association. 2005;100:322–331. [Google Scholar]
- Rubin DB. Causal Inference Through Potential Outcomes and Principal Stratification: Applications to Studies with ‘Censoring’ Due to Death. Statistical Science. 2006a;21:299–321. with discussion and rejoinder. [Google Scholar]
- Rubin DB. Matched Sampling for Causal Effects. New York: Cambridge University Press; 2006b. [Google Scholar]
- Rubin DB. “Author's reply” to letters by Pearl, Shrier and Sjolander re: The design versus the analysis of observational studies for causal effects: parallels with the design of randomized trials (2007) Statistics in Medicine. 2009;28:1420–1424. doi: 10.1002/sim.2739. [DOI] [PubMed] [Google Scholar]
- Shadish WR. Campbell and Rubin: A primer and comparison of their approaches to causal inference in field settings. Psychological Methods, to appear. 2010 doi: 10.1037/a0015916. [DOI] [PubMed] [Google Scholar]
- Speed TP. Introductory Remarks on Neyman (1923) Statistical Science. 1990;5:463–464. [Google Scholar]
- Thistlethwaite DL, Campbell DT. Regression-discontinuity analysis: an alternative to the ex-post facto experiment. Journal of Educational Psychology. 1960;51:309–317. [Google Scholar]
- West SG, Thoemmes F. Campbell's and Rubin's perspectives on causal inference. Psychological Methods, to appear. 2010 doi: 10.1037/a0015917. [DOI] [PubMed] [Google Scholar]
- Zhang J, Mealli F, Rubin DB. Evaluating the effects of job training programs on wages through principal stratification. Advances in Economics. 2008;21:119–147. [Google Scholar]
- Zhang J, Mealli F, Rubin DB. Likelihood-based analysis of job training programs using principal stratification. The Journal of the American Statistical Association. 2009;104:166–176. [Google Scholar]


