Matrix strains induced by cells: Computing how far cells can feel

Abstract

Many tissue cells exert contractile forces that mechanically couples them to elastic matrices and that influence cell adhesion, cytoskeletal organization, and even cell differentiation. However, strains within the depths of matrices are often unclear and are likely relevant not only to the fact that some matrices such as so-called basement membranes are thin relative to cell dimensions but also to defining how far cells can ‘feel’. Here we briefly present experimental results for cell spreading on thin, ligand-coated gels and for prestress in stem cells in relation to gel stiffness. We then introduce a finite element computation in which a cell is placed on an elastic matrix, while matrix elasticity and thickness are varied in order to compute and compare elastostatic deformations within the matrix. Average interfacial strains between cell and matrix show large deviations only when soft matrices are a fraction of the height and width of a cell, proving consistent with experiments. Three-dimensional (3D) cell morphologies that model stem cell-derived neurons, myoblasts, and osteoblasts show that a cylinder-shaped myoblast induces the highest strains, consistent with the prominent contractility of muscle. Groups of such cells show a weak crosstalk in matrix strains, but the cells must be much closer than a cell-width. Cells thus feel on length scales closer to that of adhesions than on cellular scales or higher.

Introduction

Cells respond to external stimuli by altering their cytoskeletal assembly, protein phosphorylation¹, and gene and protein levels^{2, 3} resulting in changes in cell shape, function, and viability^2–6. Matrix elasticity is increasingly recognized as a key factor in cellular processes ranging from motility^{1, 7–9} to adhesion^{1, 7, 10, 11} and differentiation^{3, 10, 12}. Alterations in in vivo matrix stiffness are often closely associated with disease progression, as reported in the stiffening of heart muscle during myocardial infarction due to fibrosis¹³, the softening of matrix in atherosclerosis¹⁴, or the stiffening of the muscle diaphragm in muscular dystrophy¹⁵. The cell’s ability to probe the extracellular matrix (ECM) was first documented by Harris and co-workers^{16, 17}, who observed the wrinkling of thin, flexible silicone films beneath adherent tissue cells. The traction forces transmitted through focal adhesions generate substrate displacements only when the substrate is compliant, and various gel systems have emerged that allow not only quantitative study of the tractions but also reveal surprising effects of matrix elasticity^{1, 18}.

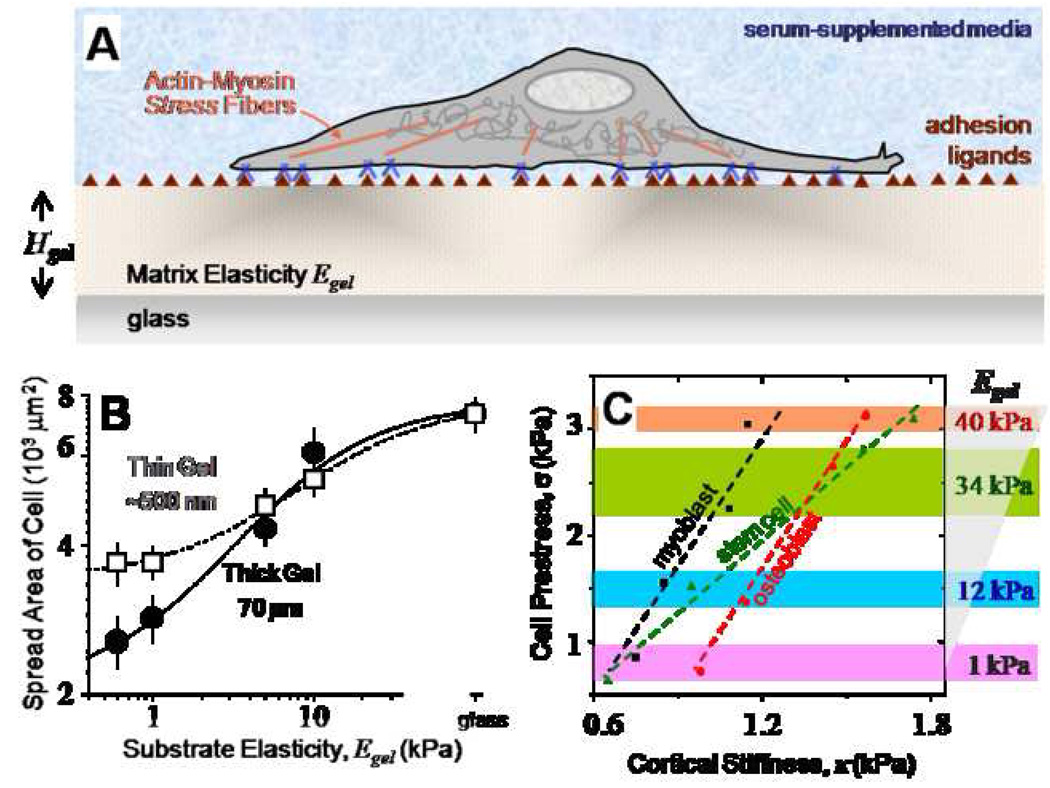
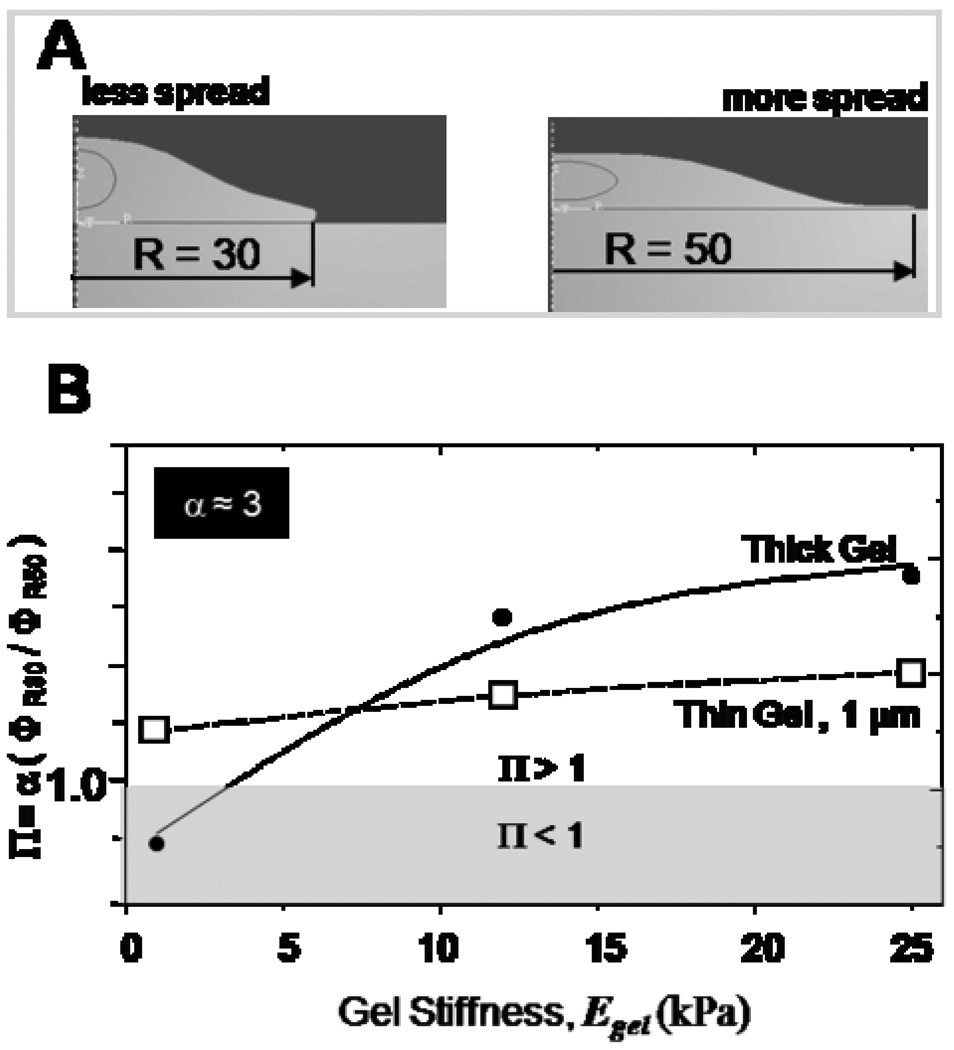
Recent work has demonstrated that mesenchymal stem cells (MSCs) cultured on thick polyacrylamide (PA) gels (H_gel = 70 µm) of varying stiffness (E_gel), but under identical growth factors, exhibit drastically different morphologies driven solely by gel stiffness¹⁹. On soft gels representative of brain tissue (0.1–1 kPa)²⁰, a majority of MSCs exhibit a neuronal, branched morphology. On moderately stiff substrates, which mimic the passive elasticity of striated muscle (E_muscle ≈ 8 – 17 kPa)¹⁰, MSCs develop a myoblast-like spindle shape. On substrates significantly stiffer than E_muscle (i.e. >30 kPa) and representative of crosslinked collagen of osteoids²¹, MSC shape is more polygonal and highly spread, resembling osteoblasts. Enhanced spreading of MSCs on thin gels (~500 nm) compared to thick gels suggests MSCs feel into their matrices on the length scales of their adhesions. Non-muscle myosin II is directly involved in this matrix sensing by pulling on actin, which in turn transmits forces to the ECM through focal adhesions (Figure 1A). Focal adhesions become smaller and less stable in the absence of these contractions²². Knocking down non-muscle myosin II expression by blebbistatin treatment completely eliminates the ability to sense matrix stiffness, thereby blocking matrix sensitive differentiation of stem cells.

Figure 1. Cell on gel culture results.

1. Gel-based matrices allows for control of substrate stiffness E_gel, control of cell adhesion by covalent attachment of adhesion ligands, and also control of thickness H_gel.
2. Cell spreading on gels increases with increasing gel stiffness. However, on thin (H_gel ~ 500 nm) soft gels, cells start feeling the rigid glass substrate resulting in enhanced spreading.
3. Cell prestress (σ) is plotted versus membrane stiffness (κ) for MSCs, C2C12 and hFOB cells on different stiffness gels. In comparison to C2C12 and hFOB cells which exhibit the same slope, MSCs are twice as mechanosensitive behaving more like C2C12 cells on intermediate stiffness gels and like hFOB cells on higher stiffness gels.

Numerous experiments conducted to understand cell response to mechanical stress have been effectively combined with finite element models to map out the contributions of structural components, computing stress and strain distributions within the cell and relate the biological influences of various types of force application^23–26. However, models to date have not adequately addressed the role of matrix properties in directing cell behavior. In this paper, our specific objective is to understand prestress-driven matrix-sensing by cells. We begin by presenting experimental results demonstrating the importance of matrix stiffness and thickness in regulating cell spreading and affecting stem cell differentiation. A simple axisymmetric finite element model is developed to compute the strain and displacement fields imposed on the underlying matrix by cellular prestress. By fixing the cell geometry and varying the matrix thickness, we determine how deep cells feel their substrates. Strain energy comparison between two spread cell shapes of almost identical volume allows us to recapitulate the differential cell spreading response on soft, thin gels. Three-dimensional simulations incorporating morphology of MSCs on different gels demonstrates distinct differences in strain maps induced by the cells on these matrices. Planar simulations of a group of cells allow us to study the mechanical crosstalk through the compliant matrix. Overall, we aim to determine the length scales and stiffness scales relevant to cells, which seem to be likely factors in cell remodeling and differentiation as well as mechano-signaling to adjacent cells via matrix changes.

Computational Model

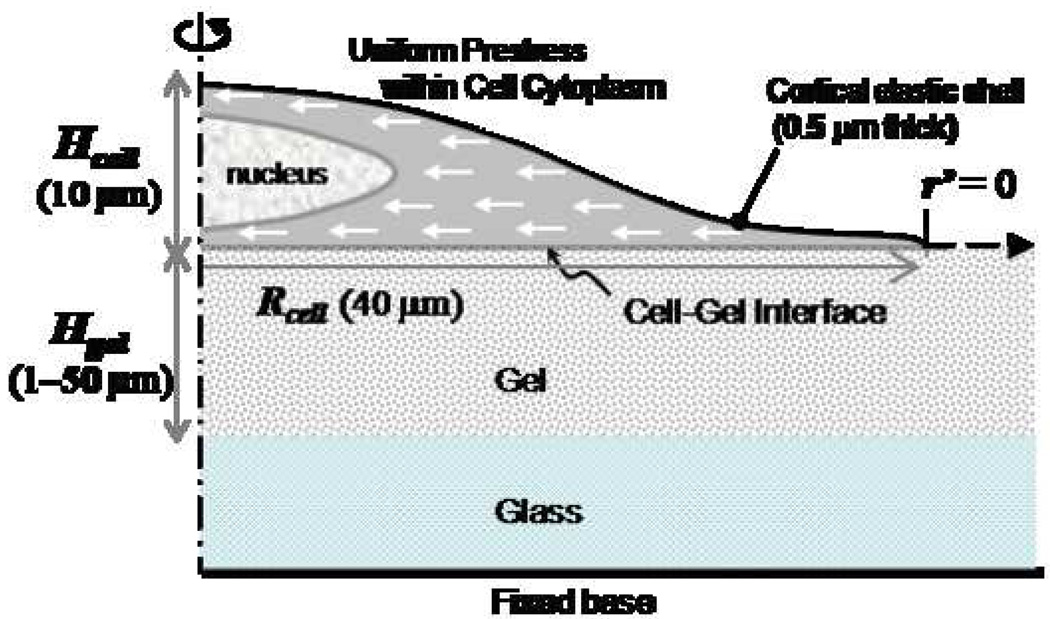
An axisymmetric finite element model has been developed to simulate substrate strains induced by cell prestress (Figure 2). The cell has three components: 1) cytoskeleton, within the cell body; 2) cortical shell, represented by a shell layer on top of the cytoskeleton encompassing the cell body, and attached to it; 3) the nucleus at the center of the cell. The physical parameters of the system include the maximum cell height along the axis of symmetry (H_cell, held constant at 10 µm), the cell radius along the cell-gel interface (R_cell, ~40 µm in length), and the gel thickness (H_gel, varied between 1–50 µm depending on the type of simulation). The gel radius is chosen to be sufficiently large to eliminate edge effects. To mimic in vitro cell cultures a zero-displacement boundary condition is imposed at the bottom surface of the glass on which the gel rests. Free stress boundary conditions are imposed at the perimeter of the cell and the lateral edges of the gel. For symmetry considerations, the centerline is constrained from moving in the radial direction. A uniform prestress, of a magnitude which matches those experimentally determined¹⁹, is specified throughout the entire cell cytoplasm except the nucleus. Comparison between individual cases is made using the measure of the logarithmic strain, a nonlinear strain measure. For a simple one dimensional case it is defined as ln (λ), where λ is the extension ratio.

Figure 2. Computational Model.

Axisymmetric cell spread on a gel with a fixed base. The gel thickness (H_gel) is varied, and the gel radius is chosen so as to minimize edge effects. A uniformly compressive prestress is specified throughout the cell cytoplasm, except in the nucleus and the outer cortex. Lateral propagation of displacement and strain are measured from the edge of the cell (r^/=0) extending radially outward.

To determine the displacement and strain fields induced within the cell monolayer, a finite element model was developed using the commercially available software Abaqus (Providence, RI), version 6.4. The cell cytoplasm, cell nucleus and the gel are modeled with homogeneous hyperelastic Neo-Hookean materials, which are isotropic and nonlinear, and exhibit instantaneous elastic responses for large strains. The initial shear modulus and bulk modulus for these materials required to determine the strain energies are computed from the Young’s modulus and Poisson’s ratio. The Young’s modulus is chosen as 1 kPa for neurons, 12 kPa for myoblasts and 34 kPa for osteoblasts. The Young’s modulus is chosen as 1 kPa for a soft gel, 12 kPa for an intermediate stiff gel, and 34 kPa or 40 kPa for stiff gels. A Poisson’s ratio of 0.45 is chosen for all the calculations. To model the experimentally observed behavior of stem cells, identical cell and gel properties are chosen for simulating the response on a substrate of given stiffness. The 0.5 µm thick cortical shell is bonded to the cell cytoplasm and modeled using homogeneous shell section. The magnitude of the Young’s modulus of the shell is determined from the experimental values reported here. The glass base has a Young’s modulus of 50 GPa and a Poisson’s ratio of 0.2.

For the axisymmetric simulations, 4-node bilinear axisymmetric quadrilateral elements are used for modeling the cell cytoplasm, nucleus and gel, and 2-node linear axisymmetric shell elements are used for the cortical layer. For the 3d simulations, 8-node linear brick elements are used for neuronal morphology for both the cell and the gel; for the myoblast morphology, 8-node linear brick elements are used for the gel and 4-node tetrahedral elements for the cell. For all the cases, the meshing is biased towards the regions of maximal deformations, namely, the cell-gel interface and the cell periphery.

As validation, the displacement and strain fields were computed for an axisymmetric solid (both with a homogeneous linear elastic material with Young’s modulus 12 kPa and Poisson’s ratio 0.5, and with a hyperelastic material with Young’s modulus 12 kPa and Poisson’s ratio 0.45) with distributed traction (100 Pa directed radially inward specified on 65 nodes) on the upper edge, and fixed on its base. For both the material descriptions, the theoretical shear modulus was compared with the experimentally determined shear modulus to validate the model.

Results

Cell on gel experimental results

While cell spreading on thick gels is remarkably independent of gel thickness²⁷ and guided by gel stiffness alone, thickness plays an increasingly important role as it approaches mechanosensing length scales in the order of a few 100 nm’s (Figure 1B). As the thin gels become softer (< 5 kPa), cells begin sensing the underlying rigid glass substrate, with the spreading response being equivalent to that on a much stiffer gel. This mechanosensitivity would expectedly be different for different cell types, and small changes in the immediate environment would affect the cells to varying extents. Comparing pluripotent cell behavior to fully differentiated cell types (C2C12 skeletal myoblasts and hFOB osteoblasts) on thick gels, the enhanced mechanosensitivity of MSCs to matrix stiffness can be demonstrated by plotting the prestress (σ) as a function of cell membrane stiffness (κ) for different stiffness gels (Figure 1C). For all the committed cell types shown here and elsewhere, i.e., myoblasts and osteoblasts^{19, 28}, prestress and membrane stiffness increase linearly with increasing matrix stiffness, and at the same rate. Interestingly, the multipotent MSCs exhibit modest mechanical properties similar to C2C12 cells on myogenic gels (12 kPa) and display higher tensile properties like hFOB cells on stiff substrates, displaying a mechanosensitivity that is twice that of either committed cell line, a potentially important trait for stem cells.

Deformation of Thick Matrices

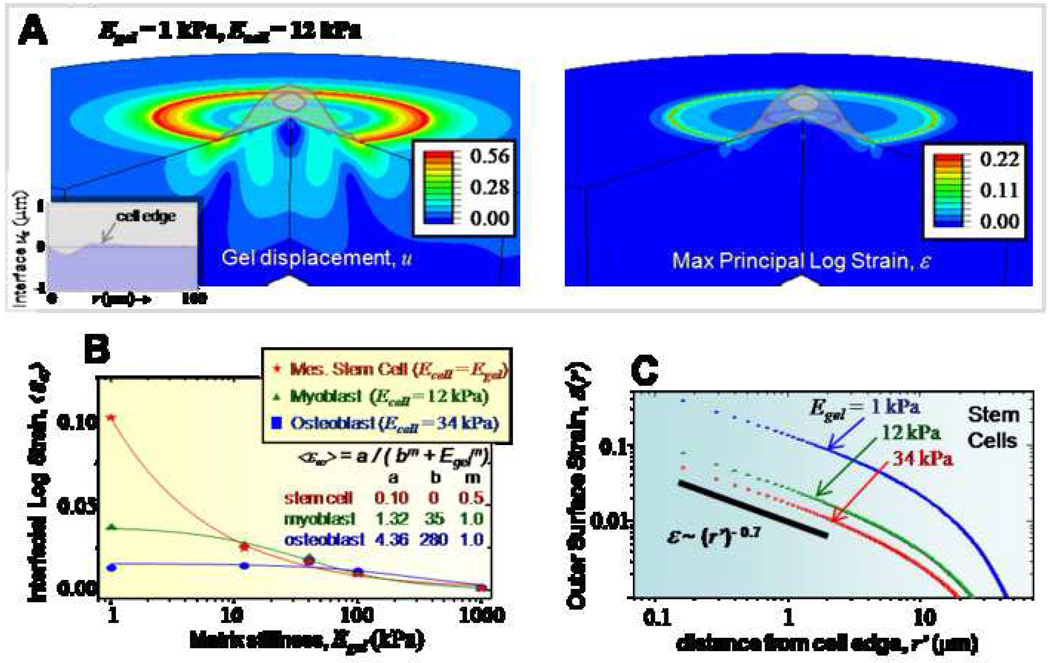
Using the axisymmetric cell-on-gel model described above, we study the sensitivity of different cell types to matrix stiffness by comparing the matrix strain fields. For these simulations, the gel thickness is chosen to be 50 µm so as to eliminate any thickness effects. Figure 3A shows representative gel displacement and strain maps for the case of a myoblast (12 kPa) on a soft gel (1 kPa), with maximum gel displacements of ~550 nm and strains of ~25 % localized on the outer edge of the cell. It is important to note that the cell-gel interface deforms both radially and transversely (z-direction), as shown in the plot of u_z (inset). For comparing the behavior of different cell types, we introduce mean interfacial logarithmic strain <ε_∞> of the gel along the cell-gel interface (Figure 3B) representative of the total work done by the cell in deforming its matrix, and computed by taking the average of the maximum principal logarithmic strain in the gel along the interface. <ε_∞> shows contrasting behavior for different cell types. For stem cells and myoblasts, <ε_∞> is maximal on the softest gels and decreases with increasing gel stiffness. In contrast, osteoblasts are relatively insensitive to gel stiffness. As expected, the mean strain approaches zero for all the different cell-types in the rigid limit (i.e., as the substrate becomes infinitely stiff). However, as the substrate becomes infinitely soft, the mean strain plateaus to some constant value for both the myoblast and the osteoblast, but diverges for the stem cell. The computed profiles were fit using the expression <ε_∞> = a/(b^m + E_gel^m), with the fit values of the parameters shown in the figure. Compared to stem cells, for myoblasts and osteoblasts, the parameter ‘b’ is orders of magnitude higher. Therefore, subtle changes in matrix stiffness would be magnified for stem cells much significantly compared to myobasts and osteoblasts, thereby confirming their increased mechanosensitivity observed experimentally. These trends above observed with <ε_∞> also holds true for the interfacial displacement <u_∞> (Supp. Figure S1A). Lateral propagation of strains is addressed by studying their decay away from the cell edge (Figure 3C, plotted for stem cells only). Independent of the gel stiffness, gel strains decay rapidly away from the cell edge, with the initial decay well approximated using power-laws with an exponent of −0.7. Similar to surface strains, surface displacements decay exponentially in a stiffness-independent manner over a characteristic length of 10 µm (Supp. Figure S1B).

Figure 3. Cell responses on thick matrices.

1. The displacement and strain map induced by a model cell (E_cell = 12 kPa) on a soft gel (E_gel = 1 kPa). Peak displacement and strain occur on the cell edge and decrease both inside and outside. The displacements decay to zero well before hitting the gel base. Inset shows the z-displacement of the cell-gel interface.
2. <ε_∞> are plotted for different stiffness gels for models of various cell types. Stem cells show the greatest sensitivity to gel stiffness, but power-law decays with E_gel of <ε> indicate minimal sensitivity to very stiff substrates.
3. Lateral strains decay with distance, and can be fit over the first 2 µm’s by a moderately steep power-law.

Depth-Sensing by Cells: Effect of Gel Thickness

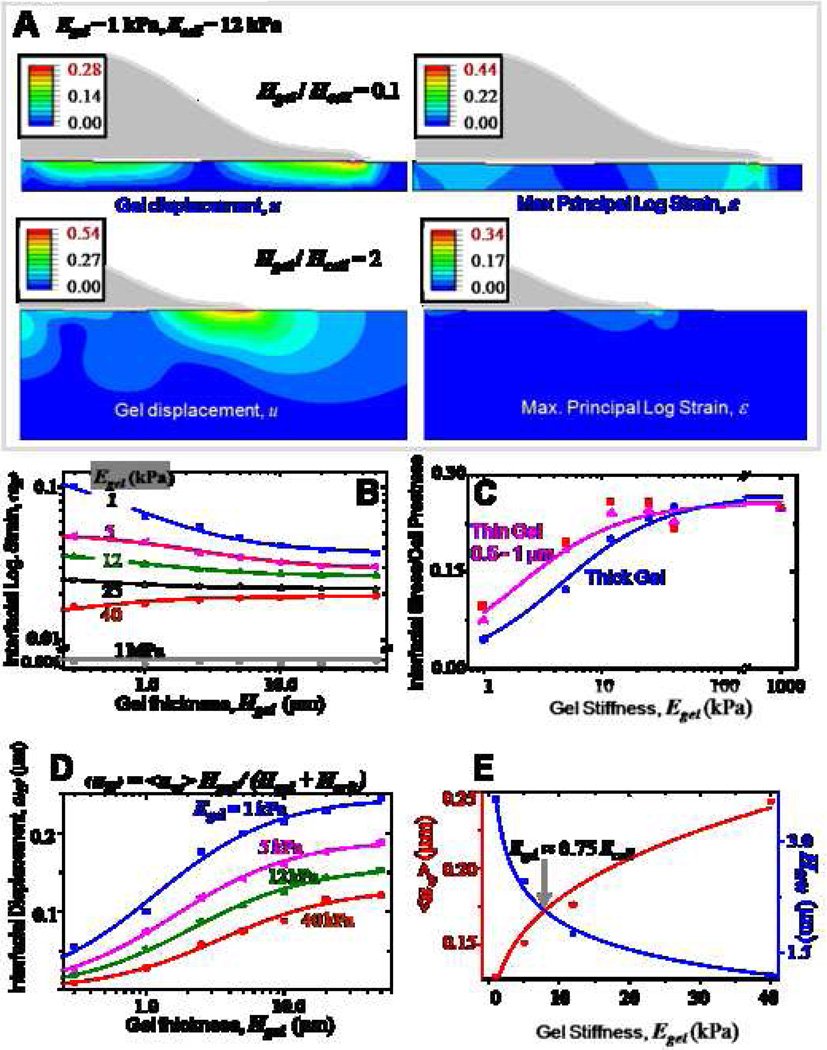
Cell sensitivity to matrix thickness was assessed by performing simulations for varying gel thickness using the same axisymmetric cell-on-gel model. In these simulations, the cell stiffness and cell geometry are held constant, and the ratio of gel thickness to cell height is varied over four orders of magnitude from 0.006 to 5.0. Figure 4A shows the displacement and strain maps for two different gel thicknesses, the ratios being 0.1 and 2.0 respectively. For the thicker gel, both displacements and strains decay to zero well before reaching the gel base, while for the thinner gel, constrained by the glass substrate the displacement and strain fields were altered significantly. The strongest dependence of the mean interfacial logarithmic strain (<ε_H>) on gel thickness is observed on the softest gels with more than 50 % reduction occurring within the first 2 µm. This dependence is weaker for intermediate and stiff gels (Figure 4B). Strains are negligible on very stiff matrices which cells are unable to deform - on a 1 MPa gel, the mean strain is roughly constant at 0.1 %. For a gel of given stiffness, with increasing gel thickness, the mean strain levels off to a constant value dictated solely by the gel stiffness and captures the response on thick matrices (Figure 3). Interestingly, the mean stress ratio (mean interfacial stress (E_gel * <ε>) normalized by cell prestress) plotted for thin (0.5 – 1 µm) and thick gels (Figure 4C) exhibits a trend very similar to the spreading response observed on these gels (Figure 1B). A higher stress ratio indicative of more efficient transmission of tractions to the substrate is thus higher for thin gels compared to thick gels on soft substrates. The mean interfacial displacement curves were fitted using hyperbolic functions for gels of varied elasticity (Figure 4D), thus yielding gel-stiffness dependent critical gel thickness (H_crit) and characteristic interfacial displacement on thick gels (u_∞). A mechanosensing length scale is defined by H_crit, which scales nonlinearly with gel stiffness. Maximum sensitivity of H_crit and <u_∞> to gel stiffness occurs in the range of 1 – 10 kPa (i.e., in the range of E_cell), with a crossover at 8 kPa (0.75 * E_cell) (Figure 4E). Individual interfacial strain components (<ε_rr>, <ε_zz>, <ε_rz>, <ε_θθ>) plotted versus gel thickness for different values of E_gel have different transition regimes (Supp. Figure S2); of these the radial strain and the shear strain prove to be the most significant, and the minimum transition gel thickness of 1 – 2 µm for these two strains agrees well with the results obtained above with stress ratio and H_crit.

Figure 4. Depth-sensing by cells: Effect of gel thickness.

Gel thickness (H_gel) and gel elasticity are varied while cell stiffness is a constant 12 kPa.

1. A. Representative displacement and strain maps induced by an axisymmetric cell on two different thickness gels (H_gel/H_cell = 0.1 and 2 respectively).
2. B. <ε_H> decreases with increasing gel thickness, and shows greatest sensitivity to gel thickness on soft substrates, with >50% reduction within the first 2 µm.
3. C. The ratio of the interfacial stress to the cell prestress increases with gel stiffness and saturates, and similar to cell spreading is higher for thin and soft gels.
4. D. Cell-gel interfacial <u> for increasing gel thickness saturates beyond a given gel thickness, representative of the mechanosensing length scale of the cell.
5. E. Hyperbolic fits to <u> yield constants ‘a’ and H_crit. ‘a’, indicative of gel deformability, decreases with increase in gel stiffness. H_crit, the critical gel thickness beyond which a cell cannot feel its substrate, increases with increasing gel stiffness. These two parameters crossover at a critical stiffness of ~8 kPa.

Cell Spreading Energetics

The above results demonstrate the existence of a critical gel thickness within which cells feel their substrates. By varying the fixed cell geometry used in these simulations we can explore the differential cell spreading response on thin gels (Figure 1B). Cell spreading here is simulated by choosing two cell geometries with different spread shape but same volume (Figure 5A) and comparing their strain energies to determine the energetically favorable shape on a given substrate. The two spread shapes, labeled R₃₀ and R₅₀, have respective cell-gel interface radii of 30 µm (less spread) and 50 µm (more spread). Mean strain energies within the cell for these two configurations are respectively computed as Φ_R30 and Φ_R50, and we find that the less spread cell always has a lower mechanical energy than the more spread cell. However, the experiments of Fig.1B show that a less spread shape is preferred only on gels that are thick and soft (with E_gel < 5–10 kPa), and so we multiply the purely mechanical energy ratio (Φ_R30/Φ_R50) by an efficiency factor α, which we propose can account for different metabolic-to-mechanical energy conversion rates (eg. ATP hydrolysis) in the two different spread shapes. We then plot this relative energy index as Π = α (Φ_R30/Φ_R50) in Fig. 5B.

Figure 5. Cell spreading energetics.

Cell spreading on thin gels is studied by comparing strain energies between two spread shapes of a cell (R₃₀ and R₅₀ respectively). The relative energy index (Π) provides a basis for identifying the energetically favored shape on a given substrate. Consistent with experiments, the maximally spread shape is favored on thin gels on substrates of all stiffnesses. In contrast, the least spread shape is only favored on thick gels which are relatively soft (E_gel < 5 kPa).

Only for α ≈ 3 do we obtain results that conform to the experimental trends for more spread versus less spread of Fig. 1B. With thin gels, Π is always greater than 1 and thus indicates that the more spread cell shape (R₅₀) is energetically favored on these gels irrespective of the gel stiffness, whereas with thick gels and only for E_gel < 5 kPa is the less spread shape energetically favored with Π < 1. The results are thus made consistent with the experimental results, suggesting that if a minimum cellular energy principle governs cell spreading, then it might be based on metabolic energy inputs and different conversion efficiencies in the more or less spread cell shapes.

Three-Dimensional Simulations: Representative Strain maps induced by MSCs

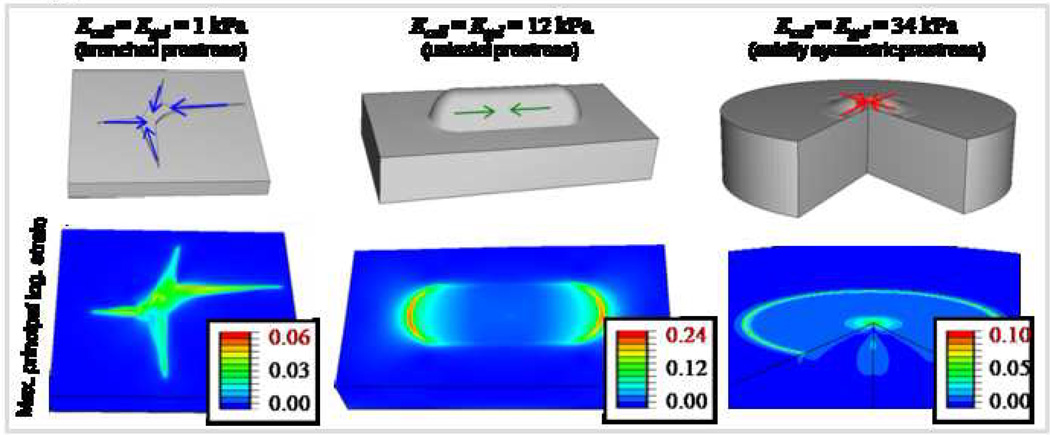
Since all previous calculations have assumed axisymmetric cell geometry, three dimensional finite element simulations were performed taking into account the variation of stem cell morphology on different substrates. Figure 6 shows the geometry and loading of models representing different cell morphologies, with the gel fixed at its base to a rigid support. The prestress distribution in the cell on different substrates depends on cell morphology, and is branched on a soft gel (1 kPa), uniaxial on an intermediate stiffness gel (12 kPa), and axisymmetric on a stiff gel (34 kPa). In contrast to maximum strains of 6 % and 10 % imposed by the model MSC on a soft gel or on a stiff gel, it is 20 % on an intermediate stiffness gel. The peak strain, highest for the spindle-shaped morphology on an intermediate stiffness gel representative of a myoblast, but much lower for the branched morphology on soft gel representative of a neuron, or the axisymmetric morphology on stiff gel representative of an osteoblast, is consistent with the prominent contractility of muscle.

Figure 6.

Three dimensional simulations: Representative strain maps induced by stem cells differentiated into – from left to right – a branched neuron, cylindrical myoblast, or axisymmetric osteoblast on either a soft, medium or stiff substrate. The prestress direction is assumed to match the cell symmetry, and the prestress magnitude taken from experiments.¹⁹ The strain maps induced by the model stem cell are distinct on different gels, and maximum strains of 20% are obtained below the ‘myoblast’ shaped cell on an intermediate stiffness substrate.

Mechanical crosstalk between cells

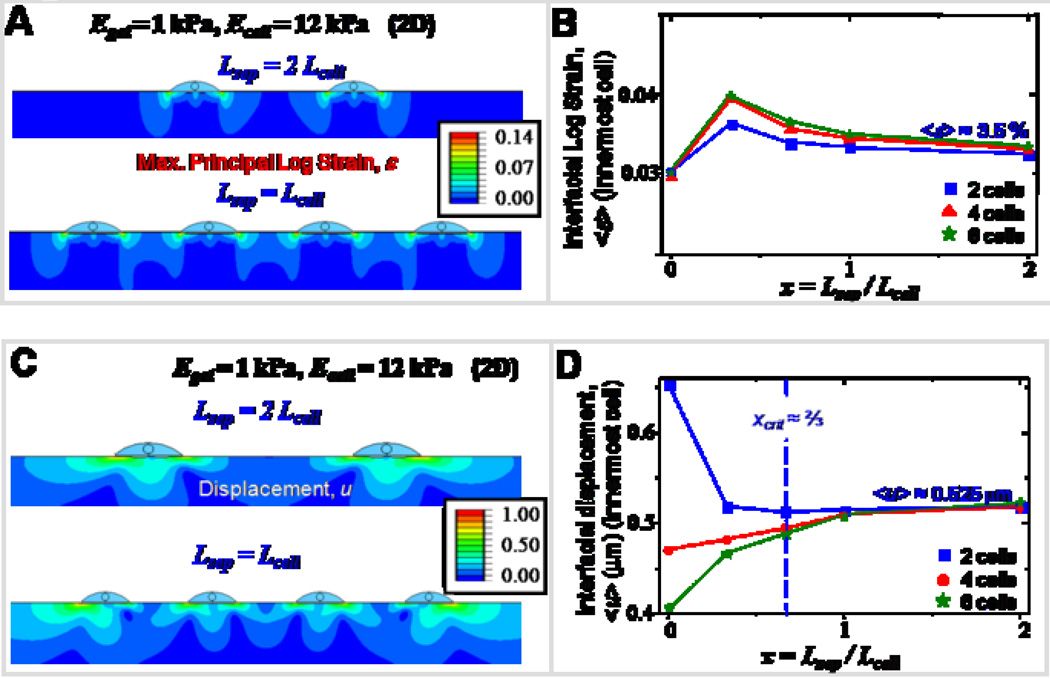
Tissue formation, growth and functioning all require both cell-ECM and cell-cell interactions, yet few simulations have considered how cell interactions overlap. The underlying principle of mechanical crosstalk has been shown both theoretically^29–31, and experimentally¹⁰ in the preferential alignment of cells on compliant matrices. Here, we have used a planar (2D) cells-on-gel model to study collective interaction of cells, with the total number of cells varied between two and six, and the cell spacing ratio x (L_sep / L_cell) varied between 0 and 2. Negligible differences in strain maps for two different spacing ratios (Figure 7A) suggests that in both cases the cell spacing is larger than the threshold spacing below which cells begin sensing the presence of their neighbors. <ε> plotted for the innermost cell as a function of x (Figure 7B) remains roughly constant (~3.5 %) suggesting a weak crosstalk between the cells. The divergent behavior in <u> for small cell-cell separations (Figure 7C) arises due to the spatial asymmetry in cells pulling on the matrix as opposed to pulling each other. For two cells only, when the spacing is small, the displacement and strain maps are asymmetric with respect to the center of each cell, as the inner edges do not deform much, being restricted by each other; in contrast, the outer edges easily deform the matrix giving rise to large deformations and strains on the outer edges, thereby giving a moderately large value for the mean displacement (Figure 7D). For the case of six or eight cells, <u> is minimal due to the presence of neighboring cells pulling the matrix in opposite directions. For large separations, <u> saturates to a value independent of the number of cells depending only on the matrix stiffness.

Figure 7. Mechanical crosstalk between cells.

Mechanical crosstalk of adjacent cells through their matrix is studied by varying the number of interacting cells and the spacing between them. The number of cells is varied from two to six in increments of two, and the cell-cell spacing is varied from zero to two cell lengths. For these simulations, the cell and gel stiffness are held constant at 12 kPa and 1 kPa respectively.

1. A. Representative strain maps of the gel obtained for two different systems, namely, two cells spaced two cell lengths apart, and four cells spaced one cell length apart.
2. B. <ε> plotted as function of spacing ratio remains moderately constant at 3.5 % suggesting weak crosstalk between cells.
3. C. Representative displacement maps of the gel obtained for two different systems, namely, two cells spaced two cell lengths apart, and four cells spaced one cell length apart.
4. D. <u> plotted for the innermost cell shows divergent behavior. For two cells only, <u> is maximum with zero spacing, and decreases with increasing cell spacing and then levels off to a value of ~0.525 µm. For six cells, <u> increases with increasing cell spacing and then saturates. Beyond the critical cell spacing of ~2/3 * L_cell, the curves collapse onto one another.

Discussion

In this paper, we have studied the strain maps induced by a contractile cell on its substrate, and have namely addressed the effects of matrix stiffness and thickness on the overall response. Matrix sensitive differentiation of stem cells to neurons, myoblasts or osteoblasts highlights the strong influence of a cell’s elastic microenvironment in regulating cellular processes and serves as a central motivation in identifying and decoupling the effects of the individual factors.

Even with our simple axisymmetric finite element model of a prestressed cell-on-gel, we observe increased mechanosensitivity of stem cells to matrix stiffness similar to that in vitro ^{19, 32} relative to differentiated cells such as myoblasts and osteoblasts. Since prestress values are comparable, and major differences in mean interfacial strain values is observed mainly on the soft gels, the increased mechanosensitivity of stem cells is probably due to its ability to match its compliance with that of its matrix (i.e., E_cell = E_gel). The limited mechanosensitivity of myoblasts and osteoblasts in comparison to stem cells is also captured by the fit parameter ‘b’ which is orders of magnitude higher for myoblasts and osteoblasts.

Our simulations assume uniform cellular prestress and continuous adhesions between the cell and its substrate. However, DiMilla and co-workers, who used discrete adhesions in a generalized adhesion model, also conclude that cell behavior is highly linked to the contractile state of the cells.³³ By simulating three different prestress distributions, namely, uniform prestress, edge prestress (i.e. cell prestress prescribed only near the cell periphery), and interfacial prestress (i.e., cell prestress prescribed only in the cell-gel interface), and comparing strain distributions, we find that the peak strain of 21% obtained with edge prestress compares well with the 23% strain obtained here for uniform prestress (Supp. Figure S3). In contrast, the interfacial prestress distribution induces minimal displacement and strain in the matrix. Further, with an edge prestress there is negligible displacement or strain near the cell center. Thus, given a strain map induced by a cell it is possible to qualitatively judge the prestress distribution in the cell.

Contrary to traction force measurements which do not account for bead displacements in a vertical direction, profiles of the deformed cell-gel interface clearly show vertical displacements that vary in a spatial manner, with regions where the cell pushes in on its matrix (towards the center) with little or no radial displacement, and regions where it actively pulls the matrix (towards the periphery). Gel surface displacements and strains decay rapidly away from the cell periphery with a higher displacement gradient obtained for a soft gel. The characteristic decay length-scale of 10 µm translates to roughly 0.25 R_cell. The presence of one another felt by adjacent cells within this length scale might drive mechanosensitive alignment leading to some characteristic spatial arrangement. This has been observed with myoblasts that preferentially align over distances of 5–10 cell widths,¹⁰ with a bias towards soft matrices where strains decay over longer ranges and matrices have higher baseline displacements.

Depth-sensing by cells addressed here in simulation confirms experimental results from here and elsewhere²⁷. Hyperbolic fits to the mean interfacial displacements yield a crossover gel stiffness of 8 kPa, a set point that falls in the range of many behavioral crossovers for various cell types, e.g. very spread smooth muscle cells and fibroblasts^{18, 34}, onset of cancer metastasis from normal breast ductile cells³⁵, etc. Constrained displacements of thinner matrices limit the extent of displacement propagation in a vertical direction thereby leading to strain accumulation, which is likely to be present in thin basement membranes. Thus mean strains are largest on the thinnest and softest gels, and decrease rapidly with increasing thickness and stiffness, with the asymptotes representing the responses on thick matrices. Our measures of stress ratio (Figure 4C) and relative energy index (Fig. 5B) both capture the phenomena of differential cell spreading on thin gels. The stiffness-dependent behavior of the stress ratio reflects the cell’s ability to transmit tractions to its substrate: higher stress ratios on soft thin gels compared to thick gels indicate a higher effective stiffness probed by the cell. In addition, when we model less spread versus more spread cells and account for possible differences in metabolic-to-mechanical conversion rates, we show that the less spread cell is favored on soft and thick gels only when the conversion ratio has a value (α ≈ 3) that corresponds to less efficient conversion in the less spread shape. Metabolic profiling could perhaps be used to directly test this proposition, but it has been clear since the very first ‘cell on gel’ study¹ that phosphorylation in signaling pathways (derived from ATP, GTP, etc.) is blunted in less spread cells on thick soft gels.

Using mean interfacial strain as a metric, we have shown that large deviations in interfacial strain are observed only when soft matrices are a fraction of the height and width of the cell. Therefore, matrices with stiffness less than 8 kPa and thickness less than 2 µm are expected to have greatest influence in affecting cell behavior. Consistent with this, no detectable differences in smooth muscle cell spreading have been observed between 5 µm and 70 µm thick polyacrylamide gels²⁷. However, literature estimates of relevant mechanosensing length scales have varied from measures of a couple of microns to several tens of microns. These differences arise from association of the critical thickness to the cell length³⁶, cell height²⁷, magnitude of surface displacements^{37, 38}, or size of focal adhesions³⁹. Using finite-layer elasticity theory, Maloney et al. have estimated a critical thickness of ~1.5 µm for a focal adhesion of 1 µm dimension⁴⁰. However, using the same finite-layer theory, Merkel et al. report values of tens of microns as relevant to cell mechanosensing length scales⁴¹. As per Maloney et al., this apparent contradiction can be resolved by considering the length-scale relevant to the measurements⁴⁰. Intriguingly, our simple model which lacks focal adhesions is sufficient to predict the critical thickness of 1–2 µm of depth-sensing with soft gels.

Using laser nano-ablation, Kumar et al. have demonstrated that incision of a single stress fiber bundle can lead to significant relaxation of a compliant ECM visualized by movement of embedded beads⁴². Ablation-induced structural reorganization observed in cells on compliant substrates, but not in cells on glass highlights that the matrix-mediated coupling between cells permissible on compliant substrates. Using our cells-on-gel model, we show that cell-cell crosstalk is possible only when cells are much less than one cell-width apart. Further, such crosstalk is dependent on the substrate stiffness, with more crosstalk possible on softer substrates.

In summary, taking the physical features of the cell and its substrate into account, through our computations of deformations and strains induced by a cell on its environment, we have shown that cells sense their surroundings in the length scales closer to that of adhesions than on cellular scales or higher.